Combined Description of the Total and Differential Cross Sections and the ${\rho}$-Parameter for $\boldsymbol{p(\bar{p})p}$ Scattering over the Energy Region of $\boldsymbol{\sqrt{s}\geqslant 7}$ GeV and for all Values of $\boldsymbol{t<0}$

Abstract

The results of a combined description of data on the differential and total scattering cross sections and the $\rho$-parameter for $p(\bar{p})p$ collisions in tuning the parameters of an analytic model constructed in order to describe data over a broad region of kinematical variables for $\sqrt{s}\gtrsim 7$ GeV and all currently available experimental data on $t$ are presented. The experimental data were taken from the COMPAS group (IHEP) compilations and the CLM compilations and were supplemented with data from the FNAL-COLLIDER-D0 and CERN-LHC-TOTEM experiments and with cosmic-ray data from the Pierre Auger Observatory (PAO).

INTRODUCTION

New data obtained by measuring the observables $d\sigma/dt$, $\sigma_{\mathrm{tot}}$, and $\rho$ of the elastic scattering of antiprotons and protons on protons at maximum energies in collider experiments and in cosmic rays [1–7] revealed the need for tuning almost all of the models intended for describing experimental data in order to refine the predictions obtained on the basis of these models for measurable quantities (see Fig. 4 in [1]). Here, we present the results of a combined analytic description of all published experimental data obtained for the aforementioned observables in collider experiments¹ for $\sqrt{s}\gtrsim 7$ GeV and in the observations of cosmic-ray interactions with atmospheric nuclei at high energies over the whole interval of experimental data for invariant momentum transfers $t$.

EXPERIMENTAL DATA

Experimental data on the differential cross sections [8] for elastic scattering of antiprotons and protons on protons in terms of the variables ($\sqrt{s}$, $t$, $d\sigma/dt\left({s,t}\right)$) are distributed near some two-dimensional surfaces for which analytic models intended for obtaining the best description of the data on the basis of the least squares method are chosen. The projection of these distributions onto the ($t$, $d\sigma/dt$) plane is shown in Fig. 1, where general features of the surfaces and their relative arrangement can be seen:

• 1. a coordinated behavior of the two surfaces for $|t|\gtrsim 0.16$ GeV${}^{2}$, which is similar to their intersection and subsequent coming closer together (for $|t|\to 0$) or the merger of the surfaces in the region of Coulomb–nuclear interference within the experimental errors (for a more detailed picture, see Fig. 2);

• 2. a weak energy dependence of the ‘‘band’’ of intersection and merger of the surfaces;²

• 3. a manifestation of dips (shoulders) on the surfaces in the region of $\left|t\right|\gtrsim 0.16$ GeV${}^{2}$ near the region of Coulomb–nuclear interference from the side of higher collision energies.³

Fig. 1.

Differential cross sections for elastic (closed symbols) $pp$ and (open symbols) $\bar{p}p$ collisions. For some points, we do not indicate the lower error, since it goes to the region of negative values.

Fig. 2.

Partition of a data sample and theoretical curves obtained within our model for the differential cross sections at various values of $\sqrt{s}$ (the closed and open symbols represent data for, respectively, $pp$ and $\bar{p}p$ scattering). The dashed curves correspond to the theoretical results for $\bar{p}p$ scattering.

Fig. 2.

(Contd.)

This data set was formed on the basis of the well-known CLM compilation [9], whose data file was checked by us on the basis of the Landolt–Börnstein reference books [10–12] and the HEPDATA and COMPAS databases. The CLM file was refined: pieces of incorrect information that were noticed by us were removed, the gaps were filled, and new experimental data published after 2006 were added.

Text files with data on the cross sections and $\rho$-parameter can be found on the Particle Data Group Web site and in our network files [13–20].

DESCRIPTION OF THE MODEL

In order to describe the total cross sections $\sigma^{\textrm{tot}}$, the $\rho$-parameter, and the differential cross sections $d\sigma/dt$, we use the expressions⁴

$$\sigma_{\pm}^{\textrm{tot}}\left(s\right)=\frac{\textrm{Im}\ T_{\pm}\left({s,t=0}\right)}{\sqrt{s\left({s-4m_{p}^{2}}\right)}},$$

$$\rho_{\pm}\left(s\right)=\frac{\textrm{Re}\ T_{\pm}\left({s,t=0}\right)}{\textrm{Im}\ T_{\pm}\left({s,t=0}\right)},$$

$$\frac{d\sigma_{\pm}}{dt}\left({s,t}\right)=\frac{\left|{T_{\pm}\left({s,t}\right)+T_{\pm}^{\textrm{c}}\left({s,t}\right)}\right|^{2}}{16\pi\left({\hslash c}\right)^{2}s\left({s-4m_{p}^{2}}\right)},$$

where $T_{\pm}\left({s,t}\right)$ and $T_{\pm}^{\textrm{c}}\left({s,t}\right)$ are, respectively, the nuclear and Coulomb amplitudes (in mb GeV${}^{2}$ units); $m_{p}$ is the proton mass; and $\left({\hslash c}\right)^{2}=0.389379\ldots$ (in mb GeV${}^{2}$ units).

Introducing the notation⁵

$$\hat{s}\left({s,t}\right)\equiv\hat{s}=\frac{-t+2s-4m_{p}^{2}}{2s_{0}},\quad s_{0}=t_{0}=1[\textrm{GeV}^{2}],$$

$$\tilde{s}=\ln\hat{s}-\frac{i\pi}{2},\quad\tilde{\tau}=\sqrt{-t/t_{0}}\ln\tilde{s},$$

we reduce the nuclear amplitude to a form of a linear combination of the $c$-even ($F_{+}$) and $c$-odd ($F_{-}$) Regge amplitudes; that is,

$$T_{\pm}\left({s,t}\right)=F_{+}\left({\hat{s},t}\right)\pm F_{-}\left({\hat{s},t}\right).$$

In turn, the even–odd Regge amplitudes for $F_{\pm}\left({\hat{s},t}\right)$ are represented in the form

$$F_{+}\left({\hat{s},t}\right)=F_{+}^{\textrm{H}}\left({\hat{s},t}\right)+F_{+}^{P}\left({\hat{s},t}\right)+F_{+}^{PP}\left({\hat{s},t}\right) $$

$${}+F_{+}^{R}\left({\hat{s},t}\right)+F_{+}^{RP}\left({\hat{s},t}\right)+N_{+}\left({{s},t}\right),$$

$$F_{-}\left({\hat{s},t}\right)=F_{-}^{\textrm{MO}}\left({\hat{s},t}\right)+F_{-}^{O}\left({\hat{s},t}\right)+F_{-}^{OP}\left({\hat{s},t}\right) $$

$${}+F_{-}^{R}\left({\hat{s},t}\right)+F_{-}^{RP}\left({\hat{s},t}\right)+N_{-}\left({s,t}\right),$$

where $F_{+}^{\textrm{H}}\left({\hat{s},t}\right)$ is the Heisenberg–Froissart contribution [21] (triple-Regge pole), $F_{-}^{\textrm{MO}}\left({\hat{s},t}\right)$ is the triple-Regge pole for the maximal odderon, $F_{+}^{P}\left({\hat{s},t}\right)$ is the simple Regge pole for the Pomeron, $F_{-}^{O}\left({\hat{s},t}\right)$ is the simple Regge pole for the odderon, $F_{+}^{PP}\left({\hat{s},t}\right)$ describes the Pomeron–Pomeron exchange, $F_{-}^{OP}\left({\hat{s},t}\right)$ describes the Pomeron–odderon exchange, $F_{\pm}^{R}\left({\hat{s},t}\right)$ stands for the contributions of secondary $c$-even and $c$-odd Reggeons, $F_{\pm}^{RP}\left({\hat{s},t}\right)$ is the contribution of $c$-even and $c$-odd Reggeon–Pomeron branch points, and $N_{\pm}\left({s,t}\right)$ stands for correction terms (see below) associated with the asymptotic QCD contributions to the amplitudes. With allowance for the fitting parameters determined below, all of these contributions are represented in the form⁶

$$\frac{F_{+}^{\textrm{H}}\left({\hat{s},t}\right)}{i\hat{s}}$$

$${}=\begin{pmatrix}{H_{1}\dfrac{2J_{1}\left({K_{+}\tilde{\tau}}\right)}{K_{+}\tilde{\tau}}e^{b_{+1}t}\ln^{2}\tilde{s}}\\ {+H_{2}J_{0}\left({K_{+}\tilde{\tau}}\right)e^{b_{+2}t}\ln\tilde{s}}\\ {+H_{3}\left[{J_{0}\left({K_{+}\tilde{\tau}}\right)-K_{+}\tilde{\tau}J_{1}\left({K_{+}\tilde{\tau}}\right)}\right]e^{b_{+3}t}}\end{pmatrix},$$

$$\frac{F_{-}^{\textrm{MO}}\left({\hat{s},t}\right)}{\hat{s}}=\begin{pmatrix}{O_{1}\dfrac{\sin\left({K_{-}\tilde{\tau}}\right)}{K_{-}\tilde{\tau}}e^{b_{-1}t}\ln^{2}\tilde{s}}\\ {+O_{2}\cos\left({K_{-}\tilde{\tau}}\right)e^{b_{-2}t}\ln\tilde{s}}\\ {+O_{3}e^{b_{-3}t}}\end{pmatrix},$$

$$F_{+}^{P}\left({\hat{s},t}\right)=-C_{P}e^{b_{P}t}e^{\frac{-i\pi}{2}\alpha_{P}\left(t\right)}\left({\hat{s}}\right)^{\alpha_{P}\left(t\right)},$$

$$F_{-}^{O}\left({\hat{s},t}\right)=-iC_{O}e^{b_{O}t}e^{\frac{-i\pi}{2}\alpha_{O}\left(t\right)}\left({\hat{s}}\right)^{\alpha_{O}\left(t\right)},$$

$$F_{+}^{PP}\left({\hat{s},t}\right)=\frac{-C_{PP}}{\ln\tilde{s}}e^{b_{PP}t}e^{\frac{-i\pi}{2}\alpha_{PP}\left(t\right)}\left({\hat{s}}\right)^{\alpha_{PP}\left(t\right)},$$

$$F_{-}^{OP}\left({\hat{s},t}\right)=\frac{-iC_{OP}}{\ln\tilde{s}}e^{b_{OP}t}e^{\frac{-i\pi}{2}\alpha_{OP}\left(t\right)}\left({\hat{s}}\right)^{\alpha_{OP}\left(t\right)},$$

$$F_{\pm}^{RP}\left({\hat{s},t}\right)=\frac{tF_{RP}^{\pm}}{\ln\tilde{s}}e^{b_{RP}^{\pm}t}i^{\frac{-1\pm 1}{2}}e^{\frac{-i\pi}{2}\alpha_{RP}^{\pm}\left(t\right)}\left({\hat{s}}\right)^{\alpha_{RP}^{\pm}\left(t\right)},$$

$$F_{\pm}^{R}\left({\hat{s},t}\right)=\pm C_{R}^{\pm}e^{b_{R}^{\pm}t}i^{\frac{-1\pm 1}{2}}e^{\frac{-i\pi}{2}\alpha_{R}^{\pm}\left(t\right)}\left({\hat{s}}\right)^{\alpha_{R}^{\pm}\left(t\right)},$$

$$\alpha_{P}\left(t\right)=1+\alpha^{\prime}_{P}t,$$

$$\alpha_{R}^{\pm}\left(t\right)=\alpha_{R}^{\pm}\left(0\right)+{\alpha^{\prime}}^{\pm}_{\!\!R}\left(t\right)t,$$

$$\alpha_{O}\left(t\right)=1+\alpha^{\prime}_{O}t,$$

$$\alpha_{OP}\left(t\right)=1+\frac{\alpha^{\prime}_{P}\alpha^{\prime}_{O}}{\alpha^{\prime}_{P}+\alpha^{\prime}_{O}}t,$$

$$\alpha_{PP}\left(t\right)=1+\frac{\alpha^{\prime}_{P}}{2}t,$$

$$\alpha_{RP}^{\pm}\left(t\right)=\alpha_{R}^{\pm}\left(0\right)+\frac{\alpha^{\prime}_{P}{\alpha^{\prime}}_{\!\!R}^{\pm}}{\alpha^{\prime}_{P}+{\alpha^{\prime}}_{\!\!R}^{\pm}}t.$$

The terms $F_{\pm}\left({s,t}\right)$ are supplemented above with the correction terms $N_{\pm}\left({s,t}\right)$ associated with QCD asymptotic behavior; that is,

$$N_{\pm}\left({s,t}\right)=-i^{\frac{-1\pm 1}{2}}\hat{s}N_{\pm}\ln\tilde{s}\frac{\left({t/t_{0}}\right)}{\left({1-t/t_{\pm}}\right)^{5}}.$$

Similar corrections were used in [22]. The experimental large-$|t|$ behavior in the $t^{-4}$ form is known. The theoretical motivation of $N_{-}\left({s,t}\right)$ as three-gluon odderon exchange was given long ago by Donnachie and Landshoff [23]. The motivation of $N_{+}\left({s,t}\right)$ is less obvious, but we can also interpret it as the $c$-even part of the contribution of three-gluon exchange.

The model that we described above includes 36 unknown parameters (determined below from a fit to experimental data). Their list given immediately below includes fixed ones printed in boldface: $H_{1}$, $H_{2}$, $H_{3}$, $K_{+}$, $C_{P}$, $C_{PP}$, $C_{R}^{+}$, $C_{RP}^{+}$, ${\boldsymbol{\alpha}}^{\textbf{+}\prime}_{\textbf{R}}\textbf{ = 0.8}$, $\alpha^{\prime}_{P}$, $b_{+1}$, $b_{+2}$, $b_{+3}$, $\boldsymbol{b_{P}}=0$, $b_{PP}$, $b_{R}^{+}$, $b_{RP}^{+}$, $N_{+}$, $t_{+}$, ${\boldsymbol{O}}_{\textbf{1}}\textbf{ = 0}$, $O_{2}$, $O_{3}$, $K_{-}$, $C_{O}$, $C_{OP}$, $C_{R}^{-}$, $C_{RP}^{-}$, $\alpha_{R}^{-}(0)$, ${\boldsymbol{\alpha}}^{-\prime}_{\textbf{R}}\textbf{ = 0.8}$, $\alpha^{\prime}_{O}$, $\boldsymbol{b}_{\textbf{-1}}\textbf{ = }0$, $b_{-2}$, $b_{-3}$, $b_{O}$, $b_{OP}$, $b_{R}^{-}$, $b_{RP}^{-}$, $N_{-}$, $t_{-}$, $\boldsymbol{A}_{\textbf{MO}}\textbf{ = 0}$, $A_{O}$.

In addition, we note the following:

• 1. We set $O_{1}\equiv 0$ since the fitting of the whole set of parameters shows that this parameter is extremely small.

• 2. We excluded the parameters ${\alpha}_{\!R}^{\pm\prime}\equiv 0.8$ from the fitting procedure.

• 3. We supplemented the terms $F_{-}^{\textrm{MO}}\left({\hat{s},t}\right)$ and $F_{-}^{O}\left({\hat{s},t}\right)$ with the empirical correction terms $\left({1+A_{\textrm{MO}}t}\right)$ and $(1+A_{O}t)$, respectively, but we set $A_{\textrm{MO}}$ to zero, since the fitting of the whole set of parameters showed that this parameter is extremely small.

• 4. Upon free fitting of all parameters, without any exception, the parameter $b_{p}$ became negative, which resulted in an indefinite growth; for this reason, we restricted variations of this parameter in an ad hoc manner, not permitting it to become negative, with the result that it vanished (yet another fixed parameter).

The Coulomb corrections are taken into account in a dipole form as⁷

$$T_{\pm}^{C}\left({s,t}\right)=\pm e^{\left[{\pm i\alpha\Phi_{\pm}^{NC}\left({s,t}\right)}\right]}\times 8\pi\left({\hslash c}\right)^{2}\alpha\frac{s}{t}\left({1\!-\!\frac{t}{\Lambda^{2}}}\right)^{-4}\!\!,$$

where $\Phi_{\pm}^{NC}\left({s,t}\right)$ is the phase-shift for Coulomb–nuclear interaction:

$$\Phi_{\pm}^{NC}\left({s,t}\right)=\ln\left[{-\frac{t}{2}\left({B_{\pm}\left(s\right)+\frac{8}{\Lambda^{2}}}\right)}\right] $$

$${}+\gamma-\frac{4t}{\Lambda^{2}}\ln\left[{\frac{-4t}{\Lambda^{2}}}\right]-\frac{2t}{\Lambda^{2}}.$$

This form of the phase shift for the Coulomb–nuclear interference was taken from [24] ($\Lambda=\sqrt{0.71}$ [GeV]).

In order to simplify the ensuing calculations, we modify the expression for the slope of the diffraction cone as follows:

$$B_{\pm}\left(s\right)=\left\{{\frac{d}{dt}\ln\left[{\frac{d\sigma_{\pm}}{dt}\left({s,t}\right)}\right]}\right\}_{t=0}$$

$${}\overbrace{\longrightarrow}^{\textrm{replace}}B_{\pm}\left(s\right)=\frac{\sigma_{\pm}\left(s\right)}{4\pi\left({\hslash c}\right)^{2}}.$$

RESULTS OF FITTING AND PARAMETRIZATION OF OBSERVABLES

Recent phenomenological treatments of data on $d\sigma/dt$, $\sigma_{\mathrm{tot}}$, and $\rho$ in terms of analytic parametrizations [24–27] beyond the region of the Coulomb–nuclear interference resulted in presenting ‘‘the best combined descriptions of the data’’ before the appearance of the data from the CERN-LHC-TOTEM experiment. Our attempts at reproducing the results reported in [24] failed. This might be associated with the fact that the some portions of experimental data were discarded in that study without any appropriate explanation—probably with the aim of obtaining an acceptable value of $\chi^{2}$. We dispensed with discarding arrays of experimental data and processed all experimental points without any exception.On the basis of the expressions used in [24], we developed our own (extended) version of data parametrization, taking into account the effect of the Coulomb–nuclear interference.

Although there are a great many parameters in the model, we were unable to obtain a satisfactory $\chi^{2}$ value of $\chi^{2}/\textrm{DoF}\cong 1$. For all experimental data, $\chi^{2}/\textrm{DoF}=1.62$. This is a record $\chi^{2}$ value, but it is substantially greater than unity, so that a rigorous standard procedure for calculating the errors in the parameters by the Hessian method is inapplicable here.

Therefore, we employ the procedure of a so-called direct propagation of the errors. We will describe this procedure in detail elsewhere, only mentioning it briefly here.

We refer to an ordered set of parameter values for the global minimum based on input experimental data as the global parameter vector.

Further, we perform a random shift of experimental data under conditions of a Gaussian distribution within the total error of each experimental measurement, whereupon we construct a new fit to the data, thereby obtaining a new parameter vector. After accumulating a significant sample of such vectors, we perform a statistical analysis of these sets, extracting from them errors in the parameters and use them to calculate the errors in the observables (total and differential cross sections and $\rho$-parameters).

RESULTS OF DESCRIBING EXPERIMENTAL DATA

The parameter values and the errors in them as obtained from the results of fitting and processing are listed in Table 1. Further, we address the problem of agreement between the experimental data on the differential cross sections and the theoretical curves at various energies. In Fig. 2, we present data taken from Fig. 1 and broken down into the energy intervals specified in the figure, indicating the numbers of points in these energy regions, Npt, and respective values of $\chi^{2}/\textrm{Npt}$.

Table 1. Values of model parameters and errors in them

By and large, the result of discarding, in an ad hoc manner, not more than 5${\%}$ of experimental points in the differential cross sections alone (we mean points deviating from the theoretical curve by three and more standard errors) is that the total $\chi^{2}/\textrm{DoF}$ value becomes equal to or less than unity.

The theoretical description agrees fairly well with the experimental data in all regions. In order to illustrate this agreement, we present a typical behavior of the theoretical curve (with allowance for the errors) and the experimental data at the energy of 7 TeV (see Fig. 3).

Fig. 3.

Theoretical curves (with allowance for the errors) and experimental points corresponding to $d\sigma/dt$ at $\sqrt{s}=7$ TeV for (a) $pp$ and (b) $\bar{p}p$ scattering. These curves differ substantially only in the vicinities of local minima.

Figure 4 illustrates a smooth shift of a local minimum (dip) for pp collisions within our model as the energy changes. The curves are presented as a corridor of errors (1$\sigma$) with allowance for the uncertainties in the fitted parameter values. The total ($\sigma_{\textrm{tot}}$), elastic ($\sigma_{\textrm{elastic}}$), and inelastic ($\sigma_{\textrm{inelastic}}$) scattering cross sections are presented in Fig. 5 for (upper panel) $pp$ and (lower panel) $\bar{p}p$ collisions.

Fig. 4.

Theoretical curves representing $d\sigma/dt$ (with allowance for the errors) for $pp$ collisions at $\sqrt{s}=$ (1) $12$ GeV, (2) $7$ TeV, and (3) $14$ TeV. The local minima move leftward with increasing energy.

Fig. 5.

Theoretical curves (for $\sqrt{s}\geqslant 7$ GeV) and experimental points (total set from the database) representing the total, elastic, and inelastic scattering cross sections for $pp$ and $\bar{p}p$ collisions.

The elastic scattering cross section $\sigma_{\textrm{elastic}}$ can be evaluated as

$$\sigma_{\textrm{elastic}}\left(s\right)=\int\limits_{t=0}^{\infty}\left({\frac{d\sigma_{\pm}}{dt}}\right)_{\textrm{nucl}}\left({s,t}\right)dt,$$

where $\left({d\sigma_{\pm}/dt}\right)_{\textrm{nucl}}$ was calculated without the Coulomb term $T_{\pm}^{\textrm{c}}\left({s,t}\right)$ in the total scattering amplitude; that is,

$$\left({\frac{d\sigma_{\pm}}{dt}}\right)_{\textrm{nucl}}\left({s,t}\right)=\frac{\left|{T_{\pm}\left({s,t}\right)}\right|^{2}}{16\pi\left({\hslash c}\right)^{2}s\left({s-4m_{p}^{2}}\right)}.$$

The inelastic cross section was set to the following difference:

$$\sigma_{\textrm{inelastic}}=\sigma_{\textrm{tot}}-\sigma_{\textrm{elastic}}.$$

It can be seen that the experimental data on the elastic, inelastic, and total cross sections are described quite satisfactorily (a numerical characteristic of this description is given in Fig. 6).

Fig. 6.

Experimental data (total set) and theoretical curves representing (a, b) the differential cross sections for (c, d) $\sqrt{s}\geqslant 7$ GeV and $\sqrt{s}\geqslant 5$ GeV and (e,f) the $\rho$-parameters for ${pp}$ and $\bar{p}p$ scattering. Figures 6a, 6c, and 6e give the results based on the original model, while Figs. 6b, 6d, and 6f give their counterparts based on the model where the odderon contribution is discarded. The differential and total cross sections are visually indistinguishable in these graphs, while the behavior of the $\rho$-parameter changes drastically (compare Figs. 6e and 6f).

In our opinion, the fact that the curves of the $\rho$-parameter, first, intersect and, second, diverge at higher energies (see Fig. 6) is an important special feature of the model being considered. Earlier, we have never obtained the results that were published in the most recent PDG reviews or in [28] (this is likely due to the presence of the odderon in the model description).

For this reason, we modified slightly our model by suppressing the odderon in the total cross sections and $\rho$-parameter for $t\to 0$. For this, we set $t=0$ in the expressions for the total cross sections and discarded terms corresponding to odderon poles in the amplitude. A theoretical description of the behavior of the differential cross sections $d\sigma_{\pm}/dt$ and total cross sections $\sigma_{\pm}$ remains nearly unchanged upon going over from one of these two cases to the other. The difference in the $\chi^{2}/\textrm{DoF}$ values is also insignificant.

However, the behavior of the $\rho$-parameter undergoes a drastic change at high values of the c.m. collision energy $\sqrt{s}$. Earlier, our group had analyzed a large number of various theoretical descriptions [29] of the behavior of $\sigma_{\textrm{tot}}$ and the $\rho$-parameter in the absence of the odderon; in all of those cases, the curves representing the $\rho$-parameter for $pp$ and $\bar{p}p$ collisions gradually come closer to each other (without undergoing intersection) and become indistinguishable within the corridor of errors of the theoretical curves for $\sqrt{s}$ values of about several hundred GeV units. In the original model, these curves, first, intersect and, second, diverge ever more strongly as the energy grows (see Fig. 6). This fact indicates that the inclusion of odderon poles in models for describing differential cross sections in not mandatory. This permits simplifying relevant expressions and reducing the number of model parameters. Figure 7 illustrates a general three-dimensional behavior of the shape of surfaces of differential cross sections versus $\sqrt{s}$ and $\left|t\right|$ over the whole energy region being considered.

Fig. 7.

Behavior of the $d\sigma/dt$ surfaces versus $\sqrt{s}$ and $\left|t\right|$ for (a) $pp$ and (b) $\bar{p}p$ collisions on a logarithmic scale along both axes.

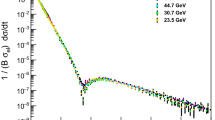
In [30], one can follow the behavior of the curve representing $d\sigma/dt\left({|t|}\right)$ for (red curve) $pp$ and (blue curve) $\bar{p}p$ collisions in response to a change in the energy over the interval of $7 \, \textrm{GeV}\leqslant\sqrt{s}\leqslant 14$ TeV.

In conclusion, we present a graph that illustrates the accuracy of the description of experimental data on the basis of our model in the region of the first local minimum (see Fig. 8).

Fig. 8.

Behavior of the theoretical curve (with allowance for the errors in the calculation) representing $d\sigma/dt$ for $pp$ collisions at $\sqrt{s}=7$ TeV in the region of the first local minimum.

More precise data on all model parameters and on versions of the description will be obtained after the appearance of new results from the LHC at the energies of 13 and 14 TeV on the differential and total cross sections, as well as on the values of the $\rho$-parameter.