Massless Electronic Excitations in Graphene Near Coulomb Impurities

Abstract

We study low-energy massless electronic excitations in a graphene monolayer near a pointlike Coulomb impurity. We assume that such excitations are described by the Dirac model. We construct a family of self-adjoint Hamiltonians corresponding to these excitations for any charge of the impurity and perform their spectral analysis. It is shown that in this case, the structure of electron excitation spectra differs qualitatively from the corresponding spectra of massive excitations. The obtained results are used for analyzing the local surface density of electron states in graphene and its dependence of the choice of self-adjoint Hamiltonians.

1 INTRODUCTION

The presence of impurities and defects can noticeably change the electronic properties of graphene. For example, the presence of charged impurities such as Coulomb centers substantially affects the mobility of charge carriers [1]. For this reason, analysis of the properties of graphene in the case of interaction of carriers with the Coulomb centers is important for understanding the electron transport in the presence of impurities (see [2–6]). This problem is technically simplified because low-energy electron excitations in a graphene monolayer in an external electromagnetic field are successfully described by the Dirac model, in which these excitations are chiral Dirac fermions in 2 + 1 dimensions [7, 8].

A correct description of such excitations (which will be often referred to as quasiparticles in further analysis) near a pointlike Coulomb impurity requires a correct definition of the Dirac Hamiltonian as a self-adjoint (henceforth, s.a.) operator in the corresponding Hilbert space. For the motion of an electron in the Coulomb field, the problem of determining the Hamiltonian as an s.a. operator is nontrivial only for nuclei with large Z (Z > 119), which do not appear in laboratory conditions; for Coulomb impurities in graphene, this threshold is much lower because of the properties of Dirac quasiparticles in the Dirac model of graphene.

It should be noted that depending on the structure of the substrate on which graphene is synthesized; a gap can appear (or not appear) between the valence band and the conduction band in the electron spectrum. This is determined by the properties of the interaction between the graphene layer and the substrate, which breaks the symmetry between sublattices, but preserves the translational symmetry. For a nonzero gap, low-energy electron excitations in the Dirac model are massive fermions, while for zero gap between the valance and conduction bands, these excitations are massless fermions. The gap width can be changed by varying the chemical composition and concentration of the substrate [9].

In the previous publication [10] with the participation of the authors, with the help of the theory of s.a. extensions of symmetric operators, a family of s.a. Hamiltonians describing electron excitations in gapped graphene for any value of the impurity charge. Based on the Krein method of guiding functionals, the spectral analysis of such Hamiltonians was performed. In particular, their spectra and the corresponding complete sets of (generalized) eigenfunctions were determined. The choice of s.a. Hamiltonians from all analytically possible operators is a separate physical problem. It should be noted the results of this study cannot be used directly in the massless case because the domains of s.a. Dirac Hamiltonians for gapped graphene vanish in the massless limit (for graphene with zero gap). For this reason, the case of gapless graphene requires separate investigation, which forms the subject of this study.

In this study, we consider the problem of correct definition of a Dirac Hamiltonian as an s.a. operator for quasiparticles in gapless graphene in the presence of a Coulomb impurity with an arbitrary charge Z. We present analysis of all aspects of this problem based on the theory of s.a. extensions of symmetric operators [11–13]. We construct the family of all possible s.a. Hamiltonians, the members of which differ in the parameters of corresponding extensions (therefore, are parameterized by them) and perform their spectral analysis. For this purpose, we construct generalized eigenfunctions of all such Hamiltonians for any impurity charge. This problem is technically reduced to analysis of the spectra of corresponding s.a. 1D partial radial Hamiltonians. It is shown that the spectra of such Hamiltonians are continuous and occupy the entire real $\mathbb{R}$ axis in contrast to the massive case, where there are both discrete and continuous spectra.

The article is organized as follows. In Section 2, the definitions of basic concepts and relations explaining the formulation of the problem are considered. In Section 3, the analytically rigorous procedure of reducing the problem of construction of an s.a. rotationally invariant Dirac Hamiltonian in complete Hilbert space to the problem of constructing s.a. 1D partial radial Hamiltonians with a certain angular momentum is described. In Section 4, the general solution to radial equations for the massless Dirac equation in the 2 + 1 dimensions is analyzed. In Section 5, the s.a. partial radial Hamiltonians with an arbitrary admissible value of angular momentum j are constructed. Section 6 is devoted to the description of peculiarities of the complete Hamiltonian for the model under consideration depending on impurity charge Z. In Section 7, the obtained results are used for analyzing the local density of states in graphene. Brief conclusions are formulated in Section 8.

2 DIRAC EQUATION IN 2 + 1 DIMENSIONS FOR A MASSLESS CHARGED PARTICLE IN THE COULOMB FIELD

We operate in the framework of the Dirac model in the 2 + 1 dimensions for charged quasiparticles near a Coulomb impurity. Let us suppose that the Coulomb impurity with charge Z is located at the origin of the Cartesian system of coordinates with the x and y axes lying in the graphene plane. With account for macroscopic permittivity $\epsilon$, the potential produced by the impurity has form

$$V(\rho ) = - \frac{{Z{{e}^{2}}}}{\epsilon }\frac{1}{\rho },\quad \rho = {\text{|}}{\mathbf{r}}{\text{|}} = \sqrt {{{x}^{2}} + {{y}^{2}}} ,\quad {\mathbf{r}} = (x,y).$$

We denoted by K_s the Dirac points, the coordinates of which in the Brillouin zone are chosen in form K_s = (4πs/(3a), 0), where a = 2.46 Å is the lattice constant and s = ±1 is the isospin quantum number.

Total Hilbert space ${{\mathfrak{H}}_{{{\text{tot}}}}}$ of quantum states of quasiparticles is the direct orthogonal sum of two Hilbert spaces ${{\mathfrak{H}}_{s}}$, s = ±1, each of which is connected with corresponding Dirac point K_s. Spaces ${{\mathfrak{H}}_{s}}$ are the Hilbert spaces of 2D doublets, so that

$$\begin{gathered} {{\mathfrak{H}}_{{{\text{tot}}}}} = {{\mathfrak{H}}_{{\text{1}}}} \otimes {{\mathfrak{H}}_{{ - 1}}}, \\ {{\mathfrak{H}}_{{\text{1}}}} = {{\mathfrak{H}}_{{ - 1}}} = \mathfrak{H} = {{L}^{2}}({{\mathbb{R}}^{2}}) \oplus {{L}^{2}}({{\mathbb{R}}^{2}}). \\ \end{gathered} $$

In view of the long-range nature of the Coulomb field, the intervalley processes are disregarded, and transitions between Hilbert spaces ${{\mathfrak{H}}_{s}}$ are not considered. Therefore, the total effective Hamiltonian ${{\hat {H}}_{{{\text{tot}}}}}$ of quasiparticles is the direct orthogonal sum of two Hamiltonians ${{\hat {\mathcal{H}}}_{s}}$, s = ±1, each of which is acting in corresponding Hilbert space ${{\mathfrak{H}}_{s}}$ and can be considered separately.

In the Dirac model, quasiparticles near each Dirac point K_s are described by the effective massless Dirac equation [14]:

$${{{\check{\mathcal{H}}}}_{s}}{{\Psi }_{s}}=\mathcal{E}{{\Psi }_{s}},\quad s=\pm 1,$$

(1)

where wavefunctions Ψ_s are doublets depending on r, Ψ_s = Ψ_s(r) = {ψ_sα(r), α = 1, 2}, components ψ_sα(r) being the envelopes of the Bloch functions in two graphene sublattices A and B, respectively, and ${{{\check{\mathcal{H}}}}_{s}}$ are the differential operations corresponding to the Dirac equation in the 2 + 1 dimensions,

$$\begin{matrix} {{{\check{\mathcal{H}}}}_{s}}=\hbar {{\mathsf{v}}_{\text{F}}}\left( -i\,[s{{\sigma }_{x}}{{\partial }_{x}}+{{\sigma }_{y}}{{\partial }_{y}}]-\frac{q}{\rho } \right), \\ g=\frac{1}{\hbar {{\mathsf{v}}_{\text{F}}}}\frac{Z{{e}^{2}}}{\epsilon }={{\alpha }_{\text{F}}}\frac{Z}{\epsilon }={{\alpha }_{\text{F}}}{{Z}_{\text{eff}}}, \\ {{Z}_{\text{eff}}}=\frac{Z}{\epsilon }. \\ \end{matrix}$$

(2)

Here, ${{{v}}_{{\text{F}}}}$ ≈ 10⁶ cm/s is the Fermi velocity, α_F = e²/($\hbar {{{v}}_{{\text{F}}}}$) is the fine structure constant for graphene, and {σ_x, σ_y, σ_z} are the Pauli matrices. Introducing notation ${{\check{{H}}}_{s}}$ = ($\hbar {{{v}}_{{\text{F}}}}$)^–1${{\check{{\mathcal{H}}}}_{s}}$ and E = ($\hbar {{{v}}_{{\text{F}}}}$)^–1$\mathcal{E}$, we write Eq. (1) in the following form:

$${{\check{{H}}}_{s}}{{\Psi }_{s}}(\mathbf{r})=E{{\Psi }_{s}}(\mathbf{r}),\quad s=\pm 1,$$

where differential operations ${{\check{{H}}}_{s}}$ in polar coordinates ρ, ϕ (x = ρcosϕ, y = ρsinϕ) have form

$$\begin{matrix} {{\check{{H}}}_{s}}=-i(s\cos \phi {{\sigma }_{x}}+\sin \phi {{\sigma }_{y}})\frac{\partial }{\partial \rho } \\ +\frac{i}{\rho }(s\sin \phi {{\sigma }_{x}}-\cos \phi {{\sigma }_{y}})\frac{\partial }{\partial \phi }-\frac{g}{\rho }. \\ \end{matrix}$$

(3)

To impart the physical meaning to the corresponding quantum-mechanical eigenvalue problem, we must, proceeding from differential operations ${{\check{{H}}}_{s}}$, construct corresponding Hamiltonians ${{\hat {H}}_{s}}$ as the s.a. operators with certain domains in Hilbert space $\mathfrak{H}$ = L²(${{\mathbb{R}}^{2}}$) $\oplus$ L²(${{\mathbb{R}}^{2}}$). In solving this problem, we follow the ideas formulated in [10], where a similar problem is considered for corresponding massive quasiparticles.

By definition, variable j takes half-integer positive and negative values, j = ±(n + 1/2), n ∈ ${{\mathbb{Z}}_{ + }}$, while variable Z takes nonnegative integer values, Z ∈ ${{\mathbb{Z}}_{ + }}$. In further analysis, it will be more convenient to treat variable Z as a quantity assuming continuous values and lying on the nonnegative vertical half-plane, Z ∈ ${{\mathbb{R}}_{ + }}$, and to return to its natural integer values when necessary.

3 REDUCTION TO THE RADIAL PROBLEM

Let us begin with the definition of initial symmetric operators $\hat {H}_{s}^{{{\text{in}}}}$ Hilbert space $\mathfrak{H}$ = L²(${{\mathbb{R}}^{2}}$) $\oplus$ L²(${{\mathbb{R}}^{2}}$), which are associated with the corresponding differential expressions (3) for ${{\check{{H}}}_{s}}$. Since the coefficient function of the differential expressions for ${{\check{{H}}}_{s}}$ are smooth outside of the origin, we choose the space of smooth compactly supported doublets for domains D($\hat {H}_{s}^{{{\text{in}}}}$) of operators $\hat {H}_{s}^{{{\text{in}}}}$.

To avoid the problems with a singularity of the Coulomb potential at the origin of coordinates, we impose the additional requirement of vanishing doublets D($\hat {H}_{s}^{{{\text{in}}}}$) in a certain neighborhood of the origin, which is generally different for each doublet. It should be noted that the domains D($\hat {H}_{s}^{{{\text{in}}}}$) (which are the same for both values of s) are dense in $\mathfrak{H}$. Therefore, operators $\hat {H}_{s}^{{{\text{in}}}}$ are defined as

$$\hat{H}_{s}^{\text{in}}=\left\{ \begin{aligned} & D(\hat{H}_{s}^{\text{in}})=\{\Psi (\mathbf{r}):{{\psi }_{\alpha }}(\mathbf{r})\in C_{0}^{\infty }({{\mathbb{R}}^{2}}\backslash \{ 0 \} ) \}, \\ & \hat{H}_{s}^{\text{in}}\Psi \mathrm{(}\mathbf{r}\mathrm{)=}{{\check{{H}}}_{s}}\Psi (\mathbf{r}). \\ \end{aligned} \right.$$

Operator $\hat {H}_{s}^{{{\text{in}}}}$ defined in this way is obviously symmetric.

We construct s.a. Hamiltonians ${{\hat {H}}_{s}}$ as s.a. extensions of corresponding initial symmetric operators $\hat {H}_{s}^{{{\text{in}}}}$. We require that operators ${{\hat {H}}_{s}}$, as well as initial symmetric operators $\hat {H}_{s}^{{{\text{in}}}}$, be rotationally invariant. The meaning of this requirement will be explained below.

There exist two different unitary representations U_s of rotational group Spin(2) in $\mathfrak{H}$, which are connected with corresponding operators U_s. Generator ${{\hat {J}}_{s}}$ of the representation of group U_s, which is known as the angular momentum operator (there are two such operators), is an s.a. operator in $\mathfrak{H}$, which is defined on absolutely continuous doublets periodic in ϕ ∈ [0, 2π] and associated with differential expression

$${{\check{{J}}}_{s}}=-i\frac{\partial }{\partial \phi }+s\frac{{{\sigma }_{z}}}{2}.$$

For each s, Hilbert space $\mathfrak{H}$ can be represented as a direct orthogonal sum of subspaces ${{\mathfrak{H}}_{{sj}}}$, which are eigenspaces of angular momentum operator ${{\hat {J}}_{s}}$ and correspond to its all eigenvalues j,

$$\begin{gathered} \mathfrak{H} = \sum\limits_j{}^ \oplus {\,{{\mathfrak{H}}_{{ - 1,j}}}} = \sum\limits_j{}^ \oplus {\,{{\mathfrak{H}}_{{ + 1,j}}}} , \\ j = \pm 1{\text{/}}2, \pm 3{\text{/}}2,... \\ \end{gathered} $$

(4)

Subspace ${{\mathfrak{H}}_{{sj}}}$ with given s and j consists of doublets Ψ_sj of form

$${{\Psi }_{{sj}}}({\mathbf{r}}) = \frac{1}{{\sqrt {2\pi \rho } }}{{e}^{{ij\phi }}}\left( \begin{gathered} {{e}^{{ - is\phi /2}}}f(\rho ) \\ - is{{e}^{{is\phi /2}}}g(\rho ) \\ \end{gathered} \right) \in {{\mathfrak{H}}_{{sj}}},$$

(5)

which are eigenfunctions of operator ${{\hat {J}}_{s}}$,

$${{\hat{J}}_{s}}{{\Psi }_{sj}}(\mathbf{r})={{\check{{J}}}_{s}}{{\Psi }_{sj}}(\mathbf{r})=j{{\Psi }_{sj}}(\mathbf{r}).$$

It should be noted that the spectra of operators ${{\hat {J}}_{{ - 1}}}$ and ${{\hat {J}}_{1}}$ coincide. Functions f(ρ) and g(ρ) are referred to as radial functions. In the language of physics, expansions (4) and (5) correspond to the expansion of doublets Ψ(r) ∈ $\mathfrak{H}$ in the eigenfunctions of two different angular momentum operators ${{\hat {J}}_{{ - 1}}}$ and ${{\hat {J}}_{1}}$.

In further analysis, the following fact is significant. Let ${{\mathbb{L}}^{2}}$(${{\mathbb{R}}_{ + }}$) be the Hilbert space of radial doublets,

$$F(\rho ) = \left( \begin{gathered} f(\rho ) \\ g(\rho ) \\ \end{gathered} \right) \in {{\mathbb{L}}^{2}}({{\mathbb{R}}_{ + }}),$$

with scalar product

$$\begin{gathered} ({{F}_{1}},{{F}_{2}}) = \int\limits_0^\infty {F_{1}^{ + }(\rho ){{F}_{2}}(\rho )d\rho } \\ = \int\limits_0^\infty {[\overline {{{f}_{1}}(\rho )} {{f}_{2}}(\rho ) + \overline {{{g}_{1}}(\rho )} {{g}_{2}}(\rho )]} d\rho , \\ \end{gathered} $$

so that ${{\mathbb{L}}^{2}}$(${{\mathbb{R}}_{ + }}$) = L²(${{\mathbb{R}}_{ + }}$) $\oplus$ L²(${{\mathbb{R}}_{ + }}$). Then expression (5) and relation

$${\text{||}}{{\Psi }_{{sj}}}{\text{|}}{{{\text{|}}}^{2}} = \int\limits_0^\infty {[{\text{|}}f(\rho ){{{\text{|}}}^{2}} + \,{\text{|}}g(\rho ){{{\text{|}}}^{2}}]d\rho } $$

indicate that space ${{\mathfrak{H}}_{{sj}}}$ ⊂ $\mathfrak{H}$ is unitarily equivalent to Hilbert space ${{\mathbb{L}}^{2}}$(${{\mathbb{R}}_{ + }}$),

$${{\Psi }_{{sj}}}({\mathbf{r}}) = {{V}_{{sj}}}F(\rho ),\quad F(\rho ) = V_{{sj}}^{{ - 1}}{{\Psi }_{{sj}}}({\mathbf{r}}).$$

(6)

The initial symmetric operators $\hat {H}_{s}^{{{\text{in}}}}$ are rotationally invariant. Namely, each operator $\hat {H}_{s}^{{{\text{in}}}}$ is invariant to representation U_s of the rotational group. Therefore, each subspace ${{\mathfrak{H}}_{{sj}}}$ (eigenspace of generator ${{\hat {J}}_{s}}$ with eigenvalue j) reduces operator $\hat {H}_{s}^{{{\text{in}}}}$. In other words, operator $\hat {H}_{s}^{{{\text{in}}}}$ commutes with projectors P_sj onto subspaces ${{\mathfrak{H}}_{{sj}}}$ (see [15]). This in turn indicates the following. Let us suppose that

$${{\Psi }_{s}}({\mathbf{r}}) = \sum\limits_j^{} {{{\Psi }_{{sj}}}({\mathbf{r}}) \in D(\hat {H}_{s}^{{{\text{in}}}}).} $$

Then

$${{\Psi }_{{sj}}} = {{P}_{{sj}}}{{\Psi }_{s}} \in D(\hat {H}_{s}^{{{\text{in}}}}),\quad \hat {H}_{s}^{{{\text{in}}}}{{\Psi }_{s}} = \sum\limits_j^{} {\hat {H}_{{sj}}^{{{\text{in}}}}{{\Psi }_{{sj}}},} $$

where operators $\hat {H}_{{sj}}^{{{\text{in}}}}$ = P_sj$\hat {H}_{s}^{{{\text{in}}}}$P_sj = $\hat {H}_{s}^{{{\text{in}}}}$P_sj are the so-called parts of operator $\hat {H}_{s}^{{{\text{in}}}}$, which are acting in ${{\mathfrak{H}}_{{sj}}}$. The rule of action of these operators is given by the first-order differential operation in variable ρ, which will be given below. Thus, each initial symmetric operator $\hat {H}_{s}^{{{\text{in}}}}$ is the direct orthogonal sum of its parts,

$$\hat {H}_{s}^{{{\text{in}}}} = \sum\limits_j{}^ \oplus {\,\hat {H}_{{sj}}^{{{\text{in}}}}} ,$$

so that analysis of rotationally invariant operator $\hat {H}_{s}^{{{\text{in}}}}$ is reduced to analysis of operators $\hat {H}_{{sj}}^{{{\text{in}}}}$.

Each operator $\hat {H}_{{sj}}^{{{\text{in}}}}$ is a symmetric operator acting in subspace ${{\mathfrak{H}}_{{sj}}}$. It obviously induces symmetric operator ${{\hat {h}}_{{{\text{in}}}}}$(Z, j, s) in Hilbert space ${{\mathbb{L}}^{2}}$(${{\mathbb{R}}_{ + }}$), which is unitarily equivalent to operator $\hat {H}_{{sj}}^{{{\text{in}}}}$,

$${{\hat {h}}_{{{\text{in}}}}}(Z,j,s)F = V_{{sj}}^{{ - 1}}\hat {H}_{{sj}}^{{{\text{in}}}}{{\Psi }_{{sj}}},\quad {{\Psi }_{{sj}}} = {{V}_{{sj}}}F.$$

Operator ${{\hat {h}}_{{{\text{in}}}}}$(Z, j, s) is defined as

$${{\hat{h}}_{\text{in}}}(Z,j,s)=\left\{ \begin{aligned} & {{D}_{{{h}_{\text{in}}}(Z,j,s)}}=\mathbb{C}_{0}^{\infty }({{\mathbb{R}}_{+}}) \\ & {{{\hat{h}}}_{n}}(Z,j,s)F(\rho )=\check{{h}}\,(Z,j,s)F(\rho ), \\ \end{aligned} \right.$$

(7)

where $\mathbb{C}_{0}^{\infty }$(${{\mathbb{R}}_{ + }}$) = $C_{0}^{\infty }$(${{\mathbb{R}}_{ + }}$) $\oplus$ $C_{0}^{\infty }$(${{\mathbb{R}}_{ + }}$). Differential operation $\check{{h}}\,$(Z, j, s),

$$\begin{gathered} \check{{h}}\,(Z,j,s)=-i{{\sigma }_{y}}\frac{d}{d\rho }+\frac{\kappa }{\rho }{{\sigma }_{x}}-\frac{g}{\rho }, \\ \kappa =-sj,\quad g={{\alpha }_{F}}{{\epsilon }^{-1}}Z, \\ \end{gathered}$$

(8)

will be referred to as the partial radial differential operations.

The construction of s.a. rotationally invariant Hamiltonians ${{\hat {H}}_{s}}$ as s.a. extensions of initially symmetric operators $\hat {H}_{s}^{{{\text{in}}}}$ is reduced to the construction of s.a. partial radial Hamiltonians $\hat {h}$(Z, j, s) in ${{\mathbb{L}}^{2}}$(${{\mathbb{R}}_{ + }}$) as s.a. extensions of initial symmetric partial radial operators ${{\hat {h}}_{{{\text{in}}}}}$(Z, j, s). Namely, let operators $\hat {h}$(Z, j, s) be such extensions. They obviously induce s.a. extensions ${{\hat {H}}_{{sj}}}$ = V_sj$\hat {h}$(Z, j, s)$V_{{sj}}^{{ - 1}}$ of initial symmetric operators $\hat {H}_{{sj}}^{{{\text{in}}}}$ in subspaces ${{\mathfrak{H}}_{{sj}}}$. Then the direct orthogonal sum of partial operator ${{\hat {H}}_{{sj}}}$,

$${{\hat {H}}_{s}} = \sum\limits_j{}^ \oplus {\,{{{\hat {H}}}_{{sj}}},} $$

(9)

is a rotationally invariant extension of initial symmetric operator $\hat {H}_{s}^{{{\text{in}}}}$. Any s.a. rotationally invariant extension of initial symmetric operator $\hat {H}_{s}^{{{\text{in}}}}$ has structure (9). The spectrum of Hamiltonian $\hat {H}_{s}^{{}}$ is given by the combination of the spectra of partial radial Hamiltonians,

$${\text{spec}}\hat {H}_{s}^{{}} = {{ \cup }_{j}}{\text{spec}}\hat {h}(Z,j,s),$$

and the corresponding eigenfunctions associated with ${{\mathfrak{H}}_{{sj}}}$ are obtained from the eigenfunctions of operators $\hat {h}$(Z, j, s) in ${{\mathbb{L}}^{2}}$(${{\mathbb{R}}_{ + }}$) using transformation V_sj; see relation (6).

4 GENERAL SOLUTION TO RADIAL EQUATIONS

Let us now consider the general solution to the system of two linear ordinary differential equations for functions f(ρ) and g(ρ),

$$\begin{gathered} \check{{h}}\,(Z,j,s)F(\rho )=WF(\rho ), \\ F(\rho )=\left( \begin{matrix} f(\rho ) \\ g(\rho ) \\ \end{matrix} \right),\quad W\in \mathbb{C}, \\ \end{gathered}$$

(10)

which is required for analyzing the spectrum and eigenfunctions of partial radial Hamiltonians. Real values of W will be henceforth denoted by letter E. For our analysis, it is sufficient to consider the values of W belonging to the upper complex half-plane, W = E + iy, y ≥ 0. We will also be interested in limit W → E + i0.

System (10) written in components has form

$$\begin{gathered} \frac{{df}}{{d\rho }} + \frac{\kappa }{\rho }f(\rho ) - \left( {W + \frac{g}{\rho }} \right)g(\rho ) = 0, \\ \frac{{dg}}{{d\rho }} - \frac{\kappa }{\rho }g(\rho ) + \left( {W + \frac{g}{\rho }} \right)f(\rho ) = 0. \\ \end{gathered} $$

(11)

Further, we will refer to Eqs. (11) as radial equations. Let us write the general solution to radial equations, following the standard procedure [12, 16]. We perform the following substitution of functions and variables:

$$f(\rho ) = {{z}^{\Upsilon }}{{e}^{{ - z/2}}}[Q(z) + P(z)],$$

$$g(\rho ) = i{{z}^{\Upsilon }}{{e}^{{ - z/2}}}[Q(z) - P(z)],$$

$$z = - 2iW\rho ,\quad {{\Upsilon }^{2}} = {{\kappa }^{2}} - {{g}^{2}}.$$

In the new variables and for the new function, we obtain

$$\begin{gathered} z\frac{{{{d}^{2}}Q(z)}}{{d{{z}^{2}}}} + (\beta - z)\frac{{dQ(z)}}{{dz}} - \alpha Q(z) = 0, \\ P(z) = - \frac{1}{\kappa }\left( {z\frac{d}{{dz}} + \alpha } \right)Q(z), \\ \beta = 1 + 2\Upsilon ,\quad \alpha = {{\alpha }_{ + }},\quad {{\alpha }_{ + }} = \Upsilon - ig. \\ \end{gathered} $$

(12)

It can be seen that Eq. (12) for function Q(z) is the known confluent hypergeometrical equation. Let us suppose that $\Upsilon$ ≠ –n/2, n ∈ $\mathbb{N}$. In this case, the general solution to the confluent hypergeometrical equation is a linear combination of standard hypergeometric functions Φ(α, β; z) and Ψ(α, β; z),

$$Q(z) = A\Phi (\alpha ,\beta ;z) + B\Psi (\alpha ,\beta ;z)$$

where A and B are arbitrary constants and

$$\begin{gathered} \Psi (\alpha ,\beta ;z) = \frac{{\Gamma (1 - \beta )}}{{\Gamma (\alpha - \beta + 1)}}\Phi (\alpha ,\beta ;z) \\ + \frac{{\Gamma (\beta - 1)}}{{\Gamma (\alpha )}}{{z}^{{1 - \beta }}}\Phi (\alpha - \beta + 1,2 - \beta ;z). \\ \end{gathered} $$

Using relations

$$\begin{gathered} \left( {z\frac{d}{{dz}} + \alpha } \right)\Phi (\alpha ,\beta ;z) = \alpha \Phi (\alpha + 1,\beta ;z), \\ \left( {z\frac{d}{{dz}} + \alpha } \right)\Psi (\alpha ,\beta ;z) = \alpha (\alpha - \beta - 1)\Psi (\alpha + 1,\beta ;z), \\ \end{gathered} $$

$$\alpha - \beta + 1 = - {{\alpha }_{ - }},\quad {{\alpha }_{ + }}{{\alpha }_{ - }} = {{\kappa }^{2}},$$

$${{\alpha }_{ - }} = \Upsilon + ig,\quad a = \frac{\alpha }{\kappa },$$

we obtain the general solution to system (11) in form

$$Q(z) = \tilde {A}\Phi (\alpha ,\beta ;z) + B\Psi (\alpha ,\beta ;z),$$

$$P(z) = - \tilde {A}a\Phi (\alpha + 1,\beta ;z) + B\kappa \Psi (\alpha + 1,\beta ;z).$$

As follows from equalities

$$\Phi (\alpha + 1,\beta ;z) = {{e}^{z}}\Phi (\beta - \alpha - 1,\beta ; - z),$$

$$i\frac{{1 + a}}{{1 - a}} = \frac{{\kappa + \Upsilon }}{g},$$

we can write the general solution to the radial equations in the following form:

$$\begin{gathered} F(\rho ,\Upsilon ,W) = AX(\rho ,\Upsilon ,W) \\ + B{{z}^{\Upsilon }}{{e}^{{ - z/2}}}[\Psi (\alpha ,\beta ;z){{\varrho }_{ + }} - \kappa \Psi (\alpha + 1,\beta ;z){{\varrho }_{ - }}], \\ {{\varrho }_{ \pm }} = {{( \pm 1,i)}^{T}},\quad \tilde {A} = \frac{{{{{( - 2iW)}}^{{ - \Upsilon }}}}}{{1 - a}}A, \\ \end{gathered} $$

(13)

where we have introduced doublet X(ρ, $\Upsilon$, W),

$$\begin{gathered} X(\rho ,\Upsilon ,W) = {{z}^{\Upsilon }}[{{e}^{{ - z/2}}}\Phi (\alpha ,\beta ;z){{\varrho }_{ + }} \\ \, + e{{a}^{{z/2}}}\Phi (\alpha + 1,\beta ;z){{\varrho }_{ - }}] \\ = \frac{{1 - a}}{2}{{( - 2iW\rho )}^{\Upsilon }}[{{\Phi }_{ + }}(\rho ,\Upsilon ,W) + {{\Phi }_{ - }}(\rho ,\Upsilon ,W)\Xi ]{{d}_{ + }}, \\ \end{gathered} $$

$$\begin{gathered} {{\Phi }_{ + }}(\rho ,\Upsilon ,W) = {{e}^{{iW\rho }}}\Phi (\alpha ,1 + 2\Upsilon , - 2iW\rho ) \\ \, + {{e}^{{ - iW\rho }}}\Phi ({{\alpha }_{ - }},1 + 2\Upsilon ,2iW\rho ), \\ \end{gathered} $$

$$\begin{gathered} {{\Phi }_{ - }}(\rho ,\Upsilon ,W) = \frac{1}{{iW}}[{{e}^{{iW\rho }}}\Phi (\alpha ,1 + 2\Upsilon , - 2iW\rho ) \\ \, - {{e}^{{ - iW\rho }}}\Phi ({{\alpha }_{ - }},1 + 2\Upsilon ,2iW\rho )], \\ \end{gathered} $$

$$\Xi = \left( {\begin{array}{*{20}{c}} 0&W \\ { - W}&0 \end{array}} \right),\quad {{d}_{ \pm }} = {{\left( {1,\frac{{\kappa \pm \Upsilon }}{g}} \right)}^{T}}.$$

Henceforth, we will use some particular solutions to the radial equations, which correspond to a certain set of constants A and B and parameter $\Upsilon$.

We introduce new quantity ${{\Upsilon }_{ + }}$ as follows:

$${{\Upsilon }_{ + }} = {{\Upsilon }_{ + }}(g,j) = \left\{ \begin{gathered} \gamma = \sqrt {{{\kappa }^{2}} - {{g}^{2}}} \geqslant 0,\quad g \leqslant {\text{|}}\kappa {\text{|}}{\text{,}} \hfill \\ i\sigma = i\sqrt {{{g}^{2}} - {{\kappa }^{2}}} ,\quad \sigma > 0. \hfill \\ \end{gathered} \right.$$

This quantity as a function of parameter g has zero values at points g = g_c(j) = |κ| = |j|. When ${{\Upsilon }_{ + }}$ ≠ 0 (g ≠ g_c(j)), we have two linearly independent solutions F₁ and F₂, which form the following fundamental set of solutions to system (11):

$$\begin{gathered} {{F}_{1}}(\rho ;W) = F(\rho ,{{\Upsilon }_{ + }},W){{{\text{|}}}_{{A = 1,B = 0}}} \\ = {{\rho }^{{{{\Upsilon }_{ + }}}}}{{d}_{ + }} + O({{\rho }^{{{{\Upsilon }_{ + }} + 1}}}),\quad \rho \to 0, \\ \end{gathered} $$

$$\begin{gathered} {{F}_{2}}(\rho ;W) = F(\rho , - {{\Upsilon }_{ + }},W){{{\text{|}}}_{{A = 1,B = 0}}} \\ = {{\rho }^{{ - {{\Upsilon }_{ + }}}}}{{d}_{ - }} + O({{\rho }^{{ - {{\Upsilon }_{ + }} + 1}}}),\quad \rho \to 0. \\ \end{gathered} $$

It should be noted that both doublets F₁ and F₂ are real-valued integer functions of W. Their Wronskian can be found easily, Wr(F₁, F₂) = –2${{\Upsilon }_{ + }}$g^–1. If Im W > 0, both doublets F₁(ρ; W) and F₂(ρ; W) increase exponentially for ρ → ∞. For real values of W = E, doublets F₁ and F₂ can be written in terms of the Coulomb functions [17],

$$\begin{gathered} {{\mathcal{F}}_{\alpha }}(\eta ;r) = \frac{{{\text{|}}\Gamma (\alpha + 1 + i\eta ){\text{|}}}}{{\Gamma (2\alpha + 2)}}{{(2r)}^{\alpha }}r{{e}^{{ - \pi \eta /2 - ir}}} \\ \, \times \Phi (\alpha + 1 - i\eta ,2\alpha + 2,2ir). \\ \end{gathered} $$

For ${{\Upsilon }_{ + }}$ = γ, we have

$$\begin{gathered} {{F}_{1}}(\rho ;W) = \frac{{2\Gamma (2\gamma ){{e}^{{ - \pi \tilde {g}/2}}}}}{{{\text{|}}\Gamma (\gamma - i\tilde {g}){\text{|}}}}{\text{|}}2E{{{\text{|}}}^{{ - \gamma }}}({{u}_{ + }}(\gamma ){{\mathcal{F}}_{{\gamma - 1}}}( - \tilde {g},{\text{|}}E{\text{|}}\rho ) \\ - \operatorname{sgn} (sjE){{u}_{ - }}(\gamma ){{\mathcal{F}}_{\gamma }}( - \tilde {g},{\text{|}}E{\text{|}}\rho )), \\ {{F}_{2}}(\rho ;E) = {{F}_{1}}(\rho ;E){{{\text{|}}}_{{\gamma \to - \gamma }}}, \\ {{u}_{ + }}(\Upsilon ) = \left( \begin{gathered} 1 \\ \frac{{\Upsilon - sj}}{g} \\ \end{gathered} \right),\quad {{u}_{ - }}(\Upsilon ) = \left( \begin{gathered} \frac{{\Upsilon - sj}}{g} \\ 1 \\ \end{gathered} \right), \\ \tilde {g} = \operatorname{sgn} (E)g. \\ \end{gathered} $$

(14)

For ${{\Upsilon }_{ + }}$ = iσ, σ > 0, we have another representation:

$$\begin{gathered} {{F}_{1}}(\rho ;E) = 2\Gamma (2i\sigma )\sqrt {\frac{{(\sigma - \tilde {g})\sinh (\sigma - \tilde {g})}}{\pi }} \\ \times \,{{e}^{{ - \pi \tilde {g}/2}}}{\text{|}}2E{{{\text{|}}}^{{ - i\sigma }}}\left[ {{{u}_{ + }}(i\sigma ){{\mathcal{F}}_{{i\sigma - 1}}}{{{( - \tilde {g},{\text{|}}E{\text{|}}\rho )}}_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}} \right. \\ \left. { - \frac{{sj}}{{\tilde {g} - \sigma }}{{u}_{ - }}(i\sigma ){{\mathcal{F}}_{{i\sigma }}}( - \tilde {g},{\text{|}}E{\text{|}}\rho )} \right], \\ {{F}_{2}}(\rho ;E) = \overline {{{F}_{1}}(\rho ;E)} . \\ \end{gathered} $$

One more useful solution F₃ is given by expression (13) for A = 0, $\Upsilon$ = ${{\Upsilon }_{ + }}$, and a special choice of parameter B = B(W),

$$\begin{gathered} {{F}_{3}}(\rho ;W) = B(W){{z}^{\Upsilon }}{{e}^{{ - z/2}}}[\Psi (\alpha ,\beta ;z){{\varrho }_{ + }} \\ \, - {{b}_{ - }}\Psi (\alpha + 1,\beta ;z){{\varrho }_{ - }}] \\ = \Gamma ( - 2{{\Upsilon }_{ + }}){{F}_{1}}(\rho ;W) - \frac{{g\omega (W)}}{{2{{\Upsilon }_{ + }}}}{{F}_{2}}(\rho ;W), \\ \end{gathered} $$

where

$$\begin{gathered} \omega (W) = - i\frac{{\Gamma (1 + 2{{\Upsilon }_{ + }})\Gamma ( - {{\alpha }_{ - }})}}{{a\Gamma (\alpha )[\kappa - {{\Upsilon }_{ + }}]}}{{(2{{e}^{{ - i\pi /2}}}W)}^{{ - 2{{\Upsilon }_{ + }}}}} \\ = - {\text{Wr}}({{F}_{1}},{{F}_{3}}), \\ \end{gathered} $$

$$B(W) = \frac{1}{2}\Gamma ( - {{\alpha }_{ - }})\left[ {1 + \frac{{\kappa + {{\Upsilon }_{ + }}}}{{ig}}} \right]{{(2{{e}^{{ - i\pi /2}}}W)}^{{ - {{\Upsilon }_{ + }}}}}.$$

If ImW > 0, doublet F₃(ρ; W) decreases exponentially for ρ → ∞ (to within a certain polynomial).

5 SELF-ADJOINT RADIAL HAMILTONIANS

Since all possible s.a. partial radial Hamiltonians $\hat {h}$(Z, j, s) are associated with the general differential expression $\check{{h}}\,$(Z, j, s) in (8), and their definition boils down to the indication of their domains D_h(Z, j,s) ⊂ ${{\mathbb{L}}^{2}}$(${{\mathbb{R}}_{ + }}$). Each operator $\hat {h}$(Z, j, s) is the s.a. extension of initial symmetric operator $\hat {h}_{{{\text{in}}}}^{{}}$(Z, j, s) in (7), which is defined in space $\mathbb{C}_{0}^{\infty }$(${{\mathbb{R}}_{ + }}$) of smooth compactly supported doublets on the semi-axis ${{\mathbb{R}}_{ + }}$. At the same time, each operator $\hat {h}$(Z, j, s) is the s.a. contraction of adjoint operator $\hat {h}_{{{\text{in}}}}^{ + }$(Z, j, s) acting on the so-called natural domain of $D_{\check{{h}}\,(Z,j,s)}^{*}$(${{\mathbb{R}}_{ + }}$) for $\check{{h}}\,$(Z, j, s) consisting of doublets F(ρ) ∈ ${{\mathbb{L}}^{2}}$(${{\mathbb{R}}_{ + }}$), which are absolutely continuous in space ${{\mathbb{R}}_{ + }}$ and such that

$$\check{{h}}\,(Z,j,s)F(\rho )\in {{\mathbb{L}}^{2}}({{\mathbb{R}}_{+}}),$$

$${{D}_{{{h}_{\text{in}}}(Z,j,s)}}\subset {{D}_{h(Z,j,s)}}\subseteq D_{\check{{h}}\,(Z,j,s)}^{*}({{\mathbb{R}}_{+}}).$$

Since the coefficient functions of differential operation $\check{{h}}\,$(Z, j, s) are real-valued, the deficiency indices of initial symmetric operator ${{\hat {h}}_{{{\text{in}}}}}$(Z, j, s) are identical so that s.a. extensions $\hat {h}$(Z, j, s) exist for any values of parameters Z and j.

Following [10, 12], we construct s.a. extensions $\hat {h}$(Z, j, s) of operator ${{\hat {h}}_{{{\text{in}}}}}$(Z, j, s) as s.a. contractions of adjoint operator $\hat {h}_{{{\text{in}}}}^{ + }$(Z, j, s), which are determined by certain asymptotic s.a. boundary conditions.

Let us estimate the asymmetry of operator $\hat {h}_{{{\text{in}}}}^{ + }$(Z, j, s) in terms of (asymptotic) boundary values of doublets from its domain $D_{\check{{h}}\,(Z,j,s)}^{*}$(${{\mathbb{R}}_{ + }}$). To this end, we introduce quadratic asymmetry form ${{\Delta }_{*}}$ for operator $\hat {h}_{{{\text{in}}}}^{ + }$(Z, j, s) by relation

$$\begin{matrix} {{\Delta }_{*}}(F)=(F,\hat{h}_{\text{in}}^{+}F)-(\hat{h}_{\text{in}}^{+}F,F)=2i\operatorname{Im}(F,\hat{h}_{\text{in}}^{+}F) \\ =\int\limits_{0}^{\infty }{{{F}^{+}}(\rho )(\check{{h}}\,F)(\rho )d\rho -\int\limits_{0}^{\infty }{{{(\check{{h}}\,F)}^{+}}(\rho )F(\rho )d\rho .}} \\ \end{matrix}$$

(15)

This form shows the extent of deviation of operator $\hat {h}_{{{\text{in}}}}^{ + }$(Z, j, s) from the symmetric operator. If ${{\Delta }_{*}}$ ≡ 0, operator $\hat {h}_{{{\text{in}}}}^{ + }$(Z, j, s) is symmetric and, hence, is an s.a. operator. Then $\hat {h}_{{{\text{in}}}}^{{}}$(Z, j, s) is an essentially s.a. operator, and its only s.a. extension is adjoint operator $\hat {h}_{{{\text{in}}}}^{ + }$(Z, j, s). If ${{\Delta }_{*}}$ ≠ 0, s.a. operator $\hat {h}$(Z, j, s) is determined as a contraction of operator $\hat {h}_{{{\text{in}}}}^{ + }$(Z, j, s) onto domain D_h(Z, j,s) ⊆ $D_{\check{{h}}\,(Z,j,s)}^{*}$(${{\mathbb{R}}_{ + }}$), such that contraction of form ${{\Delta }_{*}}$ on D_h(Z, j,s) is zero, and domain D_h(Z, j,s) cannot be extended with the conservation of condition ${{\Delta }_{*}}$ ≡ 0.

Integrating by parts on the right-hand side of Eq. (15) and taking into account relations (8), we can easily see that asymmetry form ${{\Delta }_{*}}$ is given by

$${{\Delta }_{*}}(F) = [F](\infty ) - [F](0),\quad [F](\infty ) = \mathop {\lim }\limits_{\rho \to \infty } [F](\rho ),$$

$$[F](0) = \mathop {\lim }\limits_{\rho \to 0} [F](\rho ),$$

$$[F](\rho ) = - i{{F}^{ + }}(\rho ){{\sigma }_{y}}F(\rho ) = - [\overline {f(\rho )} g(\rho ) - \overline {g(\rho )} f(\rho )].$$

The quadratic integrability of doublet $\check{{h}}\,$(Z, j, s)F for F ∈ $D_{\check{{h}}\,(Z,j,s)}^{*}$(${{\mathbb{R}}_{ + }}$) implies the quadratic integrability of derivative F  '(ρ) at infinity. It follows hence that any doublet F ∈ $D_{\check{{h}}\,(Z,j,s)}^{*}$(${{\mathbb{R}}_{ + }}$) decreases at infinity, [F](∞) = 0, and asymmetry form ${{\Delta }_{*}}$ is determined by the behavior of these doublets at zero:

$$\begin{gathered} {{\Delta }_{*}}(F) = - [F](0) \\ = \mathop {\lim }\limits_{\rho \to 0} (\overline {f(\rho )} g(\rho ) - \overline {g(\rho )} f(\rho )). \\ \end{gathered} $$

(16)

To calculate this asymmetry form, we must know the explicit form of doublets F from domain of definition $D_{\check{{h}}\,(Z,j,s)}^{*}$(${{\mathbb{R}}_{ + }}$). It should be noted in this connection that these doublets can be treated as quadratically integrable solutions to nonhomogeneous differential equation $\check{{h}}\,$(Z, j, s)F(ρ) = G(ρ) with the right-hand side of G belonging to ${{\mathbb{L}}^{2}}$(${{\mathbb{R}}_{ + }}$). Any solution to this nonhomogeneous differential equation can be represented in form

$$\begin{gathered} F(\rho ) = {{c}_{1}}{{u}_{1}}(\rho ) + {{c}_{2}}{{u}_{2}}(\rho ) + {{I}_{1}}(\rho ) + {{I}_{2}}(\rho ), \\ {{c}_{1}},{{c}_{2}} = {\text{const}}, \\ {{u}_{1}}(\rho ) = {{d}_{ + }}{{\rho }^{{{{\Upsilon }_{ + }}}}}, \\ \end{gathered} $$

$$\begin{matrix} {{u}_{2}}(\rho )=\left\{ \begin{aligned} & {{d}_{-}}{{\rho }^{-{{\Upsilon }_{+}}}},\quad g\ne {{g}_{c}}(j), \\ & {{d}_{0}}(\rho ),\quad g={{g}_{c}}(j), \\ \end{aligned} \right. \\ \check{{h}}\,(Z,j,s){{u}_{k}}(\rho )=0, \\ \end{matrix}$$

(17)

$$\begin{gathered} {{d}_{ \pm }} = \left( \begin{gathered} 1 \\ (\kappa \pm {{\Upsilon }_{ + }}){\text{/}}g \\ \end{gathered} \right), \\ {{d}_{0}}(\rho ) = \left( \begin{gathered} \ln \rho - \zeta (j,s)g_{c}^{{ - 1}}(j) \\ \zeta (j,s)\ln \rho \\ \end{gathered} \right), \\ \zeta (j,s) = \operatorname{sgn} (\kappa ) = - s\operatorname{sgn} (j), \\ \end{gathered} $$

where I₁(ρ) and I₂(ρ) are particular solutions to the nonhomogeneous equation,

$$\begin{gathered} {{I}_{1}}(\rho ) = \left\{ \begin{gathered} \frac{g}{{2{{\Upsilon }_{ + }}}}\int\limits_\rho ^{{{\rho }_{0}}} {[{{u}_{1}}(\rho ) \otimes {{u}_{2}}(\rho {\kern 1pt} ')]G(\rho {\kern 1pt} ')d\rho {\kern 1pt} ',\quad \Upsilon = {{\Upsilon }_{ + }} \geqslant } \,1{\text{/}}2,\quad {{\rho }_{0}} > 0, \hfill \\ - \frac{g}{{2{{\Upsilon }_{ + }}}}\int\limits_0^\rho {[{{u}_{1}}(\rho ) \otimes {{u}_{2}}(\rho {\kern 1pt} ')]G(\rho {\kern 1pt} ')d\rho {\kern 1pt} ',\quad \Upsilon = {{\Upsilon }_{ + }} < } \,1{\text{/}}2,\quad \Upsilon = i\sigma ,\quad \sigma > 0, \hfill \\ {{g}_{c}}(j)\int\limits_0^\rho {[{{u}_{1}}(\rho ) \otimes {{u}_{2}}(\rho {\kern 1pt} ')]G(\rho {\kern 1pt} ')d\rho {\kern 1pt} ',\quad \Upsilon = 0,} \hfill \\ \end{gathered} \right. \hfill \\ {{I}_{2}}(\rho ) = \left\{ \begin{gathered} \frac{g}{{2{{\Upsilon }_{ + }}}}\int\limits_\rho ^0 {[{{u}_{2}}(\rho ) \otimes {{u}_{1}}(\rho {\kern 1pt} ')]G(\rho {\kern 1pt} ')d\rho {\kern 1pt} ',\quad \Upsilon \ne \,} 0, \hfill \\ - {{g}_{c}}(j)\int\limits_0^\rho {[{{u}_{2}}(\rho ) \otimes {{u}_{1}}(\rho {\kern 1pt} ')]G(\rho {\kern 1pt} ')d\rho {\kern 1pt} ',\quad \Upsilon = 0.} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $$

(18)

Expressions (17) and (18) allow us to find the asymptotic behavior of the doublets at zero and to calculate asymmetry form (16). It follows from expressions (17) and (18) that the behavior of doublets F at zero substantially depends on the values of parameters j and Z.

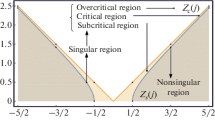
It is convenient to divide upper half-plane (j, Z) into the so-called nonsingular and singular domains, in which the problem of determining s.a. extensions ${{\hat {h}}_{{{\text{in}}}}}$(Z, j, s) has basically different solutions. These regions are divided by symmetric singular curve Z = Z_s(j), where Z_s(j) = $\alpha _{F}^{{ - 1}}\epsilon \sqrt {{{j}^{2}} - 1{\text{/}}4}$, on which g = g_s(j) = $\sqrt {{{j}^{2}} - 1{\text{/}}4}$ and ${{\Upsilon }_{ + }}$ = γ = 1/2. The nonsingular domain is defined by inequality Z ≤ Z_s(j), which is equivalent to inequality ${{\Upsilon }_{ + }}$ = γ ≥ 1/2. The singular domain is defined by inequality Z > Z_s(j), which is equivalent 0 ≤ ${{\Upsilon }_{ + }}$ = γ < 1/2 or ${{\Upsilon }_{ + }}$ = iσ, σ > 0. Since the singular curve is the upper boundary of the nonsingular domain, the value of Z_s(j) will be referred to as the maximal nonsingular value of Z for the given j.

We divide the singular domain into three subsets: subcritical, critical, and overcritical. The subcritical domain is defined by inequalities Z_s(j) < Z < Z_c(j), which is equivalent to 0 < ${{\Upsilon }_{ + }}$ = γ < 1/2, where Z_c(j) = $\alpha _{F}^{{ - 1}}\epsilon$|j|. We will call the value of Z_c(j) the critical value of Z for the given j. The critical domain is critical curve Z = Z_c(j), which is equivalent to g = g_c(j) = |j| or ${{\Upsilon }_{ + }}$ = γ = 0. The overcritical domain is defined by inequality Z > Z_c(j) = α^–1$\epsilon$|j|, which is equivalent to ${{\Upsilon }_{ + }}$ = iσ, where σ = $\sqrt {{{g}^{2}} - {{j}^{2}}}$ > 0.

Further, we construct s.a. radial Hamiltonians $\hat {h}$(Z, j, s) as s.a. extensions of operator ${{\hat {h}}_{{{\text{in}}}}}$(Z, j, s) in each of the four domains of variation of impurity charge Z.

5.1 Nonsingular Domain

Let us calculate asymmetry form (16) for nonsingular domain Z ≤ Z_s(j), ${{\Upsilon }_{ + }}$ = γ ≥ 1/2. For integrals (18), the following estimate holds:

$${{I}_{1}}(\rho ) = O({{\rho }^{{1/2}}}),\quad {{I}_{2}}(\rho ) = O({{\rho }^{{1/2}}}),\quad \rho \to 0.$$

(19)

Relations (17) imply that function u₂(ρ) ~ ρ^γ is quadratically integrable at the origin of coordinates, and function u₂(ρ) ~ ρ^–γ is not quadratically integrable. Doublets F ∈ $D_{\check{{h}}\,(Z,j,s)}^{*}$(${{\mathbb{R}}_{ + }}$) are defined by expression (17) with c₂ = 0 and behave as O(ρ^1/2) for ρ → 0. Then the asymmetry form is zero in the entire domain $D_{\check{{h}}\,(Z,j,s)}^{*}$(${{\mathbb{R}}_{ + }}$).

It follows hence that each partial radial Hamiltonian in the nonsingular domain is defined uniquely, ${{\hat {h}}_{1}}$(Z, j, s) = $\hat {h}_{{{\text{in}}}}^{ + }$ (Z, j, s). Here, subscript “1” is used as the symbol of the nonsingular domain (subscripts “2,” “3,” and “4” together with other corresponding indices will refer to certain subdomains of the singular domain).

In other words, initial symmetric operator ${{\hat {h}}_{{{\text{in}}}}}$(Z, j, s) is an essentially s.a. operator because its defect indices are (0, 0), and the domain of operator ${{\hat {h}}_{1}}$(Z, j, s) is the natural domain for $\check{{h}}\,$(Z, j, s), ${{D}_{{h{{{\kern 1pt} }_{1}}(Z,j,s)}}}$ = $D_{\check{{h}}\,(Z,j,s)}^{*}$(${{\mathbb{R}}_{ + }}$).

Let us perform spectral analysis of s.a. operator ${{\hat {h}}_{1}}$(Z, j, s). We construct the Green function of this operator:

$$\begin{gathered} G(\rho ,\rho {\kern 1pt} ';W) \\ = {{\omega }^{{ - 1}}}(W)\left\{ \begin{gathered} {{F}_{3}}(\rho ;W) \otimes {{F}_{1}}(\rho {\kern 1pt} ';W),\quad \rho > \rho {\kern 1pt} ', \\ {{F}_{1}}(\rho ;W) \otimes {{F}_{3}}(\rho {\kern 1pt} ';W),\quad \rho < \rho {\kern 1pt} '. \\ \end{gathered} \right. \\ \end{gathered} $$

For the doublet determining the guiding functional, we choose real entire doublet U₁(ρ; W) = F₁(ρ; W). As in the massive case, we can show that this guiding functional is simple (see [12]). Derivative σ'(E) of the spectral function is connected with the Green function and simple guiding functional U₁(ρ; W) by relation

$$\begin{gathered} {{U}_{1}}(c;E) \otimes {{U}_{1}}(c;E)\sigma {\kern 1pt} '(E) \\ = {{\pi }^{{ - 1}}}{\text{Im}}G(c - 0,c + 0;E + i0), \\ \end{gathered} $$

where c is an arbitrary point in interval (0; ∞).

The case of half-integer values of parameter γ = $\ell$/2, $\ell$ ∈ $\mathbb{N}$, requires additional investigation because doublet F₂(ρ; W) has a singularity of form Γ(–2γ) at point γ = $\ell$/2,

$$\mathop {\lim }\limits_{\gamma \to \ell /2} \frac{{{{F}_{2}}(\rho ;W)}}{{\Gamma ( - 2\gamma )}} = - {{a}_{\ell }}(W){{F}_{1}}(\rho ;W){{{\text{|}}}_{{\gamma = \ell /2}}},$$

$${{a}_{\ell }}(W) = 2\gamma {{[g\omega (W){{{\text{|}}}_{{\gamma = \ell /2}}}]}^{{ - 1}}},$$

where function ${{a}_{\ell }}$(W) is a polynomial in W with real coefficients:

$$\begin{gathered} {{a}_{\ell }}(W) = \frac{{{{2}^{\ell }}\pi \gamma }}{{g\ell !}}\left( {2 - \frac{\ell }{\kappa }} \right) \\ \times \frac{{{{e}^{{ - \pi g}}} - {{{( - 1)}}^{\ell }}{{e}^{{\pi g}}}}}{{[{{{( - 1)}}^{\ell }} - \cosh (2\pi g)]{\text{|}}\Gamma (ig - \ell {\text{/}}2){{{\text{|}}}^{2}}}}{{W}^{\ell }}. \\ \end{gathered} $$

In the neighborhood $\ell$ – 1 < 2γ < $\ell$ + 1, $\ell$ ∈ $\mathbb{N}$, of point γ = $\ell$/2, doublet F₂(ρ; W) can be represented as

$${{F}_{2}}(\rho ;W) = - {{a}_{\ell }}(W)\Gamma ( - 2\gamma ){{F}_{1}}(\rho ;W) + {{U}_{\ell }}(\rho ;W),$$

(20)

where doublet ${{U}_{\ell }}$(ρ; W) is real entire, has a finite limit for γ → $\ell$/2, and satisfies radial equations (11). Relation (20) implies that

$${{U}_{\ell }}(\rho ;W) = {{d}_{ - }}{{\rho }^{{ - \gamma }}} + O({{\rho }^{{1 - \gamma }}})$$

for ρ → 0.

Since doublets F₁(ρ; W) and ${{U}_{\ell }}$(ρ; W) are linearly independent, Wr(F₁, ${{U}_{\ell }}$) = –2γ/g ≠ 0, in neighborhood $\ell$ – 1 < 2γ < $\ell$ + 1 of point γ = $\ell$/2, doublet F₃(ρ, W) permits expansion

$${{F}_{3}}(\rho ;W) = \omega (W)\left[ {{{A}_{\ell }}(W){{F}_{1}}(\rho ;W) + \frac{g}{{2\gamma }}{{U}_{\ell }}(\rho ;W)} \right],$$

$${{A}_{\ell }}(W) = \Gamma ( - 2\gamma )[{{\omega }^{{ - 1}}}(W) - {{\omega }^{{ - 1}}}(W){{{\text{|}}}_{{\gamma = \ell /2}}}].$$

Then, for $\ell$ – 1 < 2γ < $\ell$ + 1, we have

$$\begin{gathered} G(c - 0,c + 0,E + i0) \\ = {{A}_{\ell }}(E + i0){{F}_{1}}(c;E) \otimes {{F}_{1}}(c;E) \\ + \frac{g}{{2\gamma }}{{F}_{1}}(c;E) \otimes {{U}_{\ell }}(c;E). \\ \end{gathered} $$

Since doublets F₁(c; E) and ${{U}_{\ell }}$(c; E) are real entire, the derivative of the spectral function can be written as

$$\sigma _{1}^{'}(E) = {{\pi }^{{ - 1}}}{\text{Im}}{{A}_{\ell }}(E + i0).$$

It should be noted that function ${{A}_{\ell }}$(E + i0) is continuous at point γ = $\ell$/2. Therefore, we can set

$$\sigma _{1}^{'}(E){{{\text{|}}}_{{\gamma = \ell /2}}} = \mathop {\lim }\limits_{\gamma \to \ell /2} \sigma _{1}^{'}(E){{{\text{|}}}_{{\gamma \ne \ell /2}}},$$

$$\sigma _{1}^{'}(E){{{\text{|}}}_{{\gamma \ne \ell /2}}} = {{\pi }^{{ - 1}}}\Gamma ( - 2\gamma ){\text{Im}}{{\omega }^{{ - 1}}}(E + i0).$$

At the point where ω(E + i0) differs from zero, the derivative of the spectral function gas form

$$\begin{gathered} \sigma _{1}^{'}(E) = {{\pi }^{{ - 1}}}\Gamma ( - 2\gamma )\operatorname{Im} {{\omega }^{{ - 1}}}(E) \\ = {{\left[ {\frac{{{\text{|}}2E{{{\text{|}}}^{\gamma }}}}{{{\text{|}}\Gamma (ig - \gamma ){\text{|}}\Gamma (2\gamma + 1)}}} \right]}^{2}} \\ \times \frac{{\pi (\kappa - \gamma ){{e}^{{\operatorname{sgn} (E)\pi g}}}}}{{\kappa (\cosh (2\pi g) - \cos (2\pi \gamma ))}} > 0. \\ \end{gathered} $$

Since function ω(E) is nonzero for all E, continuous on (–∞, 0) ∪ (0; ∞), and assumed complex values, the values of E ∈ (–∞, ∞) are points of the continuous spectrum of operator ${{\hat {h}}_{1}}$(Z, j, s). At these points of the spectrum, function $\sigma _{1}^{'}$(E) is positive, $\sigma _{1}^{'}$(E) = $Q_{1}^{2}$(E) > 0, where Q₁(E) = $\sqrt {\sigma _{1}^{'}(E)}$ is the normalization factor for the corresponding (generalized) eigenfunction U₁(ρ; E) of the continuum.

Therefore, the spectrum of each partial radial Hamiltonian ${{\hat {h}}_{1}}$(Z, j, s) in the nonsingular domain is simple (nondegenerate) and consists of only the continuous spectrum,

$${\text{spec}}{{\hat {h}}_{1}}(Z,j,s) = ( - \infty ,\infty ).$$

Orthonormal (generalized) eigenfunctions U_1E(ρ), |E| ≥ 0, of the continuum, which correspond to partial radial Hamiltonians ${{\hat {h}}_{1}}$(Z, j, s), form a complete orthonormal system in space ${{\mathbb{L}}^{2}}$(${{\mathbb{R}}_{ + }}$) in the sense of inversion formulas (see [12]) and have form

$$\begin{gathered} {{U}_{{1E}}}(\rho ) = {{Q}_{1}}(E){{F}_{1}}(\rho ;E), \\ {{Q}_{1}}(E) = \sqrt {\sigma _{1}^{'}(E)} = \frac{{{\text{|2}}E{{{\text{|}}}^{\gamma }}{{e}^{{\operatorname{sgn} (E)\pi g/2}}}}}{{{\text{|}}\Gamma (ig - \gamma ){\text{|}}\Gamma (2\gamma + 1)}} \\ \times \sqrt {\frac{{\pi (\kappa - \gamma )}}{{\kappa [\cosh (2\pi g) - \cos (2\pi \gamma )]}}} . \\ \end{gathered} $$

(21)

5.2 Subcritical Domain

In the subcritical domain of charge variation, Z_s(j) < Z < Z_c(j), relation 0 < ${{\Upsilon }_{ + }}$ = γ < 1/2 holds. Here, estimate (19) for integrals (18) remains valid. Since functions u₁(ρ) ~ ρ^γ and u₂(ρ) ~ ρ^–γ are quadratically integrable at the origin for γ < 1/2, we can write for doublets F ∈ $D_{\check{{h}}\,(Z,j,s)}^{*}$(${{\mathbb{R}}_{ + }}$)

$$F(\rho ) = {{c}_{1}}{{\rho }^{\gamma }} + {{c}_{2}}{{\rho }^{{ - \gamma }}} + O({{\rho }^{{1/2}}}),\quad \rho \to 0.$$

(22)

It follows hence that the asymmetry form is a nontrivial anti-Hermitian quadratic form in the coefficients of asymptotics (22):

$${{\Delta }_{*}}(F) = \frac{{2\gamma }}{g}(\overline {{{c}_{2}}} {{c}_{1}} - \overline {{{c}_{1}}} {{c}_{2}}).$$

This means that the deficiency indices of operator ${{\hat {h}}_{{{\text{in}}}}}$(Z, j, s) are (1, 1), and there exists a family of s.a. extensions ${{\hat {h}}_{{2,\nu }}}$(Z, j, s) of this operator, which are parameterized by parameter ν ∈ [–π/2, π/2], –π/2 ~ π/2, and are characterized by the following s.a. boundary conditions at the origin,

$$\begin{gathered} F(\rho ) = c[{{\rho }^{\gamma }}{{d}_{ + }}\cos \nu + {{\rho }^{{ - \gamma }}}{{d}_{ - }}\sin \nu ] + O({{\rho }^{{1/2}}}), \\ \rho \to 0, \\ \end{gathered} $$

(23)

where c is an arbitrary complex number. Therefore, domain ${{D}_{{{{h}_{{2,\nu }}}(Z,j,s)}}}$ of Hamiltonian ${{\hat {h}}_{{2,\nu }}}$(Z, j, s) has form

$$\begin{matrix} {{D}_{{{h}_{2,\nu }}(Z,j,s)}}=\{F(\rho ):F(\rho )\in D_{\check{{h}}\,(Z,j,s)}^{*}({{\mathbb{R}}_{+}}), \\ F\,\,\text{satisfies}\,\,(23)\}. \\ \end{matrix}$$

Let us now perform the spectral analysis of s.a. operator ${{\hat {h}}_{{2,\nu }}}$(Z, j, s). As the doublet determining the simple guiding functional, we choose real entire doublet

$${{U}_{{2,\nu }}}(\rho ;W) = {{F}_{1}}(\rho ;W)\cos \nu + {{F}_{2}}(\rho ;W)\sin \nu .$$

Let us construct the corresponding Green function:

$$\begin{gathered} G(\rho ,\rho {\kern 1pt} ';W) \\ = \omega _{1}^{{ - 1}}(W)\left\{ \begin{gathered} {{F}_{3}}(\rho ;W) \otimes {{U}_{{2,\nu }}}(\rho {\kern 1pt} ';W),\quad \rho > \rho {\kern 1pt} ', \hfill \\ {{U}_{{2,\nu }}}(\rho ;W) \otimes {{F}_{3}}(\rho {\kern 1pt} ';W),\quad \rho < \rho {\kern 1pt} ', \hfill \\ \end{gathered} \right. \\ \end{gathered} $$

$$\begin{gathered} {{\omega }_{1}}(W) = - {\text{Wr}}({{F}_{1}},{{F}_{3}}) \\ = \omega (W)\cos \nu + {{g}^{{ - 1}}}\Gamma (1 - 2\gamma )\sin \nu , \\ \end{gathered} $$

and write doublet F₃(ρ; W) in form

$${{F}_{3}}(\rho ;W) = \frac{g}{{2\gamma }}[{{\tilde {\omega }}_{1}}{{U}_{{2,\nu }}}(\rho ;W) + {{\omega }_{1}}{{\tilde {U}}_{{2,\nu }}}(\rho ;W)],$$

$${{\tilde {U}}_{{2,\nu }}}(\rho ;W) = - {{F}_{1}}(\rho ;W)\sin \nu + {{F}_{2}}(\rho ;W)\cos \nu ,$$

$${{\tilde {\omega }}_{1}}(W) = \omega (W)\sin \nu - {{g}^{{ - 1}}}\Gamma (1 - 2\gamma )\cos \nu .$$

Then

$$\begin{gathered} G(c - 0,c + 0,E + i0) \\ = \omega _{{2,\nu }}^{{ - 1}}(E + i0){{U}_{{2,\nu }}}(c;E) \otimes {{U}_{{2,\nu }}}(c;E) \\ + \frac{g}{{2\gamma }}{{U}_{{2,\nu }}}(c;E) \otimes {{{\tilde {U}}}_{{2,\nu }}}(c;E), \\ \end{gathered} $$

$$\begin{gathered} {{\omega }_{2}}(W) = \frac{{2\gamma {{\omega }_{1}}(W)}}{{g{{{\tilde {\omega }}}_{1}}(W)}} \\ = \frac{{2\gamma }}{g}\frac{{\omega (W)\cos \nu + {{g}^{{ - 1}}}\Gamma (1 - 2\gamma )\sin \nu }}{{\omega (W)\sin \nu - {{g}^{{ - 1}}}\Gamma (1 - 2\gamma )\cos \nu }}. \\ \end{gathered} $$

Doublets U_{2, ν}(ρ; E) and ${{\tilde {U}}_{{2,\nu }}}$(ρ; E) are real entire, and derivative $\sigma _{{2,\nu }}^{'}$(E) of the spectral function has form

$$\sigma _{{2,\nu }}^{'}(E) = \frac{1}{\pi }\operatorname{Im} \frac{1}{{{{\omega }_{{2,\nu }}}(E + i0)}}.$$

Function ω₂(E) is continuous, differs from zero, and ω_{2, ν}(E + i0) = ω_{2, ν}(E). This gives the following expression for the derivative of the spectral function:

$$\sigma _{{2,\nu }}^{'}(E) = \frac{{A(E)[\cot (\pi g) + \delta \sinh (\pi g)]\sin (2\pi \gamma )}}{{[\cosh (2\pi g) - \cos (2\pi \gamma )]\cos \nu + {{A}^{2}}(E){{{(\pi \gamma {\text{/}}g)}}^{2}}(1 - \cos (2\nu )) + {{B}_{\delta }}A(E)\cosh (2\nu )}},$$

$$A(E) = \frac{{\kappa - \gamma }}{{2\gamma \kappa }}{\text{|}}\Gamma (ig - \gamma ){{{\text{|}}}^{2}}\frac{{\Gamma (1 - 2\gamma )}}{{\Gamma (1 + 2\gamma )}}{\text{|}}2E{{{\text{|}}}^{{2\gamma }}},\quad \delta = \operatorname{sgn} (E),$$

$${{B}_{\delta }} = \frac{{4\pi \gamma }}{g}[{{\cos }^{2}}(\pi \gamma )\sinh (\pi g) - \delta {{\sin }^{2}}(\pi \gamma )\cosh (\pi g)].$$

Function $\sigma _{{2,\nu }}^{'}$(E) is continuous and, hence, the spectrum of operator ${{\hat {h}}_{{2,\nu }}}$(Z, j, s) is continuous and simple,

$${\text{spec}}{{\hat {h}}_{{2,\nu }}}(Z,j,s) = ( - \infty ,\infty ).$$

Ultimately, normalized (generalized) eigenfunctions U_{2, ν}(ρ) corresponding to the continuum and defined by expressions

$$\begin{gathered} {{U}_{{2,\nu ,E}}}(\rho ) = {{Q}_{{2,\nu }}}(E){{U}_{{2,\nu }}}(\rho ;E) \\ = {{Q}_{{2,\nu }}}(E)[{{F}_{1}}(\rho ;E)\cos \nu + {{F}_{2}}(\rho ;E)\sin \nu ], \\ {{Q}_{{2,\nu }}}(E) = \sqrt {\sigma _{{2\nu }}^{'}(E)} , \\ \end{gathered} $$

(24)

form a complete orthonormal system in space ${{\mathbb{L}}^{2}}$(${{\mathbb{R}}_{ + }}$) in the sense of inversion formulas.

5.3 Critical Domain

The critical domain is defined by critical curve Z = Z_c(j), on which g = g_c(j) and ${{\Upsilon }_{ + }}$ = γ = 0. It should be noted that physical values of pairs j (half-integer) and Z (integer) in this domain lie on the critical curve for very special values of the fine structure constant α_F/$\epsilon$ in graphene, α_F/$\epsilon$ = |j|/Z. In particular, if α_F/$\epsilon$ is an irrational number, none of physical pairs (j, Z) lies on the critical curve.

In this domain, the asymptotic behavior of doublets F ∈ $D_{\check{{h}}\,(Z,j,s)}^{*}$(${{\mathbb{R}}_{ + }}$) is specified by formulas (17) with account for the fact that

$${{I}_{1}}(\rho ) = O({{\rho }^{{1/2}}}\ln \rho ),\quad {{I}_{2}}(\rho ) = O({{\rho }^{{1/2}}}\ln \rho ),$$

for γ = 0, ρ → 0:

$$F(\rho ) = {{c}_{1}}{{d}_{ + }} + {{c}_{2}}{{d}_{0}}(\rho ) + O({{\rho }^{{1/2}}}\ln \rho ),\quad \rho \to 0.$$

This leads to the following expression for the symmetry form:

$${{\Delta }_{*}}(F) = g_{c}^{{ - 1}}(j)(\overline {{{c}_{1}}} {{c}_{2}} - \overline {{{c}_{2}}} {{c}_{1}}).$$

Consequently, in this domain, there also exists a one-parametric family of s.a. extensions ${{\hat {h}}_{{3,\nu }}}$(Z, j, s), ν ∈ [–π/2, π/2], –π/2 ~ π/2, which are determined by asymptotic s.a. boundary conditions

$$\begin{gathered} F(\rho ) = c[{{d}_{0}}(\rho )\cos \nu + {{d}_{ + }}\sin \nu ] + O({{\rho }^{{1/2}}}\ln \rho ), \\ \rho \to 0, \\ \end{gathered} $$

(25)

where constant doublet d₊ = d₊|_{γ = 0} = (1, ζ)^T and doublet d₀(ρ) that depends on ρ are defined by relations (17). Therefore, domain ${{D}_{{{{h}_{{3,\nu }}}(Z,j,s)}}}$ of Hamiltonian ${{\hat {h}}_{{3,\nu }}}$(Z, j, s) has form

$$\begin{matrix} {{D}_{{{h}_{3,\nu }}(Z,j,s)}}=\{F(\rho ):F(\rho )\in D_{\check{{h}}\,(Z,j,s)}^{*}({{\mathbb{R}}_{+}}), \\ F\,\,\text{satisfies conditions}\,\,(25)\}. \\ \end{matrix}$$

It should be noted that for ${{\Upsilon }_{ + }}$ = γ = 0, doublets F₁ and F₂ coincide. For this reason, for two linearly independent solutions to radial equations (11) for γ = 0, we choose two linearly independent real entire solutions $F_{1}^{{(0)}}$(ρ; W), $F_{2}^{{(0)}}$(ρ; W), and their linear combination $F_{3}^{{(0)}}$. Namely,

$$F_{1}^{{(0)}}(\rho ;W) = {{F}_{1}}(\rho ;W){{{\text{|}}}_{{\gamma = 0}}} = {{d}_{ + }} + O(\rho ),\quad \rho \to 0,$$

$$\begin{gathered} F_{2}^{{(0)}}(\rho ;W) = {{\partial }_{\gamma }}{{F}_{1}}(\rho ;W){{{\text{|}}}_{{\gamma = 0}}} - \frac{{\zeta (j,s)}}{{{{g}_{c}}(j)}}F_{1}^{{(0)}}(\rho ;W) \\ = {{d}_{0}}(\rho ) + O(\rho \ln \rho ),\quad \rho \to 0. \\ \end{gathered} $$

The corresponding Wronskian has form

$${\text{Wr}}(F_{1}^{{(0)}},F_{2}^{{(0)}}) = g_{c}^{{ - 1}}(j).$$

As an analog of doublet F₃(ρ; W) for γ = 0, we take doublet

$$\begin{gathered} F_{3}^{{(0)}}(\rho ;W) = - \mathop {\lim }\limits_{\gamma \to 0} {{F}_{3}}(\rho ;W) \\ = F_{2}^{{(0)}}(\rho ;W) + f(W)F_{1}^{{(0)}}(\rho ;W), \\ \end{gathered} $$

where

$$f(W) = {{g}_{c}}(j){{\omega }^{{(0)}}}(W),$$

$$\begin{gathered} {{\omega }^{{(0)}}}(W) = - {\text{Wr}}(F_{2}^{{(0)}},F_{3}^{{(0)}}) = g_{c}^{{ - 1}}(j)\left[ {\ln {{{(2{{e}^{{ - i\pi /2}}}W)}}_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}} \right. \\ \left. { + \frac{{\zeta (j,s) + i}}{{2{{g}_{c}}(j)}} + \psi ( - i{{g}_{c}}(j)) - 2\psi (1)} \right], \\ \end{gathered} $$

$$\psi (x) = \frac{{\Gamma '(x)}}{{\Gamma (x)}}.$$

The spectral analysis of operators ${{\hat {h}}_{{3,\nu }}}$(Z, j, s) is performed analogously to the case of the subcritical domain, and we write here only final results. As a doublet determining a simple guiding functional, we choose quantity

$${{U}_{{3,\nu }}}(W) = F_{1}^{{(0)}}(\rho ,W)\sin \nu + F_{2}^{{(0)}}(\rho ,W)\cos \nu ,$$

which is real entire in W and satisfies s.a. asymptotic boundary conditions (25). The Green function of operator ${{\hat {h}}_{{3,\nu }}}$(Z, j, s) is given by

$$\begin{gathered} G(\rho ,\rho {\kern 1pt} ';W) \\ = \omega _{3}^{{ - 1}}(W)\left\{ \begin{gathered} F_{3}^{{(0)}}(\rho ;W) \otimes {{U}_{{3,\nu }}}(\rho ';W),\quad \rho > \rho ', \hfill \\ {{U}_{{3,\nu }}}(\rho ;W) \otimes F_{3}^{{(0)}}(\rho ';W),\quad \rho < \rho ', \hfill \\ \end{gathered} \right. \\ \end{gathered} $$

$$\begin{gathered} {{\omega }_{3}}(W) = - {\text{Wr}}({{U}_{{3,\nu }}},F_{3}^{{(0)}}) \\ = g_{c}^{{ - 1}}(j)[f(W)\cos \nu - \sin \nu ]. \\ \end{gathered} $$

This gives

$$\begin{gathered} G(c - 0,c + 0,E + i0) \\ = \omega _{{3,\nu }}^{{ - 1}}(E + i0){{U}_{{3,\nu }}}(c;E) \otimes {{U}_{{3,\nu }}}(c;E) \\ \, + {{g}_{c}}(j){{U}_{{3,\nu }}}(c;E) \otimes {{{\tilde {U}}}_{{3,\nu }}}(c;E), \\ \end{gathered} $$

$${{\omega }_{{3,\nu }}}(W) = g_{c}^{{ - 1}}(j)\frac{{f(W)\cos \nu - \sin \nu }}{{f(W)\sin \nu + \cos \nu }},$$

$${{\tilde {U}}_{{3,\nu }}}(\rho ;W) = F_{1}^{{(0)}}(\rho ,W)\cos \nu - F_{2}^{{(0)}}(\rho ,W)\sin \nu .$$

Derivative $\sigma _{{3,\nu }}^{'}$(E) of this spectral function has form

$$\sigma _{{3,\nu }}^{'}(E) = \frac{1}{\pi }\operatorname{Im} \frac{1}{{{{\omega }_{{3,\nu }}}(E + i0)}}.$$

Basis function ω_{3, ν}(E) differs from zero for all E, is continuous, and takes complex values. Consequently,

$$\begin{gathered} \sigma _{{3,\nu }}^{'}(E) = \frac{1}{\pi }\operatorname{Im} \frac{1}{{{{\omega }_{{3,\nu }}}(E)}} \\ = - \frac{{{{g}_{c}}(j){{B}_{\delta }}{\text{/}}\pi }}{{(A_{\zeta }^{2} + B_{\beta }^{2}){{{\cos }}^{2}}\nu - {{A}_{\zeta }}\sin (2\nu ) + {{{\sin }}^{2}}\nu }}, \\ \end{gathered} $$

$$\begin{gathered} {{A}_{\zeta }} = \operatorname{Re} f(W) = - 2\psi (1) + \zeta (j,s)g_{c}^{{ - 1}}(j){\text{/}}2 \\ + \ln {\text{|}}2E{\text{|}} + \operatorname{Re} \psi ( - i{{g}_{c}}(j)), \\ \end{gathered} $$

$$\begin{gathered} {{B}_{\delta }} = \operatorname{Im} f(W) = (g_{c}^{{ - 1}}(j) - \pi )\frac{\delta }{2} + \operatorname{Im} \psi ( - i{{g}_{c}}(j)), \\ \delta = \operatorname{sgn} (E). \\ \end{gathered} $$

The simple spectrum of Hamiltonian ${{\hat {h}}_{{3,\nu }}}$(Z, j, s) is given by

$${\text{spec}}{{\hat {h}}_{{3,\nu }}}(Z,j,s) = ( - \infty ,\infty ).$$

Normalized (generalized) eigenfunctions U_{3, ν}(ρ) corresponding to the continuous spectrum have form

$$\begin{gathered} {{U}_{{3,\nu ,E}}}(\rho ) = {{Q}_{{3,\nu }}}(E){{U}_{{3,\nu }}}(\rho ;E) \\ = {{Q}_{{3,\nu }}}(E)[F_{1}^{{(0)}}(\rho ;E)\cos \nu + F_{2}^{{(0)}}(\rho ;E)\sin \nu ], \\ {{Q}_{{3,\nu }}}(E) = \sqrt {\sigma _{{3,\nu }}^{'}(E)} , \\ \end{gathered} $$

(26)

and form a complete orthonormal system in space ${{\mathbb{L}}^{2}}$(${{\mathbb{R}}_{ + }}$) in the sense of the inversion formulas.

5.4 Overcritical Domain

The overcritical domain is determined by conditions Z > Z_c(j) and ${{\Upsilon }_{ + }}$ = iσ, where σ = $\sqrt {{{g}^{2}} - {{j}^{2}}}$ > 0. In this domain, the asymptotic behavior of doublets F ∈ $D_{\check{{h}}\,(Z,j,s)}^{*}$(${{\mathbb{R}}_{ + }}$) is defined by expression (17), where I₁(ρ) = O(ρ^1/2) and I₂(ρ) = O(ρ^1/2) for ρ → 0:

$$F(\rho ) = {{c}_{1}}{{\rho }^{{i\sigma }}}{{d}_{ + }} + {{c}_{2}}{{\rho }^{{ - i\sigma }}}{{d}_{ - }} + O({{\rho }^{{1/2}}}),\quad \rho \to 0.$$

For the asymmetry form, we get

$${{\Delta }_{*}}(F) = 2i\sigma {{g}^{{ - 1}}}({\text{|}}{{c}_{1}}{{{\text{|}}}^{2}} - \,{\text{|}}{{c}_{2}}{{{\text{|}}}^{2}}).$$

In this domain, we are dealing again with a one-parametric family of s.a. extensions ${{\hat {h}}_{{4,\nu }}}$(Z, j, s), ν ∈ [‒π/2, π/2], –π/2 ~ π/2, which are specified by asymptotic s.a. boundary conditions:

$$\begin{gathered} F(\rho ) = c[i{{e}^{{i\nu }}}{{\rho }^{{i\sigma }}}{{d}_{ + }} - i{{e}^{{ - i\nu }}}{{\rho }^{{ - i\sigma }}}{{d}_{ - }}] + O({{\rho }^{{1/2}}}), \\ \rho \to 0. \\ \end{gathered} $$

(27)

It follows hence that domain ${{D}_{{{{h}_{{4,\nu }}}(Z,j,s)}}}$ of Hamiltonian ${{\hat {h}}_{{4,\nu }}}$(Z, j, s) has form

$$\begin{matrix} {{D}_{{{h}_{4,\nu }}(Z,j,s)}}=\{F(\rho ):F(\rho )\in D_{\check{{h}}\,(Z,j,s)}^{*}({{\mathbb{R}}_{+}}) \\ \text{and}\,\,F\,\,\text{satisfies conditions }(27)\}. \\ \end{matrix}$$

Spectral analysis of operators ${{\hat {h}}_{{4,\nu }}}$(Z, j, s) is performed analogously to the previous cases; we will write here only final results. For the doublet determining the simple guiding functional, we choose

$${{U}_{{4,\nu }}}(\rho ;W) = i{{e}^{{i\nu }}}{{F}_{1}}(\rho ,W)\sin \nu - i{{e}^{{ - i\nu }}}{{F}_{2}}(\rho ,W),$$

which is real entire in W and satisfies s.a. asymptotic boundary conditions (27). The Green function of operator ${{\hat {h}}_{{4,\nu }}}$(Z, j, s) is defined as

$$\begin{gathered} G(\rho ,\rho {\kern 1pt} ';W) \\ = \omega _{4}^{{ - 1}}(W)\left\{ \begin{gathered} {{F}_{3}}(\rho ;W) \otimes {{U}_{{4,\nu }}}(\rho {\kern 1pt} ';W),\quad \rho > \rho {\kern 1pt} ', \hfill \\ {{U}_{{4,\nu }}}(\rho ;W) \otimes {{F}_{3}}(\rho {\kern 1pt} ';W),\quad \rho < \rho {\kern 1pt} ', \hfill \\ \end{gathered} \right. \\ \end{gathered} $$

$$\begin{gathered} {{\omega }_{4}}(W) = - {\text{Wr}}({{U}_{{4,\nu }}},{{F}_{3}}) \\ = - i{{e}^{{ - i\nu }}}\frac{{\Gamma (1 - 2i\sigma )}}{g}\left[ {1 - \frac{{g\omega (W)}}{{\Gamma (1 - 2i\sigma )}}{{w}^{{2i\nu }}}} \right], \\ \end{gathered} $$

which gives

$$\begin{gathered} G(c - 0,c + 0,E + i0) \\ = \omega _{{4,\nu }}^{{ - 1}}(E + i0){{U}_{{4,\nu }}}(c;E) \otimes {{U}_{{4,\nu }}}(c;E) \\ - \frac{g}{{4\sigma }}{{U}_{{4,\nu }}}(c;E) \otimes {{{\tilde {U}}}_{{4,\nu }}}(c;E), \\ \end{gathered} $$

$${{\omega }_{{4,\nu }}}(W) = - 4i\sigma {{g}^{{ - 1}}}\frac{{1 - {{e}^{{2i\nu }}}g\omega (W){\text{/}}\Gamma (1 - 2i\sigma )}}{{1 + {{e}^{{2i\nu }}}g\omega (W){\text{/}}\Gamma (1 - 2i\sigma )}},$$

$${{\tilde {U}}_{{4,\nu }}}(\rho ;W) = {{e}^{{i\nu }}}{{F}_{1}}(\rho ,W) + {{e}^{{ - i\nu }}}{{F}_{2}}(\rho ,W).$$

Derivative $\sigma _{{4,\nu }}^{'}$(E) of the spectral function has form

$$\sigma _{{4,\nu }}^{'}(E) = \frac{1}{\pi }\operatorname{Im} \frac{1}{{{{\omega }_{{4,\nu }}}(E + i0)}}.$$

Basis function ω_{4, ν}(E) differs from zero, is continuous, and takes complex values. Then

$$\sigma _{{4,\nu }}^{'}(E) = \frac{1}{\pi }\operatorname{Im} \frac{1}{{{{\omega }_{{4,\nu }}}(E)}} = - \frac{\delta }{{4\sigma }}\frac{{{{A}_{ - }}}}{{{{A}_{ + }} + {{B}_{s}}(\nu ;E)}},$$

$$\begin{gathered} {{A}_{ \pm }} = \frac{{\pi {{g}^{2}}}}{{4\sigma j}}[{{\sinh }^{{ - 1}}}(\pi \sigma ) - {{\cosh }^{{ - 1}}}(\pi \sigma )] \\ \times \,\{ {{e}^{{2\pi \sigma }}}{{\sinh }^{{ - 1}}}(\pi [g - \delta \sigma ]) \pm {{\sinh }^{{ - 1}}}(\pi [g + \delta \sigma ])\} , \\ \end{gathered} $$

$$\begin{gathered} {{B}_{s}}(\nu ;E) = 2{\text{Re}}\{ (j + is\sigma )\Gamma ( - i(g - \sigma ))\Gamma (i(g + \sigma )) \\ \times \,{{\Gamma }^{2}}( - 2i\sigma )\exp (2i\sigma \ln {\text{|}}2E{\text{|}} - 2i\nu )\} , \\ \delta = \operatorname{sgn} (E). \\ \end{gathered} $$

The spectrum of Hamiltonian ${{\hat {h}}_{{4,\nu }}}$(Z, j, s) is simple and is given by

$${\text{spec}}{{\hat {h}}_{{4,\nu }}}(Z,j,s) = ( - \infty ,\infty ).$$

Normalized (generalized) eigenfunctions U_{4, ν}(ρ) corresponding to the continuous spectrum have form

$$\begin{gathered} {{U}_{{4,\nu }}}(\rho ) = {{Q}_{{4,\nu }}}(E){{U}_{{4,\nu }}}(\rho ;E) \\ = i{{Q}_{{4,\nu }}}(E)[{{e}^{{i\nu }}}{{F}_{1}}(\rho ,W) - {{e}^{{ - i\nu }}}{{F}_{2}}(\rho ,W)], \\ {{Q}_{{4,\nu }}}(E) = \sqrt {\sigma _{{4,\nu }}^{'}(E)} . \\ \end{gathered} $$

(28)

These functions form a complete orthonormal system in space ${{\mathbb{L}}^{2}}$(${{\mathbb{R}}_{ + }}$) in the sense of inversion formulas.

6 SELF-ADJOINT TOTAL HAMILTONIANS

In Sections 5.1–5.4, we have constructed all s.a. partial radial Hamiltonians $\hat {h}$(Z, j, s) for all values of charge Z as s.a. extensions of initial symmetric operators ${{\hat {h}}_{{{\text{in}}}}}$(Z, j, s) for any values of j and s and have analyzed spectral problems for these Hamiltonians.

We have shown that in the singular domain of variation of the impurity charge, s.a. partial radial Hamiltonians $\hat {h}$(Z, j, s) as s.a. extensions of initial symmetric operators ${{\hat {h}}_{{{\text{in}}}}}$(Z, j, s) are not defined unambiguously for each triple of parameters Z, j, s. Since deficiency indices m₊ and m_– of each symmetric operator ${{\hat {h}}_{{{\text{in}}}}}$(Z, j, s) equal (1, 1) and, hence, there exists a one-parametric family of extensions, such a family is parameterized by parameter ν ∈ [–π/2, π/2], –π/2 ~ π/2. Partial radial Hamiltonians with identical values of Z, j, s, but with different values of ν are associated with the same differential expression $\check{{h}}\,$(Z, j, s), but differ in their domains, which are the subsets of natural domain $D_{\check{{h}}\,(Z,j,s)}^{*}$(${{\mathbb{R}}_{ + }}$) for $\check{{h}}\,$(Z, j, s) and are specified by certain asymptotic boundary conditions at the origin, which contain explicitly parameter ν.

Like in the “massive” case [10] and in the 3D Coulomb problem [12], the singular domain is divided into three subsets differing in the form of asymptotic s.a. boundary conditions at the origin. In all three subdomains, for each operator ${{\hat {h}}_{{k,\nu }}}$, there exists a simple guiding functional. It follows hence that the spectrum of operator ${{\hat {h}}_{{k,\nu }}}$ is simple (nondegenerate in the terminology adopted in physics). In this case, the main instrument of spectral analysis is spectral function σ_k,ν(E) and its (generalized) derivative $\sigma _{{k,\nu }}^{'}$(E), where E, E ∈ $\mathbb{R}$, is a real-valued variable.

Expression (9) makes it possible to reconstruct all s.a. operators ${{\hat {H}}_{s}}$ associated with differential expression (3) for any value of parameter g and to describe the solution of corresponding spectral problems for all Hamiltonians ${{\hat {H}}_{s}}$.

Let us introduce, following [10], the sets of charge values for which the spectral problem is described similarly. These sets are defined by functions g_c(k) and g_s(k), which take the following values at characteristic points k = l + 1/2, l ∈ ${{\mathbb{Z}}_{ + }}$:

$${{g}_{c}}(k) = k,\quad {{g}_{s}}(k + 1) = \sqrt {{{{(k + 1)}}^{2}} - \frac{1}{4}} $$

and satisfy the following inequalities:

$${{g}_{c}}(k) < {{g}_{s}}(k + 1) < {{g}_{c}}(k + 1) < {{g}_{s}}(k + 2).$$

(29)

We introduce intervals Δ(k):

$$\Delta (0) = (0;1{\text{/}}2),$$

$$\Delta (k) = ({{g}_{c}}(k),{{g}_{c}}(k + 1)] = (k,k + 1],$$

$$(0,\infty ) = \Delta (0) \cup \left\{ {{{g}_{c}}\left( { \pm \frac{1}{2}} \right)} \right\} \cup \left( {\bigcup\limits_k^{} {\Delta (k)} } \right).$$

As follows from inequalities (29), each interval Δ(k) can be represented in form Δ(k) = ∪_{i = 1, 2, 3}Δ_i(k), where

$${{\Delta }_{1}}(k) = ({{g}_{c}}(k),{{g}_{s}}(k + 1)],$$

$${{\Delta }_{2}}(k) = ({{g}_{s}}(k + 1),{{g}_{c}}(k + 1)),$$

$${{\Delta }_{3}}(k) = \{ {{g}_{c}}(k + 1)\} .$$

In accordance with this decomposition, we define three sets G_i = ${{ \cup }_{k}}{{\Delta }_{i}}$(k), i = 1, 2, 3, and variations of coupling parameters g such that any value of g > g_c(±1/2) = 1/2 can be put in correspondence with a pair of two integers, k and i = 1, 2, 3: g ⇒ (k, i), such that g ∈ G_i. As follows from the results of Sections 5.1 and 5.2, we obtain the following classification:

$$\begin{gathered} {{U}_{E}}(\rho ) = \left\{ \begin{gathered} {{U}_{{4,\nu ,E}}}(\rho ),\quad {\text{|}}j{\text{|}} \leqslant k, \hfill \\ {{U}_{{1E}}}(\rho ),\quad {\text{|}}j{\text{|}} \geqslant k + 1, \hfill \\ \end{gathered} \right.\quad g \in {{\Delta }_{1}}(k), \hfill \\ {{U}_{E}}(\rho ) = \left\{ \begin{gathered} {{U}_{{4,\nu ,E}}}(\rho ),\quad {\text{|}}j{\text{|}} \leqslant k, \hfill \\ {{U}_{{2,\nu ,E}}}(\rho ),\quad {\text{|}}j{\text{|}} = k + 1, \hfill \\ {{U}_{{1E}}}(\rho ),\quad {\text{|}}j{\text{|}} > k + 1, \hfill \\ \end{gathered} \right.\quad g \in {{\Delta }_{2}}(k), \hfill \\ \end{gathered} $$

$${{U}_{E}}(\rho ) = \left\{ \begin{gathered} {{U}_{{4,\nu ,E}}}(\rho ),\quad {\text{|}}j{\text{|}} \leqslant k, \hfill \\ {{U}_{{3,\nu ,E}}}(\rho ),\quad {\text{|}}j{\text{|}} = k + 1, \hfill \\ {{U}_{{1E}}}(\rho ),\quad {\text{|}}j{\text{|}} > k + 1, \hfill \\ \end{gathered} \right.\quad g \in {{\Delta }_{3}}(k),$$

(30)

$$\begin{gathered} {{U}_{E}}(\rho ) = \left\{ \begin{gathered} {{U}_{{2,\nu ,E}}}(\rho ),\quad {\text{|}}j{\text{|}} = 1{\text{/}}2, \hfill \\ {{U}_{{1E}}}(\rho ),\quad {\text{|}}j{\text{|}} > 1{\text{/}}2, \hfill \\ \end{gathered} \right.\quad g \in \Delta (0), \hfill \\ {{U}_{E}}(\rho ) = \left\{ \begin{gathered} {{U}_{{3,\nu ,E}}}(\rho ),\quad {\text{|}}j{\text{|}} = 1{\text{/}}2, \hfill \\ {{U}_{{1E}}}(\rho ),\quad {\text{|}}j{\text{|}} > 1{\text{/}}2, \hfill \\ \end{gathered} \right.\quad g \in {{g}_{c}}( \pm 1{\text{/}}2). \hfill \\ \end{gathered} $$

We can now describe the spectral problem for all s.a. Dirac Hamiltonians for all values of g. It should be noted that inequality g > g_s(±1/2) = 0 and (9) lead to the following important fact: total s.a. Dirac Hamiltonian ${{\hat {H}}_{s}}$ is not defined unambiguously for each charge Z = ($\epsilon g$)/α_F.

Let us consider eigenvectors Ψ_sj(r) for s.a. Dirac Hamiltonian ${{\hat {H}}_{s}}$, which satisfy the following set of equations (see Section 3):

$${{\check{{H}}}_{s}}{{\Psi }_{sj}}(\mathbf{r})=E{{\Psi }_{sj}}(\mathbf{r}),\quad {{\hat{J}}_{s}}{{\Psi }_{sj}}(\mathbf{r})=j{{\Psi }_{sj}}(\mathbf{r}),$$

and have form Ψ_sj(r) = V_sjU_E(ρ) (see relation (6)).

For any coupling constant g, the energy spectrum of any s.a. Dirac Hamiltonian ${{\hat {H}}_{s}}$ consists of a continuum occupying axis (–∞, ∞). All doublets U_E(ρ) depend on extension parameters, quantum numbers j, parameter s, and coupling constant g in accordance with relations (30). It should be noted that the extension parameters depend on quantum numbers j as well as on parameter s.

7 LOCAL DENSITY OF STATES

The local density of states per unit surface area in graphene is defined as

$$\begin{gathered} N(\rho ;E) = \sum\limits_{E'}^{} {{\text{|}}\Psi (\rho ;E{\kern 1pt} '){{{\text{|}}}^{2}}} \delta (E - E{\kern 1pt} ') = \sum\limits_{j = - \infty }^\infty {{{n}_{j}}(\rho ;E),} \\ {{n}_{j}}(\rho ;E) = {\text{|}}{{\Psi }_{{sj}}}(\rho ;E){{{\text{|}}}^{2}} \\ \end{gathered} $$

(31)

(see [8]). Quantity N(ρ; E)dE has the meaning of the probability of finding a quasiparticle on an elementary surface area of graphene at a given point (ϕ, ρ) in the energy range from E to E + dE. It should be noted that there exists another definition of the local density of states in graphene, which is based on the calculation of the imaginary part of the Green function [18]. Substituting expression (5) into (31), we get

$${{n}_{j}}(\rho ;E) = \frac{1}{{2\pi r}}{\text{|}}{{U}_{E}}(\rho ){{{\text{|}}}^{2}},$$

where doublets U_E(ρ) for different values of charge g and angular momentum j are defined by expression (30). Equality $\check{{h}}\,$(Z, j, s) = $\check{{h}}\,$(Z, –j, –s) implies that n_j(ρ; E)|_{s = +1} = n_–j(ρ; E)|_{s = –1}. It can be seen from this relation that sum n_j(ρ; E) + n_–j(ρ; E) is independent of the choice of parameter s = ±1. Therefore, the symmetry between the choice of two sublattices in graphene in the behavior of the local density of states (31) is preserved.

Let us first consider the case of small values of coupling parameter g ∈ Δ(0). In this case, the local density of states is determined only the noncritical and subcritical domains of charge variation:

$$\begin{gathered} N(\rho ;E) = {{N}_{0}}(\rho ,{{\nu }_{1}};E) = \sum\limits_{|j| > 1/2}^{} {n_{j}^{1}(\rho ;E)} \\ \, + n_{{j = - 1/2}}^{{2,{{\nu }_{1}}}}(\rho ;E) + n_{{j = 1/2}}^{{2,{{\nu }_{1}}}}(\rho ;E), \\ \end{gathered} $$

(32)

where partial local density of states $n_{j}^{1}$(ρ; E) corresponds to the noncritical domain,

$$\begin{gathered} n_{j}^{1}(\rho ;E) = \frac{1}{{2\pi \rho }}{\text{|}}{{U}_{{1E}}}(\rho ){{{\text{|}}}^{2}} = {\text{|}}{{F}_{1}}(\rho ;E{\text{)}}{{{\text{|}}}^{2}}\sigma _{1}^{'}(E) = \frac{{{{{(2\rho {\text{|}}E{\text{|}})}}^{{2\gamma }}}{\text{|}}{{\Phi }_{\gamma }}(\rho ){{{\text{|}}}^{2}}{{e}^{{\pi g\delta }}}}}{{\rho {{\Gamma }^{2}}(1 + 2\gamma ){\text{|}}\Gamma (ig - \gamma ){{{\text{|}}}^{2}}[\cosh (2\pi g) - \cos (2\pi \gamma )]}}, \\ {{\Phi }_{\gamma }}(\rho ) = \Phi (\gamma - ig,1 + 2\gamma , - 2iE\rho ), \\ \end{gathered} $$

(33)

while $n_{j}^{{2,{{\nu }_{1}}}}$(ρ; E) corresponds to partial Hamiltonian ${{\hat {h}}_{{2,{{\nu }_{1}}}}}$(Z, j, s) in the subcritical domain, which is parameterized by parameter ν₁ of the s.a. extension,

$$n_{j}^{{2,{{\nu }_{1}}}}(\rho ;E) = \frac{1}{{2\pi \rho }}{\text{|}}{{U}_{{2{{\nu }_{1}},E}}}(\rho ){{{\text{|}}}^{2}}\frac{1}{{2{{\pi }^{2}}\rho }}\frac{{{{\varrho }_{\gamma }}(\rho ){{{\cos }}^{2}}{{\nu }_{1}} + {{\varrho }_{{ - \gamma }}}(\rho ){{{\sin }}^{2}}{{\nu }_{1}} + \operatorname{Re} (\varrho (\rho ))\sin (2{{\nu }_{1}}){\text{/}}g}}{{{{\varrho }_{\gamma }}(\infty ){{{\cos }}^{2}}{{\nu }_{1}} + {{\varrho }_{{ - \gamma }}}(\infty ){{{\sin }}^{2}}{{\nu }_{1}} + \operatorname{Re} (\varrho (\infty ))\sin (2{{\nu }_{1}}){\text{/}}g}},$$

$$\begin{gathered} {{\varrho }_{\gamma }}(\rho ) = \frac{{{\text{|}}{{\Phi }_{\gamma }}(\rho ){{{\text{|}}}^{2}}}}{{j + s\gamma }}{{\rho }^{{2\gamma }}},\quad \varrho (\rho ) = \frac{{g - i\gamma }}{j}{{\Phi }_{\gamma }}(\rho )\Phi _{{ - \gamma }}^{*}(\rho ), \\ {{\varrho }_{\gamma }}(\infty ) = \mathop {\lim }\limits_{\rho \to \infty } {{\varrho }_{\gamma }}(\rho ) = \frac{{{{\Gamma }^{2}}(1 + 2\gamma ){{e}^{{ - \delta \pi g}}}{\text{|}}2E{{{\text{|}}}^{{ - 2\gamma }}}}}{{(j + s\gamma )\Gamma (1 - ig + \gamma )\Gamma (1 + ig + \gamma )}}, \\ \end{gathered} $$

(34)

$$\varrho (\infty ) = \mathop {\lim }\limits_{\rho \to \infty } \varrho (\rho ) = \frac{{2\gamma }}{j}\frac{{\sinh (\pi [g - i\gamma ])}}{{\sin (2\pi \gamma )}}{{e}^{{ - \delta \pi (g + i\gamma )}}}.$$

In the limit g → 0, quantity $n_{j}^{1}$(ρ; E) can be expressed in terms of the Bessel functions:

$$\mathop {\lim }\limits_{g \to 0} n_{j}^{1}(\rho ;E) = [{{J}_{{|j| - 1/2}}}(E\rho ) + {{J}_{{|j| + 1/2}}}(E\rho )]\frac{{{\text{|}}E{\text{|}}}}{{4\pi }},$$

and the summation over j (disregarding the contribution $n_{j}^{{2,{{\nu }_{1}}}}$(ρ; E) from the subcritical domain) leads to the following expression for the free density of states of quasiparticles in graphene:

$$\mathop {\lim }\limits_{g \to 0} \sum\limits_{j = - \infty }^\infty {n_{j}^{1}(\rho ;E) = \frac{{{\text{|}}E{\text{|}}}}{{2\pi }}.} $$

(35)

Figure 1 shows the dependences of density of states N₀(ρ, ν₁; E) on the quasiparticle energy for ρ = 1, g = 0.3. For low energies (E → 0), we have

$$\begin{gathered} n_{j}^{1}(\rho ;E)\sim \frac{{{{{(2\rho {\text{|}}E{\text{|}})}}^{{2\gamma }}}{{e}^{{\pi g\delta }}}}}{\rho }{{\Gamma }^{{ - 2}}}(1 + 2\gamma {\text{)|}}\Gamma (ig - \gamma ){{{\text{|}}}^{{ - 2}}} \\ = {{[\cosh (2\pi g) - \cos (2\pi \gamma )]}^{{ - 1}}}. \\ \end{gathered} $$

Fig. 1.

Energy dependences of local density of states N₀(ρ, ν₁; E) for ρ = 1, g = 0.3, and ν₁ = 0, π/6. The blue line describes the local density of states in zero field.

It should be noted that if parameter ν₁ of the s.a. extension is zero, the contribution from the subcritical domain coincides with the contribution from the noncritical domain,

$$n_{j}^{{2,{{\nu }_{1}}}}(\rho ;E){{{\text{|}}}_{{{{\nu }_{1}} = 0}}} = n_{j}^{1}(\rho ;E)$$

and the density of states is determined by the noncritical domain alone,

$${{N}_{0}}(\rho ,0;E) = \sum\limits_j^{} {n_{j}^{1}(\rho ;E).} $$

If parameter ν₁ differs from zero, the contribution of terms

$${{N}_{{{\text{subcr}}}}}(\rho ,{{\nu }_{1}},E) = n_{{j = - 1/2}}^{{2,{{\nu }_{1}}}}(\rho ;E) + n_{{j = 1/2}}^{{2,{{\nu }_{1}}}}(\rho ;E)$$

to local density of states N₀(ρ, ν₁; E) leads to the emergence of local peaks even for small impurity charges (see Figs. 1 and 2). Figure 2 shows the energy dependences of quantity N_subcr(ρ, ν₁; E) for different values of parameter ν₁ for ρ = 1, g = 0.3. It can be seen that function N_subcr(ρ, ν₁; E) has a clearly manifested local peak for various values of parameter ν₁ differing from zero.

Fig. 2.

Energy dependences of contribution N_subcr(ρ, ν₁; E) for ρ = 1, g = 0.3, and different values of s.a. extension parameter ν₁.

In the vicinity of point E = 0, quantity N_subcr(ρ, ν₁; E) has asymptotic form

$$\begin{gathered} {{N}_{{{\text{subcr}}}}}(\rho ,{{\nu }_{1}},E) \\ \sim \frac{1}{{C(g)\rho }}\left[ {4{\text{tan}}\nu + 2{{\rho }^{{2\gamma }}} + \frac{{(1 - 2{{g}^{2}}){\text{ta}}{{{\text{n}}}^{2}}\nu }}{{{{g}^{2}}}}{{\rho }^{{ - 2\gamma }}}} \right] \\ \times \,{\text{|}}2E{{{\text{|}}}^{{2\gamma }}}{{e}^{{\delta \pi g}}} + O({\text{|}}2E{{{\text{|}}}^{{2\gamma + 1}}}), \\ \gamma = \sqrt {1{\text{/}}4 - {{g}^{2}}} < 1{\text{/}}2, \\ \end{gathered} $$

$$C(g) = [\cosh (2\pi g) - \cos (2\pi \gamma )]\Gamma {{(1 + 2\gamma )}^{2}}{\text{|}}\Gamma (ig - \gamma ){{{\text{|}}}^{2}}.$$

It follows hence that even for g → 0 and E → 0 for ν₁ ≠ 0, the contribution of the subcritical domain differs from expression (35) for the local density of states of a free particle in the presence of divergence in g:

$${{N}_{{{\text{subcr}}}}}(\rho ,{{\nu }_{1}},E)\sim \frac{{{\text{|}}E{\text{|}}}}{{2\pi }}\left[ {1 + \frac{{2\tan \nu }}{\rho } + \frac{1}{2}{{{\left( {\frac{{\tan \nu }}{{g\rho }}} \right)}}^{2}}} \right],$$

$$E \to 0,\quad g \to 0.$$

Nevertheless, for any value of parameter ν₁, quantity N_subcr(ρ, ν₁; E) for E → 0 behaves as |E|^2γ to within a factor, which agrees with the results obtained in [8]. Using representation (14), we can write the expression for $n_{j}^{1}$(ρ; E) in terms of the Coulomb functions (which also agrees with the results obtained in [8]):

$$n_{j}^{1}(\rho ;E) = \frac{1}{{2{{\pi }^{2}}\rho }}\frac{{{{j}^{2}}}}{{{{\gamma }^{2}}}}\left( {\mathcal{F}_{{\gamma - 1}}^{2} + \mathcal{F}_{\gamma }^{2} + \frac{{2\tilde {g}}}{{{\text{|}}j{\text{|}}}}{{\mathcal{F}}_{{\gamma - 1}}}{{\mathcal{F}}_{\gamma }}} \right),$$

$${{\mathcal{F}}_{\alpha }} = {{\mathcal{F}}_{\alpha }}( - \tilde {g};{\text{|}}E{\text{|}}\rho ).$$

For coupling parameters g = g_c(±1/2), we have the contribution to the local density of states from the critical domain:

$$\begin{gathered} N(\rho ;E) = {{N}_{1}}(\rho ,{{\nu }_{2}};E) \\ = \sum\limits_{|j| > 1/2}^{} {n_{j}^{1}(\rho ;E)} + n_{{j = - 1/2}}^{{3,{{\nu }_{2}}}}(\rho ;E) + n_{{j = 1/2}}^{{3,{{\nu }_{2}}}}(\rho ;E), \\ \end{gathered} $$

(36)

where $n_{j}^{{3,{{\nu }_{2}}}}$(ρ; E) corresponds to partial Hamiltonian ${{\hat {h}}_{{3,{{\nu }_{2}}}}}$(Z, j, s) in the critical domain, which is parameterized by s.a. extension parameter ν₂,

$$n_{j}^{{3,{{\nu }_{2}}}}(\rho ;E) = \frac{1}{{2\pi \rho }}{\text{|}}{{U}_{{3,{{\nu }_{2}},E}}}(\rho ){{{\text{|}}}^{2}} = \frac{1}{{2{{\pi }^{2}}\rho }}\frac{{\varrho _{1}^{{(0)}}(\rho ){\text{si}}{{{\text{n}}}^{2}}{{\nu }_{2}} + \varrho _{2}^{{(0)}}(\rho ){\text{co}}{{{\text{s}}}^{2}}{{\nu }_{2}} + {\text{Re}}\varrho _{3}^{{(0)}}(\rho ){\text{sin}}(2{{\nu }_{2}})}}{{\varrho _{1}^{{(0)}}(\infty ){\text{si}}{{{\text{n}}}^{2}}{{\nu }_{2}} + \varrho _{2}^{{(0)}}(\infty ){\text{co}}{{{\text{s}}}^{2}}{{\nu }_{2}} + {\text{Re}}\varrho _{3}^{{(0)}}(\infty ){\text{sin}}(2{{\nu }_{2}})}},$$

$$\varrho _{1}^{{(0)}}(\rho ) = {\text{|}}F_{1}^{{(0)}}(\rho ){{{\text{|}}}^{2}},\quad \varrho _{1}^{{(0)}}(\infty ) = - {{[{{g}_{c}}(j)\operatorname{Im} f(W)]}^{{ - 1}}},$$

$$\varrho _{2}^{{(0)}}(\rho ) = {\text{|}}F_{2}^{{(0)}}(\rho ){{{\text{|}}}^{2}},\quad \varrho _{2}^{{(0)}}(\infty ) = - g_{c}^{{ - 1}}(j)\frac{{{\text{|}}f(W){{{\text{|}}}^{2}}}}{{\operatorname{Im} f(W)}},$$

$$\varrho _{3}^{{(0)}}(\rho ) = F_{1}^{{(0)}}(\rho )F_{2}^{{(0)*}}(\rho ),$$

$$\operatorname{Re} \varrho _{3}^{{(0)}}(\infty ) = g_{c}^{{ - 1}}(j)\frac{{\operatorname{Re} f(W)}}{{\operatorname{Im} f(W)}}.$$

The contribution from the critical domain for E → 0 diverges as the square of the logarithm:

$$\begin{gathered} n_{{j = - 1/2}}^{{3,{{\nu }_{2}}}}(\rho ;E) + n_{{j = 1/2}}^{{3,{{\nu }_{2}}}}(\rho ;E) \\ \sim \frac{{2 + {{{(\ln \rho + \tan \nu )}}^{2}}}}{{{{\pi }^{2}}\rho }}{\text{|}}\operatorname{Im} f(W){\text{|}}{{\ln }^{{ - 2}}}(2{\text{|}}E{\text{|}}). \\ \end{gathered} $$

Figure 3 shows the dependences of density of states N₁(ρ, ν₂; E) on the quasiparticle energy for ρ = 1, g = 0.5.

Fig. 3.

Energy dependences of local density of states N₁(ρ, ν₂; E) for ρ = 1, g = 0.5, and ν₂ = 0, π/6. The blue line describes the local density of states in zero field.

For half-integer values of parameter g ∈ Δ₃(k), g = g_c(k), k = 3/2, 5/2, …, the contribution to the local density of states comes from the subcritical and overcritical domains; therefore, this density of states is parameterized by two s.a. extension parameters ν₂ and ν₃:

$$\begin{gathered} N(\rho ;E) = {{N}_{2}}(\rho ,{{\nu }_{2}},{{\nu }_{3}};E) \\ = \sum\limits_{|j| > k + 1}^\infty {n_{j}^{1}} (\rho ,{{\nu }_{2}},{{\nu }_{3}};E) + n_{{ - (k + 1)}}^{{3,{{\nu }_{2}}}}(\rho ;E) + n_{{k + 1}}^{{3,{{\nu }_{2}}}}(\rho ;E) \\ + \sum\limits_{|j| \leqslant k}^{} {n_{j}^{{4,{{\nu }_{3}}}}(\rho ;E),} \\ \end{gathered} $$

(37)

where $n_{j}^{{4,{{\nu }_{3}}}}$(ρ; E) corresponds to partial Hamiltonian ${{\hat {h}}_{{4,{{\nu }_{3}}}}}$(Z, j, s) in the overcritical domain, which is parameterized by s.a. extension parameter ν₃,

$$\begin{gathered} n_{j}^{{4,{{\nu }_{3}}}}(\rho ;E) = \frac{1}{{2\pi \rho }}{\text{|}}{{U}_{{4,{{\nu }_{3}},E}}}(\rho ){{{\text{|}}}^{2}}\sigma _{{4,{{\nu }_{3}}}}^{'}(E) \\ = \frac{1}{{2{{\pi }^{2}}\rho }}\frac{{{{\varrho }_{1}}(\rho ) - \operatorname{Re} \{ {{\varrho }_{2}}(\rho )\exp (2i[{{\nu }_{3}} + \sigma \ln (\rho )])\} }}{{{{\varrho }_{1}}(\infty ) - \operatorname{Re} \{ {{\varrho }_{2}}(\infty )\exp (2i[{{\nu }_{3}} + \sigma \ln (\rho )])\} }}. \\ \end{gathered} $$

(38)

Here,

$${{\varrho }_{1}}(\rho ) = \frac{g}{{2j}}\left[ {\left( {1 - \frac{\sigma }{g}} \right){\text{|}}{{\Phi }_{{ - i\sigma }}}(\rho ){{{\text{|}}}^{2}} + \left( {1 + \frac{\sigma }{g}} \right){\text{|}}{{\Phi }_{{i\sigma }}}(\rho ){{{\text{|}}}^{2}}} \right],$$

$${{\varrho }_{2}}(\rho ) = \frac{{j - is\sigma }}{g}{{\Phi }_{{i\sigma }}}(\rho )\Phi _{{ - i\sigma }}^{*}(\rho )$$

and

$$\begin{gathered} {{\varrho }_{1}}(\infty ) = \mathop {\lim }\limits_{\rho \to \infty } {{\varrho }_{1}}(\rho ) \\ = - \frac{{\delta \sigma }}{j}\frac{{{{e}^{{ - \pi \sigma }}}\sinh (\pi [g - \delta \sigma ]) + {{e}^{{\pi \sigma }}}\sinh (\pi [g + \delta \sigma ])}}{{{{e}^{{ - \pi \sigma }}}\sinh (\pi [g - \delta \sigma ]) - {{e}^{{\pi \sigma }}}\sinh (\pi [g + \delta \sigma ])}}, \\ \end{gathered} $$

$$\begin{gathered} {{\varrho }_{2}}(\infty ) = \mathop {\lim }\limits_{\rho \to \infty } {{\varrho }_{2}}(\rho ) \\ = \frac{{j - is\sigma }}{g}\frac{{{{\Gamma }^{2}}(1 + 2i\sigma ){{e}^{{ - \delta \pi g}}}}}{{\Gamma (1 - i(g - \sigma ))\Gamma (1 + i(g + \sigma ))}}. \\ \end{gathered} $$

In terms of the Coulomb wavefunctions, we have

$$n_{j}^{{4,{{\nu }_{3}}}}(\rho ;E) = \frac{1}{{2{{\pi }^{2}}\rho }}\frac{{{{{\tilde {\varrho }}}_{1}}(\rho ) - s\operatorname{sgn} (jE)\operatorname{Re} \{ {{{\tilde {\varrho }}}_{2}}(\rho )\exp (2i[{{\nu }_{3}} + \sigma \ln (\rho )])\} }}{{{{{\tilde {\varrho }}}_{1}}(\infty ) - s\operatorname{sgn} (jE)\operatorname{Re} \{ {{{\tilde {\varrho }}}_{2}}(\infty )\exp (2i[{{\nu }_{3}} + \sigma \ln (\rho )])\} }},$$

$${{\tilde {\varrho }}_{1}}(\rho ) = {\text{|}}{{\mathcal{F}}_{{i\sigma }}}{{{\text{|}}}^{2}} + \,{\text{|}}{{\mathcal{F}}_{{i\sigma - 1}}}{{{\text{|}}}^{2}} + \frac{{2{\text{|}}j{\text{|}}}}{{\tilde {g}}}\operatorname{Re} [\mathcal{F}_{{i\sigma - 1}}^{*}{{\mathcal{F}}_{{i\sigma }}}],$$

$${{\tilde {\varrho }}_{2}}(\rho ) = \left( {2{{\mathcal{F}}_{{i\sigma - 1}}}{{\mathcal{F}}_{{i\sigma }}} + \frac{{{\text{|}}j{\text{|}}}}{{\tilde {g}}}[\mathcal{F}_{{i\sigma }}^{2} + \mathcal{F}_{{i\sigma - 1}}^{2}]} \right)\frac{{sj - i\sigma }}{g}\frac{{\Gamma (2i\sigma )}}{{\Gamma ( - 2i\sigma )}}\exp [ - 2i\sigma \ln (2\rho {\text{|}}E{\text{|}})],$$

$${{\mathcal{F}}_{{i\sigma }}} = {{\left( {\frac{{\tilde {g} + \sigma }}{{\tilde {g} - \sigma }}} \right)}^{{1/4}}}{{\mathcal{F}}_{{i\sigma }}}( - \tilde {g};{\text{|}}E{\text{|}}\rho ),$$

$${{\mathcal{F}}_{{i\sigma - 1}}} = {{\left( {\frac{{\tilde {g} - \sigma }}{{\tilde {g} + \sigma }}} \right)}^{{1/4}}}{{\mathcal{F}}_{{i\sigma - 1}}}( - \tilde {g};{\text{|}}E{\text{|}}\rho ).$$

It follows from expression (38) that a change in the s.a. extension parameter leads to phase shift δ_j(ρ). Figure 4 shows the dependences of density of states N₂(ρ, ν₂, ν₃; E) on the quasiparticle energy for ρ = 1, g = 3.5.

Fig. 4.

Energy dependences of local density of states N₂(ρ, ν₂, ν₃; E) for ρ = 1, g = 3.5, and ν₂ = ν₃ = 0 and ν₂ = π/4, ν₃ = π/3. The blue line describes the local density of states in zero field.

Let us suppose that there exists a half-integer k > 1/2, such that g ∈ Δ₁(k) = [g_c(k), g_s(k + 1)]. Then the contribution to the density of states comes only from the overcritical domain:

$$\begin{gathered} N(\rho ;E) = {{N}_{3}}(\rho ,{{\nu }_{3}};E) \\ = \sum\limits_{|j| \geqslant k + 1}^{} {n_{j}^{1}(\rho ;E) + \sum\limits_{|j| < k}^{} {n_{j}^{{4,{{\nu }_{3}}}}(\rho ;E)} } . \\ \end{gathered} $$

(39)

Figure 5 shows the dependences of density of states N₃(ρ, ν₃; E) on the quasiparticle energy for ρ = 3, g = 3.7.

Fig. 5.

Energy dependences of local density of states N₃(ρ, ν₃; E) for ρ = 3, g = 3.7, and ν₃ = 0, π/3. The blue line describes the local density of states in zero field.

If, however, there exists a half-integer k > 1/2 such that g ∈ Δ₂(k) = [g_s(k + 1), g_c(k + 1)], the local density of states is parameterized by two s.a. extension parameters ν₁ and ν₃:

$$\begin{gathered} N(\rho ;E) = {{N}_{4}}(\rho ,{{\nu }_{1}},{{\nu }_{3}};E) \\ = \sum\limits_{|j| > k + 1}^{} {n_{j}^{1}(\rho ;E) + n_{{ - (k + 1)}}^{{2,{{\nu }_{1}}}}(\rho ;E)} \\ + \,n_{{k + 1}}^{{2,{{\nu }_{1}}}}(\rho ;E) + \sum\limits_{|j| < k}^{} {n_{j}^{{4,{{\nu }_{3}}}}(\rho ;E).} \\ \end{gathered} $$

(40)

Figure 6 shows the dependences of density of states N₄(ρ, ν₁, ν₃; E) on the quasiparticle energy for ρ = 3 and g = 3.48.

Fig. 6.

Energy dependences of local density of states N₄(ρ, ν₁, ν₃; E) for ρ = 3, g = 3.48 for ν₁ = ν₃ = 0 and ν₁ = π/4, ν₃ = π/2. The blue line describes the local density of states in zero field.

It should be noted that for all values of impurity charge Z, we observe the electron–hole symmetry breaking: the local density of states behaves differently for positive and negative energy values. The attractive Coulomb potential of the impurity leads to a decrease in the local density of states for negative (hole) values of energy E < 0 relative to the states with positive energy E > 0. This effect is manifested most strongly near the impurity.

It should also be noted that because of exponential factor exp(δπg) in expression (33), the contribution of the nonsingular domain is suppressed exponentially for negative energy values, and the main contribution to local densities of states N₃(ρ, ν₃; E) and N₄(ρ, ν₁, ν₃; E) comes from a finite number of terms in $\sum\nolimits_{|j| < k}^{} {n_{j}^{{4,{{\nu }_{3}}}}}$(ρ; E), which correspond to the overcritical domain. Figure 7 shows the dependences of the contributions from each domain separately for density of states N₄(ρ, ν₁, ν₃; E) on the quasiparticle energy for ρ = 3 and g = 3.48. It can be seen that the contributions from the nonsingular and subcritical domains are strongly suppresses in the range of negative energies.

Fig. 7.

Contributions of the nonsingular, subcritical, and overcritical domains to N₄(ρ, ν₁, ν₃; E).

The contribution of the overcritical domain in expressions (37), (39), and (40) leads to a much stronger rearrangement of the density of states near impurity than contribution (34) of the subcritical region for small charges g ∈ Δ(0). In Figs. 3–5, the contribution of the overcritical domain leads to the emergence of resonances in the range of negative energies, which decay with increasing distance from the impurity. With increasing impurity charge Z, the number of resonances increases, and they are shifted downwards on the energy scale. The Dirac point can be treated as the point of accumulation of an infinitely large number of resonances [8, 19]. This is due to the fact that functions $n_{j}^{{4,{{\nu }_{3}}}}$(ρ; E) in the overcritical domain oscillate with logarithmically diverging frequency 2[σln|2E| – ν₃] for E → 0 for all values of s.a. extension parameter ν₃.

8 CONCLUSIONS

It should be noted that the previous publication [10] with the participation of the authors was devoted to analysis of the spectra of massive quasiparticles in graphene near a Coulomb impurity. This study is its natural continuation. Here, we have considered the case when the effective mass of quasiparticles in graphene is zero and have shown that the structure of the electron excitation spectra in this case is qualitatively different. In particular, we have constructed a family of all possible s.a. Hamiltonians corresponding to massless charge carriers in graphene with Coulomb impurities, which are parameterized by extension parameters, and have performed their spectral analysis. It is shown that the spectrum of s.a. partial Hamiltonian is continuous, spec $\hat {h}$(Z, j, s) = (–∞, ∞) in contrast to the massive case, when both discrete and continuous spectra exist.

We have calculated the generalized eigenfunctions corresponding to s.a. partial Hamiltonians for any impurity charge (see relations (30)). Namely, the normalized (generalized) eigenfunctions are given by formulas (21) for the nonsingular domain (g ≤ g_s(j)), by formula (24) for subcritical domain (g_s(j) < g < g_c(j)), and by formula (26) for the critical domain (g = g_c(j)), and by formula (28) for the overcritical domain (g > g_c(j)). The resulting eigenfunctions proved to be significant for analysis of the local density of states (see formulas (32), (36), (37), and (40)), which depends on the s.a. extension parameters.

It should be noted that in [20], the s.a. Dirac Hamiltonians corresponding to massless charge carriers in graphene with Coulomb centers were also considered in combination with the Aharonov–Bohm field (in the 2 + 1 dimensions) except for the critical region, when Z = Z_c(j). However, substantial peculiarities of the given problem in undoped graphene were not taken into account. For this reason, the radial Hamiltonians considered in [20] were parameterized in a special manner, which does not allow one to identify them with the corresponding Hamiltonians of the real problem for graphene.