1 INTRODUCTION

It is well known that Yablonovitch and John [1, 2] demonstrated for the first time that the structure consisting of a periodic matrix made of dielectric materials (with different refractive indices) can control the propagation of an electromagnetic wave. Later, an analogous effect was also observed in other periodic structures consisting of metal/semiconductor, metal/dielectric, etc. layers. Such media with a periodic variation of the dielectric/magnetic properties on a spatial scale on the order of the optical wavelength are known as photonic crystals (PCs) due to the similarity of their structural periodicity with the periodic potential energy in semiconducting crystals. It is well known that each PC is characterized by a certain frequency range referred to as the photonic bandgap (PBG) [3]. In this frequency interval, an electromagnetic wave cannot propagate through the crystal. This unique property of PCs renders them inimitable candidates for preparing a large number of photonic elements/devices.

For preparing a PC, various chemical/optical methods and various approaches to deposition are used [4]. Laser technology was also employed for obtaining PCs after considerable advances made in the formation of the material surface structure [4]. Photonic crystals can also be self-organizing. A classical example of self-organizing PCs are cholesteric liquid crystals (CLCs). A CLC has a birefringent structure that rotates uniformly around a certain direction known as the direction of the optical axis of the medium [5]. Cholesteric liquid crystals are also interesting because the exact analytic solution to the problem of light propagation in a CLC along its optical axis is known [6, 7].

Peculiarities in light localization in a PC form a rapidly developing trend in contemporary optics and photonics. This is associated with the fundamental importance and possible applications of features of light localization. It should be noted that unlike the propagation of waves that can easily be grasped from the wave equation, localization of waves (formation of bound states) is a more complex effect. There are many methods of light interception, and all of them are implemented with the help of materials or systems in which outgoing waves are prohibited. Strong light localization is observed in the Fabry–Perot-type systems because of the multiple reflection of light from the boundaries as well as from the PC defects. Strong localization of light can also occur due to nonreciprocal reflection [8, 9]. In recent years, Anderson localization of light in disordered systems and in biological nanostructures [10], as well as light localization in nanoparticles [11], have become active fields of investigation.

In this study, we analyze some peculiarities of light localization in CLCs. We study the effect of dielectric boundaries on light localization.

2 FORMULATION OF THE PROBLEM AND BASIC RELATIONS

In analysis of optical properties of CLCs, two system of coordinates are conventionally used: (i) laboratory system of coordinates (x, y, z), where the z axis is parallel to the axis of the CLC spiral, and (ii) rotating system of coordinates (x', y', z'), where the z' axis coincides with the z axis, while the x' and y' axes are parallel to the principal directions of the permittivity tensor for each value of z'. In this case, two approaches to solving the Maxwell equations are possible [12, 13].

1. For invariable vectors of electric and magnetic fields and induction, we can transform the permittivity tensor in accordance with the law

$$\hat {\varepsilon }(z) = \hat {R}(az){{\hat {\varepsilon }}_{0}}{{\hat {R}}^{{ - 1}}}(az),$$

where

$${{\hat {\varepsilon }}_{0}} = \left( {\begin{array}{*{20}{c}} {{{\varepsilon }_{1}}}&0&{\dot {0}} \\ 0&{{{\varepsilon }_{2}}}&0 \\ 0&0&{{{\varepsilon }_{2}}} \end{array}} \right)$$

is the local permittivity tensor and \(\hat {R}\)(az) is the rotation matrix:

$$\hat {R}(az) = \left( {\begin{array}{*{20}{c}} {\cos az}&{ - \sin az}&0 \\ {\sin az}&{\cos az}&0 \\ 0&0&1 \end{array}} \right),$$

a = 2π/p, p being the CLC helix pitch.

2. For a constant permittivity tensor in the rotating system of coordinates, in which this tensor is diagonal, the vectors of electric and magnetic fields and induction can be transformed in accordance with the rule E(z) = \({{\hat {R}}^{{ - 1}}}\)(az)\(\mathcal{E}\)(z).

Although both these methods are equivalent, we will use the second method, which has certain advantages in solving certain problems. The solution of the Maxwell equations in the rotating system of coordinates for light propagating along the cholesteric axis has form

$$\mathcal{E}(z,t) = \sum\limits_{m = 1}^4 {{{\mathcal{E}}_{{0m}}}\exp (i{{k}_{m}}z)\exp ( - i\omega t),} $$
(1)

where km are the wavenumbers in the rotating system of coordinates. These wavenumbers are the solution to the dispersion equation

$$\left( {\frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}{{\varepsilon }_{1}} - k_{m}^{2} - {{a}^{2}}} \right)\left( {\frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}{{\varepsilon }_{2}} - k_{m}^{2} - {{a}^{2}}} \right) - 4{{a}^{2}}k_{m}^{2} = 0,$$
(2)

where ω/c = 2π/λ, λ being the wavelength of light in vacuum.

Using the eigenvalues of wavenumbers obtained from Eq. (2), we solve the problem of reflection, transmission, and localization of light in the case of a CLC layer. We assume that the CLC optical axis is perpendicular to the layer boundaries. On both sides, the CLC layer borders on the isotropic half-spaces with identical refractive indices ns. The boundary conditions involving the continuity of the tangential components of the electric and magnetic fields have form

$${{E}_{{ix}}} + {{E}_{{rx}}} = \sum\limits_{m = 1}^4 {({{\mathcal{E}}_{{mx}}}\cos {{\varphi }_{0}} - {{\mathcal{E}}_{{my}}}\sin {{\varphi }_{0}}),} $$
$${{H}_{{iy}}} + {{H}_{{ry}}} = \sum\limits_{m = 1}^4 {({{\mathcal{H}}_{{my}}}\cos {{\varphi }_{0}} + {{\mathcal{H}}_{{mx}}}\sin {{\varphi }_{0}}),} $$
$${{E}_{{iy}}} + {{E}_{{ry}}} = \sum\limits_{m = 1}^4 {({{\mathcal{E}}_{{my}}}\cos {{\varphi }_{0}} + {{\mathcal{E}}_{{mx}}}\sin {{\varphi }_{0}}),} $$
$${{H}_{{ix}}} + {{H}_{{rx}}} = \sum\limits_{m = 1}^4 {({{\mathcal{H}}_{{mx}}}\cos {{\varphi }_{0}} - {{\mathcal{H}}_{{my}}}\sin {{\varphi }_{0}}),} $$
$$\begin{gathered} \sum\limits_{m = 1}^4 {[{{\mathcal{E}}_{{mx}}}\exp (i{{k}_{m}}d)\cos ({{\varphi }_{0}} + ad)} \\ \, - {{\mathcal{E}}_{{my}}}\exp (i{{k}_{m}}d)\sin ({{\varphi }_{0}} + ad)] = {{E}_{{tx}}}, \\ \end{gathered} $$
$$\begin{gathered} \sum\limits_{m = 1}^4 {[{{\mathcal{H}}_{{my}}}\exp (i{{k}_{m}}d)\cos ({{\varphi }_{0}} + ad)} \\ \, + {{\mathcal{H}}_{{mx}}}\exp (i{{k}_{m}}d)\sin ({{\varphi }_{0}} + ad)] = {{H}_{{ty}}}, \\ \end{gathered} $$
$$\begin{gathered} \sum\limits_{m = 1}^4 {[{{\mathcal{E}}_{{my}}}\exp (i{{k}_{m}}d)\cos ({{\varphi }_{0}} + ad)} \\ \, + {{\mathcal{E}}_{{mx}}}\exp (i{{k}_{m}}d)\sin ({{\varphi }_{0}} + ad)] = {{E}_{{ty}}}, \\ \end{gathered} $$
$$\begin{gathered} \sum\limits_{m = 1}^4 {[{{\mathcal{H}}_{{mx}}}\exp (i{{k}_{m}}d)\cos ({{\varphi }_{0}} + ad)} \\ \, - {{\mathcal{H}}_{{my}}}\exp (i{{k}_{m}}d)\sin ({{\varphi }_{0}} + ad)] = {{H}_{{tx}}}, \\ \end{gathered} $$

where d is the thickness of the CLC layer, φ0 is the angle between the director and the x axis at the inlet surface of the CLC layer, and \({{\mathcal{E}}_{{mx}}}\), \({{\mathcal{E}}_{{my}}}\), \({{\mathcal{H}}_{{mx}}}\), and \({{\mathcal{H}}_{{my}}}\) are the electric and magnetic field components in rotating system of coordinates (x', y', z'). In [14, 15], exact analytic solutions of the boundary value problem and exact analytic expressions for the reflection and transmission coefficients were obtained (from intensity) for a diffracting proper wave in the case of the minimal influence of dielectric boundaries (i.e., for ns = \(\sqrt {{{\varepsilon }_{m}}} \) = \(\sqrt {({{\varepsilon }_{1}} + {{\varepsilon }_{2}}){\text{/}}2} \)). Analogous results for an incident wave with an arbitrary polarization and for an arbitrary value of ns were obtained in [16, 17].

Therefore, solving the boundary value problem, we can determine the values for the components of the reflected and transmitted fields, as well as for the field in the medium and, hence, analyze the peculiarities in light localization in a CLC layer.

The total electric field corresponding to the medium on the left side of the CLC layer, inside the CLC layer, and in the medium on the right side of the CLC layer (we assume that the CLC layer is located between two isotropic half-spaces z = 0 and z = d) can be written in form

$${\mathbf{E}} = \left\{ \begin{gathered} {{{\mathbf{E}}}_{i}}(z) + {{{\mathbf{E}}}_{r}}(z),\quad z < 0, \hfill \\ {{{\hat {R}}}^{{ - 1}}}(az)\mathcal{E}(z),\quad 0 < z < d, \hfill \\ {{{\mathbf{E}}}_{t}}(z),\quad z > d, \hfill \\ \end{gathered} \right.$$
(3)

where Ei, Er, and Et are the fields of incident, reflected, and transmitted waves and \({{\hat {R}}^{{ - 1}}}\)(az)\(\mathcal{E}\)(z) is the total field in the CLC layer itself.

3 RESULTS AND DISCUSSION

Each optical system has characteristic polarizations called eigen polarizations (EPs). Eigen polarizations are two polarizations of incident light, which do not change upon transmission of light through the system. These polarizations coincide with the polarizations of the eigenmodes. The EPs of the CLC layer for the normal incidence of light almost coincide with the orthogonal circular polarizations. When light is incident along the normal to the CLC layer, the wave with one of EPs diffracts from the periodic structure of the medium, while the wave with the other eigen polarization practically almost does not perceive the periodic structure of the medium. Therefore, for the normal incidence of light on a CLC, a PBG exists only for light with only one of the EPs (which will be referred to as a diffracting EP); in the case of minimal effect of dielectric boundaries, the reflection coefficient equals unity in the PBG and decreases, oscillating outside of the PBG. These oscillations are due to finiteness of the CLC layer thickness, are consequences of diffraction of light in a finite volume, and are not associated with reflections from the dielectric boundaries. The existence of dielectric boundaries (i.e., the difference of ns from \(\sqrt {{{\varepsilon }_{m}}} \)) leads to additional modulation of these oscillations outside of the PBG. The reflection minima can be determined approximately from condition

$$kd = m\pi ,\quad m = 0, \pm 1, \pm 2,...,$$
(4)

where

$$k = \sqrt {\frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{2} + {{a}^{2}} \pm \sqrt {{{{\left( {\frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}\frac{{{{\varepsilon }_{1}} - {{\varepsilon }_{2}}}}{2}} \right)}}^{2}} + 4{{a}^{2}}\frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}{{\varepsilon }_{m}}} } .$$

At the frequencies specified by this condition (and known as the edge mode frequencies), strong localization of light takes place. With increasing order of the edge modes, light localization becomes weaker. Localization of light in CLCs was analyzed theoretically for the first time in [18, 19]. This problem for a diffracting EP of a CLC was considered analytically and numerically in [20] for the minimal influence of dielectric boundaries also. Various features of light localization in CLCs were also investigated in [21–25]. We will continue below the analysis of peculiarities of light localization in a CLC layer.

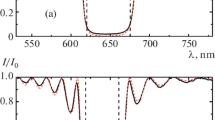
Figure 1 shows intensity distribution I(z) = |E(z)|2 outside and inside of the CLC layer at wavelength λ = 625.5 nm (within PBG near its center) in the case of the minimal influence of dielectric boundaries (i.e., for ns = \(\sqrt {{{\varepsilon }_{m}}} \)). The polarizations of light incident on the layer coincide with the first (diffracting) and second EPs, with the left and right circular polarizations and, finally, with the linear polarizations along the x and y axes.

Fig. 1.
figure 1

Intensity distribution I(z) = |E(z)|2 outside and inside of the CLC layer at wavelength λ = 625.5. nm (within the PBG near its center) in the case of the minimal influence of dielectric boundaries (i.e., for ns = \(\sqrt {{{\varepsilon }_{m}}} \)). The polarization of light incident on the layer coincides with the first (diffractive) (a) and second (b) EP with the left (c) and right (d) circular polarizations and, finally, with linear polarizations along the x (e) and y (f) axes. CLC parameters: helix pitch p = 420 nm, ε1 = 2.29, ε2 = 2.143, and layer thickness d = 50p. Vertical dashed lines in all figures correspond to the left and right boundaries of the CLC layer.

Full size image

Figure 2 shows intensity distributions I(z) = |E(z)|2 outside and inside of the CLC layer at wavelength λ = 625.5 nm (inside of the PBG near its center), at a wavelength outside of the PBG at the first short-wavelength minimum of the reflection coefficient (or just at the edge mode with m = –1), at a wavelength outside of the PBG at the first short-wavelength maximum of the reflection coefficient, and at a wavelength outside of the PBG at the second short-wavelength minimum of the reflection coefficient (or at the edge mode with m = –2 for ns = 1 (CLC layer is in vacuum) and ns = \(\sqrt {{{\varepsilon }_{m}}} \). The polarization of light incident on the layer coincides with the first and second EP.

Fig. 2.
figure 2

Intensity distribution I(z) = |E(z)|2 outside and inside of the CLC layer: (a, b) at wavelength λ = 625.5 nm (within the PBG near its center); (c, d, e, f) at a wavelength outside the PBG at the first short-wavelength minimum of the reflection coefficient (or just at the edge mode with m = –1); (g, h, i, j) at a wavelength outside of the PBG at the first short-wavelength maximum of the reflection coefficient; (k, l, m, n) at a wavelength outside of the PBG at the second short-wavelength minimum of the reflection coefficient (or at the edge mode with m = –2); (a, b, e, f, i, j, m, n) ns = 1 (the CLC layer is in vacuum); (c, d, g, h, k, l) ns = \(\sqrt {{{\varepsilon }_{m}}} \). The polarization of light incident on the layer coincides with the first (a, c, e, g, i, k, m) and second (b, d, f, h, j, l, n) IP. Parameters are the same as in Fig. 1.

Full size image

Figure 3 shows intensity distributions I(z) = |E(z)|2 outside and inside of the CLC layer at wavelength λ = 625.5 nm, at a wavelength outside of the PBG at the first short-wavelength minimum of the reflection coefficient, at a wavelength outside the PBG at the first short-wavelength maximum of the reflection coefficient, and at a wavelength outside of the PBG at the second short-wavelength minimum of the reflection coefficient for ns = 10.

Fig. 3.
figure 3

Intensity distribution I(z) = |E(z)|2 outside and inside of the CLC layer (a) at wavelength λ = 625.5 nm, (b) at a wavelength outside of the PBG at the first short-wavelength minimum of the reflection coefficient, (c) at a wavelength outside of the PBG at the first short-wavelength maximum of the reflection coefficient, and (d) at a wavelength outside of the PBG at the second short-wavelength minimum of the reflection coefficient for ns = 10. Parameters are the same as in Fig. 1.

Full size image

It follows from the figures that

(i) in the case of the minimal influence of the dielectric boundaries, the value of |E(z)|2 for the eigenmodes in the CLC layer varies smoothly;

(ii) when ns differs from \(\sqrt {{{\varepsilon }_{m}}} \) or when the polarization of incident light differs from the EP, oscillations appear in the dependence of energy of the total wave field in the CLC layer on z;

(iii) the amount of energy accumulated in the CLC layer depends on ns.

Let us now consider the influence of the dielectric boundaries on the luminous energy accumulated by the CLC layer.

We will first analyze the spectra of the averaged luminous energy density in the CLC layer for different values of ns. The averaged luminous energy density in the CLC layer can be calculated using formula

$$w = \frac{1}{d}\int\limits_0^d {{\text{|}}{\mathbf{E}}{{{\text{|}}}^{2}}dz.} $$
(5)

Figure 4 shows the spectra of w for different values of ns. Figure 5 shows the evolution of the w spectra upon a change in ns. Finally, Fig. 6 shows the dependences of w and wavelength λm of the edge modes on ns for the first three short-wavelength edge modes with m = –1, –2, and –3.

Fig. 4.
figure 4

Spectra of w for ns = 1 (1), \(\sqrt {{{\varepsilon }_{m}}} \) (2), 2.5 (3), 0.2 (4), 1.5 (5) and 10 (6). The remaining parameters are the same as in Fig. 1.

Full size image
Fig. 5.
figure 5

Evolution of the w spectra upon a change in ns. Parameters are the same as in Fig. 1.

Full size image
Fig. 6.
figure 6

Dependences of (a) w and (b) wavelength λm of the edge modes on ns for the first three short-wavelength edge modes with m = –1 (1), –2 (2), and –3 (3). Parameters are the same as in Fig. 1.

Full size image

These figures lead to the following conclusions.

1. For the minimal influence of dielectric boundaries (i.e., for ns = \(\sqrt {{{\varepsilon }_{m}}} \)), the maximal localization is observed at edge modes with m = ±1. With increasing m, the localization of the luminous energy decreases.

2. With increasing difference |ns – \(\sqrt {{{\varepsilon }_{m}}} \)|, the maximal localization is shifted towards edge modes with larger index m. The change of ns also leads to a change in the wavelengths of edge modes. For ns = \(\sqrt {{{\varepsilon }_{m}}} \), the wavelengths of short-wavelength (long-wavelength) edge modes take on a minimal (maximal) value. With increasing difference |ns – \(\sqrt {{{\varepsilon }_{m}}} \)|, the wavelength of short-wavelength (long-wavelength) edge modes increase (decrease).

3. With increasing ns, the value of w at different edge modes increases in different manners.

We have also analyzed the effect of the variation of ns on total luminous energy W localized in the CLC layer in a finite spectral range. This total energy was calculated using formula

$$W = \int\limits_{{{\lambda }_{1}}}^{{{\lambda }_{2}}} {wd\lambda .} $$
(6)

Figure 7 shows dependence W(ns). With increasing ns, the value of W increases monotonically, but not linearly.

Fig. 7.
figure 7

Dependences of W on ns; λ1 = 600 nm, λ2 = 650 nm. The remaining parameters are the same as in Fig. 1.

Full size image

4 CONCLUSIONS

In should be noted in conclusion that we have investigated peculiarities in light localization in a CLC layer in the case of normal light incidence. We have analyze the influence of dielectric boundaries on light localization and have demonstrated the strong effect of refractive index ns on the localization. The importance of our results lies, in particular, in the knowledge of exact analytic solution to the Maxwell equations for light propagating along the CLC axis and, hence, our results are correct. These results can serve as a goalpost for systems for which the exact solution is unknown. It should also be noted that according to the results of our analysis, the maximal localization is observed at the edge modes with m = ±1 in the case of the minimal influence of dielectric boundaries. With increasing difference |ns – \(\sqrt {{{\varepsilon }_{m}}} \)|, the maximal localization is shifted towards edge modes with a larger index m. A variation of ns also leads to a change in the wavelengths of the edge modes.

The importance of this research is due to the fact that in the presence of certain boundaries, modes of a new type, at which strong localization can also be observed, can appear apart from the edge modes. In recent years, systematic studies of optical Tamm modes have been launched and continued for various optical structures, in particular, in view of their possible wide application (see, for example, [26–33] and the literature cited therein). It is well known that strong localization is also observed at defect modes [33–39].