Nonlinear Interaction of Microwave Radiation with a Plasma Flow under Hybrid Resonance Conditions

Abstract

We propose a simple model of quasi-one-dimensional steady-state nonequilibrium plasma flow propagating along the axis of an open magnetic trap and sustained by an rf electromagnetic field. The model makes it possible to analyze qualitatively possible regimes of the plasma flow in the presence of induced intrinsic rf field amplified due to geometrical resonance with the plasma flow and to determine the main features and key characteristics of nonlinear absorption of the external field energy.

1 INTRODUCTION

The study of mutual influence of an rf field and a plasma through the averaged ponderomotive force originates from classical works [1–4]. Subsequently, this topic was developed in investigations of interaction of laser radiation with matter in applications associated with plasma acceleration of particles [5–9]. Emphasis was mainly laid on analysis of effects of nonlinear interaction of the rf field with an unbounded transparent plasma (self-focusing and defocusing of this field, organization of self-sustained waveguide channels, excitation of wakefields, etc.).

Along with lasers, high-power microwave radiation sources are used for producing and sustaining plasmas. Such sources produce steady-state nonequilibrium plasma in which the electron temperature considerably exceeds the ion temperature. This creates favorable conditions for effective ionization and excitation of ions by electron impacts, which makes it possible to use such plasmas in a wide range of applications [10, 11]. For a microwave discharge, there arises the problem of interaction of the rf field with the plasma formation with characteristic sizes that can be comparable with the wavelength of electromagnetic radiation. The description of such objects necessitates the consideration of effects associated with the influence of the plasma boundary, i.e., primarily geometrical (surface plasmon) resonances in the vicinity of which the rf field is substantially amplified [12]. In such conditions, the field intensity in the plasma may be high enough for the averaged ponderomotive force acting on plasma particle to noticeably affect the density of the medium. This leads to the self-consistent problem of the nonlinear interaction of the rf field with the plasma because the amplification of the field depends on the dynamics of the medium, which in turn depends on the ponderomotive force in the region of field amplification. The specific feature of this process is the resonant dependence of the ponderomotive force on the plasma parameters, which renders this process extremely sensitive to inhomogeneity of the spatial distributions of parameters.

One of important particular cases in the interaction of microwaves with a compact dense plasma formation is the microwave discharge that is required for applications associated with development of sources of hard UV radiation and high-multiplicity ions and that can be treated essentially as a directed plasma flow with a varying cross section [13–16]. Apart from the ponderomotive force, plasma inhomogeneity is also determined by the flow dynamics; therefore, a consistent description of gas dynamics of the flow and the dynamics of the resonant electric field induced in the discharge is of fundamental importance for correct construction of the theory of nonlinear absorption of the sustaining field in microwave discharges of this type.

In this study, we propose a simple model of a quasi-one-dimensional steady-state plasma flow propagating along the axis of an open magnetic trap and sustained by an external rf field. The model makes it possible to investigate qualitatively possible regimes of the plasma flow in the presence of a resonantly amplified internal rf field and to determine the main features and key characteristics of nonlinear absorption of microwave radiation.

2 SCATTERING AND ABSORPTION OF RF FIELD BY A HOMOGENEOUS PLASMA CYLINDER

Let us consider the auxiliary problem of scattering of an incident monochromatic electromagnetic wave by a homogeneous plasma cylinder of radius a placed into an external uniform static magnetic field (Fig. 1a). This is a standard problem in the diffraction theory, the solutions to which for an arbitrary relation between the wavelength and the cylinder transverse size in the form of an expansion in cylindrical harmonics are well known for isotropic [17, 18] as well as anisotropic [12, 19] dielectric response. If the cylinder diameter is much smaller than the wavelength, this problem can be solved in the quasi-static approximation [18, 20]. In this approximation, the variation of the external field on the outer boundary of the cylinder can be ignored.

Fig. 1.

(Color online) Explanation to the model of nonlinear interaction of an rf field with a plasma formation.

We assume that the dependence on coordinate z is harmonic, and the wave is incident on the plasma cylinder at a certain angle θ to its axis. We also assume that the size of the cylinder is much smaller than the wavelength in the plasma; therefore, we assume that the field in the cylinder is uniform in the transverse coordinate. Thus, the field inside and outside the cylinder can be written as

$${{{\mathbf{\tilde {E}}}}^{{\operatorname{int} }}} = {{{\mathbf{E}}}^{{\operatorname{int} }}}\exp (i{{k}_{0}}z\cos \theta - i\omega t),$$

$${{{\mathbf{\tilde {E}}}}^{{{\text{ext}}}}} = {{{\mathbf{E}}}^{{{\text{ext}}}}}\exp (i{{k}_{0}}z\cos \theta - i\omega t),$$

where E^int and E^ext are the complex amplitudes of the internal and external fields.

When the external field is directed along the cylinder generatrix, an additional simplification appears because the gyrotropy axis of the dielectric response coincides with the cylinder axis. In this case, the problems of excitation of plasma oscillations by rf field E parallel to the cylinder axis and perpendicular to it can be considered independently. It is also known that resonant amplification of the field for scattering by a cylindrical object which is much smaller than the wavelength is possible only for the incident field transverse relative to the cylinder axis [20]. This amplification is associated with the excitation of the electric dipole resonance in the system. Therefore, we can consider only the transverse component of the incident field. Such a description of the wave incident on the cylinder is equivalent to expansion of the incident field in cylindrical waves and inclusion of only cylindrical (TE and TM) waves with azimuthal number m = 1 [18].

When the above conditions hold, the field outside the cylinder can be written as

$${{{\mathbf{E}}}^{{{\text{out}}}}} = {{{\mathbf{E}}}^{0}} + \pi {{a}^{2}}\left( {\frac{{4({\mathbf{P}} \cdot {{{\mathbf{r}}}_{ \bot }}){{{\mathbf{r}}}_{ \bot }}}}{{{{r}^{4}}}} - \frac{{2{\mathbf{P}}}}{{{{r}^{2}}}} + i\pi {{{\tilde {k}}}^{2}}{\mathbf{P}}} \right),$$

((1))

where E⁰ is the complex amplitude of the incident wave field, P is the complex amplitude of the polarization vector, r_⊥ = (x, y) is the radius vector component perpendicular to the cylinder axis, and ${{\tilde {k}}^{2}}$ = $k_{0}^{2}$(1 + cos²θ)/2. The last term on the right-hand side of expression (1) describes the influence of radiation corrections on wave scattering (radiation friction)¹ [20, 21]. In the absence of dissipation, it is this term that limits the magnitude of the field in the cylinder at resonance.

The induced polarization is determined by field E^int excited in the cylinder:

$${\mathbf{P}} = \hat {\chi }{{{\mathbf{E}}}^{{\operatorname{int} }}},\quad \hat {\chi } = \frac{1}{{4\pi }}(\hat {\varepsilon } - 1),$$

where $\hat {\chi }$ and $\hat {\varepsilon }$ are the dielectric susceptibility and permittivity tensors, respectively. By joining the tangential components of field strength and the normal components of induction of the external and internal electric field at the plasma cylinder boundary, we obtain

$$(1 + (2\pi - i{{\pi }^{2}}{{\tilde {k}}^{2}}{{a}^{2}})\hat {\chi }){{{\mathbf{E}}}^{{\operatorname{int} }}} = {{{\mathbf{E}}}^{0}}.$$

((2))

This result is equivalent to the case of dipole scattering of a transverse polarized wave relative to the axis of an isotropic dielectric cylinder up to the substitution of scalar polarizability χ for tensor $\hat {\chi }$.

For the Stix electric field components

$$\left( \begin{gathered} {{E}_{ + }} \\ {{E}_{ - }} \\ {{E}_{{||}}} \\ \end{gathered} \right) = \left( \begin{gathered} ({{E}_{x}} + i{{E}_{y}}){\text{/}}\sqrt 2 \\ ({{E}_{x}} - i{{E}_{y}}){\text{/}}\sqrt 2 \\ {{E}_{z}} \\ \end{gathered} \right),$$

((3))

the permittivity tensor for a cold plasma in an external uniform magnetic field is diagonal:

$${{P}_{ \pm }} = \frac{{{{\varepsilon }_{ \pm }} - 1}}{{4\pi }}E_{ \pm }^{{\operatorname{int} }},\quad {{P}_{{||}}} = \frac{{{{\varepsilon }_{{||}}} - 1}}{{4\pi }}E_{{||}}^{{\operatorname{int} }},$$

((4))

where ε_± and ε_|| are defined as

$${{\varepsilon }_{ \pm }} = 1 - \frac{{\omega _{p}^{2}}}{{\omega (\omega \pm {{\omega }_{B}} + i\nu )}},$$

$${{\varepsilon }_{{||}}} = 1 - \frac{{\omega _{p}^{2}}}{{\omega (\omega + i\nu )}}.$$

Here, ω_p is the electron plasma frequency, ω_B is the electron cyclotron frequency, and ν is the effective frequency of collisions of electrons. Generally speaking, the expression for ε_± also contains the terms associated with the existence of the ion component; however, the corresponding ion frequency for a microwave discharge are much lower than the radiation frequency and, hence, these terms can be omitted.

Using relations (2) and (4), we obtain the following expression for the field intensity in the plasma cylinder:

$$\frac{{{\text{|}}E_{ \pm }^{{\operatorname{int} }}{{{\text{|}}}^{2}}}}{{{\text{|}}E_{ \pm }^{0}{{{\text{|}}}^{2}}}}\, = \,\frac{{4{{\omega }^{2}}({{\nu }^{2}} + {{{(\omega \pm {{\omega }_{B}})}}^{2}})}}{{4{{{(\nu \omega \, + \,\pi {{{\tilde {k}}}^{2}}{{a}^{2}}\omega _{p}^{2}{\text{/}}4)}}^{2}}\, + \,{{{(\omega _{p}^{2}\, - \,2\omega (\omega \pm {{\omega }_{B}}))}}^{2}}}}.$$

((5))

It can be seen that if conditions

$${\text{|}}\omega _{p}^{2} - 2\omega (\omega \pm {{\omega }_{B}}){\text{|}}\sim (\nu \omega + \omega _{p}^{2}\pi {{\tilde {k}}^{2}}{{a}^{2}}{\text{/}}4) \ll \omega _{p}^{2}$$

((6))

are satisfied in the given case, the field is abruptly amplified. The resonance

$$\omega = {{\Omega }_{ \pm }} \equiv \frac{1}{2}(\sqrt {2\omega _{p}^{2} + \omega _{B}^{2}} \mp {{\omega }_{B}})$$

((7))

corresponding to such conditions is a geometrical resonance with the plasma cylinder. In the Stix notation, this corresponds to ε_±(ω) = –1 for ν → 0. The term “resonant” will be henceforth referred to quantities in the vicinity of this resonance.

It can be seen from expression (5) that in the vicinity of the cyclotron resonance (ω = ω_B), resonance field component E_– rotating in the same direction as electrons assumes the smallest value |$E_{ - }^{{\operatorname{int} }}$| ~ ν²ω²|E⁰|²/$\omega _{p}^{4}$; i.e., it does not penetrate into a dense plasma.

Let us define the energy characteristics of radiation, viz., volumetric power density q^e of extinction, q^a of absorption, and q^s = q^e – q^a of scattering. Extinction and absorption of radiation are defined as [22]

$$\begin{gathered} {{q}^{e}} = \frac{1}{2}\operatorname{Re} ({\mathbf{j}}{\text{*}} \cdot {{{\mathbf{E}}}^{0}}), \\ {{q}^{a}} = \frac{1}{2}\operatorname{Re} ({\mathbf{j}}{\text{*}} \cdot {{{\mathbf{E}}}^{{\operatorname{int} }}}), \\ \end{gathered} $$

where j = ∂P/∂t = –iω$\hat {\chi }$E^int. Using these relations as well as relations (2) and (4), we obtain

$$q_{ \pm }^{a} = \frac{{8\nu {{\omega }^{2}}\omega _{p}^{2}W_{ \pm }^{0}}}{{4{{{(\nu \omega + \pi {{{\tilde {k}}}^{2}}{{a}^{2}}\omega _{p}^{2}{\text{/}}4)}}^{2}} + {{{(\omega _{p}^{2} - 2\omega (\omega \pm {{\omega }_{B}}))}}^{2}}}},$$

((8))

$$q_{ \pm }^{s} = \frac{{8\pi {{{\tilde {k}}}^{2}}{{a}^{2}}\omega \omega _{p}^{4}W_{ \pm }^{0}}}{{4{{{(\nu \omega + \pi {{{\tilde {k}}}^{2}}{{a}^{2}}\omega _{p}^{2}{\text{/}}4)}}^{2}} + {{{(\omega _{p}^{2} - 2\omega (\omega \pm {{\omega }_{B}}))}}^{2}}}},$$

((9))

where $W_{ \pm }^{0}$ = |$E_{ \pm }^{0}$|²/16π is the average energy density of the Stix field components of the incident wave. Obviously, the expressions for the energy characteristics contain the same resonance factor as expression (5) for the intensity; i.e., geometrical resonance (7) also determines absorption and scattering efficiencies of the incident field energy. If both circular components are present in the expansion of incident field in the Stix components (3), the corresponding energy characteristics must be added.

Generally speaking, the power of the wave incident of the plasma column can be absorbed not only due to collisions of electrons and ions, but also due to generation of plasma waves because of inhomogeneity of the plasma across the z axis. The geometrical resonance effect itself is a rough process [20]; for this reason, in our formulation, the absorption associated with the generation of plasma waves can be considered qualitatively by redefining effective collision frequency ν. One of possible ways involves the selection of such a value of ν, that absorption quality factor Q_± assumes a preset value (known, for example, from numerical simulation). In terms of this paper, the absorption Q_± factor can be written as

$${{Q}_{ \pm }} = \frac{{{{\Omega }_{ \pm }}W_{ \pm }^{{\operatorname{int} }}}}{{q_{ \pm }^{a}}} \approx \frac{{{{\Omega }_{ \pm }}{{{({{\Omega }_{ \pm }} \pm {{\omega }_{B}})}}^{2}}}}{{2\nu \omega _{p}^{2}}},$$

where $W_{ \pm }^{{\operatorname{int} }}$ = |$E_{ \pm }^{{\operatorname{int} }}$|²/16π is the electric field energy density in the plasma. Therefore, the above relation can be treated as the equation for ν. Henceforth, we will not specify the origin of the imaginary correction to the radiation frequency and will treat ν as an extrinsic parameter of the problem.

3 MODIFICATION OF THE PLASMA FLOW UNDER THE ACTION OF THE PONDEROMOTIVE FORCE

Let us consider the equations describing a steady-state flow of singly ionized plasma in the hydrodynamic approximation [23, 24]:

$$\begin{gathered} \frac{{\partial {{n}_{{e,i}}}}}{{\partial t}} + {\text{div}}({{n}_{{e,i}}}{{{\mathbf{u}}}_{{e,i}}}) = 0, \\ {{m}_{{e,i}}}{{n}_{{e,i}}}\left( {\frac{{\partial {{{\mathbf{u}}}_{{e,i}}}}}{{\partial t}} + ({{{\mathbf{u}}}_{{e,i}}}\nabla ){{{\mathbf{u}}}_{{e,i}}}} \right) + \nabla ({{n}_{{e,i}}}{{T}_{{e,i}}}) = {{{\mathbf{f}}}_{{e,i}}}, \\ \end{gathered} $$

((10))

where n_e,i are the number densities of the electron and ion plasma components, u_e,i are directional velocities of the components, p_e,i are their pressures, f_e,i is the volume density of the external force acting on electrons or ions, and m_e,i are their masses.

On the scale of variation of all gasdynamic plasma characteristics of interest to our analysis, the plasma satisfies the quasi-neutrality condition: number densities n_e,i of electrons and ions and velocities u_e,i of their directional motion coincide and equal n and u, respectively. In analysis of the plasma flow propagating in the axial region of an open magnetic trap, the force exerted on the plasma component by the external magnetic field can be taken into account approximately as the flux of a continuous medium along the tube with a variable cross section:

$$S(z) = {{S}_{0}}{{B}_{0}}{\text{/}}B(z),$$

where B(z) is the magnetic field induction on the z axis of the trap. We will mark by subscript “0” the values of physical quantities in a magnetic plug, viz., at the peak of the external magnetic field. In the conditions of resonant absorption of the rf field energy by electrons, we will assume that their temperature considerably exceeds the ion component temperature (T_e ≫ T_i). The high electron temperature leads to a high electron thermal conductivity, which enables us to assume that the electron temperature does not change along the flow. In these approximations, by averaging the flow characteristics over cross section S(z), we obtain quasi-one-dimensional balance equations for particle and momentum fluxes in the case of the steady-state plasma flow, which are analogous to those used in [13–15]:

$$\frac{d}{{dz}}(Snu) = 0,$$

((11))

$$\frac{d}{{dz}}(S{{m}_{i}}n{{u}^{2}}) + S\frac{d}{{dz}}(n{{T}_{e}}) = S\langle {{f}_{z}}\rangle ,$$

((12))

where 〈f_z〉 is the projection of the density of the averaged force exerted on plasma electrons by the rf field (ponderomotive force) onto the z axis. The corresponding force acting on ions is omitted due to the difference in the masses of electrons and ions. For the same reason, we neglect in Eq. (12) the directional electron momentum flux as compared to the ion momentum flux. The ion pressure is negligibly small as compared to the electron pressure due to the difference in the temperatures of the components. Passing to a one-liquid model, the terms corresponding to the forces exerted by the field of charge separation are mutually cancelled out due to the quasi-neutrality condition.

The ponderomotive force can be written in form [8]

$$\langle {{f}_{z}}\rangle = - n\frac{{d\Phi }}{{dz}}.$$

Here, Φ is the potential of the averaged force acting on a solitary electron in the external rf electromagnetic field in the presence of a constant magnetic field [25],

$$\Phi = \frac{{{{e}^{2}}}}{{4{{m}_{e}}\omega }}\left( {\frac{{{\text{|}}E_{z}^{{\operatorname{int} }}{{{\text{|}}}^{2}}}}{\omega } + \frac{{{\text{|}}E_{ - }^{{\operatorname{int} }}{{{\text{|}}}^{2}}}}{{\omega - {{\omega }_{B}}(z)}} + \frac{{{\text{|}}E_{ + }^{{\operatorname{int} }}{{{\text{|}}}^{2}}}}{{\omega + {{\omega }_{B}}(z)}}} \right),$$

((13))

where e is the electron charge. Since there is no resonant amplification of the longitudinal electric field component, we will ignore the first terms in potential (13).

In this paper, we consider the case when characteristic scale l of the longitudinal plasma inhomogeneity is much larger than the scales of the transverse inhomogeneity and the wavelength of the heating field,

$$a \ll 2\pi {\text{/}}{{k}_{0}} \ll l.$$

((14))

In these conditions, we can assume that local rf field E^int is defined by relation (1) in which ${{\tilde {k}}^{2}}$ is replaced by differential operator

$${{\tilde {k}}^{2}} \to \frac{1}{2}\left[ {k_{0}^{2} + {{{\left( {{{k}_{z}} - i\frac{d}{{dz}}} \right)}}^{2}}} \right] \approx {{\tilde {k}}^{2}} - i{{k}_{0}}\cos \vartheta \frac{d}{{dz}}.$$

Equation (2) for the internal field in this case takes form

$$\left( {1 + \left( {2\pi - i{{\pi }^{2}}{{a}^{2}}\hat {\chi }\left( {{{{\tilde {k}}}^{2}} - i{{k}_{0}}\cos \vartheta \frac{d}{{dz}}} \right)} \right)} \right){{{\mathbf{E}}}^{{\operatorname{int} }}} = {{{\mathbf{E}}}^{0}}.$$

Considering expression (4) for the Stix components of the plasma polarization, we can verify that the derivative with respect to the coordinate can be ignored when condition (14) in which the longitudinal inhomogeneity scale is defined as

$$l\sim \max ((\nu {\text{/}}\omega ){{L}_{{pl}}},{{({{k}_{0}}a)}^{2}}{{L}_{{pl}}}).$$

Here, L_pl ~ (dlnB/dz)^–1 are the inhomogeneity scales for the external magnetic field and the plasma density, which coincide in order of magnitude. The physical meaning of the resultant condition is quite clear: the inhomogeneity scale for the electrodynamic problem is determined by the size of the region of resonant field enhancement, which is determined either by dissipation (proportional to ∝ν) or by scattering (proportional to ∝(k₀a)²). If this region is much larger than the wavelength, we can define the internal field using local expression (5) in which a, ω_p, and ω_B are functions of coordinate z:

$$\begin{gathered} a = \sqrt {\frac{{S(z)}}{\pi }} ,\quad {{\omega }_{p}} = \sqrt {\frac{{4\pi {{e}^{2}}}}{{{{m}_{e}}}}n(z)} , \\ {{\omega }_{B}} = \frac{{{{S}_{0}}{{\omega }_{{B0}}}}}{{S(z)}}. \\ \end{gathered} $$

((15))

In other words, in analysis of the electrodynamic part of the problem, the plasma flow can be considered as a set of homogeneous cylindrical objects with parameters distributed in accordance with the solutions to hydrodynamic equations (see Fig. 1b). This is the main assumption forming the basis of the model considered below.

Substituting relations (15) into geometrical resonance condition (7), we can define “resonant number density”

$$n_{{{\text{res}}}}^{ \pm }(z) = \frac{{{{m}_{e}}{{\omega }^{2}}}}{{2\pi {{e}^{2}}}}\left( {1 \pm \frac{{{{\omega }_{B}}(z)}}{\omega }} \right),$$

((16))

where superscripts “±” correspond to circular components E₊ and E_–. The difference between two resonant number densities for different Stix components exceeds in most cases the maximal possible spread in the plasma density in the trap.² Therefore, the existence of geometrical resonance with one of the circular field components guarantees the absence of resonance with the other component. For definiteness, we will henceforth consider the field of the incident wave containing only the E₊ component corresponding to the larger value of the resonant number density. With allowance for relation (5), potential Φ of the ponderomotive force acting on electrons can be written as

$$\begin{gathered} \Phi = \frac{{{{e}^{2}}{{{({{E}^{0}})}}^{2}}}}{{{{m}_{e}}}} \\ \, \times \frac{{\omega (\omega + {{\omega }_{B}})}}{{4{{{(\nu \omega + \pi {{{\tilde {k}}}^{2}}{{a}^{2}}\omega _{p}^{2}{\text{/}}4)}}^{2}} + {{{(\omega _{p}^{2} - 2\omega (\omega + {{\omega }_{B}}))}}^{2}}}}. \\ \end{gathered} $$

This expression was obtained in approximation ν ≪ ω + ω_B; otherwise, by virtue of condition (6), resonant amplification of the field is not manifested.

4 BASIC EQUATIONS

If the electron temperature is independent of the coordinate, set of equations (11), (12) can be reduced to the first two integrals:

$$\begin{gathered} Snu = {{S}_{0}}{{n}_{0}}c, \\ \frac{{{{u}^{2}}}}{{2{{c}^{2}}}} - \ln \left( {\frac{{uS}}{{c{{S}_{0}}}}} \right) + w(\phi - {{\phi }_{0}}) = \frac{1}{2}, \\ \end{gathered} $$

((17))

where c = $\sqrt {{{T}_{e}}{\text{/}}{{m}_{i}}}$ is the “isothermal” ion acoustic velocity, w = $E_{0}^{2}$/8πn₀m_ic² is the specific density of the incident wave energy, ϕ = 8πn₀Φ/$E_{0}^{2}$ is the dimensionless potential of the average ponderomotive force,

$$\phi = \frac{{2\tilde {\omega }_{p}^{2}(1 + {{{\tilde {\omega }}}_{B}})}}{{4{{{(\tilde {\nu } + \pi {{{\tilde {k}}}^{2}}{{a}^{2}}\omega _{p}^{2}{\text{/}}4)}}^{2}} + {{{(\tilde {\omega }_{p}^{2} - 2(1 + {{{\tilde {\omega }}}_{B}}))}}^{2}}}}\frac{{{{n}_{0}}}}{n},$$

((18))

where ${{\tilde {\omega }}_{p}}$ = ω_p/ω, ${{\tilde {\omega }}_{B}}$ = ω_B/ω, and $\tilde {\nu }$ = ν/ω is the electron plasma, electron cyclotron, and collision frequencies normalized to the radiation frequency.

The integration constants in Eqs. (17) were chosen in accordance with the familiar boundary condition of equality of the flow velocity and the sound velocity at the peak of the magnetic field: u₀ = c. This condition holds in the case when the coordinate dependence of velocity of the flow contains a smooth transition through the sound barrier [15, 26]. Here, we assume that the plasma is produced by a source located in the vicinity of a magnetic plug and initially has no directional velocity, acquiring it only as a result of relaxation to the steady-state flow. In this case, the flow stabilized in the trap is subsonic, while outside it, it is supersonic.

From the physical point of view, the first relation in (17) is the conservation law for the particle flux during the propagation along the z axis, while the second relation is the effective Bernoulli law. The nonlinear interaction of the field and the flow in expressions (17) is determined by the term proportional to parameter w. Choosing the form of spatial dependence ${{\tilde {\omega }}_{B}}$(z) and the value of normalized plasma frequency ${{\tilde {\omega }}_{p}}$(0) at magnetic field maximum, we can also determine unambiguously the position of the geometrical resonance satisfying condition (7) in the framework of the model. In the linear approximation, the coordinates of the cross sections in which the geometrical resonance is realized can be determined from equation

$${{n}_{{{\text{res}}}}}({{z}_{{{\text{res}}}}}) = {{n}_{{{\text{lin}}}}}({{z}_{{{\text{res}}}}}),$$

((19))

where n_res(z) is defined by expression (16) and n_lin(z) is the solution to system of basic equations (17) for w = 0.

We will perform below the qualitative analysis of possible plasma flows in the conditions of the nonlinear interaction with the external rf field.

5 CONTINUOUS FLOWS

Let us choose the parameters of the problem so that (i) conditions (6) ensuring substantial amplification of the resonant field are satisfied and (ii) resonance condition (19) holds in the trap. For definiteness, we specify the following model profile of the external magnetic field:

$$B(z) = \frac{{{{B}_{0}}}}{{(R - 1){{{\sin }}^{2}}(\pi z{\text{/}}L) + 1}},$$

where L is the trap length and R is the mirror ratio. Let us consider a modification of the plasma flow depending on the relative field energy density w of the incident wave, the remaining parameters being fixed.

Case with w = 0. An example of solution of set (17) for the plasma density in the absence of the rf electromagnetic field is given in Fig. 2. In the subsonic flow, the density is maximal at the center of the trap and decreases monotonically with increasing distance from it. Conversely, the resonant density is minimal at the center and maximal at the points corresponding to the external magnetic field maximum.

Fig. 2.

(Color online) Distributions of plasma density n(z) (solid curve) and resonant density n_res (dashed curve) in the linear absorption regime (w = 0). The trap length is L = 26 cm, mirror ratio is R = 3.7, ${{\tilde {\omega }}_{{B0}}}$ = 1, ${{\tilde {\omega }}_{{p0}}}$ = 1.5, $\tilde {\nu }$ = 0.001, and $\tilde {k}$a = 0.05.

Case with w < $w_{1}^{*}$. For a finite field energy density, as long as w is quite small, the effect of the external rf field on the plasma characteristics is local. This case is illustrated in Fig. 3, which shows the characteristic dependences of the plasma density and the linear saturation power density on the z coordinate. We will henceforth characterize this case as a weak nonlinearity regime. An increase of w to above a certain threshold value $w_{1}^{*}$ leads to the emergence of a singularity near the resonance, which is associated with the ambiguity in the solution to system (17). The emerging singularity violates the above assumption concerning the parametric dependence of the field characteristics on the coordinate along the flow. In this case, Eqs. (17) do not permit continuous solutions any longer, but solutions with a discontinuity of gasdynamic characteristics formally remain possible.

Fig. 3.

(Color online) Distributions of plasma density n(z), resonant density n_res(z), and linear absorption power density $q_{ + }^{a}$(z)S(z). The energy density of the incident wave field is w = 1.5 × 10^–7. Other parameters are the same as in Fig. 2. Fine dot-and-dash line shows for comparison the n(z) dependence for w = 0.

Case with w > $w_{2}^{*}$. However, upon a further increase of parameter w to above a certain level $w_{2}^{*}$, the solution to system (17) turns out to be unambiguous again. We will refer to this case as the strong nonlinearity regime. The characteristic dependences of the plasma density and absorption power are given in Fig. 4. Resonance in the strong nonlinearity limit is not localized any longer since the sustaining electromagnetic radiation prevents via the ponderomotive force the increase in the plasma density at the trap center to above the resonance level. As a result, there exists an extended region of the flow, which is characterized by an increased value of the absorbed power.

Fig. 4.

(Color online) Same as in Fig. 3 for w = 1.5 × 10^–4.

6 FLOWS WITH DISCONTINUITIES

We can assume that in the case of slow application of the rf field, there must exist a transition between the weak and strong nonlinearity limits, which is continuous in energy density w. The emergence of a singularity violates the initial approximations of the model in a region which is small as compared with the characteristic scales of magnetic configuration and with the radiation wavelength. If we admit the possibility of discontinuity of plasma density n and flow velocity u in this region, it is possible to unambiguously restore steady-state flows for an arbitrary energy density of the field of the incident wave even in the formulation of the problem considered here. Certainly, in applications, a continuous transition between the values of plasma characteristics before and after discontinuity is realized; however, this region cannot ensure an appreciable contribution to absorption in view of the smallness of this region as compared to the wavelength.

For determining the exact positions of the corresponding surfaces of discontinuity, we consider the energy balance equations for electrons and ions of the plasma [23]:

$${{n}_{{e,i}}}\frac{{d{{U}_{{e,i}}}}}{{dt}} + {{p}_{{e,i}}}{\text{div}}{\mathbf{u}} + {\text{div}}{{{\mathbf{Q}}}_{{e,i}}} = {{q}_{{e,i}}} + q_{{e,i}}^{{**}},$$

((20))

$${{n}_{{e,i}}}{{T}_{{e,i}}}\frac{{d{{s}_{{e,i}}}}}{{dt}} + {\text{div}}{{{\mathbf{Q}}}_{{e,i}}} = {{q}_{{e,i}}},$$

((21))

where U_e,i is the internal energy, s_e,i is the entropy, T_e,i is the temperature, Q_e,i is the heat flux density, and q_e,i and $q_{{e,i}}^{{**}}$ are the densities of the amount of heat and of the nonthermal energy supplied by unit time to the electron and ion fractions, respectively.

The amount of heat supplied to ions due to q_i and div Q_i and, hence, the change in the entropy equal zero. Using Eqs. (10) and (21), we eliminate q_e and Q_e from Eq. (20) for electrons and then sum the result with Eq. (20) for ions. In the constant electron temperature approximation, this ultimately gives

$$dU = - {{p}_{e}}d{v} + {{T}_{e}}ds + (q_{e}^{{**}} + q_{i}^{{**}})dt,$$

((22))

where ${v}$ = 1/n is the specific volume of the plasma and U is the total internal energy of plasma electrons and ions. The last term in Eq. (22), which is responsible for the nonthermal power, receives a contribution only from the work of the ponderomotive force acting on electrons (work done by the electric field of charge separation is cancelled out during the summation of contributions from electrons and ions). Therefore, ($q_{e}^{{**}}$ + $q_{i}^{{**}}$)dt = nΦ_ed${v}$. As a result, Eq. (22) takes the standard form of the basic thermodynamic relation:

$${{T}_{e}}ds = dU + ({{p}_{e}} + n{{\Phi }_{e}})d{v}.$$

The expression in the parentheses can be treated as a new effective pressure

$$\mathcal{P} \equiv n({{T}_{e}} + {{\Phi }_{e}}) = {{m}_{i}}{{c}^{2}}{{{v}}^{{ - 1}}}(1 + w\phi ({v})),$$

((23))

where ϕ(${v}$) is defined by formula (18). In accordance with the terminology used in [27], expression (23) defines the isotherm of the equation of state. An example of such an isotherm is given in Fig. 5 (solid curve). It can easily be seen that dependence $\mathcal{P}$(${v}$) of the effective pressure on specific volume in the isothermal process in the vicinity of geometrical resonance is generally nonmonotonic. The existence of an unstable ascending branch indicates that a jump (phase transition) from one descending branch to another is possible.

Fig. 5.

(Color online) Actual isotherm (dashed curve) and the isotherm of the equation of state near resonance (solid curve). Field energy is w = 1.4 × 10^–4. Other parameters are the same as in Fig. 2.

In the case of a classical Van der Waals gas, this leads to the replacement of the unstable region on isotherm $\mathcal{P}$(${v}$) by formal solution $\mathcal{P}$ = const, which corresponds to simultaneous existence of two phases in the system [27]. In our case of the spatially inhomogeneous system, the isobaric region of the actual isotherm must be modified so as to ensure the fulfillment of relation (17). Namely, eliminating wϕ with the help of relation (23), we can write the effective Bernoulli law in form

$$\frac{1}{2}{{\left( {{{n}_{0}}{v}\frac{{{{S}_{0}}}}{S}} \right)}^{2}} - \ln ({{n}_{0}}{v}) + \frac{{{v}\mathcal{P}}}{{{{m}_{i}}{{c}^{2}}}} - w{{\phi }_{0}} = \frac{3}{2}.$$

((24))

Simultaneous fulfillment of conditions (23) and (24) determines binodal points ${{{v}}_{1}}$ and ${{{v}}_{2}}$, at which a state with a single phase is realized (see Fig. 5). The values of the work done by the medium upon a transition from the initial to the final state along the isotherm of equation of state (23) and actual isotherm (24), which will be henceforth denoted by ${{\mathcal{P}}_{{(23)}}}$ and ${{\mathcal{P}}_{{(24)}}}$, must coincide:

$$\int\limits_{{{{v}}_{1}}}^{{{{v}}_{2}}} {{{\mathcal{P}}_{{(23)}}}({v})d{v} = \int\limits_{{{{v}}_{1}}}^{{{{v}}_{2}}} {{{\mathcal{P}}_{{(24)}}}({v})d{v}{\text{.}}} } $$

((25))

Here, ${{{v}}_{1}}$ and ${{{v}}_{2}}$ are defined as the roots of equation ${{\mathcal{P}}_{{(23)}}}$(${v}$) = ${{\mathcal{P}}_{{(24)}}}$(${v}$). Condition (25) can hold only for a certain value of spatial coordinate z, on which the integrand and the integration boundaries depend parametrically. Therefore, integral condition (25) is analogous to the well-known condition of equality of areas for a phase transition in a real gas (Maxwell’s equal area rule); however, in the case of the inhomogeneous problem, it determines not binodal points ${{{v}}_{1}}$ and ${{{v}}_{2}}$, but the spatial position of the region in which the phase transition considered here occurs.

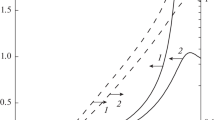
Further, we assume that if the steady-state flow is possible in principle for the preset extrinsic parameters and condition (25) can be satisfied in the bulk of the discharge, the “phase transition” necessarily occurs. Analysis of the possibility of stabilization of metastable states for a plasma flow is a separate problem that is beyond the scope of this paper. Thus, the theory constructed here makes it possible to describe any flow intermediate between the strong and weak nonlinearity limits (i.e., a flow for $w_{1}^{*}$ < w < $w_{2}^{*}$). A transition from weak to strong nonlinearity is illustrated in Fig. 6. In the strong nonlinearity regime for w > $w_{2}^{*}$, condition (25) of equality of areas cannot be satisfied at any point of space; therefore, the solutions to Eqs. (17) contain no singularities.

Fig. 6.

(Color online) Plasma density and linear absorption power density for variation of energy density w of incident radiation from 0 to 5 × 10^–4. The increase in the energy density corresponds to a displacement of the discontinuity to the center. Other parameters are the same as in Fig. 2.

7 BIFURCATION VALUES OF FIELD INTENSITY

The formalism of effective phase transitions makes it possible to establish the values of electromagnetic energy density $w_{1}^{*}$ and $w_{2}^{*}$ in the incident wave, for which a transition to the weak and strong nonlinearity regimes occurs.

Boundary $w_{1}^{*}$ of the weak nonlinearity regime is defined as the minimal value of w, for which an ascending segment of the isotherm of equation of state ${{\mathcal{P}}_{{(23)}}}$(${v}$) appears. The change from the monotonicity of the isotherm is preceded by the emergence of the inflection point in the vicinity of geometrical resonance (19); i.e.,

$$\begin{gathered} d{{\mathcal{P}}_{{(23)}}}({v}){\text{/}}d{v} = 0, \hfill \\ {{d}^{2}}{{\mathcal{P}}_{{(23)}}}({v}){\text{/}}d{{{v}}^{2}} = 0 \hfill \\ \end{gathered} $$

((26))

for z = z_res. Using expression (18) and (23), we can obtain the minimal value of w for which condition (26) can be satisfied:

$$w_{1}^{*} \approx \frac{{64}}{{3\sqrt 3 }}\frac{{n_{0}^{2}}}{{n_{{{\text{res}}}}^{2}}}{{\left( {\frac{{\tilde {\nu }}}{{\tilde {\omega }_{p}^{2}(0)}} + \frac{{\pi {{{(\tilde {k}a)}}^{2}}{{n}_{{{\text{res}}}}}}}{{4{{n}_{0}}}}} \right)}^{3}},$$

((27))

where n_res is the resonant density of the plasma at point z_res. For examples of numerical calculations considered here, our analytic estimate of energy density $w_{1}^{*}$ ensures relative error smaller than 10%.

Boundary $w_{2}^{*}$ of the strong nonlinearity regime is the largest value of w at which the flow is still discontinuous. For our model of the magnetic field (trap with magnetic plugs), this boundary can be defined as the value of w for which the discontinuity occurs exactly at the magnetic field minimum (center of the trap; see Fig. 6). In the case of strong resonant rf field amplification, which is of interest to our analysis, when conditions (6) are satisfied, the integral over the isotherm of equation of state ${{\mathcal{P}}_{{(23)}}}$(${v}$) in law (25) of equality of areas can be simplified using the fact that wϕ(${v}$) is a function with a sharp peak in the vicinity of ${{{v}}_{{{\text{res}}}}}$ (see Fig. 5). In this case, the integral on the left-hand side of equation (25) of equality of areas can be split into two integrals:

$$\int\limits_{{{{v}}_{1}}}^{{{{v}}_{2}}} {{{\mathcal{P}}_{{(23)}}}({v})d{v} \approx {{T}_{e}}\int\limits_{{{{v}}_{1}}}^{{{{v}}_{{{\text{res}}}}}} {\frac{{d{v}}}{{v}} + \frac{{{{T}_{e}}}}{{{{{v}}_{{{\text{res}}}}}}}\int\limits_{ - \infty }^\infty {w\phi ({v})d{v}{\text{.}}} } } $$

In the case of a large difference in magnetic field values (S/S₀ ≫ 1), the real isotherm is close to constant, ${{\mathcal{P}}_{{(24)}}}$(${v}$) ≈ const (as in a spatially homogeneous system). Under the above assumptions, we can evaluate all integrals in the equal area rule and obtain an algebraic equation for $w_{2}^{*}$. Its solution in the case when the discontinuity occurs at the magnetic field minimum can be written as

$$\begin{gathered} w_{2}^{*} \approx \frac{1}{\pi }\left( {\frac{{\tilde {\nu }}}{{\tilde {\omega }_{p}^{2}(0)}} + \frac{{\pi {{{(\tilde {k}a)}}^{2}}n_{{{\text{res}}}}^{*}}}{{4{{n}_{0}}}}} \right){{\psi }_{2}}(\xi ), \\ {{\psi }_{2}}(\xi ) = 2(\xi - \ln (\xi + 1)), \\ \end{gathered} $$

((28))

where ξ = $\sqrt e$n₀/$n_{{{\text{res}}}}^{*}$ and $n_{{{\text{res}}}}^{*}$ is the resonant density at the magnetic field minimum. Function ψ₂(ξ) ≈ ξ² for not very large values of ξ is simplified. The results of comparison of the resultant analytic estimate with the results of numerical simulation will be considered in the next section.

8 ABSORPTION POWER IN THE NONLINEAR REGIME

Let us apply the model developed here to analysis of the dependence of absorbed microwave radiation power on flow parameters. The most interesting in this case is the dependence of the absorbed power on energy density w of radiation introduced into the plasma.

Figure 7 shows the dependences of the absorbed rf field power on w in the conditions of resonant absorption for different positions of linear resonance (see inset) and for fixed ratios of the collision frequency to the frequency of the incident radiation $\tilde {\nu }$ and transverse size of the flow to radiation wavelength $\tilde {k}$a. In the linear regime, total absorbed power linear in w (quadratic in the incident field amplitude). In the nonlinear regime, the absorbed power increases faster than w! This effect can be explained as follows. With increasing field amplitude, the region in which the averaged ponderomotive force prevents the increase in density to above the resonance level expands; in this case, the field in the entire region becomes resonantly amplified. The absorbed power increases with the growth of the field amplitude faster than in the linear regime due to the expansion of the resonant interaction region. It can be seen from numerical calculations that the dependence is effectively saturated (the growth rate decreases) upon a transition to the strong nonlinearity regime for w ≈ $w_{2}^{*}$. At this point, the region of resonant interaction of the rf field with the flow occupies the entire volume located between two geometrical resonances (19).

Fig. 7.

(Color online) Dependences of the absorption power on energy density w of the field for different values of ${{\tilde {\omega }}_{{B0}}}$ = 1.9 (1), 1.6 (2), 1.3 (3), 1.0 (4), and 0.7 (5). Dashed lines are analytic estimates of bifurcation values of energy density $w_{2}^{*}$ (28) and absorption power $P_{{{\text{abs}}}}^{*}$ (32). The inset shows the plasma density in limit w = 0 and the resonant plasma density for indicated values of ${{\tilde {\omega }}_{{B0}}}$ (numbers on the curves correspond to those in the main figure). Other parameters are the same as in Fig. 2. The power is normalized to P_norm = ωn₀T_eS₀L/2.

Critical value $P_{{{\text{abs}}}}^{*}$ of the power at which the kink is observed on the curves in Fig. 7 can be estimated from the following physical considerations. We assume that for w = $w_{2}^{*}$, the rf field is present only in the central region of the discharge confined between two geometrical resonances. In this range, the plasma density is approximately equal to its resonance value, while outside this region, the plasma density is not perturbed, i.e.,

$$n(z) \approx \left\{ \begin{gathered} {{n}_{{{\text{res}}}}}(z)\quad {\text{for}}\quad {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} }}{}_{{{\text{res}}}}} < z < {{{\bar {z}}}_{{{\text{res}}}}}, \hfill \\ {{n}_{{{\text{lin}}}}}(z)\quad {\text{for}}\quad z < {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} }}{}_{{{\text{res}}}}}\quad {\text{or}}\quad z > {{{\bar {z}}}_{{{\text{res}}}}}, \hfill \\ \end{gathered} \right.$$

((29))

where ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} }{}_{{{\text{res}}}}}$ and ${{\bar {z}}_{{{\text{res}}}}}$ are determined from the condition of continuous joining of solutions, which coincides with expression (19). Such a coordinate dependence of the plasma density is ensured due to the action of the ponderomotive force; potential ϕ(z) corresponding to this force in resonant amplification region ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} }{}_{{{\text{res}}}}}$ < z < ${{\bar {z}}_{{{\text{res}}}}}$ can be determined from the effective Bernoulli law

$$w(\phi - {{\phi }_{0}}) = \ln \left( {\frac{{\sqrt e {{n}_{0}}}}{{{{n}_{{{\text{res}}}}}}}} \right) - \frac{1}{2}{{\left( {\frac{{{{n}_{0}}{{S}_{0}}}}{{{{n}_{{{\text{res}}}}}S}}} \right)}^{2}}.$$

((30))

It should be noted for methodological purpose that the distribution of resonantly amplified electromagnetic field, which ensures density distribution (29), is in fact established due to small detuning |n – n_res| ≪ n. In deriving formula (30) from the “nonresonant” Bernoulli law, we can ignore this detuning and determine its magnitude using perturbation theory by equating the potential obtained from “electrodynamic” definition (18) to potential (30).

Using definitions (8) and (18), we can express total absorption power $P_{{{\text{abs}}}}^{*}$ in terms of the potential of the ponderomotive force:

$$P_{{{\text{abs}}}}^{*} = \frac{{4\tilde {\nu }}}{{\tilde {\omega }_{{p0}}^{2}}}\omega {{n}_{0}}{{T}_{e}}\int\limits_{{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} }}{}_{{{\text{res}}}}}}^{{{{\bar {z}}}_{{{\text{res}}}}}} {w(\phi - {{\phi }_{0}})S(z)dz.} $$

In the range of parameters of interest to our analysis, the value of this integral can be estimated by retaining only the first (leading) term in expression (30) for the potential, disregarding the variation of the plasma cross section in the region of resonant interaction and assuming that the coordinate dependence of the resonant plasma density is quadratic:

$${{n}_{{{\text{res}}}}}(s) = \bar {n} - \frac{{(z - {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} }}{}_{{{\text{res}}}}})(z - {{{\bar {z}}}_{{{\text{res}}}}})}}{{{{{({{L}_{{{\text{res}}}}}{\text{/}}2)}}^{2}}}}(n_{{{\text{res}}}}^{*} - \bar {n}).$$

((31))

Here, $n_{{{\text{res}}}}^{*}$ is the resonant density at the magnetic field minimum; $\bar {n}$ is the density at the resonance region boundaries (for estimates, we can connect this quantity with the plasma density at magnetic field maxima, $\bar {n}$ ≈ $\sqrt e$n₀); and L_res = ${{\bar {z}}_{{{\text{res}}}}}$ – ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} }{}_{{{\text{res}}}}}$ is the length of the resonance region (Fig. 8). As a result of simplifications performed above, the expression for the critical absorption power assumes the following quite simple form:

$$\begin{gathered} P_{{{\text{abs}}}}^{*} \approx \frac{{8\tilde {\nu }}}{{\tilde {\omega }_{{p0}}^{2}}}\omega {{n}_{0}}{{T}_{e}}{{V}_{{{\text{res}}}}}{{\psi }_{1}}(\xi ), \\ {{\psi }_{1}}(\xi ) = (\sqrt \xi - \arctan \sqrt \xi ){\text{/}}\sqrt \xi \approx \xi , \\ \end{gathered} $$

((32))

where V_res = RS₀L_res is the effective volume of the resonant interaction region and ξ = $\sqrt e$n₀/$n_{{{\text{res}}}}^{*}$ – 1. As expected, the absorption power increases in proportion to the increase in the volume of the region of interaction and is the higher the lower the resonant density at the trap center; the dependence on the collision frequency is linear. The values of $w_{2}^{*}$ and $P_{{{\text{abs}}}}^{*}$ obtained in accordance with formulas (28) and (32) are marked by horizontal and vertical lines in Fig. 7. We can see that our results are in satisfactory agreement with the results of simulation.

Fig. 8.

(Color online) (a) Dependences of plasma density (solid curve), plasma density in the linear approximation (fine dot-and-dash curve), and approximate quadratic dependence of plasma density (31) (dot-and-dash curve) on the coordinate along the flow. Vertical lines mark positions ${{\bar {z}}_{{{\text{res}}}}}$ and ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} }{}_{{{\text{res}}}}}$ of linear resonance. Horizontal line is $\bar {n}$ = $\sqrt e$n₀. (b) Normalized linear absorption power density obtained as a result of simulation (solid curve) and its approximate value 8$\tilde {\nu }$Sln($\sqrt e$n₀/n_res)/$\tilde {\omega }_{{p0}}^{2}$S₀ (dot-and-dash curve). Parameter w = 1.5 × 10^–4; other parameters are the same as in Fig. 2.

The effect of expansion of the resonant interaction region due to tuning of the plasma density to the resonant value may turn out to be significant in experiments aimed at attaining high multiplicity of ionization in microwave discharges. For example, when a plasma is sustained by radiation at frequency 37.5 GHz for plasma densities close to experimental values [28] and for an analogous magnetic configuration, the expected absorption power may differ from its value obtained disregarding nonlinear effects by more than 10% even for w > 0.003. The electron temperature in such experiments is estimated as 10–50 eV. If we assume that absorption is collisional, the rf field amplitude in range 2–5 kV/cm is sufficient for the manifestation of nonlinear effects. Fields of such strength can be reached in contemporary microwave generators and are realized in plasma experiments.

9 CONCLUSIONS

Based on the theory developed in this study, we can conclude that resonant heating of a small-diameter plasma flow occurs at geometrical resonance $\omega _{p}^{2}$ = 2ω(ω ± ω_B) or, in the Stix terminology, for ε_± = –1. The efficiency of this heating is mainly determined by the volume of the resonant interaction region, which increases with the field amplitude due to tuning of the plasma density to the resonant value as a result of action of the averaged ponderomotive force.

We have considered the simplest qualitative problem of the plasma flow with a fixed (single) degree of ionization disregarding radiation losses. However, the “electrodynamic” part of the problem is independent of these peculiarities. Therefore, our formalism permits direct generalization to the case of a plasma flow with a more complicated (varying) ion composition and line radiation losses, which is topical in the context of optimization of contemporary experiments. Analysis of the effect of pressure on the balance of ionization and excitation of ions by electron impact in a nonequilibrium multicharged plasma flow, which is based on the theory developed by the authors [15, 16], requires separate consideration.