Theory of the Laue Diffraction of X Rays in a Thick Single Crystal with an Inclined Step on the Exit Surface. II: Analytical Solution

Abstract

The analytical solution of the problem of the Laue diffraction of an X-ray spherical wave in a single crystal with an inclined step on the exit surface has been obtained. The general equations are used for the specific case of plane wave diffraction in a thick crystal under the Borrmann conditions. It is shown that, provided that the crystal thickness increases from the side of the reflected beam, the reflected-wave relative amplitude is determined by three complex terms. This may formally lead to interference and an increase in the intensity in maxima by a factor of 9 as compared with the crystal without a step. The equation for the transmitted beam contains only two terms, and the corresponding increase in intensity cannot be by more than a factor of 4. The results of analytical calculations coincide with the results obtained by numerical methods and presented in the first part of the work.

INTRODUCTION

In this paper, we report the results of the work the first part of which was published in [1]. The problem of spatial distribution (in the beam cross section) of the intensities of transmitted and reflected waves is solved theoretically for the case of Laue diffraction of X rays in a thick single crystal with an inclined step on its exit surface. This problem was solved numerically in the first part of the work. A significant redistribution of the reflected-beam intensity was observed in the transition region between the step boundary and the boundary of Borrmann triangle with a vertex at the lower step boundary: the intensity maxima increased by a factor of more than 7 in comparison with the intensity before the step. It should also be noted that the transmitted-beam intensity, averaged over the interference region, and the total intensity of the two beams are reduced significantly, which indicates violation of the Borrmann conditions.

It was shown in [1] that the problem can be divided for convenience into two stages. In the first stage, a plate-shaped crystal is under consideration and the solution is found using the Fourier transform method (as was made in [2–6]). In the second stage, one must solve the Takagi equations [7]. If the sample lattice is not strained but the sample shape has a complex boundary, these equations can be solved in the integral form [8–14]. In some cases, the integral form of equations excludes a direct solution to the problem but yields an equation that can sometimes be solved analytically.

Specifically this case is implemented in the problem of Laue diffraction in a single crystal with an inclined step on its exit surface (the object of our consideration). In this paper, we report the results of analytical solution for the second stage of the problem. The method that was first applied in [15] is used.

FORMULATION OF THE PROBLEM AND ITS ANALYTICAL SOLUTION

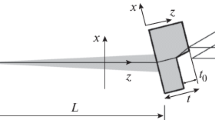
The schematic of the numerical experiment was reported in the first part of the work. It is assumed that a monochromatic spherical wave from a point X-ray source, located at a distance L from the sample, is incident on a plate-shaped single crystal of thickness t (maximum thickness). There is an inclined step of height t₀ on the exit crystal surface. We assume that the wave functions E₀(x) and E_h(x) for the transmitted and reflected beams, respectively, are known at the thickness z = t₁ = t – t₀.

In the second stage, one must solve the Takagi equations [7]

$$\frac{2}{i}\frac{{\partial {{E}_{0}}}}{{\partial {{s}_{0}}}} = {{X}_{0}}{{E}_{0}} + {{X}_{{ - h}}}{{E}_{h}}\exp (i{\mathbf{hu}}),$$

(1)

$$\frac{2}{i}\frac{{\partial {{E}_{h}}}}{{\partial {{s}_{h}}}} = [{{X}_{0}} + 2{{\alpha }_{q}}]{{E}_{h}} + {{X}_{h}}{{E}_{0}}\exp ( - i{\mathbf{hu}}).$$

(2)

Here, X_0,h,–h = Kχ_0,h,–h, where K = 2π/λ is the wave number; χ₀, χ_h, and χ_–h are the Fourier components of the crystal polarizability for the reciprocal-lattice vectors 0, h, and –h, respectively; the coordinates s₀ and s_h are counted along the propagation directions of the transmitted and reflected waves, respectively; u is the displacement vector due to the possible lattice strain; the parameter of deviation from the Bragg condition is α_q = K(θ – θ₀)sin 2θ_B; and λ is the X-ray wavelength. The angle θ–θ₀ describes the crystal angular position with respect to the incident beam.

Let us consider the case where α_q = 0 and there are no strains in the crystal (u = 0). For a perfect crystal, one can solve Eqs. (1) and (2) in the integral form in terms of known fields E₀ and E_h at some boundary in the Borrmann triangle, whose vertex is located at the observation point and sides are oriented along the directions of the transmitted (s₀) and reflected (s_h) waves [8–14]. The case where the thickness t₁ of crystal planar part exceeds greatly the diffraction focusing length [6, 16]: t_df = L|χ_h|F, where F = 1/(sin θ_Bsin 2θ_B) and θ_B is the Bragg angle. In this case, the wave function is almost constant on the horizontal x axis in the step region (thickness t₁), which corresponds to plane wave was considered in [1].

In contrast to [1], we will consider the case of a plane wave incident on a crystal, with the Bragg conditions exactly satisfied. The distance between the point source and crystal should be much larger than the diffraction focusing length L_df = t₁C, where С = (|χ_h|F)^–1. For t₁ = 1 mm, this length is L_d = 32.9 m. Note that the incident beam can easily be collimated on third-generation synchrotron radiation sources using a compound refractive lens [17].

Figure 1а shows the sample shape in the region of step on the exit surface, as well as the Borrmann triangle in which at least one wave function depends on the x coordinate. We apply the approach that was proposed for the first time in [15]. It implies consideration of the difference in the wave functions for the sample under study, E_k(r), and for the plate-shaped sample, A_k(z), rather than the real wave functions. Note that the function A_k(z) for a plane wave is known in the analytical form. Obviously, the integral equations for the differences will be the same; however, the boundary conditions differ significantly, because the difference in the wave functions is zero in the region where the crystal is homogeneous along the x axis.

Fig. 1.

(a) Exit crystal boundary in the form of step and a Borrmann triangle, in which at least one field depends on the x coordinate. (b) Different versions of step inclination at different values of parameter R = tan θ/tan θ_B (with indication of the values of parameter R).

Thus, we consider the functions

$${{e}_{k}}({\mathbf{r}}) = ({{E}_{k}}({\mathbf{r}}) - {{A}_{k}}(z))F_{0}^{{ - 1}}(z),\quad k = 0,h,$$

(3)

where

$${{A}_{k}}(z) = {{C}_{k}}{{F}_{0}}(z)F_{h}^{{ - 1}}(z),\quad {{F}_{{0,h}}} = \exp (i{{X}_{{0,h}}}z{\text{/}}2{{\gamma }_{0}}).$$

(4)

Here, γ₀ = cos θ_B and the coefficients C_k depend on the normalization. For a plane wave, they are equal to ± 0.5 at k = 0, h, respectively. Note that the fields e_k(r) are nonzero only in the acd triangle (Fig. 1а).

According to the integral formulation of theory [12], the function e_h(p) at a point p on the segment ab can be expressed in terms of the functions on the ad and db lines. Taking into account that the field differences on the ad line are zero, we obtain a solution in the form

$${{e}_{h}}(p) = {{e}_{h}}(p{{'}}) - \int\limits_{dp'} {d{{s}_{0}}} \frac{{\partial R}}{{\partial {{s}_{0}}}}{{e}_{h}} - \frac{i}{2}{{X}_{h}}\int\limits_{dp'} {d{{s}_{h}}} R{{e}_{0}},$$

(5)

$$R = {{J}_{0}}(X{{(({{s}_{{0p}}} - {{s}_{0}})({{s}_{{hp}}} - {{s}_{h}}))}^{{1/2}}}),$$

(6)

where X = (X_hX_–h)^1/2 and s_0p and s_hp are the coordinates of point p. Hereinafter, we denote the nth-order Bessel function as J_n(x). At the same time, the function e₀(p') on the db line is a solution to the integral equation

$${{e}_{0}}(p{{'}}) = \int\limits_{dp'} {d{{s}_{h}}} \frac{{\partial R}}{{\partial {{s}_{h}}}}{{e}_{0}} + \frac{i}{2}{{X}_{{ - h}}}\int\limits_{dp'} {d{{s}_{0}}} R{{e}_{h}}$$

(7)

if the function e_h(r) is known on this line. In the case under consideration, the db line is straight. We introduce coordinates ξ and ξ_η for the points on the dp'  line and at the point p'. The old and new coordinates are interrelated as follows:

$$\begin{gathered} z = \cos {{\theta }_{{\text{B}}}}({{s}_{0}} + {{s}_{h}}) = \xi \cos \theta , \\ x = \sin {{\theta }_{{\text{B}}}}({{s}_{0}} - {{s}_{h}}) = -\xi \sin \theta . \\ \end{gathered} $$

(8)

Let us denote the argument of the Bessel function in (6) as A. Taking into account (8), one can easily find that, on the db line,

$$\begin{gathered} {{s}_{0}} = {{\gamma }_{1}}\xi {\kern 1pt} {\kern 1pt} ,\quad {{s}_{h}} = {{\gamma }_{2}}\xi {\kern 1pt} {\kern 1pt} , \\ A = b({{\xi }_{\eta }} - \xi ),\quad b = X{{({{\gamma }_{1}}{{\gamma }_{2}})}^{{1/2}}}, \\ \end{gathered} $$

(9)

where

$${{\xi }_{\eta }} = {{\xi }_{0}} - \eta {{D}_{1}},\quad {{\xi }_{0}} = \frac{{{{t}_{0}}}}{\gamma },\quad {{D}_{1}} = \frac{{{{\gamma }_{0}}}}{{\sin ({{\theta }_{B}} - \theta )}},$$

(10)

$$\begin{gathered} {{\gamma }_{1}} = \frac{{\sin ({{\theta }_{{\text{B}}}} - \theta )}}{{\sin 2{{\theta }_{{\text{B}}}}}},\quad {{\gamma }_{2}} = \frac{{\sin ({{\theta }_{{\text{B}}}} + \theta )}}{{\sin 2{{\theta }_{{\text{B}}}}}}, \\ \gamma = \cos \theta . \\ \end{gathered} $$

(11)

Here, ξ_η and η are the lengths of segments dp' and pb, respectively. Then we determine the dependence of the intensities of transmitted and reflected waves on the parameter η.

The integral in (7) is calculated over the coordinate ξ in the range from zero to ξ_η. For simplicity, we will make a replacement of variables ξ → ξ_η – ξ, which does not change the integration limits. Then the derivative can be written as

$$\frac{{\partial R}}{{\partial {{s}_{h}}}} = \frac{1}{2}X{{\left( {\frac{{{{s}_{0}}}}{{{{s}_{h}}}}} \right)}^{{1/2}}}{{J}_{1}}(A) = \frac{1}{2}X{{\left( {\frac{{{{\gamma }_{1}}}}{{{{\gamma }_{2}}}}} \right)}^{{1/2}}}{{J}_{1}}(b\xi ).$$

(12)

As a result, Eq. (7) takes the following form after the replacement of variables:

$$\begin{gathered} {{e}_{0}}({{\xi }_{\eta }}) = \frac{b}{2}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{0}}({{\xi }_{\eta }} - \xi ){{J}_{1}}(b\xi ) \\ + \;\frac{i}{2}{{X}_{{ - h}}}{{\gamma }_{1}}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{h}}({{\xi }_{\eta }} - \xi ){{J}_{0}}(b\xi ). \\ \end{gathered} $$

(13)

On the right-hand side there are integrals in the form of convolutions. Integral equation (13) can be solved applying the Laplace transform

$$e(q) = \int\limits_0^\infty {d\xi } \exp ( - q\xi ){{e}_{0}}(\xi )$$

(14)

and using its property, according to which a convolution of two functions is transformed into the product of their transforms. Then we arrive at

$${{e}_{0}}(q) = \frac{b}{2}{{e}_{0}}(q){{[{{J}_{1}}(b\xi )]}_{q}} + \frac{i}{2}{{X}_{{ - h}}}{{\gamma }_{1}}{{e}_{h}}(q){{[{{J}_{0}}(b\xi )]}_{q}}.$$

(15)

The square brackets indicate a Laplace transform of the function they contain; this transform depends on the argument q. The handbook [18] contains integral no. 6.646.1, which can be transformed as follows:

$$\begin{gathered} {{\left[ {{{{\left( {\frac{\xi }{{\xi + a}}} \right)}}^{{n/2}}}{{J}_{n}}(b{{{[\xi (\xi + a)]}}^{{1/2}}})} \right]}_{q}} \\ = \frac{{{{b}^{n}}\exp ({{a}_{2}}(q - u))}}{{u{{{(q + u)}}^{n}}}}, \\ \end{gathered} $$

(16)

where

$${{a}_{2}} = a{\text{/}}2,\quad u = {{({{q}^{2}} + {{b}^{2}})}^{{1/2}}}.$$

(17)

Then we substitute (16) at a = n = 0 into (15) and make the following calculations, using the designation W = iX_–hγ₁/2:

$$\begin{gathered} {{e}_{0}}(q) = W{{e}_{h}}(q)\left( {\frac{{{{{[{{J}_{0}}(b\xi )]}}_{q}}}}{{1 - (b{\text{/}}2){{{[{{J}_{1}}(b\xi )]}}_{q}}}}} \right) \\ = \;\frac{{W{{e}_{h}}(q)}}{{u - ({{b}^{2}}{\text{/}}2){{{(u + q)}}^{{ - 1}}}}}. \\ \end{gathered} $$

(18)

It can be shown that the denominator in the right-hand side of (18) is equal to (u + q)/2 and the inverse function 2/(u + q) is the Laplace transform of function U(bξ), where

$$U(x) = 2\frac{{{{J}_{1}}(x)}}{x}.$$

(19)

After the inverse replacement of variables ξ → ξ_η – ξ, we obtain a solution to integral Eq. (13) in the form

$${{e}_{0}}({{\xi }_{\eta }}) = \frac{i}{2}{{X}_{{ - h}}}{{\gamma }_{1}}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } U(b[{{\xi }_{\eta }} - \xi ]){{e}_{h}}(\xi ).$$

(20)

Let us consider Eq. (5). In this case, the situation is more difficult, because the argument of the Bessel function depends on the coordinates of point p on the ab line. These coordinates are z_p = t₀ = ξ₀cos θ and x_p = –ξ₀sin θ – η. The coordinates of the point on the segment dp' are determined by (8). As a result of simple calculations we easily arrive at

$$\begin{gathered} {{s}_{{op}}} - {{s}_{o}} = {{\gamma }_{1}}{{\xi }_{d}}, \\ {{s}_{{hp}}} - {{s}_{h}} = {{\gamma }_{2}}({{\xi }_{d}} + a),\quad {{\xi }_{d}} = {{\xi }_{\eta }} - \xi {\kern 1pt} {\kern 1pt} , \\ \end{gathered} $$

(21)

$$\begin{gathered} R = {{J}_{0}}(b{{\sigma }_{\xi }}),\quad \frac{{\partial R}}{{\partial {{s}_{0}}}} = \frac{{b{{\varsigma }_{\xi }}}}{{2{{\gamma }_{1}}}}{{J}_{0}}(b{{\sigma }_{\xi }}), \\ a = \varepsilon \eta ,\quad \varepsilon = {{D}_{1}} + {{D}_{2}}, \\ \end{gathered} $$

(22)

$$\begin{gathered} {{\sigma }_{\xi }} = {{\left( {{{\xi }_{d}}[{{\xi }_{d}} + a]} \right)}^{{1/2}}}, \\ {{\varsigma }_{\xi }} = {{\left( {\frac{{{{\xi }_{d}} + a}}{{{{\xi }_{d}}}}} \right)}^{{1/2}}},\quad {{D}_{2}} = \frac{{{{\gamma }_{0}}}}{{\sin ({{\theta }_{{\text{B}}}} + \theta )}}. \\ \end{gathered} $$

(23)

Taking into account the above-described relations, Eq. (5) can be written as

$$\begin{gathered} {{e}_{h}}(\eta ) = {{e}_{h}}({{\xi }_{\eta }}) - \frac{b}{2}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{h}}(\xi ){{\varsigma }_{\xi }}{{J}_{1}}(b{{\sigma }_{\xi }}) \\ - \;\frac{i}{2}{{X}_{h}}{{\gamma }_{2}}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{0}}(\xi ){{J}_{0}}(b{{\sigma }_{\xi }}). \\ \end{gathered} $$

(24)

These integrals are also convolutions of two functions; therefore, it is convenient to use the Laplace transform (however, we have functions of more complex arguments in this case). Let us apply a Laplace transform to the third term in (24) and substitute (18). Taking into account formula (16), we obtain

$$\begin{gathered} \frac{b}{2}{{e}_{h}}(q)\frac{{b\exp ({{a}_{2}}(q - u))}}{{u(q + u)}} \\ = \;\frac{b}{2}{{e}_{h}}(q){{\left[ {{{{\left( {\frac{\xi }{{\xi + a}}} \right)}}^{{1/2}}}{{J}_{1}}(b{{{[\xi (\xi + a)]}}^{{1/2}}})} \right]}_{q}}. \\ \end{gathered} $$

(25)

Having made a transition from the q space back to the ξ space and added the first term, we obtain the following expression for the sum of the second and the third terms:

$$ - \frac{b}{2}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{h}}(\xi ){{J}_{1}}(b{{\sigma }_{\xi }})\left[ {{{{\left( {\frac{{{{\xi }_{d}} + a}}{{{{\xi }_{d}}}}} \right)}}^{{1/2}}} - {{{\left( {\frac{{{{\xi }_{d}}}}{{{{\xi }_{d}} + a}}} \right)}}^{{1.2}}}} \right].$$

(26)

Performing calculations for the wave function of the reflected beam on the ab line, we obtain a more convenient formula instead of (24):

$$\begin{gathered} {{e}_{h}}(\eta ) = {{e}_{h}}({{\xi }_{\eta }}) - \frac{1}{4}{{b}^{2}}\varepsilon \eta \int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{h}}(\xi ) \\ \times \;U(b{{([{{\xi }_{\eta }} - \xi ][{{\xi }_{\eta }} - \xi + \varepsilon \eta ])}^{{1/2}}}). \\ \end{gathered} $$

(27)

This formula expresses the unknown function e_h(η) on the ab line in terms of the known function e_h(ξ) on the bd line. This function is known, because the function E_h(r) on this line is simply transferred from the de line in the reflected-beam direction (i.e., its values at points p' and p'' are identical, and the difference can easily be calculated).

The formula for the function e₀(η) on the ab line can be obtained similarly to (24) with some evident changes:

$$\begin{gathered} {{e}_{0}}(\eta ) = \frac{b}{2}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{0}}(\xi )\frac{1}{{{{\varsigma }_{\xi }}}}{{J}_{1}}(b{{\sigma }_{\xi }}) \\ + \;\frac{i}{2}{{X}_{{ - h}}}{{\gamma }_{1}}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{h}}(\xi ){{J}_{0}}(b{{\sigma }_{\xi }}). \\ \end{gathered} $$

(28)

Let us apply a Laplace transform to the first term on the right-hand side, taking into account (25), and substitute expression (18) for e₀(q). As a result, we obtain an expression equal to the second term if J₀(bσ_ξ) is replaced by J₂(bσ_ξ)ζ$_{\xi }^{{ - 2}}$. Correspondingly, we arrive at

$$\begin{gathered} \frac{{{{J}_{0}}(b{{\sigma }_{\xi }})({{\xi }_{d}} + a) + {{J}_{2}}(b{{\sigma }_{\xi }}){{\xi }_{d}}}}{{{{\xi }_{d}} + a}} \\ = \;\frac{{U(b{{\sigma }_{\xi }}){{\xi }_{d}} + {{J}_{2}}(b{{\sigma }_{\xi }})a}}{{{{\xi }_{d}} + a}}. \\ \end{gathered} $$

(29)

Here, the relation J₀ + J₂ = U is used. The solution can be written as

$${{e}_{0}}(\eta ) = \frac{i}{2}{{X}_{{ - h}}}{{\gamma }_{1}}\int\limits_0^{{{\xi }_{\eta }}} {d\xi {{U}_{1}}({{\xi }_{\eta }} - \xi ,\eta ){{e}_{h}}(\xi )} ,$$

(30)

where

$${{U}_{1}}(\xi ,\eta ) = \frac{{\xi U(b{{{[\xi (\xi + \varepsilon \eta )]}}^{{1/2}}}) + \varepsilon \eta {{J}_{0}}(b{{{[\xi (\xi + \varepsilon \eta )]}}^{{1/2}}})}}{{\xi + \varepsilon \eta }}.$$

(31)

The functions on the bc line can be calculated more easily. In particular, the field E_h(r) on this line is simply transferred from the de line in the reflected-beam direction; in the case of incident plane wave, it is independent of the x coordinate. The field E₀(r) is transferred from the bd line in the transmitted-beam direction. Therefore, the fields at points p₀ and p' are similar. The field E₀(r) on the bd line is calculated from formula (20).

RESULTS AND DISCUSSION

Let us consider the same parameters as in the first part of the study: the photon energy E = ħω = 10 keV, t₁ = 1 mm, silicon crystal, reflection 220, and Bragg angle θ_B = 18.84°. Taking into account (4), one can obtain the following expression for the function e_h(ξ) on the bd line:

$${{e}_{h}}(\xi ) = {{C}_{h}}F_{h}^{{ - 1}}({{t}_{1}})[F_{0}^{{ - 1}}(\gamma \xi ) - F_{h}^{{ - 1}}(\gamma \xi )].$$

(32)

It is convenient to analyze the ratio of the beam intensities over the total thickness t in a crystal with a step with respect to the corresponding ratio for a crystal without a step. To this end, we will consider the ratio R_h(η) = E_h(η)/A_h(t) on the ab line. Then, taking into account (4), we derive from (27)

$${{R}_{h}}(\eta ) = 1 + {{g}_{h}}(\gamma {{D}_{1}}\eta ) - {{G}_{h}}(\eta ),$$

(33)

where

$$\begin{gathered} {{G}_{h}}(\eta ) = \frac{1}{4}{{b}^{2}}\varepsilon \eta \int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{g}_{h}}({{t}_{0}} - \gamma \xi ) \\ \times \;U(b{{([{{\xi }_{\eta }} - \xi ][{{\xi }_{\eta }} - \xi + \varepsilon \eta ])}^{{1/2}}}), \\ \end{gathered} $$

(34)

$${{g}_{h}}(x) = C{{F}_{0}}(x) - {{F}_{h}}(x),\quad C = {{F}_{h}}({{t}_{0}})F_{0}^{{ - 1}}({{t}_{0}}).$$

(35)

It is also convenient to make a replacement of variables ξ = ξ_η – ξ₁ in the integral G_h(η) without changing the integration limits. Finally, we arrive at

$$\begin{gathered} {{G}_{h}}(\eta ) = \frac{1}{4}{{b}^{2}}\varepsilon \eta \int\limits_0^{{{\xi }_{\eta }}} {d{{\xi }_{1}}} \\ \times \;{{g}_{h}}(\gamma {{D}_{1}}\eta + \gamma {{\xi }_{1}})U(b{{({{\xi }_{1}}[{{\xi }_{1}} + \varepsilon \eta ])}^{{1/2}}}). \\ \end{gathered} $$

(36)

Note that the second and third terms in (33) are zero at η = η_m = t₀/γD₁, and the ratio is equal to unity (i.e., the solution is continuous at the Borrmann triangle boundary). At η = 0, the parameter R_h(0) = F_h(t₀)/F₀(t₀), and the relative intensity depends only slightly on the step height; however, the real intensity is independent of the step height and equals to the field intensity at the thickness t₁.

Thus, the formula for the relative intensity contains three terms; the second and the third are complex. Therefore, if the absolute values of all three terms are close, they in sum can formally increase the intensity by a factor of 9. As was shown in [1], a numerical calculation leads to an increase in the intensity peaks by a factor of more than 7. The mechanism of this increase can be understood by analyzing formula (33).

Taking into account (4), one can derive from formula (30) a formula for R₀(η) = E₀(η)/A₀(t) ratio on the ab line:

$${{R}_{0}}(\eta ) = 1 - {{G}_{{01}}}(\eta ),$$

(37)

where

$${{G}_{{01}}}(\eta ) = \frac{i}{2}{{X}_{{ - h}}}{{\gamma }_{1}}\int\limits_0^{{{\xi }_{\eta }}} {d{{\xi }_{1}}} {{g}_{h}}(\gamma {{D}_{1}}\eta + \gamma {{\xi }_{1}}){{U}_{1}}({{\xi }_{1}},\eta ).$$

(38)

Formula (37) contains only two terms; i.e., the intensity maximum can formally increase by a factor of 4.

Let us consider the ratio R₀(η) = E₀(η)/A₀(t) on the bd line. In this case, the coordinate η is counted from the point b to the point d, and ξ_η = ξ₀ – ηD₂. The point p' corresponds to the point p₀ in Fig. 1a. Having made the same transformations as before, we obtain

$${{R}_{0}}(\eta ) = F_{0}^{{ - 1}}(\gamma {{D}_{2}}\eta )[{{F}_{h}}(\gamma {{D}_{2}}\eta ) - {{G}_{{02}}}(\eta )],$$

(39)

where

$${{G}_{{02}}}(\eta ) = \frac{i}{2}{{X}_{{ - h}}}{{\gamma }_{1}}\int\limits_0^{{{\xi }_{\eta }}} {d{{\xi }_{1}}} {{g}_{h}}(\gamma {{D}_{2}}\eta + \gamma {{\xi }_{1}})U(b{{\xi }_{1}}).$$

(40)

Formula (39) was derived taking into account that field strength E₀ at the points η on the segment bc and ξ_η on the segment bd is the same and that C_h = –C₀. At η = 0, formula (39) yields the same value as (37), and at η = η_m = t₀/γD₂ the expression can be written as F_h(t₀)/F₀(t₀) (i.e., it slightly exceeds unity, because a real field is not absorbed at height t₀ and the denominator in the ratio corresponds to the thickness t).

Figure 1b shows three types of step inclination, which can be characterized by different values of parameter R = tan θ/tan θ_B when the angle θ is counted as shown in Fig. 1а. Figure 2 presents the distributions of the relative intensity I/I₀= |R_0,h|² of the transmitted (T) and reflected (R) beams on the Borrmann triangle base ac, calculated from formulas (33), (37), and (39) at t₀ = 0.2 mm and R = 0.5, 0, and –0.5, respectively. The calculation results obtained by the numerical method [1] for the same parameters coincide with the data of this study. It is of interest that the calculation result of [1] for L = 2 m barely differs from the result shown in Fig. 2a. The reason is that a thick crystal forms a divergent spherical wave at a small distance from a point radiation source, which almost coincides in the step region with a plane wave.

Fig. 2.

Dependences of the relative intensity of the (T) transmitted and (R) reflected beams on the element of exit surface coinciding with the Borrmann triangle base (ac line in Fig. 1а) at x₀ = 68.2 µm and R = (a) 0.5, (b) 0, and (c) –0.5.

The calculations showed that the most interesting results are obtained at a positive, close-to-unity value of parameter R. In this case, the reflected-beam intensity oscillates with a short period and has the largest values (close to 9) in maxima. However, this does not occur always but depends periodically on the step height.

The relative reflected-beam intensity exceeds that of the incident beam at |R| < 1. At |R| > 1, formulas (33), (37), and (39) are not applicable, and the calculation must be performed in a different way. Note that there is some correlation between the intensity maxima and minima of the transmitted and reflected beams (they occur simultaneously). That is why these oscillations differ from the extinction oscillations of plane wave intensity in dependence on the crystal thickness, when the transmitted-beam intensity is transferred into the reflected-beam intensity and vice versa.