Central Peak in the Raman Spectra of Quartz Crystals in a Wide Temperature Range

Abstract

The spectral intensity of Raman scattering in quartz crystals has been calculated in a wide temperature range including the point of the α–β phase transition. It is established that a central peak is present in the scattered radiation spectrum at different temperatures with allowance for the interaction between the fundamental soft mode and an additional low-frequency oscillator. The intensity and half-width of the central peak are calculateed in a wide temperature range.

INTRODUCTION

Raman spectra of quartz crystals have been studied by many researchers (see, e.g., [1–3]). The temperature behavior of two lines of the A₁ symmetry in the Raman spectrum with frequencies of Ω = 207 and 466 cm^–1 at room temperature (Ω = ω₀ – ω'; ω₀ and ω' are the frequencies of excitation line and Raman scattering, respectively) was investigated in [1]. The Raman line at a frequency of 466 cm^–1 was broadened with an increase in temperature; however, its frequency changed only slightly. This line remained in the Raman spectrum above the phase-transition point (T_c = 846 K). The line at 207 cm^–1 was also significantly broadened upon heating of crystal and did not exhibit any frequency shifts. According to the well-known soft-mode theory [4–6], the low-frequency fundamental A₁-type oscillation of a quartz crystal (with a frequency of 207 cm^–1 at room temperature) should play the role of the soft mode responsible for the phase transition in this crystal. As was established in the experiments [7, 8], the frequency of this mode does not tend to zero while approaching the phase-transition point; therefore, this oscillation cannot be considered as the classical soft mode. In this case, an additional (non-fundamental) mode arising at room temperature in the form of a weak band with a frequency of 147 cm^–1 serves as the soft mode. This mode shifts significantly in frequency to the excitation line with an increase in temperature [7, 8].

When studying the structural α–β phase transition in quartz in a narrow temperature range, the effect of sharp increase (by 3–4 orders of magnitude) in the scattered light intensity (classified as the opalescence effect, similar to that occurring near liquid–vapor phase transitions) near the phase transition was previously found [9–11]. It was suggested in [12] that the opalescence observed in [9–11] is related to the static effect of formation of many twin domains near the incommensurate phase transition in a narrow temperature range (T – T_c ≈ 1.8 K) [13, 14]. The opalescence in quartz crystals can also be explained based on the dynamic mechanism related to the increase in the amplitude of the soft mode, the frequency of which anomalously decreases at the phase-transition point, and the corresponding increase in the Raman spectrum intensity. The sharp Raman peak near the phase-transition point at Ω → 0 corresponds to the so-called central peak.

Many researchers have been engaged in the problem of the central peak in Raman spectra for different crystals [15–18]. It was previously suggested that the central peak can be observed only in a narrow temperature range near the phase-transition point. However, it has been recently stated that this peak may be located far from the phase-transition temperature. For example, for lithium niobate [16, 17] and lithium tantalate [18] crystals, the central peak in Raman spectra was observed at temperatures much lower than the phase-transition temperature (including room temperature).

The purpose of this study was to theoretically analyze the Raman spectra of quartz in a wide temperature range (including the α–β phase transition point) and theoretically investigate the characteristics of the central peak and the possibility of its occurrence at different temperatures (including those far from the phase-transition point).

CALCULATION OF THE RAMAN SCATTERING INTENSITY USING THE MODEL OF TWO COUPLED OSCILLATORS

The behavior of the soft mode in Raman spectra of quartz in a wide temperature range was simulated in [19, 20]; however, the characteristics of the central peak far from the phase-transition point were not investigated. A comparative analysis of the results obtained taking into account one effective soft mode and considering the strong interaction between the soft mode and an additional low-frequency oscillator was not performed as well.

The experiments aimed at studying Raman spectra near phase transitions showed that one must take into account the interaction between the fundamental soft mode and some non-fundamental low-frequency oscillation, the nature of which has not been exactly determined [19, 20]. According to [4–6], this non-fundamental oscillation is characterized by fairly strong damping, i.e., corresponds to the relaxation process.

To calculate the Raman intensity with allowance for the interaction between the soft mode and the low-frequency non-fundamental mode, one should analyze the spectrum of two interacting oscillators. We will write the equations of motion of two coupled oscillators, one of which corresponds to the non-fundamental mode ζ(t), while the other corresponds to the soft mode ∆η(t) = ξ(t), responsible for the lattice instability [19, 20]:

$$\begin{gathered} {{m}_{1}}{\ddot {\zeta }} = - {{{\gamma }}_{1}}{\zeta } - {{{\delta }}_{1}}{\dot {\zeta }} - {\varkappa }({\zeta } - {\xi }), \\ {{m}_{2}}{\ddot {\xi }} = - {{{\gamma }}_{2}}{\xi } - {{{\delta }}_{2}}{\dot {\xi }} - {\varkappa }({\xi } - {\zeta }). \\ \end{gathered} $$

(1)

Here, m₁ (m₂), γ₁ (γ₂), and δ₁ (δ₂) are, respectively, the mass, elasticity coefficient, and damping coefficient for the first (second) oscillators and ϰ is the elastic interaction constant between the two oscillators. A solution to the system of equations (1) can be sought for in the form

$$\zeta (t) = {{\zeta }_{0}}\exp (i\Omega t),$$

$$\xi (t) = {{\xi }_{0}}\exp (i\Omega t).$$

Substituting these solutions into (1) and collecting terms, we obtain

$$\begin{gathered} {{\zeta }_{0}}({{m}_{1}}{{\Omega }^{2}}-{{\gamma }_{1}}-\varkappa -i\Omega {{\delta }_{1}}) + \varkappa {{\xi }_{0}} = 0, \\ {{\zeta }_{0}}\kappa + {{\xi }_{0}}({{m}_{2}}{{\Omega }^{2}}-{{\gamma }_{2}}-\varkappa -i\Omega {{\delta }_{2}}) = 0. \\ \end{gathered} $$

(2)

Matrix M_ij of the coefficients of system (2) has the form

$$\begin{gathered} {{M}_{{ij}}} \\ = \left( {\begin{array}{*{20}{c}} {{{m}_{1}}{{{\Omega }}^{2}}\, - \,{{{\gamma }}_{1}}\, - \,{\varkappa }\, - \,i{\Omega }{{{\delta }}_{1}}}&{\varkappa } \\ {\varkappa }&{{{m}_{2}}{{{\Omega }}^{2}}\, - \,{{{\gamma }}_{2}}\, - \,{\varkappa }\, - \,i{\Omega }{{{\delta }}_{2}}} \end{array}} \right), \\ \end{gathered} $$

(3)

and the corresponding Green tensor ${{G}_{{ij}}} = M_{{ij}}^{{ - 1}}$ is

$$\begin{gathered} {{G}_{{ij}}} = \frac{1}{{{\text{det}}({{M}_{{ij}}})}} \\ \times \;\left( {\begin{array}{*{20}{c}} {{{m}_{2}}{{{\Omega }}^{2}}\, - \,{{{\gamma }}_{2}}\, - \,{\varkappa }\, - \,i{\Omega }{{{\delta }}_{2}}}&{ - {\varkappa }} \\ { - {\varkappa }}&{{{m}_{1}}{{{\Omega }}^{2}}\, - \,{{{\gamma }}_{1}}\, - \,{\varkappa }\, - \,i{\Omega }{{{\delta }}_{1}}} \end{array}} \right), \\ \end{gathered} $$

(4)

where det(M_ij) = (m₁Ω² – γ₁ – ϰ – iΩδ₁)(m₂Ω² – γ₂ – ϰ – iΩδ₂) – ϰ².

In correspondence with the Nyquist theorem [4–6], the Raman spectrum intensity can be written as

$$I(\Omega ,T) = A\frac{{kT}}{{\hbar \Omega }}{\eta }_{0}^{2}\operatorname{Im} \sum\limits_{i,j = 1,2} {{{p}_{i}}{{p}_{j}}{{G}_{{ij}}}} .$$

(5)

Here, A is the normalization factor and η₀ is the equilibrium value of the order parameter. According to [4–6], we have η₀² = b(T_c – T)^2β (β = 1/2 in the case of a second-order phase transition and b is a constant). Coefficients p_i and p_j characterize the relative contribution from the oscillators. Substituting components G_ij into (5), we obtain

$$I({\Omega },~T) = A\frac{{kT}}{\hbar }{\eta }_{0}^{2}\frac{{({{{\delta }}_{1}}{{f}_{2}} + {{{\delta }}_{2}}{{f}_{1}})({{f}_{2}}p_{1}^{2} + {{f}_{1}}p_{2}^{2} - 2{{p}_{1}}{{p}_{2}}{\varkappa }) - ({{{\delta }}_{2}}p_{1}^{2} + {{{\delta }}_{1}}p_{2}^{2})({{f}_{1}}{{f}_{2}} - {{{\varkappa }}^{2}} - {{{\Omega }}^{2}}{{{\delta }}_{1}}{{{\delta }}_{2}})}}{{{{{({{f}_{1}}{{f}_{2}} - {{{\varkappa }}^{2}} - {{{\Omega }}^{2}}{{{\delta }}_{1}}{{{\delta }}_{2}})}}^{2}} + {{{\Omega }}^{2}}{{{({{{\delta }}_{1}}{{f}_{2}} + {{{\delta }}_{2}}{{f}_{1}})}}^{2}}}},$$

(6)

where f_1,2 = m_1,2Ω² – γ_1,2 – ϰ.

We use the approximation in which m₁ = m₂ = 1. It follows from (6) that, with allowance for the normalization factor, one of parameters p₁ and p₂ can be assumed to be unity, because only the ratio of their values affects the result. Furthermore, we assume that p₂ = 1.

Parameter γ₁ characterizes the spectral position of the intensity maximum of the low-frequency mode at Ω ≈ 0 and γ₂ indicates the spectral position of the intensity maximum of the soft mode Ω₀: γ₂ ∼ $\Omega _{0}^{2}$ ∼ (T_c – T). We assume that γ₁ = 1 and write the temperature dependence for γ₂ in the form γ₂ = A₀(T_c – T).

To determine the other parameters in (6), we performed a comparison of the calculated I(Ω, T) values with the experimental isofrequency (Ω = const) and isothermal (T = const) dependences I(Ω, T) for quartz that were obtained in [19, 20] in the x(zz)y scattering geometry. In particular, we compared the experimental and calculated values of the peak position and peak half-width for the soft mode at different temperatures. For the soft mode half-width, we find that ∆Ω₀ ≈ 80 cm^–1, and the temperature dependence of this parameter was disregarded.

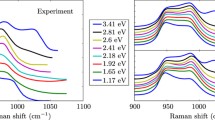
Figure 1 shows the experimental [19, 20] and calculated isofrequency temperature dependences of the Raman spectrum intensity for quartz, i(Ω, T_c – T) = I(Ω, T)/T, at fixed Ω values. Satisfactory agreement (Fig. 1) between the theory and experimental data was obtained at the following parameters: δ₁ = 50, δ₂ = 75, A₀ = 143, p₁ = 0.001, p₂ = 1, ϰ = 50.

Fig. 1.

Experimental (dots) [19, 20] and calculated (solid lines) from formula (6) temperature dependences of the Raman intensity of quartz i(Ω, T_c – T) = I(Ω, T)/T at Ω = (1) 40, (2) 50, and (3) 60 cm^–1. The calculation was performed with the following parameters: δ₁ = 50, δ₂ = 75, A₀ = 143, p₁ = 0.001, p₂ = 1, and ϰ = 50.

ANALYSIS OF THE CENTRAL PEAK INTENSITY AND HALF-WIDTH AT DIFFERENT PARAMETERS OF OSCILLATORS

Let us consider the intensity and half-width of the central peak in the Raman spectrum of quartz in dependence of temperature far from the phase transition and near it. We will also investigate the dependence of these quantities on parameters p₁ and p₂ in (6).

The temperature dependence of the maximum intensity of the central peak (Ω = 0 in relation (6)) has the form

$$\begin{gathered} I = {{I}_{0}}{\text{ }}T({{T}_{c}} - T) \\ \times \;\frac{{[{\varkappa }({{p}_{1}} + {{p}_{2}}) + {{p}_{1}}{{{\gamma }}_{2}}]_{{}}^{2}{{{\delta }}_{1}} + [{\varkappa }({{p}_{1}} + {{p}_{2}}) + {{p}_{2}}{{{\gamma }}_{1}}]_{{}}^{2}{{{\delta }}_{2}}}}{{{{{[{{{\gamma }}_{{\text{1}}}}{{{\gamma }}_{2}} + {\varkappa }({{{\gamma }}_{1}} + {{{\gamma }}_{2}})]}}^{2}}}}. \\ \end{gathered} $$

(7)

It follows from (7) that I = 0 at T = T_c. At the temperature T = T_max, which is close to the transition point (T_max < T_c), the central-peak intensity (7) has a sharp maximum. Taking into account that p₁$\ll$p₂ (from comparison of the experimental [19, 20] and calculated Raman spectra of quartz), we obtain an approximate expression for T_max:

$${{T}_{{{\text{max}}}}} = {{T}_{c}} - \frac{{{\varkappa }{{{\gamma }}_{1}}{{T}_{c}}}}{{{{A}_{0}}{{T}_{c}}({\varkappa } + {{{\gamma }}_{1}}) + 2{\varkappa }{{{\gamma }}_{1}}}}.$$

(8)

Intensities I(0, T) of the central peak (Ω = 0) in dependence of temperature at different values of parameter p₁ (p₂ = 1) are given in Table 1 and Fig. 2. As follows from (8), the intensity I(0, T) at the considered parameters has a maximum at T_max = 845.993 K.

Table 1.   Values of the maximum intensity I(0, T) and half-width ΔΩ(T) of the central peak at different temperatures and parameters p₁

Fig. 2.

Temperature dependences of the Raman intensity of quartz at Ω = 0 and parameters p₁ = (1) 0.0001, (2) 0.001, (3) 0.005, and (4) 0.01.

It can be seen in Table 1 that, with an increase in temperature from T = 300 K to the phase-transition point, the intensity increases from 0.02 to 956.3 (i.e., by a factor of about 50 000) at p₁ = 0.0001, by a factor of about 20 000 at p₁ = 0.001, and by a factor of 500 at p₁ = 0.01. It can be seen in Table 1 and Fig. 2 that, for p₁ > 0.005, the central-peak intensity begins to decrease with an increase in temperature above a certain value; afterwards, this parameter starts increasing. At p₁ < 0.005, the central-peak intensity monotonically increases with an increase in temperature. Note that the results obtained at p₁ = 0.0001–0.001 are in good agreement with the experimental data of [9–11], according to which the central-peak intensity increases by a factor of about 10⁴ near the phase-transition point.

Figure 3 shows the spectrum of the central peak at different temperatures near the phase-transition point and far from it. As one can see, the central peak may occur not only near the phase transition but also in a wide temperature range far from T_c. It can be seen in Fig. 3a that the shape of spectrum far from the phase-transition point barely changes with temperature. While approaching T_c, one can observe an anomalous increase in the intensity of the central peak and a sharp decrease in its half-width (Fig. 3b).

Fig. 3.

Shapes of the spectra I(Ω, T) of the Raman central peak of quartz at different temperatures (p₁ = 0.001): (a) T = (1) 300, (2) 500, (3) 700, and (4) 800 K; (b) T = (1) 845, (2) 845.5, and (3) 845.9 K.  

For a temperature range far from the phase-transition point, we have an approximate expression for the Raman intensity near the central peak (Ω = 0–10 cm^–1):

$$I = {{I}_{0}}\frac{T}{{A_{0}^{2}({{T}_{c}}~-~T)}}\left\{ {{{{\delta }}_{2}} + {{{\delta }}_{1}}\frac{{{{{[{\varkappa } + {{p}_{1}}{{A}_{0}}({{T}_{c}}~-~T)]}}^{2}}}}{{{{{\kappa }}^{2}} + 2{\varkappa }{{{\gamma }}_{1}} + {\delta }_{1}^{2}{{{\Omega }}^{2}}}}} \right\}.$$

(9)

Using formula (9), we find the expression for the central peak half-width ∆Ω(T) far from T_c:

$${\Delta \Omega } = \frac{{2\sqrt {{\varkappa }({\varkappa } + 2{{{\gamma }}_{1}})} }}{{{{{\delta }}_{1}}}}.$$

(10)

It follows from formula (10) that the parameter ∆Ω is temperature-independent far from the phase-transition point. We have ∆Ω = 2.04 cm^–1 for the parameters under consideration.

Values of the central peak half-width ∆Ω(T) calculated from exact formula (6) at different temperatures and different parameters p₁ are listed in Table 1. The obtained values ∆Ω(T) = 2.03–2.08 cm^–1 in the temperature range T = 300–800 K are in good agreement with the value calculated from formula (10) (2.04 cm^–1). At T = 840 K, one can observe an increase in the central peak half-width in comparison with its values at temperatures of 300–800 K; a sharp decrease in ΔΩ(T) (by two orders of magnitude) occurs at further approaching the phase-transition point. It can be seen in Table 1 that, in the larger part of the temperature range under consideration, ΔΩ(T) depends weakly on the parameter p₁ and is completely independent of this parameter in the range of p₁ = 0.0001–0.001.

It was shown in [16–18] that the central peak half-width near the phase-transition point for lithium niobate and lithium tantalate crystals can be written as

$$\Delta {\Omega }(T) = A\frac{{{{T}_{c}} - T}}{{{{T}_{c}}}}.$$

(11)

Figure 4a shows the corresponding dependence ∆Ω(T) for quartz crystals near the phase-transition point. The calculated ∆Ω(T) values are shown by dots in Fig. 4a. One can see that the obtained dependence ∆Ω(T) in the temperature range of T_c – T ≤ 6 K is close to linear; thus, relation (11) is also satisfied for quartz near T_c.

Fig. 4.

Temperature dependences of the half-width and intensity of the central peak in the quartz Raman spectrum (p₁ = 0.001): (a) central peak half-width near T_c and its extrapolation by formula (11) at A = 1280 cm^–1; (b, c) dependences I(Ω, T) at Ω = (1) 0, (2) 0.05, (3) 0.1, (4) 0.5, (5) 1, and (6) 2 cm^–1.

Figures 4b and 4c show the calculated temperature dependences of the Raman intensity for quartz I(Ω, T) near T_c. It can be seen that the central-peak intensity sharply increases with a decrease in Ω from 2 cm^–1 to zero. At Ω ≈ 0, the Raman opalescence effect is observed near T_c, which can be explained by the anomalous increase in the soft mode amplitude while approaching the phase-transition point in quartz.

The expression for the Raman intensity corresponding to the absence of the low-frequency oscillator can be derived from formula (6) at p₁ = 0 and κ = 0:

$$I{\text{ }} = {\text{ }}{{I}_{0}}\frac{{T({{T}_{c}} - T){{{\delta }}_{2}}}}{{{\text{(}}{{{\gamma }}_{2}} - {{m}_{2}}\Omega _{{}}^{2}{\text{)}}_{{}}^{{\text{2}}} + {\delta }_{{\text{2}}}^{{\text{2}}}\Omega _{{}}^{2}}}.$$

(12)

This expression at m₂ = 1 is consistent with the formula obtained in [19, 20] for the reduced intensity within the approximation of one soft mode. We find the position of the soft-mode intensity maximum from formula (12):

$${{{\Omega }}_{0}} = \sqrt {{{{\gamma }}_{2}} - {{{\delta }}_{2}}^{2}{\text{/}}2} {\kern 1pt} {\kern 1pt} .$$

(13)

Proceeding from (12), the peak half-width of the soft mode far from the phase-transition point can be presented in the form

$$\Delta {{{\Omega }}_{0}}(T) = {{{\delta }}_{2}}\left( {1 + \frac{{{\delta }_{2}^{2}}}{{4({{{\gamma }}_{2}} - {\delta }_{2}^{2})}}} \right).$$

(14)

Figure 5 shows the temperature dependences of the Raman intensity I(Ω, T) for the quartz soft mode calculated from formulas (6) and (12). Figure 5a demonstrates the dependences of the intensity I(Ω, T) of the Stokes (Ω > 0) and anti-Stokes (Ω < 0) spectral components calculated based on relation (6) for the model of two coupled oscillators in a wide temperature range (including the phase-transition point in a quartz crystal). One can see a peak corresponding to the lattice soft mode and the central peak (both far from the transition point and near it). While approaching T_c, the central-peak intensity anomalously increases. The dependences I(Ω, T) at different temperatures are given in Figs. 5b and 5c. The corresponding dependences calculated from formula (12) with allowance for only one soft mode are shown by dotted lines. At low frequencies (Ω ≈ 0), the solid and dotted curves differ significantly (Figs. 5b, 5c, insets). The central peak is completely absent in the dotted curve far from the phase-transition point. The obtained curves almost coincide far from the central-peak region. In this case, it is sufficient to use approximation (12) to analyze the soft-mode spectrum. However, as can be seen in Figs. 5b and 5c, approximation (12) is insufficient for analysis of the central-peak characteristics, and one should perform calculation from formula (6) taking into account the interaction between the soft mode and the low-frequency oscillator.

Fig. 5.

(a) Raman scattering intensity I(Ω, T) calculated for a quartz crystal at p₁ = 0.001. Frequency dependences of I(Ω, T) at different temperatures: (b) T = (1) 300, (2) 720, and (3) 819 K; (c) T = (4) 830 and (5) 840 K. Dotted lines are the dependences calculated from formula (12) with allowance for only the soft mode. Central-peak regions are shown on an enlarged scale in the insets.

CONCLUSIONS

The Raman spectra for the soft mode of a quartz crystal were calculated in a wide temperature range with allowance for the interaction between the soft mode and the low-frequency non-fundamental oscillator. It was established that the spectral intensity of the low-frequency Raman scattering sharply increases while approaching the phase-transition temperature T_c. It was shown that the scattered radiation spectrum of a quartz crystal contains the central peak, occurring not only near the phase transition but also in a wide temperature range far from T_c.

The central-peak intensity at room temperature is much lower than that near the phase transition (by a factor of 10⁴). It was shown that central peak half-width barely changes far from the phase-transition point and linearly decreases while approaching T_c.

The presence of the central peak in a wide temperature range in quartz crystals makes it possible to implement phase-matching conditions for nonlinear optical processes in these crystals due to the contribution to the quasi-momentum conservation law from the mode that corresponds to the central peak and is characterized by zero frequency and nonzero quasi-momentum.

Note that the performed simulation has a general character and is applicable not only to quartz but also other crystals undergoing a structural phase transition with a soft mode.