Physical Libration of the Moon: An Extended Problem

Abstract

The work is devoted to the study of the physical libration of the Moon. Interest in the traditional topic related to the rotation of the Moon is stirred up by the activity of many countries regarding the development of circumlunar space. Scientifically, the main agenda is to consider the viscosity of the core. At this stage of the theory development, such effects as indirect and direct perturbations from the planets were considered, the 4th order harmonic was included in the gravitational potential of the Moon, and the mean tidal potential was also considered. The inclusion of the described effects in the equations of the Moon’s rotation led to a significant improvement in the solution when compared with the corresponding data from the DE421 theory, although the residual differences still remain greater than the 1 ms accuracy required by the theory. The influence of the direct effect from the planets was milliseconds. The influence of the 4th harmonic manifested itself as a systematic shift of the order of 0.85$''$ in the residual differences in libration in longitude. Considering the tide made it possible to reduce the residual differences in latitude by almost an order of magnitude. In this case, the main factor that reduces the residual differences is changes in the second-order Stokes coefficients. The calculations were carried out using the DE421 ephemeris built at NASA Jet Propulsion Laboratory.

1 INTRODUCTION

In this study, factors are considered that make it possible to improve the accuracy of the theory of the Moon’s physical libration in comparison with the theory previously constructed for a solid Moon model within the framework of the main problem of physical libration [1, 2]. It should be noted that many works have been devoted to the study of the dynamic properties of the Moon. The Earth-Moon system is one of the most interesting objects to study. First, seismographs were placed on the Moon, which provided independent confirmation of the presence of a lunar core [3, 4] and the existence of a molten layer at the core/mantle interface. Secondly, there are high-precision gravimetric measurements carried out during many space missions, including Kaguya and GRAIL, in which accurate mascon maps were built, and high-precision values of Stokes coefficients in the expansion of the Moon’s gravitational field were determined [5]. The refined values of the Stokes coefficients confirmed the compression of the lunar core [6]. Third, to date, long-term lunar laser ranging (LLR) has achieved high accuracy (several tens of millimeters) in determining the distance between the Earth and the Moon, which made it possible to create high-precision ephemerides of the Moon, one of which is the DE421 ephemeris [7]. Considering the new data and using the DE421 ephemeris, Ramboux and Williams [6] constructed an empirical series of parameters of the lunar physical libration (LPhL), which is, in fact, the most accurate analytical description of the lunar rotation today. All of this would be impossible without the development of the LPhL theory itself, in which the correct interpretation of the LLR data is permissible, modeling of the described effects is carried out. This ultimately improves the accuracy of predicting the Moon’s position in orbit, the position of objects on the lunar surface, and, of course, clarification of the internal structure parameters of the lunar body.

Dissipative processes were also discovered, which are due to a shift at the equatorial node on the ecliptic by a magnitude (in modulus) 5.81$''$, which is equivalent to the angle of deviation of the rotation pole from the Cassini plane, equal to 0.263$''$. Williams et al. [8], and even earlier Yoder [9], and Dickey et al. [10], proposed two possible sources of dissipation: solid-body tides from the Earth and the Sun and dissipation at the core-mantle boundary. It was shown that these effects can be considered independently of each other. The processing of long-term observations of LLR showed that the tidal delay is about 4 h [8].

The inclusion of these internal effects in the model of the Moon’s rotation requires not only complex theoretical calculations, but also the use of high-precision observations that are sensitive to these effects. The most obvious is the installation of additional seismographs on the lunar surface, in which it would accurately identify the inner structure of the Moon. Another solution is to mount the telescope on the lunar surface. With such a telescope available, it will be possible to introduce corrections to the LPhL theory to reduce the discrepancies between the observed positions of the stars and the theoretically calculated ones. This idea is planned to be implemented in the ILOM mission [11, 12].

Thus, to study the fine effects of the Moon’s rotation, it is necessary to have an instrument that allows one to calculate and make appropriate adjustments to the calculation of the LPhL to reduce the residual differences. Thus, we first built a numerical LPhL-theory, which in its internal content fully corresponded to the analytical theory of Petrova [2]: the equations included a model of an absolutely rigid Moon, the gravitational potential of which was described by second and third order harmonics, the orbital motion of the Moon was specified by the analytical theory [13] constructed in the framework of the Hill problem, i.e., description of the Moon motion in the plane three-body problem Sun–Earth–Moon. The accuracy of the analytical theory [2], determined by comparison with similar analytical theories, was not very high $\sim {\kern 1pt} 0.05'' {-} 0.1{\kern 1pt} ''$. The obtained numerical solution [1] differed from the corresponding analytical one only in libration in longitude: the residual differences had an amplitude $\sim {\kern 1pt} 2''$ at the resonance frequency $(2l - 2F)$. This difference, we believe, is due to the inaccuracy of the analytical solution when obtaining the amplitudes of the resonant and with small denominators of the terms.

At this stage of our research, we are considering a more accurate model of lunar rotation. First, the modern numerical ephemeris defined by the DE421 theory shall be the focus. It was this model, and not the later, that was chosen in order to be able to compare the obtained LPhL solution with the semiempirical Ramboux and Williams series [6], which were also obtained on the basis of DE421. We needed to make such a comparison in order to check the correctness of our operations to extract both the parameters of the motion of the Moon’s mass center and the LPhL parameters from the dynamic model.

Secondly, we refine the numerical values of the parameters included in the developed theory. The solution of differential equations by the numerical method within the framework of the Cauchy problem requires the setting of the initial conditions for the sought variables, which are the libration angles and the canonical momentum conjugate to them. Inaccuracy in the initial data leads to the appearance of false near-resonant harmonics in the solution. In our case, the libration in longitude is most sensitive to inaccuracies in the initial values, in which the described effect manifests itself at periods close to 3 years. Therefore, we carefully verified the initial conditions for the libration variables with the DE421 ephemeris.

Thirdly, we make an approximate account of the lunar body deformation due to solid-body tides, introducing average corrections to the lunar inertia tensor obtained in [8] based on the analysis of laser data.

And fourthly, in addition to indirect accounting for perturbations from the planets, realized through the transition to a dynamic ephemeris, we consider the direct perturbations from the planets.

After introducing each of the described effects into our numerical theory of LPhL, we obtain residual differences when comparing our results with the data extracted from DE421, which coincide with calculations based on semiempirical series [6] with a high accuracy. As a result, the obtained differences, which do not exceed 1.2$''$ for libration in longitude and 2$''$ in latitude, show that we are using the correct algorithm for working with a dynamic ephemeris and that the effects we have introduced bring our solution increasingly closer to the results obtained with the help of semiempirical series. In conclusion, we discuss the nature of the remaining residuals and analyze the possible unaccounted effects that can reduce the amplitude of the residual differences.

2 OBTAINING THE MOON’S ORBIT FROM DE421

The staff members of the NASA Jet Propulsion Laboratory (JPL) wrote two programs for the primary processing of ephemeris files containing Chebyshev coefficients. The first program converts the original data into a binary format, and the second one carries out Chebyshev interpolation at a given time moment.

The Pleph function (ET, NTARG, NCTR, R), which implements interpolation, is written in Fortran:

ET is the date in Julian days;

NTARG is the index of the object, the coordinates of which we want to obtain (see Table 1);

Table 1.   NTARG values

NCTR is the index of the object, relative to which we want to obtain the coordinates of the celestial body NTARG; and

R is the set of coordinates and their derivatives.

The coordinate system laid down in the ephemeris is geocentric with the equator of the J2000 epoch tilted at ${{\varepsilon }_{0}}=84381.406''$ to the ecliptic of the epoch. When constructing a numerical LPhL-theory, we use the direction cosines of the vector radii directed from the Moon’s center to the centers of the Earth and the Sun. The transition from rectangular components to the direction cosines of the radius vector (to a rotating ecliptic coordinate system) is implemented in the following way:

1. Rotation of the equatorial coordinate system at an angle ${{\varepsilon }_{0}}$

$$\left( {\begin{array}{*{20}{c}} {{{X}_{{{\text{ecl}}}}}} \\ {{{Y}_{{{\text{ecl}}}}}} \\ {{{Z}_{{{\text{ecl}}}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos({{\varepsilon }_{0}})}&{\sin({{\varepsilon }_{0}})} \\ 0&{ - \sin({{\varepsilon }_{0}})}&{\cos({{\varepsilon }_{0}})} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {R(1)} \\ {R(2)} \\ {R(3)} \end{array}} \right).$$

2. Calculation of the longitude $\lambda$ and latitude $\beta$ of the object (Earth/Sun) with the transition to a rotating frame of reference by subtracting the mean motion ${{n}_{{{\text{sider}}}}}$ from longitude

$${{n}_{{{\text{sider}}}}} = F + \Omega - 180^\circ ,$$

$$\lambda = \left\{ \begin{gathered} 2\pi - {{\cos}^{{ - 1}}}\left( {\tfrac{{{{X}_{{{\text{ecl}}}}}}}{{\sqrt {X_{{{\text{ecl}}}}^{2} + Y_{{{\text{ecl}}}}^{2}} }}} \right) - n,\quad {{Y}_{{{\text{ecl}}}}} < 0 \hfill \\ {{\cos}^{{ - 1}}}\left( {\tfrac{{{{X}_{{{\text{ecl}}}}}}}{{\sqrt {X_{{{\text{ecl}}}}^{2} + Y_{{{\text{ecl}}}}^{2}} }}} \right) - n,\quad {{Y}_{{{\text{ecl}}}}} > 0, \hfill \\ \end{gathered} \right.$$

$$\beta = \tfrac{\pi }{2} - {{\cos}^{{ - 1}}}\left( {\tfrac{{{{Z}_{{{\text{ecl}}}}}}}{{\sqrt {X_{{{\text{ecl}}}}^{2} + Y_{{{\text{ecl}}}}^{2} + Z_{{{\text{ecl}}}}^{2}} }}} \right).$$

3. Calculation of the direction cosines of the radius vectors Moon–Earth and Moon–Sun:

$${{a}_{{{\text{ecl}}}}} = \frac{{\sqrt {X_{{{\text{ecl}}}}^{2} + Y_{{{\text{ecl}}}}^{2}} }}{{\sqrt {X_{{{\text{ecl}}}}^{2} + Y_{{{\text{ecl}}}}^{2} + Z_{{{\text{ecl}}}}^{2}} }}\cos(\lambda );$$

$${{b}_{{{\text{ecl}}}}} = \frac{{\sqrt {X_{{{\text{ecl}}}}^{2} + Y_{{{\text{ecl}}}}^{2}} }}{{\sqrt {X_{{{\text{ecl}}}}^{2} + Y_{{{\text{ecl}}}}^{2} + Z_{{{\text{ecl}}}}^{2}} }}\sin(\lambda );$$

$${{c}_{{{\text{ecl}}}}} = \frac{{{{Z}_{{{\text{ecl}}}}}}}{{\sqrt {X_{{{\text{ecl}}}}^{2} + Y_{{{\text{ecl}}}}^{2} + Z_{{{\text{ecl}}}}^{2}} }}.$$

The obtained parameters are necessary for calculating the potential energy of the system. The potential energy considers the interaction of the Moon with the Earth (through harmonics of the 2nd, 3rd, and 4th orders) and with the Sun (harmonic of the 2nd order). The formulas used are given in [1].

To check the calculation correctness of the orbit parameters, we compared the values we obtained based on the DE421, DE430, and DE431 ephemeris with the values taken from the HORIZONS web-interface database,¹ with the DE431mx model. The residual differences calculated by us and similar differences obtained in [7] are given in Table 2.

Table 2.   Residual differences between different orbital theories $\Delta$ in the components of the Earth relative to the Moon over an interval of 80 years

Since the differences between DE431 and Horizons are millionths of a meter, our calculation algorithm can be considered correct.

3 DEVELOPMENT OF AN ALGORITHM FOR EXTRACTING LIBRATION PARAMETERS FROM DE421

3.1 Semiempirical Series of Observations

The DE421 model was also chosen by us because it was used to construct the semiempirical Ramboux and Williams series [6], which today are the most accurate analytical representation of the observed physical libration in the form of series:

$$\begin{gathered} f(t) = \sum\limits_{j = 1}^m \,{{a}_{j}}{{t}^{j}} + \sum\limits_{i = 1}^n \,[({{C}_{i}} + \varepsilon _{i}^{c}t)\cos({{\varphi }_{i}}(t)) \\ + \;({{S}_{i}} + \varepsilon _{i}^{s}t)\sin({{\varphi }_{i}}(t))]{\kern 1pt} {\kern 1pt} . \\ \end{gathered} $$

(1)

Series (1) can be correctly called semi-empirical ones [14], since the numerical values of their coefficients and frequencies, presented through the fundamental Delaunay arguments (Table 3), were obtained not from the solution of the differential equations of the LPhL, but as a result of a complex multiparameter analysis of the residual differences obtained by comparing numerical solution of DE421 for LPhL with data of long-term laser observations. In other words, the series [6] are, in its own way, an analytical interpretation of the LPhL parameters obtained from observations. They do not fully comply with DE421, since they also contain low-amplitude terms ${{U}_{n}}$ ($\le {\kern 1pt} 0.03''$), which are absent in DE421, but they are present in observations. Barkin et al. [14] showed that the nature of these terms is due to the presence of Free Core Nutation (FCN), and the terms with the status correspond to harmonics derived from FCN [15].

Table 3.   Fragment of the table of semiempirical series [6]

Series [6] are used by us for the procedure of checking the algorithm (see below, Section 3.2) for extracting the parameters of the Moon’s libration. To do this, we have implemented a program for calculating the components of the Moon’s libration according to formula (1) using tables [6] and calculated the same parameters using the algorithm given in Section 3.2. As a result, we got good agreement in residual differences. All the numerical values of the parameters used for the calculation by formulas (1) are given in Tables 4–6.

Table 4.   Delaunay parameters [16], parameters of motion of the lunar node (epoch) and general precession

Table 5.   Longitude parameters of planets of the ecliptic of the epoch [17]

Table 6.   The polynomial coefficients ${{a}_{j}}$ for the libration parameters in the Euler angles and for the direction cosines of the ecliptic ${{P}_{1}}$, ${{P}_{2}}$, relative to the system of the main axes of inertia of the Moon

3.2 Extracting LPhL Parameters from Numerical Ephemeris DE421

To obtain the libration angles of the Moon from the DE421 ephemeris, we used the Pleph function. For this, the necessary parameters were set NCTR = 0, NTARG = 15. The set returned by the function contains the values of the Euler angles that determine the system’s position of the main axes of inertia of the Moon relative to ICRF. To obtain the classical libration angles $\rho$, $\tau$, and $I\sigma$, the following transformation algorithm was used [18]:

(1) transition to the ICRF system using the Euler angles obtained by performing the Pleph function;

(2) transition to the equatorial coordinate system;

(3) determination of the vector directed to the descending node of the lunar equator on the ecliptic;

(4) calculation of Euler angles in an ecliptic coordinate system based on scalar and vector transformations;

(5) extraction of libration angles $\rho$, $\tau$, and $I\sigma$ from Euler angles.

Having performed all the necessary calculations using this algorithm, we extracted the values of the LPhL parameters from DE421, calculating ${{\tau }^{c}}$, ${{\rho }^{c}}$, and $I{{\sigma }^{c}}$ over an interval of 200 years, starting from J2000, with a step of 1 day. The obtained values were compared with the values ${{\tau }^{e}}$, ${{\rho }^{e}}$, and $I{{\sigma }^{e}}$, calculated by series (1) at the same time interval. The residual differences $\Delta \tau = {\text{|}}{{\tau }^{c}} - {{\tau }^{e}}{\text{|}}$, $\Delta \rho = {\text{|}}{{\rho }^{c}} - {{\rho }^{e}}{\text{|}}$, and $I\Delta \sigma =$ $I\; \times \;{\text{|}}{{\sigma }^{c}} - {{\sigma }^{e}}{\text{|}}$ presented in Fig. 1 were compared with the analogous values obtained in [8] (see Fig. 2).

Fig. 1.

Differences in the libration angles $\tau$, $\rho$, and $I\sigma$, obtained by comparing the data extracted from DE421 according to the developed algorithm, and calculated by the series [6].

Fig. 2.

Differences in latitude. The lower plot shows the difference in declination [6].

Analysis of the obtained differences showed that the discrepancy with the data [6] does not exceed 20 mas (marcsec) for all three angles. For libration in the slope $\rho$ over the given time interval, our calculations show a small trend, the nature of which is we haven’t figured out yet. However, within the accuracy required at this stage, the results obtained indicate both the correctness of the algorithm used by us for working with the DE421 numerical ephemeris, and the correct choice of the values of the parameters used.

3.3 Formation of Numerical Constants and Initial Values for the LPhL

As mentioned above, in order to solve differential equations within the framework of the Cauchy problem, it is necessary to correctly set the initial conditions. In addition, since the transition to the numerical orbit of the DE ephemeris was carried out, the used parameters, constants, and initial values for the libration angles and conjugate momenta must also be adjusted in accordance with the DE421 parameters (Table 7).

Table 7.   Constants included in the numerical integration model

The theory of physical libration that we are developing is based on the J2000 ecliptic, this must be borne in mind if it is necessary, for example, to go to the ecliptic of date. In this case, this would be the longitudes of the ascending node $\Omega$ from the ecliptic of date epoch from the node J2000, calculated by the coefficients in Table 4, as well as the inclination of the Earth’s equator to the ecliptic ${{\varepsilon }_{0}}$.

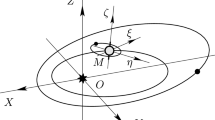
Let us consider an algorithm for calculating the initial conditions for the physical libration parameters. Recall that DE421 contains the traditional Euler angles and it is possible to determine the libration parameters $\tau$, $\rho$, and $I\sigma$ from them. In the theory we are developing, we operate with angles $\mu ,\;\nu ,\;\pi$ (see Table 6, Fig. 3) that determine the trihedron position of the Moon’s axes of inertia (dynamic coordinate system—DCS), directly relative to the ecliptic. They are also called aircraft angles [1]. The angles $\nu$ and $\pi$ are similar in meaning to the direction cosines of the ecliptic ${{P}_{1}}$, ${{P}_{2}}$, and the libration angle in longitude $\mu \sim \tau {{ + }^{2}}\left( {\tfrac{I}{2}} \right)\sin(2F)$ [2]. To bring into agreement these two different ways of describing the LPhL and to obtain the correct initial values for the angles $\mu$, $\nu$, and $\pi$, we need to program the transition from the DCS to the ecliptic system through the aircraft angles, and then the reverse transition from the ecliptic to the DCS, but already through the Euler angles $(\psi$, $\theta$, $\phi )$.

Fig. 3.

Libration angles $\mu$, $\nu$, and $\pi$. Selenocentric ecliptic coordinate system. The system $(\overline X$, $\overline Y$, $\overline Z )$ is an ecliptic system that rotates uniformly at the speed of the mean motion of the Moon. Frame $(\vec {x}$, $\vec {y}$, $\vec {z})$ represents DCS.

The mathematically necessary transition between the ecliptic and dynamic coordinate systems is carried out using rotation matrices, the rotation angles in which are either aircraft angles or Euler angles. This gives us a reason to relate different types of libration angles through the product of rotation matrices:

$${{R}_{x}}( - \pi ){{R}_{y}}(\nu ){{R}_{z}}(M) = {{R}_{z}}(\psi ){{R}_{x}}( - \theta ){{R}_{z}}(\varphi ).$$

(2)

Here, the angle $M = L + \mu$, where $L$ is the mean longitude of the Moon, measured from the axis directed to the vernal equinox.

$$\begin{gathered} \sin(\nu ) = \sin(\psi )\sin(\theta ), \\ \sin(\pi )\cos(\nu ) = \cos(\psi )\sin(\theta ), \\ \end{gathered} $$

$$\begin{gathered} \sin(M)\cos(\nu ) = \cos(\psi )\sin(\varphi ) \\ \, + \sin(\psi )\cos(\theta )\cos(\varphi ), \\ \end{gathered} $$

(3)

$$\begin{gathered} \cos(M)\cos(\nu ) = \cos(\psi )\cos(\varphi ) \\ \, - \sin(\psi )\cos(\theta )\sin(\varphi ). \\ \end{gathered} $$

Thus, Eqs. (3) enable us to obtain the initial values of the aircraft angles based on the Euler angles taken from DE421. To calculate the rate of change of angles, we differentiated expression (3) over time and obtained the necessary relations:

$$\begin{gathered} \dot {\nu }\cos(\nu ) = \dot {\psi }\cos(\psi )\sin(\theta ) + \dot {\theta }\sin(\psi )\cos(\theta ), \\ \dot {\pi }\cos(\pi )\cos(\nu ) = \dot {\nu }\sin(\pi )\sin(\nu ) \\ \, - \dot {\psi }\sin(\psi )\sin(\theta ) + \dot {\theta }\cos(\psi )\cos(\theta ), \\ \end{gathered} $$

$$\begin{gathered} \dot {M}\cos(M)\cos(\nu ) = \dot {\nu }\sin(M)\sin(\nu ) \\ \, - \dot {\psi }\sin(\psi )\sin(\varphi ) + \dot {\varphi }\cos(\psi )\cos(\varphi ) \\ \end{gathered} $$

(4)

$$\begin{gathered} \, + \dot {\psi }\cos(\psi )\cos(\theta )\sin(\varphi ) \\ \, - \dot {\theta }\sin(\psi )\sin(\theta )\cos(\varphi ) \\ \, + \dot {\varphi }\sin(\psi )\cos(\theta )\sin(\varphi ). \\ \end{gathered} $$

The LPhL equations, which are based on the canonical Hamilton equations, include not the velocities, but the momenta conjugate to the angular coordinates. To obtain canonical momenta, we use the features of Hamilton’s approach when working with canonical variables. According to [1], the projections of the angular velocity $\Omega$ of the Moon’s rotation in DCS are determined by the formulas:

$$\begin{gathered} {{\Omega }_{x}} = - \dot {M}\sin(\nu ) - \dot {\pi }, \\ {{\Omega }_{y}} = - \dot {M}\cos(\nu )\sin(\pi ) + \dot {\nu }\cos(\pi ), \\ {{\Omega }_{z}} = \dot {M}\cos(\nu )\cos(\pi ) + \dot {\nu }\sin(\pi ). \\ \end{gathered} $$

(5)

Substituting the projections of the angular velocity into the formula for calculating the kinetic energy $T$ of a solid body and considering that the canonical momenta are defined as ${{p}_{i}} = \tfrac{{\partial T}}{{\partial \mathop {\dot {q}}\nolimits_i }}$, where ${{q}_{1}} = \mu$, ${{q}_{2}} = \nu$, and ${{q}_{3}} = \pi$, we obtain the following expressions for them:

$$\begin{gathered} {{p}_{3}} = A{{\Omega }_{x}}, \\ {{p}_{2}} = B{{\Omega }_{y}}\cos(\pi ) + {{\Omega }_{z}}\sin(\pi ), \\ {{p}_{1}} = {{\Omega }_{z}}\cos(\nu )\cos(\pi ) - A{{\Omega }_{x}}\sin(\nu ) \\ \, - B{{\Omega }_{y}}\cos(\nu )\sin(\pi ). \\ \end{gathered} $$

(6)

In the transition to the portable frame of reference, tied to the DCS, the canonical momentum will be reduced by the value of the mean rotation velocity of the Moon $n$ [1]: ${{({{p}_{1}})}_{{{\text{DCS}}}}} = {{p}_{1}} - n$. As a result, Eqs. (5) and (6) allow calculating the necessary initial values for the canonical momenta.

Thus, we get the opportunity, firstly, based on the Euler angles extracted from DE421, to calculate the initial values of the libration parameters ${{\mu }^{0}}$, ${{\nu }^{0}}$, ${{\pi }^{0}}$ and their conjugate momenta $p_{1}^{0}$, $p_{2}^{0}$, $p_{3}^{0}$ in order to correctly carry out the numerical integration of the libration equations we have constructed, and secondly, to test the quality of the numerical solution $\mu (t)$, $\nu (t)$, $\pi (t)$ we obtain by comparing with the data calculated by the series [6].

4 ACCOUNTING FOR THE DIRECT AND INDIRECT INFLUENCE OF PLANETS ON THE LPhL

Indirect perturbations induced by the planets arise due to the influence of planets on the motion of the Moon’s mass center. Previously, we used the analytical theory of orbital motion [13], which was constructed for the limited problem of three bodies: the Earth, Moon, and Sun. At this stage, we come to the modern numerical orbit DE421, which was built considering perturbations from both planets and even asteroids. We carried out a number of tests (Sections 2 and 3) confirming the correctness of our transition to a new theory of motion of the lunar mass center. One of the assumptions that we put into our theory of libration is the fact that we consider the rotational and orbital motion of the Moon to be independent. The effect of spin-orbital interaction has a very small contribution to the accuracy of the rotational theory [19]. Therefore, our assumption is justified and it allows us, without changing the equations of rotation, to transfer calculations from one orbital theory to another one. Naturally, the transition to a new orbit also led to a recalculation of the initial data already for the numerical integration of the libration equations, which, in general, ensures an increase in the accuracy of the libration theory. Thus, the transition to ephemeris D421 provided us with automatic accounting for indirect perturbations induced by the planets.

To include direct perturbations from the planets, we have introduced the interaction effects of the Moon with Venus and Jupiter into the second harmonic of the selenium potential. Perturbations from other planets are not yet considered by us due to either their small masses or their great distances.

We obtained two solutions: $\mu$, $\nu$, $\pi$ without considering the direct perturbations from the planets and ${{\mu }^{p}}$, ${{\nu }^{p}}$, ${{\pi }^{p}}$ with consideration to these perturbations, and analyzed the obtained differences in these solutions $\Delta {{\mu }^{p}} = {\text{|}}{{\mu }^{p}} - \mu {\kern 1pt} {\text{|}}$, $\Delta {{\nu }^{p}} = {\text{|}}{{\nu }^{p}} - \nu {\kern 1pt} {\text{|}}$, $\Delta {{\pi }^{p}} = {\text{|}}{{\pi }^{p}} - \pi {\kern 1pt} {\text{|}}$ in order to estimate the contribution of disturbances from the planets to the libration angles. According to our calculations, it turned out that the behavior of $\Delta {{\nu }^{p}}$ and $\Delta {{\pi }^{p}}$ is practically the same; therefore, we show the differences only for two angles: $\Delta {{\mu }^{p}}$ and $\Delta {{\nu }^{p}}$ in Fig. 4.

Fig. 4.

Contribution of perturbations from planets to libration in longitude and libration in latitude.

Behavior analysis of the residual differences indicates that the contribution of perturbations from the planets is only a fraction of a milliarcsecond, which is much less than the required accuracy of both theory and observations. The obtained amplitudes of planetary contributions fully agree with the data of a similar work [20], which independently confirms the correctness of our calculations.

5 APPROXIMATE ACCOUNTING FOR THE TIDAL DEFORMATION OF THE LUNAR BODY

The model of an absolutely solid Moon is no longer consistent with the level of accuracy of modern observations. For adequate processing of data from the latest satellite missions and long-term series of laser ranging, it is necessary to consider the potential not of a solid but of a lunar body deformable due to tidal interaction with the Earth and the Sun. Due to solid-body tides, the body of the Moon “breathes” with an amplitude of about $\pm 10$ cm per month. In addition, the gravitational field and, accordingly, the physical libration are subject to the influence of tides. In [21], a thorough analysis of high-precision data on satellite tracking in the GRAIL mission [5] was carried out, based on the construction of a mathematical model of the lunar potential, including both elastic deformations and dissipation effects caused by the viscous properties of the lunar body and internal processes in the heated mantle on the depth of the outer liquid core.

In our study, we are not yet ready to solve the problem to the extent that it has been done by scientists from the NASA JPL laboratory, which have many years of experience in the development of the theory of the Moon’s rotation and the construction of geophysical models of its internal structure. But since we have set the task to develop our own instrument for describing the lunar rotation with the required accuracy, we made the first step in this direction at this stage—an approximate account of tidal deformation.

The essence of the method we use is that tidal deformation causes small constant changes in the inertia moments of the Moon $(A$, $B$, $C$, $\gamma$, $\beta )$, and in the second-order Stokes coefficients ${{C}_{{20}}}$ and ${{C}_{{22}}}$. The values of these averaged constants were obtained by analyzing laser observations [8]. Based on these data, we have developed an algorithm for accounting for mean tidal deformations.

(1) First, we calculate the solid-state components of the moments of inertia

$${{A}_{{{\text{Rigid}}}}} = \frac{{1 - \gamma \beta }}{{1 + \beta }},$$

$${{B}_{{{\text{Rigid}}}}} = \frac{{1 + \gamma }}{{1 + \beta }},$$

(7)

$$\frac{C}{{mR_{{{\text{Rigid}}}}^{2}}} = \frac{{ - 2{{c}_{{20}}}(1 + \beta )}}{{2\beta - \gamma + \beta \gamma }}.$$

(2) Then, we introduce the empirically determined in [8] corrections for the mean tide. Let $\overline {{{C}_{r}}} = \tfrac{c}{{m{{R}^{2}}}}$ be the normalized moment of inertia of the Moon, then due to tidal deformation, the moments of inertia will receive some corrections in the form:

$$A = {{A}_{{{\text{Rigid}}}}} + \frac{{\Delta A({{k}_{2}},s)}}{{\overline {{{C}_{r}}} }},$$

$$B = {{B}_{{{\text{Rigid}}}}} + \frac{{\Delta B({{k}_{2}},s)}}{{\overline {{{C}_{r}}} }},$$

$$C = {{C}_{{{\text{Rigid}}}}} + \frac{{\Delta A({{k}_{2}},s)}}{{\overline {{{C}_{r}}} }},$$

(8)

$${{C}_{{20}}} = {{C}_{{20{\text{Rigid}}}}} + \Delta {{C}_{{20}}},$$

$${{C}_{{22}}} = {{C}_{{22{\text{Rigid}}}}} + \Delta {{C}_{{22}}}.$$

(3) The Love numbers ${{k}_{2}}$ and the spherical term $s$ are presented in Table 7.

When solving the LPhL problem within the framework of the main problem [1, 2], the main moments of inertia were set in units of the main moment of inertia ${{C}_{{{\text{Rigid}}}}}$. With this approach, we can assume that ${{C}_{{{\text{Rigid}}}}} = 1$. Following this adopted system, all the main moments of inertia in (8) are also given in units of ${{C}_{{{\text{Rigid}}}}}$.

To check how significantly the corrections made for the tide will affect the quality of our solution, we first obtained our solid-state solution ${{\mu }^{r}}(t)$, ${{\nu }^{r}}(t)$, ${{\pi }^{r}}(t)$, built on the basis of the DE421 ephemeris, considering the corresponding constants (Table 7) and the initial values calculated from (3)–(6). Then, corrections (8) were made to the differential equations of LPhL, constructed earlier [1], and a numerical solution ${{\mu }^{d}}(t)$, ${{\nu }^{d}}(t)$, ${{\pi }^{d}}(t)$ was obtained, considering the mean tide. Based on the Euler angles extracted from DE421 and reduction formulas (3)–(6), we obtained the solution ${{\mu }^{{421}}}(t)$, ${{\nu }^{{421}}}(t)$, ${{\pi }^{{421}}}(t)$ on the same inter-val. Then, we constructed two types of residual di-fferences: $\Delta {{\mu }^{r}} = \left| {{{\mu }^{r}} - {{\mu }^{{421}}}} \right|$, $\Delta {{\nu }^{r}} = \left| {{{\nu }^{r}} - {{\nu }^{{421}}}} \right|$, $\Delta {{\pi }^{r}} = \left| {{{\pi }^{r}} - {{\pi }^{{421}}}} \right|$, $\Delta {{\mu }^{d}} = \left| {{{\mu }^{d}} - {{\mu }^{{421}}}} \right|$, $\Delta {{\nu }^{d}} = \left| {{{\nu }^{d}} - {{\nu }^{{421}}}} \right|$, $\Delta {{\pi }^{d}} = \left| {{{\pi }^{d}} - {{\pi }^{{421}}}} \right|$. Figure 5 presents plots of the behavior of both types of residuals. From the analysis of the plots in Fig. 5, it follows that the tide significantly affects the libration in latitude at the angles $\nu$ and $\pi$, but does not have a significant effect on the amplitude of libration in longitude $\mu$. In addition, the libration in longitude contains a fictitious frequency, the period of which is 1023.4 days, which is close to the resonance period of the system (1056.13 days). Similar harmonics are manifested in the libration in latitude: for $\nu$, the period of the fictitious harmonic is 27.22 days; and for $\pi$—27.16 days, while the resonance periods in latitude are 27.185 (for $I\sigma$) and 27.239 days (for $\rho$). The appearance of fictitious harmonics ${{\mu }^{r}}(t)$ or ${{\mu }^{d}}(t)$ in the solution either indicates that the initial values calculated by us do not correspond to the model laid down in equations [1]. This also explains the gradually increasing residual differences in both types of solutions. The DE421 solution was obtained considering many factors: a viscoelastic model with dissipation for the tidal potential, considering the differential rotation of the core and mantle, non-inertial forces (Coriolis force and centrifugal force), higher degrees of decomposition of the selenopotential, starting from the fourth harmonic, and direct perturbations from the planets (Jupiter and Venus).

Fig. 5.

Residual differences between the DE421 solution and the solution for the solid-body model (left) and the tidal model (right). All solutions are obtained in the angles $\mu$, $\nu$, $\pi$.

6 INFLUENCE OF THE 4TH HARMONIC OF THE SELENOPOTENTIAL

Analytical estimates show that the contribution to the perturbing potential from the 4th harmonic, and even more so from the 5th and 6th harmonics, is many times less compared to the 2nd and 3rd harmonics: $\tfrac{{{{U}_{3}}}}{{{{U}_{2}}}} \sim 3 \times {{10}^{{ - 4}}}$ and $\tfrac{{{{U}_{4}}}}{{{{U}_{2}}}} \sim 3 \times {{10}^{{ - 6}}}$. However, at the current level of requirements for the accuracy of the theory, the contribution of the 4th harmonic is significant. Having received a verified expression for the harmonic through the direction cosines (9), see below. We included it in the Hamiltonian and compared the obtained solution with the solution without considering this harmonic. Constructed residual differences $\Delta {{\mu }^{{(4)}}} = \left| {{{\mu }^{{(4)}}} - \mu } \right|$, $\Delta {{\nu }^{{(4)}}} = \left| {{{\nu }^{{(4)}}} - \nu } \right|$, $\Delta {{\pi }^{{(4)}}} = \left| {{{\pi }^{{(4)}}} - \pi } \right|$ are shown in Fig. 6

$$\begin{gathered} U(\rho ,\theta ,\varphi ) = \frac{{GM}}{\rho }\left( {1 + \mathop {\left( {\frac{a}{\rho }} \right)}\nolimits^2 } \right. \\ + \;[{{c}_{{20}}}{{P}_{2}}(\cos\theta ) + {{c}_{{22}}}\cos(2\lambda ){{P}_{{22}}}(\cos\theta )] \\ \end{gathered} $$

$$\begin{gathered} \, + \sum\limits_{n = 3}^\infty \,\sum\limits_{m = 0}^n \,\mathop {\left( {\frac{a}{\rho }} \right)}\nolimits^n [{{c}_{{nm}}}\cos(m\lambda ) \\ \left. {\mathop + \limits_{_{{_{{}}}}}^{^{{^{{}}}}} \;{{s}_{{nm}}}\sin(m\lambda )]{{P}_{{nm}}}(\cos\theta )} \right), \\ \end{gathered} $$

$$\begin{gathered} {{U}_{4}} = \frac{{G{{M}_{e}}}}{{a_{{em}}^{3}}}{{M}_{m}}{{a}^{2}}\mathop {\left( {\frac{{{{a}_{{em}}}}}{\rho }} \right)}\nolimits^5 \mathop {\left( {\frac{a}{{{{a}_{{em}}}}}} \right)}\nolimits^2 [\Lambda ]{\kern 1pt} {\kern 1pt} , \\ \\ [\Lambda ] = 0.375{{c}_{{40}}} + 7.5{{c}_{{42}}} - 15{{c}_{{42}}}u_{1}^{2} + 105{{c}_{{44}}}u_{1}^{4} \\ \\ \, - 15{{s}_{{42}}}{{u}_{1}}{{u}_{2}} + 420{{s}_{{44}}}u_{1}^{3}{{u}_{2}} - 630{{c}_{{44}}}u_{1}^{2}u_{2}^{2} \\ \\ - \;420{{s}_{{44}}}{{u}_{1}}u_{2}^{3} + 105{{c}_{{44}}}u_{2}^{4} - 7.5{{c}_{{41}}}{{u}_{1}}{{u}_{3}} \\ \\ + \;420{{c}_{{43}}}u_{1}^{3}{{u}_{3}} - 7.5{{s}_{{41}}}{{u}_{2}}{{u}_{3}} - 420{{s}_{{43}}}u_{2}^{3}{{u}_{3}} \\ \\ + \;3.75{{c}_{{40}}}u_{3}^{2} - 60{{c}_{{42}}}u_{3}^{2} + 105{{c}_{{42}}}u_{1}^{2}u_{3}^{2} \\ \\ + \;105{{s}_{{42}}}{{u}_{1}}{{u}_{2}}u_{3}^{2} + 17.5{{c}_{{41}}}{{u}_{1}}u_{3}^{3} + 17.5{{s}_{{41}}}{{u}_{2}}u_{3}^{3} \\ \\ + \;4.375{{c}_{{40}}}u_{3}^{4} + 52.5{{c}_{{42}}}u_{3}^{4} - 315{{c}_{{43}}}{{u}_{1}}{{u}_{3}}(1 - u_{3}^{2}) \\ \\ + \;315{{s}_{{43}}}{{u}_{2}}{{u}_{3}}(1 - u_{3}^{2}), \\ \end{gathered} $$

(9)

where ${{c}_{{ij}}},{{s}_{{ij}}}$ are the Stokes coefficients, ${{a}_{{em}}}$ is the mean Earth–Moon distance, $a$ is the mean Moon radius, $\rho$ is the instantaneous Earth–Moon distance, ${{M}_{{e/m}}}$ is the Earth/Moon mass, respectively, and ${{u}_{i}}$ is the directing radius-vectors of the perturbing body relative to the Moon center.

Fig. 6.

Contribution of the 4th harmonic to the LPhL solution.

Analyzing the residual differences in Fig. 6, we see that the contribution of the 4th harmonic to libration in longitude manifests itself both in the form of a constant shift by 0.9$''$ and in the form of periodic changes with amplitude of about 0.9$''$ and a period of 1056 days. Our previous calculations showed a similar manifestation of the 3rd harmonic of the selenopotential in libration [1], which describes the “pear-shaped” form of the Moon. As a result, the elongated “nose of the pear” carries out librational oscillations about the direction, which is approximately 200$''$ displaced to the east relative to the average direction to the Earth. But it turns out that the 4th harmonic also causes a permanent shift in the position of the x axis relative to the average direction to the Earth, but the magnitude of this shift is 2 orders of magnitude less than the contribution from the 3rd harmonic.

As for the contribution of the 4th harmonic to the libration in latitude, it is less noticeable compared to the effect on longitude. The inclusion in the selenium potential ${{U}_{4}}$ leads to the appearance of a long-period component, the nature of which we cannot yet explain: in the integration interval of 15 years, the harmonic period is no more than a quarter of this period.

7 CONCLUSIONS

The study of the celestial body rotation is the most important tool for studying its structure and for constructing a high-precision coordinate-time support system for solving navigation problems. For the Moon, both directions are very relevant. To date, on the basis of modern satellite data on the gravitational field of the Moon and thanks to the computer-mathematical analysis of a large number of long-term laser observations of the Moon, the JPL NASA laboratory has developed high-precision numerical theories of the DE series, which describe the spin-orbital dynamics of the lunar body. Dynamic ephemerides allow not only to adequately describe modern observations, and to clarify many parameters of the internal structure of the lunar body, the dynamic theory is a constantly evolving tool that allows one to study more and more subtle effects that determine lunar dynamics. Therefore, we were tasked to develop our own physical, mathematical and computer tools for describing the lunar rotation in a numerical way.

In work [1], we developed a numerical theory of physical libration for a model of a solid Moon. In this paper, we have shown the factors and methods, in which we were able to significantly improve the accuracy of the developed theory.

First of all, a necessary transition is made from a less accurate analytical theory of orbital motion to the numerical ephemeris DE421. The correctness of the algorithm developed by us for the inclusion of a numerical ephemeris (Sections 2 and 3) was verified by analyzing the residual differences when comparing our solution with similar solutions for the parameters of motion of the Moon’s mass center (Table 2).

The theory we are developing is based on the libration angles $\mu$, $\nu$, and $\pi$, which describe the trihedron position of the Moon’s axes of inertia (DCS) relative to the ecliptic, similarly to aircraft angles in aerodynamics (Fig. 2). In the numerical ephemeris DE, to describe the LPhL, the Euler angles and the corresponding librational corrections to them $\tau$, $\rho$, and $I\sigma$ are used. To check the correctness of this quantity extraction from the dynamic theory and for an a-dequate comparison of the results of the proper solution $\mu$, $nu$, and $\pi$, with the DE421 data, we constructed Eqs. (3)–(6), which allow us to carry out the transition from Euler angles to aircraft angles. These equations also made it possible to adequately calculate the initial conditions for the integration of libration equations and to verify the numerical values of the parameters included in the developed theory (Sec-tions 3.2 and 3.3).

The programs for calculating $\tau$, $\rho$, and $I\sigma$, developed by us, based on semiempirical series (1) constructed by Ramboux and Williams [6], significantly simplified the procedure for comparing our own results with actually observed data, since series [6] is an analytical representation of LPhL observations obtained on the basis of analysis of laser ranging measurements (Section 3.1).

Having checked the correctness of the algorithms for extracting data from the DE421 theory, we began to improve the model of the Moon’s rotation in the theory we are developing.

First, the transfer of our calculations to the DE421 ephemeris made it possible to automatically consider indirect perturbations from the Solar System planets, the effect of which is incorporated in the calculations of the motion of the lunar center mass.

Secondly, we included the interaction potential of the Moon with Venus and Jupiter (Section 4) in the equation of the second harmonic of the selenopotential, as well as estimated the contribution of this effect to the parameters of the Moon’s rotation (Fig. 4): it does not exceed a few milliarcseconds, which is in good agreement with similar data of [20].

Thirdly, we made an approximate account of the tidal deformation of the lunar body by including the constant additions determined in [8] in the tensor of inertia and the second-order Stokes coefficients based on the laser observation analysis. The inclusion of this effect when compared with the DE421 data reduced the amplitude of the residual differences in latitude by one order of magnitude. At the same time, we showed that the main role in this improvement of the results is played by the inclusion of tidal deformations in the Stokes coefficients; the effect of additions to the moments of inertia had practically no effect on the solution.

And finally, the selenium potential includes the 4th harmonic, due to which it was possible to get rid of the systematic difference in the libration in longitude from the systematic difference in the previous model [1] when compared with DE421. At the same time, in comparison with the 3rd harmonic, the 4th harmonic makes a small contribution to the permanent shift of the “nose of the Moon” relative to the average direction to the Earth (Section 6).

As a result, all of the above effects allowed us to build an improved LPhL model in comparison with the previous version [1]. Our improved theory differs from DE421 in the following way: variations of residual differences in the libration angle in longitude $\mu$ are from 1.1$''$ to 0.75$''$, in the angle $\nu$ they change from ‒2.3$''$ to 1.8$''$ and in the libration angle $\pi$ from –1.5$''$ to 2.7$''$.

Of course, the amplitude of the residual differences is still large enough to discuss achieving the required accuracy of our theory. Therefore, we are not going to stop there and still are developing methods and mathematical apparatus for including such effects as the influence of the Earth’s shape on the selenopotential, a more accurate rather than an approximate account of tidal phenomena, as well as the inclusion of a liquid core in the lunar body structure in the simplest Poincaré model.