Propagation of Elastic Waves in Dynamically Self-Similar Structures (Dynamic Fractals)

Abstract

The concept of a dynamically self-similar structure (dynamic fractal) is introduced, consisting in the similarity of the dynamic parameters of the cell generatrices. Elastic wave propagation in unbranched dynamically self-similar structures is investigated. It is shown that such structures are equivalent in frequency to a periodic structure with additional fixation; however, the nature of wave propagation in them significantly differs. A dynamic fractal can feature both attenuated waves and waves that increase along the length of the structure; the intensity of wave attenuation is stronger than in a periodic structure.

INTRODUCTION

Currently, there is increasing interest in the wave properties of periodic structures consisting of complex cells. Such structures include, in particular, metamaterials possessing unusual wave properties not found in nature, such as acoustic invisibility [1, 2]. Therefore, the study of wave propagation in such media is of paramount importance.

However, the class of periodic structures can be significantly expanded and supplemented with a class of self-similar fractal structures. According to B. Mandelbrot [3], distinctive features of fractals are “self-similarity, invariance with respect to zooming or scaling, and invariance with multiplicative changes in scale. In short, a self-similar object appears unchanged after both increasing and decreasing its size”.

Mandelbrot’s well-known geometric fractals [3, 4] describe structures that are similar in their geometric parameters. Their distinguishing feature is nonintegral dimensionality. Fractals can generally be considered as systemically relating local and global orders. It is this class of structures that prevails in nature and technology. Works by L.M. Lyamshev, V.V. Zosimov, and I.A. Urusovsky are devoted to the study of the wave and acoustic properties of fractal structures [5–7]. In these studies, elastic oscillations and waves in materials with a geometrically fractal structure were studied and their dispersion equations were found. Oscillations of fractal clusters are also studied, which are characterized by dependence of elastic properties on the scale of strain.

Nevertheless, the dynamic properties of a system determine its elastic–inertial parameters. Therefore, it is of interest to study the wave properties of structures consisting of cells similar in dynamic parameters, not geometric. For this, it is necessary to introduce the dynamic fractal concept, in contrast to Mandelbrot’s geometric fractals. To this end, scaling of the system parameters that determine its dynamic properties is logically required, i.e., the elastic and inertial parameters [8, 9].

SELF-SIMILAR STRUCTURE AND MATERIALS IN MECHANICS: DYNAMIC FRACTALS

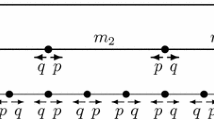
First, let us consider the simplest discrete unbranched one-dimensional structure consisting of masses connected by elastic elements.

Definition. We call structures in which the elastic and inertial parameters change with the same scale γ for each cell of the structure (or subsystem) dynamically self-similar (dynamic fractal):

$${{K}_{s}} = {\gamma }{{K}_{{s - 1}}},\,\,\,\,{{J}_{s}} = {\gamma }{{J}_{{s - 1}}},$$

(1)

K_s is the stiffness and J_s is the inertial parameter of the sth cell. This definition of a dynamic fractal is also true for structures in which the number of degrees of freedom of the cell generatrices is greater than unity. Moreover, each coordinate can have its own scaling factors (point 5).

A necessary consequence of conditions (1) is the equality of the partial frequencies for all cell generatrices:

$$\begin{gathered} {\nu }_{s}^{2} = {{\left( {{{K}_{s}} + {{K}_{{s - 1}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{K}_{s}} + {{K}_{{s - 1}}}} \right)} {{{J}_{s}}}}} \right. \kern-0em} {{{J}_{s}}}} = {\nu }{{_{{s + 1}}^{2}}^{{}}} = {{\left( {{{K}_{{s + 1}}} + {{K}_{s}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{K}_{{s + 1}}} + {{K}_{s}}} \right)} {{{J}_{{s + 1}}}}}} \right. \kern-0em} {{{J}_{{s + 1}}}}} \\ = {\text{const}} = {{{\nu }}^{2}}\,\,\,\,(s = 1....N). \\ \end{gathered} $$

(2)

The condition for equality of partial frequencies (2) is the condition of the dynamic self-similarity of structure (dynamic fractal).

We now consider an infinite discrete one-dimensional chain in which the sth cell consists of a concentrated mass m_s and springs with stiffness k_s. Let the elastic and inertial parameters change with the same scale γ from cell to cell (Fig. 1a). Then, the stiffness and mass for the element s + 1 is

$${{k}_{{s + 1}}} = {\gamma }{{k}_{s}},\,\,\,\,{{m}_{{s + 1}}} = {\gamma }{{m}_{s}}.$$

(3)

Fig. 1.

(a) Dynamically self-similar rod structure with concentrated masses, (b) equivalent periodic structure with same eigenfrequencies, (c) partial subsystem of dynamically self-similar structure.

Therefore, such a structure is a dynamic fractal.

The elastic coefficients needed to determine the partial frequencies of the cell generatrix are found with fixed cell boundaries (Fig. 1c). (If compliance coefficients are used in the equations, then the partial frequencies are determined for free cell boundaries.) For this chain

$${\nu }_{s}^{2} = {{\left( {{{k}_{{s - 1}}} + {{k}_{s}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{k}_{{s - 1}}} + {{k}_{s}}} \right)} {{{m}_{s}}}}} \right. \kern-0em} {{{m}_{s}}}}.$$

Condition (2) for the equality of the partial frequencies for each cell is fulfilled:

$$\begin{gathered} {\nu }_{s}^{2} = {{\left( {{{k}_{{s - 1}}} + {{k}_{s}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{k}_{{s - 1}}} + {{k}_{s}}} \right)} {{{m}_{s}}}}} \right. \kern-0em} {{{m}_{s}}}} = {\nu }_{{s + 1}}^{2} \\ = {{\left( {{{k}_{s}} + {{k}_{{s + 1}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{k}_{s}} + {{k}_{{s + 1}}}} \right)} {{{m}_{{s + 1}}}}}} \right. \kern-0em} {{{m}_{{s + 1}}}}} = {{{\nu }}^{2}} = {\text{const}}. \\ \end{gathered} $$

Comment. Note that conditions (2) for a dynamic fractal do not always coincide with the geometric similarity (scaling) conditions used in Mandelbrot geometric fractals. Indeed, let the elastic elements simulate longitudinal stiffness of a rod equal to Ef_s/l_s, and the inertial element be represented as a stiff ball of radius R (Fig. 1a), i.e., m_s=${{4\rho \pi R_{s}^{3}} \mathord{\left/ {\vphantom {{4\rho \pi R_{s}^{3}} 3}} \right. \kern-0em} 3}$ (here F_s is the cross-sectional area of the sth cell; l_s is its length). The geometric scaling conditions are F_s+1= γ²F_s, l_s= γl_s, R_s = γR_s. Obviously, in this case, conditions (2) for a dynamic fractal are not satisfied:

$${\nu }_{{s + 1}}^{2} = \frac{3}{4}\frac{{E{{F}_{S}}{{{\gamma }}^{{2s}}}}}{{{\rho }{{{\gamma }}^{{4s}}}{{l}_{s}}R_{s}^{3}}} = \frac{{{\nu }_{s}^{2}}}{{{{{\gamma }}^{2}}}} \ne {\text{const}}.$$

The inverse is also true: conditions (1), (2) can be satisfied without geometric similarity of all elements, only some of them. Let, e.g.,

$${{F}_{{s + 1}}} = {{{\gamma }}^{2}}{{F}_{s}},\,\,\,\,{{l}_{{s + 1}}} = {\gamma }{{l}_{s}},\,\,\,\,{{R}_{{s + 1}}} = {{{\gamma }}^{{1/3}}}{{R}_{s}}.$$

Despite the fact that the radius of the ball varies with a different similarity coefficient, γ^1/3, conditions (2) are satisfied:

$$\begin{gathered} {\nu }_{{s + 1}}^{2} = \frac{{E{{F}_{{s + 1}}}}}{{{\rho }{{l}_{{s + 1}}}{{4{\pi }{{R}_{{s + 1}}}^{3}} \mathord{\left/ {\vphantom {{4{\pi }{{R}_{{s + 1}}}^{3}} 3}} \right. \kern-0em} 3}}} \\ = \frac{3}{4}\frac{{E{{F}_{s}}{{{\gamma }}^{2}}}}{{{\rho }{{l}_{s}}{\gamma }{{{\left( {{{{\gamma }}^{{s/3}}}{{R}_{s}}} \right)}}^{3}}}} = {\nu }_{s}^{2} = {\text{const}}. \\ \end{gathered} $$

Thus, fulfillment of conditions (1), (2) for a dynamic fractal requires different scaling of the geometric parameters, which is a certain generalization of a geometric fractal.

FREQUENCY EQUIVALENCE OF DYNAMIC-SELF-SIMILAR AND PERIODIC STRUCTURES: DISPERSION EQUATION

The equation of the dynamically self-similar discrete structure shown in Fig. 1a can be written as finite difference equations. Thus, the equation for the s + 1st cell is

$$ - {{k}_{s}}{{x}_{s}} + ( - {{m}_{{s + 1}}}{{{\omega }}^{2}} + {{k}_{s}}(1 + {\gamma })){{x}_{{s + 1}}} - {\gamma }{{k}_{s}}{{x}_{{s + 2}}} = 0.$$

(4)

Where ${{{\mathbf{X}}}^{T}} = \left[ {{{x}_{1}},{{x}_{2}},{{x}_{3}}...{{x}_{n}}} \right]$, x_{s +1} is the displacement of the s + 1st mass and ${\omega }$ is natural oscillation frequency.

Equation (4) is the general form of the equation of a discrete dynamically self-similar chain structure (Fig. 1). For γ < 1, we obtain a structure with decreasing parameters along the length, and for γ > 1, increasing.

We replace the variables in (4):

$${{x}_{s}} = {{{{{\tilde {x}}}_{s}}} \mathord{\left/ {\vphantom {{{{{\tilde {x}}}_{s}}} {{{{\left( {\sqrt {\gamma } } \right)}}^{s}}}}} \right. \kern-0em} {{{{\left( {\sqrt {\gamma } } \right)}}^{s}}}}.$$

(5)

As a result, we find the equation for the s + 1st cell in new variables:

$$\begin{gathered} {{ - {{k}_{s}}{{{\tilde {x}}}_{s}}} \mathord{\left/ {\vphantom {{ - {{k}_{s}}{{{\tilde {x}}}_{s}}} {\sqrt \gamma }}} \right. \kern-0em} {\sqrt \gamma }} + \left( { - {{m}_{s}}{{{\omega }}^{2}} + \frac{{{{k}_{s}}(1 + {\gamma })}}{{\gamma }}} \right){{{\tilde {x}}}_{{s + 1}}} \\ - \,\,{{{{k}_{s}}{{{\tilde {x}}}_{{s + 2}}}} \mathord{\left/ {\vphantom {{{{k}_{s}}{{{\tilde {x}}}_{{s + 2}}}} {\sqrt \gamma }}} \right. \kern-0em} {\sqrt \gamma }} = 0. \\ \end{gathered} $$

Assuming ${{k}_{s}} = {{k}_{1}}{{{\gamma }}^{s}},$${{m}_{s}} = {{m}_{1}}{{{\gamma }}^{s}}$, we see that this equation is valid for any number s, since the ratio of its coefficients does not depend on s. It is convenient to write it in a form that describes the sth cell:

$$\begin{gathered} {{ - {{k}_{1}}{{{\tilde {x}}}_{{s - 1}}}} \mathord{\left/ {\vphantom {{ - {{k}_{1}}{{{\tilde {x}}}_{{s - 1}}}} {\sqrt {\gamma } }}} \right. \kern-0em} {\sqrt {\gamma } }} + \left( { - {{m}_{1}}{{{\omega }}^{2}} + \frac{{{{k}_{1}}(1 + {\gamma })}}{{\gamma }}} \right){{{\tilde {x}}}_{s}} \\ - \,\,\,{{{{k}_{1}}{{{\tilde {x}}}_{{s + 1}}}} \mathord{\left/ {\vphantom {{{{k}_{1}}{{{\tilde {x}}}_{{s + 1}}}} {\sqrt {\gamma } }}} \right. \kern-0em} {\sqrt {\gamma } }} = 0. \\ \end{gathered} $$

(6)

Equation (6) describes the periodic structure in Fig. 1b. The partial frequencies of each mass ${\nu }_{s}^{2} = {{\left( {{{k}_{{s - 1}}} + {{k}_{s}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{k}_{{s - 1}}} + {{k}_{s}}} \right)} {{{m}_{s}}}}} \right. \kern-0em} {{{m}_{s}}}}$ are identical by virtue of condition (3), the rigidity between the masses is ${{{{k}_{1}}} \mathord{\left/ {\vphantom {{{{k}_{1}}} {\sqrt {\gamma } }}} \right. \kern-0em} {\sqrt {\gamma } }},$ but at the same time there is additional fixation of the masses $k^{*} = \frac{{{{k}_{1}}(1 + {\gamma })}}{{\gamma }}$ – $\frac{{2{{k}_{1}}}}{{\sqrt {\gamma } }}$ = $\frac{{{{k}_{1}}{{{(1 - \sqrt {\gamma } )}}^{2}}}}{{\gamma }}.$ Therefore, the value of the elastic elements in the structure in Fig. 1b is the same for each cell and is determined only by the similarity coefficient.¹ In the range 0.16 < γ < 6.76, the stiffness of the additional fixation is less than the stiffness connecting the masses: $k^{*} < {{{{k}_{1}}} \mathord{\left/ {\vphantom {{{{k}_{1}}} {\sqrt \gamma }}} \right. \kern-0em} {\sqrt \gamma }}.$

The partial solution to Eq. (6) has the form [10, 11]

(7)

ω is the eigenfrequency and μ is the wave parameter characterizing the phase change upon transition from element s to s + 1. Here μ = κl, where κ is the wavenumber and l is the cell length.

Substituting (7) into (6), we find the dispersion equation for the periodic structure in Fig. 1b:

—for real μ: $- {{m}_{1}}{{{\omega }}^{2}} + \frac{{{{k}_{1}}(1 + {\gamma })}}{{\gamma }} - 2\frac{{{{k}_{1}}}}{{\sqrt {\gamma } }}\cos {\mu } = 0,$${{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{k}_{1}} = {{{{m}_{s}}} \mathord{\left/ {\vphantom {{{{m}_{s}}} {{{k}_{s}} = }}} \right. \kern-0em} {{{k}_{s}} = }}{{\nu }^{2}} = {\text{const}}}}} \right. \kern-0em} {{{k}_{1}} = {{{{m}_{s}}} \mathord{\left/ {\vphantom {{{{m}_{s}}} {{{k}_{s}} = }}} \right. \kern-0em} {{{k}_{s}} = }}{{\nu }^{2}} = {\text{const}}}};$

—for purely imaginary ${\mu } = i{\mu }{\kern 1pt} {{'}}$: $- {{m}_{1}}{{{{\omega }}}^{2}} + \frac{{{{k}_{1}}(1 + {{\gamma }})}}{{{\gamma }}} - 2\frac{{{{k}_{1}}}}{{\sqrt {{\gamma }} }}\operatorname{c} {\text{h}{\mu }}{\kern 1pt} {{'}} = 0.$

Figure 2a shows the dispersion curve for γ = 0.5 (ω₀ = 0.41ν, ω* = 2.41ν); Fig. 2b, the dispersion surface as a function of parameter γ.

Fig. 2.

(a) Dispersion curve for γ = 0.5: ω₀ = 0.41ν, ω* = 2.41ν; (b) dispersion surface as function of similarity coefficient.

The linear transformation of coordinates (5) does not change the frequency properties; therefore, the dynamic fractal in Fig. 1a and the periodic structure in Fig. 1b have the same frequencies. The periodic structure is a mechanical bandpass filter with a harmonic signal passband: ω₀ < ω < ω* (Fig. 2a), where

$${\omega }_{0}^{2} = {{\nu }^{2}}\frac{{{{{\left( {1 - \sqrt {\gamma } } \right)}}^{2}}}}{{\gamma }},\,\,\,\,{{{\omega }}^{{*2}}} = {{\nu }^{2}}\frac{{{{{\left( {1 + \sqrt {\gamma } } \right)}}^{2}}}}{{\gamma }}.$$

(8)

The passband is $\Delta {\omega = \omega *} - {{{\omega }}_{0}}.$ Here,

—for a chain decreasing in length, as follows from (8), $\Delta {\omega = 2\nu }{\text{,}}$ i.e., the passband width is independent of parameter γ and coincides with the that of the periodic structure without additional fixation. However, the boundary frequencies themselves, and therefore the location of the passband, depend on γ;

—for a chain increasing in length, $\Delta {\omega = \omega *} - \left| {{{{\omega }}_{0}}} \right|$ = ${{2{\nu }} \mathord{\left/ {\vphantom {{2{\nu }} {\sqrt {\gamma } }}} \right. \kern-0em} {\sqrt {\gamma } }},$ i.e., the passband width is inversely proportional to $\sqrt \gamma$ and ${\omega *} + {{{\omega }}_{0}} = 2{\nu }{\text{.}}$ For sufficiently large ${\gamma }$, the passband in the limit becomes very narrow and is located near the partial frequency ν; i.e., the system is tuned to only one specific frequency.

These results are confirmed by Table 1, which presents the boundary frequencies of the passband depending on coefficient γ. It follows from the table that in a chain decreasing in length (γ < 1), the lower passband boundary decreases with increasing γ and tends to 0, as in a periodic chain without fixation. In a chain increasing in length (γ > 1), conversely, as γ increases, the lower passband boundary increases.

Table 1.   Boundaryfrequencies of passbands for various coefficients γ

However, the difference in the squares of the cutoff frequencies does not depend on the type of chain

$$\Delta {{{\omega }}_{2}} = {{{\omega }}^{{*2}}} - {\omega }_{0}^{2} = \frac{{4{{k}_{1}}}}{{{{m}_{1}}\sqrt {\gamma } }} = {{{\nu }}^{2}}\frac{4}{{\sqrt {\gamma } }},$$

where Δω₂ is proportional to the difference in the kinetic energy of the system in the passband.

Transformation of coordinates (5) is the transformation of quadratic forms describing the potential and kinetic energy: ${{{\mathbf{x}}}^{T}}{\mathbf{Kx}} = {{{\mathbf{\tilde {x}}}}^{T}}{\mathbf{\tilde {K}\tilde {x}}},$${{{\mathbf{\dot {x}}}}^{T}}{\mathbf{M\dot {x}}} = {{{\mathbf{\tilde {\dot {x}}}}}^{T}}{\mathbf{\tilde {M}\tilde {\dot {x}}}}.$ Therefore, the dynamic fractal and corresponding periodic structure are equivalent in energy.

WAVE PROPAGATION IN DYNAMICALLY SELF-SIMILAR STRUCTURES

The nature of wave propagation in periodic and dynamically self-similar structures (dynamic fractal) is significantly different. Therefore, it is of interest to study the wave behavior of a dynamic fractal in and outside of the passband. The wave in such a structure, as can be seen from coordinate transformation (5), is obtained from the corresponding wave in the periodic structure in Fig. 1b by proportionally changing the oscillation amplitude of each section by ${1 \mathord{\left/ {\vphantom {1 {\sqrt {\gamma } }}} \right. \kern-0em} {\sqrt {\gamma } }}$ times. Figure 3 shows the higher natural oscillation form of a dynamic fractal with fixed ends. For the periodic structure in Fig. 1b, this is known to be a sinusoid in which adjacent masses are in antiphase. In a dynamic fractal (Fig. 1a), the oscillation amplitude is obtained by increasing (for γ < 1) the corresponding amplitude of the periodic structure by ${1 \mathord{\left/ {\vphantom {1 {\sqrt {\gamma } }}} \right. \kern-0em} {\sqrt {\gamma } }}$ times (or decreasing amplitude for γ > 1). Therefore, we obtain a wave with constantly increasing (decreasing) amplitudes (Figs. 3a, 3b). The envelope of this wave is the exponent. Thus, in a dynamic fractal with increasing length parameters in the passband, the level of oscillations decreases, while in a fractal with decreasing parameters, conversely, significant gain of the input signal can be achieved.

Fig. 3.

Natural oscillation forms of dynamically self-similar structure for ω₀ < ω < ω*: (a), (b) chain with parameters decreasing with length, γ < 1; (c), (d) chain with parameters increasing with length, γ > 1.

Unexpected wave properties acquire dynamic fractals in the opacity band. For a periodic structure (γ = 1), in these bands, as is known, exponential attenuation of the harmonic signal occurs along the chain [11]:

$${{X}_{s}} = A{{( - 1)}^{s}}{{e}^{{ - {{\mu }}\,s}}},\,\,\,\,{\text{ch}{\mu }} = (1 - {{{{{{\omega }}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{{\omega }}}^{{\text{2}}}}} {{\text{2}}{{{{\nu }}}^{2}}}}} \right. \kern-0em} {{\text{2}}{{{{\nu }}}^{2}}}}).$$

However, in dynamic fractals, not only attenuation is possible, but also amplification of the harmonic signal and even transformation of the opacity band into a passband. Indeed, the solution for the dynamic fractal, taking into account the transformation of coordinates (5), has the form

Therefore, the wavenumber is complex and the wave is inhomogeneous. Figure 2b can be considered as a dispersion surface in the complex plane, assuming ${\gamma = exp(2\alpha )}{\text{.}}$ In this case, the phase velocity becomes a complex quantity c_ph = ω/κ = ω/l(μ + iα).

For a dynamic fractal with increasing parameters (γ > 1) (Fig. 3b), both in and outside of the passband of the periodic structure, only an increase in the attenuation rate equal to μ + iα is possible: $X_{s}^{*} = A{{( - 1)}^{s}}\exp ( - \left( {{\mu + }i{\alpha }} \right)s)$.

However, a dynamic fractal with decreasing parameters has the following features: in such a system γ < 1; therefore ${\alpha }$ < 0, which means essentially negative damping. In this case, three different situations arise:

—if |α| > μ, then the opacity band disappears and waves appear in it, the amplitude of which increases along the chain with speed exp((|α| – μ)s),

—if |α| < μ, then attenuated waves arise; the attenuation rate is $X_{s}^{*} = A{{( - 1)}^{s}}\exp ( - \left( {{\mu } - \left| {\alpha } \right|} \right)s),$

—if |α| = μ > 1, then frequency Ω of transparency of the harmonic signal appears.

Table 2 shows the values of Ω for a chain with decreasing parameters in the opacity bands for various scale factors γ = 0.2, 0.5, 0.8.

As calculations show, in the first opacity band, 0 < ω < ω₀ and for all values γ the inequality |α| > μ. Therefore, this reject opacity band for the dynamic fractal disappears and the oscillation amplitude increases in proportional to exp(|α| – μ), while μ decreases when approaching the boundary frequency of interval ω₀.

In the second opacity band ($\omega > \omega {\text{*}}$) an excitation frequency Ω exists that is unique for each value γ for which |α| = μ > 1. This is the frequency of the harmonic signal. Then, for ω* < ω < Ω, the coefficient |α| > μ. In this range, the passband also disappears and waves appear that increase along the length of the structure with intensity exp(|α| – μ). However, as follows from Table 1, this range is very small, the frequencies Ω are located quite close to the boundary in opacity ranges, and this range decreases with an increase in γ < 1. For ω > Ω, the opacity band remains, but the attenuation intensity in it is equal to exp(μ – |α|), which is less than in the periodic system γ = 1.

Webster’s Equation. We note a certain analogy with the acoustic wave propagation in waveguides of variable cross section, which are described by Webster’s equation [12]:

$$\frac{1}{{S(x)}}\frac{\partial }{{\partial x}}\left( {S(x)\frac{{\partial p}}{{\partial x}}} \right) = \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}p}}{{\partial {{t}^{2}}}}.$$

(9)

Let the cross-sectional area change exponentially $S(x) = {{S}_{0}}\exp ({\beta }x).$ Depending on the sign of β, we obtain a structure decreasing or increasing in length. From (9), we find

$${\beta }\frac{{\partial p}}{{\partial x}} + \frac{{{{\partial }^{2}}p}}{{\partial {{x}^{2}}}} = \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}p}}{{\partial {{t}^{2}}}}.$$

Thus, a dissipative equation was obtained. The dispersion equation

$${{\omega }^{2}} - 2i\beta = {{\kappa }^{2}}{{c}^{2}}.$$

The phase velocity in this case depends on frequency and, in addition, is complex [13]. Depending on the sign of β, there will be either damped or increasing oscillations:

$${{c}_{{ph}}} = \frac{{\omega }}{{\varkappa }} = c{{\left( {1 + 2i\frac{{\beta }}{{\omega }}} \right)}^{{ - 1/2}}}.$$

The acoustic wave propagation in more complex systems with variable acoustic wall conductivity was studied in [14, 15]. It has been proven that the velocity of the wave can decrease and even vanish not reaching the edge of tube. The wave equation in this case is the generalized Webster equation.

DYNAMIC FRACTALS WITH MULTIDIMENSIONAL CELLS

In the preceding sections, one-dimensional chain structures were considered with cells having only one degree of freedom. However, in exactly the same way, we can investigate unbranched structures with multidimensional cells. As an example, let us consider propagation of bending waves in dynamically self-similar step section beam with disks attached (Fig. 4). We examine the waves in the vertical plane, taking into account the inertia of rotation of the cross section. We assume sectors of the beams are weightless; the inertial elements of the disks are mass m_s and inertia J_s. Movement of the sth node is described by a two-dimensional vector ${{{\mathbf{X}}}_{s}}$ with coordinates [$y,{\theta }$], where y is node motion and ${\theta }$ is the angle of rotation. We use a finite element model of the beam; in this case, each element of the beam system will be represented as one finite element. Such idealization is permissible for the low-frequency range if the length of the section does not exceed one-quarter of the wavelength [8].

Fig. 4.

Dynamically self-similar beam with step section.

Fig. 5.

Equivalent regular structure for dynamically self-similar beam.

The stiffness matrix of a planar beam finite element has the form [8, 16]

$$\begin{gathered} {\mathbf{K}} = \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{K}}}_{{11}}}}&{{{{\mathbf{K}}}_{{12}}}} \\ {{{{\mathbf{K}}}_{{21}}}}&{{{{\mathbf{K}}}_{{22}}}} \end{array}} \right];\,\,\,\,{{{\mathbf{K}}}_{{11}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{12EI}}{{{{l}^{3}}}}}&{\frac{{6EI}}{{{{l}^{2}}}}} \\ {\frac{{6EI}}{{{{l}^{2}}}}}&{\frac{{4EI}}{l}} \end{array}} \right], \\ {{{\mathbf{K}}}_{{12}}} = {{{\mathbf{K}}}^{T}}_{{21}} = \left[ {\begin{array}{*{20}{c}} { - \frac{{12EI}}{{{{l}^{3}}}}}&{ - \frac{{6EI}}{{{{l}^{2}}}}} \\ {\frac{{6EI}}{{{{l}^{2}}}}}&{\frac{{2EI}}{l}} \end{array}} \right], \\ \\ {{{\mathbf{K}}}_{{22}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{12EI}}{{{{l}^{3}}}}}&{ - \frac{{6EI}}{{{{l}^{2}}}}} \\ { - \frac{{6EI}}{{{{l}^{2}}}}}&{\frac{{4EI}}{l}} \end{array}} \right] = {\mathbf{T}}{{{\mathbf{K}}}_{{11}}}{\mathbf{T}},\,\,\,\,{\mathbf{T}} = \left[ {\begin{array}{*{20}{c}} 1&{} \\ {}&{ - 1} \end{array}} \right]. \\ \end{gathered} $$

(10)

${{{\mathbf{K}}}_{{ij}}}$ are the blocks of stiffness and inertia matrices of the finite element for the first and second end faces of the beam, respectively. The equation for the $s$th node of a beam of variable section is

$${{{\mathbf{K}}}_{{12}}}{{{\mathbf{x}}}_{{s - 1}}} + \left( {{{{\mathbf{K}}}_{{11}}} + {{{\mathbf{K}}}_{{22}}}} \right){{{\mathbf{x}}}_{s}} + {{{\mathbf{K}}}_{{21}}}{{{\mathbf{x}}}_{{s + 1}}} = {\mathbf{P}}.$$

(11)

Let the bending stiffness for each section ${{12E{{I}_{s}}} \mathord{\left/ {\vphantom {{12E{{I}_{s}}} {{{l}_{s}}^{3}}}} \right. \kern-0em} {{{l}_{s}}^{3}}}$ vary with the similarity coefficient γ. A fractal beam with geometric self-similarity satisfies this condition if the radius of the section and its length vary in the same γ ratio. Then, ${{12E{{I}_{s}}} \mathord{\left/ {\vphantom {{12E{{I}_{s}}} {{{l}_{s}}^{3}}}} \right. \kern-0em} {{{l}_{s}}^{3}}}$ = ${{12E{{I}_{{s - 1}}}{{{\gamma }}^{4}}} \mathord{\left/ {\vphantom {{12E{{I}_{{s - 1}}}{{{\gamma }}^{4}}} {{{{\gamma }}^{3}}l_{{s - 1}}^{3}}}} \right. \kern-0em} {{{{\gamma }}^{3}}l_{{s - 1}}^{3}}}$ = ${{{\gamma }12E{{I}_{{s - 1}}}} \mathord{\left/ {\vphantom {{{\gamma }12E{{I}_{{s - 1}}}} {l_{{s - 1}}^{3}}}} \right. \kern-0em} {l_{{s - 1}}^{3}}},$${{4E{{I}_{s}}} \mathord{\left/ {\vphantom {{4E{{I}_{s}}} {{{l}_{s}}}}} \right. \kern-0em} {{{l}_{s}}}} = {{{\gamma }}^{3}}{{4E{{I}_{{s - 1}}}} \mathord{\left/ {\vphantom {{4E{{I}_{{s - 1}}}} {{{l}_{{s - 1}}}}}} \right. \kern-0em} {{{l}_{{s - 1}}}}}.$

Each block of the stiffness matrix ${{{\mathbf{K}}}_{s}}$ for the sector s can be written as

$${{{\mathbf{K}}}_{{ij,s}}} = {{{\mathbf{\Gamma }}}^{{s/2}}}{{{\mathbf{K}}}_{i}}_{{j,1}}{{{\mathbf{\Gamma }}}^{{s/2}}}(i,j = 1,2),\,\,\,\,{\mathbf{\Gamma }} = \left[ {\begin{array}{*{20}{c}} {\gamma }&{} \\ {}&{{{{\gamma }}^{3}}} \end{array}} \right],$$

where ${{{\mathbf{K}}}_{i}}_{{j,s}}$ are the corresponding matrix blocks of the sth element.

To satisfy the dynamic fractal conditions, it is necessary that the inertial elements of the disk—weight m_s and moment of inertia J_s—change at the same scale, i.e., ${{m}_{s}} = {\gamma }{{m}_{{s - 1}}},$${{J}_{s}} = {{{\gamma }}^{3}}{{J}_{{s - 1}}}.$

Thus, in contrast to a one-dimensional cell, here each degree of freedom can have its own similarity coefficient; therefore, now we need to introduce the similarity matrix G. Then, Eq. (11) for the fractal beam in matrix form is

$$\begin{gathered} {{{\mathbf{\Gamma }}}^{{\left( {s - 1} \right)/2}}}{{{\mathbf{K}}}_{{21,s - 1}}}{{{\mathbf{\Gamma }}}^{{\left( {s - 1} \right)/2}}}{{{\mathbf{x}}}_{{s - 1}}} \\ + \,\,( - {{\omega }^{2}}{{{\mathbf{M}}}_{s}} + {{{\mathbf{\Gamma }}}^{{\left( {s - 1} \right)/2}}}{{{\mathbf{K}}}_{{22,s - 1}}}{{{\mathbf{\Gamma }}}^{{\left( {s - 1} \right)/2}}} \\ + \,\,{{{\mathbf{\Gamma }}}^{{{s \mathord{\left/ {\vphantom {s 2}} \right. \kern-0em} 2}}}}{{{\mathbf{K}}}_{{11,s}}}{{{\mathbf{\Gamma }}}^{{{s \mathord{\left/ {\vphantom {s 2}} \right. \kern-0em} 2}}}}){{{\mathbf{x}}}_{s}} + {{{\mathbf{\Gamma }}}^{{{s \mathord{\left/ {\vphantom {s 2}} \right. \kern-0em} 2}}}}{{{\mathbf{K}}}_{{12,s}}}{{{\mathbf{\Gamma }}}^{{{s \mathord{\left/ {\vphantom {s 2}} \right. \kern-0em} 2}}}}{{{\mathbf{x}}}_{{s + 1}}} = 0, \\ \end{gathered} $$

where ${{{\mathbf{M}}}_{s}} = \left[ {\begin{array}{*{20}{c}} {{{m}_{s}}}&{} \\ {}&{{{J}_{s}}} \end{array}} \right].$

This is a finite difference equation with variable coefficients depending on s. We apply, as above, transformation of coordinates ${{{\mathbf{x}}}_{s}} = {\mathbf{x}}_{s}^{*}{{\Gamma }^{{ - s/2}}}.$ Then, under the new coordinates, we find for the sth node of the beam

$$\begin{gathered} {{{\mathbf{\Gamma }}}^{{ - 1/2}}}{{{\mathbf{K}}}_{{21}}}{\mathbf{x}}_{{s - 1}}^{*} + ( - {{{\mathbf{M}}}_{s}}{{\omega }^{2}} + {{{\mathbf{\Gamma }}}^{{ - 1/2}}}{{{\mathbf{K}}}_{{22}}}{{{\mathbf{\Gamma }}}^{{ - 1/2}}} \\ + \,\,{{{\mathbf{K}}}_{{11}}}){\mathbf{x}}_{s}^{*} + {{{\mathbf{K}}}_{{12}}}{{{\mathbf{\Gamma }}}^{{ - 1/2}}}{\mathbf{x}}_{{s + 1}}^{*} = 0. \\ \end{gathered} $$

(12)

Thus, we have obtained a finite difference equation with coefficients independent of the cell number, i.e., the equation of a periodic structure. For a physical interpretation of the elastic part of Eq. (12), we represent the expression in parentheses as

$$\begin{gathered} {{{\mathbf{K}}}_{{11}}} + {{{\mathbf{\Gamma }}}^{{ - 1/2}}}{{{\mathbf{K}}}_{{22}}}{{{\mathbf{\Gamma }}}^{{ - 1/2}}} = {{{\mathbf{\Gamma }}}^{{ - 1/2}}}({{{\mathbf{K}}}_{{11}}} + {{{\mathbf{K}}}_{{22}}}){{{\mathbf{\Gamma }}}^{{ - 1/2}}} + \Delta {\mathbf{K}}, \\ \Delta {\mathbf{K}} = {{{\mathbf{K}}}_{{11}}} - {{{\mathbf{\Gamma }}}^{{ - 1/2}}}{{{\mathbf{K}}}_{{11}}}{{{\mathbf{\Gamma }}}^{{ - 1/2}}}. \\ \end{gathered} $$

Note that Eq. (12) describes a regular structure consisting of identical beam elements of form (10), but with additional fixation $\Delta {\mathbf{K}}$ at each node. This additional fastening is the beam, the stiffness of which is proportional to the difference between the stiffnesses of the beams of the first and second sectors.

In conclusion, note that the dynamic fractals discussed above can be considered elements of a metamaterial. They can find successful application due to their compactness, as well as an increase in damping/amplification of the input signal.

Table 2.   Values of passband frequency Ω of harmonic signal in the second opacity band ($\omega > {\omega *}$)

CONCLUSIONS

(1) The concept of a dynamically self-similar structure (dynamic fractal) is introduced, which consists in similarity of the dynamic parameters of the cell generatrices.

(2) The frequency equivalence of the dynamic fractal and the periodic structure with additional fastening of the mass is proved.

(3) In dynamic fractals with parameters increasing in length, a stronger attenuation in the oscillation level occurs compared to periodic structures, which is important for vibroisolation systems.

(4) In dynamic fractals with decreasing parameters in length:

—there are inhomogeneous waves with amplification of the input signal, which distinguishes a dynamic fractal from a periodic structure in which signal amplification does not occur;

—the passband of the harmonic signal of the dynamic fractal is in the region the opacity band of the periodic structure, but quite close to its boundary.

(5) In multidimensional unbranched chains, each degree of freedom can have its own similarity coefficient; therefore, it is necessary to consider the similarity matrix.