INTRODUCTION

The last few decades have passed under the sign of advanced development of microsystem technology for various purposes (for example, see [1–3]). This is connected not only with their power efficiency and low material consumption, but also with the emergence of devices, where the use of such equipment is the only possible one. For example, such a situation is realized when creating new generation computers or in different medical applications. Most of these devices have some fluid flow. Of course, such flows are also typical in various natural objects and systems.

The difficulty of experimental studies of fluid flows in microchannels and nanochannels is quite obvious. A natural alternative to the experimental study of these flows is their modeling. At the same time often standard hydrodynamic approaches are used in the assumption that fluid transport coefficients in microchannels and nanochannels are the same as in the volume. For obvious reasons, the viscosity cannot be measured in such channels. The only method to determine it is molecular modeling. Unfortunately, the well-known method of molecular dynamics (MD) is inapplicable for modeling processes of the transfer of rarefied gas, since it requires a huge number of molecules (the characteristic channel size must be much larger than the free path length of gas molecules). Earlier we developed a method of stochastic molecular modeling (SMM) for modeling rarefied gas transport coefficients [4–6]. This method is able to simulate with high accuracy the coefficients of diffusion and viscosity of both monoatomic and polyatomic rarefied gases. The aim of this work is to simulate the viscosity of rarefied gases in nanochannels using the SMM method. For this purpose the method [4–6] is first generalized for modeling the gas transport processes in confined conditions. Its applicability is demonstrated on the modeling of self-diffusion of rarefied gas molecules in nanochannels.

SMM METHOD IN CONFINED CONDITIONS

The main idea of the SMM method is based on two formal factors. The first is obvious: the molecular nature of a substance. The stunning success of direct molecular modeling has been demonstrated by the MD method, which is widely used in physics, mechanics, chemistry and biology. However, the MD method, based on solution of Newton equations for particles of the modeling system, does not provide the real phase trajectories [7, 8]. Dynamical chaos takes place in molecular systems. Adequate data can be obtained only by the averaging of a large number of independent phase trajectories of the modeled system. The second factor follows from here: modeling of the phase trajectories stochastically and then computation of any observables by averaging by a large number of such trajectories.

For modeling transfer processes in confined conditions, the SMM method [4–6] must be transformed. First, in confined conditions it is necessary to take into account the interaction of gas molecules with the channel wall. For this reason, despite the fact that a rarefied gas is modeled, the transport coefficients of which depend only on the molecule velocities [9], now it is necessary to simulate evolution of the considered system both in velocity space and in configuration space.

The interaction of gas molecules with the boundary in this work is described using specular or specular-diffuse laws of reflection [10]. During specular reflection the molecule velocity along the surface does not change, and the normal component changes its sign. During diffuse reflection the velocity of the reflected molecule is played out according to the Maxwell distribution function. During specular-diffuse reflection a fraction of molecules θ interacts with the wall diffusely, and (1 − θ), specularly, where θ is the so-called accommodation coefficient.

This work is devoted to modeling the transport coefficients of weakly nonequilibrium gas, in which the fluxes are proportional to the gradients of corresponding hydrodynamic variables. In general they are determined by fluctuation-dissipative theorems [8, 11], according to which the transport coefficients are integrals of two-time correlation functions of corresponding dynamical variables. Importantly, these correlation functions are calculated by the equilibrium distribution function. This particularly means that the dissipative coefficients (of viscosity, heat conductivity, diffusion, etc.) are determined by equilibrium microfluctuations of the medium. In accordance with this, for the purposes of this work, it is necessary to simulate the equilibrium state of the system. The equivalence of fluctuational-dissipative theorems to formulas of the kinetic theory of gases for calculating the transport coefficients was proven in works [12, 13] (see also [8]).

At the initial moment of time the molecules are distributed uniformly in the volume according to the predefined density n. The molecule velocities vi are played out in the modeling cell in accordance with the Maxwell distribution at the predefined temperature T. The interaction of the molecules with each other is described by an arbitrary pair potential. In this work we used the Lennard–Jones potential [6–12].

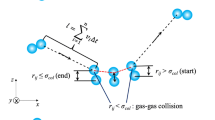
Simulation of the dynamics of gas molecules begins with making list of them, which includes the coordinates and velocities of all molecules of the system at some moment of time. Then the computation time of a single phase trajectory ts is split into steps with the duration τi = σ/\({{{v}}_{{i,\max }}}\), where σ is the effective molecule size and \({{{v}}_{{i,\max }}}\) is the maximal value of the molecule velocity at step i. We assume that at the moment of time t the molecules have velocities v1, v2, …, vN, coordinates r1, r2, …, rN, and it is necessary to generate their corresponding values at the moment of time (t + τ1). First the position of the molecule i is determined, it is shifted in configuration space according to its velocity: \({\mathbf{r}}_{1}^{'}\) = r1 + v1τ1. If the molecule reaches a wall, then its velocity changes according to the reflection law and taking the new velocity into account, the final spatial coordinate is determined.

If the molecule i does not reach a wall, then its collision with fluid molecules is played out. Since rarefied gas is considered, then the probability of collision of the molecule i for time τ1 is determined on the basis of kinetic theory [9]: Pc1 = \(4{{\tau }_{1}}n{{\sigma }^{2}}\sqrt {(\pi kT{\text{/}}m)} \) (k is the Boltzmann constant and m is the mass of the molecule). For this purpose, a number u, which is uniformly distributed for the segment [0, 1], is generated. If this number is less than or equal to Pc1, then collision occurs. In order to realize this, a molecule j is randomly selected from the remaining (N − 1) molecules. Then the velocities of the molecules i and j are changed according to the laws of elastic collision:

$${\mathbf{v}}_{i}^{'} = {{{\mathbf{v}}}_{i}} + ({{{\mathbf{v}}}_{{ij}}} \cdot {\mathbf{e}}){\mathbf{e}},\quad {\mathbf{v}}_{j}^{'} = {{{\mathbf{v}}}_{j}} + ({{{\mathbf{v}}}_{{ji}}} \cdot {\mathbf{e}}){\mathbf{e}},$$
(1)

where vji = (vj − vi) is the vector of relative velocity, e is a unit vector directed from the center of the molecule j towards the center of the molecule i.

The realization of relation (1) requires a certain accuracy. The motion of this pair of molecules occurs in a plane determined by the vectors rji = rj − ri and vji and begins with the distance 0 ≤ b ≤ σ/2 (b is the impact parameter). At the same time the amount of motion M = m(rji × vji), M = \(m{{{v}}_{{ji}}}b\) is maintained relative to the center of the field as well as energy E, which equals \(m{v}_{{ji}}^{2}{\text{/}}2\). Next it is necessary to connect the vector e with scattering parameters. The corresponding procedure is described in detail in [5].

If the generated number u turned out to be greater than the average collision probability, then the molecule i does not collide in the time interval τ1 and its velocity does not change. A similar procedure is performed sequentially for all N molecules. As a result, by the end of time (t + τ1) the complete list of phase variables of the system (coordinates and velocities) is formed. After the list is formed by the moment of time (t + τ1) the next time interval is selected and the procedure is repeated until the predetermined computation time ts = τ1 + τ2 + … + τk runs out. The computation results in a complete set of coordinates and velocities of the modeled system at sequential moments of time.

MODELING OF THE SELF-DIFFUSION COEFFICIENT IN A NANOCHANNEL

Testing of the described SMM algorithm in the general case is a complicated task due to the absence of real reliable experimental data on measuring the transfer coefficients and there is little hope to obtain them. For this purpose, in this work we modeled the self-diffusion coefficient D of rarefied argon at atmospheric pressure and a temperature of 273 K. Testing is possible, since the value of the self-diffusion coefficient along a sufficiently long channel must correspond to its value in the bulk.

The modeling cell was selected in the form of a rectangular parallelepiped, along the axes of which periodic boundary conditions were used. Intermolecular interaction was described by the Lennard−Jones potential, the effective molecule diameter σ was equal to 0.311 nm, and the depth of the potential well \(\epsilon {\text{/}}k\) = 116 K [14]. The self-diffusion coefficient D was calculated on the basis of the fluctuation-dissipative theorem [8, 11], which couples it with the autocorrelation function of velocity (ACFV) \({{\chi }_{{{vv}}}}\) of the molecules by the relation

$$D = \frac{1}{3}\int\limits_0^\tau {{{\chi }_{{{vv}}}}(0,t)dt} ,\quad {{\chi }_{{{vv}}}}(t) = \frac{1}{{Nl}}\sum\limits_{i = 1}^N {\sum\limits_{\alpha = 1}^l {[{{{\mathbf{v}}}_{i}}(t) \cdot {{{\mathbf{v}}}_{i}}(t + \alpha \Delta t)],} } $$
(2)

where τ is the so-called plateau value of time of computation of integral (2), l is the number of time intervals, at which ACFV was computed, and Δt is the step of integration over time.

According to (2), evolution of ACFV completely and entirely determines the self-diffusion coefficient. For rarefied gas, all the correlation functions, including ACFV (2), must attenuate exponentially with a relaxation time comparable with the free path time of its molecules [8]. The situation in the nanochannel is different. The interaction of gas molecules with the channel walls leads to the fact that ACFV along the channel gains a negative branch, the depth and size of which depend on the channel height. In this way, the diffusion of gas molecules in the channel is nonisotropic. It should proceed along the channel in the same way as in the bulk; here the medium is unrestricted. Indeed, computations show that the ACFV of gas molecules quickly attenuates exponentially along the channel.

In the bulk, the value of the diffusion coefficient measured in the experiment is obtained only when function (2) reaches the plateau value. The time of reaching the plateau value corresponds to the attenuation of ACFV. Evolution of the self-diffusion coefficient of argon along the channel with a square cross-section, which equals 100σ2 (about 10 nm2), is presented in Fig. 1a. Here the interaction of gas molecules with the wall was described by specular law, and time here and further is normalized to the free path time of the molecules. The self-diffusion coefficient was averaged by a thousand phase trajectories. Coefficient (2) along the channel reaches the plateau value for a time of about 15–20 free path times of the molecules. On the contrary, evolution of the diffusion coefficient across the channel (see Fig. 1b) is much more complicated, first some growth is observed and then it steadily decreases and tends to zero. At the same time this occurs quite quickly, the corresponding time will be determined by the channel height.

Fig. 1.
figure 1

Evolution of the self-diffusion coefficient along (a) and across the channel (b).

Full size image

The coefficient of self-diffusion of the molecules can also be determined using the Einstein relation for the root-mean-square displacement of the molecules:

$${{R}^{2}}(t) = \frac{1}{{Nl}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{l - 1} {{{{[{{{\mathbf{r}}}_{i}}(j\Delta t) - {{{\mathbf{r}}}_{i}}(t + j\Delta t)]}}^{2}}} } = 6Dt.$$
(3)

This obviously implies corresponding relations, which determine the root-mean-square displacements along each axis. Figure 2a presents evolution Y2 (diffusion along the channel). It proceeds according to law (3) and Y2 grows linearly with time. On the other hand, root-mean-square displacement across the channel (X2) is presented in Fig. 2b for channels of different heights: the dotted line corresponds to a channel with a height of 50σ, and the dashed line, to 30σ. The root-mean-square displacement across the channel stops depending on time, and this means that the corresponding diffusion coefficient tends to zero.

Fig. 2.
figure 2

Evolution of the root-mean-square displacement of gas molecules along (a) and across (b) the channel.

Full size image

The above-mentioned absence of isotropy of the coefficient of self-diffusion of argon molecules in the nanochannel is quite expected. The SMM method gives a qualitatively physically quite reasonable result. However, its use requires a clear understanding of how accurately the algorithm allows calculating the transport coefficients of rarefied gases. This can be established. The coefficient of self-diffusion along the channel must correspond to the value in the bulk and it can be comparable with the experimental data. Clearly, the accuracy of modeling will depend on the channel length, and thus on the number of molecules in the cell. As an example of studying this dependence, Table 1 shows the comparison of the calculated data of the self-diffusion coefficient of argon in a channel with a square cross section of 100σ2 under normal conditions. The first line shows the number of molecules in the cell, second, the channel length, third, the calculated value of the self-diffusion coefficient, and the last, the relative error in comparison with the experimental value. The length of the channel L changed from 1000σ to 32 000σ (i.e., from about 0.3 to 100 μm). In the last case it could already be expected that the self-diffusion coefficient will be close to the corresponding value in the bulk. It really turned out to be like this. The experimental value of the self-diffusion coefficient in the bulk equals 0.156 cm2/s [15] and the modeling accuracy at the maximal channel length turned out to be about one percent (see Table 1). A similar result is also obtained for channels of any other cross section.

Table 1. Relative error of computation of the self-diffusion coefficient at various lengths of the channel L
Full size table

It is clear that in the general case, in stochastic modeling of the phase trajectories, the accuracy should substantially depend on the number of independent phase trajectories l used for averaging. The performed systematic calculations showed that the modeling accuracy here, as in the bulk, is well described by the relation Δ ∼ \({\text{1/}}\sqrt l \).

MODELING OF THE VISCOSITY COEFFICIENT IN A NANOCHANNEL

Now let us consider modeling the viscosity of argon at atmospheric pressure and a temperature of 273 K. The channel has a square cross section, its height varied from 20σ to 1607σ.

The viscosity coefficient was averaged by a thousand independent phase trajectories. The viscosity coefficient was determined by the relation (V is the volume of the system)

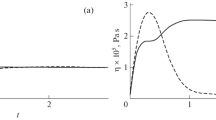
$$\eta = \frac{1}{{3VkT}}\int\limits_0^\tau {\left\langle {{\boldsymbol{\sigma }}(0):{\boldsymbol{\sigma }}(t)} \right\rangle dt} ,\quad {\boldsymbol{\sigma }}(t) = \frac{1}{{Nl}}\sum\limits_{j = 1}^l {\sum\limits_{i = 1}^N {m[{{{\mathbf{v}}}_{i}}(j\Delta t){{{\mathbf{v}}}_{i}}(j\Delta t)].} } $$
(4)

A nanochannel is a significantly nonisotropic system. Thus, the process of impulse transfer along and across the channel, which determines corresponding contributions to the viscosity coefficient, must be different as well. The value of the viscosity coefficient (4) is determined by the integral of the corresponding correlation function. The evolution of this correlation function χn normalized to the initial values along and across the channel is presented in Fig. 3a. The correlation function across the channel has a characteristic negative tail conditioned by the interaction of argon molecules along (solid line) and across (dashed line) the nanochannel with the wall. In this example, interaction with the wall was described by a specular law and the channel height was equal to 50σ. The presence of the negative tail leads to the fact that the contribution of molecules across the channel into the viscosity coefficient turns out to be almost twenty times less than along the channel. The corresponding values are presented in Fig. 3b. In this way, the complete viscosity coefficient of gas in the channel is almost three times lower than in the bulk.

Fig. 3.
figure 3

Evolution of the normalized correlation function (a) and viscosity coefficient (b).

Full size image

The law of interaction of gas molecules with the wall will substantially change impulse transfer in the system. For example, in a channel with a height of 50σ at θ = 0 (specular reflection) the viscosity coefficient constitutes 0.82 × 10–5 Pa s, at θ = 0.5, 2.76 × 10–5 Pa s, and at θ = 1 (purely diffuse reflection), 5.07 × 10–5 Pa s. The corresponding value of the viscosity coefficient in the volume was 2.14 × 10–5 Pa s. Thus, when the accommodation coefficient changes from zero to unity, the gas viscosity coefficient changes more than six times.

Naturally, anisotropy of the viscosity is a universal property and takes place for any gases. In this work besides argon we studied the viscosity of crypton, xenon and neon. The parameters of the potentials of intermolecular interaction for these gases are significantly different: Kr is σ = 0.36 nm, \(\epsilon {\text{/}}k\) = 171 K, Ne is σ = 0.279 nm, \(\epsilon {\text{/}}k\) = 35.7 K, Xe is σ = 0.41 nm, \(\epsilon {\text{/}}k\) = 221 K [14]. Table 2 presents comparison of the calculated and experimental values on viscosity on a channel with square cross section and specular walls, its height constituted 17 nm and length, 390 nm. The first line shows data of the viscosity coefficient along the channel ηa, second, the experimental values [16], third, the relative error of modeling, and the last, the relation of the viscosity coefficient along the channel to its value across the channel ηc. The largest anisotropy is recorded for neon. It can be seen in Table 2 that anisotropy grows with decreasing the Lennard–Jones potential well and increasing the characteristic molecule size σ. The latter, in confined conditions, is generally quite an important factor, since while maintaining the specified pressure and temperature, the numerical density will significantly change. Indeed, the characteristic volume of molecules, such as neon and xenon, differs by more than three times.

Table 2. Comparison of the viscosity coefficients in the nanochannel
Full size table

CONCLUSIONS

Boltzmann’s kinetic theory basically provides a method for calculating the transport coefficients of a rarefied gas. This method, however, is not trivial and requires a consistent solution of the system of integral equations [9]. The situation becomes complicated for multiatomic gases and in the case, when it is necessary to take into account internal degrees of freedom (for example, see [17–19]). Traditional kinetic theory does not allow calculation of the gas transport coefficients in a nanochannel at all. This requires use of the kinetic equation with a source term, which described the interaction of gas molecules with the wall [20].

In this work the SMM method is generalized for modeling the transport coefficients of a rarefied gas in confined conditions including nanochannels. Its performance is demonstrated using the example of calculating the self-diffusion coefficient of rarefied argon. It was shown that the accuracy of the method grows with increasing number of molecules in the cell and the number of phase trajectories used for averaging. The relative modeling error in the volume is as follows: Δ ∼ \({\text{1/}}\sqrt {lN} \) [4–6]. However, in confined conditions, the situation is more complicated. To achieve a given accuracy, at a certain channel cross section, its length should be at least a certain one. Otherwise, the required plateau value of the corresponding transfer coefficient will simply not be achieved.

The SMM method is genetically connected with the well-known method of direct statistical modeling (DSM) by Bird [21], which has been successfully implemented in recent decades for computing flows of rarefied gases. At present many different implementations of this method are known [22–24]. DSM simulates a nonequilibrium state, and to calculate the transport coefficients, it is sufficient (and necessary!) to study the equilibrium state. If DSM solves the spatially uniform problem, realization of collision dynamics can be accomplished by various, but ideologically similar techniques. The SMM algorithm uses one of the simplest. Spatially nonuniform problems, including the problems of internal and external flows, are solved by DSM in a substantially different way. In fact, some mesh method is also involved. Finally, we can add that the SMM method, strictly speaking, has no relation to the Monte Carlo method. A stochastic process is not constructed here, which would be a solution to the kinetic equation. For the DSM method, such approaches are known.

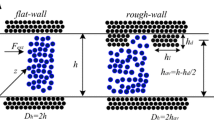
Studying the gas viscosity in a nanochannel shows that impulse transfer processes and thus the viscosity as well in these channels are nonisotropic. By varying the wall materials, it is possible to control the average viscosity of gas in the channel. Usually, real channels have roughness. Its presence leads to an increase in the surface area of the channel. This means that the nonisotropy of gas transfer in such channels will be more pronounced than in a channel with smooth walls. Thus, the presence of roughness may lead to its decrement as well. It all depends on the nature of interaction of gas molecules with the surface.

Finally, it is important to have an answer to the question when the processes of impulse transfer become practically isotropic. An indirect answer to this question is given in Fig. 4, which shows the dependence of the ratio of the viscosity coefficient of argon along the channel to its value across the channel (ηr = ηa/ηc), on the channel height. In computations, the specular law of interaction of the molecules with walls was used. Here dots correspond to simulation data, the approximation (continuous curve) is built by them such that hr ∼ h–0.59. The dashed line in Fig. 4 corresponds to isotropic viscosity (hr = 1). Analysis of the presented dependence shown that nonisotropy of the viscosity can be observed not only in nanochannels, but also in microchannels.

Fig. 4.
figure 4

Dependence of the relation of the viscosity coefficient of argon along and across the channel on its height.

Full size image

The nature of flows in confined conditions is determined by corresponding transfer processes, the experimental studies of which are complicated for obvious reasons. It is only possible to obtain some integral information, which is interpreted using classical hydrodynamic representations. As a result, it is indicated that in such flows, on the one hand, the slip length can increase significantly, and on the other hand, a significant increase in the viscosity coefficient is observed (see, for example, [1–3, 24]). These two conclusions are mutually contradictory: the first fixes a significant decrease in hydraulic resistance, and the second, its increase. The study of the viscosity of the gas, presented in this work, shows that in practice, both results can be practically realized.