Conical Singular Points and Vector Fields

Abstract

We consider several examples of mechanical systems the configuration spaces of which have the form of smooth manifolds with a unique singular point: two intersecting (or tangent) curves on a two-dimensional torus, four curves on a four-dimensional torus with a common point, and a two-dimensional cone (cusp) in ${{\mathbb{R}}^{6}}$. The main problem presented in this paper is the calculation of the (co)tangent space above the singular point by means of various theoretical approaches. Outside singular points, the motion of the mechanisms in question is described in the context of classical mechanics. However, in the neighborhood of a singular point, terms like “tangent vector” and “cotangent vector” must have conceptually new definitions. In this paper, the approach of the theory of “differential spaces” is used. In the case of a conical singular point, to calculate (co)tangent space, we use two various differential structures: the algebra of functions locally constant near the cone vertex and the algebra of restrictions of smooth functions from enveloping space to a cone. In the first case, tangent and cotangent spaces at the cone vertex are zero. In the second case, the algebra of functions on the cotangent bundle consists of functions locally constant on the cotangent layer above the singular point.

1 INTRODUCTION

In the general case, a mechanical system has the form of a system of material points and distributed bodies, the movements of which are restricted (connected). Configuration space of the system represents a smooth manifold M. Thus, positions of the hinge mechanism are given by the coordinates of the vertices and the angles of rotation of the rods. If the configuration space of the hinge mechanism contains singular points, then it is impossible to apply the concepts of differential geometry and classical mechanics to describe its movement. To formulate problems concerning kinematics in this case, it is necessary to use methods of the geometry of singular spaces.

There are several approaches to constructing differential geometry on sets for which the structure of a smooth manifold is not specified. In differential calculus over commutative algebras [1, 2], all concepts of differential geometry (such as points, tangent vectors, and vector fields) are formulated in terms of the algebra of functions. In the obtained algebraic terms, the concept of “smoothness” is no longer present. Other theories, such as differential spaces [3, 4] and Frölicher spaces [5], in addition to the algebra of functions, also consider the original point space on which topology is assigned.

In [6], we consider the case in which the configuration space of a mechanical system near a singular point represents a union of two smooth curves. In the present paper, on the basis of this mechanism, we construct mechanisms whose configuration spaces represent four smooth curves, a cone, or a cusp. The dynamics on the union of several curves can be divided (formally) into several movements separately for each curve; however, for a cone or a cusp, such a representation does not exist. For singular points, a set of velocity vectors of smooth curves passing through a singular point is considered. In studies of the kinematics of mechanisms, methods of differential spaces are used. Two differential structures on a cone, their (co)tangent spaces at a singular point, and phase space T *X are considered.

2 CONFIGURATION SPACES WITH SINGULAR POINTS

Consider several examples of mechanical systems with singularities of configuration space. They are obtained on the basis of a singular pendulum. The configuration spaces of these mechanisms represent two intersecting (or tangent) curves, four intersecting (or tangent) curves, and a cone or a cusp.

2.1 Singular Pendulum

Consider flat double pendulum ABC with rods AB and BC. Point A is fixed (a fixed hinge), whereas point C moves only along a given curve γ (e.g., an ellipse) [7]. Friction in the model is not taken into account. We call this mechanism a “singular pendulum.” Each possible position of the mechanism is given by a pair of angles (φ, ψ) of deviations of rods AB and BC from a vertical straight line. The condition that point C moves only along the given curve γ specifies an additional relation on angles φ and ψ (Fig. 1). Angle u measures the deviation of straight line AC from the AX axis (taking into account the angle sign).

Fig. 1.

Singular pendulum.

Theorem [7]. The configuration space of the singular pendulum lies on a two-dimensional torus (with coordinates (φ, ψ)) and represents in the general case two smooth curves c₁ and c₂ without common points. We can choose a curve γ in such a way the curves c₁ and c₂ have a single common point ω. Geometrically, point ω corresponds to the following configuration of the mechanism: rods AB and BC are codirectional (and directed parallel to the AX axis) at u = 0.

Note that, locally, it is possible to arrange any degree of a touch of curves c₁ and c₂ at common point ω.

2.2 Double Singular Pendulum

We modify a singular pendulum by adding a symmetrical pendulum to it. Note that the singular pendulum can be constructed as follows: a double ABC pendulum is “attached” to point C on a given curve γ and fixed point A. Analogously, we can add symmetrically another double pendulum ADC. The second pendulum can have the same lengths of rods |AB| and |BC| or other lengths. With two identical (symmetrical) pendulums ABC and ADC, we obtain a mechanism similar to “scissors” (Fig. 2). We obtain a “double singular pendulum.” The configuration space of a double singular pendulum has the form of four smooth curves with a common point.

Fig. 2.

Double singular pendulum.

2.3 Rotating Singular Pendulum

The configuration spaces of singular and double singular pendulums are one-dimensional manifolds with singular points. It is also possible to construct two-dimensional manifolds with singular points. For example, assume that the vertical axis of a singular pendulum is stationary and the plane of the pendulum Π rotates around the AX axis. Each position of the flat pendulum outside a singular point is matched by an additional degree of freedom: the rotation of the pendulum around the vertical axis (Fig. 3). We call this mechanism a “rotating singular pendulum.” Vertices B(x₁, y₁, z₁) and C(x₂, y₂, z₂) are located now in ${{\mathbb{R}}^{3}}$. The configuration space of the pendulum in coordinates (φ, ψ, ξ) is the surface of rotation. Angles φ and ψ correspond to the deviations of rods AB and BC from the vertical axis (coordinates on the torus), whereas ξ is the angle of rotation of the pendulum in the plane orthogonal to vertical axis AX. When rotated by angle ξ = π, the pendulum passes into a symmetrical position and remains in the same plane. Coordinates of the pendulum in space ${{\mathbb{R}}^{{3 + 3}}}$ have the following form:

$${{x}_{1}} = {{l}_{1}}\cos \varphi ,\quad {{x}_{2}} = {{l}_{1}}\cos \varphi + {{l}_{2}}\cos \psi ,$$

$${{y}_{1}} = {{l}_{1}}\sin \varphi \cos \xi ,\quad {{y}_{2}} = ({{l}_{1}}\sin \varphi + {{l}_{1}}\sin \psi )\cos \xi ,$$

(1)

$${{z}_{1}} = {{l}_{1}}\sin \varphi \sin \xi ,\quad {{z}_{2}} = ({{l}_{1}}\sin \varphi + {{l}_{2}}\sin \psi )\sin \xi .$$

Fig. 3.

Rotating singular pendulum.

2.4 Spatial Singular Pendulum

Consider another modification of a singular pendulum. For example, point A and curve γ lie in the same (fixed) plane Π, while vertex C of pendulum ABC can move freely along curve γ. The two-link ABC can freely rotate around the AC axis at a fixed position of vertex C. We call this mechanism a “spatial singular pendulum.” The only singular point of this mechanism corresponds to a singular point of the singular pendulum: rods AB and BC must be codirectional at u = 0. Outside a singular point, the mechanical system has two degrees of freedom (Fig. 4). Distance |AC|(u) = d(u) is a smooth function of angle u. If u = 0 corresponds (locally) to the minimum or maximum value of d(u), then we must have d'(0) = 0.

Fig. 4.

Spatial singular pendulum.

We find the dependence of the coordinates of points B(x₁, y₁, z₁) and C(x₂, y₂, z₂) on angles u, θ, and ξ. Note that, when rotating around the AX axis, the x coordinates of points B and C do not change. Since point A and curve γ lie in common plane Π, straight line AC also lies in plane Π. Angle u measures the deviation of straight line AC from vertical straight line AX in plane Π. Angle θ measures the deviation of rod AB from straight line AC in the ABC plane. Angle ξ indicates the angle of rotation of point B relative to straight line AC lying in plane Π (Fig. 4). To determine angle ξ, we can construct plane Π₁ (passing through point B) orthogonal to straight line AC. Assume that Π₁ intersects AC at point N. From point N in plane Π, draw straight line NM perpendicular to straight line AC. Angle ξ is the angle between straight lines NM and NB.

Proposition. The configuration space of a spatial singular pendulum has a singularity of the type of a conical (or cuspidal) singular point.

Proof. We find the coordinates of point B. Note that its coordinates can be obtained with three rotations around certain axes. If we rotate straight line AC by angle –u (Fig. 4) around point A in plane Π, then the straight line AC ' will be parallel to the AX axis. Point C will move to C ' and point B will move to B'. If we then rotate point B' by angle –ξ around the AC ' (or AX) axis, then point B'' will lie in plane Π (Oxy plane).

Acting in reverse order, we obtain the following sequence of steps. Consider point B'' = (l₁ cos θ, l₁ sin θ, 0) in plane Π. We turn point B'' by angle ξ in the plane orthogonal to the AX axis and passing through point B''. We then rotate straight line AC ' in plane Π by angle u relative to the AX axis. We obtain the coordinates of vertices B and C:

$${{x}_{1}} = {{l}_{1}}\cos \theta \cos u - {{l}_{1}}\cos \xi \sin u\sin \theta ,\quad {{x}_{2}} = d(u)\cos u,$$

$${{y}_{1}} = {{l}_{1}}\cos \theta \sin u + {{l}_{1}}\cos \xi \cos u\sin \theta ,\quad {{y}_{2}} = d(u)\sin u,$$

(2)

$${{z}_{1}} = {{l}_{1}}\sin \xi \sin \theta ,\quad {{z}_{2}} = 0.$$

At u = 0, angle θ is also zero. In Eqs. (2), at u = 0, θ = 0, and any ξ, we obtain the same coordinates of points B and C. Their values are B = (l₁, 0, 0) and C = (d(0), 0, 0). The velocity vector of the mechanical system at a singular point depends on angle ξ, with which the spatial pendulum moves to a singular point. In fact, the velocity vector at u → 0 and θ → 0 is determined by the following expression:

$$\begin{gathered} {{\left. {({{{\dot {x}}}_{1}},{{{\dot {y}}}_{1}},{{{\dot {z}}}_{1}},{{{\dot {x}}}_{2}},{{{\dot {y}}}_{2}},{{{\dot {z}}}_{2}})} \right|}_{{(u = 0,\theta = 0)}}} = (0,{{l}_{1}} + {{l}_{1}}\theta {\kern 1pt} '(0)\cos \xi ,{{l}_{1}}\theta {\kern 1pt} '(0)\sin \xi ,d{\kern 1pt} '(0),d(0),0)\dot {u}(0) \\ = [(0,{{l}_{1}},0,d{\kern 1pt} '(0),d(0),0) + {{l}_{1}}\theta {\kern 1pt} '(0) \cdot (0,\cos \xi ,\sin \xi ,0,0,0)]\dot {u}(0). \\ \end{gathered} $$

(3)

Hence, the velocity vector of point B at a singular point depends on limit value ξ. In the general case, configuration space X has a conical singular point: the directions of tangent vectors from (3) at a given value of $\dot {u}(0)$ form a circle in ${{\mathbb{R}}^{6}}$, and the value of $\dot {u}(0)$ = 0 is matched by one point (0, 0, 0, 0, 0, 0).

If θ'(0) = 0 and d'(0) = 0, then the expression for the tangent vector (3) is simplified,

$${{\left. {({{{\dot {x}}}_{1}},{{{\dot {y}}}_{1}},{{{\dot {z}}}_{1}},{{{\dot {x}}}_{2}},{{{\dot {y}}}_{2}},{{{\dot {z}}}_{2}})} \right|}_{{(u = 0,\theta = 0)}}} = (0,{{l}_{1}},0,0,d(0),0) \cdot \dot {u}(0),$$

and does not depend on angle ξ. Therefore, X has a feature of the cusp type at a singular point for θ'(0) = 0 and d '(0) = 0, because the velocity vectors of all smooth curves on X have only one direction at a singular point.

It is also possible to modify a spatial singular pendulum to distinguish angle ξ with which point B comes to a singular point (it is matched by the value of angle u = 0). For example, rod AB can be added by an additional rod DE. In this case, point D is located on segment AB and rod DE itself is attached in such a way that it is always contained in the plane passing through points A, B, and C. It is assumed that rod AB cannot rotate around its axis. Then, for different angles ξ, with which vertex B comes to a singular point, we will obtain geometrically different configurations of a modified spatial singular pendulum.

The motion of a singular pendulum can be divided into two independent motions, in which the coordinates of the vertices change smoothly. However, for a mechanism with a cuspidal singular point, it is no longer possible to distinguish a finite set of possible one-dimensional movements. To consider the kinematics of a spatial singular pendulum, it is necessary to use methods of the geometry of singular spaces.

3 DIFFERENTIAL STRUCTURES ON A CONE

To determine the differential equation by geometric methods, it is necessary to construct a vector field on the phase space of the system. In the case of space with singularities, these concepts need to be given accurate definitions. In the case of smooth manifolds, these definitions must coincide with the standard concepts of differential geometry: tangent vectors, vector fields, etc. Generalizations are based on the fact that many concepts of differential geometry can be formulated, e.g., in algebraic terms that do not use the concept of “smoothness.”

3.1 Differential Spaces

We present several calculations for differential spaces on a cone (or a cusp). First, we describe the necessary “dictionary” of terms.

Consider topological space X and the algebra of functions F on it. For  f ∈ F, we have the definition for smooth shell sc(F) (or a smooth closure) of algebra F:

$$sc(F) = \{ g({{f}_{1}}, \ldots ,{{f}_{k}}),{{f}_{i}} \in F,g \in {{C}^{\infty }}({{\mathbb{R}}^{k}},\mathbb{R}),k \in \mathbb{N}\} .$$

Taking the second smooth shell does not change the algebra: sc(sc(F)) = sc(F).

Definition. A pair (X, F) is called a differential space if (1) algebra F coincides with its smooth closure: F = sc(F) and (2) function f is contained in algebra F if and only if, for any point x ∈ X, there exist open neighborhood U_x and function g ∈ F such that ${{\left. f \right|}_{{{{U}_{x}}}}}$ = ${{\left. g \right|}_{{{{U}_{x}}}}}$ (every local function from F is contained in F).

Definition. Assume that (X, F) and (Y, G) are differential spaces. The mapping h : X → Y is called “smooth,” if for any function f ∈ G, composition h $\circ$ f lies in the set of functions F.

Definition. Assume that (X, F) is a differential space and point x ∈ X. Linear operator Δ : F → $\mathbb{R}$ is called a “tangent vector” at point x ∈ X if for it the Leibniz identity

$$\Delta (fg) = \Delta (f)g(x) + f(x)\Delta (g)$$

holds.

The set of all tangent vectors at point x ∈ X is tangent space T_xX. Tangent space T_xX has a natural linear structure. Similarly, tangent vectors can be obtained using smooth curves.

Definition. Curve c : $\mathbb{R}$ → X is called “smooth” if, for any function f ∈ F, composition f $\circ$ c : $\mathbb{R}$ → $\mathbb{R}$ is a smooth function.

The velocity vector of a smooth curve at point x,

$${{\Delta }_{{c,x}}}(f) = (f \circ c){\kern 1pt} '(0),$$

is a tangent vector in the operator sense; ${{\Delta }_{{c,x}}} \in {{T}_{x}}X$.

Definition. Assume that (X, F) is a differential space. Linear operator Δ : F → F is called an (operator) vector field if for it the Leibniz identity

$$\Delta (fg) = \Delta (f)g + f\Delta (g)$$

holds.

We denote by D(F) the set of vector fields of algebra F (or differentiations of algebra F). For vector field V ∈ D(F), the value of the field at point ${v}$ = ${{V}_{x}}(f)$ = ${{\left. {V(f)} \right|}_{x}}$ determines tangent vector ${v} \in {{T}_{x}}X$.

Covectors in the singular case can be considered as differentials of functions from the algebra.

Definition. Suppose that  f ∈ F. Differential of the function f at point x ∈ X is the linear mapping df : T_xX → $\mathbb{R}$ acting by the rule

$$d{{f}_{x}}({v}) = {v}(f).$$

We denote the set of all differentials (or covectors) at point x ∈ X by $T_{x}^{*}X$. For the differential space (X, F_X), its tangent bundle TX = ${{ \cup }_{{x \in X}}}{{T}_{x}}X$ can also be endowed with the structure of differential space. For the algebra of functions on the tangent bundle, we can take the prototypes of functions in the projection of π : TX → X and the differentials of the functions

$${{F}_{{TX}}} = sc(\{ \pi \circ f,f \in {{F}_{X}}\} \cup \{ df,f \in {{F}_{X}}\} ).$$

(4)

The cotangent space T*X = ${{ \cup }_{{x \in X}}}{{T}_{x}}X$ can also be endowed with a structure of differential space:

$${{F}_{{T{\text{*}}X}}} = sc(\{ \pi \circ f,f \in {{F}_{X}}\} \cup \{ V^*,V \in D({{F}_{X}})\} ).$$

(5)

Operator V* acts on covector df at point x ∈ X as follows:

$$(V{\kern 1pt} ^*{\kern 1pt} (df))(x) = {{V}_{x}}(df).$$

The principle of localization [2]. Suppose that (X, F) is a differential space. Assume that there is function η ∈ F with the following properties: we can find two neighborhoods U₁ and U₂ of point x (x ∈ U₁ ⊂ U₂ ⊂ U) such that η = 1 in neighborhood U₁ and η = 0 outside neighborhood U₂. The value of vector field Δ : F → F can be determined “locally”: Δ( f )|_x = Δ( f |_U)|_x.

Assume that, in neighborhood U of point x, algebra F |_U is isomorphic to algebra C^∞(${{\mathbb{R}}^{n}}$) for some n. By the principle of localization, vector fields outside singular points coincide with vector fields for smooth manifolds. We use this fact in order to, first, calculate vector fields outside a singular point and, then, find conditions for coefficients of vector fields.

We now investigate two differential structures on cone X.

3.2 Constant Functions near the Vertex

Consider the algebra of functions A_c that are locally constant near the vertex of the cone (such functions on the cone are considered, e.g., in ([4], pp. 5–12)):

$${{A}_{c}} = \{ {{\left. f \right|}_{X}}|f \in {{C}^{\infty }}({{\mathbb{R}}^{3}}),\exists {{U}_{0}}:{{\left. f \right|}_{{{{U}_{0}}}}} \equiv \operatorname{const} \} .$$

Proposition. Vector fields for a differential space (X, A_c) turn to zero at a singular point. Tangent space T₀X and cotangent space $T_{0}^{*}X$ have zero dimension.

Proof. Consider vector fields for the differential space (X, A_c). There is smooth function η_ε equal to 1 in the (ε/2)-neighborhood of the vertex of the cone and equal to zero outside ball B_ε(s) for any ε > 0. According to the principle of localization, vector fields outside a singular point have the forms of ordinary smooth vector fields. Conversely, if there is smooth (outside the vertex of the cone) vector field Δ, then for function f ∈ A_c there exists neighborhood U of the vertex of the cone such that f |_U = const. Then,

$${{\left. {\Delta (f)} \right|}_{s}} = {{\left. {\Delta ({{{\left. f \right|}}_{U}})} \right|}_{s}} = {{\left. {\Delta (0)} \right|}_{s}} = 0.$$

If for each vector field Δ ∈ D(A_c) we determine a value at a singular point as zero, then we obtain operator Δ : A_c → A_c: any function has a neighborhood in which it is constant and becomes zero when differentiated locally.

The tangent space at a singular point is zero, because tangent vectors are also localizable:

$${{\Delta }_{x}}(f) = {{\Delta }_{x}}({{\left. f \right|}_{U}}) = {{\Delta }_{x}}(c) = 0.$$

This means that the tangent space at a singular point is zero. Cotangent space $T_{s}^{*}X$ is then also zero. The structure of functions on the cotangent bundle is as follows:

$$V{\kern 1pt} ^*{\kern 1pt} (df) = {{V}_{x}}(f) = {{V}_{x}}({{\left. f \right|}_{U}}) = 0.$$

Hence, the tangent and cotangent spaces for the cone at a singular point are zero.

A smooth curve on X can pass the vertex of the cone with only zero velocity vector or zero momentum. However, then the curve’s state at the vertex of the cone coincides with the state of rest.

3.3 Functions on the Cone

Consider algebra A = ${{\left. {{{C}^{\infty }}({{\mathbb{R}}^{3}})} \right|}_{X}}$ of the restrictions of smooth functions from enveloping space ${{\mathbb{R}}^{3}}$ to cone X.

Proposition. For differential space (X, A), operator tangent space T₀X and cotangent space $T_{0}^{*}X$ have dimension 3.

Proof. Embedding a cone into space ${{\mathbb{R}}^{3}}$ gives a description of the tangent space at the vertex of the cone. In fact, the constraint pr : ${{C}^{\infty }}({{\mathbb{R}}^{3}})$ → A is surjective. The mapping of tangent spaces d|pr| : T₀A → ${{T}_{0}}{{\mathbb{R}}^{3}}$ is then injective (see ([2], pp. 160–165)). Consequently, the dimension of the tangent space at the vertex of the cone is not greater than 3. From the vertex of the cone can come three curves γ₁, γ₂, and γ₃ whose tangent vectors $\gamma _{1}^{'}(0)$, $\gamma _{2}^{'}(0)$, and $\gamma _{3}^{'}(0)$ are not coplanar at a singular point. The tangent vector of each curve gives the operator tangent vector ${{\Delta }_{{{{\gamma }_{i}},0}}}$, i = 1, 2, 3. The standard coordinate tangent vectors

$${{\left. {\frac{\partial }{{\partial x}}} \right|}_{0}},\quad {{\left. {\frac{\partial }{{\partial y}}} \right|}_{0}},\quad {{\left. {\frac{\partial }{{\partial z}}} \right|}_{0}}$$

are expressed in terms of vectors ${{\Delta }_{{{{\gamma }_{i}},0}}}$ and represent linearly independent tangent vectors at the vertex of the cone. Hence, tangent space T₀X is three-dimensional.

For differential df of function f from algebra A and any tangent vector ${v}$ ∈ T₀A, the following relation holds:

$${{d}_{0}}f({v}) = {v}(f) = \left( {{{{\left. {{{c}_{1}}\frac{\partial }{{\partial x}}} \right|}}_{0}} + {{{\left. {{{c}_{2}}\frac{\partial }{{\partial y}}} \right|}}_{0}} + {{{\left. {{{c}_{3}}\frac{\partial }{{\partial z}}} \right|}}_{0}}} \right)f = \frac{{\partial f}}{{\partial x}}(0){{d}_{0}}x({v}) + \frac{{\partial f}}{{\partial y}}(0){{d}_{0}}y({v}) + \frac{{\partial f}}{{\partial z}}(0){{d}_{0}}z({v}).$$

The covectors d₀x, d₀y, and d₀z then generate cotangent space $T_{0}^{*}X$ and are linearly independent. Hence, the cotangent space at the singular point has dimension 3.

Since algebra A outside the singular point coincides with the algebra of smooth functions on a plane, the cotangent space outside the singular point is two-dimensional.

Proposition. For differential space (X, A), vector fields V ∈ D(A) turn to zero at the vertex of the cone.

Proof. In the general case, for subset Y of Cartesian space ${{\mathbb{R}}^{N}}$, the following condition is met. For differential space (Y, C^∞(${{\mathbb{R}}^{N}}$)|_Y), vector field V ∈ D(C^∞(${{\mathbb{R}}^{N}}$)|_Y) can be continued to a smooth vector field on the enveloping space ${{\mathbb{R}}^{N}}$ (see [3]). Space ${{\mathbb{R}}^{N}}$ is endowed with a standard differential structure (${{\mathbb{R}}^{N}}$, C^∞(${{\mathbb{R}}^{N}}$)).

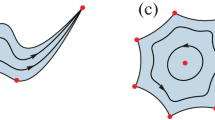
Assume that vector field V is a continuation of vector field W from the cone to space ${{\mathbb{R}}^{3}}$. Consider three curves γ₁, γ₂, and γ₃ coming from the vertex of cone S such that tangent vectors $\gamma _{1}^{'}(0)$, $\gamma _{2}^{'}(0)$, and $\gamma _{3}^{'}(0)$ are not coplanar. For a smooth vector field in ${{\mathbb{R}}^{3}}$ tangent to the cone outside the vertex, we can consider the corresponding tangent planes to the cone ${{T}_{{{{\gamma }_{1}}(t)}}}$, ${{T}_{{{{\gamma }_{2}}(t)}}}$, and ${{T}_{{{{\gamma }_{3}}(t)}}}$ along curves γ₁, γ₂, and γ₃. Because of the smoothness of field V when t → 0, tangent vector V(0) must be contained at the intersection of tangent planes ${{T}_{{{{\gamma }_{1}}(0)}}}$, ${{T}_{{{{\gamma }_{2}}(0)}}}$, and ${{T}_{{{{\gamma }_{3}}(0)}}}$. However, the intersection ${{T}_{{{{\gamma }_{1}}(0)}}}$ ∩ ${{T}_{{{{\gamma }_{2}}(0)}}}$ ∩ ${{T}_{{{{\gamma }_{3}}(0)}}}$ consists of only one point, namely, the vertex of the cone. Thus, vector V(0) is zero; therefore, the value at the vertex of the cone of the original field W(0) represents a zero vector.

Accordingly, since the value of vector field W tangent to the cone is zero at the vertex of cone S, the coefficients of vector field W (such that V|_X = W) tend to zero when approaching a singular point. We now describe functions on T *X.

Proposition. Functions on cotangent bundle T*X have the following properties: (1) they are smooth functions on T *X\$T_{0}^{*}X$, with their value being constant in the layer above a singular point $T_{0}^{*}X$, and (2) they are continuous functions when x → 0.

Proof. Outside the singular point, the algebra of functions A coincides with the algebra of smooth functions on the plane; therefore, outside the vertex of the cone, the cotangent bundle coincides with the usual bundle.

Consider generating functions of algebra F_T*X. According to the definition, these are functions of two kinds: liftings of functions f of algebra A with projection π : T *X → X and functions V* for V ∈ D(A). Liftings π $\circ$ f ( f ∈ A) are constant in layer $T_{0}^{*}X$. For vector field V ∈ D(A), the value of V( f )|₀ is zero. Then, at points w ∈ $T_{0}^{*}X$, the values of the generating functions are constant. Hence, in a smooth shell, they are constant on the layer $T_{0}^{*}X$.

Functions on cotangent bundle T *X go to a constant when x → 0. In fact, functions of the form π $\circ$ f ( f  ∈ A) tend to a constant value f(0) when x → 0 for the part of the cone without the singularity T *X\$T_{0}^{*}X$. The effect of “covector” fields on differentials of the functions V *(df ) → 0 when x → 0, because the coefficients of vector fields in enveloping space ${{\mathbb{R}}^{3}}$ tend to zero when x → 0. Hence, functions f ∈ F_T*X are not only constant on layer $T_{0}^{*}X$, but also tend to this value when x → 0.

3.4 Functions on Cone Blowing

Consider the mapping h : $\mathbb{R}$ × S¹ → ${{\mathbb{R}}^{3}}$, which represents a parameterization of cone X:

$$h:(x,\varphi ) \to (x,\psi (x)\cos \varphi ,\psi (x)\sin \varphi ).$$

Here, function ψ(x) denotes the distance from the point (x, 0, 0) ∈ Ox to the point on the cone in the plane tilted at angle φ to plane Oxy. Outside the set {0} × S¹, the mapping h is a diffeomorphism to the set X \0. If there is a curve of motion of a mechanism on the cone (and this curve is smooth before a singular point and after it), then it must also rise to a curve (on the cylinder), which can be discontinuous only at points on the circle {0} × S¹. The cylinder itself Cil = $\mathbb{R}$ × S¹ with the coordinates (x, φ) can be considered as a cone blowing, which must carry more information than a cone as a set of points: the cylinder also contains directions with which the curves approach the vertex of the cone.

Consider the differential structure on the cylinder obtained by the mapping h: these are functions of the type g = h*( f ), f ∈ ${{\left. {{{C}^{\infty }}({{\mathbb{R}}^{3}})} \right|}_{X}}$. They have the following property:

$${{\left. {g(x,\varphi )} \right|}_{{{{S}^{1}}}}} = {{\left. {f(x,\psi (x)\cos \varphi ,\psi (x)\sin \varphi )} \right|}_{{x = 0}}} = f(0,0,0) = \operatorname{const} .$$

Hence, the functions are constant on circle S¹. If X is a cusp (ψ'(0) = 0), then

$${{\left. {\frac{{\partial g}}{{\partial x}}} \right|}_{{{{S}^{1}}}}} = \frac{{\partial f}}{{\partial x}}(0,0,0) = \operatorname{const} .$$

Consider as a cone-singularity model cylinder Cil and the following algebra of functions on it:

$${{A}_{{{{S}^{1}}}}} = \{ f \in {{C}^{\infty }}(Cil):{{\left. f \right|}_{{{{S}^{1}}}}} \equiv \operatorname{const} \} .$$

We calculate vector fields for space (Cil, ${{A}_{{{{S}^{1}}}}}$) in coordinates x, y = φ.

Proposition. Vector fields Δ for differential space (Cil, ${{A}_{{{{S}^{1}}}}}$) are arranged as follows:

$$\Delta = a(x,y)\frac{\partial }{{\partial x}} + b(x,y)\frac{\partial }{{\partial y}},$$

(6)

where a and b are smooth and 2π-periodic for y functions on plane u ${{\left. a \right|}_{{{{S}^{1}}}}}$ ≡ 0.

Proof. Consider vector fields for ${{A}_{{{{S}^{1}}}}}$. According to the principle of locality outside a singular point, vector fields represent ordinary vector fields with smooth coefficients. Accordingly, outside circle S¹ on the cylinder, we obtain that vector field Δ acts on function f ∈ ${{A}_{{{{S}^{1}}}}}$ as follows:

$$\Delta (f) = a(x,y)f_{x}^{'} + b(x,y)f_{y}^{'}.$$

An arbitrary function f ∈ ${{A}_{{{{S}^{1}}}}}$ by the Hadamard lemma can be presented as follows:

$$f = c + xg(x,y),\quad g \in {{C}^{\infty }}({{\mathbb{R}}^{2}}).$$

(7)

For f(x, y) = x, we obtain that a(x, y) ∈ ${{A}_{{{{S}^{1}}}}}$. Consider functions g, which represent products of coordinate functions: g = $k(x)m(y)$. Functions k and m now can be arbitrary smooth functions. After substitution in (6), we obtain the condition

$$ak(x)m(y) + bxk(x)m{\kern 1pt} '(y) \in {{A}_{{{{S}^{1}}}}}.$$

Assume that function k(x) is positive; we then divide the left and right sides by k(x):

$$am(y) + bxm{\kern 1pt} '(y) = h \in {{A}_{{{{S}^{1}}}}}.$$

Consider function m(y) such that m'(y) > 0. Then, from the last expression, it follows that bx = (h – am)/m' is a smooth function. Hence, the value of function bx on S¹ is determined. Consider now function m(y) with the properties

$$m(0) = 1,\quad m{\kern 1pt} '(0) = 0,\quad m(1) = 2,\quad m{\kern 1pt} '(1) = 0.$$

Assume that ${{\left. {(am(y) + bxm{\kern 1pt} '(y))} \right|}_{{{{S}^{1}}}}}$ = c. We obtain

$$am(0) + bxm{\kern 1pt} '(0) = c,\quad am(1) + (bx) \cdot m{\kern 1pt} '(1) = c;$$

it follows that a(0, 0) = c and 2a(0, 1) = c. Since a ∈ ${{A}_{{{{S}^{1}}}}}$, it is necessary that ${{\left. a \right|}_{{{{S}^{1}}}}}$ ≡ 0.

Thus, for function f = xy, we obtain that ay + bx ∈ ${{A}_{{{{S}^{1}}}}}$. With allowance for ${{\left. a \right|}_{{{{S}^{1}}}}}$ ≡ 0, we obtain the consequence bx ∈ ${{A}_{{{{S}^{1}}}}}$. For function f = xy², we have ay² + 2bxy ∈ ${{A}_{{{{S}^{1}}}}}$; it follows that bxy ∈ ${{A}_{{{{S}^{1}}}}}$. Hence, two conditions are met: bx ∈ ${{A}_{{{{S}^{1}}}}}$ and (bx)y ∈ ${{A}_{{{{S}^{1}}}}}$. If bx is not identically equal to zero on S¹, then, when multiplied by y, there are two points in which the values of (bx)y differ. Hence, ${{\left. {(bx)} \right|}_{{{{S}^{1}}}}}$ = 0. Now, with allowance for bx ∈ ${{A}_{{{{S}^{1}}}}}$, ${{\left. {bx} \right|}_{{{{S}^{1}}}}}$ = 0, we obtain by the Hadamard lemma bx = 0 + xh(x, y). Then, b ∈ C^∞(${{\mathbb{R}}^{2}}$). Hence, it is necessary that a, b ∈ C^∞(${{\mathbb{R}}^{2}}$), ${{\left. a \right|}_{{{{S}^{1}}}}}$ = 0. However, these conditions are also sufficient: if a, b ∈ C^∞(${{\mathbb{R}}^{2}}$), ${{\left. a \right|}_{{{{S}^{1}}}}}$ = 0, then vector field (6) transforms functions from ${{A}_{{{{S}^{1}}}}}$ to functions from ${{A}_{{{{S}^{1}}}}}$.

Hence, vector fields of form (6) describe all vector fields for algebra ${{A}_{{{{S}^{1}}}}}$. Note that the coefficient for the derivative of the y coordinate differs from zero on circle S¹. Consequently, vector fields do not turn to zero at points of S¹. However, their action as operators leads to zero values; i.e., their action cannot be observed.

4 CONCLUSIONS

For the described example of a spatial singular pendulum, the configuration space of which is a cone or a cusp, two structures are considered. In the structure with functions constant near the vertex of the cone, the cotangent space at a singular point is zero: here, the system must not come out of a state of rest. In the second structure, the functions on cotangent bundle T*X are continuous and their values are constant in the layer above singular point $T_{0}^{*}X$. The results are similar to the results of calculations for the one-dimensional case [8].

The formulation of the general problems of constructing differential calculus such that there is zero tangent or cotangent space represents the next step in the study of kinematics problems on singular spaces.