Wave Propagation in Functionally-Graded Nanoplates Embedded in a Winkler–Pasternak Foundation with Initial Stress Effect

Abstract

This paper presents the analysis of wave propagation in functionally-graded (FG) nanoplates on a Winkler–Pasternak foundation. The investigation is carried out in the framework of nonlocal elasticity theory and a new four-unknown higher-order displacement theory including indeterminate integral terms. Hamilton’s principle and Navier’s method are used to obtain the frequency relations of FG nanoplates for different conditions by solving an eigenvalue problem. The obtained results for the frequency and phase velocity of wave propagation in an FG nanoplate are compared with recent outcomes of similar research.

1. INTRODUCTION

Composite and functionally-graded materials are special composites whose properties vary continuously along with their thickness. They are used in many various applications, such as reactor vessels, airplanes, space vehicles, biomedical industries, defense industries, and other engineering applications [1, 2]. Currently, different aspects of nanocomposite behavior are being extensively studied. Aghababaei and Reddy [3] analyzed the small-scale effects and the quadratic variation of shear stress across the thickness of a nanoplate to study the free vibration and bending within the third-order shear strain theory. Hedayatrasa et al. [4] proposed a numerical modeling solution using the 2D time-domain spectral finite element method and high-order Chebyshev polynomials as approximation functions for the analysis of wave propagation in FG materials. Abdelmalek et al. [5] analyzed the effect of temperature and humidity on the vibration response of laminated plates utilizing a micromechanical approach and a refined nth-order shear deformation theory. Wang et al. [6] examined the effects of the small scale on bending wave characteristics in nanoplates using nonlocal continuum theory. Guo et al. [7] introduced an element-free kp-Ritz method to approximate the field of displacements for the generalized regularized long wave equation. Also, many published articles are concerned with the analysis of FG nanostructures based on higher-order shear deformation theories and distinct refined theories [8–11].

Belmahi et al. [12] discussed the vibration of carbon nanotube beams embedded in a polymer matrix on polymer Winkler elastic foundations using nonlocal theories of elasticity with arbitrary effects of boundary conditions. Naceri et al. [13] analyzed sound wave propagation in armchair SWCNTs under thermal environment. The literature contains new and modified shear and normal strain theories [14–19]. Much attention is paid to the study of wave propagation and vibration in microplate structures of functionally-graded carbon nanotube reinforced composites [20–23]. Arani et al. [24] discussed the wave frequency behavior in a piezoelectric composite microplate reinforced with FG carbon nanotubes having different material properties across the thickness on a visco-Pasternak foundation based on Eringen’s nonlocal elasticity theory. Sobhy and Zenkour [25, 26] discussed the axial magnetic field and porosity effects on wave propagation in bi-layer FG graphene platelet-reinforced nanobeams and nanoplates. Mehar et al. [27] presented a mathematical method based on a finite element model and the nonlocal theory of elasticity for the response analysis of a nanoplate structure. Abazid et al. [28] considered the wave propagation in FG porous graphene platelet reinforced nanoplates under in-plane mechanical load and Lorentz magnetic force in the context of a new quasi-3D plate theory. Different methods and models based on Eringen’s nonlocal theory are discussed in [12, 29–31]. Other models based on the higher-order nonlocal gradient theory are presented in [32, 33]. There are dissimilar types of strain gradient elasticity in the literature [34–39]. Nonlocal theory can only predict the softening response in contrast to strain gradient theory that describes the stiffening structural behavior of materials [37].

This work presents the analysis of wave propagation in FG nanoplates utilizing a higher-order shear strain theory that provides more precise estimates of transverse shear stresses. In addition, employing a new integral variable displacement field across the thickness of FG nanoplates leads to a decline in the number of unknowns. Navier’s method is used to explain the propagation equations and to assess the frequency and phase velocity of wave propagation in FG nanoplates resting on a Winkler–Pasternak foundation. The influence of the nonlocal parameter, wavenumber, volume fraction index, shear modulus, and spring coefficients on the phase velocity and wave propagation frequency is investigated.

2. MATHEMATICAL MODELS

2.1. Eringen’s Nonlocal Elasticity

Let us consider the Eringen nonlocal elasticity model assuming that the stress state at a reference point is considered to be dependent not only on the strain state at that point but also on the strain states at all body points. The basic relations of nonlocal elasticity theory for an FG nanoplate are given by [6, 8, 13, 16, 40]

$${\sigma _{ij,j}} = 0,$$

$${\sigma _{ij}}(x) = \int {\alpha (|x - x'|,\;\tau ){C_{ijkl}}{\varepsilon _{kl}}(x'){\rm{d}}V(x),} \;\forall x \in V,$$

((1))

$${\varepsilon _{ij}} = {1 \over 2}({u_{i,j}} + {u_{j,i}} + {u_{k,i}}{u_{k,j}}),$$

where C_ijkl is the elastic modulus tensor of classical (local) elasticity, ε_ij and σ_ij are the strain and stress tensors, respectively, and u_i is the displacement vector. In addition, α(|x – x′|, τ) is the nonlocal modulus, |x – x′| is the Euclidean distance, and τ = e₀a/l, where l is the external characteristic length, e₀ is a constant appropriate to the type of material, and a is an internal characteristic length of such a material (e.g., C–C bond length, lattice spacing, or granular distance).

The constitutive equation of nonlocal elasticity theory may be expressed as [6, 8, 13, 16]

$$(1 - {\xi ^2}{\nabla ^2}){\sigma _{ij}} = {C_{ijkl}}{\varepsilon _{kl}},$$

((2))

where the parameter ξ = e₀a is defined above, and ${\nabla ^2}$ is the Laplace operator.

2.2. Material Properties of an FG Nanoplate

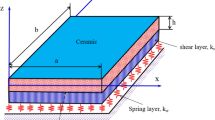
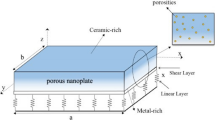
Consider a nanoplate of thickness h, width b, and length a (Fig. 1). The FG nanoplate is embedded in a Winkler–Pasternak foundation and exposed to initial stress as shown in Fig. 1. A wave propagates in the nanoplate along the x and y directions. Suppose that the initial stress along the x direction equals the initial stress along the y direction. It is also assumed that the FG nanoplate is made of a ceramic phase (denoted by c) mixed with a metal phase (denoted by m), with the material composition varying along the z axis, i.e., only across the thickness. Thus, the material properties of the FG nanoplate, such as Young’s modulus E and mass density, can be expressed as [8–11]

$$P(z) = ({P_{\rm{c}}} - {P_{\rm{m}}}){V_{\rm{f}}}(z) + {P_{\rm{m}}},$$

((3))

where P_m and P_c are the properties of metal and ceramics. The volume fraction of ceramics is defined by

$${V_{\rm{f}}}(z) = {\left( {{{2z + h} \over {2h}}} \right)^N}.$$

((4))

From Eqs. (3) and (4) we can write the Young modulus and mass density of the FG nanoplate:

$$E(z) = ({E_{\rm{c}}} - {E_{\rm{m}}}){\left( {{{2z + h} \over {2h}}} \right)^N} + {E_{\rm{m}}},\;\rho (z) = ({\rho _{\rm{c}}} - {\rho _{\rm{m}}}){\left( {{{2z + h} \over {2h}}} \right)^N} + {\rho _{\rm{m}}}.$$

((5))

Fig. 1.

Wave propagation in the FG nanoplate embedded in a Winkler–Pasternak foundation with initial stress.

2.3. Model with Indeterminate Integral Variables

The present work is developed based on the assumptions of trigonometric shear strain theory, in which the in-plane displacements contain an integral component:

$$u(x,y,z,t) = {u_0}(x,y,t) - z{{\partial {w_0}} \over {\partial x}} + {s_1}f(z)\int {\theta (x,y,t){\rm{d}}x,} $$

$$v(x,y,z,t) = {v_0}(x,y,t) - z{{\partial {w_0}} \over {\partial y}} + {s_2}f(z)\int {\theta (x,y,t){\rm{d}}y,} $$

((6))

$$w(x,\;y,\;z,\;t) = {w_0}(x,\;y,\;t),$$

where t is the time, u₀, v₀, w₀, θ are four unknowns of the displacements of the mean surface of the plate, f(z) is the shape function that describes the distribution of transverse shear stresses and strains across the plate thickness. The constants s₁ and s₂ depend on the plate geometry. In this study, we take the function f(z) as follows:

$$f(z) = {{3\pi } \over 2}h\tanh {z \over h} - {{3\pi } \over 2}z{{\mathop{\rm sech}\nolimits} ^2}{1 \over 2}.$$

((7))

In linear elasticity, the displacement-strain relation associated with Eq. (6) is expressed in the following form:

((8))

where

((9))

The integral terms used in the displacement field equations can be determined using Navier’s solution and can be given by

$$\int {\theta {\rm{d}}x} = A'{{\partial \theta } \over {\partial x}},\;{\partial \over {\partial y}}\int {\theta {\rm{d}}x} = A'{{{\partial ^2}\theta } \over {\partial x\partial y}},\;\int {\theta {\rm{d}}y} = B'{{\partial \theta } \over {\partial y}},\;{\partial \over {\partial x}}\int {\theta {\rm{d}}y} = B'{{{\partial ^2}\theta } \over {\partial x\partial y}}.$$

((10))

According to the type of solution used (Navier’s solution in our case), the coefficients A′, B′, k₁ and k₂ are chosen and defined as follows:

$$A' = - {1 \over {k_1^2}},\;B' = - {1 \over {k_2^2}},\;{s_1} = k_1^2,\;{s_2} = k_2^2.$$

((11))

The constitutive equations of FG nanoplates in linear elasticity are given by

((12))

where

$${Q_{11}} = {Q_{22}} = {{E(z)} \over {1 - {\nu ^2}}},\;{Q_{12}} = {Q_{21}} = {{\nu E(z)} \over {1 - {\nu ^2}}},\;{Q_{44}} = {Q_{55}} = {Q_{66}} = {{E(z)} \over {2(1 + \nu )}}.$$

((13))

The stress resultants (N_i, M^b_i, M^s_i) and (S^s_xz, S^s_yz) for the FG nanoplate can be expressed by integrating Eq. (12) over the nanoplate thickness:

$$({N_i},\;M_i^b,\;M_i^s) = \int\limits_{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} {{\sigma _i}\{ 1,\;z,\;f(z)\} {\rm{d}}z,} \;i = x,\;y,\;xy,$$

$$(S_{xz}^s,\;S_{yz}^s) = \int\limits_{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} {g(z)\{ {\tau _{xz}},\;{\tau _{yz}}\} {\rm{d}}z.} $$

((14))

Replacing Eq. (12) in Eq. (14) gives the following expressions in which the resulting stresses from the proposed model can be obtained in terms of strains and stiffness elements:

((15))

$$S - {\xi ^2}{\nabla ^2}S = {A^s}\gamma ,$$

where

$$N = {\{ {N_x},\;{N_y},\;{N_{xy}}\} ^{\rm{t}}},\;{M^b} = {\{ M_x^b,\;M_y^b,\;M_{xy}^b\} ^{\rm{t}}},\;{M^s} = {\{ M_x^s,\;M_y^s,\;M_{xy}^s\} ^{\rm{t}}},$$

$$\varepsilon = {\{ \varepsilon _x^0,\;\varepsilon _y^0,\;\varepsilon _{xy}^0\} ^{\rm{t}}},\;{k^b} = {\{ k_x^b,\;k_y^b,\;k_{xy}^b\} ^{\rm{t}}},\;{k^s} = {\{ k_x^s,\;k_y^s,\;k_{xy}^s\} ^{\rm{t}}},$$

$$S = {\{ S_{xz}^s,\;S_{yz}^s\} ^{\rm{t}}},\;\gamma = {\{ \gamma _{xz}^0,\;\gamma _{yz}^0\} ^{\rm{t}}},$$

((16))

The stiffness terms of this approach are defined as

$$({A_{ij}},\;{B_{ij}},\;{D_{ij}},\;B_{ij}^s,\;D_{ij}^s,\;H_{ij}^s) = \int\limits_{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} {{Q_{ij}}\{ 1,\;z,\;{z^2},\,f(z),\;zf(z),\;{{[f(z)]}^2}\} {\rm{d}}z,} \;i,\;j = 1,\,2,\;6,$$

((17))

$$(A_{44}^s,\;A_{55}^s) = \int\limits_{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} {\{ {Q_{44}},\,{Q_{55}}\} {{[g(z)]}^2}{\rm{d}}z.} $$

Here we use Hamilton’s principle to get the equations of motion. This principle can be given by the following analytical relation:

$$\int\limits_0^t {(\delta {U_P} + \delta {U_F} + \delta K - \delta V){\rm{d}}t} = 0,$$

((18))

where δU_P and δU_F are the components of change in the strain energy, δK is the kinetic energy change, and δV is the potential energy change:

$$\delta {U_P} = \int\limits_V {({\sigma _x}\delta {\varepsilon _x} + {\sigma _y}\delta {\varepsilon _y} + {\sigma _{xy}}\delta {\varepsilon _{xy}} + {\tau _{xz}}\delta {\gamma _{xz}}} + {\tau _{yz}}\delta {\gamma _{yz}}){\rm{d}}V = \int\limits_A {({N_x}\delta \varepsilon _x^0 + {N_y}\delta \varepsilon _y^0 + {N_{xy}}\delta \varepsilon _{xy}^0} $$

$$ + M_x^b\delta k_x^b + M_y^b\delta k_y^b + M_{xy}^b\delta k_{xy}^b + M_x^s\delta k_x^s + M_x^s\delta k_x^s + M_{xy}^s\delta k_{xy}^s + S_{xz}^s\delta \gamma _{xz}^s + S_{yz}^s\delta \gamma _{yz}^s){\rm{d}}A.$$

((19))

The change in the strain energy of the Winkler–Pasternak foundation can be expressed as

$$\delta {U_F} = {1 \over 2}\int\limits_A {[{K_{\rm{W}}}w(x,y,t) + {K_{\rm{g}}}{\nabla ^2}w(x,y,t)]{\rm{d}}x{\rm{d}}y,} $$

((20))

where K_W and K_g are the transverse and shear stiffness coefficients of the foundation, respectively.

The kinetic energy change can be given by

$$\delta K = \int\limits_V {(\dot u\delta \dot u + \dot v\delta \dot v + \dot w\delta \dot w)\rho (z){\rm{d}}V} = \int\limits_A {\left\{ {{I_0}({{\dot u}_0}\delta {{\dot u}_0} + {{\dot v}_0}\delta {{\dot v}_0} + \dot w\delta {{\dot w}_0})} \right.} $$

$$ - {I_1}\left( {{{\dot u}_0}{{\partial \delta {{\dot w}_0}} \over {\partial x}} + {{\partial {{\dot w}_0}} \over {\partial x}}\delta {{\dot u}_0} + {{\dot v}_0}{{\partial \delta {{\dot w}_0}} \over {\partial y}} + {{\partial {{\dot w}_0}} \over {\partial y}}\delta {{\dot v}_0}} \right)$$

$$ + {J_1}\left[ {{S_1}A'\left( {{{\dot u}_0}{{\partial \delta \dot \theta } \over {\partial x}} + {{\partial \dot \theta } \over {\partial x}}\delta {{\dot u}_0}} \right) + {S_2}B'\left( {{{\dot v}_0}{{\partial \delta \dot \theta } \over {\partial y}} + {{\partial \dot \theta } \over {\partial y}}\delta {{\dot v}_0}} \right)} \right]$$

$$ + {I_2}\left( {{{\partial \delta {{\dot w}_0}} \over {\partial x}}{{\partial {{\dot w}_0}} \over {\partial x}} + {{\partial \delta {{\dot w}_0}} \over {\partial y}}{{\partial {{\dot w}_0}} \over {\partial y}}} \right)$$

$$ - {J_2}\left[ {{S_1}A'\left( {{{\partial {{\dot w}_0}} \over {\partial x}}{{\partial \delta \dot \theta } \over {\partial x}} + {{\partial \dot \theta } \over {\partial x}}{{\partial \delta {{\dot w}_0}} \over {\partial x}}} \right) + {S_2}B'\left( {{{\partial {{\dot w}_0}} \over {\partial y}}{{\partial \delta \dot \theta } \over {\partial y}} + {{\partial \dot \theta } \over {\partial y}}{{\partial \delta {{\dot w}_0}} \over {\partial y}}} \right)} \right]$$

$$ + {J_3}\left. {\left[ {{{({S_1}A')}^2}\left( {{{\partial \delta \dot \theta } \over {\partial x}}{{\partial \dot \theta } \over {\partial x}}} \right) + {{({S_2}B')}^2}\left( {{{\partial \delta \dot \theta } \over {\partial y}}{{\partial \dot \theta } \over {\partial y}}} \right)} \right]} \right\}{\rm{d}}A,$$

((21))

where the upper dot denotes the differentiation with respect to the time variable t, ρ(z) is the mass density, and (I, J) are the mass inertias specified by

$$({I_0},\;{I_1},\;{I_2}) = \int\limits_{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} {\{ 1,\;z,\;{z^2}\} \rho (z){\rm{d}}z,} \;({J_1},\;{J_2},\;{J_3}) = \int\limits_{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} {\{ f(z),\;zf(z),\;{f^2}(z)\} \rho (z){\rm{d}}z.} $$

((22))

The potential energy of the applied load can be stated as

$$V = {1 \over 2}\int\limits_A {\left[ {N_x^0{{{\partial ^2}{w_0}(x,\;y,\;t)} \over {\partial {x^2}}} + 2N_{xy}^0{{{\partial ^2}{w_0}(x,\;y,\;t)} \over {\partial x\partial y}} + N_y^0{{{\partial ^2}{w_0}(x,\;y,\;t)} \over {\partial {y^2}}}} \right]{\rm{d}}x{\rm{d}}y,} $$

((23))

with

$$N_x^0 = N_y^0 = {N_0},\;N_{xy}^0 = 0.$$

((24))

By substituting Eqs. (19)–(21), (23) into Eq. (18) and integrating by parts and separately isolating the coefficients u₀, v₀, w₀ and θ, we obtain the wave propagation equations

$$\delta {u_0}:\;{{\partial {N_x}} \over {\partial x}} + {{\partial {N_{xy}}} \over {\partial y}} = (1 - {\xi ^2}{\nabla ^2})\left( {{I_0}{{\ddot u}_0} - {I_1}{{\partial {{\ddot w}_0}} \over {\partial x}} + {S_1}A'{J_1}{{\partial \ddot \theta } \over {\partial x}}} \right),$$

$$\delta {v_0}:\;{{\partial {N_{xy}}} \over {\partial x}} + {{\partial {N_y}} \over {\partial y}} = (1 - {\xi ^2}{\nabla ^2})\left( {{I_0}{{\ddot v}_0} - {I_1}{{\partial {{\ddot w}_0}} \over {\partial y}} + {S_2}B'{J_1}{{\partial \ddot \theta } \over {\partial y}}} \right),$$

$$\delta {w_0}:\;{{{\partial ^2}M_x^b} \over {\partial {x^2}}} + 2{{{\partial ^2}M_{xy}^b} \over {\partial x\partial y}} + {{{\partial ^2}M_y^b} \over {\partial {y^2}}} + (1 - {\xi ^2}{\nabla ^2})\bar N - (1 - {\xi ^2}{\nabla ^2}){f_e} = (1 - {\xi ^2}{\nabla ^2})$$

$$ \times \left[ {{I_0}{{\ddot w}_0} + {I_1}\left( {{{\partial {{\ddot u}_0}} \over {\partial x}} + {{\partial {{\ddot v}_0}} \over {\partial y}}} \right) - {I_2}\left( {{{{\partial ^2}{{\ddot w}_0}} \over {\partial {x^2}}} + {{{\partial ^2}{{\ddot w}_0}} \over {\partial {y^2}}}} \right) + {J_2}\left( {{S_1}A'{{{\partial ^2}\ddot \theta } \over {\partial {x^2}}} + {S_2}B'{{{\partial ^2}\ddot \theta } \over {\partial {y^2}}}} \right)} \right],$$

((25))

$$\delta \theta :\; - {S_1}M_x^s - {S_2}M_y^s - ({S_1}A' + {S_2}B'){{{\partial ^2}M_{xy}^s} \over {\partial x\partial y}} + {S_1}A'{{\partial S_{xz}^s} \over {\partial x}} + {S_2}B'{{\partial S_{yz}^s} \over {\partial y}} = (1 - {\xi ^2}{\nabla ^2})$$

$$ \times \left[ { - {J_1}\left( {{S_1}A'{{\partial {{\ddot u}_0}} \over {\partial x}} + {S_2}B'{{\partial {{\ddot v}_0}} \over {\partial y}}} \right) + {J_2}\left( {{S_1}A'{{{\partial ^2}{{\ddot w}_0}} \over {\partial {x^2}}} + {S_2}B'{{{\partial ^2}{{\ddot w}_0}} \over {\partial {y^2}}}} \right) - {J_3}\left( {{{({S_1}A')}^2}{{{\partial ^2}\ddot \theta } \over {\partial {x^2}}} + {{({S_2}B')}^2}{{{\partial ^2}\ddot \theta } \over {\partial {y^2}}}} \right)} \right],$$

with

$${f_e} = {K_{\rm{W}}}w(x,\;y,\;t) - {K_{\rm{g}}}{\nabla ^2}w(x,\;y,\;t),$$

$$\bar N = {N_0}{{{\partial ^2}{w_0}(x,\;y,\;t)} \over {\partial {x^2}}} + {N_0}{{{\partial ^2}{w_0}(x,\;y,\;t)} \over {\partial {y^2}}}$$

((26))

and

$${N_0} = h{\sigma _0}.$$

((27))

We assume that the solutions for u₀, v₀, w₀, and θ describe waves propagating in the xy plane in the form

((28))

where U, V, W, X are the wave amplitude coefficients, k₁, k₂ are respectively the wavenumbers of wave propagation along the x and y axes, and ω is the frequency. So, with the aid of the above solutions, the wave propagation equations appeared in Eqs. (25) become

$$([K] - {\omega ^2}[M]\{ \Delta \} = \{ 0\} ,$$

((29))

where

$$\{ \Delta \} = {\{ U,\;V,\;W,\;X\} ^{\rm{t}}}.$$

((30))

Substituting Eq. (28) into Eq. (15), we obtain

((31))

The frequency relations of wave propagation in the FG nanoplate are provided by

$$\left| {[K] - {\omega ^2}[M]} \right| = \{ 0\} .$$

((32))

Assuming k₁ = k₂ = k, the roots of Eq. (31) can be given as follows:

$${\omega _i} = {W_i}(k),\;i = 1,\;2,\;3,\;4.$$

((33))

They correspond to the wave modes M₀, M₁, M₂ and M₃, respectively. The wave modes M₀ and M₃ correspond to the bending wave, while M₁ and M₂ correspond to the extension wave. The phase velocity of wave propagation in the FG nanoplate is expressed as

$${C_i} = {{{W_i}(k)} \over k},\;i = 1,\;2,\;3,\;4.$$

((34))

3. NUMERICAL RESULTS AND DISCUSSION

3.1. Comparison of Results

The mathematical formulation of the new model based on a four-unknown higher-order theory including indeterminate integral variables allows the analysis of wave propagation in FG nanoplates. In this work, the wave propagation in FG nanoplates is analyzed using the solution methodology based on a higher-order shear strain theory, which is schematically represented in Fig. 2.

Fig. 2.

Solution methodology for the problem of wave propagation in FG nanoplates based on a higher-order shear strain theory.

Several numerical examples are studied and discussed to verify the accuracy of the new theory with indeterminate integral variables for the prediction of wave propagation in FG nanoplates. The results obtained by this theory are compared with those of the third-order, first-order and classical nonlocal theories. The dimensionless quantity for the natural frequency is

$$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \omega } = \omega h\sqrt {{\rho \over G}} .$$

This analysis is performed for a nanoplate for various values of the aspect ratio and nonlocal parameters. The results are reported in Tables 1 and 2. The outcomes obtained by the current theory are compared with the results of the closed-form solution derived by Aghababaei and Reddy [3]. It can be noticed that nonlocal theories predict natural frequencies smaller than those of local theories, especially for high-mode frequencies (Table 2). Thus, local theories overestimate frequencies. Employing a new integral variable displacement field through the thickness of the FG nanoplate, the summation of the integral terms in the displacement field leads to a reduction in the number of unknowns. Note that the integrals do not have limits. In the present study, only four unknown displacement terms are considered instead of five terms in ordinary first- and third-order shear deformation theories [3]. The field of axial displacements uses the hyperbolic secant shear function in terms of thickness ordered to include the effect of the transverse shear strain across the thickness.

Table 1. Comparison of dimensionless first-mode frequencies $(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \omega } = {\omega _{11}}h\sqrt {{\rho \mathord{\left/ {\vphantom {\rho G}} \right. \kern-\nulldelimiterspace} G}} )$ for a simply supported isotropic nanoplate (a = 10, E = 30 × 10⁶, ν = 0.3)

Table 2. Comparison of dimensionless natural frequencies $(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \omega } = {\omega _{11}}h\sqrt {{\rho \mathord{\left/ {\vphantom {\rho G}} \right. \kern-\nulldelimiterspace} G}} )$ for a simply supported square isotropic plate (a = 10, E = 30 × 10⁶, ν = 0.3)

To validate the wave propagation results obtained by the present theory of the indeterminate integral with four variables, comparisons were made with the results of Wang et al. [6]. Let us consider the case of isotropic plates with h = 0.34 nm and the following mechanical characteristics: E = 1.06 TPa, ν = 0.25, ρ = 2.25 g/cm³, K_W = 1.13 × 10¹⁸ Pa/m, and K_g = 2 N/m.

This comparison is made for various values of the scale coefficient ξ = 0 to 2 nm. The results are shown in Figs. 3–7. It should be indicated that the data obtained by Wang et al. [6] are based on the nonlocal continuum model of classical theory. According to Figs. 3–6, the results of this study are in good agreement with the results reported in [6].

Fig. 3.

Comparison of the frequency relations for a flexural wave obtained using a classical nonlocal nanoplate model, without initial stress (color online).

Fig. 4.

Comparison of the frequency relations for a flexural wave obtained using a classical nonlocal nanoplate model, with tensile stress (color online).

Fig. 5.

Comparison of the frequency relations for a flexural wave obtained using a classical nonlocal nanoplate model for different values of compressive load (color online).

Fig. 6.

Comparison of the frequency relations for flexural wave propagation in nanoplates on a Winkler foundation obtained using a classical nonlocal nanoplate model (tensile load σ₀ = 0.005E) (color online).

Fig. 7.

Comparison of the frequency relations for flexural wave propagation in nanoplates obtained using a classical nonlocal nanoplate model, with the influence of the shear layer stiffness (tensile load σ₀ = 0.005E) (color online).

We analyze a simply supported isotropic nanoplate with the following parameters: a = 10, E = 30 × 10⁶, ν = 0.3, ρ = 1.

3.2. Parametric Study

The mechanical properties of FG nanoplates are believed to correspond to the values listed in Table 3. The values of the nonlocal parameter ξ (nm) are considered to be zero up to 3 nm [6, 17]. The Winkler and Pasternak coefficients are taken from [6]. The final solutions were obtained using the analytical procedure of Navier’s method described above in Sect. 2. To study the influence of the parameters affecting the frequency and phase velocity of wave propagation in FG nanoplates, parametric studies were carried out to observe the effect of the power-law index of the material (N), the nonlocal parameter, and the coefficients of the elastic medium (K_W and K_g). The nonlocal elasticity (ξ ≠ 0) and classical (local) elasticity (ξ = 0) models were considered.

Table 3. Elastic properties of FG nanoplates [6, 9–11]

The frequency curves of FG and isotropic (N = 0) nanoplates versus the nonlocal parameter ξ are illustrated in Fig. 8 for three values of the material index (N = 0.5, 1, and 2). It is noted that when the scale coefficient increases, the frequency curves for isotropic and FG nanoplates decrease, and this reduction is particularly significant for the FG nanoplates with the material power-law index N = 2. This means that a nanoplate with isotropic properties is more rigid than an FG nanoplate.

Fig. 8.

Effect of the material index on the frequency of wave propagation in FG nanoplate, with k₁ = k₂ = 10⁹ m^–1, K_W = K_g = 0 (color online).

The curves of the frequency and phase velocity of FG nanoplates with N = 2 versus the wavenumbers for different nonlocal parameter values are shown in Figs. 9 and 10. The outcomes of the two figures imply that with the increasing nonlocal parameter the frequency and phase velocity decrease for all wavenumber values. The effect of the nonlocal parameter, i.e., the small-scale effect, reduces the frequency and phase velocity. Moreover, as shown in Fig. 10, the phase velocities are sensitive to the small-scale coefficient for large wavenumbers k > 0.5, while the dependence is insignificant at k < 0.5.

Fig. 9.

Effect of the nonlocal parameter on the frequency of wave propagation in FG nanoplate, with N = 2, K_W = K_g = 0 (color online).

Fig. 10.

Effect of the nonlocal parameter on the phase velocity of wave propagation in FG nanoplate, with N = 2, K_W = K_g = 0 (color online).

The frequency curves of the FG nanoplate versus the material index N for different values of the nonlocal parameter are shown in Fig. 11. As the nonlocal parameter increases, the frequency curves decrease. The same behavior of the frequency curves is observed with the increasing material index N.

Fig. 11.

Variation of wave propagation frequency with material index for different values of the nonlocal parameter, with k₁ = k₂ = k = 10⁹ m^–1, K_W = K_g = 0 (color online).

The dependences of the frequency on the Pasternak and Winkler moduli K_g and K_W for different values of the nonlocal parameter are displayed in Figs. 12 and 13, respectively, for the material index N = 2. One can see that when the Pasternak or Winkler coefficients increase, the frequency curves also increase for all nonlocal parameter values. This means that the increase in the Pasternak and Winkler coefficients parallels the increase in the stiffness of the FG nanoplate. Moreover, comparison of the effect of K_g and K_W on the frequency curves indicates that the impact of the Pasternak modulus is greater than that of the Winkler modulus.

Fig. 12.

Variation of frequency with shear modulus parameter (K_W = 0) with N = 2, k₁ = k₂ = k = 10⁹ m^–1 (color online).

Fig. 13.

Variation of frequency with Winkler modulus parameter (K_g = 0) with N = 2, k₁ = k₂ = k = 10⁹ m^–1 (color online).

The frequency and phase velocity curves versus the wavenumber k for three values of the initial stress under tensile load are shown in Figs. 14 and 15, respectively. The curves are plotted for the nonlocal parameter ξ = 0.5 nm and the material index N = 2. It can be noted that as the wavenumber k increases, the frequency and phase velocity curves increase for all values of the initial tensile stress.

Fig. 14.

Variation of frequency with wavenumber for different values of initial stress under tensile load, with N = 2, ξ = 0.5 nm, K_W = K_g = 0 (color online).

Fig. 15.

Variation of phase velocity with wavenumber for different values of initial stress under tensile load, with N = 2, ξ = 0.5 nm, K_W = K_g = 0 (color online).

The frequency curve of FG nanoplates versus the nonlocal parameter for different types of foundation and the material index N = 2 are shown in Fig. 16. Four cases are considered: Winkler medium (K_W = 0.5, K_g = 0), Pasternak medium (K_W = 0, K_g = 2), Winkler–Pasternak medium (K_W = 0.5, K_g = 2), and without an elastic medium (K_W = K_g = 0). It can be seen that taking into account the elastic medium increases the nanoplate frequency and thus leads to a more rigid structure. In addition, the impact of the Pasternak medium on the nanoplate frequency curve is greater than that of the Winkler medium. It can be said that the Winkler parameters can describe the normal load of the elastic medium, while the Pasternak parameters describe both the transverse shear and the normal loads of the elastic medium. The effect of the coupled Winkler–Pasternak medium on the frequency curve of the FG nanoplate is greater than that of the Pasternak medium for the nonlocal parameter less than 2.5.

Fig. 16.

Comparison of the frequency ratios of the FG nanoplate depending on the type of foundation (color online).

4. CONCLUSIONS

This paper considered the wave propagation response of an FG nanoplate embedded in a Winkler–Pasternak medium based on a higher-order Eringen’s nonlocal theory and a new displacement field introducing indeterminate integral variables. The effect of the following parameters on the frequency and phase velocity of FG nanoplates was discussed: nonlocal parameter, material power-law index (N), wavenumbers, and the type of elastic medium. It was assumed that the nanoplate was a mixture of metal (Al) and ceramics (Al₂O₃), with the properties changing through the nanoplate thickness. Navier’s method and procedure were applied to determine the frequency and phase velocity of FG nanoplates. The formulas for the case of homogeneous isotropic nanoplates can be found as a special case. The results obtained were compared with the literature results. The following remarks can be drawn from this study:

1. The use of indeterminate integral terms allows reducing the number of propagation equations and variables. We can say that this model is simple and efficient for the analysis of the wave characteristics of FG nanoplates.

2. The variation of the material index influences the wave propagation frequency of FG nanoplates. It is shown that the frequency of wave propagation in FG nanoplates is lower than that in isotropic ceramic nanoplates.

3. The small-scale effect increases the frequency and phase velocity of wave propagation in FG nanoplates. The difference between nonlocal and local theories is significant for a high value of the nonlocal parameter.

4. The nonlocal parameter effect plays an important role in the study of the frequency behavior of FG nanoplates for larger wavenumbers. The phase velocities are more sensitive to the small-scale coefficient for large values of wavenumbers and less sensitive for smaller wavenumbers.

5. The wave propagation frequency and phase velocity become low with the increasing initial tensile stress.

6. An increase in the Winkler foundation modulus and the shear layer stiffness increase the wave propagation frequency and phase velocity.

7. Taking into account the type of elastic medium increases the propagation frequency of the waves in FG nanoplates.