Abstract
The service life and brittle fracture of steel structures at subzero temperatures is predicted with purely empirical methods based on impact bending test results or fracture mechanics criteria. Force, energy and deformation methods of fracture mechanics are used for a comparative assessment of fracture toughness in safety-related structures operating under harsh environment conditions. However, such methods are not efficient enough for the design of welded engineering components and structures due to their complex shapes, welding factors, and loading conditions. This has led to the development of specific physical methods for brittle fracture prediction. This paper proposes a method based on the application of the known brittle fracture criterion to a small material volume ahead of the crack tip (pre-fracture zone). A mathematical model was developed to describe the loading of the pre-fracture zone in a part made of an elastic-plastic material. The effect of mechanical characteristics of the material and service temperature on the brittle fracture resistance of the part was evaluated using the proposed method. The design coefficients were calculated and the functional dependencies were verified using the literature experimental data on the critical stress intensity factors obtained at subzero temperatures. A comparative analysis of the experimental and numerical results showed that the curves calculated by the proposed method are consistent with the test results. This work confirms the applicability of physical models of brittle fracture which use the mechanical characteristics of steel more suitable for engineering applications.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1. INTRODUCTION
The fracture mechanics methods used to select steels for safety-related structures [1–6] are not suitable for fracture toughness prediction of complex welded structures made from small-thickness rolled sheets. This problem is solved by physical methods of brittle fracture prediction which use different limiting states of the material at the crack tip [7–11].
Here we continue to develop a method for predicting the brittle fracture behavior of a part with a crack. The method is based on applying a generalized theory of brittle fracture in accordance with the Neuber–Novozhilov approach to the pre-fracture zone ahead of the crack tip [11–13]. The basic principles of the method were verified earlier by test data of various specimens obtained from determining the fracture mechanics criteria. The tests were conducted at subzero temperatures so that we could estimate the temperature dependence of the critical stress intensity factor.
A similar relationship was obtained with the proposed method. By comparing these dependences, we checked the adequacy of the analytical dependence and the calculated value of the cleavage stress S0. In this work, the cleavage stress of low-alloy structural steels is assumed to be linearly related to the steel yield stress σy, i.e., S0 = Cσy.
2. MATHEMATICAL MODEL OF BRITTLE FRACTURE
Brittle fracture prediction for a part with a crack can be done by applying the force criterion of the generalized theory of brittle fracture to the pre-fracture zone ahead of the crack tip, which consists of two conditions [8, 9, 11, 14]:
Here, σir and σ1r are the average stress intensity and the average first principal stress in the pre-fracture zone during elastic-plastic deformation, σyT is the yield stress of a given material determined at the test (loading) temperature, and S0 is the temperature-independent mode I (cleavage) stress. Expressions (1) are the crack initiation conditions. The crack growth conditions are not considered in this study.
It is convenient to represent the loading of the pre-fracture zone in a part made of an elastic-plastic material in dimensionless coordinates [13]:
where r0 = 0.5 mm is the characteristic size of the pre-fracture zone [11].
The stress variation in the pre-fracture zone was investigated by the finite element method on solid models of elastic-plastic material [12, 13, 15]. The parameter sr(k) does not depend on temperature. A typical sr(k) curve for a plate with an edge, through-thickness, or surface crack is divided into three stages (Fig. 1, curve 1). The first stage at 0 < k ≤ k1 corresponds to nearly elastic deformation of the material in the crack tip region. The second one at k1 < k ≤ k2 reflects the evolution of a small plastic zone accompanied by an increase in the stress-strain stiffness factor of the state ηr = σ1r/σir (curve 2) [14]. In the third stage at k > k2, the stress-strain stiffness factor decreases, while the plastic zone size and the plastic strain intensity grow rapidly.
Analysis of the loading of the pre-fracture zone suggested that brittle fracture can occur only at the second stage of deformation at k1 < k ≤ k2, under the second condition (1). If brittle fracture does not occur at k ≤ k2, then at the third stage at k > k2 fracture will be preceded by pronounced plastic deformation. The value of kс for which σ1r = S0 depends on temperature. Taking into account Eqs. (2), we write σ1r = srσyT and represent the strength condition in the form sr ≤ sc, where sc = S0/σyT. At sr > sc (curve 3), ductile fracture occurs in the interval k > k2. With decreasing temperature, the yield stress increases and the right-hand side of the condition sc = S0/σyT will decrease (Fig. 1, curve 4). Brittle fracture will occur at k = kс.
This method was implemented using a mathematical model that establishes the functional relationship sr(k) in the first two stages of loading at k ≤ k2 [12]. The model reads:
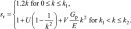 (3)
(3)
The coefficients U and V for plates with different cracks under uniaxial loading were determined by generalizing the data of finite element calculations [12, 13, 15]. The following dependences were obtained: for edge cracks at a/B < 0.1
for through-thickness cracks at a/B < 0.1
for semi-elliptical surface cracks
In these expressions, a is the characteristic crack size (Fig. 2) and Gp is the plastic hardening modulus for the bilinear approximation of the tensile curve. The influence of this parameter on brittle fracture occurrence is small, as it occurs with plastic strains not exceeding 1–2%. Therefore, Gp was determined here using a simplified approach suitable for describing the initial portion of the true tensile curve for mild steels with tensile elongation δ5 = 0.18–0.22. The value σB for such steels is achieved at an elongation of approximately 0.5δ5, and the relative decrease in the specimen diameter as a result of uniform plastic elongation is approximately ψ = 0.1. Hence the tangent of the slope angle of the second portion of the true tensile curve can be calculated by the formula [11]
where σy, σB, δ5 are the yield strength, ultimate strength, and tensile elongation obtained at a temperature of 20°C.
The coefficients U and V for compact specimens and prismatic specimens tested for bending [5, 6] were determined in a finite element study according to the procedure from [12, 15]. It was found that the coefficient U for compact and prismatic specimens at a/B = 0.3–0.5 is independent of the crack size and can be taken equal to U = 1.6 and V = 1 (Fig. 3a). The maximum stress-strain stiffness factor for compact specimens is achieved at k2 = 6–7 (Fig. 3b). The plastic strain intensity epr in the pre-fracture zone at k = k2 reaches about 4% (Fig. 3c). Deviation from the power-law dependence in the range k < 3 is due to the fact that not the entire pre-fracture zone is in the plastic state. The second deviation of the power-law dependence epr(k) at k2 > 5.5–6.0 is associated with a rapid expansion of the plastic zone. In the elastic calculation, the stress-strain stiffness factor η for these specimens does not exceed 2. The value of η = 2.5 corresponding to plane strain conditions is achieved only if a local plastic zone appears ahead of the crack tip. Approximately the same results were obtained for prismatic specimens under bending.
The plastic strain intensity in the pre-fracture zone at k1 < k ≤ k2 is satisfactorily described by the relationship (Fig. 2c)
at ζ = 0.2–0.4.
Using conditions (1) and model (3), we can calculate the critical value of the stress intensity factor K1c corresponding to brittle fracture. Assuming that in brittle fracture the second condition is satisfied by equality at sr = sc and taking into account the relation σ1r = scσyT, we get the equation
The quantity S0 will be represented as the sum S0 = S0c + ΔS0, consisting of the temperature-independent base part and the additional component ΔS0(ep) depending on plastic deformation ep that precedes fracture [14, 16]. The base part will be considered proportional to the yield stress determined at a temperature of 20°С and will be written as S0c = Cσy.
If the plastic zone ahead of the crack tip is very small compared to the size of the crack and the thickness of the part, the plastic strain intensity of the pre-fracture zone can be represented as [12]
Then, assuming that at small strain the additional component is proportional to the plastic strain, we write the expression for determining the plastic component in the form
where Y is the material constant with the dimension of stresses (Pa). As a result, the cleavage stress is described by the function
Substituting model sr(k) (3) and cleavage stress (7) into Eq. (6), we find the critical value of kc, which is the solution to Eq. (6). In the first stage of deformation, the average plastic strain intensity in the pre-fracture zone is nearly zero; therefore, the first condition (1) is not satisfied. It can be satisfied in the second stage of deformation at k1 < k ≤ k2; then the fracture condition takes the form
The critical value of kc is the solution to this equation
Here,
γT = σyT/σy is the temperature hardening coefficient of steel. We determined this coefficient for low-alloy steels using the expression [17]
where T is the temperature in °С.
Using the critical value of kc from solution (8) and formula (2), we can calculate the critical value of the stress intensity factor as
Thus, the critical stress intensity factor within the considered model is a function of the yield stress σy, plastic hardening modulus Gp, and temperature hardening coefficient γT, which depends on the type of steel and test temperature T. The parameters of this dependence are the quantities C and Y. The second parameter characterizes an increase in the cleavage stress as a result of plastic deformation. In view of very limited data, we assumed Y ≈ 800 MPa for all steels in this work. The value of C was selected from the condition that the calculated curves are close to test results.
3. SPECIMEN TEST RESULTS
The parameters of the proposed model were determined and its adequacy was verified using test results of various steel specimens, for which KIc was measured at negative temperatures. These results are compared with the analytical estimates obtained with the above formulas.
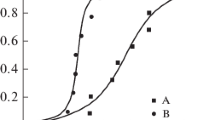
1. The KIc values were experimentally determined in [18] during bending tests on prismatic specimens with a notch and a fatigue crack in accordance with the standard test method [5]. The specimens were made of low-alloy A517-F steel, whose properties are given in Table 1 (No. 1). The calculated hardening modulus is Gp = 1750 MPa (4). The specimen dimensions (thickness × width) were 25.4 × 76.2 mm and 50.8 × 203 mm. The crack size was 0.25–0.40 of the specimen width. The experimental values of KIc obtained for these specimens are shown in Fig. 4. The figure also shows the curve plotted by Eq. (9) with the substituted parameters U = 1.6 and С = 2.7 (curve 1).
Test temperature dependence of KIc. Test on A517-F steel specimens with a thickness of 25.4 (♦) and 50.8 mm (○). Test on A572 steel specimens at strain rate \(\dot e = {10^{ - 3}}\) (■) and 10 1/s (Δ). Calculations by Eq. (9) at C = 2.7 for steel A517-F (1) and A572 (2, 3).
2. Bending test results for prismatic specimens made of A572 Grade 50 steel (Table 1, No. 2) are reported in [3]. The hardening modulus is defined as Gp = 1670 MPa (4). The values of KIc were obtained at negative temperatures. The bending test results shown in Fig. 4 were obtained at normal (\(\dot e = {10^{ - 3}}\) 1/s) and high strain rate \((\dot e = 10\) 1/s). The normal strain rate corresponds to the curve plotted by the proposed method (9) with the substitution of the parameters U = 1.6 and С = 2.7 (curve 2). Assuming that an increase in the loading rate is manifested in the same way as a decrease in temperature, the KIc(T) curve was calculated for the same values of U and C, but the estimated temperature was lower by 60°С in comparison with the real one (curve 3).
3. Test results for normalized and tempered double-cantilever beam specimens made of low-alloy UXW steel are given in [19] (Table 1, No. 3). The hardening modulus Gp = 2620 MPa (4). The experimental values of KID obtained for such specimens after crack arrest are compared in Fig. 5 with the curve calculated by Eq. (9) with the parameter U = 1.6 corresponding to the compact specimen, at C = 2.7.
Test temperature dependence of KID for UXW steel. ● and ○—experimental values obtained before and after general yield of the specimen. Curve 1 was calculated by Eq. (9) at C = 2.7.
4. Test results for compact wedge-opening-load (WOL) specimens [5] are reported in [20]. The specimens were made of low-alloy ASTM A302B steel; its post-annealing properties are indicated in Table 1 (No. 4). The hardening modulus Gp = 1670 MPa (4). The experimental values of KIc are compared in Fig. 6a with the curve calculated by Eq. (9) at U = 1.6 and C = 2.7.
Test temperature dependence of KIc for steel A302B (a) and A533B (b). ○ and □—experimental values. The curves were calculated by Eq. (9) at C = 2.7 (1) and 3.0 (2).
5. In [21], compact specimens of A533B steel were tested at negative temperatures (Fig. 6b). The steel was subjected to heat treatment, including austenitization for 4 h at 843°С with water quenching, tempering for 30 min at 660°С to a thickness of 25 mm, holding for 25 h at 610°С, furnace cooling to 315°С, and then air cooling. The mechanical characteristics of the heat-treated steel are presented in Table 1 (No. 5). The hardening modulus for this material was Gp = 3850 MPa. The dimensions of the compact specimens conformed to the ASTM standards [5], i.e., the thickness t and length a of the crack were at least 2.5(KIc/σy)2. The thickness of the test specimens was 25, 51, 102, and 152 mm. Two series of tests were performed in which the KIc values were obtained at different negative temperatures. The test results for both series are shown in Fig. 6b. The same figure illustrates the temperature dependences of KIc calculated by Eq. (9) at U = 1.6 and C = 3 (curve 2).
6. Test results of welded 10CrSiNiCu steel specimens are presented in [22] (Table 1, No. 6). The hardening modulus Gp = 1548 MPa. The specimens of width B = 300 mm consisted of four welded strips of thickness t = 40 mm. After welding they were tested for rupture in the temperature range from 0 to –130°С (Fig. 7a). The concentrator was a narrow gap of length 2a = 120 mm between the adjacent edges of the two central plates. Taking into account that the concentrator in these specimens is formed by a welded joint, its tip is not the tip of a sharp notch, and the material in which the crack is initiated differs from the base one. The critical values of the stress intensity factor were calculated from the fracture stress for the specimens. The value of sr was determined using Eq. (3). However, since these specimens had a crack with the relative size 2a/B = 0.4 exceeding the above limits, a specific finite element analysis was carried out. Due to the lack of more accurate data, the concentrator was modeled as a mathematical notch with a straight front along the entire specimen thickness. Based on this calculation, we derived the following expression for the parameter:
Test temperature dependence of KIc for welded 10CrSiNiCu steel specimens. ○—experimental values. Curve 1 was calculated for the base metal by Eq. (9) at C = 2.6.
Satisfactory convergence of the calculated Kc(T) curves (9) with the experimental ones was obtained at C = 2.6. The calculation was carried out using the mechanical characteristics of the base metal (Fig. 7b, curve 1).
4. DISCUSSION OF RESULTS
We considered the results of studies on the fracture behavior of parts with cracks in subzero temperature conditions [3, 18–22]. The tests were conducted in different laboratories using different methods and mostly aimed at determining the critical values of the stress intensity factor. The test specimens were made of low-alloy steels and had concentrators in the form of a crack or crack-like notch. The test results were used to evaluate the temperature dependence of KIc. All tests showed that KIc for the studied steels reaches its minimum at low temperature (about –80 ÷ –120°C) and grows with temperature rise. The scatter of KIc values within one series of tests was approximately ±(15–20)%.
Using these results, we verified the brittle fracture assessment method based on criterion (1) and the model of elastic-plastic deformation of the pre-fracture zone (3). We did this by calculating the critical stress intensity factor KIc (9) for the test specimens from the cited works. The initial data for the calculations were the yield stresses σy, plastic hardening moduli Gp, and test temperatures T. The value of the coefficient C was determined from the condition that the calculated curve is close to the scatter plot of experimental KIc values. Taking this into account, the cleavage stress S0c = Cσy for the considered steels was found to be equal to S0c = (2.6–3.0) σy.
In all the tests considered, specimen fracture occurred at the second stage of deformation of the pre-fracture zone, at k1 < kc < k2, and only at very low temperature kc was approaching k1 = 1.2 (Fig. 6a).
The behavior of the calculated KIc(T) curves for the given values of C agrees in most cases with the experimental data. For A517F, A572, A302B steel specimens without heat treatment and heat-treated UXW steel specimens, the coefficient C was found to be equal to 2.7. A different situation was observed in tests on A533B steel subjected to complex heat treatment. The calculated curve was approximated to the experimental values using the value C = 3 (Fig. 5b). This deviation is probably caused by a significant improvement of the steel structure as a result of multistage heat treatment.
An opposite deviation was observed when processing the test results of welded 10CrSiNiCu steel specimens, for which C = 2.6 (Fig. 7). The first difference of these specimens from all the others is in the structure of the concentrator tip. It is formed not by a fatigue crack, but by a burn-through defect between two plates. In addition, there were residual welding stresses in the specimen, and the metal in which the crack propagated was subjected to welding.
The dependence of the coefficient C on any characteristics of steel has not yet been observed. The determination of this coefficient requires more extensive experimental research.
For A517-F and A572 steels (at low loading rate), the experimental values of KIc increase considerably with increasing temperature (Fig. 4). The calculation of KIc in the given range by the proposed method gives underestimated values. This method does not take into account the rate of deformation. A preliminary assessment of the strain rate effect by a relative decrease in temperature shows that this quantity can really be taken into account using the corresponding yield stress increase factor (Fig. 4, A572 steel). However, the determination of its type and value requires additional study.
The general curve (Fig. 8) shows the values of the coefficient kc for compact and bending specimens of A517-F, A5721, UXW, and A302B steels used in the above references. Symbols indicate the experimental values of kc,test calculated with the KIc values determined from the test results as in Eqs. (2):
Test temperature dependence of kc. The values were calculated from experimental data: ○—UXW steel; ◊—A302B; Δ—A517-F; ■—A572. Curve 1 was calculated by Eq. (8) at C = 2.7 and U = 1.6.
The solid line shows the curve calculated by Eq. (8) with the averaged parameters Gp = 1500 MPa, Y = 800 MPa, C = 2.7, and U = 1.6. The summary curve shows that the calculation results by the proposed method for C = 2.7 agree with the experimental data for low-alloy steels in the as-received or annealed states.
Thus, the verification of the model by comparison with test results for low-carbon low-alloy steels showed that the model satisfactorily describes the dependence of the critical stress intensity factor on the subzero temperature value in brittle fracture. This is done using the standard mechanical characteristics of steels.
The analytical model for the loading of the pre-fracture zone eliminates the need for an elastic-plastic calculation of a metal structure by the design model of a structure with a crack. This is very convenient for practical application, because design calculations are time consuming and are not an engineering practice.
5. CONCLUSIONS
The proposed method of brittle fracture prediction was shown to adequately describe the dependence of the KIc values on low subzero temperatures for low-carbon low-alloy steels.
The cleavage stress estimate in the form S0c = Cσy was obtained by comparison with experimental data. For low-carbon low-alloy steels in the as-received or annealed state C = 2.7. For steel subjected to multistage heat treatment C = 3.0, which confirms the grain size dependence of the cleavage stress [14]. It can be assumed that after collecting a sufficient amount of experimental data this quantity can be normalized according to the type and condition of steel.
The developed method is based on using the standard mechanical characteristics of steel, which is advantageous at the design stage of engineering structures and components.
REFERENCES
Matvienko, Yu.G., Models and Criteria of Fracture Mechanics, Moscow: Fizmatlit, 2006.
Zhu, X.K. and Joyce, J.A., Review of Fracture Toughness (G, K, J, CTOD, CTOA) Testing and Standardization, Eng. Fract. Mech., 2012, vol. 85, pp. 1–46.
Barsom, J.M. and Rolf, S.T., Fracture and Fatigue Control in Structures. Application of Fracture Mechanics, Englewood Cliffs, New Jersey: Prentice-Hall, Inc., 1987.
Matvienko, Yu.G., Trends in Nonlinear Fracture Mechanics for Mechanical Engineering Problems, MoscowIzhevsk: Institute for Computer Research, 2015.
Standard Test Method for Plane-Strain Fracture Toughness of Metallic Materials. Designation: E 399–90 (Reapproved 1997), Annual Book of ASTM Standards, vol. 03.01.
GOST 25.506-85. Strength Calculations and Tests. Mechanical Testing Methods of Metals. Determination of Crack Resistance Characteristics (Fracture Toughness) under Static Loading, Moscow: Standartinform, 2005.
Sibilev, A.V. and Mishin, V.M., Cold Brittleness Criterion of Steel Specimens Based on the Local Failure Criterion, Fund. Issl. Tekh. Nauki, 2013, no. 4, pp. 843–847.
Kryzhevich, G.B., Integral Failure Criteria in Numerical Low-Temperature Strength Calculations of Marine Facilities, Transactions KSRC, 2018, no. 1(383), pp. 29–42.
Kotrechko, S.A., Meshkov, Yu.Ya., and Mettus, G.S., Model of the Failure of Steel under Conditions of Stress Concentration, Strength of Materials, 1992, vol. 24, no. 12, pp. 749–753.
Sokolov, S. and Grachev, A., Local Criterion for Strength of Elements of Steelwork, Mech. Eng. Res. Ed., 2018, vol. 12, no. 5, pp. 448–453.
Sokolov, S.A., Grachev, A.A., and Vasiliev, I.A., Strength Analysis of a Structural Element with a Crack under Negative Climatic Temperatures, Vestnik Mashinostroen., 2019, no. 11, pp. 42–46.
Sokolov, S.A. and Tulin, D.E., Modeling of Elastoplastic Stress States in Crack Tip Regions, Phys. Mesomech., 2021, no. 3, pp. 237–242. https://doi.org/10.1134/S1029959921030024
Vasiliev, I.A. and Sokolov, S.A., Investigation of Elastic-Plastic Stress-Strain State of a Plate with a Crack, Deform. Razrush. Mater., 2020, no. 3, pp. 16–20.
Kopelman, L.A., Fundamentals of the Theory of Strength of Welded Structures, SPb: Lan, 2010.
Tulin, D.E., Investigation of the Stress-Strain State of a Plate with a Semi-Elliptical and Through-Thickness Crack, Deform. Razrush. Mater., 2021, no. 4, pp. 15–18.
Karzov, G.P., Margolin, B.Z., and Shvetsova, V.A., Physical and Mechanical Modeling of Fracture Processes, SPb: Politekhnika, 1993.
Sokolov, S.A., Vasiliev, I.A., and Tulin, D.E., Change in the Yield Strength of Structural Steels at Subzero Temperatures, Deform. Razrush. Mater., 2021, no. 7, pp. 27–34.
Barsom, J.M. and Rolfe, S.T., K1c Transition-Temperature Behavior of A517-F Steel, Eng. Fract. Mech., 1971, vol. 2, pp. 341–357.
Radon, J.C. and Turner, C.E., Fracture Toughness Measurements on Low Strength Steels, in Proc. 2nd Int. Conf. on Fracture, Brighton (England), London: Chapman & Hall, Ltd., 1969, p. 165.
Wessel, E.T., Clark, W.G., and Wilson, W.K., Engineering Methods for the Design and Selection of Materials Against Fracture, Westinghouse Research Laboratories, Final Tech. Report No. DA-30-069-AMC-602(T), 1966.
Wessel, E.T., Clark, W.G., and Pryle, W.H., Fracture Mechanics Technology Applied to Heavy Section Steel Structures, in Proc. 2nd Int. Conf. on Fracture, Brighton (England), London: Chapman & Hall, Ltd., 1969.
Andreev, V.V. and Anikovskiy, V.V., Effect of Test Temperature on Static Strength of Welded 10CrSiNiCu Steel Joints with Sharp Defects, Trudy LPI, 1974, no. 336, pp. 42–44.
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Fizicheskaya Mezomekhanika, 2021, Vol. 24, No. 3, pp. 67–75.
Rights and permissions
About this article
Cite this article
Sokolov, S.A., Tulin, D.E. Mathematical Model of Brittle Fracture of a Cracked Part. Phys Mesomech 25, 72–79 (2022). https://doi.org/10.1134/S1029959922010088
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1029959922010088





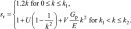 (3)
(3)





