Detailed research on the entire variety of processes occurring during the boiling of a liquid is of interest both from a purely scientific and from a practical point of view and is relevant to this day. An elementary act of the boiling process is the growth of a vapor bubble, described by a complex problem in which the equations of hydrodynamics and heat transfer should be solved concurrently. Attempts to obtain the law of vapor bubble growth have a long history, from classical works [1–5] to numerous modern studies [6, 7].

It should be noted that, when constructing mathematical models for vapor bubble growth, the authors propose to take into account various factors, dynamic, kinetic, thermal, and others, that determine this process. Since the factors change at one process stage or another depending on the properties of the two-phase system considered, various assumptions are used to solve the problem, allowing us to construct simplified mathematical models in which a single fundamental mechanism controlling the process is selected. The major, most popular of them are [8] the dynamic inertial model, in which the bubble grows exclusively due to inertial effects; the dynamic viscous model, in which bubble growth is limited by viscous forces; and the energy kinetic model, which attempts to take into account the kinetics of the phase transition and the energy thermal model. The latter is the most common in the literature. In this model, bubble growth is due to the supply of heat to the interface from the external superheated layers of the liquid; all the heat is spent on evaporation. In this model the bubble radius depends on time as a power function with an exponent of 1/2. The proportionality coefficient is a function of the Jacob number and is found by different authors in different ways. The most famous is the Plesset–Zwick formula [1], which is valid for large Jacob numbers. A sufficiently complete analytical solution of the problem in integral form was obtained by Scriven [4]. Along with this, various empirical dependencies gained popularity [9].

Analysis of the energy thermal model shows that, despite its widespread use, it has a limited scope. In particular, this is reflected in the fact that a number of approximations made in it result in a solution with an infinite bubble growth rate at the initial moment of time, which is physically incorrect. In this regard, attempts are being made to create various kinds of hybrid models that simultaneously take into account both dynamic and thermal effects [10–13], which turns out to entail significant difficulties. This work aims to find an approximate analytical solution to this problem, which would correctly describe all stages of vapor bubble growth.

Suppose that a vapor bubble originated and began to grow at the initial moment of time in a uniformly superheated liquid. The system of equations describing this process includes the well-known classical equations written as applied to this problem, taking into account the specifics of liquid evaporation. For solving the problem, let us use the approximation of a uniform equilibrium bubble, according to which the vapor in the bubble is saturated and the temperature and pressure are uniform [14].

The bubble dynamics is described by the momentum equation (modified Rayleigh equation):

$$\frac{1}{R}~\frac{{\text{d}}}{{{\text{d}}t}}({{{v}}_{{lR}}}{{R}^{2}}) - \frac{{{v}_{{lR}}^{2}}}{2} = \frac{{{{p}_{{lR}}} - p_{l}^{i}}}{{{{\rho }_{l}}}},$$
(1)

where R is the bubble radius; t is time; p is pressure; ρ is density; \({{{v}}_{{lR}}}\) is the radial velocity of the liquid at the boundary of the bubble, which, in the presence of a phase transition, differs from the bubble growth rate \(\dot {R}\) and is related to it as \({{\rho }_{l}}(\dot {R} - {{{v}}_{{lR}}}) = j\), where j is the density of the vapor flow formed during the evaporation of the liquid. Hereinafter, the subscripts l and \({v}\) denote the liquid and vapor phases; superscripts i and f are the initial and final states, respectively; the subscript R stands for the value of the quantity at the interface.

The boundary conditions reflecting the conservation laws of mass, momentum, and energy are written as follows:

$${{\rho }_{{v}}}\dot {R} + \frac{1}{3}{{\dot {\rho }}_{{v}}}R = j;$$
(2)
$${{p}_{{lR}}} = {{p}_{{v}}} + j{{{v}}_{{lR}}} - \frac{{2\sigma }}{R} - 4{{\eta }_{l}}\frac{{{{{v}}_{{lR}}}}}{R};$$
(3)
$${\text{L}} = {{\lambda }_{l}}{{\left( {\frac{{\partial {{T}_{l}}}}{{\partial r}}} \right)}_{{r = R}}}~,$$
(4)

where σ is surface tension; η is dynamic viscosity; L is specific heat of the phase transition; λ is the coefficient of thermal conductivity; and T is the temperature.

This system of equations is closed by the heat problem, in which the dynamics of the temperature field in the liquid is described by the heat equation:

$$\frac{{\partial \left( {{{\rho }_{l}}{{c}_{l}}{{T}_{l}}} \right)}}{{\partial t}} + {{{v}}_{l}}~\frac{{\partial \left( {{{\rho }_{l}}{{c}_{l}}{{T}_{l}}} \right)}}{{\partial r}} = \frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}~\left( {{{\lambda }_{l}}{{r}^{2}}~\frac{{\partial {{T}_{l}}}}{{\partial r}}} \right),$$
(5)

where r is the radial coordinate with the origin at the center of the bubble; \({{{v}}_{l}}\left( r \right) = {{{v}}_{{lR}}}~{{\left( {\frac{R}{r}} \right)}^{2}}\) is the radial velocity of the liquid (which is obtained from the continuity equation under the assumption that the liquid is incompressible); and с is the heat capacity. Further, the quantities characterizing the thermophysical properties of the liquid are assumed constant.

At the initial moment of time, the temperature of the liquid is uniform and greater than the saturation temperature at pressure \(p_{l}^{i}\) (pressure far from the bubble): \({{({{T}_{l}})}_{{t = 0}}} = {{T}^{i}} > {{T}^{s}}(p_{l}^{i})\). Far from the bubble, the temperature field remains unperturbed: \({{({{T}_{l}})}_{{r \to \infty }}} = {{T}^{i}}\). On the bubble surface, the condition of local thermodynamic equilibrium is satisfied: \({{({{T}_{l}})}_{{r = R}}} = {{T}^{s}}\left( {{{p}_{{v}}}} \right)\). Here and below, the superscript s denotes the value of the quantity on the saturation line.

The problem should be supplemented by the equation of state of the vapor in the bubble and the dependence of the saturation pressure on temperature, which in the general case have the following form:

$${{\rho }_{{v}}} = {{\rho }_{{v}}}\left( {{{p}_{{v}}},{{T}_{{v}}}} \right);$$
(6)
$${{p}_{{v}}} = {{p}^{s}}\left( {{{T}_{{v}}}} \right)\quad {\text{or}}\quad {{T}_{{v}}} = {{T}^{s}}\left( {{{p}_{{v}}}} \right).$$
(7)

These can be both model and more accurate empirical dependencies. As a rule, the Mendeleev–Clapeyron equation is used as the equation of state, assuming the vapor to be an ideal gas, and the Clapeyron–Clausius equation is used for the equilibrium curve. Admittedly this somewhat narrows the generality of both the problem statement itself and the solutions obtained. However, in most cases, this is quite sufficient to ensure an acceptable accuracy of the solution obtained. Note also that dependencies (6) and (7) uniquely define functions \({{T}^{s}}\left( {{{p}_{{v}}}} \right)\) and \({{p}^{s}}\left( {{{\rho }_{{v}}}} \right)\), which will appear later.

In the general case, the formulated problem (even without taking into account inertial effects) can be solved only numerically. However, we can propose an approach that provides a basis to construct an approximate solution for the problem in almost the entire time range of bubble evolution. From a mathematical point of view, it is convenient to construct it after passing from variables (t, r) to variables \((t,\chi )\), where χ = \(\frac{r}{{R(t)}}\), thereby reducing the boundary value problem to a problem with fixed boundaries (similarly to how it was done in [15] when solving the problem of diffusion growth of a gas bubble).

Heat equation (5) takes the following form:

$$\frac{{{{R}^{2}}}}{{{{a}_{l}}}}\frac{{\partial {{\Theta }_{l}}}}{{\partial t}} = \left( { - \frac{\alpha }{{{{\chi }^{2}}}} + \frac{2}{\chi } + \beta \chi } \right)\frac{{\partial {{\Theta }_{l}}}}{{\partial \chi }} + \frac{{{{\partial }^{2}}{{\Theta }_{l}}}}{{\partial {{\chi }^{2}}}},$$
(8)

where \({{\Theta }_{l}} = \frac{{{{T}_{l}} - T_{l}^{i}}}{{\Delta T_{l}^{i}}}\) is dimensionless temperature; \(\Delta T_{l}^{i} = T_{l}^{i} - {{T}^{s}}(p_{l}^{i})\) is the initial superheating of the liquid; \(\alpha = \frac{{{{{v}}_{{lR}}}R}}{{{{a}_{l}}}}\) and \(\beta = \frac{{\dot {R}R}}{{{{a}_{l}}}}\) are functions of time; and a = \(\frac{\lambda }{{\rho c}}\) is the thermal conductivity.

The initial and boundary conditions are written as follows:

$${{({{\Theta }_{l}})}_{{t = 0}}} = 0;\quad {{({{\Theta }_{l}})}_{{\chi = 1}}} = {{\Theta }^{s}}\left( {{{{\bar {\rho }}}_{{v}}}} \right);\quad {{({{\Theta }_{l}})}_{{\chi \to \infty }}} = 0,$$
(9)

where \({{\bar {\rho }}_{{v}}} = \frac{{{{\rho }_{{v}}}}}{{{{\rho }_{l}}}}\) is the dimensionless vapor density.

Passing to the analysis of Eq. (8), let us note that the structure of the solution depends on the behavior of the control functions \(\alpha = \alpha (t)\)and \(\beta = \beta (t)\). At the initial stage of bubble evolution its growth rate is small; therefore, the quantities \(\alpha ,\beta \ll 1\). Then the term \(\frac{2}{\chi }\) in parentheses on the right side of Eq. (8) becomes the leading term in comparison with the rest. In this case, Eq. (8) is reduced to the equation known for the heat problem, the solution of which decreases asymptotically. As the system evolves further, the structure of the solution changes due to the monotonic growth of α, β. But it still contains an asymptotically decreasing term. However, taking into account α, β leads to a temperature distribution for which the initial stage of the process becomes irrelevant. Such a solution for the temperature can be found under the condition that the right side of Eq. (8) vanishes, and, taking into account conditions (9), it is given by the formula

$${{\Theta }_{l}}\left( {\tau ,\chi } \right) = {{\Theta }^{s}}\left( {{{{\bar {\rho }}}_{{v}}}} \right)\frac{{\int\limits_0^{1/\chi ~} {{\text{exp}}\{ - \alpha \zeta - \beta {{\zeta }^{{ - 2}}}{\text{/}}2\} d\zeta } }}{{\int\limits_0^1 {{\text{exp}}\{ - \alpha \zeta - \beta {{\zeta }^{{ - 2}}}{\text{/}}2\} d\zeta } }}.$$
(10)

Solution (10) is not stationary from the point of view of mathematics, since it depends on time by \(\alpha = \alpha (t)\), \(\beta = \beta (t)\), so it is natural to call it quasi-stationary. In this case, numerical calculations for (8) show that the relaxation time of a quasi-stationary state is significantly less than the duration of the entire process of bubble evolution. This means that solution (10) quite accurately describes the dynamics of the temperature field that forms around the bubble throughout its growth.

Modifying the original system of equations (1)–(4) and substituting the obtained temperature profile (10) into the dimensionless equation (4), we get the following system of first-order differential equations:

$$\frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = \frac{{\Delta p_{{v}}^{i}}}{{{{\rho }_{l}}{{a}_{l}}}}{{\Pi }^{s}}\left( {{{{\bar {\rho }}}_{\nu }}} \right) - \frac{{2\sigma }}{{{{\rho }_{l}}{{a}_{l}}}}\frac{1}{R} - \frac{{4{{\eta }_{l}}}}{{{{\rho }_{l}}}}\frac{\alpha }{R} - \frac{{{{a}_{l}}}}{2}\frac{{{{\alpha }^{2}}}}{{{{R}^{2}}}};$$
$$\frac{{{\text{d}}{{{\bar {\rho }}}_{{v}}}}}{{{\text{d}}t}} = \frac{{3{{a}_{l}}\left( {\beta \left( {1 - {{{\bar {\rho }}}_{{v}}}} \right) - \alpha } \right)}}{{{{R}^{2}}}};$$
$$\frac{{{\text{d}}R}}{{{\text{d}}t}} = \frac{{{{a}_{l}}\beta }}{R},$$
(11)

where \(\Pi = \frac{{{{p}_{{v}}} - p_{l}^{i}}}{{\Delta p_{{v}}^{i}}}\) is the dimensionless pressure and \(\Delta p_{{v}}^{i} = {{p}^{s}}(T_{l}^{i}) - p_{l}^{i}\) is the initial excess vapor pressure due to liquid superheating. Function \(\beta = \beta \left( {\alpha ,{{{\bar {\rho }}}_{{v}}}} \right)\) is implicitly given by the equation

$$\begin{gathered} (\beta - \alpha )\mathop \smallint \limits_0^1 {\text{exp}}\{ \{ \alpha (1 - \zeta ) + \beta (1 - {{\zeta }^{{ - 2}}}){\text{/}}2\} {\text{d}}\zeta \\ = ~\, - K{{u}^{{ - 1}}}~{{\theta }^{s}}({{{\bar {\rho }}}_{{v}}}), \\ \end{gathered} $$
(12)

and functions \({{\Pi }^{s}}\left( {{{{\bar {\rho }}}_{{v}}}} \right)\) and \({{\theta }^{s}}\left( {{{{\bar {\rho }}}_{{v}}}} \right)\) are obtained from (6) and (7); Ku \( = \frac{{\text{L}}}{{{{c}_{l}}\Delta T_{l}^{i}}}\) is the Kutateladze number characterizing the initial degree of metastability. Using this approach, the solution of the heat problem is actually reduced to solving the transcendental equation (12).

Thus, the problem was reduced to solving a system of three ordinary differential equations of the form \(\frac{{{\text{d}}{\mathbf{y}}}}{{{\text{d}}t}} = {\mathbf{f}}({\mathbf{y}})\), where \({\mathbf{y}} = (\alpha ,{{\bar {\rho }}_{{v}}},R)\) is the desired vector function, and the function f(y) is given by the right-hand side of Eqs. (11).

As the bubble grows, the pressure in it gradually decreases and asymptotically tends to the pressure of the surrounding liquid; the vapor density in the bubble and the temperature of the liquid at the interface tend to constant values: \({{\rho }_{{v}}} \to \rho _{{v}}^{f};~{{({{\Theta }_{l}})}_{{\chi = 1}}} \to - 1\), where \(\rho _{{v}}^{f}\) is the vapor density at pressure \(p_{l}^{i}\). At this stage of the process, which, by the way, can be described within the framework of the energy thermal model, the bubble growth is determined exclusively by heat transfer to the interface, the temperature field in the liquid becomes stationary, the functions α and β become constants, and the solution of the boundary value problem is precisely self-similar:

$$\begin{gathered} {{\Theta }_{l}}\left( \chi \right) = - \frac{{\int\limits_0^{1/\chi } {{\text{exp}}\{ - {{\beta }^{f}}(\zeta (1 - \bar {\rho }_{{v}}^{f}) + {{\zeta }^{{ - 2}}}{\text{/}}2)\} {\text{d}}\zeta } }}{{\int\limits_0^1 {{\text{exp}}\{ - {{\beta }^{f}}(\zeta (1 - \bar {\rho }_{{v}}^{f}) + {{\zeta }^{{ - 2}}}{\text{/}}2)\} {\text{d}}\zeta } }};~ \\ R = \sqrt {2{{\beta }^{f}}{{a}_{l}}t} . \\ \end{gathered} $$
(13)

Note that a similar solution was obtained by Scriven [4]. At this stage coefficient βf, appearing in Eq. (13), is a function of only the Jacob number Ja = \({{(\bar {\rho }_{{v}}^{f}{\text{Ku}})}^{{ - 1}}} = \frac{{{{\rho }_{l}}}}{{\rho _{{v}}^{f}}}\frac{{{{c}_{l}}\Delta T_{l}^{i}}}{{\text{L}}}\) and is found from the following integral equation (which directly follows from Eq. (12)):

$${{\beta }^{f}}\mathop \smallint \limits_0^{1~{{\;}}} {\text{exp}}\left\{ {\left. {{{\beta }^{f}}\left( {\left( {1 - \zeta } \right)(1 - \bar {\rho }_{{v}}^{f}) + \frac{{1 - {{\zeta }^{{ - 2}}}}}{2}} \right)} \right\}} \right.{\text{d}}\zeta = {\text{Ja}}{\text{.}}$$
(14)

In the case of small and large superheating at \(\bar {\rho }_{{v}}^{f} \ll 1\), Eq. (14) has the following approximate solutions:

$${{\beta }^{f}} \approx Ja\quad {\text{at}}\quad Ja \ll 1;$$
$${{\beta }^{f}} \approx \left( {\frac{6}{\pi }} \right){{\left( {Ja + \frac{4}{9}} \right)}^{2}}\quad {\text{at}}\quad Ja \gg 1.$$

The latter coincides with the well-known Plesset–Zwick solution [1] (if we do not take into account the additive correction to the Jacob number, which significantly improves this asymptotic approximation).

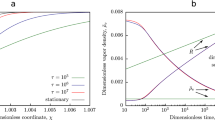
Figure 1 presents the time dependences of the bubble radius and liquid temperature at the interface, plotted for water at atmospheric pressure and the initial superheating of 50 K; they clearly illustrate the mechanism of vapor bubble growth in a superheated liquid, which combines dynamic and thermal effects. The initial bubble size was assumed to be 1.1 Rcr, where Rcr = \(\frac{{2\sigma }}{{~\Delta p_{{v}}^{i}}}\) is the critical radius at zero initial growth rate and a vapor temperature equal to the temperature of the surrounding liquid. As can be seen from the figure, the difference between the calculation results obtained by direct numerical simulation of the initial system of equations (1)–(7) and based on the derived semi-analytical solution (11) and (12) is rather small, which shows the consistency of the latter (the same was observed in the calculations for other superheating cases and for other liquids). Note also that the self-similar solution (13) and (14) is valid only on large times, since it is essentially asymptotic; that is, it is bounded as applied to real systems, especially in the case of great superheating, where the characteristic time of the transition stage can be a much more characteristic observation time.

Fig. 1.
figure 1

Dependence of the bubble radius \(R\) (1) and liquid superheating at the interface \(\Delta {{T}_{{lR}}}\); (2) on time: solid line, the obtained semi-analytical solution (11) and (12); dashed line, direct numerical simulation; dash-dotted line, the self-similar solution (13) and (14).

Full size image

Thus, we have obtained a relatively simple semi-analytical solution to the problem of the vapor bubble growth in an initially homogeneously superheated liquid, which simultaneously describes both the inertial and thermal effects controlling this process, and can serve as a good alternative to direct numerical calculations.