INTRODUCTION

It is convenient to solve the problem of the hydrodynamic interaction of two spheres moving in a potential flow of an ideal fluid using the method of generalized Lagrange coordinates. The coordinates of the centers of spheres and their radii are accepted as generalized coordinates, and their time derivatives are respectively taken as generalized velocities. The kinetic energy of the fluid is the Lagrange function. Such a method of solving the problem was first used by Kelvin and Tait [1], who obtained an expression for the kinetic energy of two spheres balls located far from each other. The exact expression for the kinetic energy of the fluid with solid spheres moving along the line of their centers was derived by Hicks [2] using the image method. Voinov [3–5] generalized the Hicks method for the motion of spheres of variable radii and obtained a general expression for the kinetic energy. In [6], a technique was developed for obtaining asymptotic expansions of the hydrodynamic interaction force with respect to a small gap between the spheres in the vicinity of their contact. With the help of this technique, the main logarithmic asymptotics for the small gap was calculated for solid spheres, and the next term of the expansion was found in [6]. In [7], it was shown how to find the main asymptotics of the forces of hydrodynamic interaction of bodies without using the exact solution. To do this, it suffices to single out the singular asymptotics of the velocity field in the vicinity of the contact.

It should be noted that the constant terms in the asymptotic expansion of hydrodynamic interaction forces are very important for studying the convergence of spheres of variable radius along with the logarithmic asymptotics. This study is devoted to constructing these terms. It opens the possibility of studying the process of approaching two pulsating gas bubbles up to their contact and to find the conditions under which no merging of bubbles occurs.

AN EXACT EXPRESSION FOR THE KINETIC ENERGY

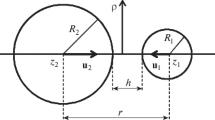
The motion of two spheres of radii \({{a}_{1}}\) and \({{a}_{2}}\) along the line of their centers in a potential flow of an ideal fluid is considered. The velocities of the centers of spheres are \({{u}_{1}}\) and \({{u}_{2}}\), respectively, and they are directed towards each other (Fig. 1). The kinetic energy \(T\) of the fluid is calculated using the potential of the velocity field. Its general expression first obtained by Voinov is given in [4, 5, 8]:

$$\begin{gathered} \frac{T}{{2\pi \rho }}\, = \,\sum\limits_{i = 1}^2 ({{A}_{i}}u_{i}^{2}\, + \,B{{u}_{i}}{{u}_{k}}\, + \,{{D}_{i}}\dot {a}_{i}^{2}\, + \,E{{{\dot {a}}}_{i}}{{{\dot {a}}}_{k}}\, + \,{{C}_{{ik}}}{{u}_{i}}{{{\dot {a}}}_{k}}\, + \,{{C}_{{ii}}}{{u}_{i}}{{{\dot {a}}}_{i}}), \\ i \ne k,\quad i,k = 1,2, \\ \end{gathered} $$
$$\begin{gathered} 2{{A}_{1}} = \frac{{a_{1}^{3}}}{3} + \sum\limits_{n = 1}^\infty \mathop {\left( {\frac{{{{a}_{1}}}}{{A_{n}^{1}}}} \right)}\nolimits^3 ,\quad 2B = \sum\limits_{n = 1}^\infty \mathop {\left( {\frac{{{{a}_{2}}}}{{B_{n}^{1}}}} \right)}\nolimits^3 , \\ {{D}_{1}} = a_{1}^{3} + \sum\limits_{n = 1}^\infty \frac{{a_{1}^{3}}}{{A_{n}^{1}}}\left[ {1 + ({{{(B_{n}^{2})}}^{2}} - 1)\ln\left( {1 - \frac{1}{{{{{(B_{n}^{2})}}^{2}}}}} \right)} \right], \\ \end{gathered} $$
((1))
$$\begin{gathered} E = \frac{{{{{({{a}_{1}}{{a}_{2}})}}^{2}}}}{r} + \frac{{{{{({{a}_{1}}{{a}_{2}})}}^{2}}}}{{{{a}_{2}}}}\sum\limits_{n = 1}^\infty \left( {\frac{1}{{B_{{n + 1}}^{2}}} - B_{n}^{1}\ln\left( {1 + \frac{1}{{B_{{n + 1}}^{2}B_{n}^{1}}}} \right)} \right), \\ {{C}_{{11}}} = \sum\limits_{n = 1}^\infty \frac{{a_{1}^{3}}}{{{{{(A_{n}^{1})}}^{2}}B_{n}^{2}}},\quad {{C}_{{12}}} = \sum\limits_{n = 1}^\infty \frac{{a_{1}^{3}}}{{{{{(B_{n}^{2})}}^{2}}A_{{n - 1}}^{1}}}. \\ \end{gathered} $$
Fig. 1.
figure 1

Problem formulation.

Full size image

The series for \({{A}_{2}},{{D}_{2}},{{C}_{{21}}},{{C}_{{22}}}\) are obtained by permutation of 1 by 2 in the corresponding formulas. The coefficients \(A_{n}^{i},B_{n}^{i}\) can be calculated from the recurrence relations for the distance between the centers of the spheres \(r = {{x}_{2}} - {{x}_{1}}\):

$$\begin{array}{*{20}{c}} {B_{n}^{i} = \frac{r}{{{{a}_{i}}}}A_{{n - 1}}^{k} - \frac{{{{a}_{k}}}}{{{{a}_{i}}}}B_{{n - 1}}^{i},\quad A_{n}^{i} = \frac{r}{{{{a}_{i}}}}B_{n}^{k} - \frac{{{{a}_{k}}}}{{{{a}_{i}}}}A_{{n - 1}}^{i},} \end{array}$$
((2))

and the initial conditions \(A_{0}^{i} = 1\), \(B_{0}^{i} = 0\). It should be noted that \(B,E\) are independent of subscripts because the equality \({{a}_{1}}B_{n}^{1} = {{a}_{2}}B_{n}^{2}\) holds.

The series of coefficients \({{A}_{i}},B,{{D}_{i}},E,{{C}_{{ii}}},{{C}_{{ik}}}\) for the kinetic energy converge as geometric progressions excluding the points of contact at which they converge as \(1{\text{/}}{{n}^{3}}.\)

EXPANSION IN THE VICINITY OF CONTACT

For the coefficients \(A_{n}^{i},B_{n}^{i}\), recurrence relations (2) can be solved as in [6, 9]:

$$\begin{gathered} A_{n}^{i} = \frac{{{{\tau }^{{n + 1}}} - {{\tau }^{{ - n - 1}}} + ({{\tau }^{n}} - {{\tau }^{{ - n}}}){{a}_{i}}{\text{/}}{{a}_{k}}}}{{\tau - {{\tau }^{{ - 1}}}}}, \\ B_{n}^{i} = \frac{{({{\tau }^{n}} - {{\tau }^{{ - n}}})r{\text{/}}{{a}_{i}}}}{{\tau - {{\tau }^{{ - 1}}}}}, \\ \end{gathered} $$

where \(\tau \) is the root of the equation r2τ = \(({{a}_{1}}\tau \, + \,{{a}_{2}})({{a}_{1}}\, + \,{{a}_{2}}\tau )\).

These expressions can be simplified by using the substitution \(\tau = {{e}^{\varepsilon }}\) [10]:

$$A_{n}^{i} = \frac{r}{{{{a}_{k}}}}\frac{{\sinh (n\varepsilon + {{\varepsilon }_{i}})}}{{\sinh \varepsilon }},\quad B_{n}^{i} = \frac{r}{{{{a}_{i}}}}\frac{{\sinh n\varepsilon }}{{\sinh \varepsilon }}.$$

In this case, \(\sinh {{\varepsilon }_{i}} = \frac{{{{a}_{k}}}}{r}\sinh \varepsilon \) and \(\varepsilon \) is found from the equation \({{r}^{2}} = a_{1}^{2} + a_{2}^{2} + 2{{a}_{1}}{{a}_{2}}\cosh\varepsilon \). Thus tending to the contact \(r \to {{a}_{1}} + {{a}_{2}}\), we obtain that \(\varepsilon \to 0\) and the following limit expressions for \(A_{n}^{i},B_{n}^{i}\) at \(\varepsilon = 0\):

$$A_{n}^{i} = \frac{{n + {{\alpha }_{k}}}}{{{{\alpha }_{k}}}},\quad B_{n}^{i} = \frac{n}{{{{\alpha }_{i}}}},\quad {{\alpha }_{i}} = \frac{{{{a}_{i}}}}{{{{a}_{1}} + {{a}_{2}}}}.$$
((3))

Previously, Voinov proposed to determine the derivative \(\frac{{\partial T}}{{\partial r}}\) in the vicinity of the contact using the following transformations [6]:

$$\begin{gathered} \sum\limits_{n = 1}^\infty \,f(n,\varepsilon ) = \sum\limits_{n = 1}^{[1/\varepsilon ]} \,f(n,0) \\ - \,\int\limits_1^{1/\varepsilon } f (x,0)dx + \int\limits_1^\infty f (x,\varepsilon )dx + O(\varepsilon ). \\ \end{gathered} $$
((4))

Applying transformation (4) to A1 and B, Voinov found that [6]

$$\begin{array}{*{20}{c}} {\frac{1}{{\mathop {a'}\nolimits^2 }}\frac{{\partial B}}{{\partial h}} = \frac{1}{4}\ln\frac{h}{{2a'}} + \frac{1}{3} - \frac{\gamma }{2} + \frac{1}{2}(1 - 3{{\alpha }_{1}}{{\alpha }_{2}})\zeta (3) + O(h{\text{ln}}h),} \\ \begin{gathered} \frac{1}{{\mathop {a'}\nolimits^2 }}\frac{{\partial {{A}_{1}}}}{{\partial h}} = \frac{1}{4}\ln\frac{h}{{2a'}} + \frac{1}{3} - \frac{\gamma }{2} \\ + \frac{1}{2}\sum\limits_{n = 1}^\infty \left[ {\frac{1}{n} - \frac{{n(n + 1)(n - 1 + 3{{\alpha }_{2}})}}{{{{{(n + {{\alpha }_{2}})}}^{4}}}}} \right] + O(h\ln h), \\ \end{gathered} \\ {a' = \frac{{{{a}_{1}}{{a}_{2}}}}{{{{a}_{1}} + {{a}_{2}}}},\quad h = r - {{a}_{1}} - {{a}_{2}}} \end{array}$$

and noticed that the series difference \(\frac{1}{{{a'}^{2}}}\frac{{\partial {{A}_{1}}}}{{\partial h}} - \frac{1}{{{a'}^{2}}}\frac{{\partial B}}{{\partial h}}\) for the coefficient \({{A}_{1}}\) remains finite when the spheres approach their contact. It turns out that all other coefficients of kinetic energy \({{D}_{1}},E,{{C}_{{11}}}{\text{/}}2,{{C}_{{12}}}{\text{/}}2\), have this property instead of only \({{A}_{1}}\). This observation simplifies the deduction of the logarithmic and next terms of the asymptotic expansions for them.

Indeed, this property implies that all the coefficients of the kinetic energy have the same structure in the vicinity of the contact

$$\frac{1}{{\mathop {a'}^2 }}\frac{{\partial X}}{{\partial h}} = \frac{1}{4}\ln\frac{h}{{2a'}} + {{X}_{1}} + O(h\ln h),$$
((5))

where X is an arbitrary kinetic-energy coefficient and \({{X}_{1}}\) depends only on the radii of the spheres and does not depend on h.

The expansions for the coefficients A1, B, D1, E, \({{C}_{{11}}}{\text{/}}2,{{C}_{{12}}}{\text{/}}2\) are obtained by integrating using formula

$$\begin{gathered} X(h) = {{X}_{0}} + \int\limits_0^h {\frac{{dX}}{{dh}}} \\ = {{X}_{0}} + {a'}^{2}h\left( {\frac{1}{4}\left( {\ln\left( {\frac{h}{{2a'}}} \right) - 1} \right) + {{X}_{1}}} \right). \\ \end{gathered} $$
((6))

This is the desired trinomial expansion of an arbitrary coefficient \(X(h)\) containing the constant term \({{X}_{0}}\) and terms like \(h\ln h\) and h. We omit the remaining terms of the order of smallness of \({{h}^{2}}\ln h\) and higher.

The expression for \({{X}_{0}}\) can be obtained from exact series (1) by substituting limit values (3) in them. We write out the dependencies of \({{X}_{0}}\) and \({{X}_{1}}\) for each kinetic-energy coefficient. For the first two coefficients \({{A}_{1}}\) and B, they have the following form:

$$\begin{array}{*{20}{c}} \begin{gathered} {{X}_{0}} = a_{1}^{3}\left( {\frac{1}{6} + \frac{1}{2}\sum\limits_{n = 1}^\infty \mathop {\left( {\frac{{{{\alpha }_{2}}}}{{n + {{\alpha }_{2}}}}} \right)}\nolimits^3 } \right), \\ {{X}_{1}} = \frac{1}{3} - \frac{\gamma }{2} + \frac{1}{2}\sum\limits_{n = 1}^\infty \left[ {\frac{1}{n} - \frac{{n(n + 1)(n - 1 + 3{{\alpha }_{2}})}}{{{{{(n + {{\alpha }_{2}})}}^{4}}}}} \right], \\ \end{gathered} \\ {{{A}_{1}} = {{X}_{0}} + {a'}^{2}h\left( {\frac{1}{4}\left( {\ln \left( {\frac{h}{{2a'}}} \right) - 1} \right) + {{X}_{1}}} \right),} \\ {{{X}_{0}} = \frac{1}{2} {a'}^{3}\zeta (3),\quad {{X}_{1}} = \frac{1}{3} - \frac{\gamma }{2} + \frac{1}{2}(1 - 3{{\alpha }_{1}}{{\alpha }_{2}})\zeta (3),} \\ {B = {{X}_{0}} + {a'}^{2}h\left( {\frac{1}{4}\left( {\ln \left( {\frac{h}{{2a'}}} \right) - 1} \right) + {{X}_{1}}} \right).} \end{array}$$
((7))

The remaining coefficients \({{D}_{1}},E,{{C}_{{11}}}{\text{/}}2,{{C}_{{12}}}{\text{/}}2\), are calculated similarly by formula (6) in which only the expressions for \({{X}_{0}}\) and \({{X}_{1}}\) vary:

$$\begin{gathered} {{D}_{1}}{\text{:}}\,{{X}_{0}} = a_{1}^{3} + a_{1}^{3}\sum\limits_{n = 1}^\infty \frac{{{{\alpha }_{2}}}}{{n + {{\alpha }_{2}}}}\left[ {1 + \left( {\frac{{{{n}^{2}}}}{{\alpha _{2}^{2}}} - 1} \right)\ln \left( {1 - \frac{{\alpha _{2}^{2}}}{{{{n}^{2}}}}} \right)} \right], \\ {{X}_{1}} = \frac{1}{3} - \frac{\gamma }{2} + \sum\limits_{n = 1}^\infty \left[ {\frac{1}{{6n}} + \frac{{(n - 1)(n + 1 - 3{{\alpha }_{2}})}}{{3n\alpha _{2}^{2}}}} \right. \\ \left. { \times \left( {1 + \frac{{{{n}^{2}}}}{{\alpha _{2}^{2}}}\ln \left( {1 - \frac{{\alpha _{2}^{2}}}{{{{n}^{2}}}}} \right)} \right) + \frac{{\alpha _{1}^{2} - (n + 1){{\alpha }_{2}}}}{{3n{{{(n + {{\alpha }_{2}})}}^{2}}}}} \right], \\ \end{gathered} $$
$$\begin{gathered} E{\text{:}}\,{{X}_{0}} = \frac{{{{{({{a}_{1}}{{a}_{2}})}}^{2}}}}{{{{a}_{1}} + {{a}_{2}}}}\left[ {1 + \sum\limits_{n = 1}^\infty \frac{1}{{n + 1}}} \right. \\ \left. { \times \left( {1 - \frac{{n(n + 1)}}{{{{\alpha }_{1}}{{\alpha }_{2}}}}\ln \left( {1 + \frac{{{{\alpha }_{1}}{{\alpha }_{2}}}}{{n(n + 1)}}} \right)} \right)} \right], \\ {{X}_{1}} = \frac{1}{3} - \frac{\gamma }{2} - \frac{1}{2} + \sum\limits_{n = 1}^\infty \left[ { - \frac{1}{{6(n + 1)}} + \frac{{{{n}^{2}} - 1 + 3{{\alpha }_{1}}{{\alpha }_{2}}}}{{3(n + 1){{\alpha }_{1}}{{\alpha }_{2}}}}} \right. \\ \times \left( {1 - \frac{{n(n + 1)}}{{{{\alpha }_{1}}{{\alpha }_{2}}}}\ln \left( {1 + \frac{{{{\alpha }_{1}}{{\alpha }_{2}}}}{{n(n + 1)}}} \right)} \right) \\ \left. { + \,\,\frac{{{{{({{\alpha }_{1}} - {{\alpha }_{2}})}}^{2}}}}{{3(n + 1)(n + {{\alpha }_{1}})(n + {{\alpha }_{2}})}}} \right], \\ \end{gathered} $$
((8))
$$\begin{gathered} {{C}_{{11}}}{\text{/}}2{\text{:}}\,{{X}_{0}} = \frac{{a_{1}^{3}}}{2}\sum\limits_{n = 1}^\infty \frac{{\alpha _{2}^{3}}}{{n{{{(n + {{\alpha }_{2}})}}^{2}}}}, \\ {{X}_{1}} = \frac{1}{3} - \frac{\gamma }{2} \\ + \sum\limits_{n = 1}^\infty \left[ {\frac{{2{{\alpha }_{2}}{{n}^{2}} + 3(\alpha _{1}^{3} + \alpha _{2}^{3} + \alpha _{2}^{2})n + {{\alpha }_{2}}(\alpha _{1}^{3} + \alpha _{2}^{3} + 3\alpha _{2}^{2})}}{{6n{{{(n + {{\alpha }_{2}})}}^{3}}}}} \right], \\ {{C}_{{12}}}{\text{/}}2{\text{:}}\,{{X}_{0}} = \frac{{a_{1}^{3}}}{2}\sum\limits_{n = 1}^\infty \frac{{\alpha _{2}^{3}}}{{{{n}^{2}}(n - 1 + {{\alpha }_{2}})}}, \\ {{X}_{1}} = \frac{1}{3} - \frac{\gamma }{2} + \sum\limits_{n = 1}^\infty \left[ {\frac{{ - {{\alpha }_{1}}{{n}^{2}} + (3n - 2{{\alpha }_{1}})(\alpha _{1}^{3} + \alpha _{2}^{3})}}{{6{{n}^{2}}{{{(n - {{\alpha }_{1}})}}^{2}}}}} \right] \\ \end{gathered} $$

where \(\gamma \approx 0.577216\) is the Euler constant and the remaining coefficients of the kinetic energy can be obtained by permutation of 1 and 2.

All series for \({{X}_{0}}\) in formulas (7) and (8) are cited in [3–6]. The series for \({{X}_{1}}\) in formulas (8) were not calculated previously, but their contribution to the force is comparable with that from the series for \({{X}_{0}}\).

PARTICULAR CASES

For spheres of identical radii \({{a}_{1}} = {{a}_{2}} = a\), the following substitution \({{\alpha }_{1}} = {{\alpha }_{2}} = 1{\text{/}}2,a' = a{\text{/}}2\) should be made in the kinetic energy coefficients formulas. Approximately calculating the numerical series in them, we obtain

$$\begin{gathered} {{A}_{1}} = {{A}_{2}} = {{a}^{3}} \times 0.192567 \\ + \frac{{{{a}^{2}}}}{4}h\left( {\frac{1}{4}\left( {\ln \left( {\frac{h}{a}} \right) - 1} \right) + 0.403378} \right), \\ B = {{a}^{3}} \times 0.0751286 \\ + \frac{{{{a}^{2}}}}{4}h\left( {\frac{1}{4}\left( {\ln \left( {\frac{h}{a}} \right) - 1} \right) + 0.194983} \right), \\ \end{gathered} $$
$$\begin{gathered} {{D}_{1}} = {{D}_{2}} = {{a}^{3}} \times 1.05634 \\ + \frac{{{{a}^{2}}}}{4}h\left( {\frac{1}{4}\left( {\ln \left( {\frac{h}{a}} \right) - 1} \right) + 0.148441} \right), \\ E = {{a}^{3}} \times 0.52088 \\ + \frac{{{{a}^{2}}}}{4}h\left( {\frac{1}{4}\left( {\ln \left( {\frac{h}{a}} \right) - 1} \right) - 0.581959} \right), \\ \end{gathered} $$
((9))
$$\begin{gathered} {{C}_{{11}}} = {{C}_{{22}}} = {{a}^{3}} \times 0.0731523 \\ + \frac{{{{a}^{2}}}}{4}h\left( {\frac{1}{2}\left( {\ln \left( {\frac{h}{a}} \right) - 1} \right) + 0.596124} \right), \\ {{C}_{{12}}} = {{C}_{{21}}} = {{a}^{3}} \times 0.281914 \\ + \frac{{{{a}^{2}}}}{4}h\left( {\frac{1}{2}\left( {\ln \left( {\frac{h}{a}} \right) - 1} \right) + 0.003238} \right). \\ \end{gathered} $$

At the contact of spheres h = 0 the numerical values of all coefficients were calculated in [3–5, 10]. No numerical values of the coefficients of \(h\) for Di, E, \({{C}_{{ii}}},{{C}_{{ik}}}\) were calculated previously.

Of interest is the case of the motion of spheres of identical radii and velocities \({{\dot {a}}_{1}} = {{\dot {a}}_{2}} = \dot {a},\,\,{{u}_{1}} = {{u}_{2}} = u\), respectively. In this case, the kinetic energy determines the force acting on the sphere near the plane and has the form

$$\frac{T}{{2\pi \rho }} = P{{u}^{2}} + 2Qu\dot {a} + R{{\dot {a}}^{2}}.$$
((10))

The numerical values of the coefficients can be found using Eqs. (9)

$$\begin{array}{*{20}{c}} \begin{gathered} P = 2{{A}_{1}} + 2B \\ = {{a}^{2}}[0.53539a + 0.0491804h + 0.25h\ln (h{\text{/}}a)], \\ \end{gathered} \\ \begin{gathered} 2Q = 2{{C}_{{12}}} + 2{{C}_{{11}}} \\ = {{a}^{2}}[0.710132a - 0.200319h + 0.5h\ln (h{\text{/}}a)], \\ \end{gathered} \\ \begin{gathered} R = 2{{D}_{1}} + 2E \\ = {{a}^{2}}[3.15443a - 0.466759h + 0.25h\ln (h{\text{/}}a)]. \\ \end{gathered} \end{array}$$
((11))

HYDRODYNAMIC FORCE NEAR CONTACT

The hydrodynamic force acting on the first sphere can be found using the Lagrange formula:

$${{F}_{1}} = - \frac{d}{{dt}}\frac{{\partial T}}{{\partial \mathop {\dot {x}}\nolimits_1 }} + \frac{{\partial T}}{{\partial {{x}_{1}}}} = - \frac{d}{{dt}}\frac{{\partial T}}{{\partial {{u}_{1}}}} - \frac{{\partial T}}{{\partial h}}.$$

Using Eq. (1), we obtain that

$$\begin{gathered} \frac{{{{F}_{1}}}}{{ - 2\pi \rho }} = \frac{d}{{dt}}(2{{A}_{1}}{{u}_{1}} + 2B{{u}_{2}} + {{C}_{{11}}}{{{\dot {a}}}_{1}} + {{C}_{{12}}}{{{\dot {a}}}_{2}}) \\ + \frac{{\partial {{A}_{1}}}}{{\partial h}}u_{1}^{2} + 2\frac{{\partial B}}{{\partial h}}{{u}_{1}}{{u}_{2}} + \frac{{\partial {{A}_{2}}}}{{\partial h}}u_{2}^{2} \\ \end{gathered} $$
$$\begin{gathered} + \frac{{\partial {{D}_{1}}}}{{\partial h}}\dot {a}_{1}^{2} + 2\frac{{\partial E}}{{\partial h}}{{{\dot {a}}}_{1}}{{{\dot {a}}}_{2}} + \frac{{\partial {{D}_{2}}}}{{\partial h}}\dot {a}_{2}^{2} + \frac{{\partial {{C}_{{11}}}}}{{\partial h}}{{u}_{1}}{{{\dot {a}}}_{1}} \\ + \frac{{\partial {{C}_{{12}}}}}{{\partial h}}{{u}_{1}}{{{\dot {a}}}_{2}} + \frac{{\partial {{C}_{{21}}}}}{{\partial h}}{{u}_{2}}{{{\dot {a}}}_{1}} + \frac{{\partial {{C}_{{22}}}}}{{\partial h}}{{u}_{2}}{{{\dot {a}}}_{2}}. \\ \end{gathered} $$

Taking into account Eqs. (7) and (8), we can single out the main asymptotics for the force at \(h \to 0\):

$$\frac{{{{F}_{1}}}}{{2\pi \rho }} = \frac{d}{{dt}}\left( {\frac{1}{2}{a'}^{2}h\ln \left( {\frac{h}{{2a'}}} \right)\dot {h}} \right) - \frac{1}{4}{a'}^{2}\ln \left( {\frac{h}{{2a'}}} \right){{\dot {h}}^{2}},$$

which agrees with [7]. If the distance between the spheres does not change, that is, \(\dot {h} = - {{u}_{1}} - {{u}_{2}} - {{\dot {a}}_{1}} - {{\dot {a}}_{2}}\) = 0, the logarithmic feature disappears as was indicated by Voinov in [4] without derivation.

We obtain an exact formula for the force acting on the sphere of variable radius a near the plane using Eq. (10) and its approximate expression using Eq. (11):

$$\begin{gathered} \frac{{{{F}_{1}}}}{{ - 2\pi \rho }} = \frac{d}{{dt}}\left( {Pu + Q\dot {a}} \right) + \frac{{\partial P}}{{\partial h}}{{u}^{2}} + 2\frac{{\partial Q}}{{\partial h}}u\dot {a} + \frac{{\partial R}}{{\partial h}}{{{\dot {a}}}^{2}} \\ = \frac{d}{{dt}}\left[ {{{a}^{2}}\left( {(0.355066a - 0.100159h){{{\dot {a}}}_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}} \right.} \right. \\ \left. {\left. {\, + (0.53539a + 0.0491804h)u - h\frac{1}{4}\ln\left( {\frac{h}{a}} \right)\frac{{\dot {h}}}{2}} \right)} \right] \\ \, + {{a}^{2}}\left( {0.29918{{u}^{2}} + 0.299681u{{{\dot {a}}}_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}} \right. \\ \left. {\, - 0.216759{{{\dot {a}}}^{2}} + \frac{1}{4}\ln\left( {\frac{h}{a}} \right)\frac{{\mathop {\dot {h}}\nolimits^2 }}{4}} \right), \\ \end{gathered} $$

where h/2 is the distance between the sphere and the plane, \(u + \dot {a} = - \dot {h}{\text{/}}2\).

At \(\dot {h} = 0\), we obtain \(u = - \dot {a}\) and

$$\frac{{{{F}_{1}}}}{{ - 2\pi \rho }} = \frac{d}{{dt}}\left( {(Q - P)\dot {a}} \right) + \frac{{\partial (P - 2Q + R)}}{{\partial h}}{{\dot {a}}^{2}}.$$

From this formula at h = 0, we find the force acting on the sphere with constant contact with the plane:

$$\begin{gathered} {{F}_{1}} = 2\pi \rho \left( {0.180324\frac{d}{{dt}}({{a}^{3}}\dot {a}) + 0.217259{{a}^{2}}{{{\dot {a}}}^{2}}} \right) \\ = 2\pi \rho {{a}^{2}}(0.758232{{{\dot {a}}}^{2}} + 0.180324a\ddot {a}). \\ \end{gathered} $$

In [4] the force is given in the following form:

$${{F}_{1}} = 2\pi \rho {{a}^{2}}(0.75821{{\dot {a}}^{2}} + 0.18032a\ddot {a}).$$

In case the bubble radius changes periodically, the average force is \(\langle {{F}_{1}}\rangle \) = 2πρa2 × \(0.217259\langle {{\dot {a}}^{2}}\rangle ,\) which corresponds to the attraction force.

ACKNOWLEDGMENTS

This study was supported by the Russian Science Foundation, project no. 14-19-01633.