Viscous Sublayer

Abstract

The eddy viscosity and the eddy diffusivity are calculated for the viscous sublayer in turbulent flow near a solid surface by using Fourier transforms of a spectral element of the velocity profiles, the pressure, and the concentration. The different spectral elements are assumed to behave independently of each other in this region, and the magnitudes are plotted as functions of distance from the wall. The tangential velocity profiles show a slope of unity on log–log plots against distance y from the wall, while the normal component shows a slope of 2. The concentration profiles generally show a slope of unity except near the outer limit of the viscous sublayer. There is also a dependence on the value of the Schmidt number as well as the concentration fluctuation assumed to prevail at a distance of δ₀ at the outer limit of the viscous sublayer. When the normal velocity fluctuation is correlated with either the streamwise velocity fluctuation or with the concentration fluctuation, one infers a slope for the eddy viscosity or the eddy diffusivity of 3. The eddy diffusivity shows more structure than the eddy viscosity and can differ substantially from the latter in the depths of the viscous sublayer.

INTRODUCTION

It is apparent since 1932 that turbulent fluctuations are present in the viscous sublayer [1, 2]. They merely decay as a solid surface is approached. Levich [3, Section 4, p. 29] suggests that in this region different eddies behave independently, so that their behavior is governed by their individual magnitudes at the outer limit δ₀ of the viscous sublayer.

Levich [3, Section 4, p. 29] says, “In the viscous sublayer Re is less than unity, and the second-order terms in the Navier–Stokes equations are small compared to the first-order terms. The velocity distribution in a viscous sublayer can therefore be determined by linear equations only. If a certain spectrum of eddies penetrates a viscous sublayer, the interaction between separate eddies ceases. The flow then becomes a sum of independent periodic motions, whose period T remains constant throughout the viscous sublayer.”

Vorotyntsev et al. [4] treat the sublayer and conclude that the eddy viscosity is proportional to y³ but that the eddy diffusivity begins to deviate from the eddy kinematic viscosity within the viscous sublayer, showing a y⁴ dependence just within the sublayer but having a y³ dependence deep in the layer whose coefficient depends on the diffusion coefficient D. In his summary of statistical treatments of this situation, Martemianov [5] reaches similar conclusions but determines that in the y³ region the eddy diffusivity is proportional to the square root of D.

ANALYSIS

Separate the velocity into a steady component and a fluctuating component:

$${\mathbf{v}} = {\mathbf{\bar {v}}} + {\mathbf{v'}}.$$

(1)

Substitute into the continuity equation, and eliminate the term for the steady component:

$$\nabla \cdot {\mathbf{v'}} = 0.$$

(2)

Substitute into the momentum equation:

$$\begin{gathered} \frac{{\partial {\mathbf{\bar {v}}} + {\mathbf{v}}{\kern 1pt} '}}{{\partial t}} + \nabla \cdot [({\mathbf{\bar {v}}} + {\mathbf{v}}{\kern 1pt} ')({\mathbf{\bar {v}}} + {\mathbf{v}}{\kern 1pt} ')] = {\nu }\nabla \cdot \nabla ({\mathbf{\bar {v}}} + {\mathbf{v}}{\kern 1pt} ') \\ - \,\,\frac{1}{{\rho }}\nabla (\mathcal{P} + \mathcal{P}{\kern 1pt} '{\text{)}}. \\ \end{gathered} $$

(3)

When 𝒫 is taken to be the dynamic pressure, no gravitational acceleration is necessary. Take the average of this equation:

$$\frac{{\partial {\mathbf{\bar {v}}}}}{{\partial t}} + \nabla \cdot ({\mathbf{\bar {v}\bar {v}}} + \left\langle {{\mathbf{v}}{\kern 1pt} '{\mathbf{v}}{\kern 1pt} '} \right\rangle ) = {\nu }\nabla \cdot \nabla {\mathbf{\bar {v}}} - \frac{1}{\rho }\nabla \bar {\mathcal{P}},$$

(4)

where the angular bracket also denotes the average, since it is difficult to put a bar on top of this quantity. Subtract this from Eq. (3):

$$\begin{gathered} \frac{{\partial {\mathbf{v}}{\kern 1pt} '}}{{\partial t}} + \nabla \cdot {\mathbf{\bar {v}v}}{\kern 1pt} ' + \nabla \cdot {\mathbf{v}}{\kern 1pt} '{\mathbf{\bar {v}}} + \nabla \cdot {\mathbf{v}}{\kern 1pt} '{\mathbf{v}}{\kern 1pt} ' - \nabla \cdot \left\langle {{\mathbf{v}}{\kern 1pt} '{\mathbf{v}}{\kern 1pt} '} \right\rangle \\ = {\nu }\nabla \cdot \nabla {\mathbf{v}}{\kern 1pt} ' - \frac{1}{{\rho }}\nabla \mathcal{P}{\kern 1pt} '. \\ \end{gathered} $$

(5)

Within the viscous sublayer, v' should be small compared with the steady term, and the square should be negligible. While this may not be true at the outer limit of the viscous sublayer, it becomes valid deeper in the viscous sublayer, and Eqs. (2) and (5) could thus describe variations of the fluctuating quantities within the viscous sublayer. For mass transfer within this layer, at moderate to high Schmidt numbers, a similar approximation should apply to fluctuations of the concentration. This derivation of the equations governing the fluctuations is inspired by Vorotyntsev et al. [4].

We thus have a linear problem for the variation of the fluctuations within the viscous sublayer. Furthermore, the viscous sublayer is very thin, and the average velocities depend only on y and in fact, ${{{\bar {v}}}_{x}}$ = βy, where β is a constant. Thus, ${{{\bar {v}}}_{y}}$ = ${{{\bar {v}}}_{z}}$ = 0. Eventually we may want to relax the strict linearity of ${{{\bar {v}}}_{x}}$, in which case ${{{\bar {v}}}_{y}}$ will no longer be zero. (Compare with the universal velocity profile.) The governing differential equations for the fluctuating components of the velocity become

$$\frac{{\partial {\text{v}}_{x}^{'}}}{{\partial x}} + \frac{{\partial {\text{v}}_{y}^{'}}}{{\partial y}} + \frac{{\partial {\text{v}}_{z}^{'}}}{{\partial z}} = 0,$$

(6)

$$\begin{gathered} \frac{{\partial {\text{v}}_{x}^{'}}}{{\partial t}} + \beta y\frac{{\partial {\text{v}}_{x}^{'}}}{{\partial x}} + \beta {\text{v}}_{y}^{'} \\ = {\nu }\left( {\frac{{{{\partial }^{2}}{\text{v}}_{x}^{'}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{\text{v}}_{x}^{'}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{\text{v}}_{x}^{'}}}{{\partial {{z}^{2}}}}} \right) - \frac{1}{\rho }\frac{{\partial \mathcal{P}{\kern 1pt} '}}{{\partial x}}, \\ \end{gathered} $$

(7)

$$\frac{{\partial {\text{v}}_{y}^{'}}}{{\partial t}} + {\beta }y\frac{{\partial {\text{v}}_{y}^{'}}}{{\partial x}} = {\nu }\left( {\frac{{{{\partial }^{2}}{\text{v}}_{y}^{'}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{\text{v}}_{y}^{'}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{\text{v}}_{y}^{'}}}{{\partial {{z}^{2}}}}} \right) - \frac{1}{{\rho }}\frac{{\partial \mathcal{P}'}}{{\partial y}},$$

(8)

$$\frac{{\partial {\text{v}}_{z}^{'}}}{{\partial t}} + {\beta }y\frac{{\partial {\text{v}}_{z}^{'}}}{{\partial x}} = {\nu }\left( {\frac{{{{\partial }^{2}}{\text{v}}_{z}^{'}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{\text{v}}_{z}^{'}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{\text{v}}_{z}^{'}}}{{\partial {{z}^{2}}}}} \right) - \frac{1}{{\rho }}\frac{{\partial \mathcal{P}'}}{{\partial z}}.$$

(9)

We recognize that we can eliminate the pressure fluctuation by taking the curl of the equation of motion. We also recognize that, on the basis of Eq. (6), we can express the fluctuating velocity components as the curl of a vector stream function. However, we also recognize that we can easily become confused.

For boundary conditions, we expect the fluctuating velocity components to vanish at y = 0 and to assume values at the outer boundary of the viscous sublayer that reflect the turbulent fluctuations in the outer flow.

Because the equations are linear in the viscous sublayer, the eddies do not interact, and we can express the fluctuating components in Fourier series which reflect periodic behavior in time and in the downstream direction x and in the cross flow direction z. Thus, we write

$${\text{v}}_{x}^{'} = \operatorname{Re} \{ {{V}_{x}}(y)\exp (i{{k}_{x}}x + i{{k}_{z}}z + i\omega t)\} ,$$

(10)

$${\text{v}}_{y}^{'} = \operatorname{Re} \{ {{V}_{y}}(y)\exp (i{{k}_{x}}x + i{{k}_{z}}z + i\omega t)\} ,$$

(11)

$${\text{v}}_{z}^{'} = \operatorname{Re} \{ {{V}_{z}}(y)\exp (i{{k}_{x}}x + i{{k}_{z}}z + i\omega t)\} ,$$

(12)

$$\mathcal{P}' = \operatorname{Re} \{ P(y)\exp (i{{k}_{x}}x + i{{k}_{z}}z + i\omega t)\} .$$

(13)

Each spectral component can be identified by the values of k_x, k_z, and ω, and each spectral component can be treated separately from all the others. If we knew the spectrum of the external turbulence, say outside a distance y = δ₀, this would constitute the boundary condition on the viscous sublayer at this distance. We then want to solve for the variation of V_x, V_y, V_z, and P as functions of y from y = 0 to y = δ₀. Since we do not know the external spectrum, we must guess values for V_x, V_y, V_z, and P at y = δ₀, perhaps trying to match the expected value of the eddy kinematic viscosity at δ₀.

Now substitute the Fourier forms (10) to (13) into Eqs. (6)–(9).

$$i{{k}_{x}}{{V}_{x}} + \frac{{d{{V}_{y}}}}{{dy}} + i{{k}_{z}}{{V}_{z}} = 0,$$

(14)

$$\begin{gathered} i\omega {{V}_{x}} + \beta yi{{k}_{x}}{{V}_{x}} + \beta {{V}_{y}} \\ = \nu \left( { - k_{x}^{2}{{V}_{x}} + \frac{{{{d}^{2}}{{V}_{x}}}}{{d{{y}^{2}}}} - k_{z}^{2}{{V}_{x}}} \right) - \frac{{i{{k}_{x}}P}}{\rho }, \\ \end{gathered} $$

(15)

$$\begin{gathered} i\omega {{V}_{y}} + \beta yi{{k}_{x}}{{V}_{y}} \\ = \nu \left( { - k_{x}^{2}{{V}_{y}} + \frac{{{{d}^{2}}{{V}_{y}}}}{{d{{y}^{2}}}} - k_{z}^{2}{{V}_{y}}} \right) - \frac{1}{\rho }\frac{{dP}}{{dy}}, \\ \end{gathered} $$

(16)

$$i\omega {{V}_{z}} + \beta yi{{k}_{x}}{{V}_{z}} = \nu \left( { - k_{x}^{2}{{V}_{z}} + \frac{{{{d}^{2}}{{V}_{z}}}}{{d{{y}^{2}}}} - k_{z}^{2}{{V}_{z}}} \right) - \frac{{i{{k}_{z}}P}}{\rho }.$$

(17)

We could eliminate P from two of these equations, but that would be unnecessarily complicated.

Next make the problem dimensionless by introducing y⁺ = (y/ν)(τ₀/ρ)^0.5 and dimensionless Fourier coefficients and a dimensionless pressure. The velocity functions V_x, V_y, and V_z, can be understood to be divided by the value of V_x at y = δ₀. The parameters and dependent variables are defined according to:

$${{K}_{x}} = {{k}_{x}}\frac{\nu }{{{\text{v*}}}},{\text{ }}{{K}_{z}} = {{k}_{z}}\frac{\nu }{{{\text{v*}}}}{\text{, where v*}} = \sqrt {\frac{{{{\tau }_{0}}}}{\rho }} ,$$

(18)

$$\Omega = \omega {\text{ }}\frac{\nu }{{{{{\left( {{\text{v*}}} \right)}}^{2}}}}{\text{, }}B = \beta {\text{ }}\frac{\nu }{{{{{\left( {{\text{v*}}} \right)}}^{2}}}}{\text{, and }}p = \frac{P}{{\rho {\text{v*}}}}.$$

(19)

Equations (14)–(17) become

$$i{{K}_{x}}{{V}_{x}} + \frac{{d{{V}_{y}}}}{{d{{y}^{ + }}}} + i{{K}_{z}}{{V}_{z}} = 0,$$

(14′)

$$\begin{gathered} i\Omega {{V}_{x}} + B{{y}^{ + }}i{{K}_{x}}{{V}_{x}} + B{{V}_{y}} \\ = - K_{x}^{2}{{V}_{x}} + \frac{{{{d}^{2}}{{V}_{x}}}}{{d{{y}^{ + }}^{2}}} - K_{z}^{2}{{V}_{x}} - i{{K}_{x}}p, \\ \end{gathered} $$

(15′)

$$i\Omega {{V}_{y}} + B{{y}^{ + }}i{{K}_{x}}{{V}_{y}} = - K_{x}^{2}{{V}_{y}} + \frac{{{{d}^{2}}{{V}_{y}}}}{{d{{y}^{ + }}^{2}}} - K_{z}^{2}{{V}_{y}} - \frac{{dp}}{{d{{y}^{ + }}}},$$

(16′)

$$i\Omega {{V}_{z}} + B{{y}^{ + }}i{{K}_{x}}{{V}_{z}} = - K_{x}^{2}{{V}_{z}} + \frac{{{{d}^{2}}{{V}_{z}}}}{{d{{y}^{ + }}^{2}}} - K_{z}^{2}{{V}_{z}} - i{{K}_{z}}p.$$

(17′)

In this way, the kinematic viscosity ν, the density ρ, and the wall stress τ₀ are eliminated, and the formulation is designed to accommodate all such values as may arise in turbulent flows. (The pressure should be made compatible with the dimensionless velocities. Since we do not use p directly, this may not be important.) B can be made to be equal to 1, since very close to the wall, v_x is proportional to y and this is commonly expressed as $v_{x}^{ + }$ = y⁺ on plots of downstream velocity versus distance from the wall in turbulent flow.

For numerical solution, Eqs. (15′) and (17′) should treat the second derivatives with central differences. Equation (14′) should be treated as a first order equation with backward differences; one essentially integrates the continuity equation with known profiles of the tangential velocity components v_x and v_z to yield the normal velocity component v_y. Equation (16′) should be treated as a first order equation for the pressure fluctuations p, with known profiles of the velocity components. The second derivative of V_y can be replaced by first derivatives of V_x and V_z by substituting Eq. (14′). The treatment of boundary conditions is tricky when there is a gradient term, here the gradient of p but frequently a gradient of electric potential. Compare the treatment of the von Kármán transformation for laminar flow to a rotating disk, where three equations (the continuity equation and the radial and angular components of the momentum equation) determine the three velocity components, and subsequently the pressure distribution is determined (if needed) from the axial component of the momentum equation. (Compare Section 15.4 in [6].) If the gradient of a variable is known throughout a field, the value of the variable need be specified at only one point in the field. The same is true of state functions in thermodynamics. In the present case, one can in principle eliminate the pressure from Eqs. (15′) and (17′) by means of Eq. (16′). This is equivalent to eliminating the pressure from the full equation of motion by taking the curl of the equation, but the introduction of additional integration constants is avoided. Thus, the boundary conditions do not actually include the value of V_y at y = δ₀, and the pressure fluctuations do not go to zero at the wall.

Figure 1 presents results obtained by numerical solution of the equations developed here. Much further work is required to consider the spectrum of the turbulence at y = δ₀, in developing the eddy viscosity from the Fourier results, and in developing the eddy diffusivity.

Fig. 1.

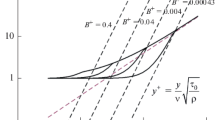
Calculated profiles of the fluctuating components of the velocity and of the pressure for one component of the Fourier spectrum (for K_x = K_z = Ω = 1). Here, B is taken to be 1. V_x, V_y, and V_z are taken to be zero at the wall. V_x and V_z and p are taken to be 1 at y⁺ = 1. While the fluctuations are comparable in the three coordinate directions in the outer turbulent flow, the normal component decreases with a slope of 2 (in the log–log plot) in the inner part of the viscous sublayer, while the tangential components are nearly equal to each other and adopt a slope of 1. The pressure fluctuations persist with little change all the way to the surface.

FLUCTUATIONS OF CONCENTRATION

Modeling of mass transfer permits calculation of a profile of the eddy diffusivity. The concentration profile obeys the equation of convective diffusion

$$\frac{{\partial {{c}_{i}}}}{{\partial t}} + \nabla \cdot ({\mathbf{v}}{{c}_{i}}) = \mathcal{D}\nabla \cdot \nabla {{c}_{i}}.$$

(20)

With boundary conditions of

$${{c}_{i}} = {{c}_{0}}{\text{ at }}y = 0{\text{ and }}{{c}_{i}} \to {{c}_{\infty }}{\text{ as }}y \to \infty ,$$

(21)

it is convenient to work with a dimensionless concentration defined as

$$\theta = \frac{{{{c}_{i}} - {{c}_{0}}}}{{{{c}_{\infty }} - {{c}_{0}}}}{\text{.}}$$

(22)

In terms of steady and fluctuating quantities, Eq. (20) becomes

$$\frac{{\partial \bar {\theta } + \theta {\kern 1pt} '}}{{\partial t}} + \nabla \cdot \left[ {({\mathbf{\bar {v}}} + {\mathbf{v}}{\kern 1pt} ')(\bar {\theta } + \theta {\kern 1pt} ')} \right] = \mathcal{D}\nabla \cdot \nabla (\bar {\theta } + \theta {\kern 1pt} '),$$

(23)

and the averaged equation becomes

$$\frac{{\partial \bar {\theta }}}{{\partial t}} + \nabla \cdot \left[ {{\mathbf{\bar {v}}}\bar {\theta } + \left\langle {{\mathbf{v'}}\theta {\kern 1pt} '} \right\rangle } \right] = \mathcal{D}\nabla \cdot \nabla \bar {\theta }.$$

(24)

This is like the original equation but averaged and with the presence of the turbulent transport term. Subtraction from the preceding equation gives the equation governing the fluctuations of concentration

$$\frac{{\partial \theta {\kern 1pt} '}}{{\partial t}} + \nabla \cdot \left[ {{\mathbf{\bar {v}}}\theta {\kern 1pt} ' + {\mathbf{v}}{\kern 1pt} '\bar {\theta } + {\mathbf{v}}{\kern 1pt} '\theta {\kern 1pt} ' - \left\langle {{\mathbf{v'}}\theta {\kern 1pt} '} \right\rangle } \right] = \mathcal{D}\nabla \cdot \nabla \theta {\kern 1pt} ',$$

(25)

similar to Eq. (5).

We drop the two quadratic terms on the premise that they are negligible deep in the viscous sublayer. We make the same assumptions with respect to the average velocity, namely that the x component can be approximated by βy and that the y and z components are zero. The average concentration depends also only on y. Equation (25) then simplifies to

$$\frac{{\partial \theta {\kern 1pt} '}}{{\partial t}} + \beta y\frac{{\partial \theta {\kern 1pt} '}}{{\partial x}} + {\text{v}}_{y}^{'}\frac{{\partial \bar {\theta }}}{{\partial y}} = \mathcal{D}\left( {\frac{{{{\partial }^{2}}\theta {\kern 1pt} '}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\theta {\kern 1pt} '}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\theta {\kern 1pt} '}}{{\partial {{z}^{2}}}}} \right),$$

(26)

similar to Eq. (7). The fluctuations in concentration are caused by the fluctuations in velocity (see the third term in this equation) and can be represented by a similar Fourier series:

$$\theta ' = \operatorname{Re} \{ C(y)\exp (i{{k}_{x}}x + i{{k}_{z}}z + i\omega t)\} ,$$

(27)

where C belongs to the same spectral component as the fluctuating velocity components treated earlier. Consequently, the transformed Eq. (26) becomes

$$i\omega C + \beta yi{{k}_{x}}C + {{V}_{y}}\frac{{\partial \bar {\theta }}}{{\partial y}} = \mathcal{D}\left( { - k_{x}^{2}C + \frac{{{{d}^{2}}C}}{{d{{y}^{2}}}} - k_{z}^{2}C} \right).$$

(28)

The similarity to Eq. (15) should be apparent. Notable differences are the replacement of the kinematic viscosity with the diffusion coefficient, the absence of a pressure term, and the replacement of β with the derivative of the average concentration profile. For a dimensionless form, the Definitions (18) and (19) yield

$$\begin{gathered} i\Omega C + B{{y}^{ + }}i{{K}_{x}}C + {{{\text{V}}}_{y}}\frac{{\partial \bar {\theta }}}{{\partial {{y}^{ + }}}} \\ = \frac{\mathcal{D}}{\nu }\left( { - K_{x}^{2}C + \frac{{{{d}^{2}}C}}{{d{{y}^{ + }}^{2}}} - K_{z}^{2}C} \right). \\ \end{gathered} $$

(29)

For boundary conditions we might expect

$$C = 0{\text{ at }}{{y}^{ + }} = 0{\text{ and }}C \to {\text{0 as }}{{y}^{ + }} \to \delta _{0}^{ + },$$

(30)

at least for moderately high Schmidt numbers where the diffusion layer is expected to lie entirely within the viscous sublayer.

Some calculated results are shown in Fig. 2.

Fig. 2.

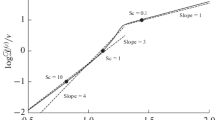
Magnitudes of the fluctuations in concentration for four different Schmidt numbers Sc, ranging from 1 to 1000. Solid curves use the zero boundary condition for θ′ at y⁺ = $\delta _{0}^{ + }$ = 1. Then the concentration fluctuations are due entirely to velocity fluctuations within the viscous sublayer. The curves with short dashes set θ′ to 1 at y⁺ = δ₀, which might be more appropriate for Sc = 1 because the diffusion layer can extend somewhat beyond the viscous sublayer. For Sc = 1000, the two curves nearly coincide except for y⁺ values very close to $\delta _{0}^{ + }$. Dashed lines show for comparison slopes of 1 and 2.

At Sc = 1, the Reynolds analogy might hold (where v_x and c_i profiles may be very similar, because the governing equations are similar, and consequently the Stanton number may be close to half the friction factor). At higher Schmidt numbers, substantial differences show up, and StSc^2/3 becomes proportional to the square root of the friction factor. Some features in the curves in Fig. 2 may arise from the boundary condition at y⁺ = $\delta _{0}^{ + }$. For Sc = 1, substantial concentration fluctuations may come from the external flow, but for higher Sc, the diffusion layer lies within the viscous sublayer, and the zero boundary condition may be more appropriate.

For turbulent flow, the derivative of the average concentration can be expected to follow [7]

$$\frac{{d\bar {\theta }}}{{d{{y}^{ + }}}} = \frac{{\gamma {\text{ S}}{{{\text{c}}}^{{1/3}}}}}{{1.2092}}\frac{1}{{1 + {{\xi }^{3}}}},{\text{ where }}\xi = \gamma {\text{ S}}{{{\text{c}}}^{{1/3}}}{{y}^{ + }}{\text{,}}$$

(31)

and γ = B⁺ as used in [7] for the coefficient of y³ in the expression of the eddy viscosity. See in particular Eqs. (37) and (39) in [8]. (For turbulent flow, the edge of the diffusion layer is broader than for laminar flow because of the mixing effect of the eddy diffusivity. Contrast this equation with Figs. 17.1 and 17.66 in [6]. Figure 3 shows the two profiles; for turbulent flow, the average concentration does not reach the bulk value until much larger values of ξ.)

Fig. 3.

Profile of average concentration for turbulent shear flow and for a laminar boundary layer, such as that found on a rotating disk. The dimensionless distance ξ in the diffusion layer is defined appropriately for the two different systems.

It is possible that the assumption of the y³ dependence of the eddy diffusivity influences the outcome of the slopes on Fig. 2, which in turn may influence the conclusions obtained for the eddy diffusivity itself. For this reason, the calculations were redone with an exponent of 1/4 for Sc in Eq. (31) and with an exponent of 4 on ξ in the denominator. The results are shown in Fig. 4. There is little difference; in particular, the slopes do not appear to change.

Fig. 4.

Concentration fluctuations recalculated with the changes mentioned in the text to ensure that the form of Eq. (31) is not influencing the slopes in Figs. 2 and 4.

EDDY DIFFUSIVITY AND EDDY KINEMATIC VISCOSITY

A procedure to calculate profiles of the turbulent transport coefficients would be to pick several spectral points, somewhere between 1 and 100, chosen to represent points characteristic of the actual turbulence. For each spectral point, one would calculate the averages 〈V_yC〉 for mass transfer and 〈V_yV_x〉 for the Reynolds stress. The different spectral points would not expect to be correlated with each other. Hence, one can take the average for each spectral point. This means taking the magnitude of the combined real and imaginary parts, it being assumed that the average of the different angles would yield a number of order 1 and about the same for all spectral points. One needs to be dividing by the flux density or the stress at the surface. This should be automatic for the dimensionless formulations.

The result of such an effort is shown in Fig. 5.

Fig. 5.

Profiles of the relative magnitude of the eddy diffusivity 𝒟^(t) and the eddy kinematic viscosity ν^(t). The Schmidt number is a parameter for the diffusivities, and again, the boundary condition was taken as C = 1 for the short dashed lines and C = 0 for the solid lines, both boundary conditions applying at y⁺ = $\delta _{0}^{ + }$ = 1. The boundary conditions provide some distortion near the maximum value. The eddy kinematic viscosity is positioned just above the short dashed line for Sc = 1. Dot-dash lines provide comparison for slopes of 3 and 4.

It is presumed that the lines for all spectral points will generally have the same slope, so that, when one averages over the spectrum, one obtains the same slopes apparent for the individual spectral points.

DISCUSSION

Vorotyntsev et al. [4, 5] develop predictions for the eddy diffusivity in the viscous sublayer by a more complicated method but still using the same basic concept of treating the velocity and concentration fluctuations. They conclude that the eddy diffusivity varies as y⁴, apparently in a region near the outer limit of the viscous sublayer. One can infer such a y⁴ dependence from Fig. 5 (seen for Sc = 100 and 1000) and a corresponding y² dependence for the concentration fluctuation from Figs. 2 or 4. They also conclude a y³ dependence deeper in the viscous sublayer but with a coefficient proportional to the square root of the diffusion coefficient. We verify here the y³ dependence, but not necessarily the dependence on the diffusion coefficient. Figures 2 and 4 do show a dependence on the Schmidt number. One should keep in mind that the diffusion layer lies deeper in the viscous sublayer as Sc increases [9]. For example, the outer limit of the diffusion layer at Sc = 1000 should be approximately at y⁺ = 0.08, although this transition should be much less sharp for turbulent flow than for laminar flow, as mentioned in connection with Fig. 3. [11–13] provide additional perspective on these matters, including behavior at lower Schmidt numbers, which are also covered here in Figs. 2, 3, and 5.

UNCERTAINITIES

The behavior of turbulent mass transfer in the viscous sublayer is not completely resolved. Equation (29) requires the derivative of the average concentration in order to compute the fluctuations. However, the calculation of the average concentration requires a profile of the eddy diffusivity, which comes from the fluctuations. The development of Fig. 4 suggests that one can guess the average concentration profile and that the choice made has only a weak effect on the result. One can do better by iterating between the two. In fact, one can do even better by doing this with the whole profile. Figure 5 provides the whole profile for the eddy diffusivity in the viscous sublayer, hinting at slopes of both 3 and 4. On can use this profile in Eq. (29) to calculate a new profile of fluctuating concentration and eventually come to a consistent profile for average concentration and for eddy diffusivity. It should be noted that this procedure does not involve or require any use of analogies among heat, mass, and momentum transfer.

This problem is also present in the treatment of the velocity profiles. The average velocity profile was used to select a value of β. Fortunately, it is clear that B = 1 in much of the viscous sublayer, and a similar iteration process can be implemented as long as one does not go too far outside the viscous sublayer.

CONCLUSIONS

The behavior of the eddy viscosity and the eddy diffusivity in the viscous sublayer can be explored by treating individual Fourier components since eddies behave independently of each other in this region. Vorotyntsev et al. [4] inspired our derivation of the governing equations for the fluctuations (Eqs. (6) through (9) and (25)). Within the viscous sublayer, the fluctuations of the normal component of the velocity are proportional to y² while those of the tangential components and of the concentration are proportional to y. Consequently, both the eddy viscosity and the eddy diffusivity should be proportional to y³. The latter two are not equal to each other, and the eddy diffusivity shows some dependence on the Schmidt number. The concentration fluctuations are produced by the steady concentration gradient interacting with the fluctuating normal component of the velocity. Consequently they should be absent in the bulk turbulent flow at high Schmidt numbers because this is then outside the diffusion layer. On the other hand, for Sc = 1, the concentration fluctuations should reach to the center line of a pipe and resemble the fluctuation of the normal velocity component [10]. Thus, there is a quandary as to the proper boundary condition for the concentration fluctuations at the outer limit of the viscous sublayer, depending on the Schmidt number. It would be desirable to treat more spectral components at the same time so as to be more quantitative about the magnitudes of the turbulent quantities and how they evolve in the region from y⁺ = 1 to 30.

TURBULENT FLOW IN A PIPE

One might be able to approach a valid treatment of fully developed turbulence in a pipe. The steady, fully developed flow has only an axial velocity component, and this depends only on radial position. The average axial pressure drop is the same at each axial and radial position, although there may be a radial average pressure variation as discussed below.

Thus one could express the fluctuations as a sum of a finite number of spectral components of a form similar to that used in the present linear problem:

$${\text{v}}_{r}^{'} = \Sigma [\operatorname{Re} \{ {{V}_{r}}(r)\exp (i{{k}_{\theta }}\theta + i{{k}_{z}}z + i\omega t)\} ],$$

(A.1)

$${\text{v}}_{{\theta }}^{'} = \Sigma [\operatorname{Re} \{ {{V}_{\theta }}(r)\exp (i{{k}_{\theta }}\theta + i{{k}_{z}}z + i\omega t)\} ],$$

(A.2)

$${\text{v}}_{z}^{'} = \Sigma [\operatorname{Re} \{ {{V}_{z}}(r)\exp (i{{k}_{\theta }}\theta + i{{k}_{z}}z + i\omega t)\} ],$$

(A.3)

$$\mathcal{P}{\kern 1pt} ' = \Sigma [\operatorname{Re} \{ P(r)\exp (i{{k}_{\theta }}\theta + i{{k}_{z}}z + i\omega t)\} ].$$

(A.4)

The problem is reduced to finding the radial dependence of V_r, V_θ, V_z, and P for these spectral components. This is a formidable problem, but still simpler than solving directly for fluctuating components in time and space. This method of treating interacting Fourier components could also be used in the present problem for extending the valid range farther into the outer turbulent flow for a single spectral component.

Is there a variation of average pressure with radial position in this pipe flow? I thought I found one in about 1963, but I have lost any notes on it. The averaged radial component of the equation of motion is

$$\begin{gathered} \frac{1}{2}\frac{{\partial \left\langle {{\text{v}}_{r}^{'}{\text{v}}_{r}^{'}} \right\rangle }}{{\partial r}} + \left\langle {\frac{{{\text{v}}_{{\theta }}^{'}}}{r}\frac{{\partial {\text{v}}_{r}^{'}}}{{\partial \theta }}} \right\rangle \\ + \left\langle {{\text{v}}_{z}^{'}\frac{{\partial {\text{v}}_{r}^{'}}}{{\partial z}}} \right\rangle - \,\,\frac{{\partial \left\langle {{\text{v}}_{\theta }^{'}{\text{v}}_{\theta }^{'}} \right\rangle }}{r} = - \frac{1}{\rho }\frac{{\partial \bar {\mathcal{P}}}}{{\partial r}}. \\ \end{gathered} $$

(A.5)

Even if the third term on the left is zero, the fourth term would be expected to generate a nonzero contribution. The first term will generate a zero result overall, since it can be integrated and the correlation should be zero at both the center and the pipe wall. The second term should be zero since the angular fluctuation should not be correlated with the radial fluctuation (fluctuations of the angular velocity should be equally probable in the plus and minus θ directions).