INTRODUCTION

Polymer brushes, that is, monolayers formed by macromolecules densely grafted to an impermeable surface, have been attracting the unflagging attention of researchers for several decades. The strong overlapping of the grafted macromolecules and their immobility cause a considerable extension of chains as compared to their unperturbed size in the direction perpendicular to the grafting surface. Among the unique properties of polymer brushes, barrier (protection against nonspecific sorption of proteins and biological overgrowth of surfaces and stabilization of colloidal dispersions) and tribological properties (reduction of friction between surfaces coated with polymer brushes) are of great practical importance [1–5].

Modification of the surface with grafted polymers opens the possibility of creating smart surfaces capable of responding to external stimuli (exposure to light and varying temperature and solvent composition) by changing the conformations of macromolecules forming a brush [6–8]. Owing to the dense grafting and strong overlapping of the chains, these changes are “consistent,” which provides a well-defined response of a brush to an external stimulus. Mixed brushes formed by macromolecules of various chemical nature can act as such smart surfaces [9]. In this case, changes in external conditions can affect the hydrophilicity or hydrophobicity of the surface.

Another classic example of smart or stimuli-responsive brushes is polyelectrolyte brushes, the state of which can be controlled by changing the ionic strength of the solution (salt concentration in the solution) or pH, if the brush is formed by chains of an ionizable (pH-sensitive) polyelectrolyte.

Speaking of smart and stimuli-responsive brushes, it is worth noting that the brush can be a “matrix” for a switch based on a single chain embedded into the brush which differs from brush-forming chains in chemical nature and/or degree of polymerization. In [10–12], the chain embedded in the brush was capable of adsorbing on the grafting surface (and the chains forming the brush were inert to it). Then the “matrix” brush served as a kind of barrier located near the attracting surface. This makes the adsorption transition not smooth, as in the case of ordinary adsorption on the plane, but sharp (in this case, naturally, the energy of attraction of the units to the surface corresponding to the adsorption transition increases compared with that in the absence of the barrier).

Of great interest are brushes in which branched macromolecules are grafted to the surface. Relatively recently, attention has been drawn to the possibility of using macromolecules of complex branched architecture as a material for creating polymer brushes. Theoretically, brushes made of grafted, regularly branched macromolecules have been studied since the mid-1990s [13–15]. The development of methods for the synthesis of regularly branched macromolecules (in particular, dendrons) and the development of methods for their grafting to the surface made it possible to create such brushes in the laboratory [16]. In addition, “dendronized polymers”—the analogs of graft copolymers, in which the side chains are regularly branched dendrons [17, 18]—were obtained.

The attractiveness of dendron brushes is that, by grafting one macromolecule (one dendron) by its root spacer, a large amount of polymer material can be bound to the surface via a single grafting point. At the same time, the thickness of the brush is limited by the limiting span of the dendron. This enables one to create thinner and denser layers compared to brushes composed of linear chains.

The simplest approach to constructing an analytical theory of dendron brushes involves the use of a Flory-type mean-field approach—an analog of the Alexander–de Gennes model [19, 20] for an ordinary brush of linear macromolecules. This approach allows one to obtain power-law dependences for the main characteristics of the brush, such as brush thickness, polymer density in the brush, and equilibrium free energy, on system parameters (for a neutral brush made of dendrons with flexible spacers, these are the grafting density, spacer length, number of generations, and functionality of branching points). A theory of this type was first proposed by D. Boris and M. Rubinstein [21] for dendrimers (actually, spherical dendron brushes) and generalized for planar, spherical, and cylindrical geometries by M. Kröger et al. [22]. An essential point in the development of theories of this kind was the assumption concerning the mechanism of extension of dendron spacers. According to [23], there are two limiting scenarios of dendron extension. In the first case, only one “longest path” is stretched in the dendron connecting its point of grafting to the surface to one of the free ends. In another extreme case, all dendron spacers are equally stretched.

The first analytical theory of dendron brushes taking into account the nonuniformity of the density profile and the unequal stretching of dendrons in the brush was proposed by G.T. Picket in 2001 for a planar brush [24]. It was based on the assumption that the monomer units of dendrons are in the field of a quadratic (parabolic) self-consistent potential, as in the case of the brush consisting of linear macromolecules. This potential includes the so-called topological coefficient, which depends on the number of generations, the functionality of branching points, and the length of the spacers in the dendron.

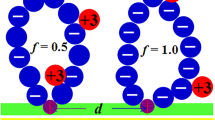
As further analysis showed, the theory based on the quadratic potential and the infinite Gaussian extensibility of the dendron spacers is valid only in the region of low grafting densities. Studies of dendron brushes by the numerical Scheutjens–Fleer self-consistent field calculations [23] and computer simulations [25, 26] using the models with the finite extensibility of polymer chains (dendron spacers) made it possible to reveal that grafted dendron brushes have a nontrivial internal structure. At a high grafting density, the dendrons in the brush are divided into several groups (or “populations”), which vary in the degree of stretching [23, 26, 27]. This is clearly manifested even by the simplest representative of the class of dendron brushes—brushes made of dendrons of the first generation or brushes composed of arm-grafted stars [25, 28]. For them, at a high grafting density, two populations of stars coexist in the brush and the brush becomes two-layered. Some stars have a strongly, almost ultimately, stretched arm, by which they are grafted to the surface (“stem”). The free arms of such stars are directed from the grafting surface toward the solvent and form the outer layer. The remaining stars are stretched weakly and fill the inner near-surface layer of the brush. A schematic representation of the brush made of grafted stars with the two-population (two-layered) structure is given below.

The two-population structure of brushes made of stars was studied in detail [28–31]. It was found that the main reason of the two-population structure is the finite extensibility of the arms of stars; under the Gaussian (that is, infinite) extensibility of the arms, it is impossible to obtain the two-population structure.

Until recently, the studies of dendron brushes concerned mainly uncharged systems. At the same time, polymer brushes composed of branched polyelectrolytes are of undoubted interest; their research began relatively recently. O.V. Borisov and E.B. Zhulina developed the analytical theory of dendron brushes made of a strong polyelectrolyte [32]. Brushes made of dendrons of arbitrary generation were considered in the framework of the scaling analysis and a brush model with a uniform density profile. A more detailed self-consistent field (SCF) theory was proposed in the same paper for brushes made of dendrons of the first generation or brushes of polyelectrolyte stars arm-grafted to the surface. When constructing the theory, the Gaussian elasticity of the star arms, that is, their infinite extensibility, was assumed. As already indicated, this approach does not allow one to describe the situation with the division of stars into two populations and the separation of brushes into two layers. It should be noted that in polyelectrolyte brushes the chains are stretched more strongly than those in neutral brushes (due to the osmotic pressure of counterions in the “osmotic” regime or renormalization of the second virial coefficient in the “salt” regime); therefore, in the polyelectrolyte brush, the division of dendrons into populations will be even more pronounced.

The present work is devoted to the theoretical study of brushes formed by grafted polyelectrolyte stars (charged first-generation dendrons) with a fixed degree of ionization (the case of strong polyelectrolyte) using the Scheutjens–Fleer self-consistent field approach and the construction of a “minimal” Flory-type theory describing the conformational properties of such brushes. Particular attention will be paid to the formation of a layered two-population structure.

MODEL AND RESEARCH METHODS

The System under Study

Consider a planar brush made of grafted stars, each of which contains p arms consisting of n monomer units. Monomer unit size a is taken as the unit length. Stars are grafted onto an impenetrable planar surface at the density σ (the number of stars per unit grafting surface). The brush is immersed in a solvent, which thermodynamic quality with respect to the polymer is characterized by the Flory parameter χ. In this paper, we restrict ourselves to considering the case of an athermal solvent corresponding to χ = 0. The arms of stars are linear chains of polyelectrolytes with a fixed degree of ionization of the arms α (strong polyelectrolyte). The ions of monovalent salt are also present in the solution, the volume fraction of salt ions is 2Φs.

Analytical Theory

According to the two-population structure of the brush made of stars, the stars in the brush are divided into two groups or “populations.” Near the grafting surface, stars with weakly stretched arms predominate. Stars belonging to the second population are characterized by a strongly stretched arm, by which the star is grafted to the surface (“stem”), and their free arms are directed to the periphery of the brush.

The simplest Flory-type mean-field theory for a two-layered brush made of stars was proposed by H. Merlitz et al. [29]. It combined the elements of the Alexander–de Gennes model with the allowance for the division of stars into two populations (Fig. 1a). It was believed that the polymer density in the brush is constant; that is, the polymer concentration in two layers is the same (Fig. 1b). Another feature of the model was the neglect of the elastic contribution of weakly stretched stars to free energy. It was assumed to be negligibly small compared to the similar contribution of strongly stretched stars and to the contribution of volume interactions (polymer–polymer and polymer–solvent). For strongly stretched stars, their final extensibility was taken into account. Later on, the authors of [29] applied a similar analytical approach to the description of brushes made of second-generation dendrons [33].

Fig. 1.
figure 1

(Color online) (a) Two types of stars in the “two-layered” brush and (b) one-step and (c) two-step approximation of the profile of the volume fraction of polymer in the “two-layered” brush of stars.

Full size image

In [31], we used the approach developed in [29], introducing a single change into it; namely, the condition of constant polymer density inside the brush was eliminated: the density profile had a two-step form (Fig. 1c). Such a difference in density does not mean that there is a density jump at the boundary between the layers; it corresponds to the difference in the average density of the polymer in the layers.

A drawback of the model developed in [31] was that the stretching of stars belonging to a weakly extended population was not taken into account. According to self-consistent field calculations [28] and Langevin [25] and Brownian [26] dynamics simulations, the distribution of the branching points of stars from the weakly extended population turns out to be quite wide (Fig. 3), so that not all stars in it are stretched weakly. By ignoring the stretching of stars from the “near-surface” population when constructing the theory, we thereby make this population of stars thermodinamically more advantageous and artificially reduce the fraction of strongly stretched stars. In polyelectrolyte brushes, electrostatic interactions additionally stretch the macromolecules forming the brush, and this requires a more accurate consideration of the stretching of stars.

Fig. 2.
figure 2

(Color online) (a) Three types of stars in the brush and (b) three-step approximation of the profile of the volume fraction of polymer in the brush of stars.

Full size image
Fig. 3.
figure 3

(Color online) (a) The density profile of the polymer, the distribution of (b) branching points and (c) end groups, and (d) the density profiles of salt counterions and ions for the brush of polyelectrolyte stars grafted with a grafting density σ = 0.1 and the number of arms p = 3. The degree of ionization of the arms of stars α = (1) 0, (2) 0.1, (3) 0.3, and (4) 0.5. Volume fraction of salt in solution Φs = 10–4. Color drawings can be viewed in the electronic version.

Full size image

One way to take into account the elastic contribution of weakly stretched stars is to divide such stars into two groups, selecting moderately stretched stars in a separate “class.” Thus, all the stars in the brush will be artificially divided into three groups and the brush itself will be divided into three parts with thicknesses H1, H2, and H3 (Fig. 2a). We will assume that, within each of the groups, the stars are stretched equally. For example, for all strongly stretched stars, branching points are located at the same distance from the grafting surface (Fig. 2a) equal to H1 + H2 and the ends of the free arms are situated at distance H = H1 + H2 + H3. Let the fraction of such stars be equal to λ1.

The second group of stars is moderately stretched stars. Suppose that the stars of this group are stretched so that their free ends are located at the same distance from the grafting surface as the branching points of strongly stretched stars, H1 + H2, and the branching points are at distance H1 from the grafting surface. Let us denote the fraction of such moderately stretched stars of the total number of stars λ2.

Finally, we will still assume that the remaining stars, whose fraction is λ3 = 1 – λ1 – λ2, are very weakly (slightly) stretched and completely located in the near-surface layer with a thickness of H1; their contribution to the conformational free energy will not be taken into account.

In accordance with this idea, the brush is divided into three layers (Fig. 2b). In the first layer adjacent to the grafting surface, there are very weakly stretched stars, “stems” of moderately stretched stars, and a part of “stems” of strongly stretched stars. In the second layer, there are free arms of moderately stretched stars and parts of stems of strongly stretched stars. Note once again that the first and second layers are two parts of the near-surface layer, in which stars of the population with weakly stretched arms are located [25, 26, 28].

Within the framework of the proposed model, the density profile of the polymer in the brush has a three-step form: in the first layer with thickness H1, the density is φ1; in the second layer with thickness H2, φ2 < φ1; and in the outer layer with thickness H3 = H ‒ H1 – H2, φ3 < φ2 < φ1.

Taking into account the above assumptions, the density of the polymer in the layers is given by expressions

$$\begin{gathered} {{\varphi }_{1}} = \frac{{{{\lambda }_{1}}\left[ {{{H}_{1}}{\text{/}}\left( {{{H}_{1}} + {{H}_{2}}} \right)} \right] + {{\lambda }_{2}} + p{{\lambda }_{3}}}}{{{{H}_{1}}}}~n\sigma \\ = \sigma \left[ {\frac{{{{\lambda }_{1}}}}{{{{\zeta }_{1}} + {{\zeta }_{2}}}} + \frac{{{{\lambda }_{2}}}}{{{{\zeta }_{1}}}} + \frac{{p{{\lambda }_{3}}}}{{{{\zeta }_{1}}}}} \right], \\ \end{gathered} $$
(1)
$$\begin{gathered} {{\varphi }_{2}} = \frac{{{{\lambda }_{1}}\left[ {{{H}_{2}}{\text{/}}\left( {{{H}_{1}} + {{H}_{2}}} \right)} \right] + \left( {p - 1} \right){{\lambda }_{2}}}}{{{{H}_{2}}}}~n\sigma \\ = \sigma \left[ {\frac{{{{\lambda }_{1}}}}{{{{\zeta }_{1}} + {{\zeta }_{2}}}} + \frac{{\left( {p - 1} \right){{\lambda }_{2}}}}{{{{\zeta }_{2}}}}} \right], \\ \end{gathered} $$
(2)
$${{\varphi }_{3}} = \frac{{(p - 1){{\lambda }_{1}}}}{{{{H}_{3}}}}~n\sigma = \sigma ~\frac{{(p - 1){{\lambda }_{1}}}}{{{{\zeta }_{3}}}},$$
(3)

where ζi = Hi/n is the height of layers i = 1, 2, 3 reduced to the length of the star arm. Here we took into account that the “stem” of a strongly stretched star from the first group is stretched homogeneously; therefore, the fraction of “stem” units in the layer H1 and H2 is H1/(H1 + H2) and H2/(H1 + H2), respectively.

The free energy of the brush consists of the following contributions:

$$F = {{F}_{{{\text{conf}}}}} + {{F}_{{{\text{int}}}}} + {{F}_{{{\text{sol}}}}} + {{F}_{{{\text{ion}}}}}.$$
(4)

Here Fconf is the conformational free energy, Fint is the contribution of polymer-solvent interaction, Fsol is the contribution of the translational entropy of solvent molecules, and Fion is the contribution related to the translational entropy of mobile ions present in the system.

The contribution to the conformational free energy Fconf is provided only by stars of the first and second groups (strongly and moderately stretched). It can be easily calculated if we accept that the “stem” of the star from the ith group (i = 1 or 2) is stretched by force fi. Then each of q = p – 1 free arms, which are stretched homogeneously and equally, is subjected to the action of force fi/q, since the balance of forces acting from the “stem” side and free arms should be fulfilled at the branching point. Thus, force fi acts as a parameter that can be conveniently used to calculate the elastic free energy of stretched stars. This means a temporary transition to a thermodynamic ensemble of a fixed force.

Consider a freely-jointed chain on a simple cubic lattice stretched by the applied force fi directed along the axis Oz. The statistical weight of one monomer unit in the field of force fi is calculated as follows:

$${{w}_{i}} = {{\lambda }_{z}}{{e}^{{{{f}_{i}}}}} + {{\lambda }_{z}}{{e}^{{ - {{f}_{i}}}}} + {{\lambda }_{{xy}}}{{e}^{0}} = \frac{2}{3} + \frac{1}{3}\cosh {{f}_{i}},$$
(5)

where λz = 1/6 is the probability of a step along axis Oz and λxy = 1 – 2λz = 2/3 is the probability of a step in plane Oxy. (Hereinafter, energy is expressed in kBT units). Since in the freely-jointed chain the units are independent, the statistical sum of the chain can be represented as the product of the statistical sums of the individual units, that is, the statistical sum of the stem \({{Z}_{{{\text{stem}},\;i}}} = w_{i}^{n}\). The logarithm of the statistical sum gives the Gibbs free energy of the “stem” of the star from the ith group:

$${{G}_{{{\text{stem}},~i}}} = - \log {{Z}_{{{\text{stem}},~i}}} = - n\log \left( {\frac{2}{3} + \frac{1}{3}\cosh {{f}_{i}}} \right).$$
(6)

The average distance between chain ends is obtained by differentiating the Gibbs free energy with respect to the force, which is a parameter conjugate to the distance; therefore,

$${{H}_{1}} + {{H}_{2}} = - \frac{{\partial {{G}_{{{\text{stem}},~1}}}}}{{\partial {{f}_{1}}}} = n~\frac{{\sinh {{f}_{1}}}}{{2 + \cosh {{f}_{1}}}},$$
$${{H}_{1}} = - \frac{{\partial {{G}_{{{\text{stem}},~2}}}}}{{\partial {{f}_{2}}}} = n~\frac{{\sinh {{f}_{2}}}}{{2 + \cosh {{f}_{2}}}}.$$
(7)

In a similar manner, we obtain the Gibbs free energy for one free arm of a star, which, as already noted, is subjected to the action of tensile force fi/q:

$${{G}_{{{\text{arm}},~i}}} = - n\log \left[ {\frac{2}{3} + \frac{1}{3}\cosh \left( {{{f}_{i}}{\text{/}}q} \right)} \right].$$
(8)

The Gibbs free energy of a strong (i = 1) or moderately (i = 2) stretched star has the form

$$\begin{gathered} {{G}_{i}} = - n\log \left[ {\frac{2}{3} + \frac{1}{3}\cosh {{f}_{i}}} \right] \\ \, - nq\log \left[ {\frac{2}{3} + \frac{1}{3}\cosh \left( {{{f}_{i}}{\text{/}}q} \right)} \right]. \\ \end{gathered} $$
(9)

To pass from the Gibbs free energy G to the Helmholtz free energy F, we will use the Legendre transform: F = G + Hf, where H is the average distance between the ends of the chain stretched by force f related to the Gibbs free energy H = –∂G/∂f. As a result, the Helmholtz conformational free energy taking into account the contribution of two types of stars (strongly and moderately stretched) may be written as

$$\begin{gathered} \frac{{{{F}_{{{\text{conf}}}}}}}{n} = {{\lambda }_{1}}\left\{ { - \log \left[ {\frac{2}{3} + \frac{1}{3}\cosh {{f}_{1}}} \right]} \right. \\ \left. {\, - q\log \left[ {\frac{2}{3} + \frac{1}{3}\cosh \left( {{{f}_{1}}{\text{/}}q} \right)} \right] + \left( {{{\zeta }_{1}} + {{\zeta }_{2}} + {{\zeta }_{3}}} \right){{f}_{1}}} \right\} \\ \, + {{\lambda }_{2}}\left\{ { - \log \left[ {\frac{2}{3} + \frac{1}{3}\cosh {{f}_{2}}} \right]} \right. \\ \left. {\, - q\log \left[ {\frac{2}{3} + \frac{1}{3}\cosh \left( {{{f}_{2}}{\text{/}}q} \right)} \right] + \left( {{{\zeta }_{1}} + {{\zeta }_{2}}} \right){{f}_{2}}} \right\}, \\ \end{gathered} $$
(10)

where φj is the volume fraction of the polymer in the layers; j = 1, 2, 3 is set by expressions (1)–(3), and the reduced layer height ζj is defined as follows:

$${{\zeta }_{1}} = \frac{{\sinh {{f}_{2}}}}{{2 + \cosh {{f}_{2}}}},$$
(11)
$${{\zeta }_{2}} = \frac{{\sinh ({{f}_{2}}{\text{/}}q)}}{{2 + \cosh ({{f}_{2}}{\text{/}}q)}},$$
(12)
$${{\zeta }_{3}} = \frac{{\sinh ({{f}_{1}}{\text{/}}q)}}{{2 + \cosh ({{f}_{1}}{\text{/}}q)}}.$$
(13)

In this case, it should be taken into account that force f1 stretches the stem of a strongly stretched star at the distance (in reduced units)

$${{\zeta }_{1}} + {{\zeta }_{2}} = \frac{{\sinh {{f}_{1}}}}{{2 + \cosh {{f}_{1}}}},$$
(14)

which gives the condition relating forces f1 and f2:

$$\frac{{\sinh {{f}_{1}}}}{{2 + \cosh {{f}_{1}}}} = \frac{{\sinh {{f}_{2}}}}{{2 + \cosh {{f}_{2}}}} + \frac{{\sinh ({{f}_{2}}{\text{/}}q)}}{{2 + \cosh ({{f}_{2}}{\text{/}}q)}}.$$
(15)

From Eq. (15), we can obtain an explicit expression for force f1 as a function of f2:

$${{f}_{1}} = \log \frac{{1 + A}}{{\sqrt {3{{A}^{2}} + 1} - 2A}}.$$
(16)

Here

$$A = A({{f}_{2}}) = \frac{{\sinh {{f}_{2}}}}{{2 + \cosh {{f}_{2}}}} + \frac{{\sinh ({{f}_{2}}{\text{/}}q)}}{{2 + \cosh ({{f}_{2}}{\text{/}}q)}}.$$
(17)

The free energy of polymer–polymer and polymer–solvent interactions per grafted star is expressed as

$${{F}_{{{\text{int}}}}} = \mathop \sum \limits_{i = 1}^3 {{n}_{i}}~\chi ~\left( {1 - {{\varphi }_{i}}} \right),$$
(18)

where summation is carried out over the layers (Fig. 2b) and ni is the number of monomer units per star which are located in the ith layer. This value can be rewritten as

$${{F}_{{{\text{int}}}}} = n~\mathop \sum \limits_{i = 1}^3 \frac{{{{\varphi }_{i}}{{\zeta }_{i}}}}{\sigma }~~\chi \left( {1 - {{\varphi }_{i}}} \right)$$
(19)

(χ is the Flory parameter). It is assumed that salt counterions and ions are equivalent to solvent molecules in terms of their interaction with the polymer; therefore, the same value of the Flory parameter χ is used for them.

Reference System: Polyelectrolyte Solution in Equilibrium with Salt Solution

To study the properties of brushes made of grafted polyelectrolyte stars, it is necessary to take into account the corresponding contribution associated with immobilized (bound to the polymer) and mobile (counterions and co-ions of the dissociated salt) charges to the free energy of the brush. We will assume that the condition of local electroneutrality is fulfilled for the brush: the counterions necessary to neutralize the charges immobilized on the brush stars are kept inside the brush; therefore, the brush as a whole remains electrically neutral. Then the main contribution to free energy will be provided by the osmotic pressure of the trapped counterions and the entropy of the mobile counterions. Outside the brush, the system will also be assumed to be locally electrically neutral.

For accurate calculation of the contribution associated with immobilized and mobile charges to free energy, it is convenient to consider the reference system, that is, a solution of an infinitely long PE chain with a fixed charge α which is in equilibrium with a solution of a univalent salt (e.g., NaCl) [34].

The chain is located in a cell with a semi-impermeable wall through which solvent and mobile ions can pass, while the polymer chain cannot pass. It is assumed that the polymer solution is homogeneous and the volume fraction of the polymer in this part of the cell is constant and equal to φp. The solution also contains solvent molecules (water), which occupy a fraction of volume equal to φ0, and positively and negatively charged ions with volume fractions φ+ and φ–, respectively. In the framework of the lattice model, we will assume that the monomer unit, solvent molecule, and positively or negatively charged ions occupy one lattice unit. Accordingly, the incompressibility condition must be satisfied

$${{\varphi }_{p}} + {{\varphi }_{0}} + {{\varphi }_{ + }} + {{\varphi }_{ - }} = 1.$$
(20)

The volume fractions of positively and negatively charged ions (cations and anions) in solution are related by the electroneutrality condition

$${{\varphi }_{ + }} = {{\varphi }_{ - }} + \alpha {{\varphi }_{{\text{p}}}}.$$
(21)

In the external medium, the polymer is absent; there are only solvent molecules and mobile ions, the volume fraction of which is equal to Φ+ and Φ–. For the external medium, the conditions of electroneutrality

$${{\Phi }_{ + }} = {{\Phi }_{ - }}.$$
(22)

and incompressibility

$${{\Phi }_{0}} + {{\Phi }_{ + }} + {{\Phi }_{ - }} = 1$$
(23)

(Φ0 is the volume fraction of solvent in the external medium) should be fulfilled. Let us denote Φs = Φ+ = Φ–; then Φ0 = 1 – 2Φs.

The free energy of a polymer solution is the free energy of mixing

$${{F}_{{{\text{mix}}}}} = V{{f}_{{{\text{mix}}}}} = V~~\left[ {f\left( {{{\varphi }_{p}}} \right) - \mathop \sum \limits_i {{\varphi }_{i}}\mu _{i}^{{{\text{out}}}}} \right].$$
(24)

Here V is the volume of the system occupied by the polymer, f is the density of free energy in the brush, fmix is the density of the free energy of mixing in the brush, \(\mu _{i}^{{{\text{out}}}}\) is the chemical potential of the ith component (solvent molecules and ions; that is, i = 0, +, –) in the external medium, and φi is the volume fraction of these components in the brush. The subtraction of the contributions in expression (24) is required to account for the changes in the free energy of the components upon their mixing with the polymer (upon transition from the external solution to the part containing the polymer).

The expression for the free energy density in the part occupied by the polymer contains only the entropy contributions of low molecular weight components (we believe that there is no additional attraction or repulsion between them, which corresponds to a zero value of the Flory parameter χij = 0):

$$f = {{\varphi }_{0}}\log {{\varphi }_{0}} + {{\varphi }_{ + }}\log {{\varphi }_{ + }} + {{\varphi }_{ - }}\log {{\varphi }_{ - }}.$$
(25)

The chemical potential of low molecular weight components in the external medium is \(\mu _{i}^{{{\text{out}}}}\) = logΦi (i = 0, +, –). Thus, the free energy of mixing per unit volume (density of the free energy of mixing) is

$$\begin{gathered} {{f}_{{{\text{mix}}}}} = f - {{{\Phi }}_{0}}\log {{{\Phi }}_{0}} - {{{\Phi }}_{ + }}\log {{{\Phi }}_{ + }} - {{{\Phi }}_{ - }}\log {{{\Phi }}_{ - }} \\ = {{\varphi }_{0}}\log \frac{{{{\varphi }_{0}}}}{{{{{\Phi }}_{0}}}} + {{\varphi }_{ + }}\log \frac{{{{\varphi }_{ + }}}}{{{{{\Phi }}_{ + }}}} + {{\varphi }_{ - }}\log \frac{{{{\varphi }_{ - }}}}{{{{{\Phi }}_{ - }}}} \\ = [1 - 2{{\varphi }_{ - }} - (1 + \alpha ){{\varphi }_{p}}]\log \frac{{1 - 2{{\varphi }_{ - }} - (1 + \alpha ){{\varphi }_{p}}}}{{1 - 2{{{\Phi }}_{s}}}} \\ \, + ({{\varphi }_{ - }} + \alpha {{\varphi }_{p}})\log \frac{{{{\varphi }_{ - }} + \alpha {{\varphi }_{p}}}}{{{{{\Phi }}_{s}}}} + {{\varphi }_{ - }}\log \frac{{{{\varphi }_{ - }}}}{{{{{\Phi }}_{s}}}}. \\ \end{gathered} $$
(26)

This expression should be minimized with respect to φ–: dfmix/dφ– = 0, which leads to the relation

$$\frac{{{{\varphi }_{ - }} + \alpha {{\varphi }_{p}}}}{{{{{\Phi }}_{s}}}}~~\frac{{{{\varphi }_{ - }}}}{{{{{\Phi }}_{s}}}} = {{\left[ {\frac{{1 - 2{{\varphi }_{ - }} - (1 + \alpha ){{\varphi }_{p}}}}{{1 - 2{{{\Phi }}_{s}}}}} \right]}^{2}}.$$
(27)

This condition is similar to the Donnan membrane equilibrium condition; it takes into account the explicit volume of ions and represents a quadratic equation with respect to φ–, which is convenient to solve by making the substitution φ– = y – αφp/ 2. Then φ+ = y + αφp/2, y = (φ+ + φ–)/2, and φ0 = 1 – φp – 2y, and Eq. (27) takes the form

$$\left[ {{{y}^{2}} - {{{\left( {\frac{{\alpha {{\varphi }_{p}}}}{2}} \right)}}^{2}}} \right]{{(1 - 2{{{\Phi }}_{s}})}^{2}} = {{(1 - {{\varphi }_{p}} - 2y)}^{2}}{\Phi }_{s}^{2}$$
(28)

or

$$\begin{gathered} (1 - 4{{{\Phi }}_{s}}){{y}^{2}} + 4{\Phi }_{s}^{2}(1 - {{\varphi }_{p}})y - {{(1 - {{\varphi }_{p}})}^{2}}{\Phi }_{s}^{2} \\ - {{\left( {\frac{{\alpha {{\varphi }_{p}}}}{2}} \right)}^{2}}{{(1 - 2{{{\Phi }}_{s}})}^{2}} = 0. \\ \end{gathered} $$
(29)

Note that the dependence on the degree of ionization α is contained only in the last term of the left side of the equation. Its solution is given by the following expression

$$y = y\left( {{{\varphi }_{p}}} \right) = \frac{{\left( {1 - 2{{{\Phi }}_{s}}} \right)\sqrt {{\Phi }_{s}^{2}{{{\left( {1 - {{\varphi }_{p}}} \right)}}^{2}} + {{{\left( {\frac{{\alpha {{\varphi }_{p}}}}{2}} \right)}}^{2}}\left( {1 - 4{{{\Phi }}_{s}}} \right)} - 2{\Phi }_{s}^{2}\left( {1 - {{\varphi }_{p}}} \right)}}{{1 - 4{{{\Phi }}_{s}}}}.$$
(30)

Taking into account that

$$\begin{gathered} {{\varphi }_{ - }} = y - \frac{{\alpha {{\varphi }_{p}}}}{2},\quad {{\varphi }_{ + }} = y + \frac{{\alpha {{\varphi }_{p}}}}{2}, \\ {{\varphi }_{0}} = 1 - {{\varphi }_{p}} - 2y, \\ \end{gathered} $$
(31)

we obtain the expression for the free energy density:

$$\begin{gathered} {{f}_{{{\text{mix}}}}}\left( {{{\varphi }_{p}}} \right) = \left( {1 - {{\varphi }_{p}} - 2y} \right)\log \frac{{1 - {{\varphi }_{p}} - 2y}}{{1 - 2{{{\Phi }}_{s}}}} \\ + \left( {y\, - \,\frac{{\alpha {{\varphi }_{p}}}}{2}} \right){\text{log}}\frac{{y\, - \,\alpha {{\varphi }_{p}}{\text{/}}2}}{{{{{\Phi }}_{s}}}}\, + \,\left( {y\, + \,\frac{{\alpha {{\varphi }_{p}}}}{2}} \right){\text{log}}\frac{{y\, + \,\alpha {{\varphi }_{p}}{\text{/}}2}}{{{{{\Phi }}_{s}}}} \\ = \left( {1 - {{\varphi }_{p}}} \right)\log \frac{{1 - {{\varphi }_{p}} - 2y}}{{1 - 2{{{\Phi }}_{s}}}} + \frac{{\alpha {{\varphi }_{p}}}}{2}\log \frac{{y + \alpha {{\varphi }_{p}}{\text{/}}2}}{{y - \alpha {{\varphi }_{p}}{\text{/}}2}}. \\ \end{gathered} $$
(32)

This expression includes contributions of the translational entropy of mobile ions and solvent molecules (that is, the contributions Fion and Fsol in expression (4) for the free energy of the brush).

Free Energy of a Brush Made of Polyelectrolyte Stars with a Fixed Charge

The free energy of the brush composed of PE stars is given by the expression

$$\begin{gathered} \frac{F}{n} = {{\lambda }_{1}}\left\{ { - \log \left[ {\frac{2}{3} + \frac{1}{3}\cosh {{f}_{1}}} \right]} \right. \\ \,\left. { - q\log \left[ {\frac{2}{3} + \frac{1}{3}\cosh ({{f}_{1}}{\text{/}}q)} \right] + ({{\zeta }_{1}} + {{\zeta }_{2}} + {{\zeta }_{3}}){{f}_{1}}} \right\} \\ \, + {{\lambda }_{2}}\left\{ { - \log \left[ {\frac{2}{3} + \frac{1}{2}\cosh {{f}_{2}}} \right]} \right. \\ \left. {\, - q\log \left[ {\frac{2}{3} + \frac{1}{3}\cosh ({{f}_{2}}{\text{/}}q)} \right] + ({{\zeta }_{1}} + {{\zeta }_{2}}){{f}_{2}}} \right\} \\ \, + \sum\limits_{i = 1}^3 {\frac{{{{\zeta }_{i}}}}{\sigma }\left[ {(1 - {{\varphi }_{i}})\log \frac{{1 - {{\varphi }_{i}} - 2y({{\varphi }_{i}})}}{{1 - 2{{\Phi }_{s}}}}} \right.} \\ \left. { + \frac{{\alpha {{\varphi }_{i}}}}{2}\log \frac{{y({{\varphi }_{i}}) + \alpha {{\varphi }_{i}}{\text{/}}2}}{{y({{\varphi }_{i}}) - \alpha {{\varphi }_{i}}{\text{/}}2}} + \chi (1 - {{\varphi }_{i}})} \right], \\ \end{gathered} $$
(33)

where φi is the volume fraction of the polymer in the ith layer (Eqs. (1)–(3)), ζi is the reduced height of the ith layer (Eqs. (11)–(13)), and the dependence y(φi) is given by expression (30).

Brush free energy F turns out to be a function of four variables: f1, λ1, f2, and λ2; here, variables f1 and f2 are related by condition (15). Minimization of free energy was carried out numerically by introducing the Lagrange multiplier related to the condition (15).

The Numerical Scheutjens–Fleer Self-Consistent Field Method

In this work were carried out using the numerical Scheutjens–Fleer self-consistent field method, which is widely used to model grafted polymer layers—polymer brushes. The Scheutjens–Fleer method and its modifications for studying polymer brushes of various types were repeatedly described in the literature; therefore, in this paper, we allow ourselves to omit a detailed description of this method, which can be found, for example, in the monograph [35]. Features of the implementation of the self-consistent field method for brushes made of grafted stars are described in [28].

To solve the problem of a planar brush, the so-called single-gradient version of the Scheutjens–Fleer method is used which is based on the assumption that the brush is laterally uniform, the x and y components of the gradient of the polymer volume fraction parallel to the grafting plane of chains are equal to zero, and only the z component of the density gradient perpendicular to the plane is not equal to zero. This means that the density of the polymer is only a function of z: φ = φ(z). Electrostatic interactions in the system are taken into account in the framework of the Poisson–Boltzmann equation [36].

In the present work, the calculations were performed using the SFBox program developed at Wageningen University (Netherlands), which allows one to obtain the density distributions of the polymer as a whole and of individual segments, including branching points and end groups, as well as integral thermodynamic characteristics, for example, the free energy. It is important that, in this case, there is no need to make assumptions concerning the nature of the conformations of stars in the brush, introducing the corresponding model simplifications, to which one must resort when constructing the analytical theory.

RESULTS AND DISCUSSION

Numerical Self-Consistent Field Modeling Results

In the self-consistent field calculations, the results of which are presented in this paper, brushes composed of stars containing arms of n = 100 units immersed in an athermal solvent, which corresponds to the zero value of the Flory parameter χ = 0, were studied. Consider a brush of three-arm stars (p = 3) with a constant grafting density (σ = 0.1) immersed in a solution with a low salt concentration (Φs = 10–4). Figure 3a shows the evolution of the polymer concentration profile in the brush φ(z) with variation in the degree of ionization of grafted stars, z is the distance from the grafting surface. The density of the polymer in the brush monotonically decreases from the grafting surface to the periphery. As the degree of ionization increases, the thickness of the brush grows (the distance from the grafting plane z at which the density vanishes) while the maximum density at the grafting surface and the average density of the polymer in the brush both decrease. Thus, it can be concluded that there is a general increase in the stretching of stars in the brush in the direction perpendicular to the grafting plane with an increase in the degree of ionization of the arms.

A more detailed analysis of the brush structure follows from the distributions of branching points of stars (nbp) and end groups of free arms (ne). To compare these distributions for brushes with different grafting densities, it is convenient to normalize them to unity and represent them in the form

$${{n}_{{{\text{bp}}}}}(z) = \frac{{{{\varphi }_{{{\text{bp}}}}}(z)}}{\sigma },\quad {{n}_{{\text{e}}}}(z) = \frac{{{{\varphi }_{{\text{e}}}}(z)}}{{\left( {p - 1} \right)\sigma }},$$
(34)

where φbp(z) and φe(z) are the density profiles of branching points and end groups. This normalization ensures equality of the area under the curves nbp(z) and ne(z) to unity.

Figure 3b shows the evolution of the distribution of the branching point with increasing charge density on the arms of polyelectrolyte stars. In a neutral star, the distribution is virtually unimodal—there is one pronounced maximum and a small shoulder on the right. Increasing the degree of ionization of the arms α leads to broadening of the distribution, which corresponds to a general extension of the chains and an increase in the thickness of the brush, and transformation of the right shoulder into a full maximum, the height and sharpness of which grow with increasing α. The maximum position is limited by z = n = 100, which corresponds to the full stretching of the “stem.” At the same time, the extended near-surface part of the distribution does not vanish; this means the absence of “dead zones” for the branching points in the brush.

Very similar changes also occur in the distribution of the ends (Fig. 3c): in the absence of charges on the arms, there is one maximum and a small “shoulder,” which becomes more pronounced and becomes a maximum with an increase in the degree of ionization, and the distribution width as a whole increases with increasing α.

This type of distribution of the ends and branching points corresponds, as was shown in [23] and proved in [28], to the division of stars in the brush into two populations: there is a part of stars with a strongly, extremely stretched stem, which corresponds to a sharp maximum on the right on the distribution of branching points nbp(z) in Fig. 3b, and free arms of stars directed into the solvent, which corresponds to the peripheral part of the distribution ne(z) in Fig. 3c. At the same time, there is another population of stars in the brush that are stretched fairly weakly—they correspond to the extended parts of the distribution profiles of branching points and ends that begin at the grafting surface. The number of stars with a strongly stretched stem increases with increasing degree of ionization, which is associated with an increase in the number of counterions held in the brush (Fig. 5d) and an increase in the osmotic pressure that stretches the brush.

Fig. 4.
figure 4

(Color online) (a) The density profile of the polymer, the distribution of (b) branching points and (c) end groups, and (d) the density profiles of salt counterions for the polyelectrolyte brush made of stars with the number of arms p = 3. The degree of ionization of the arms α = (1) 0 and (2–5) 0.3; grafting density σ = 0.1; salt concentration Φs = (2) 10–1, (3) 10–2, (4) 10–3, and (1, 5) 10–4.

Full size image
Fig. 5.
figure 5

(Color online) Charge density distribution in the polyelectrolyte brush of stars with the number of arms p = 3 and the degree of ionization of the arms α = 0.3 grafted with a grafting density of σ = 0.1. Φs = (1) 10–1, (2) 10–2, (3) 10–3, and (4) 10–4.

Full size image

Effect of Salt Concentration on the Structure of a Brush Made of Stars

The effect of salt concentration on the structure of a polyelectrolyte brush made of stars is illustrated in Fig. 4, which presents the data for the brush composed of three-arm stars p = 3 with a fixed degree of ionization of the arms α = 0.3.

It follows from the polymer density profile (Fig. 4a) that, with increasing salt concentration, the brush becomes denser and its height decreases. This is due to the fact that the charge of star arms is screened: the number of salt counterions and coions outside increases (Fig. 4d) and the release of the stars’ own counterions outside becomes disadvantageous in terms of the entropy. They remain inside the brush, forming a “coat” around the chains. In Figs. 4b and 4c, the bimodal distributions of branching points and end groups, respectively, are also seen. This finding indicates the division of stars into two populations, especially at low salt concentrations.

To verify that the condition of local electroneutrality in the brush is satisfied, the distribution of charge density in the system φq(z) = αφ(z) + φ–(z) – φ+(z) was calculated. As follows from Fig. 5, the local charge density in the brush is zero and only insignificant but compensated deviations from zero are observed at the borders of the brush: near the grafting surface of stars and on the periphery.

Above, we described the two-population structure of the brush made of stars using various polymer distributions in the system: the polymer density profile and the distributions of branching points and ends. To characterize the structure of the brush, it is also helpful to use its integral characteristics, such as the average density of the polymer in the brush and the fraction of strongly stretched stars, which make it possible to unveil general patterns of the behavior of the brushes with a change in various external parameters.

Since existence of the two-population brush structure is indicated by both the distribution of branching points and the distribution of ends, two methods can be proposed for determining the fraction of strongly stretched stars in the brush λ1 (Figs. 1a, 2a). Using normalized distributions, λ1 can be calculated as follows:

$${{\lambda }_{1}} = \mathop \sum \limits_{z \geqslant {{z}_{{{\text{min,}}\,j}}}} {{n}_{j}}(z),$$
(35)

where j = bp or e (branching points or ends) and the lower limit of summation z = zmin,j corresponds to the right minimum on the curve nj(z) The value of λ calculated from the distribution of branching points (j = bp) is the fraction of units with a strongly stretched “stem,” and the value of λ1 found from the distribution of ends (j = e) is the fraction of stars forming an external “brush” with arms directed toward the periphery. As was shown for neutral brushes [28], both methods give the same value of λ1. This indicates that the arms directed toward the periphery of the brush belong to stars with the strongly stretched “stem,” which confirms the proposed two-population structure of stars in the brush. In the case of the brush made of polyelectrolyte stars, the definition of λ1 in two ways also gives the same values.

Another integral characteristic, average polymer density in the brush φ, can be obtained from the polymer density profile φ(z):

$$\varphi = \frac{{\sum\limits_z^{} {\varphi (z)\varphi (z)} }}{{\sum\limits_z^{} {\varphi (z)} }}.$$
(36)

The results of calculating these characteristics according to the self-consistent field approach and comparison with the data obtained by numerically solving the equations of the analytical theory developed in the previous sections will be presented below.

Effect of the Degree of Ionization on the Structure of a Brush Made of Stars

Figures 6 and 7 show the volume fraction of the polymer and the fraction of strongly stretched stars λ1 as a function of the grafting density of stars for brushes composed of three- and five-arm stars which are obtained at low (Φs = 10–4) and high (Φs = 0.1) salt concentrations. First note that the range of variation in grafting density is bounded above by a value less than unity. This is the maximum possible grafting density, at which the polymer density in the brush is maximal, and the brush itself does not contain solvent molecules. In this case, the volume of the brush per star (V = H/σ) is occupied by the star itself and the trapped counterions in order to fulfill the electroneutrality condition; that is, V = (1 + α)pn. Equating the expressions for the volume, we arrive at the dependence of the height of the solvent-free brush on the grafting density: H = N(1 + α)σ, where N = np is the total number of monomer units in the star. The maximum possible brush height is twice the arm length: Hmax = 2n; therefore, the maximum allowable density of grafting of polyelectrolyte stars with a degree of ionization α to the surface of the brush is

$${{\sigma }_{{{\text{max}}}}} = \frac{2}{{p(1 + \alpha )}}.$$
(37)
Fig. 6.
figure 6

(Color online) Dependences of the average volume fraction of polymer φ on grafting density σ in brushes made of stars with p = (a, b) 3 and (c, d) 5. The degree of ionization of the arms of stars α = (1) 0, (2) 0.1, (3) 0.3, and (4) 0.5; Φs = (a, c) 10‒4 and (b, d) 10–1. Points are the results of numerical modeling, and curves are the results of the theory.

Full size image
Fig. 7.
figure 7

(Color online) Dependences of the fraction of strongly stretched stars λ1 with p = (a, b) 3 and (c, d) 5 on the grafting density σ. The degree of ionization of the arms of stars α = (1) 0, (2) 0.1, (3) 0.3, and (4) 0.5; Φs = (a, c) 10–4 and (b, d) 10–1; λmax = (a, b) 0.75 and (c, d) 0.624. Points are the results of numerical modeling, and curves are the results of the theory. The horizontal line shows the maximum possible fraction of strongly stretched stars.

Full size image

The above expression can be rewritten in a more general form for a brush made of regularly branched dendrons of arbitrary generation with identical spacers \(~{{\sigma }_{{{\text{max}}}}} = \mathcal{N}{\text{/}}[N(1 + \alpha )]\), where \(\mathcal{N}\) is the number of monomer units in the maximum path connecting the point of grafting of the dendron to the surface to any of its end groups (for a star \(\mathcal{N}\) = 2n) and N is the total number of units in the dendron (for a star N = np). The maximum allowable grafting density decreases with increasing α, since the number of counterions that must be trapped in the brush grows and this requires additional volume.

The maximum grafting density corresponds to the average volume fraction of polymer equal to φmax= 1/(1 + α), and the fraction of stars with the extremely stretched stem λ1(σmax) = p/[2(p – 1)] [30], which is independent of the degree of ionization α.

With an increase in the grafting density, the average polymer density and the fraction of strongly stretched stars in the brush grow because, owing to compaction of the brush, the stars are forced to be located on its periphery. Similar effects are also caused by an increase in the number of arms in grafted stars. The fraction of strongly stretched stars also increases with increasing degree of ionization, although the average density of the polymer decreases. This fact can be explained by an increase in the number of counterions trapped in the brush and, as a consequence, by a rise in the osmotic pressure, which leads to the stretching of stars. This also contributes to the transition of stars to the upper population. An increase in the salt concentration in the solution causes screening of the charge and decrease in the stretching and swelling of the stars in the brush and, as a result, a decrease in λ1. Note that the results of the analytical theory are in quantitative agreement with the average polymer density obtained from numerical SCF calculations. The more stars are stretched in the brush (that is, the higher the grafting density, the number of star arms, and the degree of ionization and the lower the salt concentration), the better this agreement is.

On the Need to Take into Account the Stretching of Stars from a Weakly Stretched Population

In the present work, the theory describing the two-population structure of brushes made of grafted polyelectrolyte stars was developed. It is based on the three-step approximation of the density profile and the division of the stars that make up the brush into three groups in order to allow for the elastic free energy of stars belonging to a weakly stretched population (Fig. 2). In earlier theories based on one-step (Fig. 1a, [29]) and two-step (Fig. 1b, [31]) approximations of the density profile and separation of stars into two groups, corresponding to the division into two populations, the stretching of weakly stretched stars was neglected. It is clear that, for the brushes made of polyelectrolyte stars, the theory relying on this simpler model can be developed. Such calculations were also carried out within the framework of this study. The dependences shown in Fig. 8 indicate that the model with the two-step approximation of the profile and neglecting the elastic contribution of weakly stretched stars is insufficient for an adequate description of brushes made of polyelectrolyte stars. This primarily concerns the case of a low salt concentration and a high degree of ionization, where the electrostatic effects are more pronounced. Obviously, the model with the three-step approximation of the density profile is expected to give a more accurate estimate for the average volume fraction of the polymer in the brush. In addition, it leads to a higher fraction of strongly stretched stars, since a partial account of the elastic energy of weakly stretched stars reduces the advantage of this population compared to the “two-step” model.

Fig. 8.
figure 8

(Color online) Dependences of (a) the average volume fraction of polymer φ and (b) the fraction of strongly stretched stars λ1 of three arms on the grafting density σ at the degree of ionization of the arms of stars α = (1) 0.1 and (2) 0.5 in the brush immersed in solution with a low salt concentration Φs = 10–4. Points are the results of numerical modeling, and curves are the results of the theory for models with the two-step (dashed lines) and three-step (solid lines) approximation of the density profile.

Full size image

CONCLUSIONS

This work is devoted to the theoretical study of the planar brush of grafted polyelectrolyte stars with a fixed degree of ionization of monomer arm units immersed in a salt solution. It is known that the characteristic feature of brushes made of stars is formation of a layered structure with the division of stars into two populations; therefore, this effect and the influence of the charge of arms and the concentration of salt in the system on it were given special attention. The system was investigated by using two approaches: on one hand, modeling was performed using the numerical Scheutjens–Fleer self-consistent field approach, which allows obtaining detailed information on the structure of the brush in the form of distributions of polymer density, branching points, end groups, and mobile cations and anions. On the other hand, a simple Flory-type analytical theory was developed with the three-step approximation of the density profile of the polymer in the brush and the isolation of three groups of stars in the brush—strongly, moderately, and weakly stretched. Electrostatic effects were taken into account in the theory under the local electroneutrality approximation, and the correctness of such an approximation was confirmed by SCF modeling. To calculate the contribution associated with the entropy of mobile ions to the free energy, the reference system, that is, a single infinitely long chain of polyelectrolyte occurring in solution in equilibrium with the external medium, was considered. The theory also takes into account explicitly the finite volume of ions.

It was shown that an increase in the number of stars with an extremely stretched arm, by which the star grafts to the surface, is facilitated by an increase in the grafting density, the number of arms, or the degree of ionization of the arms. In the latter case, the average brush density decreases, while in the former two cases it increases. It is shown that the theory describes well the results of SCF modeling. The best agreement is observed at a high degree of ionization, a large number of arms, and a high grafting density. We should note that in this range of parameters, numerical SCF calculations become more time-consuming. The developed approach can be generalized to the case of a brush formed by ionizable (pH-sensitive) stars and to another type of lattice or continuum model for brush-forming macromolecules.