1 INTRODUCTION

1.1 Motivation

In this paper, the problem of controlling modern communication networks is considered from the point of view of optimization and stochastic modeling. To solve problems of this type, we need to represent and analyze the mathematical model arising in the simulation of large-scale broadband networks. It is expected that, in future communication networks, there appear applications that will be able to change their data transmission rates according to the available network capacity. An example of such a network is TCP traffic through the Internet.

The key issue addressed in this paper is how the available capacity of the network is to be allocated among competing flows. The use of available capacities by consumers is controlled by correcting the link prices.

Thus, we consider the problem of optimizing resource allocation in computer networks with a large number of links. The links are used by consumers (users), whose number can also be very large. The goal of this study is to determine a resource allocation mechanism, where the resources are understood as available capacities of network links. Additionally, it is necessary to ensure stable performance of the system and to prevent overloads. As an optimality criterion, we use the sum of the utilities of all users of the computer network.

Originally, standard resource allocation problems reducing to the maximization of the aggregate utility of users in the case of shared use of available resources were considered in [1]. Resource allocation in computer networks was investigated in the recent work [2]. Proposed in [3], the mechanisms of decentralized resource allocation drew much attention in economic studies (see, e.g., [4–6] and references therein). In this paper, following [7, 8], we consider various mechanisms of price adjustment. The proposed approaches are of practical importance due to their decentralized nature, which means that the price of an individual link is established and adjusted relying only on the reactions of users employing this link, rather than on the reactions of all network users. In the case of such an adjustment mechanism, all links perform independently.

Additionally, one of the approaches proposed in this paper relies on the stochastic projected subgradient method and overcomes the following difficulty arising in actual networks: data packets sent by users arrive at a link at different times, so the total traffic through the link is not known in practice. This difficulty is obviated by applying stochastic methods. They can do without the exact value of total traffic, managing only with its estimate, which can be obtained using the traffic of a single user. The idea of using the stochastic projected subgradient method for solution of this problem was proposed in [2].

1.2 Content of This Paper

This paper is organized as follows. The formulation of the problem and the construction of its dual are described in Section 2. Additionally, we state all necessary assumptions for the primal problem. In Section 3, the problem is solved by applying Nesterov’s fast gradient method [9], whose complexity bound is found to be \(O\left( {\tfrac{1}{{\sqrt \varepsilon }}} \right)\). In Section 4, this problem is solved using the stochastic projected subgradient method with \(O\left( {\tfrac{1}{{{{\varepsilon }^{2}}}}} \right)\) complexity bounds.

In Section 5, the problem is solved by applying the ellipsoid method, which is well suited for low-dimensional problems, and an algorithm for constructing the accuracy certificate for this method is described. We present complexity bounds on the order of \(O\left( {{{m}^{2}}\ln\tfrac{1}{\varepsilon }} \right)\), where \(m\) is the number of links in the network. A regularization technique for recovering the solution of the primal problem from the solution of the dual one if the method is not primal-dual is described in Section 6. The regularized problem is solved using the random gradient extrapolation method in Section 7. Its complexity bounds are presented, which are on the order of \(O\left( {\tfrac{1}{{\sqrt \varepsilon }}\ln\tfrac{1}{\varepsilon }} \right)\), where the logarithmic factor appears due to the regularization of the dual problem.

Numerical experiments supporting the theoretical results obtained in the preceding sections are presented in Section 8.

Additionally, for each algorithm, we describe its distributed computation in the context of the problem under consideration.

2 FORMULATION OF THE PROBLEM

Consider a computer network with \(m\) links and \(n\) users (or nodes), see Fig. 1.

Fig. 1.
figure 1

Example of a computer network with \(m = 6\) and \(n = 3\).

Full size image

The users exchange data packets through a fixed set of links. The network structure is specified by the routing matrix \(C = (C_{i}^{j}) \in {{{\mathbf{R}}}^{{m \times n}}}\). The matrix columns \({{{\mathbf{C}}}_{i}} \ne 0\), \(i = 1, \ldots ,n\), are \(m\)-dimensional Boolean vectors such that \(C_{i}^{j} = 1\) if node \(i\) uses link \(j\) and \(C_{i}^{j} = 0\) otherwise. The link capacities are described by a vector \({\mathbf{b}} \in {{{\mathbf{R}}}^{m}}\) with strictly positive components.

The users estimate the performance of the network with the help of utility functions \({{u}_{k}}({{x}_{k}})\), \(k = 1, \ldots ,n\), where \({{x}_{k}} \in {{{\mathbf{R}}}_{ + }}\) is the rate of data transmission from the \(k\)th user. As an optimality criterion for the system, we use the sum of the utility functions for all users [1].

The problem of maximizing the aggregate utility of the network under constraints imposed on the link capacities is stated as follows:

$$\mathop {\max}\limits_{\left\{ {C{\mathbf{x}} = \sum\limits_{k = 1}^n \,{{{\mathbf{C}}}_{k}}{{x}_{k}}} \right\} \leqslant {\mathbf{b}}} \left\{ {U({\mathbf{x}}) = \sum\limits_{k = 1}^n \,{{u}_{k}}({{x}_{k}})} \right\},$$
(1)

where \({\mathbf{x}} = ({{x}_{1}}, \ldots ,{{x}_{n}}) \in \mathbb{R}_{ + }^{n}\). The solution of this problem is an optimal resource allocation \({\mathbf{x}}\text{*}\).

Consider the standard transition to the dual problem for (1). Given a vector of dual multipliers \(\boldsymbol{\lambda} = ({{\lambda }_{1}}, \ldots ,{{\lambda }_{m}}) \in \mathbb{R}_{ + }^{m}\), which can be interpreted as the price vector of the links, the dual objective function is defined as

$$\varphi (\boldsymbol{\lambda} ) = \mathop {\max}\limits_{{\mathbf{x}} \in {\mathbf{R}}_{ + }^{n}} \left\{ {\sum\limits_{k = 1}^n \,{{u}_{k}}({{x}_{k}}) + \left\langle {\boldsymbol{\lambda} ,{\mathbf{b}} - \sum\limits_{k = 1}^n \,{{{\mathbf{C}}}_{k}}{{x}_{k}}} \right\rangle } \right\} = \left\langle {\boldsymbol{\lambda} ,{\mathbf{b}}} \right\rangle + \sum\limits_{k = 1}^n \,\left( {{{u}_{k}}({{x}_{k}}(\boldsymbol{\lambda} )) - \left\langle {\boldsymbol{\lambda} ,{{{\mathbf{C}}}_{k}}{{x}_{k}}(\boldsymbol{\lambda} )} \right\rangle } \right),$$
(2)

here, the users choose optimal data transmission rates \({{x}_{k}}\) by solving the optimization problem

$${{x}_{k}}(\boldsymbol{\lambda} ) = \mathop {\arg\,\max}\limits_{{{x}_{k}} \in {{{\mathbf{R}}}_{ + }}} \,\left\{ {{{u}_{k}}({{x}_{k}}) - {{x}_{k}}\left\langle {\boldsymbol{\lambda} ,{{{\mathbf{C}}}_{k}}} \right\rangle } \right\}.$$
(3)

Let \({\mathbf{x}}(\boldsymbol{\lambda} )\) denote the vector with components \({{x}_{k}}(\boldsymbol{\lambda} )\). Then, to find optimal prices \(\boldsymbol{\lambda} \text{*}\), we need to solve the problem

$$\mathop {\min}\limits_{\boldsymbol{\lambda} \in {\mathbf{R}}_{ + }^{m}} \varphi (\boldsymbol{\lambda} ).$$
(4)

Assume that the Slater condition is satisfied for the primal problem. Then, by virtue of strong duality, both primal and dual problems have solutions. By using the Slater condition, it is possible to compactify the solution of the dual problem. Assume that the solution of the dual problem satisfies the estimate

$${{\left\| {\lambda \text{*}} \right\|}_{2}} \leqslant R.$$

Here, \(R\) has no effect on the performance of the considered algorithms, but is only involved in their convergence rate estimates.

The basic idea of this paper is to apply various optimization methods for solving dual problem (4) with the addition of primal-dual analysis of these methods, which makes it possible to recover the solution of primal problem (1). In this sense, we develop the approach addressed in our previous works [10–21]. The basic difference is that we consider inequality constraints and analyze stochastic algorithms in the terms of estimates with high probability, rather than on average.

2.1 Strongly Concave Utility Functions

In some sections, we assume that the utility functions \({{u}_{k}}({{x}_{k}})\), \(k = 1, \ldots ,n\), are strongly concave with a constant \(\mu \). In this subsection, we describe the properties of the dual problem under this assumption.

Proposition 1 (Demyanov–Danskin–Rubinov theorem, see [22, 23]). Suppose that, for any \(\boldsymbol{\lambda} \in {{\mathbb{R}}_{ + }}\), it holds that \(\varphi (\boldsymbol{\lambda} ) = \mathop {\max}\limits_{{\mathbf{x}} \in X} F({\mathbf{x}},\boldsymbol{\lambda} )\), where \(F({\mathbf{x}},\boldsymbol{\lambda} )\) is a convex and smooth function of \(\boldsymbol{\lambda} \) with a maximum reached at the only point \(x(\boldsymbol{\lambda} )\). Then \(\nabla \varphi (\boldsymbol{\lambda} ) = {{\nabla }_{\boldsymbol{\lambda} }}F(x(\boldsymbol{\lambda} ),\boldsymbol{\lambda} )\).

Proposition 2 (see [24]). Suppose that the functions \({{u}_{k}}({{x}_{k}})\) are \(\mu \)-strongly concave for all \(k = 1, \ldots ,n\). Then function (2), where \({{x}_{k}}(\boldsymbol{\lambda} ),\) \(k = 1, \ldots ,n\), solve problem (3), is \(n{{m}^{2}}{\text{/}}\mu \)-smooth, i.e., the gradient of the function \(\varphi (\boldsymbol{\lambda} )\) satisfies the Lipschitz condition with constant \(L = n{{m}^{2}}{\text{/}}\mu \):

$$\mathop {\left| {\left| {\nabla \varphi ({{\boldsymbol{\lambda} }^{2}}) - \nabla \varphi ({{\boldsymbol{\lambda} }^{1}})} \right|} \right|}\nolimits_2 \leqslant L{{\left\| {{{\boldsymbol{\lambda} }^{2}} - {{\boldsymbol{\lambda} }^{1}}} \right\|}_{2}}.$$

The proof of the proposition can be found in the Appendix.

2.2 Concave Utility Functions

Now we assume that the utility functions \({{u}_{k}}({{x}_{k}})\), \(k = 1, \ldots ,n\), are concave, but not strongly concave. Then the dual problem is not smooth. In this subsection, we describe some properties of subgradients of the dual problem under these assumptions.

The subgradient of dual problem (4) is defined as

$$\nabla \varphi (\boldsymbol{\lambda} ) = {\mathbf{b}} - C{\mathbf{x}}.$$

Since \({\mathbf{x}}\) is a bounded rate of data transmission and the vector \({\mathbf{b}}\) is also bounded, we see that the subgradients of the dual problem are bounded. Thus, there exists a positive constant \(M\) such that

$${{\left\| {\nabla \varphi (\boldsymbol{\lambda} )} \right\|}_{2}} \leqslant M.$$
(5)

As a rough estimate from above for the constant \(M\) in (5), we can use \(O(n\sqrt m )\). The multiplier \(n\) appears because there are \(n\) terms and \(\sqrt m \) is used as an estimate for the dependence of the \(2\)-norm on the vector dimension \(m\).

3 FAST GRADIENT METHOD

In this section, we assume that the utility functions \({{u}_{k}}({{x}_{k}})\), \(k = 1, \ldots ,n\), are strongly concave with a constant \(\mu \); therefore, the dual problem is smooth.

Dual problem (4) is solved by applying Nesterov’s fast gradient method (FGM) in the following version (PDFGM method, see Algorithm 1).

Algorithm 1.  Primal-Dual Fast Gradient Method (PDFGM)

Input: \({{u}_{k}}({\mathbf{x}}),\) \(k = 1, \ldots ,n\), are strongly concave utility functions for each user; \({{\boldsymbol{\lambda} }^{0}}\) is the initial price vector, \({{\alpha }_{t}}: = \tfrac{{t + 1}}{2}\), \({{A}_{{ - 1}}}: = 0\), \({{A}_{t}}: = {{A}_{{t - 1}}} + {{\alpha }_{t}} = \tfrac{{(t + 1)(t + 2)}}{4}\), and \({{\tau }_{t}}: = \tfrac{{{{\alpha }_{{t + 1}}}}}{{{{A}_{{t + 1}}}}} = \tfrac{2}{{t + 3}}\), \(t = 0,1, \ldots ,N - 1\).

1: for \(t = 0,1, \ldots ,N - 1\)

2:  Compute \(\varphi ({{\boldsymbol{\lambda} }^{t}})\), \(\nabla \varphi ({{\boldsymbol{\lambda} }^{t}})\)

3:  \({{{\mathbf{y}}}^{t}}: = \mathop {\left[ {{{\boldsymbol{\lambda} }^{t}} - \tfrac{1}{L}\left( {{\mathbf{b}} - \sum\nolimits_{k = 1}^n {{{{\mathbf{C}}}_{k}}{{x}_{k}}({{\boldsymbol{\lambda} }^{t}})} } \right)} \right]}\nolimits_ + \)

4:  \({{{\mathbf{z}}}^{t}}: = \mathop {\left[ {{{\boldsymbol{\lambda} }^{0}} - \tfrac{1}{L}\sum\nolimits_{j = 0}^t {{{\alpha }_{j}}} \left( {{\mathbf{b}} - \sum\nolimits_{k = 1}^n {{{{\mathbf{C}}}_{k}}{{x}_{k}}({{\boldsymbol{\lambda} }^{j}})} } \right)} \right]}\nolimits_ + \)

5:  \({{\boldsymbol{\lambda} }^{{t + 1}}}: = {{\tau }_{t}}{{{\mathbf{z}}}^{t}} + (1 - {{\tau }_{t}}){{{\mathbf{y}}}^{t}}\)

6:  \({{{\mathbf{\hat {x}}}}^{{t + 1}}}: = \tfrac{1}{{{{A}_{{t + 1}}}}}\sum\nolimits_{j = 0}^{t + 1} {{{\alpha }_{j}}{\mathbf{x}}({{\boldsymbol{\lambda} }^{{\mathbf{j}}}})} \)

7: end for

8: return \({{\boldsymbol{\lambda} }^{N}}\), \({{{\mathbf{\hat {x}}}}^{N}}\)

3.1 Distributed Method

The problem under consideration can also be solved using the distributed version of FGM, which means that each link can compute an optimal data transmission rate only relying on the reactions of the users that employ this link without interacting with the other links.

The process occurring at the \(t\)th iteration for link \(j\) can be described as follows.

1. Given information received from the users after the preceding iteration with index \(t - 1\) (vector \({{{\mathbf{x}}}^{t}} = {\mathbf{x}}({{\boldsymbol{\lambda} }^{t}})\)), the link \(j\) computes

$$y_{j}^{t} = \mathop {\left[ {\lambda _{j}^{t} - \frac{1}{L}\left( {{{b}_{j}} - \sum\limits_{k = 1}^n \,C_{k}^{j}x_{k}^{t}} \right)} \right]}\nolimits_ + .$$

Here, \(C_{k}^{j} \ne 0\) only for users employing the link \(j\). Therefore, to compute this step, the link needs only information from the users employing this link.

2. Similarly, the link \(j\) computes

$$z_{j}^{t} = \mathop {\left[ {\lambda _{j}^{0} - \frac{{{{\alpha }_{j}}}}{L}\left( {{{b}_{j}} - \sum\limits_{k = 1}^n \,C_{k}^{j}x_{k}^{t}} \right)} \right]}\nolimits_ + .$$

3. After obtaining values at two preceding steps, link \(j\) computes the price for the next iteration \(t + 1\):

$$\lambda _{j}^{{t + 1}} = {{\tau }_{t}}z_{j}^{t} + (1 - {{\tau }_{t}})y_{j}^{t}$$

and sends out this information to all users connected to it.

4. The users compute the optimal data transmission rates \({{{\mathbf{\hat {x}}}}^{{t + 1}}}\); specifically, for user \(k\), we obtain

$${{x}_{k}}({{\boldsymbol{\lambda} }^{{t + 1}}}) = \mathop {\arg\,\max}\limits_{{{x}_{k}} \in {{{\mathbf{R}}}_{ + }}} \,\left( {{{u}_{k}}({{x}_{k}}) - {{x}_{k}}\sum\limits_{j = 1}^m \,\lambda _{j}^{{t + 1}}C_{k}^{j}} \right),$$

where, by the definition of the matrix \(C\), the user needs only data from the links it employs. Next, the user computes the optimal rate

$$\hat {x}_{k}^{{t + 1}} = \frac{{{{A}_{t}}\hat {x}_{k}^{t} + x_{k}^{{t + 1}}}}{{{{A}_{{t + 1}}}}}.$$

Remark 1. A disadvantage of this algorithm is that each link has to know the reactions of all users that employ it at every iteration step. Unfortunately, in actual networks, users do not transmit data simultaneously, so it is rather difficult to collect this information for the link. However, if complete information on the users is available, the link can establish an equilibrium price more quickly.

3.2 Estimation of the Convergence Rate of FGM

Before proving the convergence of FGM for the problem under consideration, we state the key lemma necessary for estimating the residuals in the constraints and the duality gap after running PDFGM.

Lemma 1. Suppose that Algorithm 1 starts at an initial point \({{\boldsymbol{\lambda} }^{0}}\) lying in the Euclidean ball of radius \(R\) centered at the origin. Then, after performing \(N\) iterations of Algorithm 1, it holds that

$${{A}_{N}}\varphi ({{{\mathbf{y}}}^{N}}) - {{A}_{N}}U({{{\mathbf{\hat {x}}}}^{N}}) + 2\hat {R}{{A}_{N}}\mathop {\left\| {\mathop {(C{{{{\mathbf{\hat {x}}}}}^{N}} - {\mathbf{b}})}\nolimits_ + } \right\|}\nolimits_2 \leqslant \tfrac{{37L{{{\hat {R}}}^{2}}}}{9},$$
(6)

where \({{{\mathbf{\hat {x}}}}^{N}} = \tfrac{1}{{{{A}_{N}}}}\sum\nolimits_{t = 0}^{N - 1} {{{\alpha }_{t}}{\mathbf{x}}({{\boldsymbol{\lambda} }^{t}})} \) and \(\hat {R} = 3R\).

The proof of the lemma can be found in the Appendix.

Now we formulate a theorem on the convergence rate estimate for Algorithm 1.

Theorem 1. Suppose that Algorithm 1 starts at an initial point \({{\boldsymbol{\lambda} }^{0}}\) lying in the Euclidean ball of radius \(R\) centered at the origin. Then, after performing

$$N = \left\lceil {\frac{{2\hat {R}}}{3}\sqrt {\frac{{37L}}{\varepsilon }} } \right\rceil $$

iterations of Algorithm 1, it holds that

$$U({\mathbf{x}}\text{*}) - U({{{\mathbf{\hat {x}}}}^{N}}) \leqslant \varepsilon ,\quad \mathop {\left\| {\mathop {(C{{{{\mathbf{\hat {x}}}}}^{N}} - {\mathbf{b}})}\nolimits_ + } \right\|}\nolimits_2 \leqslant \frac{\varepsilon }{{\hat {R}}},$$

where \({{{\mathbf{\hat {x}}}}^{N}} = \tfrac{1}{{{{A}_{N}}}}\sum\nolimits_{t = 0}^{N - 1} {{{\alpha }_{t}}{\mathbf{x}}({{\boldsymbol{\lambda} }^{t}})} \), \({\mathbf{x}}\text{*}\) is an optimal solution of problem (1), and \(\hat {R} = 3R\).

Proof. Let \(\operatorname{Opt} [P]\) denote the optimal value in the original primal problem (1), and let \(\operatorname{Opt} [D]\) denote the optimal value in the dual problem (4). By the weak duality, we have

$$\operatorname{Opt} [D] \geqslant \operatorname{Opt} [P].$$

Moreover, for all \({\mathbf{x}} \in \mathbb{R}_{ + }^{n}\), the optimal solution \(\boldsymbol{\lambda} \text{*}\) of dual problem (4) satisfies

$$\operatorname{Opt} [P] \geqslant U({\mathbf{x}}) - \left\langle {\boldsymbol{\lambda} \text{*},\mathop {\left( {\sum\limits_{k = 1}^n \,{{{\mathbf{C}}}_{k}}{{x}_{k}} - {\mathbf{b}}} \right)}\nolimits_ + } \right\rangle \geqslant U({\mathbf{x}}) - \hat {R}\mathop {\left\| {\mathop {(C{\mathbf{x}} - {\mathbf{b}})}\nolimits_ + } \right\|}\nolimits_2 .$$
(7)

Then

$$\begin{gathered} \varphi ({{{\mathbf{y}}}^{N}}) - U({{{{\mathbf{\hat {x}}}}}^{N}}) = \varphi ({{{\mathbf{y}}}^{N}}) - U({{{{\mathbf{\hat {x}}}}}^{N}}) + \operatorname{Opt} \text{[}P] - \operatorname{Opt} [P] + \operatorname{Opt} [D] - \operatorname{Opt} [D] = \underbrace {(\operatorname{Opt} [D] - \operatorname{Opt} [P])}_{ \geqslant 0} \\ \, + (\operatorname{Opt} [P] - U({{{{\mathbf{\hat {x}}}}}^{N}})) + \underbrace {(\varphi ({{{\mathbf{y}}}^{N}}) - \operatorname{Opt} [D])}_{ \geqslant 0}\;\mathop \geqslant \limits^{(7)} \; - {\kern 1pt} \left\langle {\boldsymbol{\lambda} \text{*},{{{({\mathbf{b}} - C{{{{\mathbf{\hat {x}}}}}^{N}})}}_{ + }}} \right\rangle \geqslant - \hat {R}{\kern 1pt} {{\left\| {{{{(C{{{{\mathbf{\hat {x}}}}}^{N}} - {\mathbf{b}})}}_{ + }}} \right\|}_{2}}. \\ \end{gathered} $$

Substituting the last inequality into (6) yields the estimate

$$\hat {R}{{\left\| {{{{(C{{{{\mathbf{\hat {x}}}}}^{N}} - {\mathbf{b}})}}_{ + }}} \right\|}_{2}} \leqslant \frac{{37L{{{\hat {R}}}^{2}}}}{{9{{A}_{N}}}}.$$

Consequently, \(\varphi ({{{\mathbf{y}}}^{N}}) - U({{{\mathbf{\hat {x}}}}^{N}}) \geqslant - \tfrac{{37L{{{\hat {R}}}^{2}}}}{{9{{A}_{N}}}}\). On the other hand, it follows from (6) that \(\varphi ({{{\mathbf{y}}}^{N}}) - U({{{\mathbf{\hat {x}}}}^{N}}) \leqslant \tfrac{{37L{{{\hat {R}}}^{2}}}}{{9{{A}_{N}}}}\). Therefore,

$$\left| {\varphi ({{{\mathbf{y}}}^{N}}) - U({{{{\mathbf{\hat {x}}}}}^{N}})} \right| \leqslant \frac{{37L{{{\hat {R}}}^{2}}}}{{9{{A}_{N}}}}.$$

Since \(\varphi ({{{\mathbf{y}}}^{N}}) \geqslant \operatorname{Opt} [D] = \varphi ({\mathbf{y}}\text{*}) \geqslant \operatorname{Opt} [P] = U({\mathbf{x}}\text{*})\), we have

$$U({\mathbf{x}}\text{*}) - U({{{\mathbf{\hat {x}}}}^{N}}) \leqslant \frac{{37L{{{\hat {R}}}^{2}}}}{{9{{A}_{N}}}} = \frac{{148L{{{\hat {R}}}^{2}}}}{{9(N + 1)(N + 2)}} \leqslant \frac{{148L{{{\hat {R}}}^{2}}}}{{9{{N}^{2}}}} \leqslant \varepsilon .$$

Expressing \(N\) from the last inequality gives the estimate from the condition of the theorem.

4 STOCHASTIC PROJECTED SUBGRADIENT METHOD

Consider the original problem (1), now assuming that the utility functions \({{u}_{k}}({{x}_{k}})\), \(k = 1, \ldots ,n\), are concave, but not strongly concave. In this case, dual problem (4) becomes nonsmooth. Accordingly, for its solution, we propose the stochastic projected subgradient method. For the first time, the idea of using this method for solving the given problem was proposed in [2].

Consider the probability space \(\left( {\Omega ,\mathcal{F},\mathbb{P}} \right)\). Suppose that a sequence of independent random variables \(\{ {{\xi }^{t}}\} _{{t = 0}}^{\infty }\) uniformly distributed on \(\{ 1, \ldots ,n\} \) is defined on \(\left( {\Omega ,\mathcal{F},\mathbb{P}} \right)\), i.e.,

$$\mathbb{P}({{\xi }^{t}} = i) = \frac{1}{n},\quad i \in \{ 1, \ldots ,n\} .$$

If there is an oracle producing the stochastic subgradient of the dual function \(\nabla \varphi (\boldsymbol{\lambda} ,\xi )\), i.e.,

$$\nabla \varphi (\boldsymbol{\lambda} ,\xi ) = {\mathbf{b}} - n{{C}_{\xi }}{{x}_{\xi }}(\boldsymbol{\lambda} ),$$

then

$$\mathbb{E}{\kern 1pt} [{\mathbf{b}} - n{{C}_{{{{\xi }_{t}}}}}{{x}_{{{{\xi }_{t}}}}}({{\boldsymbol{\lambda} }^{t}})\,{\text{|}}\,{{\xi }^{t}}] = {\mathbf{b}} - \sum\limits_{k = 1}^n \,{{{\mathbf{C}}}_{k}}{{x}_{k}}({{\boldsymbol{\lambda} }^{t}}) = \nabla \varphi ({{\boldsymbol{\lambda} }^{t}})$$

Algorithm 2. Primal-Dual Stochastic Projected Subgradient Method (PDSPSGM), Version 1

Input: \({{u}_{k}}({\mathbf{x}}),\) \(k = 1, \ldots ,n\), are concave utility functions for each user, and \(\beta \) is the step of the method.

1: \({{\boldsymbol{\lambda} }^{0}}: = 0\)

2: for \(t = 1, \ldots ,N - 1\)

3:  Compute \(\nabla \varphi ({{\boldsymbol{\lambda} }^{{t - 1}}},\xi )\)

4:  \({{\boldsymbol{\lambda} }^{t}}: = {{[{{\boldsymbol{\lambda} }^{{t - 1}}} - \beta ({\mathbf{b}} - n{{C}_{{{{\xi }^{{t - 1}}}}}}{{x}_{{{{\xi }^{{t - 1}}}}}}({{\boldsymbol{\lambda} }^{{t - 1}}}))]}_{ + }}\)

5:  \({{{\mathbf{\hat {x}}}}^{{t + 1}}}: = \tfrac{1}{{t + 1}}\sum\nolimits_{j = 0}^t {{\mathbf{x}}({{\boldsymbol{\lambda} }^{j}})} \)

6:  \({{\hat {\boldsymbol{\lambda} }}^{{t + 1}}}: = \tfrac{1}{{t + 1}}\sum\nolimits_{j = 0}^t {{{\boldsymbol{\lambda} }^{j}}} \)

7: end for

8: return \({{\hat {\boldsymbol{\lambda} }}^{N}},\;{{{\mathbf{\hat {x}}}}^{N}}\)

Therefore, the stochastic subgradient is an unbiased estimator of the subgradient.

An optimal solution of problem (2) is sought using PDSPSGM. We describe two versions of this method (see Algorithms 2 and 3). Algorithm 2 relies on a complete model of reconstructing the vector \({\mathbf{x}}(\boldsymbol{\lambda} )\) at every iteration. However, the computation of \({\mathbf{x}}(\boldsymbol{\lambda} )\) is nearly equivalent in complexity to the computation of a complete subgradient of \(\varphi (\boldsymbol{\lambda} )\). Therefore, the basic algorithm is Algorithm 3, in which the vector \({\mathbf{x}}(\boldsymbol{\lambda} )\) is reconstructed using an incomplete stochastic model, which means that only one component of the vector \({\mathbf{x}}(\boldsymbol{\lambda} )\) is updated at every iteration step, while the others remain unchanged. In the proof of the convergence theorem, we first establish the convergence estimate for Algorithm 2 and then show that the approximate solution of the primal problem produced by Algorithm 3 is close in accuracy to the solution obtained using Algorithm 2.

Algorithm 3.  Primal-Dual Stochastic Projected Subgradient Method (PDSPSGM), Version 2

Input: \({{u}_{k}}({\mathbf{x}}),\) \(k = 1, \ldots ,n\), are concave utility functions for each user, and \(\beta \) is the step of the method.

1: \({{\boldsymbol{\lambda} }^{0}}: = 0\)

2: for \(t = 1, \ldots ,N - 1\)

3:  Compute \(\nabla \varphi ({{\boldsymbol{\lambda} }^{{t - 1}}},\xi )\)

4:  \({{\boldsymbol{\lambda} }^{t}}: = {{[{{\boldsymbol{\lambda} }^{{t - 1}}} - \beta ({\mathbf{b}} - n{{C}_{{{{\xi }^{{t - 1}}}}}}{{x}_{{{{\xi }^{{t - 1}}}}}}({{\boldsymbol{\lambda} }^{{t - 1}}}))]}_{ + }}\)

5:  \({\mathbf{\tilde {x}}}_{{{{\xi }^{t}}}}^{{t + 1}}: = \tfrac{t}{{t + 1}}{\mathbf{\tilde {x}}}_{{{{\xi }^{t}}}}^{t} + \tfrac{1}{{t + 1}}n{{x}_{{{{\xi }^{t}}}}}({{\lambda }^{t}})\), \({\mathbf{\tilde {x}}}_{j}^{{t + 1}}: = {\mathbf{\tilde {x}}}_{j}^{t}\) for \(j \ne {{\xi }^{t}}\)

6:  \({{\hat {\boldsymbol{\lambda} }}^{{t + 1}}}: = \tfrac{1}{{t + 1}}\sum\nolimits_{j = 0}^t {{{\boldsymbol{\lambda} }^{j}}} \)

7: end for

8: return \({{\hat {\boldsymbol{\lambda} }}^{N}},\;{{{\mathbf{\tilde {x}}}}^{N}}\)

4.1 Distributed Method

Let us describe how the distributed version of the stochastic projected subgradient method can be applied for solving the problem under consideration.

The process occurring at the \(t\)th iteration for link \(j\) is as follows:

1. Given the information received from the links after the preceding iteration with index \(t - 1\), the random user \({{\xi }^{t}}\) transmits data at the optimal rate

$${{x}_{{{{\xi }^{t}}}}}({{\boldsymbol{\lambda} }^{{t + 1}}}) = \mathop {\arg\,\max}\limits_{{{x}_{{{{\xi }^{t}}}}} \in {{{\mathbf{R}}}_{ + }}} \,\left( {{{u}_{{{{\xi }^{t}}}}}({{x}_{{{{\xi }^{t}}}}}) - {{x}_{{{{\xi }^{t}}}}}\sum\limits_{j = 1}^m \,\lambda _{j}^{{t + 1}}C_{{{{\xi }^{t}}}}^{j}} \right),$$

where, by the definition of the matrix \(C,\) the information required for the user is only from the links used by the user.

2. The link \(j\) computes the price for the next iteration based on the reaction of this user:

$$\lambda _{j}^{{t + 1}} = {{[\lambda _{j}^{t} - \beta ({{b}_{j}} - nC_{{{{\xi }^{t}}}}^{j}x_{{{{\xi }^{t}}}}^{t})]}_{ + }}.$$

Here, \(C_{{{{\xi }^{t}}}}^{j} \ne 0\) only for users employing link \(j.\) Therefore, the price changes only for actual links of the user transmitting data.

Remark 2. The main advantage of this method is that the link changes the price relying only on the reactions of a single user, which makes the problem formulation much closer to the situation occurring in actual networks, where users do not transmit data simultaneously.

4.2 Estimation of the Convergence Rate of the Stochastic Projected Subgradient Method

Before proving the main theorem on convergence rate estimates for the proposed methods, we state the necessary assumptions for the problem under study. Assume that there exists a positive constant \(M = O(n\sqrt m )\) such that

$${{\left\| {\nabla \varphi (\lambda ,\xi )} \right\|}_{2}} \leqslant M.$$
(8)

This assumption holds, since the data transmission rate \({\mathbf{x}}\) is bounded and the capacity vector \({\mathbf{b}}\) is bounded as well in view of the physical considerations. Therefore, by its definition, the stochastic subgradient is also bounded.

Additionally, we assume that

$$\mathbb{E}\left[ {\exp\left( {\frac{{\mathop {\left\| {\nabla \varphi (\lambda ,\xi ) - \nabla \varphi (\lambda )} \right\|}\nolimits_2^2 }}{{{{\sigma }^{2}}}}} \right)} \right] \leqslant \exp(1),$$

where \(\sigma \) is a positive numerical constant and the order of dependence on \(n\) and \(m\) is the same as for \(M\).

To estimate the convergence rate of Algorithm 3, it is necessary to assume that \({{u}_{k}}({{x}_{k}}),k = 1, \ldots ,n\), are Lipschitz continuous functions with constant \({{M}_{{{{u}_{k}}}}}\). Then \(U({\mathbf{x}})\) is a Lipschitz continuous function with a constant \({{M}_{U}}\):

$$\forall {\mathbf{x}},{\mathbf{y}}\quad \left| {U({\mathbf{x}}) - U({\mathbf{y}})} \right| \leqslant {{M}_{U}}{{\left\| {{\mathbf{x}} - {\mathbf{y}}} \right\|}_{2}},$$

where \({{M}_{U}} = O(\sqrt n )\). It may happen that \({{u}_{k}}({{x}_{k}})\) is a Lipschitz continuous function everywhere, except, for instance, the point \(0\). An example of such a function is \({{u}_{k}}({{x}_{k}}) = \ln{{x}_{k}}\), which is one of the most widespread utility functions. However, by the specific features of the problem, there always exist \(\bar {\varepsilon } > 0\) and \(\underline \varepsilon > 0\) such   that \(x_{k}^{*} \geqslant \underline \varepsilon \) and \(x_{k}^{*} \leqslant \bar {\varepsilon }\). Then the problem can be solved on the compact set \(Q = \left\{ {{\mathbf{x}}:\underline \varepsilon \leqslant {{x}_{k}} \leqslant \bar {\varepsilon },\;k = 1, \ldots ,n} \right\}\), and the considered function \({{u}_{k}}({{x}_{k}}) = \ln{{x}_{k}}\) becomes Lipschitz continuous on \(Q\). In the general case, a concave utility function \(u(x)\) is Lipschitz continuous on a compact set lying in the relative interior of the domain of \(u(x)\).

Suppose that

$$\mathbb{E}\left[ {\exp\left( {\frac{{\mathop {\left\| {{\mathbf{x}}(\boldsymbol{\lambda} \lambda ,\xi ) - {\mathbf{x}}(\boldsymbol{\lambda} )} \right\|}\nolimits_2^2 }}{{\sigma _{x}^{2}}}} \right)} \right] \leqslant \exp(1),$$

where \({{\sigma }_{x}} = O(\sqrt n )\) is a positive numerical constant and

$${\mathbf{x}}(\boldsymbol{\lambda} ,\xi ) = {{(0, \ldots ,n{{x}_{\xi }}(\boldsymbol{\lambda} ), \ldots ,0)}^{{\text{T}}}}.$$

Below is the key lemma necessary for obtaining convergence rate estimates for the residual in the constraints and the duality gap after running PDSPSGM.

Lemma 2. Suppose that Algorithm 3 starts at the initial point \({{\boldsymbol{\lambda} }^{0}} = 0\) with a step \(\beta \). Then, after performing \(N\) iterations of Algorithm 3, with probability 1 – 4\(\delta \),

$$\begin{gathered} \varphi ({{{\hat {\boldsymbol{\lambda} }}}^{N}}) - U({{{{\mathbf{\tilde {x}}}}}^{N}}) + 2R\mathop {\left\| {{{{[C{{{{\mathbf{\tilde {x}}}}}^{N}} - {\mathbf{b}}]}}_{ + }}} \right\|}\nolimits_2 \leqslant {{C}_{1}}\frac{{{{R}^{2}}\sigma \sqrt {g(N)J} }}{{\sqrt N }} + \frac{{2{{R}^{2}}}}{{\beta N}} + \frac{{\beta {{M}^{2}}}}{2} \\ \, + \frac{{\sqrt 2 \left( {1 + \sqrt {3\ln\tfrac{1}{\delta }} } \right)}}{{\sqrt N }}\left( {{{M}_{U}}{{\sigma }_{x}} + 2R\left( {\sigma + {{\sigma }_{x}}\sqrt {{{\lambda }_{{{\text{max}}}}}({{C}^{{\text{T}}}}C)} } \right)} \right), \\ \end{gathered} $$

where

$${{\hat {\boldsymbol{\lambda} }}^{N}} = \frac{1}{N}\sum\limits_{t = 0}^{N - 1} \,{{\boldsymbol{\lambda} }^{t}},$$
$${{{\mathbf{\tilde {x}}}}^{N}} = \frac{1}{N}\sum\limits_{t = 0}^{N - 1} \,{\mathbf{x}}({{\boldsymbol{\lambda} }^{t}},{{\xi }^{t}}),$$

\({{C}_{1}}\) is a positive numerical constant, \(g(N) = \ln\left( {\tfrac{N}{\delta }} \right) + \ln\ln\left( {\tfrac{F}{f}} \right)\),

$$F = 2{{\sigma }^{2}}N{{(2\beta )}^{N}}\left( {2{{R}^{2}} + 2{{\beta }^{2}}{{M}^{2}} + \beta {{R}^{2}} + 24\ln\frac{N}{\delta }\beta {{\sigma }^{2}}N} \right),$$

\(f = {{\sigma }^{2}}{{R}^{2}}\),

$$J = \max\left\{ {1,\quad \frac{1}{R}\beta {{C}_{1}}\sqrt {{{\sigma }^{2}}g(N)} + \sqrt {\frac{1}{{{{R}^{2}}}}{{\beta }^{2}}C_{1}^{2}{{\sigma }^{2}}g(N) + \frac{{2{{R}^{2}} + 2{{\beta }^{2}}{{M}^{2}}}}{{{{R}^{2}}}}} } \right\},$$

and \(R\) is determined by the condition \({{\left\| {\boldsymbol{\lambda} \text{*}} \right\|}_{2}} \leqslant R\).

The proof of the lemma can be found in the Appendix.

Now we formulate a theorem on the convergence rate estimate for Algorithm 3.

Theorem 2. Suppose that Algorithm 3 starts at the initial point \({{\boldsymbol{\lambda} }^{0}} = 0\) with step \(\beta = \tfrac{R}{{M\sqrt N }}\). Define

$$A = \sqrt 2 \left( {1 + \sqrt {3\ln\frac{1}{\delta }} } \right)\left( {{{M}_{U}}{{\sigma }_{x}} + 2R\left( {\sigma + {{\sigma }_{x}}\sqrt {{{\lambda }_{{{\text{max}}}}}({{C}^{{\text{T}}}}C)} } \right)} \right) + 2.5RM.$$

Then, after performing

$$N = O\left( {\left\lceil {\frac{{{{A}^{2}}}}{{{{\varepsilon }^{2}}}}\ln\left( {\frac{{MR}}{{\varepsilon \delta }}} \right)} \right\rceil } \right)$$

iterations of Algorithm 3, with probability 1 – 4\(\delta \),

$$U({\mathbf{x}}\text{*}) - U({{{\mathbf{\tilde {x}}}}^{N}}) \leqslant \varepsilon ,\quad \mathop {\left\| {{{{(C{{{{\mathbf{\tilde {x}}}}}^{N}} - {\mathbf{b}})}}_{ + }}} \right\|}\nolimits_2 \leqslant \frac{\varepsilon }{R},$$

where \({{{\mathbf{\tilde {x}}}}^{N}} = \tfrac{1}{N}\sum\nolimits_{t = 0}^{N - 1} {{\mathbf{x}}({{\boldsymbol{\lambda} }^{t}},{{\xi }^{t}})} \) and \({\mathbf{x}}\text{*}\) is an optimal solution of problem (1).

Proof. The beginning of the proof is the same as for Theorem 1, but we use the estimate from Lemma 2. As a result, for the step \(\beta = \tfrac{R}{{M\sqrt N }}\), we obtain

$$\frac{{\sqrt 2 \left( {1 + \sqrt {3\ln\tfrac{1}{\delta }} } \right)}}{{\sqrt N }}\left( {{{M}_{U}}{{\sigma }_{x}} + 2R\left( {\sigma + {{\sigma }_{x}}\sqrt {{{\lambda }_{{{\text{max}}}}}({{C}^{{\text{T}}}}C)} } \right)} \right) + \frac{{5RM}}{{2\sqrt N }} + {{C}_{1}}\frac{{{{R}^{2}}\sigma \sqrt {g(N)J} }}{{\sqrt N }},$$

moreover, up to constants, \(g(N) \approx \ln\left( {\tfrac{N}{\delta }} \right)\) and \(J \approx \max\left\{ {1,\beta \sqrt {g(N)} } \right\}\). Next, we find \(N\) for which the estimate becomes less than \(\varepsilon \).

We introduce the following notation:

$$A = \sqrt 2 \left( {1 + \sqrt {3\ln\frac{1}{\delta }} } \right)\left( {{{M}_{U}}{{\sigma }_{x}} + 2R\left( {\sigma + {{\sigma }_{x}}\sqrt {{{\lambda }_{{{\text{max}}}}}({{C}^{{\text{T}}}}C)} } \right)} \right) + 2.5RM,$$
$$B = {{C}_{1}}{{R}^{2}}\sigma .$$

It is necessary to obtain the minimum estimate on the iteration number \(N\) required for achieving the prescribed accuracy \(\varepsilon \). For \(J = 1\), we obtain

$$\sqrt N = \left\lceil {\frac{{A + B\sqrt {\ln\left( {\tfrac{N}{\delta }} \right)} }}{\varepsilon }} \right\rceil .$$
(9)

Substituting \(N\) recursively, we derive from (9) the complexity bound

$$N = O\left( {\left\lceil {\frac{{{{A}^{2}}}}{{{{\varepsilon }^{2}}}}\ln\left( {\frac{{MR}}{{\varepsilon \delta }}} \right)} \right\rceil } \right).$$

For \(J = \beta \sqrt {g(N)} = \tfrac{{R\sqrt {g(N)} }}{{M\sqrt N }}\), we assume that

$$\frac{A}{{\sqrt N }} + \frac{{Bg(N)R}}{{MN}} = \frac{A}{{\sqrt N }} + \frac{{\bar {B}g(N)}}{N} \leqslant \varepsilon .$$

Since the minimum \(N\) is needed, replacing the last inequality with equality and solving the resulting equation, we obtain

$$\sqrt N = \left\lceil {\frac{{A + \sqrt {{{A}^{2}} + 4\varepsilon \bar {B}\ln\left( {\tfrac{N}{\delta }} \right)} }}{{2\varepsilon }}} \right\rceil .$$

By analogy with the case \(J = 1\), this equality yields the estimate

$$N = O\left( {\left\lceil {\frac{{{{A}^{2}}}}{\varepsilon }\ln\left( {\frac{{MR}}{{\varepsilon \delta }}} \right)} \right\rceil } \right).$$

The worst of the complexity bounds for \(J = 1\) and \(J = \beta \sqrt {g(N)} \) is the estimate from the condition of the theorem.

5 ELLIPSOID METHOD

In this section, the original problem (1) is solved by applying the ellipsoid method [25]. This method can be used when the dual problem has a low dimension (\(m\)) or when high accuracy of the solution is required. The method is primal-dual, i.e., the solution of the primal problem can be recovered from the solution of the dual problem.

Consider the original problem (1) and its dual (2). As in the preceding section, the functions \({{u}_{k}}({{x}_{k}})\), \(k = 1, \ldots ,n\), are assumed to be concave, but not strongly concave. Additionally, we assume that the solution of the dual problem lies in the Euclidean ball of radius \(R\) centered at the origin, i.e., \({{\left\| {\boldsymbol{\lambda} \text{*}} \right\|}_{2}} \leqslant R\). As an initial point of the method, we use the zero vector \({{\boldsymbol{\lambda} }^{0}} = 0\). The problem is solved on the set

$${{\Lambda }_{{2R}}} = \left\{ {\boldsymbol{\lambda} \in \mathbb{R}_{ + }^{m}:{{{\left\| \boldsymbol{\lambda} \right\|}}_{2}} \leqslant 2R} \right\}.$$

Let us describe the ellipsoid method (Algorithm 4), which is used to solve the dual problem.

Algorithm 4.  Ellipsoid Method

Input: \({{u}_{k}}({{x}_{k}}),k = 1, \ldots ,n\), are concave utility functions

1: \({{B}_{0}}: = 2R \cdot {{I}_{n}}\), \({{I}_{n}}\) is the identity matrix

2: for \(t = 0, \ldots ,N - 1\)

3:  Compute \(\nabla \varphi ({{\boldsymbol{\lambda} }^{t}})\)

4:  \({{{\mathbf{q}}}_{t}}: = B_{t}^{{\text{T}}}\nabla \varphi ({{\boldsymbol{\lambda} }^{t}})\)

5:  \({{{\mathbf{p}}}_{t}}: = \frac{{B_{t}^{{\text{T}}}{{{\mathbf{q}}}_{t}}}}{{\sqrt {{\mathbf{q}}_{t}^{{\text{T}}}{{B}_{t}}B_{t}^{{\text{T}}}{{{\mathbf{q}}}_{t}}} }}\)

6:  \({{B}_{{t + 1}}}: = \frac{m}{{\sqrt {{{m}^{2}} - 1} }}{{B}_{t}} + \left( {\frac{m}{{m + 1}} - \frac{m}{{\sqrt {{{m}^{2}} - 1} }}} \right){{B}_{t}}{{{\mathbf{p}}}_{t}}{\mathbf{p}}_{t}^{{\text{T}}}\)

7:  \({{\lambda }^{{t + 1}}}: = {{\lambda }^{t}} - \frac{1}{{m + 1}}{{B}_{t}}{{{\mathbf{p}}}_{t}}\)

8: end for

9: return \({{\boldsymbol{\lambda} }^{N}}\)

To reconstruct the solution of the primal problem from the solution of the dual one, it is necessary to determine the accuracy certificate \(\xi \) for the ellipsoid method. Recall that the accuracy certificate is a sequence of weights \(\xi = \{ {{\xi }_{t}}\} _{{t = 0}}^{{N - 1}}\) such that

$${{\xi }_{t}} \geqslant 0,\quad \sum\limits_{t = 0}^{N - 1} \,{{\xi }_{t}} = 1.$$

In our case, the accuracy certificate is constructed in the course of running the ellipsoid method (see Algorithm 5); its general scheme can be described as follows [26].

1. Find the “narrowest strip” containing the ellipsoid \({{Q}_{N}}\) remaining after iteration \(N\), i.e., a vector \({\mathbf{h}}\) such that the following inequality holds on \({{Q}_{N}}\):

$$\mathop {\max}\limits_{\boldsymbol{\lambda} \in {{Q}_{N}}} \left\langle {{\mathbf{h}},\boldsymbol{\lambda} } \right\rangle - \mathop {\min}\limits_{\boldsymbol{\lambda} \in {{Q}_{N}}} \left\langle {{\mathbf{h}},\boldsymbol{\lambda} } \right\rangle \leqslant 1.$$
(10)

For the ellipsoid method, all \({{Q}_{N}}\) are represented in the form

$${{Q}_{N}} = \{ {{B}_{N}}{\mathbf{z}} + {{\lambda }^{N}}:{{{\mathbf{z}}}^{{\text{T}}}}{\mathbf{z}} \leqslant 1\} .$$

Then, to solve (10), we need to perform a singular value decomposition \({{B}_{N}} = UDV,\) where \(U\) and \(V\) are orthogonal matrices and \(D\) is a diagonal matrix with positive diagonal elements. Next, the desired vector \({\mathbf{h}}\) is determined as \({\mathbf{h}} = 1{\text{/}}(2{{\sigma }^{i}}\text{*}) \cdot U{{{\mathbf{e}}}^{i}}\text{*}\), where \({{i}_{*}}\) is the index of the smallest diagonal element of \(D\), \({{\sigma }^{i}}\text{*}\) is the value of this element, and \({{{\mathbf{e}}}^{i}}\) are the vectors of the standard basis.

2. For the vectors \({{{\mathbf{h}}}^{ + }} = \left[ {{\mathbf{h}}, - \left\langle {{\mathbf{h}},{{\boldsymbol{\lambda} }^{N}}} \right\rangle } \right]\) and \({{{\mathbf{h}}}^{ - }} = - {{{\mathbf{h}}}^{ + }}\), find expansions of the form

$${{{\mathbf{h}}}^{ + }} = \sum\limits_{t = 0}^{N - 1} \,{{\nu }_{t}}\left[ {\nabla \varphi ({{\boldsymbol{\lambda} }^{t}}), - \left\langle {\nabla \varphi ({{\boldsymbol{\lambda} }^{t}}),{{\boldsymbol{\lambda} }^{t}}} \right\rangle } \right] + {{{\mathbf{y}}}^{ + }},$$
$${{{\mathbf{h}}}^{ - }} = \sum\limits_{t = 0}^{N - 1} \,{{\mu }_{t}}\left[ {\nabla \varphi ({{\boldsymbol{\lambda} }^{t}}), - \left\langle {\nabla \varphi ({{\boldsymbol{\lambda} }^{t}}),{{\boldsymbol{\lambda} }^{t}}} \right\rangle } \right] + {{{\mathbf{z}}}^{ + }};$$

their existence follows from Proposition 4.1 in [26]. This step is described by Steps 6–13 in Algorithm 5 (see below).

3. From the expansion coefficients \({{\nu }_{t}}\) and \({{\mu }_{t}}\) of the vectors \({{{\mathbf{h}}}^{ + }}\) and \({{{\mathbf{h}}}^{ - }}\), respectively, derive expressions for \({{\xi }_{t}},\;t \in {{I}_{N}}\), where

$${{I}_{N}} = \{ t \leqslant N - 1:{{\boldsymbol{\lambda} }^{t}} \in \operatorname{int} {{\Lambda }_{{2R}}}\} .$$

Expansion coefficients are determined only for feasible points obtained in the course of running Algorithm 5.

Algorithm 5.  Construction of the Accuracy Certificate for the Ellipsoid Method

Input: \(N - 1\) is the number of the iteration at which the accuracy certificate is computed, and \(\mathop {\left\{ {{{B}_{t}},{{\boldsymbol{\lambda} }^{t}},\nabla \varphi ({{\boldsymbol{\lambda} }^{t}})} \right\}}\nolimits_{t = 0}^{N - 1} \) is the work protocol of the ellipsoid method after \(N\) iterations

 1: if \(\nabla \varphi ({{\boldsymbol{\lambda} }^{{N - 1}}}) = 0,\) then

 2:  \({{\xi }_{t}}: = 0\) for all \(t = 0, \ldots ,N - 2\)

 3:  \({{\xi }_{{N - 1}}}: = 1\)

 4: otherwise

 5:  \({\mathbf{h}}: = 1{\text{/}}(2{{\sigma }^{i}}\text{*}) \cdot U{{{\mathbf{e}}}^{i}}\text{*}\)

 6:  \({{{\mathbf{g}}}_{\nu }}: = {\mathbf{h}},\) \({{{\mathbf{g}}}_{\mu }}: = - {\mathbf{h}}\)

 7:  for \(t = 0, \ldots ,N - 1\)

 8:   \({\mathbf{q}}: = B_{t}^{{\text{T}}}\nabla \varphi ({{\lambda }^{t}})\)

 9:   \({{\nu }_{t}}: = {{[{\mathbf{g}}_{\nu }^{{\text{T}}}{{B}_{t}}{\mathbf{q}}]}_{ + }}{\text{/}}\left\| {\mathbf{q}} \right\|_{2}^{2}\)

10:   \({{{\mathbf{g}}}_{\nu }}: = {{{\mathbf{g}}}_{\nu }} - {{\nu }_{t}}\nabla \varphi ({{\boldsymbol{\lambda} }^{t}})\)

11:   \({{\mu }_{t}}: = {{[{\mathbf{g}}_{\mu }^{{\text{T}}}{{B}_{t}}{\mathbf{q}}]}_{ + }}{\text{/}}\left\| {\mathbf{q}} \right\|_{2}^{2}\)

12:   \({{{\mathbf{g}}}_{\mu }}: = {{{\mathbf{g}}}_{\mu }} - {{\mu }_{t}}\nabla \varphi ({{\boldsymbol{\lambda} }^{t}})\)

13:  end for

14:  \({{\xi }_{t}}: = ({{\nu }_{t}} + {{\mu }_{t}}){\text{/}}\sum\nolimits_{i \in {{I}_{N}}}^{} {({{\nu }_{i}} + {{\mu }_{i}})} ,\) \(t \in {{I}_{N}}\)

15: end if

16: return \(\mathop {\left\{ {{{\xi }_{t}}} \right\}}\nolimits_{t = 0}^{N - 1} \)

Remark 3. In contrast to FGM and the stochastic projected subgradient method, the computation of Steps 4–6 of Algorithm 4 in the ellipsoid method requires information about all gradient components, i.e., information from all users. Accordingly, it is necessary to have a common center for all links that collects information from them and performs these computations.

An estimate for the convergence rate of the ellipsoid method for the problem under study is provided by the following result.

Theorem 3 (see [26]). Suppose that Algorithm 4 starts from the initial ball \({{B}_{0}} = \{ \boldsymbol{\lambda} \in {{\mathbb{R}}^{m}}:\left\| \boldsymbol{\lambda} \right\| \leqslant 2R\} \) and the accuracy certificate \(\xi \) is produced by Algorithm 5. Then, after performing

$$N = 2m(m + 1)\left\lceil {\ln\left( {\frac{{32 \cdot 4MR}}{\varepsilon }} \right)} \right\rceil $$
(11)

iterations, it is true that

$$U({\mathbf{x}}\text{*}) - U({{{\mathbf{\hat {x}}}}^{N}}) \leqslant \varepsilon ,\quad {{\left\| {{{{[C{{{{\mathbf{\hat {x}}}}}^{N}} - {\mathbf{b}}]}}_{ + }}} \right\|}_{2}} \leqslant \frac{\varepsilon }{R},$$

where

$${{{\mathbf{\hat {x}}}}^{N}} = \sum\limits_{t \in {{I}_{N}}} \,{{\xi }_{t}}{\mathbf{x}}({{\lambda }^{t}}),\quad {{I}_{N}} = \left\{ {t \leqslant N - 1:{{\lambda }^{t}} \in \operatorname{int} {{\Lambda }_{{2R}}}} \right\}.$$

The proof of this theorem can be found in the Appendix.

6 REGULARIZATION OF THE DUAL PROBLEM

In previous sections, we considered primal-dual methods for solving the dual problem. However, there is a standard approach in which the solution of the primal problem can be recovered from the solution of the dual problem without using primal-dual methods. The key idea of this approach is a regularization of the dual problem such that the resulting regularized problem is strongly convex. In what follows, we describe this approach in detail and state lemmas relating the solutions of the primal and dual problems.

Functional (2) is regularized in the sense of Tikhonov:

$${{\varphi }_{\delta }}(\boldsymbol{\lambda} ) = \varphi (\boldsymbol{\lambda} ) + \frac{\delta }{2}\left\| \boldsymbol{\lambda} \right\|_{2}^{2}$$

and, instead of problem (4), we solve the regularized problem

$$\mathop {\min}\limits_{\boldsymbol{\lambda} \in {\mathbf{R}}_{ + }^{m}} {{\varphi }_{\delta }}(\boldsymbol{\lambda} ).$$

An optimal parameter \(\delta \) will be specified later. As in Section 5, we assume that the problem is solved on the set

$${{\Lambda }_{{2R}}} = \{ \lambda \in \mathbb{R}_{ + }^{m}:{{\left\| \boldsymbol{\lambda} \right\|}_{2}} \leqslant 2R\} .$$

For the resulting regularized function, we formulate the following lemma on the smoothness of the regularized problem.

Lemma 3. Suppose that the function \(\varphi (\boldsymbol{\lambda} )\) is \(L\)-smooth. Then the regularized function \({{\varphi }_{\delta }}(\boldsymbol{\lambda} )\) is \((L + \delta )\)-smooth, i.e., for any \({{\boldsymbol{\lambda} }^{1}}\), \({{\boldsymbol{\lambda} }^{2}} \in {\mathbf{R}}_{ + }^{m}\),

$${{\left\| {\nabla {{\varphi }_{\delta }}({{\boldsymbol{\lambda} }^{1}}) - \nabla {{\varphi }_{\delta }}({{\boldsymbol{\lambda} }^{2}})} \right\|}_{2}} \leqslant (L + \delta ){{\left\| {{{\boldsymbol{\lambda} }^{1}} - {{\boldsymbol{\lambda} }^{2}}} \right\|}_{2}}.$$
(12)

Proof. The gradient of the regularized function is given by

$$\nabla {{\varphi }_{\delta }}(\boldsymbol{\lambda} ) = \nabla \varphi (\boldsymbol{\lambda} ) + \delta \boldsymbol{\lambda} .$$

Therefore, we have

$${{\left\| {\nabla {{\varphi }_{\delta }}({{\boldsymbol{\lambda} }^{1}}) - \nabla {{\varphi }_{\delta }}({{\boldsymbol{\lambda} }^{2}})} \right\|}_{2}} = {{\left\| {\nabla \varphi ({{\boldsymbol{\lambda} }^{1}}) - \nabla \varphi ({{\boldsymbol{\lambda} }^{2}}) + \delta ({{\boldsymbol{\lambda} }^{1}} - {{\boldsymbol{\lambda} }^{2}})} \right\|}_{2}} \leqslant {{\left\| {\nabla \varphi ({{\boldsymbol{\lambda} }^{1}}) - \nabla \varphi ({{\boldsymbol{\lambda} }^{2}})} \right\|}_{2}} + \delta {{\left\| {{{\boldsymbol{\lambda} }^{1}} - {{\boldsymbol{\lambda} }^{2}}} \right\|}_{2}}.$$

By Proposition 2, this estimate implies (12).

Additionally, to estimate the convergence of the algorithm for the primal problem, we need the following auxiliary lemma concerning the relationship between the gradient estimate for the dual problem and convergence estimates with respect to the function and the residual in the constraint for the primal problem.

Lemma 4 (see [10]). Let \({\mathbf{x}}\text{*}\) be a solution of primal problem (1). Then

$${{\left\| {C{\mathbf{x}}(\boldsymbol{\lambda} ) - {\mathbf{b}}} \right\|}_{2}} \leqslant {{\left\| {\nabla {{\varphi }_{\delta }}(\boldsymbol{\lambda} )} \right\|}_{2}} + \delta {{\left\| \boldsymbol{\lambda} \right\|}_{2}},$$
(13)
$$U({\mathbf{x}}\text{*}) - U({\mathbf{x}}(\boldsymbol{\lambda} )) \leqslant {{\left\| {\nabla {{\varphi }_{\delta }}(\lambda )} \right\|}_{2}} \cdot {{\left\| \boldsymbol{\lambda} \right\|}_{2}} + \delta \left\| \boldsymbol{\lambda} \right\|_{2}^{2},$$
(14)

where \({\mathbf{x}}(\boldsymbol{\lambda} )\) is defined by (3).

Proof. By virtue of (3), we have

$$U({\mathbf{x}}(\lambda )) + \left\langle {\lambda ,{\mathbf{b}} - C{\mathbf{x}}(\lambda )} \right\rangle \geqslant U({\mathbf{x}}{\kern 1pt} {\text{*}}) + \left\langle {\lambda ,{\mathbf{b}} - C{\mathbf{x}}{\kern 1pt} {\text{*}}} \right\rangle \geqslant U({\mathbf{x}}{\kern 1pt} {\text{*}}),$$

whence

$$U({\mathbf{x}}(\boldsymbol{\lambda} )) \geqslant U({\mathbf{x}}\text{*}) - \left\langle {\boldsymbol{\lambda} ,{\mathbf{b}} - C{\mathbf{x}}(\boldsymbol{\lambda} )} \right\rangle = U({\mathbf{x}}\text{*}) - \left\langle {\boldsymbol{\lambda} ,\nabla \varphi (\boldsymbol{\lambda} )} \right\rangle .$$

Since \(\varphi (\boldsymbol{\lambda} ) = {{\varphi }_{\delta }}(\boldsymbol{\lambda} ) - \tfrac{\delta }{2}\left\| \boldsymbol{\lambda} \right\|_{2}^{2}\), it is true that

$${{\left\| {\nabla \varphi (\boldsymbol{\lambda} )} \right\|}_{2}} = {{\left\| {\nabla {{\varphi }_{\delta }}(\boldsymbol{\lambda} ) - \delta \boldsymbol{\lambda} } \right\|}_{2}} \leqslant \left\| {\nabla {{\varphi }_{\delta }}(\boldsymbol{\lambda} )} \right\| + \delta {{\left\| \boldsymbol{\lambda} \right\|}_{2}}.$$

Combining this inequality with the relation \(\nabla \varphi (\boldsymbol{\lambda} ) = {\mathbf{b}} - C{\mathbf{x}}(\boldsymbol{\lambda} )\) yields (13).

Furthermore, estimate (14) follows from

$$\begin{gathered} U({\mathbf{x}}\text{*}) - U({\mathbf{x}}(\boldsymbol{\lambda} )) \leqslant \left\langle {\boldsymbol{\lambda} ,\nabla \varphi (\boldsymbol{\lambda} )} \right\rangle \leqslant {{\left\| {\nabla \varphi (\boldsymbol{\lambda} )} \right\|}_{2}} \cdot {{\left\| \boldsymbol{\lambda} \right\|}_{2}} \\ \, \leqslant {{\left\| \boldsymbol{\lambda} \right\|}_{2}} \cdot \left( {\mathop {\left\| {\nabla {{\varphi }_{\delta }}(\boldsymbol{\lambda} )} \right\|}\nolimits_2 + \delta \mathop {\left\| \boldsymbol{\lambda} \right\|}\nolimits_2 } \right) \leqslant {{\left\| {\nabla {{\varphi }_{\delta }}(\boldsymbol{\lambda} )} \right\|}_{2}} \cdot {{\left\| \boldsymbol{\lambda} \right\|}_{2}} + \delta \left\| \boldsymbol{\lambda} \right\|_{2}^{2}. \\ \end{gathered} $$

Additionally, we need the following result concerning convergence with respect to the gradient of the regularized function.

Lemma 5. Let \(\boldsymbol{\lambda} _{\delta }^{*}\) be a solution of the regularized dual problem. Then

$$\mathop {\left\| {\nabla {{\varphi }_{\delta }}({{\boldsymbol{\lambda} }^{N}})} \right\|}\nolimits_2 \leqslant (L + \delta ){{\left\| {{{\boldsymbol{\lambda} }^{N}} - \boldsymbol{\lambda} _{\delta }^{*}} \right\|}_{2}}.$$

The proof follows immediately from Lemma 3 and the relation

$$\nabla {{\varphi }_{\delta }}(\boldsymbol{\lambda} _{\delta }^{*}) = 0.$$

We have formulated the lemmas necessary for the regularized problem. An example of applying this approach is considered in the next section.

7 RANDOM GRADIENT EXTRAPOLATION METHOD

Consider the random gradient extrapolation method [27]. Note that this method does not require updating the gradient at every iteration step. It is necessary to update only one of its components at every iteration, which considerably reduces the computations, especially for large-scale problems. Since this method is not primal-dual, Algorithm 6 has to be applied to the regularized problem.

The parameters \(\alpha \), \(\eta \), \(\tau \), and \({{\theta }_{t}}\) are specified as

$$\bar {\alpha } = 1 - \frac{1}{{n + \sqrt {{{n}^{2}} + 16nL{\text{/}}\delta } }},$$
(15)
$$\alpha = n\bar {\alpha },\quad \eta = \frac{{\delta \bar {\alpha }}}{{1 - \bar {\alpha }}},\quad \tau = \frac{1}{{n(1 - \bar {\alpha })}} - 1,\quad {{\theta }_{t}} = \mathop {\bar {\alpha }}\nolimits^{ - t} .$$
(16)

7.1 Distributed Method

This section presents a distributed version of the considered method. By way of introduction, we note that the vectors \(\mathop {\underline {\boldsymbol{\lambda}} }\nolimits_1^0 , \ldots ,\mathop {\underline {\boldsymbol{\lambda}} }\nolimits_n^0 \) are stored by the corresponding users and influence the formation of optimal data traffic for the corresponding user. As was noted in the description of the distributed FGM, the optimal traffic for a user is influenced only by the prices of the links through which this user exchanges packets. Therefore, we can assume that the only nonzero components in the vector \(\mathop {\underline {\boldsymbol{\lambda}} }\nolimits_k^t \) are those whose indices coincide with the indices of the used links.

Algorithm 6.  Random Gradient Extrapolation Method (RGEM)

Input: Parameters \(\alpha \), \(\eta \), \(\tau \), \(\{ {{\theta }_{t}}\} _{{t = 1}}^{N}\)

 1: \({{{\boldsymbol{\lambda}} }^{0}}: = {\mathbf{0}}\)

 2: \(\mathop {\underline {\boldsymbol{\lambda}} }\nolimits_i^0 : = {{{\boldsymbol{\lambda}} }^{0}}\), \(i = 1, \ldots ,n\)

 3: \({{y}_{{ - 1}}} = {{y}_{0}} = {\mathbf{0}}\)

 4: for \(t = 1, \ldots ,N\)

 5:     Choose \({{k}_{t}}\) at random from the set \(\{ 1, \ldots ,n\} \) uniformly over all values

 6:  \({\mathbf{\tilde {y}}}_{k}^{t}: = {\mathbf{y}}_{k}^{{t - 1}} + \alpha ({\mathbf{y}}_{k}^{{t - 1}} - {\mathbf{y}}_{k}^{{t - 2}}),\) \(k = 1, \ldots ,n\)

 7:  \({{{\boldsymbol{\lambda}} }^{t}}: = \mathop {\left[ {\eta {{{\boldsymbol{\lambda}} }^{{t - 1}}} - \tfrac{1}{n}\sum\nolimits_{k = 1}^n {{\mathbf{\tilde {y}}}_{k}^{t}} } \right]}\nolimits_ + {\text{/}}(\delta + \eta )\)

 8:

 9:  \(\mathop {\underline {\boldsymbol{\lambda}} }\nolimits_{{{k}_{t}}}^t : = ({{{\boldsymbol{\lambda}} }^{t}} + \tau \mathop {\underline {\boldsymbol{\lambda}} }\nolimits_{{{k}_{t}}}^{t - 1} ){\text{/}}(1 + \tau )\)

10:  \(\mathop {\underline {\boldsymbol{\lambda}} }\nolimits_k^t : = \mathop {\underline {\boldsymbol{\lambda}} }\nolimits_k^{t - 1} \), \(k \in \{ 1, \ldots ,n\} {{\backslash }}\{ {{k}_{t}}\} \)

11:

12:  \({\mathbf{y}}_{{{{k}_{t}}}}^{t}: = {\mathbf{b}} - n{{{\mathbf{C}}}_{{{{k}_{t}}}}}{{x}_{{{{k}_{t}}}}}(\mathop {\underline {\boldsymbol{\lambda}} }\nolimits_{{{k}_{t}}}^t )\)

13:  \({\mathbf{y}}_{k}^{t}: = {\mathbf{y}}_{k}^{{t - 1}}\), \(k \in \{ 1, \ldots ,n\} {{\backslash }}\{ {{k}_{t}}\} \)

14: end for

15: \({{\bar {{\boldsymbol{\lambda}} }}^{N}}: = \left( {\sum\nolimits_{t = 0}^{N - 1} {{{\theta }_{t}}{{{\boldsymbol{\lambda}} }^{t}}} } \right){\text{/}}\sum\nolimits_{t = 1}^N {{{\theta }_{t}}} \)

16: return \({{\bar {{\boldsymbol{\lambda}} }}^{N}}\)

Let us describe the distributed algorithm at the \(t\)th iteration.

1. Using information collected from the users at the preceding iteration, link \(j\) computes

$$\tilde {y}_{{k,j}}^{t}: = y_{{k,j}}^{{t - 1}} + \alpha (y_{{k,j}}^{{t - 1}} - y_{{k,j}}^{{t - 2}}) = {{b}_{j}} - nC_{k}^{j}{{x}_{k}}(\mathop {\underline {\boldsymbol{\lambda}} }\nolimits_k^{t - 1} ) + \alpha (nC_{k}^{j}{{x}_{k}}(\mathop {\underline {\boldsymbol{\lambda}} }\nolimits_k^{t - 2} ) - nC_{k}^{j}{{x}_{k}}(\mathop {\underline {\boldsymbol{\lambda}} }\nolimits_k^{t - 1} )).$$

Note that, by the definition of the matrix \(C,\) link \(j\) needs information only from the users exchanging packets through this link.

2. The price of link \(j\) changes according to the rule

$$\lambda _{j}^{t} = {{\left[ {\eta \lambda _{j}^{{t - 1}} - \frac{1}{n}\sum\limits_{k = 1}^n \,\tilde {y}_{{k,j}}^{t}} \right]}_{ + }}{\text{/}}(\delta + \eta ).$$

3. One of the users, \({{k}_{t}}\), reacts to the price change and stores the local price vector

$$\mathop {\underline {\boldsymbol{\lambda}} }\nolimits_{{{k}_{t}}}^t = ({{{\boldsymbol{\lambda}} }^{t}} + \tau \mathop {\underline {\boldsymbol{\lambda}} }\nolimits_{{{k}_{t}}}^{t - 1} ){\text{/}}(1 + \tau ),$$

while the local prices for the other users remain unchanged, i.e., \(\mathop {\underline {\boldsymbol{\lambda}} }\nolimits_{{{k}_{t}}}^t = \mathop {\underline {\boldsymbol{\lambda}} }\nolimits_{{{k}_{t}}}^{t - 1} \).

4. The user \({{k}_{t}}\) computes

$$x_{{{{k}_{t}}}}^{t}(\mathop {\underline \lambda }\nolimits_{{{k}_{t}},j}^t ) = \mathop {\arg\,\max}\limits_{{{x}_{k}} \in {{{\mathbf{R}}}_{ + }}} \,\left( {{{u}_{k}}({{x}_{k}}) - {{x}_{k}}\sum\limits_{j = 1}^m \,\mathop {\underline \lambda }\nolimits_{{{k}_{t}},j}^t C_{k}^{j}} \right)$$

and transmits this information to the used links.

5. Link \(j\) updates the information for the user \({{k}_{t}}\):

$$y_{{{{k}_{t}},j}}^{t} = {{b}_{j}} - nC_{{{{k}_{t}}}}^{j}{{x}_{{{{k}_{t}}}}}(\mathop {\underline {\boldsymbol{\lambda}} }\nolimits_{{{k}_{t}}}^t ).$$

This information is updated by the link only if the user \({{k}_{t}}\) exchanges packets through it.

7.2 Estimation of the Convergence Rate of RGEM

Following Section 3, we consider problem (2) with \(\mu \)-strongly concave cost functions \({{u}_{k}}({{x}_{k}}),k = 1, \ldots ,n\). Recall that, since the cost functions are strongly concave, the dual problem (4) is smooth with Lipschitz constant \(L = \tfrac{{n{{m}^{2}}}}{\mu }\).

To estimate the convergence rate of the method, we need the estimate for the residual with respect to the argument from Theorem 2.1 in [27], namely,

$$\mathbb{E}\left[ {\left\| {{\boldsymbol{\lambda}} _{\delta }^{*} - {{{\boldsymbol{\lambda}} }^{N}}} \right\|_{2}^{2}} \right] \leqslant \frac{{4\Delta {{{(\bar {\alpha })}}^{N}}}}{\delta },$$
(17)

where \(\Delta = \delta \left\| {{\boldsymbol{\lambda}} _{\delta }^{*} - {{{\boldsymbol{\lambda}} }^{0}}} \right\|_{2}^{2} + \tfrac{B}{{n\delta }} + {{\varphi }_{\delta }}({{\lambda }^{0}}) - {{\varphi }_{\delta }}(\lambda _{\delta }^{*})\) and \(B = \left\| {\mathbf{b}} \right\|_{2}^{2}\).

By using (17), it is possible to prove the following convergence estimate theorem for the method as applied to problem (11).

Theorem 4. Suppose that the regularized dual problem (11) is solved by applying RGEM with parameters (15), (16), and \(\delta = \tfrac{\varepsilon }{{8{{R}^{2}}}}\) and with

$$N = \left\lceil {2\left( {n + \sqrt {{{n}^{2}} + \frac{{128nL{{R}^{2}}}}{\varepsilon }} } \right)\ln\left( {\frac{{4RA}}{\varepsilon }} \right)} \right\rceil $$

iterations, where \(A = 2\left( {LR + \tfrac{\varepsilon }{{8R}}} \right)\sqrt {6 + \tfrac{{16L{{R}^{2}}n + 8B}}{{n\varepsilon }}} \). Then

$$\mathbb{E}{\kern 1pt} [U({\mathbf{x}}\text{*}) - U({\mathbf{x}}({{\lambda }^{N}}))] \leqslant \varepsilon ,\quad \mathbb{E}\left[ {\mathop {\left\| {C{\mathbf{x}}({{\lambda }^{N}}) - {\mathbf{b}}} \right\|}\nolimits_2 } \right] \leqslant \frac{\varepsilon }{{2R}}.$$

Proof. Lemma 4 implies estimate (13) for the residual with respect to the constraints and estimate (14) for the residual with respect to the objective function. By the assumption \({\boldsymbol{\lambda}} \in {{\Lambda }_{{2R}}}\), we have

$${{\left\| {C{{{\mathbf{x}}}^{N}} - {\mathbf{b}}} \right\|}_{2}} \leqslant {{\left\| {\nabla {{\varphi }_{\delta }}({{{\boldsymbol{\lambda}} }^{N}})} \right\|}_{2}} + 2\delta R,$$
(18)
$$U({\mathbf{x}}\text{*}) - U({{{\mathbf{x}}}^{N}}) \leqslant 2R{{\left\| {\nabla {{\varphi }_{\delta }}({{{\boldsymbol{\lambda}} }^{N}})} \right\|}_{2}} + 4\delta {{R}^{2}},$$
(19)

where \({{{\mathbf{x}}}^{N}} = {\mathbf{x}}({{{\boldsymbol{\lambda}} }^{N}})\). Combining Lemma 5 with inequality (17) yields the following estimate for \({{\left\| {\nabla {{\varphi }_{\delta }}({{{\boldsymbol{\lambda}} }^{N}})} \right\|}_{2}}\):

$$\mathbb{E}\left[ {{{{\left\| {\nabla {{\varphi }_{\delta }}({{{\boldsymbol{\lambda}} }^{N}})} \right\|}}_{2}}} \right] \leqslant 2(L + \delta )\sqrt {\frac{\Delta }{\delta }} {{(\bar {\alpha })}^{{N/2}}}.$$

Let us estimate \(\Delta \). The function \({{\varphi }_{\delta }}\) with a Lipschitz continuous gradient satisfies the inequality

$${{\varphi }_{\delta }}({{{\boldsymbol{\lambda}} }^{0}}) - {{\varphi }_{\delta }}({\boldsymbol{\lambda}} _{\delta }^{*}) \leqslant \left\langle {\nabla {{\varphi }_{\delta }}({\boldsymbol{\lambda}} _{\delta }^{*}),{{\lambda }^{0}} - {{\lambda}} \text{*}} \right\rangle + \frac{{L + \delta }}{2}\left\| {{\boldsymbol{\lambda}} _{\delta }^{*} - {{{\boldsymbol{\lambda}} }^{0}}} \right\|_{2}^{2}.$$

Since \(\nabla {{\varphi }_{\delta }}({\boldsymbol{\lambda}} _{\delta }^{*}) = 0\), we obtain

$$\Delta \leqslant \delta \left\| {{\boldsymbol{\lambda}} _{\delta }^{*} - {{{\boldsymbol{\lambda}} }^{0}}} \right\|_{2}^{2} + \frac{B}{{n\delta }} + \frac{{L + \delta }}{2}\left\| {{\boldsymbol{\lambda}} _{\delta }^{*} - {{{\boldsymbol{\lambda}} }^{0}}} \right\|_{2}^{2} \leqslant (6\delta + 2L){{R}^{2}} + \frac{B}{{n\delta }}.$$

Suppose that \(\delta \) is chosen so that \(4\delta {{R}^{2}} = \tfrac{\varepsilon }{2}\). Then \(\delta = \tfrac{\varepsilon }{{8{{R}^{2}}}}\). It follows that

$$4\delta {{R}^{2}} = \frac{\varepsilon }{2},\quad 2\delta R = \frac{\varepsilon }{{4R}}.$$

Assume that \(U({\mathbf{x}}\text{*}) - U({\mathbf{x}}({{{\boldsymbol{\lambda}} }^{N}})) \leqslant \varepsilon \). Then, by virtue of (18) and (19), it is true that

$${{\left\| {\nabla {{\varphi }_{\delta }}({{{\boldsymbol{\lambda}} }^{N}})} \right\|}_{2}} \leqslant \frac{\varepsilon }{{4R}},$$

whence

$$2(L + \delta )\sqrt {\frac{\Delta }{\delta }} {{(\bar {\alpha })}^{{N/2}}} \leqslant \frac{\varepsilon }{{4R}}.$$

Taking into account

$$2(L + \delta )\sqrt {\frac{\Delta }{\delta }} \leqslant 2\left( {LR + \frac{\varepsilon }{{8R}}} \right)\sqrt {6 + \frac{{16L{{R}^{2}}n + 8B}}{{n\varepsilon }}} ,$$

we obtain the following estimate for the number of iterations:

$$N = \left\lceil {2\left( {n + \sqrt {{{n}^{2}} + \frac{{128nL{{R}^{2}}}}{\varepsilon }} } \right)\ln\left( {\frac{{4RA}}{\varepsilon }} \right)} \right\rceil ,$$

where \(A = 2\left( {LR + \tfrac{\varepsilon }{{8R}}} \right)\sqrt {6 + \tfrac{{16L{{R}^{2}}n + 8B}}{{n\varepsilon }}} \).

Remark 4. The complexity bound for Algorithm 6 can also be represented in the form \(O\left( {\max\left\{ {n,\sqrt {nL{{R}^{2}}{\text{/}}\varepsilon } } \right\}\ln\left( {\tfrac{1}{\varepsilon }} \right)} \right)\), where the logarithmic factor appears due to the necessity of regularization of the dual problem. At every iteration, only one component of the user reaction vector to changed prices is computed; accordingly, the arithmetic complexity of the operation is better than that in the case of computing all components of these vectors. For FGM, the assumptions made about the objective function are similar, but, since the complete gradient has to be computed at every iteration step, the complexity bound for the algorithm is \(O\left( {n\sqrt {L{{R}^{2}}{\text{/}}\varepsilon } } \right)\). Thus, although the theoretical convergence estimate for RGEM has the same order as for FGM, in practice the gain is obtained due to the cheaper computations within a single iteration.

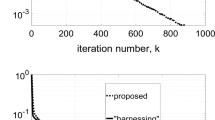
8 NUMERICAL EXPERIMENTS

The software code for numerical experiments was written in Python 3.6 and C++14. The source code for experiments and the methods considered in this paper is available at https://github.com/dmivilensky/network-resource-allocation. The running time was measured on a computer with a 2-core Intel Core i5-5250U 1.6 GHz processor and 8 GB RAM.

8.1 Strongly Convex (Quadratic) Utility Functions

Consider problem (1) for utility functions of the form

$${{u}_{k}}({{x}_{k}}) = {{a}_{k}}{{x}_{k}} - \frac{{\sigma n}}{2}x_{k}^{2},\quad {{a}_{k}} \sim \mathcal{U}(0,100),\quad \sigma = 0.1,$$

where \({{a}_{k}}\) are independent identically distributed random variables. Then problem (3) can be solved explicitly:

$${\mathbf{x}}(\lambda ) = \frac{{{{{[{\mathbf{a}} - C{\boldsymbol{\lambda}} ]}}_{ + }}}}{{n\sigma }}.$$

For a small number of users (\(n = 1500\)), the link capacities are chosen identical (in this case, \({\mathbf{b}} = (5, \ldots ,5)^{\text{T}}\)), and the demand for data transmission is uniform (\({{c}_{{ij}}} = 1\) for any \(i,j\)). For a larger number of users, the capacity vector is generated at random, so that \({{b}_{i}} \sim \mathcal{U}(1,6)\). The elements of the demand matrix are also chosen randomly and independently, so that \({{c}_{{ij}}} = 1\) with probability \(p = 0.5\) and \({{c}_{{ij}}} = 0\) with probability \(q = 0.5\).

Table 1 presents the number of iterations and the running times of the fast gradient method (FGM) and the random  gradient  extrapolation method (RGEM) for various network configurations (with \(m\) links), various numbers of users \(n\), and various values of the required accuracy \(\varepsilon \). The cases in which RGEM converges to the solution faster than FGM, despite the larger number of iterations than in FGM, are highlighted in the table. Indeed, for \(n \gg 0\), RGEM requires fewer queries for the optimal solution \({{x}_{k}}({\boldsymbol{\lambda}} )\) from users than in other algorithms, since a query at one RGEM iteration is sent to only one random user.

Table 1.   Comparison of the number of iterations and the running time of FGM and RGEM for strongly convex (quadratic) utility functions
Full size table

8.2 Convex (Logarithmic) Utility Functions

Consider the performance of the stochastic subgradient method (Algorithm 2) and the ellipsoid method (Algorithm 4) for the utility function

$${{u}_{k}}({{x}_{k}}) = \ln{{x}_{k}}.$$

In this case, an explicit solution of problem (3) is given by

$${\mathbf{x}}({\boldsymbol{\lambda}} ) = \frac{1}{{C{\boldsymbol{\lambda}} }}$$

(the operation \(1/ \cdot \) as applied to a vector is understood elementwise). For a small number of users (\(n = 1500\)), the link capacities are chosen identical (in this case, \({\mathbf{b}} = {{(5, \ldots ,5)}^{{\text{T}}}}\)) and the demand for data transmission is uniform (\({{c}_{{ij}}} = 1\) for any \(i,j\)). For a larger number of users, the capacity vector is randomly generated, so that \({{b}_{i}} \sim \mathcal{U}(1,6)\). The elements of the demand matrix are also chosen randomly and independently, so that \({{c}_{{ij}}} = 1\) with probability \(p = 0.5\) and \({{c}_{{ij}}} = 0\) with probability \(q = 0.5\).

Table 2 presents the number of iterations and the running times of the stochastic subgradient method (SGM) and the ellipsoid method for various network configurations, various numbers of users, and various values of the required accuracy. The cases in which SGM converges to the solution faster than the ellipsoid method are highlighted in the table.

Table 2.   Comparison of the number of iterations and the running time of the stochastic subgradient method and the ellipsoid method for convex (logarithmic) utility functions
Full size table

Note that, as in RGEM, only one component of the user reaction vector \({\mathbf{x}}({\boldsymbol{\lambda}} )\) to established prices has to be computed at every iteration in SGM. Thus, when the number of iterations of the method is large, the number of computed components \({{x}_{k}}({{{\boldsymbol{\lambda}} }^{t}})\) is smaller than in other algorithms, for example, in the ellipsoid method, and the same is true of the communication complexity in the case of distributed implementation.

9 CONCLUSIONS

To conclude, we note some possible directions of development of this work and briefly describe suitable methods without detailed analysis of their convergence estimates.

In Section 5, as applied to low-dimensional problems, we considered the ellipsoid method, which is primal-dual. There are other methods that are highly accurate and well suited for low-dimensional problems. An example is Vaidya’s cutting plane method [28]. However, to recover the solution of the primal problem when the dual one is solved using Vaidya’s method, we need convergence in the gradient norm for the dual problem. For this purpose, the dual problem has to be smooth, which is ensured by the strong convexity of the objective function in the primal problem (Proposition 2). If the primal problem is not strongly convex, it can be regularized as described in Section 6, but the convergence estimate will then degrade logarithmically.

Additionally, if the dual problem is sufficiently smooth, it can be solved by applying high-order methods [29, 30]. The steps of these methods can be computed on a distributed basis, since the given problem makes use of a centralized architecture in terms of the interaction of a link and the users using it. Note, however, that high-order optimal methods that require linesearch and do not have the primal-dual property apply to only preliminarily regularized dual problems.

Another direction is represented by variance reduced methods (see, e.g., [31, 32]), which are intermediate between the stochastic gradient method and FGM. However, these methods are not primal-dual either, so they apply to preliminarily regularized dual problems.

Of special interest are the Hogwild! method [33] and minibatching techniques. In this case, data are sent out not by all users simultaneously, but by more than one of them, in contrast to stochastic methods. By setting the size of the batch equal to the number of users transmitting data at a time, one can take into account the specific features of actual networks.