1 INTRODUCTION

In [1], a theory of lower (oracle) bounds on the complexity of solving constrained and stochastic convex optimization problems on sets of a simple structure was developed. In [1], methods that converge according to these lower bounds (up to logarithmic factors) were also proposed. In particular, a class of nonsmooth (stochastic) convex optimization was considered. For this class, a special method called the mirror descent method was proposed, which is optimal for this class of problems. It was known that the mirror descent method can be extended to constrained optimization problems (with the loss of a logarithmic factor compared with lower bounds). The subsequent development of numerical methods for convex optimization showed that the mirror descent method is in many respects convenient for various problems, including huge-scale optimization problems (problems in huge-dimensional spaces or with a huge number of constraints). In particular, such problems arise in truss topology design (see Example 1 in Section 4). There are various simplifications and generalizations of this method. In this paper, we follow [2] to extend the modern version of the mirror descent method to constrained stochastic optimization problems. In distinction from [1, 2], we obtain sharp bounds on the probability of large deviations and prove the primal–dual property of the method in the deterministic case. The bounds on the convergence rate of the method correspond to the lower bounds obtained in [1]; i.e., the logarithmic gap mentioned above is eliminated. An important feature of the proposed method is its simplicity, which helps use the sparseness of the problem.

In Section 2, we describe the method and prove a theorem establishing a bound on the convergence rate of the method. Note that we consider the oracle that produces not only stochastic (sub)gradients of the objective functional and functional constraint but also the value (but not realization) of the functional constraint at the point of interest. Using the theory of fast automatic differentiation (see [3]), we may conclude that such an oracle can also produce the gradient of the functional constraint (rather than the stochastic gradient). However, the fast automatic differentiation technique is developed for smooth problems (while lexicographic differentiation is used for nonsmooth problems [4]) and, secondly, certain applications require the use of the sparse stochastic (sub)gradient rather than the nonsparse full (sub)gradient. Some examples of such problems are discussed in Section 4.

In Section 3, we prove (in the deterministic case) the primal–dual property of the method. This property is useful, for instance, in the application of the proposed method to truss topology design, in which the primal and the dual problems must be solved simultaneously.

In the concluding Section 4, we discuss possible generalizations and applications. A more detailed comparative analysis with other available results is also performed.

2 MIRROR DESCENT METHOD FOR CONVEX CONSTRAINED OPTIMIZATION PROBLEMS

Consider the convex constrained optimization problem

$$f(x) \to \mathop {\min }\limits_{g\left( x \right) \leqslant 0,\;x \in Q} .$$
((1))

By an \(\left( {{{\varepsilon }_{f}},{{\varepsilon }_{g}},\sigma } \right)\)-solution of this problem, we mean an \({{\bar {x}}^{N}} \in Q \subseteq {{\mathbb{R}}^{n}}\) such that the inequality

$$f({{\bar {x}}^{N}}) - {{f}_{*}} \leqslant {{\varepsilon }_{f}} = \frac{{{{M}_{f}}}}{{{{M}_{g}}}}{{\varepsilon }_{g}},\quad g({{\bar {x}}^{N}}) \leqslant {{\varepsilon }_{g}},$$
((2))

holds with a probability \( \geqslant 1 - \sigma \), where \({{f}_{*}} = f({{x}_{*}})\) is the optimal value of the objective functional in problem (1) and \({{x}_{*}}\) is the solution of problem (1).

Define a norm \(\left\| {} \right\|\) in the primal space (the adjoint norm will be denoted by \({{\left\| {} \right\|}_{*}}\)) and a proximity function \(d(x)\) that is strongly convex with respect to this norm with a strong convexity constant \( \geqslant {\kern 1pt} 1\). Choose an initial point

$${{x}^{1}} = \arg \mathop {\min }\limits_{x \in Q} d(x),$$

where we assume that

$$d({{x}^{1}}) = 0,\quad \nabla d({{x}^{1}}) = 0.$$

Define the Bregman “distance”

$${{V}_{x}}{\kern 1pt} \left( y \right) = d{\kern 1pt} \left( y \right) - d{\kern 1pt} \left( x \right) - \left\langle {\nabla d{\kern 1pt} \left( x \right),\;y - x} \right\rangle .$$

The “size” of the solution is defined by

$$d({{x}_{*}}) = {{V}_{{{{x}^{1}}}}}({{x}_{*}}) = {{R}^{2}},$$

and the size of the set \(Q\) (for clarity, we assume that this set is bounded, but in the general case the reasoning below can be conducted accurately under certain additional assumptions, see [5]) is defined by

$$\mathop {\max}\limits_{x,y \in Q} {{V}_{x}} \left( y \right) = {{\bar {R}}^{2}}.$$

We assume that there is a sequence of independent random variables \(\left\{ {{{\xi }^{k}}} \right\}\) and sequences \(\left\{ {{{\nabla }_{x}}f(x,{{\xi }^{k}})} \right\}\), \(\left\{ {{{\nabla }_{x}}g(x,{{\xi }^{k}})} \right\}\) (\(k = 1,...,N\)) such that the following relations hold:

$${{E}_{{{{\xi }^{k}}}}}\left[ {{{\nabla }_{x}}f(x,{{\xi }^{k}})} \right] = \nabla f{\kern 1pt} \left( x \right),\quad {{E}_{{{{\xi }^{k}}}}}\left[ {{{\nabla }_{x}}g(x,{{\xi }^{k}})} \right] = \nabla g{\kern 1pt} \left( x \right);$$
((3))
$$\left\| {{{\nabla }_{x}}f(x,{{\xi }^{k}})} \right\|_{*}^{2} \leqslant M_{f}^{2},\quad \left\| {{{\nabla }_{x}}g(x,{{\xi }^{k}})} \right\|_{*}^{2} \leqslant M_{g}^{2}$$
((4))

or

$${{E}_{{{{\xi }^{k}}}}}\left[ {\left\| {{{\nabla }_{x}}f(x,{{\xi }^{k}})} \right\|_{*}^{2}} \right] \leqslant M_{f}^{2},\quad {{E}_{{{{\xi }^{k}}}}}\left[ {\left\| {{{\nabla }_{x}}g(x,{{\xi }^{k}})} \right\|_{*}^{2}} \right] \leqslant M_{g}^{2}.$$
((4'))

At each iteration step \(k = 1,...,N\), we have a stochastic (sub)gradient \({{\nabla }_{x}}f(x,{{\xi }^{k}})\) or \({{\nabla }_{x}}g(x,{{\xi }^{k}})\) at a point \({{x}^{k}}\) chosen by the method.

Let us describe the stochastic version of the mirror descent method for problems with functional constraints (this method dates to [1]).

Define the “projection” operator associated with the Bregman distance by

$${\text{Mir}}{{{\text{r}}}_{{{{x}^{k}}}}}({\text{v}}) = \arg \mathop {\min }\limits_{y \in Q} \left\{ {\left\langle {{\text{v}},y - {{x}^{k}}} \right\rangle + {{V}_{{{{x}^{k}}}}}(y)} \right\}.$$

The mirror descent method for problem (1) has the form (e.g., see [2])

$$\begin{gathered} {{x}^{{k + 1}}} = {\text{Mir}}{{{\text{r}}}_{{{{x}^{k}}}}}\left( {{{h}_{f}}{{\nabla }_{x}}f({{x}^{k}},{{\xi }^{k}})} \right)\quad {\text{if}}\quad g({{x}^{k}}) \leqslant {{\varepsilon }_{g}}, \\ {{x}^{{k + 1}}} = {\text{Mir}}{{{\text{r}}}_{{{{x}^{k}}}}}\left( {{{h}_{g}}{{\nabla }_{x}}g({{x}^{k}},{{\xi }^{k}})} \right)\quad {\text{if}}\quad g({{x}^{k}}) > {{\varepsilon }_{g}}, \\ \end{gathered} $$
((5))

where \({{h}_{g}} = {{{{\varepsilon }_{g}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{g}}} {M_{g}^{2}}}} \right. \kern-0em} {M_{g}^{2}}}\), \({{h}_{f}} = {{{{\varepsilon }_{g}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{g}}} {\left( {{{M}_{f}}{{M}_{g}}} \right)}}} \right. \kern-0em} {\left( {{{M}_{f}}{{M}_{g}}} \right)}}\), \(k = 1,...,N\). Denote by \(I\) the set of indexes \(k\) for which \(g({{x}^{k}}) \leqslant {{\varepsilon }_{g}}\). We also introduce the notation

$$\left[ N \right] = \left\{ {1,...,N} \right\},\quad J = \left[ N \right]{\backslash\text{ }}I,\quad {{N}_{I}} = \left| I \right|,\quad {{N}_{J}} = \left| J \right|,\quad {{\bar {x}}^{N}} = \frac{1}{{{{N}_{I}}}}\sum\limits_{k \in I} {{{x}^{k}}} .$$

In the theorems formulated below, it is assumed that the sequence \(\left\{ {{{x}^{k}}} \right\}_{{k = 1}}^{{N + 1}}\) is generated by method (5).

Theorem 1.Let conditions (3) and (4') hold. Then, for

$$N > \frac{{2M_{g}^{2}{{R}^{2}}}}{{\varepsilon _{g}^{2}}}\;\mathop = \limits^{{\text{def}}} \;N({{\varepsilon }_{g}})$$

it holds that \({{N}_{I}} \geqslant 1\) (with a probability \( \geqslant {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\)) and

$$E\left[ {f({{{\bar {x}}}^{N}})} \right] - {{f}_{*}} \leqslant {{\varepsilon }_{f}},\quad g({{\bar {x}}^{N}}) \leqslant {{\varepsilon }_{g}}.$$

Let conditions (3) and (4) hold. Then, for

$$N \geqslant \frac{{81M_{g}^{2}{{{\bar {R}}}^{2}}}}{{\varepsilon _{g}^{2}}}\ln \left( {\frac{1}{\sigma }} \right)$$
((6))

it holds that \({{N}_{I}} \geqslant 1\)and

$$f({{\bar {x}}^{N}}) - {{f}_{*}} \leqslant {{\varepsilon }_{f}},\quad g({{\bar {x}}^{N}}) \leqslant {{\varepsilon }_{g}}$$

with a probability \( \geqslant 1 - \sigma \); i.e., inequalities (2) are satisfied.

Proof. The first part of this theorem was proved in [2]. Here we prove the second part. According to [6], for every \(x \in Q\) such that \(g(x) \leqslant 0\), it holds that

$${{h}_{f}}{{N}_{I}}\left( {f({{{\bar {x}}}^{N}}) - f(x)} \right) \leqslant {{h}_{f}}\sum\limits_{k \in I} {\left\langle {{{E}_{{{{\xi }^{k}}}}}\left[ {{{\nabla }_{x}}f({{x}^{k}},{{\xi }^{k}})} \right],{{x}^{k}} - x} \right\rangle } \leqslant \frac{{h_{f}^{2}}}{2}\sum\limits_{k \in I} {\left\| {{{\nabla }_{x}}f({{x}^{k}},{{\xi }^{k}})} \right\|_{*}^{2}} $$
$$ + \;{{h}_{f}}\sum\limits_{k \in I} {\left\langle {{{E}_{{{{\xi }^{k}}}}}\left[ {{{\nabla }_{x}}f({{x}^{k}},{{\xi }^{k}})} \right] - {{\nabla }_{x}}f({{x}^{k}},{{\xi }^{k}}),{{x}^{k}} - x} \right\rangle } + {{h}_{g}}\sum\limits_{k \in J} {\underbrace {\left\langle {{{E}_{{{{\xi }^{k}}}}}\left[ {{{\nabla }_{x}}g({{x}^{k}},{{\xi }^{k}})} \right],{{x}^{k}} - x} \right\rangle }_{ \geqslant g({{x}^{k}}) - g(x) > {{\varepsilon }_{g}}}} $$
$$ + \;\frac{{h_{g}^{2}}}{2}\sum\limits_{k \in J} {\left\| {{{\nabla }_{x}}g({{x}^{k}},{{\xi }^{k}})} \right\|_{*}^{2}} + {{h}_{g}}\sum\limits_{k \in J} {\left\langle {{{E}_{{{{\xi }^{k}}}}}\left[ {{{\nabla }_{x}}g({{x}^{k}},{{\xi }^{k}})} \right] - {{\nabla }_{x}}g({{x}^{k}},{{\xi }^{k}}),{{x}^{k}} - x} \right\rangle } + \sum\limits_{k \in [N]} {\left( {{{V}_{{{{x}^{k}}}}}(x) - {{V}_{{{{x}^{{k + 1}}}}}}(x)} \right)} .$$

Put \(x = {{x}_{*}}\) and define

$${{\delta }_{N}} = {{h}_{f}}\sum\limits_{k \in I} {\left\langle {\nabla f({{x}^{k}}) - {{\nabla }_{x}}f({{x}^{k}},{{\xi }^{k}}),{{x}^{k}} - {{x}_{*}}} \right\rangle } + {{h}_{g}}\sum\limits_{k \in J} {\left\langle {\nabla g({{x}^{k}}) - {{\nabla }_{x}}g({{x}^{k}},{{\xi }^{k}}),{{x}^{k}} - {{x}_{*}}} \right\rangle } .$$

Then

$${{h}_{f}}{{N}_{I}}\left( {f({{{\bar {x}}}^{N}}) - f({{x}_{*}})} \right) \leqslant \frac{1}{2}h_{f}^{2}M_{f}^{2}{{N}_{I}} - \frac{1}{{2M_{g}^{2}}}\varepsilon _{g}^{2}{{N}_{J}} + {{V}_{{{{x}^{1}}}}}({{x}_{*}}) - {{V}_{{{{x}^{{N + 1}}}}}}({{x}_{*}}) + {{\delta }_{N}}$$
$$ = \frac{1}{2}\left( {h_{f}^{2}M_{f}^{2} + \frac{{\varepsilon _{g}^{2}}}{{M_{g}^{2}}}} \right){{N}_{I}} - \frac{1}{{2M_{g}^{2}}}\varepsilon _{g}^{2}N + {{R}^{2}} - {{V}_{{{{x}^{{N + 1}}}}}}({{x}_{*}}) + {{\delta }_{N}}$$
((7))
$$ = {{\varepsilon }_{f}}{{h}_{f}}{{N}_{I}} - \frac{1}{{2M_{g}^{2}}}\varepsilon _{g}^{2}N + {{R}^{2}} - {{V}_{{{{x}^{{N + 1}}}}}}({{x}_{*}}) + {{\delta }_{N}} \leqslant {{\varepsilon }_{f}}{{h}_{f}}{{N}_{I}} + \left( {{{R}^{2}} + {{\delta }_{N}} - \frac{1}{{2M_{g}^{2}}}\varepsilon _{g}^{2}N} \right).$$

The Azuma–Hoeffding inequality [7] implies that

$$P\left( {{{\delta }_{N}} \geqslant 2\sqrt 2 \bar {R}\Lambda \sqrt {h_{f}^{2}M_{f}^{2}{{N}_{I}} + h_{g}^{2}M_{g}^{2}{{N}_{J}}} } \right) \leqslant \exp \left( { - {{{{\Lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\Lambda }^{2}}} 2}} \right. \kern-0em} 2}} \right);$$

i.e.,

$$P\left( {{{\delta }_{N}} \geqslant \frac{{4\bar {R}{{\varepsilon }_{g}}}}{{{{M}_{g}}}}\sqrt {N\ln \left( {\frac{1}{\sigma }} \right)} } \right) \leqslant \sigma $$

with a probability \( \geqslant 1 - \sigma \). We assume that (the constant 81 can be decreased to \({{\left( {4 + \sqrt {18} } \right)}^{2}}\)):

$$N \geqslant \frac{{81M_{g}^{2}{{{\bar {R}}}^{2}}}}{{\varepsilon _{g}^{2}}}\ln \left( {\frac{1}{\sigma }} \right).$$

Then, with a probability \( \geqslant 1 - \sigma \), the expression in parentheses in (7) is strictly less than zero; therefore, we have the inequalities

$$f({{\bar {x}}^{N}}) - {{f}_{*}} \leqslant {{\varepsilon }_{f}},\quad g({{\bar {x}}^{N}}) \leqslant {{\varepsilon }_{g}}.$$

The last inequality follows from the fact that \(g({{x}^{k}}) \leqslant {{\varepsilon }_{g}}\) for \(k \in I\) and from the convexity of the function \(g\left( x \right)\).

3 THE PROMAL–DUAL PROPERTY OF THE METHOD

Let \(g{\kern 1pt} \left( x \right) = \mathop {\max }\limits_{l = 1,...,m} {{g}_{l}}\left( x \right)\). Consider the dual problem

$$\varphi \left( \lambda \right) = \mathop {\min }\limits_{x \in Q} \left\{ {f{\kern 1pt} \left( x \right) + \sum\limits_{l = 1}^m {{{\lambda }_{l}}{{g}_{l}}\left( x \right)} } \right\} \to \mathop {\max }\limits_{\lambda \geqslant 0} .$$
((8))

We have the inequality (weak duality)

$$0 \leqslant f{\kern 1pt} \left( x \right) - \varphi {\kern 1pt} \left( \lambda \right)\;\mathop = \limits^{{\text{def}}} \;\Delta \left( {x,\lambda } \right),\quad x \in Q,\quad g{\kern 1pt} \left( x \right) \leqslant 0,\quad \lambda \geqslant 0.$$

Denote the solution to problem (8) by \({{\lambda }_{*}}\). Assume that Slater’s conditions hold, i.e., there exists an \(\tilde {x} \in Q\) such that \(g{\kern 1pt} \left( {\tilde {x}} \right) < 0\). Then

$${{f}_{*}} = f({{x}_{*}}) = \varphi ({{\lambda }_{*}})\;\mathop = \limits^{{\text{def}}} \;{{\varphi }_{*}}.$$

In this case, the “quality” of the pair \(({{x}^{N}},{{\lambda }^{N}})\) is naturally assessed by the size of the duality gap \(\Delta ({{x}^{N}},{{\lambda }^{N}})\). The less the gap, the higher is the quality.

Let (we restrict ourselves to the deterministic case)

$$g({{x}^{k}}) = {{g}_{{l(k)}}}({{x}^{k}}),\quad \nabla g({{x}^{k}}) = \nabla {{g}_{{l(k)}}}({{x}^{k}}),\quad k \in J.$$

Set

$$\lambda _{l}^{N} = \frac{1}{{{{h}_{f}}{{N}_{I}}}}\sum\limits_{k \in J} {{{h}_{g}}I\left[ {l\left( k \right) = l} \right]} ,$$
$$I\left[ {{\text{predicate}}} \right] = \left\{ \begin{gathered} 1,\quad {\text{predicate}} = true, \hfill \\ 0,\quad {\text{predicate}} = false. \hfill \\ \end{gathered} \right.$$

Theorem 2. Let

$$\left\| {\nabla f{\kern 1pt} \left( x \right)} \right\|_{*}^{2} \leqslant M_{f}^{2},\quad \left\| {\nabla g{\kern 1pt} \left( x \right)} \right\|_{*}^{2} \leqslant M_{g}^{2}.$$

Then, for

$$N \geqslant \frac{{2M_{g}^{2}{{{\bar {R}}}^{2}}}}{{\varepsilon _{g}^{2}}} + 1,$$

it holds that \({{N}_{I}} \geqslant 1\)and

$$\Delta ({{\bar {x}}^{N}},{{\lambda }^{N}}) \leqslant {{\varepsilon }_{f}},\quad g({{\bar {x}}^{N}}) \leqslant {{\varepsilon }_{g}}.$$

Proof. According to [6], we have

$${{h}_{f}}{{N}_{I}}f({{\bar {x}}^{N}}) \leqslant \mathop {\min }\limits_{x \in Q} \left\{ {{{h}_{f}}{{N}_{I}}f{\kern 1pt} \left( x \right) + {{h}_{f}}\sum\limits_{k \in I} {\left\langle {\nabla f({{x}^{k}}),{{x}^{k}} - x} \right\rangle } } \right\} \leqslant \mathop {\min }\limits_{x \in Q} \left\{ {{{h}_{f}}{{N}_{I}}f{\kern 1pt} \left( x \right) + \frac{{h_{f}^{2}}}{2}\sum\limits_{k \in I} {\left\| {\nabla f({{x}^{k}})} \right\|_{*}^{2}} } \right.$$
$$ - \;{{h}_{g}}\sum\limits_{k \in J} {\underbrace {\left\langle {\nabla g({{x}^{k}}),{{x}^{k}} - x} \right\rangle }_{ \geqslant {{g}_{{l\left( k \right)}}}({{x}^{k}}) - {{g}_{{l\left( k \right)}}}(x)}} + \frac{{h_{g}^{2}}}{2}\sum\limits_{k \in J} {\left\| {\nabla g({{x}^{k}})} \right\|_{*}^{2}} + \left. {\sum\limits_{k \in [N]} {\left( {{{V}_{{{{x}^{k}}}}}{\kern 1pt} \left( x \right) - {{V}_{{{{x}^{{k + 1}}}}}}{\kern 1pt} \left( x \right)} \right)} } \right\} \leqslant \frac{1}{2}h_{f}^{2}M_{f}^{2}{{N}_{I}} - \frac{1}{{2M_{g}^{2}}}\varepsilon _{g}^{2}{{N}_{J}} + {{\bar {R}}^{2}}$$
$$ + \;{{h}_{f}}{{N}_{I}}\mathop {\min }\limits_{x \in Q} \left\{ {f{\kern 1pt} \left( x \right) + \sum\limits_{l = 1}^m {\lambda _{l}^{N}{{g}_{l}}\left( x \right)} } \right\} = {{\varepsilon }_{f}}{{h}_{f}}{{N}_{I}} + \left( {{{{\bar {R}}}^{2}} - \frac{1}{{2M_{g}^{2}}}\varepsilon _{g}^{2}N} \right) + {{h}_{f}}{{N}_{I}}\varphi ({{\lambda }^{N}}).$$

The subsequent reasoning repeats the reasoning in the proof of Theorem 1 (see formula (7) and the text following it).

4 CONCLUDING REMARKS

In Remarks 1 and 2, the results obtained in Sections 2 and 3 are compared with other known results.

Remark 1. The results of Theorems 1 and 2 can be found in [8, 9] for the deterministic case; however, they were proved for other methods that are close to (5) but still different from it. As in [8, 9] the main advantage of method (5) is that the bounds on its convergence rate do not include the size of the dual solution, which is involved in the bounds of other primal–dual methods and approaches (e.g., see [10]).

Remark 2. In [11, 12], another method for deriving results close to those obtained in this paper in the deterministic case is proposed. The approach used in those papers is based on the ellipsoid method instead of the mirror descent method (5). Note that in Section 5 of [11], it is shown how the violation of the constraint \(g({{\bar {x}}^{N}}) \leqslant {{\varepsilon }_{g}}\) can be avoided. In the approach described in that paper, which follows the series of works [2, 8, 9], the constraint was perturbed to ensure proper bounds on the rate of the duality gap decrease. In [11, 12], the ellipsoid method was used that guaranteed the desired bounds on the convergence rate of the accuracy certificate, which majorizes the duality gap, without constraint relaxation.

The results of Sections 2 and 3 can be further elaborated. This will be briefly described in Remarks 3–7. A more detailed presentation will be made in a future paper.

Remark 3. Using the constructs described in [13] (also see [14]), the results obtained above can be extended for the case of small nonrandom noise.

Remark 4. The method described in Section 3 can be extended for the case of arbitrary \({{\varepsilon }_{g}}\) and \({{\varepsilon }_{f}}\) not satisfying the relation \({{\varepsilon }_{f}} = {{{{M}_{f}}{{\varepsilon }_{g}}} \mathord{\left/ {\vphantom {{{{M}_{f}}{{\varepsilon }_{g}}} {{{M}_{g}}}}} \right. \kern-0em} {{{M}_{g}}}}\). In Sections 2 and 3, this relation was assumed only to simplify the calculations.

Remark 5. Similarly to [5, 13, 15], we can propose an adaptive version of the method described in Section 3 that does not require the bounds \({{M}_{f}}\) and \({{M}_{g}}\) to be known a priori. Furthermore, in the case of a bounded set \(Q\), an adaptive version of the method described in Section 2 for stochastic optimization problems can be proposed (see [15]), as well as the corresponding generalization of the method AdaGrad [15]. Moreover, using the results obtained in [16] and a special choice of steps in the adaptive method, one can obtain (in the deterministic case) sharper bounds on the convergence rate that admit, e.g., the unboundedness of the Lipschitz constant of the functional on an unbounded set \(Q\).

Remark 6. The method described in Section 3 can be extended for composite optimization problems [17] in the case when the function and the functional have a common composite.

Remark 7. Using restarts as in [18], the method described in Section 3 can be extended to strongly convex problem statements (when both the functional and the constraints are strongly convex). The key observation is as follows. If \(f{\kern 1pt} \left( x \right)\) and \(g{\kern 1pt} \left( x \right)\) are \(\mu \)-strongly convex functions with respect to the norm \(\left\| {} \right\|\) on the convex set \(Q\) and \({{x}_{*}} = \arg \mathop {\min }\limits_{x \in Q,g\left( x \right) \leqslant 0} f{\kern 1pt} \left( x \right)\) for \(x \in Q\), then \(f{\kern 1pt} \left( x \right) - f({{x}_{*}}) \leqslant {{\varepsilon }_{f}}\) and \(g{\kern 1pt} \left( x \right) \leqslant {{\varepsilon }_{g}}\) imply that

$$\frac{\mu }{2}{{\left\| {x - {{x}_{*}}} \right\|}^{2}} \leqslant \max \left\{ {{{\varepsilon }_{f}},{{\varepsilon }_{g}}} \right\}.$$

Examples 1 and 2 discussed below demonstrate the possible fields of application of the proposed version of the mirror descent method. Pay attention to how the number of constraints \(m\) appears in these bounds. In the sparse case, formulas (9) and (10) seem to be very optimistic.

Example 1. The main field of application of the proposed approach is convex problems of the form (see [2, 8])

$$f({{c}^{{\text{T}}}}x) \to \mathop {\min }\limits_{\mathop {\max }\limits_{k = 1,...,m} {{\sigma }_{k}}(A_{k}^{{\text{T}}}x) \leqslant 0,\;x \geqslant 0} ,$$

\(m \gg 1\), where \(f{\kern 1pt} \left( {} \right)\) and \({{\sigma }_{k}}{\kern 1pt} \left( {} \right)\) are convex functions (of a scalar argument) with the Lipschitz constant uniformly bounded by a known number M and the (sub)gradient of each such function can be computed in an amount of time \({\rm O}\left( 1 \right)\). As applied to truss topology design, these functions may be assumed to be linear [8]. Define the matrix

$$A = {{\left[ {{{A}_{1}},...,{{A}_{m}}} \right]}^{{\text{T}}}},$$

and assume that each column of the matrix \(A\) contains not more than \({{s}_{m}} \ll m\) nonzero elements and each row contains not more than \({{s}_{n}} \ll n\) such elements (the vector \({c}\) has no more than \({{s}_{n}}\) nonzero elements as well). The results obtained in Sections 2 and 3 imply that the proposed version of the mirror descent method (with the choice of \(\left\| {} \right\| = {{\left\| {} \right\|}_{2}}\), \(d\left( x \right) = {{\left\| x \right\|_{2}^{2}} \mathord{\left/ {\vphantom {{\left\| x \right\|_{2}^{2}} 2}} \right. \kern-0em} 2}\)) requires (Theorem 2)

$${\rm O}\left( {\frac{{{{{\rm M}}^{2}}\max \left\{ {\mathop {\max }\limits_{k = 1,...,m} \left\| {{{A}_{k}}} \right\|_{2}^{2},\left\| c \right\|_{2}^{2}} \right\}R_{2}^{2}}}{{{{\varepsilon }^{2}}}}} \right)$$

iteration steps, where \(R_{2}^{2}\) is the Euclidean distance from the start point to the solution squared and each iteration step (except for the first one) requires (see [2, 19] and the reasoning in Example 2 below)

$${\rm O}\left( {{{s}_{n}}{{s}_{m}}{{{\log }}_{2}}m} \right)$$

operations. This requires \({\rm O}\left( {m + n} \right)\) operations for additional preprocessing (to prepare the memory in a proper way). Thus, the total number of arithmetic operations is

$${\rm O}\left( {{{s}_{n}}{{s}_{m}}{{{\log }}_{2}}m\frac{{{{{\rm M}}^{2}}\max \left\{ {\mathop {\max }\limits_{k = 1,...,m} \left\| {{{A}_{k}}} \right\|_{2}^{2},\left\| c \right\|_{2}^{2}} \right\}R_{2}^{2}}}{{{{\varepsilon }^{2}}}}} \right).$$
((9))

Example 2. Assume that the matrix \(A\) and the vector \({c}\) in Example 1 are not sparse. We try to introduce randomization into the approach described in Example 1. To this end, we perform some additional preprocessing to construct a probability distribution vector from nonsparse vectors \({{A}_{k}}\). Represent these vectors by

$${{A}_{k}} = A_{k}^{ + } - A_{k}^{ - },$$

where each vector \(A_{k}^{ + }\) and \(A_{k}^{ - }\) has nonnegative components. According to this representation, we prepare the memory in such a way that the time needed to generate random variables based on the probability distributions \({{A_{k}^{ + }} \mathord{\left/ {\vphantom {{A_{k}^{ + }} {{{{\left\| {A_{k}^{ + }} \right\|}}_{1}}}}} \right. \kern-0em} {{{{\left\| {A_{k}^{ + }} \right\|}}_{1}}}}\) and \({{A_{k}^{ - }} \mathord{\left/ {\vphantom {{A_{k}^{ - }} {{{{\left\| {A_{k}^{ - }} \right\|}}_{1}}}}} \right. \kern-0em} {{{{\left\| {A_{k}^{ - }} \right\|}}_{1}}}}\) takes a time \({\rm O}\left( {{{{\log }}_{2}}n} \right)\). This can always be done as was proved in [19]. However, this requires a fairly large number of the corresponding “trees” to be stored in fast memory. The time taken by the preprocessing procedure and the amount of required memory are proportional to the number of nonzero elements in the matrix \(A\), which is too large in the case of huge-scale problems. Nevertheless, we below assume that such a preprocessing can be performed and (which is the main thing) such an amount of memory is available. In practice the preprocessing is often needed only for a small number of constraints and the problem functional, so that the required amount of memory is available. Define the stochastic (sub)gradient (the same can be made for the functional)

$${{\nabla }_{x}}g(x,{{\xi }^{k}}) = \left( {{{{\left\| {A_{{k\left( x \right)}}^{ + }} \right\|}}_{1}}{{e}_{{i({{\xi }^{k}})}}} - {{{\left\| {A_{{k\left( x \right)}}^{ - }} \right\|}}_{1}}{{e}_{{j({{\xi }^{k}})}}}} \right)\sigma _{k}^{'}(A_{{k\left( x \right)}}^{{\text{T}}}x),$$

where

$$k(x) \in {\text{Arg}}\mathop {\max }\limits_{k = 1,...,m} {{\sigma }_{k}}(A_{k}^{{\text{T}}}x);$$

moreover, it is of no importance which representative of \({\text{Arg}}\max \) is chosen;

$${{e}_{i}} = \overbrace {\underbrace {\left( {0,} \right....,0,1}_i,0,...\left. {,0} \right)}^n;$$
$$i({{\xi }^{k}}) = i\quad {\text{with the probability}}\quad {{A_{{k\left( x \right)i}}^{ + }} \mathord{\left/ {\vphantom {{A_{{k\left( x \right)i}}^{ + }} {{{{\left\| {A_{{k\left( x \right)}}^{ + }} \right\|}}_{1}}}}} \right. \kern-0em} {{{{\left\| {A_{{k\left( x \right)}}^{ + }} \right\|}}_{1}}}},\quad i = 1,...,n;$$
$$j({{\xi }^{k}}) = j\quad {\text{with the probability}}\quad {{A_{{k\left( x \right)j}}^{ - }} \mathord{\left/ {\vphantom {{A_{{k\left( x \right)j}}^{ - }} {{{{\left\| {A_{{k\left( x \right)}}^{ - }} \right\|}}_{1}}}}} \right. \kern-0em} {{{{\left\| {A_{{k\left( x \right)}}^{ - }} \right\|}}_{1}}}},\quad j = 1,...,n.$$

The results of Sections 2 and 3 imply that the proposed version of the mirror descent method (with the choice of \(\left\| {} \right\| = {{\left\| {} \right\|}_{2}}\), \(d\left( x \right) = {{\left\| x \right\|_{2}^{2}} \mathord{\left/ {\vphantom {{\left\| x \right\|_{2}^{2}} 2}} \right. \kern-0em} 2}\)) requires (here, for clearness, we restrict ourselves to the convergence in expectation in Theorem 1, i.e. without bounds on the probabilities of large deviations)

$${\rm O}\left( {\frac{{{{{\rm M}}^{2}}\max \left\{ {\mathop {\max }\limits_{k = 1,...,m} \left\| {{{A}_{k}}} \right\|_{1}^{2},\left\| c \right\|_{1}^{2}} \right\}R_{2}^{2}}}{{{{\varepsilon }^{2}}}}} \right)$$

iteration steps. The main computational complexity is in computing \(k\left( x \right)\). However, except for the first iteration step, the repeated solution of this problem can be organized efficiently. Indeed, assume that \(k({{x}^{l}})\) has already been calculated and we want to calculate \(k({{x}^{{l + 1}}})\). Since \({{x}^{{l + 1}}}\) can differ from \({{x}^{l}}\) only in two components (see [2]), \(\mathop {\max }\limits_{k = 1,...,m} {{\sigma }_{k}}(A_{k}^{{\text{T}}}{{x}^{{l + 1}}})\) can be recalculated in time \({\rm O}\left( {{{s}_{m}}{{{\log }}_{2}}m} \right)\) based on the known \(\mathop {\max }\limits_{k = 1,...,m} {{\sigma }_{k}}(A_{k}^{{\text{T}}}{{x}^{l}})\) (e.g., see [19]). Thus, the expected total number of arithmetic operations in the randomized mirror descent method is

$${\rm O}\left( {{{s}_{m}}{{{\log }}_{2}}m\frac{{{{{\rm M}}^{2}}\max \left\{ {\mathop {\max }\limits_{k = 1,...,m} \left\| {{{A}_{k}}} \right\|_{1}^{2},\left\| c \right\|_{1}^{2}} \right\}R_{2}^{2}}}{{{{\varepsilon }^{2}}}}} \right).$$
((10))

For the matrices \(A\) and the vector \(c\) all nonzero elements of which have the same order of magnitude, e.g., \({\rm O}\left( 1 \right)\), we have

$$\mathop {\max }\limits_{k = 1,...,m} \left\| {{{A}_{k}}} \right\|_{2}^{2} \simeq {{s}_{n}},\quad \mathop {\max }\limits_{k = 1,...,m} \left\| {{{A}_{k}}} \right\|_{1}^{2} \simeq s_{n}^{2},\quad \left\| c \right\|_{2}^{2} \simeq {{s}_{n}},\quad \left\| c \right\|_{1}^{2} \simeq s_{n}^{2}.$$

In this case, no advantages can be expected because formulas (9) and (10) will be similar. However, if this condition (that the nonzero elements of \(A\) and \(c\) have the same order of magnitude) holds not very accurately, certain advantages can be expected.

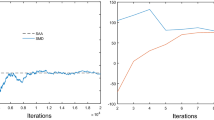
Numerical experiments confirm the estimates presented in these examples and in [2]. A more detailed description of the numerical experiments can be found in [20].

Already after this paper has been prepared for publication, we got to know the works [21–23], in which similar results were obtained. In connection with this, we note a different (simpler) technique used in this paper to obtain the main results and the treatment of the primal–dual property of the proposed method in the deterministic case.