1 INTRODUCTION

In this paper, we apply methods of linear and computer algebra to study the equilibrium orientations of a satellite (rigid body) moving in a central Newtonian force field along a circular orbit.

In the 1960s, this problem was solved by rather complicated methods. Due to solving the problem of equilibrium orientations of satellites, gravitational attitude control systems have become widespread. These systems operate based on the fact that, in a central Newtonian force field, a satellite with unequal principal central moments of inertia has 24 equilibrium orientations on a circular orbit, four of which are stable [1–3]. The dynamics of satellites with gravitational attitude control systems was considered in detail in [4].

Investigating the motion of a satellite in a central Newtonian force field on a circular orbit under the action of the gravitational torque is of considerable practical interest for developing control systems of artificial Earth satellites. An important property of gravitational attitude control systems is their capability of long-term on-orbit operation without energy and/or working fluid consumption.

In this paper, we conduct a detailed investigation of the equilibrium orientations of a satellite by using algebraic methods that have been successfully employed to study the equilibrium positions of a gyrostat satellite [5–7], dynamics of a satellite with an aerodynamic attitude control system [8], and dynamics of motion of a system of two connected bodies [9]. The equilibrium orientations of the satellite are determined by real roots of a system of algebraic equations. To find the equilibrium solutions, the system of algebraic equations is decomposed using linear algebra methods and algorithms for Gröbner basis construction [10, 11]. For this purpose, we employ the Maple computer algebra system [12]. All equilibrium orientations of the satellite on a circular orbit are determined.

Computer algebra systems are widely used to solve problems of celestial mechanics, in particular, the three-body problem [13]. For instance, using symbolic computations, new results were obtained [14–17] by investigating the classical problem of three bodies with variable masses in the general case and finding equilibrium orientations in the restricted four-body problem.

2 EQUATIONS OF MOTION

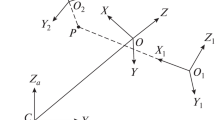
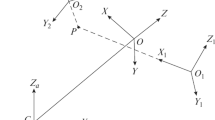
We consider the motion of the satellite (rigid body) relative to its center of mass along a circular orbit under the action of the gravitational torque. To write the corresponding equations of motion, we introduce two right-handed rectangular coordinate systems the origins of which are at the center of mass O of the satellite. In the orbital coordinate system \(OXYZ\), the OZ axis is directed along the radius vector that connects the centers of masses of the Earth and satellite, while the OX axis is directed along the linear velocity vector of the center of mass O of the satellite. Then, the OY axis is directed along the normal to the orbital plane. In the coordinate system \(Oxyz\) associated with the satellite, \(Ox\), \(Oy\), and \(Oz\) are the satellite’s principal central axes of inertia.

Let us determine the orientation of the coordinate system \(Oxyz\) relative to the orbital coordinate system by using the pitch α, yaw β, and roll γ angles. The directional cosines of the \(Ox\), \(Oy\), and \(Oz\) axes in the orbital coordinate system are expressed in terms of these angles as follows [4]:

$${{a}_{{11}}} = \cos(x,X) = \cos\alpha \cos\beta ,$$
$${{a}_{{12}}} = \cos(y,X) = \sin\alpha \sin\gamma - \cos\alpha \sin\beta \cos\gamma ,$$
$${{a}_{{13}}} = \cos(z,X) = \sin\alpha \cos\gamma + \cos\alpha \sin\beta \sin\gamma ,$$
$${{a}_{{21}}} = \cos(x,Y) = \sin\beta ,$$
$${{a}_{{22}}} = \cos(y,Y) = \cos\beta \cos\gamma ,$$
(1)
$${{a}_{{23}}} = \cos(z,Y) = - \cos\beta \sin\gamma ,$$
$${{a}_{{31}}} = \cos(x,Z) = - \sin\alpha \cos\beta ,$$
$${{a}_{{32}}} = \cos(y,Z) = \cos\alpha \sin\gamma + \sin\alpha \sin\beta \cos\gamma ,$$
$${{a}_{{33}}} = \cos(z,Z) = \cos\alpha \cos\gamma - \sin\alpha \sin\beta \sin\gamma .$$

For small satellite oscillations, the pitch corresponds to the rotation about the OY axis, yaw corresponds to the rotation about the \(OZ\) axis, and roll corresponds to the rotation about the OX axis.

Then, the equations that describe the satellite’s motion relative to its center of mass are written as follows [18]:

$$A\dot {p} + (C - B)qr - 3\omega _{0}^{2}(C - B){{a}_{{32}}}{{a}_{{33}}} = 0,$$
$$B\dot {q} + (A - C)rp - 3\omega _{0}^{2}(A - C){{a}_{{33}}}{{a}_{{31}}} = 0,$$
(2)
$$C\dot {r} + (B - A)pq - 3\omega _{0}^{2}(B - A){{a}_{{31}}}{{a}_{{32}}} = 0,$$
$$p = \bar {p} + {{\omega }_{0}}{{a}_{{21}}},\quad \bar {p} = \dot {\alpha }{{a}_{{21}}} + \dot {\gamma },$$
$$q = \bar {q} + {{\omega }_{0}}{{a}_{{22}}},\quad \bar {q} = \dot {\alpha }{{a}_{{22}}} + \dot {\beta }\sin\gamma ,$$
(3)
$$r = \bar {r} + {{\omega }_{0}}{{a}_{{23}}},\quad \bar {r} = \dot {\alpha }{{a}_{{23}}} + \dot {\beta }\cos\gamma .$$

In equations (2) and (3), A, \(B\), and \(C\) are the principal central moments of inertia of the satellite; p, q, and \(r\) are the projections of the satellite’s absolute angular velocity on \(Ox\), \(Oy\), and \(Oz\); and \({{\omega }_{0}}\) is the angular velocity of the satellite’s center of mass on a circular orbit. The dot denotes differentiation with respect to time t.

For the system of equations of motion (2) and (3), the following generalized energy integral is valid [19, 20]:

$$\begin{gathered} \frac{1}{2}(A\mathop {\bar {p}}\nolimits^2 + B\mathop {\bar {q}}\nolimits^2 + C{{{\bar {r}}}^{2}}) \\ + \;\frac{3}{2}\omega _{0}^{2}((A - C)a_{{31}}^{2} + (B - C)a_{{32}}^{2}) \\ + \;\frac{1}{2}\omega _{0}^{2}((B - A)a_{{21}}^{2} + (B - C)a_{{23}}^{2}) = {\text{const}}. \\ \end{gathered} $$
(4)

3 EQUILIBRIUM ORIENTATIONS

Suppose that all three principal central moments of inertia of the satellite are different \((A \ne B \ne C)\); then, setting \(\alpha = {{\alpha }_{0}} = {\text{const}}\), \(\beta = {{\beta }_{0}} = {\text{const}}\), and \(\gamma = {{\gamma }_{0}}\) = const in (2) and (3), we obtain the equations

$${{a}_{{22}}}{{a}_{{23}}} - 3{{a}_{{32}}}{{a}_{{33}}} = 0,$$
$${{a}_{{23}}}{{a}_{{21}}} - 3{{a}_{{33}}}{{a}_{{31}}} = 0,$$
(5)
$${{a}_{{21}}}{{a}_{{22}}} - 3{{a}_{{31}}}{{a}_{{32}}} = 0,$$

which determine the equilibrium orientations of the satellite in the orbital coordinate system. Taking into account (1), system (5) can be regarded as a system of three equations in unknowns α0, β0, and γ0.

Another (more convenient) way of closing equations (5) is to impose six orthogonality conditions on the direction cosines:

$$a_{{21}}^{2} + a_{{22}}^{2} + a_{{23}}^{2} - 1 = 0,$$
$$a_{{31}}^{2} + a_{{32}}^{2} + a_{{33}}^{2} - 1 = 0,$$
(6)
$${{a}_{{21}}}{{a}_{{31}}} + {{a}_{{22}}}{{a}_{{32}}} + {{a}_{{23}}}{{a}_{{33}}} = 0.$$

Equations (5) and (6) form a closed algebraic system of equations with respect to six direction cosines that determine the equilibrium orientations of the satellite. For this system of equations, it is required to determine all nine direction cosines, i.e., all equilibrium orientations of the satellite in the orbital coordinate system. Upon finding six direction cosines \({{a}_{{21}}}\), \({{a}_{{22}}}\), \({{a}_{{23}}}\), \({{a}_{{31}}}\), \({{a}_{{32}}}\), and \({{a}_{{33}}}\), the remaining direction cosines \({{a}_{{11}}}\), \({{a}_{{12}}}\), and \({{a}_{{13}}}\) can be determined by the following formulas taking into account that each component of the direction cosines is equal to its algebraic complement:

$${{a}_{{11}}} = {{a}_{{22}}}{{a}_{{33}}} - {{a}_{{23}}}{{a}_{{32}}},$$
$${{a}_{{12}}} = {{a}_{{23}}}{{a}_{{31}}} - {{a}_{{21}}}{{a}_{{33}}},$$
(7)
$${{a}_{{13}}} = {{a}_{{21}}}{{a}_{{32}}} - {{a}_{{22}}}{{a}_{{31}}}.$$

The cosines \({{a}_{{11}}}\), \({{a}_{{12}}}\), and \({{a}_{{13}}}\) do not vanish simultaneously.

Solutions to the system of equations (5), (6) have been studied in a number of publications. For instance, in [1, 2], it was shown that the satellite in the orbital coordinate system has 24 equilibrium orientations. In [1, 2], system (5) was solved by expressing the direction cosines in terms of Euler angles. In [3], these equilibrium orientations were obtained in an explicit and rather complex form.

4 STUDYING THE EQUILIBRIUM ORIENTATIONS OF THE SATELLITE

Equations (5) and (6) allow us to determine all equilibrium orientations of the satellite. To find the equilibrium solutions, we first use an approach based on linear algebra methods.

Let us consider the second and third equations of system (5) with respect to variables a21 and \({{a}_{{31}}}\). These equations form a homogeneous subsystem with the determinant Δ1 = \(3({{a}_{{22}}}{{a}_{{33}}} - {{a}_{{23}}}{{a}_{{32}}})\) = 3a11. If \({{a}_{{11}}} \ne 0\), then \({{a}_{{21}}} = 0\), \({{a}_{{31}}} = 0\), and equations (7) imply that a12 = \({{a}_{{13}}}\) = 0 and \(a_{{11}}^{2} = 1\).

Taking into account the expressions a22 = a11a33 – \({{a}_{{13}}}{{a}_{{31}}}\) = a11a33 and \({{a}_{{23}}} = {{a}_{{12}}}{{a}_{{31}}} - {{a}_{{11}}}{{a}_{{32}}}\) = –a11a32 obtained from the orthogonality conditions, equations (5) and (6) can be simplified as follows:

$${{a}_{{32}}}{{a}_{{33}}} = 0,$$
(8)
$$a_{{32}}^{2} + a_{{33}}^{2} = 1.$$

Equation (8) implies that either \({{a}_{{32}}} = 0\) and \(a_{{33}}^{2} = 1\) or \(a_{{32}}^{2} = 1\) and \({{a}_{{33}}} = 0\). Thus, in the case of \(a_{{11}}^{2} = 1\), we obtain eight equilibrium solutions of system (5), (6) that constitute the following two groups:

$$a_{{11}}^{2} = a_{{33}}^{2} = 1,\quad {{a}_{{22}}} = {{a}_{{11}}}{{a}_{{33}}},$$
(9)
$${{a}_{{12}}} = {{a}_{{13}}} = {{a}_{{21}}} = {{a}_{{23}}} = {{a}_{{31}}} = {{a}_{{32}}} = 0;$$
$$a_{{11}}^{2} = a_{{32}}^{2} = 1,\quad {{a}_{{23}}} = - {{a}_{{11}}}{{a}_{{32}}},$$
(10)
$${{a}_{{12}}} = {{a}_{{13}}} = {{a}_{{21}}} = {{a}_{{22}}} = {{a}_{{31}}} = {{a}_{{33}}} = 0.$$

Similarly, in the case of \(a_{{11}}^{2} = 1\), we consider the first and third equations of system (5) with respect to a22, \({{a}_{{32}}}\). These equations form a homogeneous subsystem with the determinant \({{\Delta }_{2}} = - 3({{a}_{{23}}}{{a}_{{31}}} - {{a}_{{21}}}{{a}_{{33}}})\) = –3a12. If \({{a}_{{12}}} \ne 0\), then \({{a}_{{22}}} = 0\), \({{a}_{{32}}} = 0\) and equations (7) imply that \({{a}_{{11}}} = {{a}_{{13}}} = 0\), \(a_{{12}}^{2} = 1.\) Under these conditions, from equations (5) and (6), we obtain eight equilibrium solutions included in the following two groups:

$$a_{{12}}^{2} = a_{{33}}^{2} = 1,\quad {{a}_{{21}}} = - {{a}_{{12}}}{{a}_{{33}}},$$
(11)
$${{a}_{{11}}} = {{a}_{{13}}} = {{a}_{{22}}} = {{a}_{{23}}} = {{a}_{{31}}} = {{a}_{{32}}} = 0;$$
$$a_{{12}}^{2} = a_{{31}}^{2} = 1,\quad {{a}_{{23}}} = {{a}_{{12}}}{{a}_{{31}}},$$
(12)
$${{a}_{{11}}} = {{a}_{{13}}} = {{a}_{{22}}} = {{a}_{{23}}} = {{a}_{{31}}} = {{a}_{{32}}} = 0.$$

By further considering the first and second equations of system (5) with respect to \({{a}_{{23}}}\) and \({{a}_{{33}}}\) as a homogeneous subsystem with the determinant Δ3 = \( - 3({{a}_{{21}}}{{a}_{{32}}}\) – a22a31) = 3a13, we obtain \({{a}_{{23}}} = 0\) and \({{a}_{{33}}} = 0\) for \({{a}_{{13}}} \ne 0\). Then, equations (7) imply that \({{a}_{{11}}} = {{a}_{{12}}} = 0\) and \(a_{{13}}^{2}\) = 1. Under these conditions, from equations (5) and (6), we obtain the following eight equilibrium solutions included in two groups:

$$a_{{13}}^{2} = a_{{32}}^{2} = 1,\quad {{a}_{{21}}} = {{a}_{{13}}}{{a}_{{32}}},$$
(13)
$${{a}_{{11}}} = {{a}_{{12}}} = {{a}_{{22}}} = {{a}_{{23}}} = {{a}_{{31}}} = {{a}_{{33}}} = 0;$$
$$a_{{13}}^{2} = a_{{31}}^{2} = 1,\quad {{a}_{{22}}} = - {{a}_{{13}}}{{a}_{{31}}},$$
(14)
$${{a}_{{11}}} = {{a}_{{12}}} = {{a}_{{21}}} = {{a}_{{23}}} = {{a}_{{32}}} = {{a}_{{33}}} = 0.$$

Note that each of the six groups of solutions (9)–(14) determines four equilibrium solutions (four equilibrium orientations in the orbital coordinate system). All these 24 solutions correspond to different cases of coincidence between the principal central axes of inertia of the satellite and the axes of the orbital coordinate system. Thus, the satellite with different principal central moments of inertia has 24 equilibrium orientations on a circular orbit.

5 INVESTIGATING SATELLITE EQUILIBRIUM ORIENTATIONS BY COMPUTER ALGEBRA METHODS

To solve the system of algebraic equations (5), (6), we employ algorithms for Gröbner basis construction [10, 11]. Construction of Gröbner bases is an algorithmic procedure that completely reduces a problem with a system of polynomials in many variables to a problem with a polynomial in one variable. Most modern computer algebra systems implement algorithms for Gröbner basis construction. Our investigation is carried out using the Groebner[Basis] package for Maple 17 [21]. We construct a Gröbner basis for six polynomials fi, which are the left-hand sides of the equations from system (5), (6) with six direction cosines aij (\(i = 2,3\), \(j = 1,2,3\)), by using the lexicographic ordering option plex:

G:=map(factor,Groebner[Basis]([f1,…,f6], plex(a21,…,a33))).

When using this instruction, the system executes the FGLM Gröbner basis construction algorithm developed by Faugere, Gianni, Lazard, and Mora [22]. The resulting Gröbner basis consists of 18 polynomials:

$$\begin{gathered} 1.\;{{a}_{{33}}}(a_{{33}}^{2} - 1) = 0,\quad 2.\;{{a}_{{32}}}(a_{{32}}^{2} - 1) = 0, \\ 3.\;{{a}_{{23}}}(a_{{23}}^{2} - 1) = 0,\quad 4.\;{{a}_{{22}}}(a_{{22}}^{2} - 1) = 0, \\ 5.\;a_{{21}}^{2} + a_{{22}}^{2} + a_{{23}}^{2} - 1 = 0, \\ 6.\;a_{{31}}^{2} + a_{{32}}^{2} + a_{{33}}^{2} - 1 = 0, \\ \end{gathered} $$
$$\begin{gathered} 7.\;{{a}_{{31}}}(a_{{22}}^{2} + a_{{23}}^{2} - 1) = 0, \\ 8.\;{{a}_{{21}}}(a_{{32}}^{2} + a_{{33}}^{2} - 1) = 0, \\ 9.\;1 - a_{{23}}^{2}(1 - a_{{32}}^{2}) \\ - \;a_{{22}}^{2}(1 - a_{{33}}^{2}) - a_{{33}}^{2} - a_{{32}}^{2} = 0, \\ \end{gathered} $$
(15)
$$\begin{gathered} 10.\;{{a}_{{32}}}{{a}_{{33}}} = 0,\quad 11.\;{{a}_{{31}}}{{a}_{{33}}} = 0,\quad 12.\;{{a}_{{31}}}{{a}_{{32}}} = 0, \\ 13.\;{{a}_{{23}}}{{a}_{{33}}} = 0,\quad 14.\;{{a}_{{22}}}{{a}_{{32}}} = 0,\quad 15.\;{{a}_{{22}}}{{a}_{{23}}} = 0, \\ 16.\;{{a}_{{22}}}{{a}_{{21}}} = 0,\quad 17.\;{{a}_{{21}}}{{a}_{{23}}} = 0,\quad 18.\;{{a}_{{21}}}{{a}_{{31}}} = 0. \\ \end{gathered} $$

Let us consider the first equation in (15) with respect to \({{a}_{{33}}}:{{a}_{{33}}}(a_{{33}}^{2} - 1)\) = 0. For \(a_{{33}}^{2} = 1\) (\({{a}_{{31}}} = {{a}_{{32}}}\) = a23 = 0), equations (5) imply the equalities \({{a}_{{22}}}{{a}_{{23}}} = 0\), \({{a}_{{22}}}{{a}_{{21}}} = 0\), and \({{a}_{{21}}}{{a}_{{23}}} = 0\). These equalities are also included in relations 15, 16, and 17 of the Gröbner basis (15). In this case, there are eight solutions when either \(a_{{21}}^{2} = 1\) or \(a_{{22}}^{2} = 1\), which exactly coincide with the groups of solutions (9) and (11) considered above.

From the second equation in (15), we can also obtain two groups of four solutions under the condition \(a_{{32}}^{2} = 1\) (\({{a}_{{31}}} = {{a}_{{33}}} = {{a}_{{22}}} = 0\)) when either \(a_{{21}}^{2} = 1\) or \(a_{{23}}^{2} = 1\), which also follow from the third equality of (15) and coincide with the groups of solutions (10) and (13) considered above.

Let us construct a Gröbner basis by using another lexicographic order, plex(a21,a22,a23,a32, a33,a31): to obtain a polynomial in a31:

$$\begin{gathered} 1.\;{{a}_{{31}}}(a_{{31}}^{2} - 1) = 0,\quad 2.\;{{a}_{{32}}}(a_{{32}}^{2} - 1) = 0, \\ 3.\;{{a}_{{23}}}(a_{{23}}^{2} - 1) = 0,\quad 4.\;{{a}_{{22}}}(a_{{22}}^{2} - 1) = 0, \\ 5.\;a_{{21}}^{2} + a_{{22}}^{2} + a_{{23}}^{2} - 1 = 0, \\ \end{gathered} $$
$$\begin{gathered} 6.\;a_{{31}}^{2} + a_{{32}}^{2} + a_{{33}}^{2} - 1 = 0, \\ 7.\;{{a}_{{31}}}(a_{{22}}^{2} + a_{{23}}^{2} - 1) = 0, \\ 8.\;{{a}_{{23}}}(a_{{31}}^{2} + a_{{32}}^{2} - 1) = 0,\quad 9.\;{{a}_{{21}}}{{a}_{{31}}} = 0, \\ \end{gathered} $$
(16)
$$\begin{gathered} 10.\;{{a}_{{32}}}{{a}_{{33}}} = 0,\quad 11.\;{{a}_{{31}}}{{a}_{{33}}} = 0,\quad 12.\;{{a}_{{31}}}{{a}_{{32}}} = 0, \\ 13.\;{{a}_{{23}}}{{a}_{{33}}} = 0,\quad 14.\;{{a}_{{22}}}{{a}_{{32}}} = 0, \\ 15.\;{{a}_{{22}}}{{a}_{{23}}} = 0,\quad 16.\;{{a}_{{22}}}{{a}_{{21}}} = 0,\quad 17.\;{{a}_{{21}}}{{a}_{{23}}} = 0. \\ \end{gathered} $$

The variant when \({{a}_{{31}}} = 0\) has been considered in the previous case. Let us consider the case where \(a_{{31}}^{2} = 1\) (\({{a}_{{32}}}\, = \,{{a}_{{33}}}\, = \,{{a}_{{21}}}\) = 0). Equations (5) imply that \({{a}_{{22}}}{{a}_{{23}}}\) = 0, \({{a}_{{22}}}{{a}_{{21}}} = 0\), and \({{a}_{{21}}}{{a}_{{23}}}\) = 0. These equalities are also included in relations 15, 16, and 17 of the Gröbner basis (16). In this case, there are eight solutions when either \(a_{{22}}^{2} = 1\) or \(a_{{23}}^{2} = 1\), which follow from the third and fourth equalities of (16). These solutions exactly coincide with the groups of solutions (12) and (14) considered above.

The Gröbner bases constructed imply that, for \(a_{{31}}^{2} = 1\), \(a_{{32}}^{2} = 1\), and \(a_{{33}}^{2} = 1\), each of the three cases involve eight equilibrium orientations of the satellite. In total, there are 24 equilibrium orientations of the satellite on a circular orbit (9)–(14). The same result can be obtained by constructing a Gröbner basis with the lexicographic order in \({{a}_{{21}}}\), \({{a}_{{22}}}\), \({{a}_{{23}}}\) and considering the cases where \(a_{{21}}^{2} = 1\), \(a_{{22}}^{2} = 1\), and \(a_{{23}}^{2} = 1\).

Using the left-hand side of generalized energy integral (4) as a Lyapunov function, it can be shown that, under the condition

$$B > A > C,$$
(17)

one of solutions (9) (\({{a}_{{11}}} = {{a}_{{22}}} = {{a}_{{33}}} = 1\)), a12 = a13 = a21 = \({{a}_{{23}}} = {{a}_{{31}}} = {{a}_{{32}}} = 0\), is stable [19, 20]. It is easy to verify that the remaining three solutions (9) also satisfy sufficient stability conditions (17). Thus, out of 24 equilibrium orientations, there are four stable equilibria for which the axis of the satellite’s maximum moment of inertia coincides with the normal to the orbital plane, while the axis of the satellite’s minimum moment of inertia coincides with the radius vector of the orbit. Solutions (10)–(14) do not satisfy conditions (17).

6 CONCLUSIONS

In this paper, we have investigated the equilibrium orientations of a satellite moving along a circular orbit by using methods of linear and computer algebra.

Construction of Gröbner bases is a universal method used to solve systems of algebraic equations. A significant disadvantage of this method is the exponential complexity of Gröbner basis construction algorithms. In our case, the time it took to construct a Gröbner basis on Intel Core i7 2.8 GHz with 8 Gb RAM was about 0.01 seconds. The analysis of the polynomials in the Gröbner basis has allowed us to conclude, based only on their form, that the original system of algebraic equations (5), (6) has only those solutions for which the direction cosines that determine the orientation of the satellite can take values either 0 or 1, i.e., it has only those solutions for which the axes of the orbital and satellite coordinate systems coincide.

The first method solves this problem by extracting linear subsystems from the original system while assuming that the determinants of these linear subsystems are not zero. We have not considered the cases where these determinants are zero and it is possible to obtain parametric solutions. When using the Gröbner basis method, this problem does not arise.

In turn, computer algebra methods allow one to solve the classical problem of space flight mechanics in a fairly simple form.