Tsallis Holographic Dark Energy in Bianchi Type I Universe in the Framework of $\boldsymbol{f(R)}$ Theory of Gravity

Abstract

We consider a Bianchi Type I universe filled with cold dark matter and non-interacting Tsallis holographic dark energy in the framework of $f(R)$ theory of gravity. We take the GO scale as an IR cutoff and find exact solutions of the field equations by considering a linearly varying deceleration parameter. The evolution of different cosmologically relevant parameters are studied graphically, and Statefinder diagnostics is performed in the light of recent cosmological observations. We find that our model corresponds to current accelerated expansion scenarios, and the function $f(R)\approx R$ implies that our model resembles General Relativity.

1 INTRODUCTION

General Relativity has been able to explain the evolution of the universe to a very striking accuracy, but some unexplained phenomena still evade it. Such phenomena originate from cosmology and quantum field theory and are essentially results of lack of a definitive quantum gravity theory [1]. Late-time cosmic acceleration is the latest addition to this list. According to General Relativity, the universe’s expansion should decelerate due to the effect of gravitational attraction. But the observations indicate otherwise, i.e., instead of showing deceleration, the universe is undergoing expansion with acceleration [2, 3]. This cosmic acceleration was observed not only from high-redshift surveys of Type Ia Supernovae but also from the anisotropy power spectrum of the Cosmic Microwave Background [4]. The most favored explanation for this acceleration is that the Universe is currently dominated by some form of dark energy which produces negative pressure [5].

A number of dark energy models have been proposed in the literature. However, none of them is completely satisfactory. Also, there is no satisfactory theoretical basis for the origin of this exotic matter, which is seen precisely at the epoch when one needs a source for cosmic acceleration. The simplest model is the so-called concordance model or $\Lambda$CDM model, where a cosmological constant plays the role of dark energy, and the nature of dark matter remains undetermined apart from the fact that it does not interact but gravitationally [6]. The latest observations coming from different sources seem to indicate that the energy budget of the universe is 4.9$\%$ of ordinary baryonic matter, 26.8$\%$ of dark matter and 68.3$\%$ of dark energy [4].

In the recent times, holographic dark energy has emerged as a powerful candidate to explain the consequences of dark energy. The holographic dark energy is theoretically based on the famous holographic principle by G. ‘t Hooft [7] which was later modified by Fischler and Susskind [8]. Following the work of Li [9], the density of holographic dark energy can be obtained as $\rho_{\textrm{HDE}}=3c^{2}M_{p}^{2}L^{-2}$, where $3c^{2}$ is a numerical constant, $L$ is the infrared (IR) cutoff, and $M_{p}^{2}$ is the reduced Planck mass. Different suitable choices of this IR cutoff lead to some new problems in cosmology. Tsallis and Cirto [10] in 2013 assumed some quantum modification of the horizon entropy of a black hole and proposed the entropy in the form $S=\gamma A^{\delta}$, where $\delta$ is a nonadditive parameter, $\gamma$ is a constant, and $A$ is the surface area of the event horizon. Using this entropy, the Tsallis holographic dark energy (THDE) density can be obtained as $\rho_{\textrm{THDE}}=DL^{2\delta-4}$, where $D$ is an unknown parameter, and depends on $\gamma$ and $\delta$ [11].

In this present work we use the IR cutoff as the Granda-Oliveros (GO) scale and then the THDE density $\rho_{\textrm{THDE}}=D(\alpha H^{2}+\beta\dot{H})^{-\delta+2}$, where $\alpha$ and $\beta$ are suitable constants which must satisfy the observational constraints.

Again, General Relativity is a classical theory which can describe the universe at the largest scales but surprisingly fails to describe the quantum world. In other words, General Relativity cannot be quantized [12]. There is another approach where the action of General Relativity is modified. Such modifications by introducing higher-order curvature invariants to the gravitational action have been made for a very long time. In 1919 Weyl, and in 1922, Eddington considered such modifications in the action [13, 14]. Later these modifications were revived in higher-order gravity theories. Recently, such modifications are introduced to explain the accelerated expansion. Some of the popular modified gravity theories are $f(R)$ gravity [15], $f(R,T)$ gravity [16], $f(G)$ gravity [17], $f(G,T)$ gravity [18], $f(T)$ gravity [19], etc.

The $f(R)$ theory of gravity is one of the simplest modifications of General Relativity, in which $f(R)$ is an arbitrary function of the Ricci scalar $R$. A new scalar degree of freedom appears in $f(R)$ gravity, dubbed the scalaron that is absent in General Relativity. There are three versions of $f(R)$ gravity: metric $f(R)$ gravity, Palatini $f(R)$ gravity, and metric-affine $f(R)$ gravity. The first version is the metric formalism in which the affine connection $\Gamma_{\mu\nu}^{\alpha}$ depends on $g_{\mu\nu}$. In metric $f(R)$ gravity, matter is minimally coupled to the metric. The second one uses the Palatini formalism in which $\Gamma_{\mu\nu}^{\alpha}$ and $g_{\mu\nu}$ are treated as independent variables, and the action is varied with respect to both. In metric-affine $f(R)$ gravity, one uses the Palatini variation but abandons the assumption that the action of matter is independent from the connection [20].

Recently, Ens and Santos studied $f(R)$ gravity and Tsallis holographic dark energy in the context of the FLRW metric [21]. Jawad and Chattopadhyay studied the new holographic dark energy model in the framework of modified $f(R)$ Horǎva-Lifshitz gravity [22]. Sarkar and Chattopadhyay reconstructed $f(R)$ gravity with Barrow Holographic Dark Energy (BHDE) as a form of background evolution and observed that in this case the equation of state can have a transition from quintessence to phantom [23].

In the present work, we study the anisotropic and homogeneous Bianchi Type I universe filled with pressureless cold dark matter and Tsallis Holographic Dark Energy in the framework of metric $f(R)$ theory of gravity. The paper is organized as follows: in Section 2, we give a brief introduction to $f(R)$ gravity field equations. In Section 3, we derive the field equations of the $f(R)$ gravity for the Bianchi Type I metric. Considering a generalized, linearly varying deceleration parameter proposed by Akarsu et al. [24], we solve the field equations in Section 4. In Section 5, we obtain the directional scale factors and different physical parameters of the universe. We discuss their properties graphically and perform Statefinder diagnostics in Section 6. Finally, we conclude the paper in Section 7.

2 $f(R)$ GRAVITY FIELD EQUATIONS

$f(R)$ gravity is one of the simplest modifications of Einstein’s theory of gravity. In $f(R)$ gravity, the Ricci scalar $R$ in the Einstein-Hilbert action is replaced by an arbitrary function $f(R)$ . As a result, there are changes in the gravitational geometry as described by Einstein’s field equations. One of the earliest $f(R)$ theories was proposed in [25] with $f(R)=R+R^{2}/(6M^{2})$ plus some nonlocal terms. This function could explain the cosmic inflation and also the late-time cosmic acceleration. Various other forms of the function have also been suggested in the literature to explain the present cosmic acceleration [26].

The action of $f(R)$ theory of gravity is

$$S=\frac{1}{2\kappa}\int d^{4}x\sqrt{-g}f(R)+S_{m}(g_{\mu\nu},\psi),$$

(1)

where $g$ is the determinant of the metric, $\kappa=8\pi G$, $G$ being the gravitational constant, and $\psi$ denotes matter fields.

Varying the action (1) with respect to the metric tensor $g_{\mu\nu}$, the field equations are obtained as

$$F(R)R_{\mu\nu}-\frac{1}{2}f(R)g_{\mu\nu}-\nabla_{\mu}\nabla_{\nu}F(R)$$

$${}+g_{\mu\nu}\square F(R)=\kappa(T_{\mu\nu}+\bar{T}_{\mu\nu}),$$

(2)

where $F=df(R)/dR$, $\square=\nabla^{\mu}\nabla_{\mu}$, $\nabla_{\mu}$ being the covariant derivative associated with the Levi-Civita connection of the metric. $T_{\mu\nu}$ is the stress-energy tensor of matter given by

$$T_{\mu\nu}=\frac{-2}{\sqrt{-g}}\frac{\delta L_{M}}{\delta g^{\mu\nu}}.$$

For pressureless cold dark matter, $T_{\mu\nu}=\rho_{m}u_{\mu}u_{\nu}$, $\rho_{m}$ being the energy density of cold dark matter.

For Tsallis holographic dark energy, the stress-energy tensor $\bar{T}_{\mu\nu}$ is given by

$$\bar{T}_{\mu\nu}=(\rho_{\textrm{THDE}}+p_{\textrm{THDE}})u_{\mu}u_{\nu}+p_{\textrm{THDE}}g_{\mu\nu},$$

(3)

where $\rho_{\textrm{THDE}}$ and $p_{\textrm{THDE}}$ are the energy density and pressure of THDE. In this paper, we use the natural units convention $c=8\pi G=1$. Also, time $t$ is considered to be the cosmic time (in billions of years).

3 BIANCHI TYPE I METRIC AND FIELD EQUATIONS

We consider a spatially homogeneous and anisotropic Bianchi Type I metric

$$ds^{2}=-dt^{2}+A^{2}dx^{2}+B^{2}dy^{2}+C^{2}dz^{2},$$

(4)

where $A$, $B$, and $C$ are directional scale factors which are functions of the time $t$ only. The corresponding Ricci scalar $R$ is given by

$$R=2\left(\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\ddot{C}}{C}+\frac{\dot{A}\dot{B}}{AB}+\frac{\dot{B}\dot{C}}{BC}+\frac{\dot{C}\dot{A}}{AC}\right),$$

(5)

where an over dot denotes differentiation with respect to $t$.

We assume that the universe is filled with a mixture of pressureless cold dark matter and THDE with obtained by the identification of IR cutoff GO scale given by

$$\rho_{\textrm{THDE}}=D(\alpha H^{2}+\beta\dot{H})^{-\delta+2},$$

(6)

where $H$ is the Hubble parameter, $\alpha$ and $\beta$ are constants which must satisfy the observational constraints. For $\delta=1$, the usual new holographic dark energy density can be recovered, and for $\delta=2$, the THDE behaves like a cosmological constant. For $1<\delta<2$, $\delta$ can be defined as $\delta=d/(d-1)$, $d>1$ as proposed in [27].

For the metric (4), the Hubble parameter is defined as

$$H=\frac{1}{3}\bigg{(}\frac{\dot{A}}{A}+\frac{\dot{B}}{B}+\frac{\dot{C}}{C}\bigg{)}.$$

(7)

The field equations (2) for the metric (4) in natural units are obtained as

$$\frac{\ddot{A}}{A}+\frac{\dot{A}}{A}\frac{\dot{B}}{B}+\frac{\dot{C}}{C}\frac{\dot{A}}{A}-\frac{f}{2F}-\frac{\dot{B}}{B}\frac{\dot{F}}{F}-\frac{\dot{C}}{C}\frac{\dot{F}}{F}-\frac{\ddot{F}}{F}$$

$${}=p_{\textrm{eff}},$$

(8)

$$\frac{\ddot{B}}{B}+\frac{\dot{A}}{A}\frac{\dot{B}}{B}+\frac{\dot{B}}{B}\frac{\dot{C}}{C}-\frac{f}{2F}-\frac{\dot{A}}{A}\frac{\dot{F}}{F}-\frac{\dot{C}}{C}\frac{\dot{F}}{F}-\frac{\ddot{F}}{F}$$

$${}=p_{\textrm{eff}},$$

(9)

$$\frac{\ddot{C}}{C}+\frac{\dot{B}}{B}\frac{\dot{C}}{C}+\frac{\dot{C}}{C}\frac{\dot{A}}{A}-\frac{f}{2F}-\frac{\dot{A}}{A}\frac{\dot{F}}{F}-\frac{\dot{B}}{B}\frac{\dot{F}}{F}-\frac{\ddot{F}}{F}$$

$${}=p_{\textrm{eff}},$$

(10)

$$\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\ddot{C}}{C}-\frac{f}{2F}-\frac{\dot{A}}{A}\frac{\dot{F}}{F}-\frac{\dot{B}}{B}\frac{\dot{F}}{F}-\frac{\dot{C}}{C}\frac{\dot{F}}{F}$$

$${}=-\rho_{\textrm{eff}}-p_{\textrm{eff}},$$

(11)

where $\rho_{\textrm{eff}}=(\rho_{m}+\rho_{\textrm{THDE}})/F$, and $p_{\textrm{eff}}=p_{\textrm{THDE}}/F$ are the effective energy density and pressure, respectively. The energy-momentum conservation yields

$$\dot{\rho}_{m}+\dot{\rho}_{\textrm{THDE}}+3H(\rho_{m}+\rho_{\textrm{THDE}}$$

$${}+p_{\textrm{THDE}})=0.$$

(12)

Considering the cold dark matter and THDE to be noninteracting, we can split Eq. (12) into the following two continuity equations:

$$\dot{\rho}_{m}+3H\rho_{m}=0,$$

(13)

$$\dot{\rho}_{\textrm{THDE}}+3H(\rho_{\textrm{THDE}}+p_{\textrm{THDE}})=0.$$

(14)

4 COSMOLOGICAL SOLUTIONS OF THE FIELD EQUATIONS

For the metric (4), the average scale factor $a$ is defined as

$$a=\left(ABC\right)^{1/3}.$$

(15)

From Eqs. (7)–(10), the directional scale factors $A$, $B$, $C$ in terms of $a$ can be obtained as

$$A=l_{1}ae^{m_{1}I(t)},$$

(16)

$$B=l_{2}ae^{m_{2}I(t)},$$

(17)

$$C=l_{3}ae^{m_{3}I(t)},$$

(18)

with

$$I(t)=\int\frac{1}{a^{3}F}dt,$$

(19)

where $l_{1}$, $l_{2}$, $l_{3}$ are positive constants such that $l_{1}l_{2}l_{3}=1$ and $m_{1}$, $m_{2}$, $m_{3}$ are arbitrary constants satisfying the condition $m_{1}+m_{2}+m_{3}=0$.

The integral $I(t)$ suggests that we may consider $F$ as a function of the average scale factor $a$ as

$$F=la^{n},$$

(20)

where $l$ is a constant of proportionality, and $n$ is an integer [28]. Now, to find the scale factors explicitly, we consider a generalized, linearly varying deceleration parameter proposed by Akarsu et al. [24], given as

$$q=-\frac{\ddot{a}a}{(\dot{a})^{2}}=-kt+m-1,$$

(21)

which is linear in time with a negative slope and can be considered as a generalization of Berman’s law [29, 30]. Berman’s law has been used for cosmological models obeying the Einstein equations, the Pryce-Hoyle tensor equation, Brans-Dicke relations and also in dark energy cosmological models which take into account the current acceleration of the universe. The law (21) gives a better consistency with cosmological observations as compared to Berman’s law. Integrating Eq. (21), the scale factor is obtained as

$$a=a_{1}\exp{\Big{[}\frac{2}{m}\textrm{arctanh}\Big{(}\frac{k}{m}t-1\Big{)}\Big{]}},$$

(22)

where we consider $k>0,m>0$, and $a_{1}$ is an integration constant. The argument of arctanh in Eq. (22) is $(kt/m-1)$, which is defined for $(-1,1)$. So, in our model, the universe starts at $t=0$ and ends at $t=\frac{2m}{k}$, i.e., it has a finite lifetime. By substituting the values of $m=1.6$ and $k=0.097$, it can be observed that $t\approx 33$ billion years, which is the lifetime of the universe. The energy density of the fluid and the scale factor both diverge in finite time as $t\to t_{\textrm{end}}$. This is the big rip behavior, as was first suggested by Caldwell et al. [31]. The universe begins with $q_{i}=m-1$, starts accelerating at $t_{t}=(m-1)/k$, enters into a super-exponential expansion phase at $t_{\textrm{se}}=m/k$, and ends at $q_{\textrm{end}}=-m-1$. The same has been discussed in [24]. The dark energy in our model passes into a phantom region, as shown in Figs. 8 and 14. This has been shown to be viable in a number of recent studies [32, 33] and leads into a big rip in the future.

We take $a_{1}=1$ in the present work and obtain

$$A=l_{1}\left(\frac{kt}{2m-kt}\right)^{1/m}e^{m_{1}I(t)},$$

(23)

$$B=l_{2}\left(\frac{kt}{2m-kt}\right)^{1/m}e^{m_{2}I(t)},$$

(24)

$$C=l_{3}\left(\frac{kt}{2m-kt}\right)^{1/m}e^{m_{3}I(t)}.$$

(25)

From Eq. (13), we obtain

$$\rho_{m}=\rho_{0}\left(\frac{kt}{2m-kt}\right)^{-3/m},$$

(26)

where $\rho_{0}$ is an integration constant. Also, the effective energy density of matter is obtained as

$$\rho_{m}^{\textrm{eff}}=\frac{\rho_{m}}{F}=\frac{\rho_{0}}{l}\left(\frac{kt}{2m-kt}\right)^{-(3+n)/m}.$$

(27)

From Eq. (6), the energy density and the equation of state parameter of Tsallis holographic dark energy are obtained as

$$\rho_{\textrm{THDE}}=D\left(\frac{4\xi}{t^{2}(2m-kt)^{2}}\right)^{-\delta+2},$$

(28)

$$\omega_{\textrm{THDE}}=\omega_{\textrm{THDE}}^{\textrm{eff}}=-1+(\delta-2)\frac{(2m-kt)\zeta}{6\xi},$$

(29)

where $\xi=\alpha-\beta m+\beta kt$ and $\zeta=4\beta m-4\alpha-3\beta kt$. Also, the pressure of THDE is obtained as

$$p_{\textrm{THDE}}=D\left(-1+\frac{(\delta-2)(2m-kt)\zeta}{6\xi}\right)$$

$${}\times\left(\frac{4\xi}{t^{2}(2m-kt)^{2}}\right)^{-\delta+2}.$$

(30)

The trace of the stress-energy tensor is obtained as

$$T=3p_{\textrm{THDE}}-(\rho_{m}+\rho_{\textrm{THDE}})$$

$${}=D\left(\frac{4\xi}{t^{2}(2m-kt)^{2}}\right)^{-\delta+2}-\rho_{0}\left(\frac{kt}{2m-kt}\right)^{-3/m}$$

$${}\times\left(-4+\frac{(\delta-2)(2m-kt)\zeta}{2\xi}\right).$$

(31)

Finally, the Ricci scalar $R$ and the function $f(R)$ are obtained as

$$R=24\left(\frac{m+2}{t(2m-kt)^{2}}\right),$$

(32)

$$f(R)=D\left(2-\frac{(\delta-2)(2m-kt)\zeta}{4\xi}\right)$$

$$\left(\frac{4\xi}{t^{2}(2m-kt)^{2}}\right)^{-\delta+2}+\frac{\rho_{0}}{2}\left(\frac{kt}{2m-kt}\right)^{-3/m}$$

$${}+\frac{\lambda}{t^{2}(2m-kt)^{2}}\left(\frac{kt}{2m-kt}\right)^{n/m},$$

(33)

where $\lambda=6l(2m+4-3n-n^{2}-nm)$.

Some relevant cosmological parameters are obtained as:Mean Hubble parameter,

$$H=\frac{2}{t(2m-kt)}.$$

(34)

Expansion scalar:

$$\theta=3H=\frac{6}{t(2m-kt)}.$$

(35)

Spatial volume:

$$V=a^{3}=\left(\frac{kt}{2m-kt}\right)^{3/m}.$$

(36)

Shear scalar:

$$\sigma^{2}=\frac{1}{2}\bigg{[}\bigg{(}\frac{\dot{A}}{A}\bigg{)}^{2}+\bigg{(}\frac{\dot{B}}{B}\bigg{)}^{2}+\bigg{(}\frac{\dot{C}}{C}\bigg{)}^{2}-\frac{1}{3}\theta^{2}\bigg{]}$$

$${}=\frac{m_{1}^{2}+m_{2}^{2}+m_{3}^{2}}{2l^{2}}\left(\frac{kt}{2m-kt}\right)^{-(2n+6)/m}.$$

(37)

Anisotropy parameter:

$$A_{m}=6\left(\frac{\sigma}{\theta}\right)^{2}=\frac{\left(m_{1}^{2}+m_{2}^{2}+m_{3}^{2}\right)t^{2}(2m-kt)^{2}}{12l^{2}}$$

$${}\times\left(\frac{kt}{2m-kt}\right)^{-(2n+6)/m}.$$

(38)

5 EVOLUTION OF THE RELEVANT COSMOLOGICAL PARAMETERS

In this section, we proceed to investigate the cosmological behavior of the model by studying the evolution of some cosmologically relevant parameters. From Fig. 1, it is observed that the deceleration parameter became negative when the universe was around 6 billion years old and attains a value of $q\approx-1$ at current times, which implies accelerated expansion. The deceleration parameter continues to be negative till the end of time.

From Fig. 2 it is observed that the universe starts at $t\to 0$ with $a\approx 0$, $a$ increases with time, and it increases exponentially at late times showing an accelerated expansion of the universe. Figure 3 plots the mean Hubble parameter $H$ versus cosmic time $t$, and it diverges at the beginning and at the end of the evolution. Our results obtained in Figs. 1–3 are similar to those obtained by Akarsu et al. [24]. Figure 4 shows variation of the effective energy density of dark matter with cosmic time, it is found to be decreasing in nature, as known from various cosmological observations. From Fig. 5 we observe that the early universe is highly anisotropic, and the anisotropy dies out in the course of evolution for both negative and positive values of $n$. Here, we have considered the value of $m_{1}^{2}+m_{2}^{2}+m_{3}^{2}$ equal to 0.0001 since a smaller value gives the evolution of the universe from an earlier time. A comparatively large value of $m_{1}^{2}+m_{2}^{2}+m_{3}^{2}$ shows the evolution from a later time. For $1.8<m<2$, the anisotropy of the universe has a nonzero value at the beginning i.e., at the time of big bang. For $m\geq 2$, the universe is found to be isotropic at $t=0$, but gradually the anisotropy grows and reaches a non-zero value but decays at later times and tends to zero at the end. For $m\leq 1.8$, the universe begins with high anisotropy which decays with time. For relatively smaller values of $m(\approx 0.5)$, the anisotropy decays out at very early times. For our present study, we have taken the value $m=1.6$. For large value of $k(\approx 2)$, the anisotropy of the universe dies out at the beginning, but at smaller values of $k(\approx 0.097)$, the anisotropy decays gradually and tends to zero, in agreement with the current observations. In the present study, we have considered $k=0.097$. Figure 6 shows variation of the Ricci scalar $R$ with cosmic time.

Figure 1

Evolution of the deceleration parameter $q$ with cosmic time $t$ with $k=0.097$, $m=1.6$.

Figure 2

The scale factor $a$ vs. cosmic time $t$, with $k=0.097$, $m=1.6$.

Figure 3

The Hubble parameter $H$ vs. cosmic time $t$, with $k=0.097$, $m=1.6$.

Figure 4

Evolution of the effective energy density of cold dark matter $\rho_{m}^{\textrm{eff}}$ with cosmic time $t$, with $k=0.097$, $m=1.6$, $l=1$, $\rho_{0}=1$.

Figure 5

Evolution of the anisotropy parameter $A_{m}$ with cosmic time $t$, with $k=0.097$, $m=1.6$, $m_{1}^{2}+m_{2}^{2}+m_{3}^{2}=0.0001$, $l=1$.

Figure 6

The Ricci scalar $R$ vs. cosmic time $t$, with $k=0.097$, $m=1.6$.

6 SOME PARTICULAR CASES

As already mentioned, the Tsallis holographic dark energy behaves like the usual holographic dark energy if $\delta=1$. At $\delta=2$, it behaves like a cosmological constant, and at $1<\delta<2$, $\delta$ is defined as $\delta=d/(d-1),d>1$ [27]. To study the cosmological evolution of THDE in a Bianchi Type I universe in the framework of $f(R)$ gravity, we consider the following particular cases:

Case I: $\delta=1$. In this case, we obtain

$$\rho_{\textrm{THDE}}=\frac{4D\xi}{t^{2}(2m-kt)^{2}},$$

(39)

$$\omega_{\textrm{THDE}}=\omega_{\textrm{THDE}}^{\textrm{eff}}=-1-\frac{(2m-kt)\zeta}{6\xi},$$

(40)

$$T=D\left(-4+\frac{(\delta-2)(2m-kt)\zeta}{2\xi}\right)$$

$${}\times\left(\frac{4\xi}{t^{2}(2m-kt)^{2}}\right)-\rho_{0}\left(\frac{kt}{2m-kt}\right)^{\!-3/m},$$

(41)

$$f(R)=\frac{\lambda}{t^{2}(2m-kt)^{2}}\left(\frac{kt}{2m-kt}\right)^{n/m}$$

$${}+D\frac{8\xi+\zeta(2m-kt)}{t^{2}(2m-kt)^{2}}+\frac{\rho_{0}}{2}\left(\frac{kt}{2m-kt}\right)^{\!-3/m}.$$

(42)

Figure 7 shows variation of the THDE density for $\delta=1$, and Fig. 8 variation of the EoS parameter with cosmic time $t$. We observe that the usual new holographic dark energy behaves like a phantom at late times. In Fig. 9, the trace of the stress-energy tensor $T$ is plotted against $t$, and is found to be negative at all times. Figure 10 shows the evolution of the function $f(R)$.

Figure 7

Evolution of THDE density $\rho_{\textrm{THDE}}$ with cosmic time $t$ with $D=1$, $\alpha=0.8$, $\beta=0.4$, $k=0.097$, $m=1.6$.

Figure 8

Evolution of the EoS parameter $\omega_{\textrm{THDE}}$ with cosmic time $t$, with $\alpha=0.8$, $\beta=0.4$, $k=0.097$, $m=1.6$.

Figure 9

Evolution of the trace $T$ of the stress energy tensor vs. $t$, with $D=1$, $\alpha=0.8$, $\beta=0.4$, $k=0.097$, $m=1.6$, $\rho_{0}=1$.

Figure 10

The function $f(R)$ vs. $t$, with $D=1$, $\alpha=0.8$, $\beta=0.4$, $k=0.097$, $m=1.6$, $\rho_{0}=1$, $l=1$.

Figure 11

Evolution of the trace $T$ vs. $t$, with $D=1$, $k=0.097$, $m=1.6$, $\rho_{0}=1$.

Figure 12

The function $f(R)$ vs. $t$ with $D=1$, $k=0.097$, $m=1.6$, $\rho_{0}=1$, $l=1$.

Figure 13

The THDE density $\rho_{\textrm{THDE}}$ vs. cosmic time $t$, with $D=1$, $\alpha=0.8$, $\beta=0.4$, $k=0.097$, $m=1.6$.

Figure 14

The EoS parameter $\omega_{\textrm{THDE}}$ vs. $t$, with $\alpha=0.8$, $\beta=0.4$, $k=0.097$, $m=1.6$.

Figure 15

The trace $T$ vs. $t$, with $D=1$, $\alpha=0.8$, $\beta=0.4$, $k=0.097$, $m=1.6$, $\rho_{0}=1$.

Figure 16

The function $f(R)$ vs. $t$, with $D=1$, $\alpha=0.8$, $\beta=0.4$, $k=0.097$, $m=1.6$, $\rho_{0}=1$, $l=1$.

Figure 17

Evolution of the Statefinder parameter $r$ vs. $s$, with $k=0.097$, $m=1.6$, $t=13.8$.

Case II: $\delta=2$. In this case, $\rho_{\textrm{THDE}}=D$, and $\omega_{\textrm{THDE}}=-1$, which mimics the energy density and the equation of state parameter of the cosmological constant. We have:

$$T=-4D-\rho_{0}\left(\frac{kt}{2m-kt}\right)^{-3/m},$$

(43)

$$f(R)=2D+\frac{2\lambda}{t^{2}(2m-kt)^{2}}\left(\frac{kt}{2m-kt}\right)^{n/m}$$

$${}+\frac{\rho_{0}}{2}\left(\frac{kt}{2m-kt}\right)^{-3/m}.$$

(44)

In Fig. 11, the trace $T$ of the stress energy tensor is plotted against cosmic time $t$, it is found to be negative and attains a constant value at late times. Figure 12 shows variation of the function $f(R)$ with cosmic time $t$, it is observed to be similar to that of the Ricci scalar $R$ shown in Fig. 6.

Case III: $\delta=1.4$. In this case, we plot the THDE density, EoS parameter, the trace $T$ and the function $f(R)$ versus cosmic time $t$ for the particular value $\delta=1.4$. Figure 13 shows variation of the THDE density, and Fig. 14 variation of the EoS parameter with cosmic time $t$. In this case we also observe that the THDE behaves like a phantom at late times. Figure 15 shows the trace $T$ as a function of $t$, and it is found to be negative, while Fig. 16 shows variation of the function $f(R)$ with $t$.

7 STATEFINDER DIAGNOSTICS

The Statefinder is a geometric diagnostic that characterizes the properties of dark energy in a model-independent manner [34]. It is used for distinguishing different types of dark energy. It was introduced to characterize flat universe models with cold dark matter (dust) and dark energy. It is dimensionless and is constructed from the scale factor $a$ of the universe and its time derivatives only. The parameter $r$ forms the next step in the hierarchy of geometrical cosmological parameters after the Hubble parameter $H$ and the deceleration parameter $q$, while $s$ is a linear combination of $q$ and $r$ chosen in such a way that it does not depend on the dark energy density, given as

$$r=\frac{1}{aH^{3}}\frac{d^{3}a}{dt^{3}},\quad s=\frac{r-1}{3(q-\frac{1}{2})}.$$

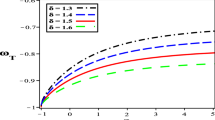
The Statefinder pair $\{r,s\}$ is algebraically related to the equation of state of dark energy and its first time derivative. For the $\Lambda$CDM model, the statefinder pair becomes (1, 0). From Fig. 17 we observe that our model admits a $\Lambda$CDM scenario at late times.

8 CONCLUSION

In this paper, we have studied a spatially homogeneous and anisotropic Bianchi Type I universe filled with cold dark matter and a non-interacting Tsallis holographic dark energy in the framework of $f(R)$ theory of gravity. Exact solutions of the field equations are obtained by considering a generalized linearly varying deceleration parameter, and we derived various parameters of cosmological importance. The cosmological behavior of the model is studied graphically, including physical and geometric properties of the relevant parameters. We also perform Statefinder diagnostics in the light of recent cosmological observations. We find that:

• Our model is a finite time model where the universe passes on from deceleration to the present accelerating epoch and will eventually enter into superexponential expansion.

• The new holographic dark energy behaves like phantom dark energy at late times, and the universe ends in a Big Rip.

• The universe starts with high anisotropy, which dies out rapidly. The anisotropy decrease is more rapid at negative values of $n$ than at positive values of $n$.

• The Ricci scalar is found to be positive and diverging at the beginning and at the end of the evolution.

• The THDE density decreases at early times and increases at late times for $\delta=1$ and 1.4, while it behaves like cosmological constant at $\delta=2$.

• The trace $T$ of the stress energy tensor is found to be negative for all the three values of $\delta$.

• The function $f(R)\approx R$ for $\delta=2$, which implies that our model resembles General Relativity .

• The Statefinder parameters pass through the point (1, 0) which corresponds to the $\Lambda$CDM model.