INTRODUCTION: SPECIFIC FEATURES OF THE FLUID DYNAMICS OF A SPRAY CONE OF A NOZZLE

Liquid spraying into a gas, e.g., by nozzles, is used in power and chemical engineering to intensify (by increasing the interfacial area) such processes as combustion or pyrolysis of liquid hydrocarbons, wet air scrubbing to remove dust and harmful gaseous impurities, and drying and granulation of polymers.

Methods of calculation of such heat- and mass-transfer processes are based on the concepts of the pattern of the formed two-phase flow in the spray cone, the forces of interaction of the drops with the gas, and elementary heat and mass transfer processes between the gas and a single drop [1, 2].

Methods of satisfactory calculation of the fluid dynamics of a spray cone and the interphase heat and mass transfer in it have not until recently been developed. This emphasizes the topicality of this work, which is a continuation of the previous studies [1–3].

Interphase heat and mass transfer processes are very often simultaneous and parallel, which complicates modeling and calculation of integrated transfer processes. The purpose of the current work is to model an integrated process comprising evaporation and cooling of water drops sprayed in air with taking into account the crisises of drag of the drops and the interphase heat and mass transfer.

Previously [2], a simpler process of interphase mass transfer (without heat transfer) was modeled and calculated, specifically, wet air scrubbing to remove harmful gaseous impurities, e.g., SO2.

Two-phase flows are mathematically modeled using two main approaches: the method of interpenetrating continua [4] and the theory of turbulent jets [5]. Using the former approach, each of the phases is considered as a continuum distributed continuously throughout space with a variable density averaged over a small volume, and the velocities of the phases are believed to be different. Using the latter approach, the concentration of the dispersed phase is assumed to be low and the velocities of the phases are assumed to be approximately equal, with the turbulence of the gas phase being taken into account.

An example of one of the first applications of the continual approach to calculating a gas–drop two-phase flow is the one-dimensional model of flow dynamics of a nozzle spray cone [6]. Subsequently, this model was used many times as a basis for modeling a number of heat- and mass-transfer chemical engineering processes with liquid spraying, in particular, evaporation of liquid hydrocarbon feedstock in carbon black production [7]. This approach should be further developed by the creation of a two-dimensional model of an axisymmetric spray cone. A number of the following important features must be taken into account.

As has been experimentally determined, the gas flow in a nozzle spray cone is a turbulent jet [1], which originates at the spray cone vertex because of the interaction of the phases. Well away from the nozzle, the jet develops independently of the drop flow and differs from a single-phase gas jet by the flow pattern and the characteristics of the turbulent friction. In particular, it has been shown that the dimensionless profiles of the axial velocity of the gas are shallower than those in a single-phase jet; a noticeable difference between the velocities of the phases has been observed, and gas pressure differences on the order of 1–10 Pa along the radius and axis of the spray cone have been detected.

Thus, in the two-dimensional model of the spray cone, it is necessary and advisable to use the continual approach, taking into account the turbulence of the jet gas flow.

Moreover, experiments have shown a significant feature of the interaction between the phases, which has been called the early crisis of drag [1] (see below). This feature must also be taken into account in calculating the spray cone and consists in the following.

The known classical drag crisis in a sphere moving in a viscous medium is a phenomenon in which the drag force and the drag coefficient of the medium at a Reynolds number of Re = Recr ≈ (2–3) × 105 decrease by a factor of approximately 4–5 times [8–12]. This is due to a transition of the laminar boundary layer near the surface of a streamlined body to a turbulent one, a shift of the flow separation line downstream the flow, and improvement of the streamlining of the body with decreasing drag [11].

The critical Reynolds value Recr depends on the degree of turbulence of the viscous medium flowing past the sphere and decreases with increasing degree of turbulence. Cases of the drag crisis of a sphere have been described even at Recr ≈ 400–2200 [10].

Nozzle liquid spraying produces drops with Sauter mean diameter d on the order of 10–4 m. At such sizes and with a significant difference between the dynamic viscosities of the liquid of the drops and the gas flowing past them (for water and air, by a factor of approximately 60 times), one can ignore the deformation of the drops and the internal flow of the liquid in them and consider them as solid balls.

The drag force on a drop past which a gas flows is typically calculated as

$$F~\,\, = \,\,{{~{{C}_{{\text{d}}}}~s~\rho ~{{V}^{2}}} \mathord{\left/ {\vphantom {{~{{C}_{{\text{d}}}}~s~\rho ~{{V}^{2}}} 2}} \right. \kern-0em} 2},$$
(1)

where V = u – w is the relative velocity of the drop in the gas, Cd is the drag coefficient, s is the central-section area of the spherical drop, ρ is the gas density, and μ is the dynamic viscosity of the gas.

In the case of a laminar flow past a ball at low Reynolds numbers Re = Vdρ/μ \( \ll \) 1, the Stokes formula Cd = 24/Re is used, and in a transition range of 2 < Re < 700, the Klyachko formula

$${{C}_{{\text{d}}}}~~ = ~\,\,{{24} \mathord{\left/ {\vphantom {{24} {{\text{Re}}}}} \right. \kern-0em} {{\text{Re}}}}{{\;}} + \,\,~{4 \mathord{\left/ {\vphantom {4 {{\text{R}}{{{\text{e}}}^{{1/3}}}}}} \right. \kern-0em} {{\text{R}}{{{\text{e}}}^{{1/3}}}}}$$
(2)

approximates well the experimental data generalized by the standard Raileigh curve [9, 8].

It has been experimentally demonstrated [1] that, in the developed turbulent flow of a nozzle spray cone at Re = Recr ≈ 100, Cd of the drops decreased by a factor of 4–7 in comparison with the values given by the Klyachko formula (2). This is the earliest crisis of drag.

In particular, for the drops moving along the axis of the spray cone, a good approximation at 40 < Re < 110 was proposed in [1]:

$${{C}_{{\text{d}}}}~\,\, = {{2000} \mathord{\left/ {\vphantom {{2000} {{{{\operatorname{Re} }}^{2}}}}} \right. \kern-0em} {{{{\operatorname{Re} }}^{2}}}}.$$
(3)

A subsequent analysis of experimental data showed that formula (3) is valid not only for the drops in the axis of the spray cone, but also for all of the drops in the volume of the spray cone at z > 0.1 m. Furthermore, to simplify calculations, one can take into account that, in the self-similar flow zone of the free spray cone, at z > 300 mm and Re > 110,

$${{C}_{{\text{d}}}}\left( {r,~z} \right)~\,\, = \,\,~{{C}_{{\text{d}}}}\left( {\operatorname{Re} } \right)~\,\, \simeq \,\,~0.1$$
(4)

with an approximate deviation of ±0.05.

The same early drag crisis was observed in a gas flow in a convergent tube past a single solid ball [3, Sect. 5.1].

As one of the possible causes of the early crisis of drag of a spherical particle, a hypothesis of the effect of the high turbulence of the gas flow was considered: this turbulence was additionally increased by the convergent tube in comparison with a free jet and was sufficient to induce the early crisis in a single solid ball [3, Sect. 5.1].

This assumption was confirmed by numerical modeling of both laminar and highly turbulent gas flow past a ball [3, Sect. 5.3].

The above suggested that, for mathematical and numerical modeling of a spray cone as a two-phase flow, taking into account all its features, to describe the motion of both phases in the same manner, it is reasonable to use a combination of the method of interpenetrating continua [4] and the theory of turbulent jets [5]. This idea was used in the two-dimensional model of the flow dynamics of the free spray cone and the two-phase flow bounded by the walls of a cylindrical apparatus [3, Sect. 7.2].

For more information on the subject of investigation, including the consideration of the early crisis of drag in the interaction between the phases in the spray cone, and also the description of the foundations of the mathematical model used in this work, the reader is referred to the previous works [2, 3]

MODELING OF THE HEAT AND MASS TRANSFER IN A FREE SPRAY FLOW PRODUCED BY A NOZZLE

The model under consideration is based on the equations of the fluid dynamics of a two-phase flow. For example, in the previous work [2], along with formula (1), such equations are Eqs. (4)–(14). The last two of them takes into account the early drag crisis in the drops in their interaction with the highly turbulent gas flow by using the experimentally determined dependence Cd(r, z). Note that, in this work, along with them, the formulas (3) and (4) are also used.

To calculate the interphase mass transfer (without considering heat transfer), this system of fluid-dynamic equations (4)–(14) was supplemented [2] with Eqs. (15)–(19), which take into account the convective transfer of the impurity gas component in the flow and from the gas to the liquid drops.

Similarly, in this work, the system of Eqs. (4)–(19) from the previous work [2] was supplemented with the below equations of convective heat transfer in each of the phases and convective mass transfer of the vapor as one of the components of the gas phase, and also with relations describing the heat and mass transfer from the liquid drops into the gas flow.

To take into account the heat transfer within the gas phase, the mathematical model can and must be supplemented with the “heat balance equation” [11, p. 436], which has also been called the “total heat transfer equation” [12, p. 277] and was before [3, Sect. 6.1] presented under number (6.8) in the form

$${{\rho ~{{c}_{v}}~dT} \mathord{\left/ {\vphantom {{\rho ~{{c}_{v}}~dT} {d\tau ~}}} \right. \kern-0em} {d\tau ~}} = \,\,~ - ~P~{\text{div}}{\mathbf{w}}~\,\, + ~\,\,{\text{div}}\left( {\lambda ~\nabla T} \right)~\,\, + \,\,~{{\Phi }_{d}}.$$
(5)

In formula (5), the last term Φd describes the dissipation of the mechanical energy of the gas into heat. It has been reported [11, 12] that, at low flow velocities and low gas compression ratio, this term can be represented as

$${{\Phi }_{d}}\,\,~ = \,\,~{\mu \mathord{\left/ {\vphantom {\mu 2}} \right. \kern-0em} 2}{{\left( {{{\partial {{w}_{i}}} \mathord{\left/ {\vphantom {{\partial {{w}_{i}}} {\partial {{x}_{k}}}}} \right. \kern-0em} {\partial {{x}_{k}}}} + ~{{\partial {{w}_{k}}} \mathord{\left/ {\vphantom {{\partial {{w}_{k}}} {\partial {{x}_{i}}}}} \right. \kern-0em} {\partial {{x}_{i}}}}} \right)}^{2}}.$$
(6)

At small differences between the temperatures of the sphere (drop) and the gas flowing past it, the viscosity μ and thermal conductivity λ of the gas (air) differ little. As calculations have shown [3, Sect. 6.2], in this case, the effect of the term Φd on the distributions of the velocities and temperatures of the gas can also be ignored. Then, Eq. (5) can be transformed to the form

$$\begin{gathered} \frac{{\partial T}}{{\partial \tau }} + {{w}_{z}}\frac{{\partial T}}{{\partial z}} + {{w}_{r}}\frac{{\partial T}}{{\partial r}} \\ = - 0.4T~{\text{div}}{\mathbf{w}} + \frac{\lambda }{{\rho ~{{c}_{v}}}}\Delta T + \frac{Q}{{\rho ~{{c}_{v}}}}. \\ \end{gathered} $$
(7)

In the transition from formula (5) to formula (7), the relation P/(ρcv) = RT/(Mcv) ≈ 0.4T was used, which follows from the ideal gas law using data on air; the heat flux Q from all the drops to the gas per unit volume of spray was also taken into account.

The notation in formulas (5)–(17) is the following: α is the liquid volume fraction; ρl is the physical density of the drops; wz and wr are the axial and radial components of the gas velocity, respectively; uz and ur are the same for the liquid, respectively; ρsv is the density of the saturated water vapor near the surface of the drop; ρv = ρv(r, z) is the density of the water vapor in air far from the drop; сv is the specific heat at constant volume; сp is the specific heat at constant pressure; cl is the specific heat of the drops; a = λ/(ρсp) is the thermal diffusivity of the gas; Pr = ν/a = 0.71 is the Prandtl number; ν = μ/ρ is the kinematic viscosity of the gas; D is the diffusion coefficient of the water vapor in the gas; PrD = ν/D = 0.64 is the diffusion Prandtl number (sometimes called the Schmidt number Sc); Vd is the drop volume; L is the specific heat of evaporation of the liquid drops; R = 8.31 J/(mol K) is the universal gas constant; and M is the molar mass of the gas. The presented numerical estimates were made using data on air at a temperature of tg = 20°C.

Using the previous results [3, Sect. 6.3], to simplify the interphase heat transfer model, the temperatures at all the points within the drop and on its surface can be taken as equal to each other (Tl = Tl(r, z)) and dependent only on the coordinates r and z of the drop in the spray cone. This gives an external problem of interphase heat transfer. Then, the density of the heat flux from a single drop with the surface temperature Tl to its surrounding gas with the temperature Tg = Tg(r, z) can be described by Newton’s law of cooling

$$q = {{k}_{t}}\left( {{{T}_{l}} - {{T}_{g}}} \right)$$
(8)

with the heat-transfer coefficient

$$~{{k}_{t}} = ~{\text{Nu}}\;{\lambda \mathord{\left/ {\vphantom {\lambda d}} \right. \kern-0em} d}.$$
(9)

The Nusselt number can be found from the Ranz-Marshall correlation [13]

$${\text{Nu}} = {{\;}}2 + 0.6{\text{R}}{{{\text{e}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}~{\text{P}}{{{\text{r}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}.$$
(10)

Then, using formula (9), the heat flux from all the drops to the gas per unit spray cone volume can be represented as

$$Q = \frac{{4q~s~\alpha }}{{{{V}_{{\text{d}}}}}} = \frac{{6q~\alpha }}{d} = \frac{{6{{k}_{t}}~\left( {{{T}_{l}} - {{T}_{g}}} \right)~\alpha }}{d}.$$
(11)

To take into account the mass transfer of the vapor in the gas flow and its mass transfer from the liquid drops to the gas by analogy with the previous work [2], where Eqs. (15)–(19) considered the interphase mass transfer of the impurity gas component, the above system of Eqs. (5)–(11) was also supplemented with Eqs. (12)–(16).

Keeping in mind the analogy between the phenomena of interphase heat and mass transfer [11], for the density of the mass flux of the vapor from a single drop to the gas, the mass-transfer equation can be written:

$${{j}_{v}} = {{k}_{m}}\left( {{{\rho }_{{sv}}} - {{\rho }_{v}}} \right),$$
(12)

which is similar to Newton’s law of cooling (8) for the heat flux density. Also by analogy with the heat-transfer coefficient, the mass-transfer coefficient from the drop to the gas can be defined:

$$~{{k}_{m}} = ~\;{\text{N}}{{{\text{u}}}_{D}}~{D \mathord{\left/ {\vphantom {D d}} \right. \kern-0em} d},$$
(13)

and the diffusion Nusselt number can be defined by analogy with Ranz-Marshall correlation (10)

$${\text{N}}{{{\text{u}}}_{{D{{\;}}}}} = {{\;}}2 + 0.6{\text{R}}{{{\text{e}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\;{\text{Pr}}_{D}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}},$$
(14)

which is well known in heat-transfer studies.

Then, using Eq. (12), the vapor mass flux from all the drops to the gas per unit spray volume can be represented by the relations

$$J = \frac{{4{{j}_{v}}~s~\alpha }}{{{{V}_{{\text{d}}}}}} = \frac{{6{{j}_{v}}~\alpha }}{d} = \frac{{6{{k}_{m}}~\left( {{{\rho }_{{sv}}} - {{\rho }_{v}}} \right)~\alpha }}{d}.$$
(15)

The equation of convection–diffusion transfer of the vapor in the gas flow with taking into account its mass transfer from the liquid drops to the gas can be written as

$$\frac{{\partial {{\rho }_{v}}}}{{\partial \tau }} + {{w}_{z}}\frac{{\partial {{\rho }_{v}}}}{{\partial z}} + {{w}_{r}}\frac{{\partial {{\rho }_{v}}}}{{\partial r}} = D\Delta {{\rho }_{v}} + J.$$
(16)

To the right-hand side of the continuity equation (4) for the gas from the previous work [2], the same term J should be added, as the last term of Eqs. (15) and (16) here. To the right-hand side of Eq. (5) from the previous work [2], to change the axial velocity wz of the gas, the term uz J/ρ should be added, which describes the thrust (momentum flux) due to the vapor inflow at the rate of evaporating drops in to the gas flow; to the right-hand side of Eq. (6) of the same system of Eq. (4)–(9) from the previous work [2], the similar term ur J/ρ should be added.

Furthermore, to take into account the heat transfer in the dispersed phase, the mathematical model should be supplemented with an equation similar to Eq. (7), but simpler:

$$\frac{{\partial {{T}_{l}}}}{{\partial \tau }} + {{u}_{z}}\frac{{\partial {{T}_{l}}}}{{\partial z}} + {{u}_{r}}\frac{{\partial {{T}_{l}}}}{{\partial r}} = - \frac{{Q + J~L}}{{\alpha ~{{\rho }_{l}}~{{c}_{l}}}}.$$
(17)

The numerator of the fraction on the right-hand side of Eq. (17) characterizes the decrease in the heat of the liquid drops due to the heat transfer to the gas (Q) and the evaporation from their surface (JL).

Without taking into account the mass-transfer crisis similar to the heat-transfer crisis [3, Sect. 6.2], formulas (10) and (14) give the values Nu ≈ NuD > 2. To take into account the heat- and mass-transfer crisis, which, like the drag crisis of the drops, is caused by the high turbulence of the gas flow, the values Nu = NuD = 2 should be used.

The system of Eqs. (1) and (4)–(12) from the previous work [2], supplemented with formulas (3)–(17) presented here, enables one to calculate the changes in the temperatures T(r, z) and Tl(r, z) of the phases in the two-phase flow of the nozzle spray cone both with and without taking into account the drag crisis in the drops and the heat- and mass-transfer crisis in the phases.

In the numerical model of the spray cone, before replacing the differential equations by their difference analogs, it is worth nondimensionalizing the variables by dividing the coordinates r and z by the initial (minimum) radius r0 = z0tanφ of the spray cone in the computational domain (z0 = 100 mm is the distance from the upper boundary of the computational domain to the nozzle hole); the velocities w, u, V, and ws, by the initial velocity u0 of the drops (liquid jet); the density ρ of air (and also water vapor), by the density ρ0 of the quiescent gas far from the spray cone; the time τ, by τ0 = r0/u0; and the temperatures T and Tl, by, e.g., T0 = 293 K. The form of Eqs. (4)–(9) from the previous work [2], and also Eqs. (7), (16), and (17) in this work remains unchanged, and at the terms on the right-hand sides of these equations, the corresponding additional coefficients emerge.

As in the previous work [2], in the transition from the above differential equations to their difference analogs using Eqs. (1) and (10)–(12) from the previous work [2] and Eqs. (3)–(4) and (8)–(15) in this work for approximating the convective terms on rectangular spatial computational grid (i, j), the Lax–Wendroff two-step explicit difference scheme was used [14]. This scheme is time-centered; therefore, the numerical effects of viscosity and diffusion on it are much weaker than in the Lax one-step scheme, and consequently, the velocity profiles of each of the phases are closer to the true ones.

For the Lax–Wendroff scheme to be stable, the Courant–Friedrichs–Lewy condition should be met [14], which, at equal grid steps Δz = Δr, has the form

$$\Delta \tau \leqslant \frac{{\Delta z}}{{\sqrt {2\left( {w_{s}^{2} + w_{z}^{2} + w_{r}^{2}} \right)} }}.$$
(18)

The diffusion terms of Eqs. (7) and (16) were approximated using an explicit scheme of the first order of accuracy [14, p. 107], for which the stability condition on a two-dimensional grid has the form

$$\Delta \tau \leqslant \frac{{{{{(\Delta z)}}^{2}}}}{{4D}}.$$
(19)

For the stability of the entire difference scheme, both conditions (18) and (19) should simultaneously be met, of which the first turned out to be stronger.

An advantage of the proposed numerical model is that it allows one to calculate all the variables using a simple explicit scheme.

A certain difficulty in constructing the numerical model was to impose suitable boundary conditions, which preserve the stability of the difference scheme. The difference scheme at the boundary points of the grid has a different form in comparison with that at internal points, because the spatial derivatives in the former case are approximated by one-sided, rather than two-sided, differences. Moreover, at the axis of symmetry (at r = iΔr = 0), the radial velocities of the phases are wr = ur = 0, and the derivatives of some variables with respect to r can also become zero.

Using experimental data, at the upper (inlet) boundary of the computational domain (j = 0), the profile of the liquid volume fraction should be set, e.g., in the triangular shape α(r, z0) = 3(rn/r0)2(1 – r/r0), where rn is the nozzle hole radius, and r0 = z0tanφ. The radial profiles of the components uz(r, z0) and ur(r, z0) of the liquid velocity should also be specified. The shape of the first of them can be taken as rectangular, trapezoidal, or more complex, whereas the second, with the consideration of the pattern of the liquid outflow from the nozzle hole, should be given as a function of the radius: ur(r, z0) = uz(r, z0)r/z0.

In the case of a free spray of a nozzle, the gas density at the lateral (external) boundary of the computational domain can be found from the Bernoulli’s equation

$$\rho = {{\rho }_{0}}\left( {1 - \frac{{w_{z}^{2} + w_{r}^{2}}}{{2w_{{s0}}^{2}}}} \right).$$

and the gas temperature is taken to be equal to its initial value T0 = 293 K.

In the calculation of the two-phase flow in a cylindrical spraying apparatus, on its wall, which is the lateral boundary of the computational grid, the conditions under which the components of the gas velocity are zero are set: wz = wr = 0; the temperatures of the gas and the liquid can be considered equal (T = Tl) at z ≥ zw = Rapp/tanφ because of the wetting of the apparatus wall with the liquid flowing down as a film.

RESULTS OF THE CALCULATION OF THE HEAT AND MASS TRANSFER OF THE PHASES IN THE FREE SPRAY CONE OF A NOZZLE

The above algorithm was implemented using the Delphi software for calculating the fluid dynamics and the heat and mass transfer in the vertically axisymmetric spray cone of a centrifugal spray nozzle with a hole diameter of dh = 2 mm.

The free spray cone was calculated using from work [2] the dependence (11) for the Reynolds stress of the gas and dependences (13) and (14) for the drag coefficient of the drops. In the calculation of the two-phase flow in the apparatus, instead of the last two dependences, formulas (3) and (4) of this work were used.

As a unit of the dimensionless spatial scale of the grid, the radius r0 = z0tanφ of the spray cone at the upper boundary of the computational domain was taken (φ = 32.5° is the spray cone half-angle, and z0 = 100 mm) and as a unit of velocity scale, the initial velocity u0 = 0.75(2Рl/ρl)1/2 of the liquid leaving the nozzle. As d, the volume-surface mean diameter d32 = 0.14 mm of the drops was used, which was measured at a water pressure at the nozzle of Рl = 5 × 105 Pa. The thermophysical characteristics of the gas were taken as for air, those of the liquid as for water. The initial temperature of the air was taken to be T0 = 293 K, that of the water drops, as Tl = 1.1T0 = 322 K.

The computations were made on a rectangular spatial domain with physical sizes rmax = hmax(i), zmax – z0 = hmax(j), and h = 4 mm. The number of grid points in the calculation of the free spray cone was varied to max(i) = max(j) = 200 at a dimensionless grid step of Δr = Δz = 1/16, which ensured sufficient approximation of the difference scheme.

The (quasi-)steady-state flow of interest was reached by the evolution of the unsteady-state solution in the “grid” time that was approximately 15–20 times longer than the characteristic time τs = (zmax − z0)/u0, in which the drops could move from the upper to the lower boundary of the computational domain without taking into account their deceleration in the gas.

Figures 1–6 present the results of the calculations of the interphase heat and mass transfer in the axisymmetric free nozzle spray cone using the proposed model.

Fig. 1.
figure 1

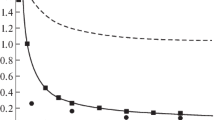
Calculated dependences of the velocities of the gas (wz[0, j]) and the drops (uz[0, j]) and their temperatures (tg[0, j] and tl[0, j], respectively) in the axis of the free spray cone. The open symbols represent the results of the calculation without taking into account the drag crisis by Klyachko formula (2) and the heat- and mass-transfer crisis using formulas (10) and (14) at Nu ≈ NuD > 2. The filled symbols represent the results of the calculation with taking into account the drag crisis by formulas (13) and (14) from the previous work [2] and the heat- and mass-transfer crisis at Nu = NuD = 2.

Full size image
Fig. 2.
figure 2

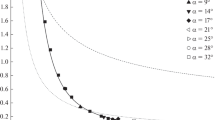
Radial profiles of the temperatures of the phases at various distances z = (100 + 4j) mm from the nozzle in the free spray cone with taking into account the drag crisis in the drops and their heat- and mass-transfer crisis with the gas. The filled and open symbols represent the reduced temperatures of the gas (tg[i, j]) and the drops (tl[i, j]) respectiveiy.

Full size image
Fig. 3.
figure 3

The same as in Fig. 2 with taking into account the drag crisis in the drops by formulas (13) and (14) from the previous work [2], but without taking into account the heat- and mass-transfer crisis at Nu ≈ NuD > 2. The notation is the same as in Fig. 2.

Full size image
Fig. 4.
figure 4

The same as in Fig. 2 without taking into account the drag crisis in the drops using formula (2), but with taking into account the heat- and mass-transfer crisis of the phases at Nu = NuD = 2. The notation is the same as in Fig. 2.

Full size image
Fig. 5.
figure 5

The same as in Fig. 2 without taking into account the drag crisis of the drops and their heat- and mass-exchange crisis with the gas. The notation is the same as in Fig. 2.

Full size image
Fig. 6.
figure 6

Changes in the centigrade temperatures 〈tg[i, j]〉 and 〈tl[i, j]〉 of the phases, averaged over a section of the two-phase flow, with distance z = 100 + 4j mm from the nozzle.

Full size image

Figure 1 shows the axial profiles of the velocities of the phases and the reduced temperatures of the gas (tg[0, j] = 10(T[0, j]/T0 – 1)) and the drops (tl[0, j] = 10(Tl[0, j]/T0 – 1)) on the axis of the free spray cone with and without taking into account the drag crisis in the drops and the interphase heat- and mass-transfer crisis. One can see that the drag crisis noticeably affects the profiles of the velocities of each of the phases: the gas flows more slowly, whereas the drops move more rapidly because of the weaker interphase momentum transfer. A similar effect is produced by the heat- and mass-transfer crisis on the temperatures of the phases near the axis of the spray cone: the gas is heated (by 10 K), and the drops are cooled (by 9 K) to a lesser extent than without the crisis (by 17 and 12 K, respectively).

Figures 2–5 present the radial profiles of the reduced temperatures of the gas (tg[i, j] = 10(T[i, j]/T0 – 1)) and the drops (tl[i, j] = 10(Tl[i, j]/T0 – 1)) at various distances z = 100 + 4j mm from the nozzle, which were calculated with and without taking into account the drag crisis of the drops and the crisis of the heat- and mass-transfer of the phases.

It is seen that the drag crisis approximately doubles the width of the temperature profiles of the drops at j = 100–150, whereas the heat- and mass-transfer crisis approximately halves the maximum height of the temperature profiles of the gas. Without taking into account the heat- and mass-transfer crisis, the reduced temperatures of the phases near the axis of the spray cone far from the nozzle are close, and with taking into account this crisis, they differ by about half. The qualitative effect of both crises is quite expectable: because of the drag crisis, the drops move more rapidly, and the gas flows more slowly than without the crisis, and because of the heat- and mass-transfer crisis, the drops are cooled, and the gas is heated to a lesser extent than without this crisis.

Figure 6 shows the dependences calculated with taking into account each of the crises for the centigrade temperatures of the phases, 〈tg[i, j]〉 and 〈tl [i, j]〉, averaged over a section of the two-phase flow, as functions of the distance z = 100 + 4j mm to the nozzle.

As one can see, despite both crises, the warm water sprayed by the nozzle in air in a free jet 1.5 m long is cooled by 22.7°C, or 77.5% of the initial difference Δt = 29.3°C of the temperatures of the phases.

CALCULATION OF THE INTERPHASE HEAT- AND MASS-TRANSFER IN A SPRAYING APPARATUS

Figure 4 in the previous work [2] shows a schematic used in the calculations of an injection sprayer containing a nozzle forming a spray cone, a cylindrical chamber coaxial with the nozzle for mixing the phases, and a separator tank for their separation. The common axis of the nozzle and the mixing chamber is vertical. The mixing chamber is open-top, and the gas flow rate is controlled by a valve at the outlet of the gas from the apparatus. The liquid collected at the bottom of the separator tank is removed through a valve.

The cylindrical chamber for mixing the phases limits the radius (r ≤ Rapp) and height (H) of the two-phase flow. The height H is related to the position jmax = n of the lower boundary of the computational domain by the formula H = zmax = (z0 + n h). The internal surface of the chamber wall is the lateral boundary of the computational domain, imax = m = RAPP/h, at which both components of the gas velocity are zero: wr(m, j) = wz(m, j) = 0.

The drops reaching the wall fall on it, wetting the internal surface below the coordinate zw = Rapp/tanφ. On the temperature of the liquid flowing as a film down the internal surface of the apparatus (at r = Rapp), the boundary condition was imposed: Tl(Rapp, z) = T0 at z < zw as the initial temperature of the gas and ∂Tl(Rapp, z)/∂r = 0 at z ≥ zw as the temperature of the drops reaching the wall at given height z.

In the proposed model of the two-phase flow, the computational domain 0 < j < n is completely within the mixing chamber.

In the calculations, the gas pressure difference ΔP was set and maintained between the lowermost and uppermost sections of the mixing chamber—the horizontal boundaries of the computational domain. From the calculated values of the axial velocity of the gas, its volumetric flow rate V through the apparatus was calculated. The variants of the calculation of the apparatus differed in gas pressure difference ΔP and in radius Rapp and height H of the mixing chamber of the apparate.

Figure 7 presents the calculated radial profiles of the reduced temperatures tg[i, j] and tl[i, j] in the spraying apparatus with taking into account of both crises: the drag crisis of the drops and the heat- and mass-transfer crisis inter the phases.

Fig. 7.
figure 7

Calculated radial profiles of the reduced temperatures tg[i, j] of the gas (filled symbols) and tl [i, j] of the liquid (open symbols) at various distances z = 100 + 4j mm from the nozzle in the spraying apparatus with taking into account the drag crisis of the drops and the heat- and mass-transfer crisis of the phases. Rapp = 144 mm, H = 1100 mm, and the gas pressure difference across the apparatus is ΔP = 7 Pa.

Full size image

The temperature difference between the phases near the axis of the apparatus (at i = 0) is seen to be noticeably higher than that near the apparatus wall (at i = n = 36).

Figure 8 presents the calculated dependences on the volumetric gas flow rate V through the apparatus for the reduced temperatures of the gas 〈tg[i, n]〉 and the liquid 〈tl[i, n]〉, averaged over the outlet section (a different one for each of the phases) of the mixing chamber. At V > 0, the gas and liquid flows are co-current, and at V < 0, they are counter-current.

Fig. 8.
figure 8

Calculated dependences on the volumetric gas flow rate V through the apparatus for the reduced temperatures of the gas 〈tg[i, n]〉 and the liquid (〈tl[i, n]〉), averaged over the outlet section (a different one for each of the phases) of the mixing chamber, at Rapp = 140 mm and H = 1100 mm.

Full size image

Figure 8 shows that, with increasing V, the liquid temperature approximately linearly decreases, as does the gas temperature at V < 0, whereas at V > 0, there is a maximum (about 30%). The position of the maximum of the gas temperature agrees with the assumption made in the previous work [1, Sect. 7.2], that the maximum efficiency of the heat and/or mass transfer of the phases in the co-current mode of a spraying apparatus can be reached at a gas flow rate close to the optimal value Vopt, which meets the condition Vopt/Vmax = 3–1/2.

Figure 9 presents the calculated dependences on the cross-sectional area S of the mixing chamber for the maximum gas flow rate Vmax (i.e., at a low pressure difference of ΔP = 0.7 Pa across the apparatus), the average reduced temperatures 〈tg[i, n]〉 and 〈tl [i, n]〉 of the phases, and also the ratio ml(n)/ml(0) of the mass flux of the liquid at the outlet section of the apparatus (i.e., the liquid that has not fallen on the apparatus wall) to the mass flux of the liquid at the inlet section.

Fig. 9.
figure 9

Calculated dependences on the cross-sectional area S of the apparatus for the maximum gas flow rate Vmax through the apparatus, the average reduced temperatures 〈tg[i, n]〉 and 〈tl[i, n]〉 of the phases, and also the ratio ml(n)/ml(0) of the liquid mass flux at the outlet section of the apparatus to the liquid mass flux at the inlet section at H = 1100 mm and gas pressure difference across the apparatus of ΔP = 0.7 Pa.

Full size image

The graphs in Fig. 9 show that, with increasing S, the average temperatures of both phases at the outlet of the mixing chamber decrease, the gas flow rate Vmax and the fraction of the liquid that has not fallen on the chamber wall increase, but more than 65% of drops have reached the wall.

Figure 10 presents the calculated dependences of the same quantities as in Fig. 9 on the apparatus height H, but at a gas pressure difference across the apparatus of ΔP = 7 Pa.

Fig. 10.
figure 10

Calculated dependences of the same quantities as in Fig. 9 on the apparatus height H at Rapp = 140 mm and gas pressure difference across the apparatus of ΔP = 7 Pa.

Full size image

One can see that, with an increase in H by a factor of 3, the volumetric flow rate V of the gas decreases no more than by a factor of 2, and the average temperature of the gas at the outlet of the mixing chamber increases approximately linearly, whereas the last quantity for the liquid changes insignificantly and irregularly, and the fraction of the liquid that has not yet fallen on the apparatus wall decreases approximately inversely proportional to H.

CONCLUSIONS

The previously proposed [2, 3] model of a nozzle spray cone with taking into account the early crisis of drag for drops and the interphase mass transfer crisis has been developed in this work by taking into account the crisis of heat and mass transfer from the drops to the gas, which is similar to the crisis of heat transfer between a ball and a gas flow [3, Sect. 6.2].

Building on the results obtained in the previous works [2, 3], in this work, new results are obtained. In particular, for a free spray cone of height H to 1.5 m, not only the axial and radial profiles of the velocities of the phases, but also the distributions of the temperatures Tg(r, z) and Tl(r, z) of the phases have been calculated with and without taking into account the drag crisis in the drops and the crisis of heat and mass transfer from them to the gas.

According to the data in Fig. 6, although the model takes into account both crises, the water in a free spray jet at distance 1.5 m from a nozzle is cooled significantly, namely, by 23°C, i.e., almost 80% of the initial difference Δt = 29°C of the temperatures of the phases.

Along with a free spray cone, the interphase heat and mass transfer has also been calculated in a gas–drop flow through a cylindrical apparatus, including the dependences of the average temperatures 〈Tl〉 and 〈Tg〉 of the phases at the outlet of the apparatus on the volumetric gas flow rate V through the apparatus.

The proposed numerical model enables one to calculate the dependences of the operating characteristics V, 〈Tl〉, and 〈Tg〉 of the spraying apparatus on its design parameters S and H and the gas pressure difference ΔP across the apparatus.

According to the data in Figs. 8–10, because of the heat- and mass-transfer crisis in the spraying apparatuses, the warm water sprayed by the nozzle into air is cooled insignificantly: under the studied conditions, it does not exceed 17.5 K, i.e., about 60% of the difference of the initial temperatures of the water and air.

The problem of determining the degree of cooling of the water flowing down the wall of the mixing chamber remains incompletely solved. A preliminary estimation of the contribution of the heat and mass transfer between the gas and the liquid flowing down as a film has shown that it is about 8% of the heat and mass transfer between the gas and the drops in the bulk of the apparatus.

NOTATION

a = λ/(ρсp)

thermal diffusivity of gas, m2/s

C d

drag coefficient of drop

c

specific heat, J/(kg K)

D

diffusion coefficient of water vapor in gas, m2/s

d = d32

volume-surface mean diameter of drops, m

d h

nozzle hole diameter, mm

H

apparatus height, mm

h

computational grid spacing, mm

i, j

nos. of computational grid points along radius and axis of flow

J

vapor mass flux from all drops to gas per unit volume, kg/(m3 s)

j v

density of vapor mass flux from single drop to gas, kg/(m3 s)

k t

heat-transfer coefficient from drop to gas, W/(m2 K)

k m

mass-transfer coefficient from drop to gas, m/s

L

specific heat of evaporation of liquid drops, J/kg

M

molar mass of gas, kg/mol

m, n

maximum values of i and j, respectively

m l

liquid drops mass flux through cross section of apparatus, kg/s

P l

gauge pressure of water in nozzle, Pa

P

gas pressure, Pa

Q

heat flux from all drops to gas per unit volume, W/m3

q

density of heat flux from single drop to gas, W/m2

R = 8.31

universal gas constant, J/(mol K)

R app

apparatus radius, mm

r

radial coordinate of points in spray cone, m

S

cross-sectional area of apparatus, m2

s

central-section area of spherical drop, mm2

T, Tl

temperatures of gas and liquid, respectively, K

t

same on Celsius scale, °C

tg, tl

reduced temperatures of gas and liquid, respectively

u

liquid velocity, m/s

V = u – w

relative drop velocity in gas, m/s

V

volumetric gas flow rate through apparatus, m3/s

V d

volume of drop, m3

Δx

change in quantity x

〈x〉

average value of quantity x

z

axial coordinate of points in spray cone, m

w, ws

gas velocity and sound velocity in gas, respectively, m/s

α

liquid volume fraction at given point of spray cone

λ

thermal conductivity of gas, W/(m K)

μ

dynamic viscosity of gas, Pa s

ν = μ/ρ

kinematic viscosity of gas

ρ, ρl, ρv, ρsv

densities of gas, liquid, vapor, and saturated vapor, respectively, kg/m3

τ and τs

time and characteristics time, respectively, s

Φd

heat release due to dissipation of mechanical energy of gas, W/m3

φ

nozzle spray cone half-angle, deg

Nu = ktd/λ, NuD = kmd/D

Nusselt number diffusion Nusselt number

Pr = ν/a,

PrD = ν/D

Prandtl number diffusion Prandtl number

Re = Vdρ/μ, Recr

Reynolds number critical Reynolds number.

SUBSCRIPTS AND SUPERSCRIPTS

0

initial value

g

Gas

l

Liquid

max

maximum value

opt

optimum value

p or v

constant pressure or volume

r

component of vector along radius of flow

z

component of vector along axis of flow