Mathematical Modeling of a Biotechnological Continuous Fermentation Process for Lactic Acid Production: A Review

Abstract

The results of an analysis of mathematical models for a continuous fermentation process for lactic acid production have been presented. Mathematical models are represented by equations with the kinetics of the formation of lactic acid for strains of the following types: strains that consume only the main substrate (most frequently, glucose) and do not form by-products; strains that form by-products; strains that consume not only the main substrate, but also the substrate that forms during synthesis from the corresponding component of raw materials; and strains that use both the substrate from the component that forms during synthesis and simultaneously form a by-product in sufficiently large amounts. Kinetic relationships take into account inhibition by biomass (X), a substrate (S), and a product (P). The resulting relationships for the concentrations of the products (in the general case, X, S, P, and B) have been presented, and, most importantly, inlet characteristics (in the general case, D, S₀, and M₀) that ensure the real implementation of the technology have been estimated. Computational relationships and algorithms for the calculation of characteristics in different variants of the formulation of problems have been given. It has been pointed out that, in most solutions, there is the possibility of obtaining characteristics that ensure a set of implementing technologies. Data on the sources of raw materials used in published scientific studies have been presented. A table with algorithms for calculating the characteristics of steady states and numerical examples of calculating the characteristics of steady states have been given.

INTRODUCTION

A study of the kinetics of a biotechnological process for lactic acid production and an analysis of a batch fermentation method [1, 2] have shown that researchers have great interest in the synthesis process with the use of strains that produce lactic acid.

In [3], it is pointed out that lactic acid is considered one of the most useful products used in the food, textile, pharmaceutical, and chemical industries as a raw material for the production of propylene glycol, acrylic acid, acetaldehyde, etc. Interest in lactic acid has increased due to the possibility of using it as a monomer for the production of biodegradable polymers (PLA).

The potential of using lactic acid for the manufacture of various products was shown in [4].

An extensive study of achievements in the field of lactic acid production by microbiological fermentation was presented in [5]. The article contains 326 scientific references. The main sections of the article are as follows: (1) Introduction, (2) Microbial Lactic Acid Producers, (3) Alternative Fermentation Substrates for Lactic Acid Production, (4) Advances in Fermentation Processes for Enhanced Lactic Acid Production, and (5) Improved Lactic Acid Fermentation with High Cell Density.

Naturally, the selection of microorganisms is the key element determining the biotechnology of the process. A list of microorganisms that produce lactic acid was presented in [6]. The list is quite impressive (61 items). The types of substrates consumed by microorganisms were also given in this article. However, as will be shown below, naturally, not all of the listed microorganisms have attracted attention for the purpose of developing a biotechnological process.

Ensuring the possibility of developing a biotechnological process for lactic acid production is associated with selecting the sources of raw materials with a comparatively low cost. Raw materials with a comparatively low cost for the production of lactic acid are listed in Table 1 [3]. Data on productivity attained in cultivation using different types of raw materials are also given in this table. Naturally, Table 1 does not exhaust the complete list of possible raw materials for the production of lactic acid.

Table 1.   Literature data on raw materials for lactic acid production

One important component for developing the technology of the process is the construction of equations for the kinetics of the process that determines the rate of the growth of a population of microorganisms and, as a consequence, the intensity of the formation of lactic acid. Kinetic relationships were presented in the review [1], and they are not considered in this study. It should only be noted that, most frequently, the form of kinetic relationships also determines the mathematical expressions of a particular mathematical model for a continuous process, since the conditions of inhibition for a particular strain of microorganisms are taken into account in some kinetic relationships and they are not taken into account in others.

The mathematical models of continuous fermentation processes can be represented by the three groups determined by the types of strains: a group of strains of microorganisms that consume only the main substrate (most frequently, glucose) and do not form by-products (or an insignificant amount of them); a group of strains of microorganisms that form a by-product which is sometimes quite valuable in a sufficiently large amount; and a group of strains of microorganisms that use, in addition to the main substrate, the components of raw materials that produce the main substrate during synthesis (with and without the formation of by-products).

Some other features of the mathematical modeling of continuous fermentation should also be pointed out. First and foremost, this is the necessity of obtaining the estimates of inlet characteristics that ensure the possibility of the real implementation of the process. Another feature is that the results of modeling make it possible to obtain a set of the estimates of inlet characteristics for the same value of productivity with respect to lactic acid Q_P (g/(L h)), where Q_P = PD; P is the concentration of lactic acid, g/L; and D is the dilution rate, h^–1. There is the possibility of obtaining estimates for optimal conditions: maxQ_P and others.

MATHEMATICAL MODELING OF CONTINUOUS FERMENTATION

A system of equations of a mathematical model for the process that pertains to the first group for strains of microorganisms that consume only the main substrate and do not form by-products has the following form:

$$ - DX + \mu X = 0;$$

(1)

$$D\left( {{{S}_{f}} - S} \right) - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\mu X = 0{\kern 1pt} ;$$

(2)

$$ - DP + \left( {\alpha \mu + \beta } \right)X = 0.$$

(3)

System of equations (1)–(3) was presented in several studies cited below.

The calculation of the characteristics of the process based on the solution to (1)–(3) depends on the form of the relationship for the specific growth rate μ. A sufficiently complete review of the forms of kinetic relationships for μ was presented in [1, 2], and it is not given here, except for the variants that are used in the present review. One of the first relationships for μ was derived in [25] and has the following form:

$$\mu = {{\mu }_{{{\text{max}}}}}\frac{S}{{{{K}_{S}} + S}}.$$

(4)

A more complex relationship was used in [26]:

$$\mu = {{\mu }_{{{\text{max}}}}}\frac{S}{{{{K}_{S}} + S + {{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{{\text{i}}}}}}} \right. \kern-0em} {{{K}_{{\text{i}}}}}}}}.$$

(5)

However, relationship (5), as well as (4), takes into account inhibition only by the concentration of substrate S, and it is very seldom used for the modeling of the continuous process.

The equation for the specific growth rate in the following form is most frequently used in modeling:

$$\mu = {{\mu }_{{{\text{max}}}}}\left( {1 - \frac{P}{{{{P}_{{{\text{max}}}}}}}} \right)\frac{S}{{{{K}_{S}} + S + {{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{{\text{i}}}}}}} \right. \kern-0em} {{{K}_{{\text{i}}}}}}}},$$

(6)

in which inhibition by the concentrations of the substrate S and the product P (lactic acid) is taken into account.

A list of constants with numerical values [27, 28], which were used in most numerical calculations in modeling, is given in Table 2.

Table 2. Numerical values of constants

STEADY STATES

An analytical solution to system of equations (1)−(3), (6) was presented in [29–31]. Block diagrams of algorithms for calculating the characteristics of steady states in different variants of the formulation of problems were also given in these publications. In the generalized form, these algorithms are given in Table 3.

Table 3.   Algorithms for calculating the characteristics of steady states for system of Eqs. (1)–(3), (6)

In addition to initial data, constants from Table 2 were used in algorithms presented in Table 3. Numerical examples of the implementation of algorithms were given in [29–31].

The graphical interpretation of steady states was presented in [29, 31–35].

The following features were pointed out:

The extremal character of the dependences of the productivity Q_P (g/(L h)) on S_f at a given value of D and on D at a given value of S_f, as well as concentration P (g/L) on S_f at a given value of D;

The presence of the multiplicity of steady states for the same value of Q_P;

The limiting value of the dilution rate D = D^lim (h^–1) at which the substrate is washed out from the fermenter without having time to enter into the synthesis process.

This emphasizes that there is the boundedness of the range of values for the inlet characteristics S_f and D that ensure the real conditions of the existence of the technology.

The following two characteristics relate to constructing the region of real implementation of the technology and are very important for estimating the capabilities of the technological process: D^lim and Q_P.

The calculation of D^lim was presented in [32, 33] using the following equation:

$${{D}^{{{\text{lim}}}}} = {{\mu }_{{\text{m}}}}\frac{{{{K}_{{\text{i}}}}{{S}_{f}}}}{{{{K}_{{\text{i}}}}{{K}_{S}} + {{K}_{{\text{i}}}}{{S}_{f}} + {{S}_{f}}}},$$

(7)

i.e., the value of D at which the substrate is washed out from the fermenter without having time to enter into the synthesis process. In this case, we have X = 0, P = 0, and S = S_f.

The maximum possible value of D^lim was also given in these publications:

$${\text{max}}{{D}^{{\lim }}} = \frac{{{{\mu }_{{\text{m}}}}}}{{1 + 2{{{\left( {\frac{{{{K}_{{\text{m}}}}}}{{{{K}_{{\text{i}}}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}},$$

(8)

which is determined only by the values of kinetic constants. For max D^lim, the value of S_f = (K_mK_i)^1/2 was obtained.

It is evident that the real value of D in the technology should satisfy the following condition:

$$0 < D < {{D}^{{{\text{lim}}}}}.$$

(9)

The second characteristic max Q_P was presented in [32] and calculated using the formula

$${\text{max}}{{Q}_{P}} = \frac{{{{\mu }_{{\text{m}}}}{{P}_{{\text{m}}}}}}{{4\left[ {1 + 2{{{\left( {\frac{{{{K}_{{\text{m}}}}}}{{{{K}_{{\text{i}}}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right]}}.$$

(10)

Formulas for calculating the following characteristics of the process were also given in [32]: X^opt, S^opt, P^opt, $S_{f}^{{{\text{opt}}}}$, and D^opt for max Q_P. The general formulation of the optimization problem was presented in [36].

The region for estimating the initial characteristics S_f and D is constructed in the form of dependence for a given value of Q_P < max Q_P:

$${{S}_{{{{f}_{{1,2}}}}}} = \frac{{B\left( D \right)}}{2}\left[ {1 \pm \sqrt {1 - \frac{{4{{K}_{{\text{m}}}}{{K}_{{\text{i}}}}}}{{{{B}^{2}}\left( D \right)}}} } \right] + \frac{{{{Q}_{P}}}}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}\left( {\alpha D + \beta } \right)}};$$

(11)

$$B\left( D \right) = {{K}_{{\text{i}}}}\left[ {\frac{{{{\mu }_{{\text{m}}}}\left( {D{{P}_{{\text{m}}}} - {{Q}_{P}}} \right)}}{{{{P}_{{\text{m}}}}{{D}^{2}}}} - 1} \right].$$

(12)

Relationships (11)–(12) were derived in [37]. The coordinates of the so-called singular points that bound the range of values for D and the range of values for S_f were also given in this publication. The quantity D₁ is the minimum value of D for both of Eqs. (11) and (12), and the quantity D₂ is the maximum value of D for both of Eqs. (11) and (12):

$${{D}_{{1,2}}}{\kern 1pt} = \frac{{{{\mu }_{{\text{m}}}}}}{{2\left[ {1 + 2{{{\left( {\frac{{{{K}_{{\text{m}}}}}}{{{{K}_{{\text{i}}}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right]}}\left[ {1 \mp \sqrt {\frac{{4{{Q}_{P}}}}{{{{P}_{{\text{m}}}}{{\mu }_{{\text{m}}}}}}\left[ {1 + 2{{{\left( {\frac{{{{K}_{{\text{m}}}}}}{{{{K}_{{\text{i}}}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right]} } \right].$$

(13)

The calculation of the corresponding values of S_f, i.e., S_f(D₁) and S_f(D₂), was presented.

Two more singular points for the range of allowable values, namely, $S_{f}^{{{\text{max}}}}$ and $S_{f}^{{{\text{min}}}}$, were calculated using the necessary condition with respect to D:

$${\text{for}}\,\,S_{f}^{{{\text{max}}}}:\frac{{d{{S}_{{{{f}_{1}}}}}}}{{dD}} = 0;\,\,\,\,{\text{for}}\,\,S_{f}^{{{\text{min}}}}:\frac{{d{{S}_{{{{f}_{2}}}}}}}{{dD}} = 0.$$

(14)

The values of D for $S_{1}^{{{\text{max}}}}$ and D for $S_{2}^{{{\text{min}}}}$ were calculated. Thus, a portrait of the allowable values of S_f and D for any Q_P < maxQ_P was determined.

Relationships that substantiate the existence of the multiplicity of steady states for the process under consideration were presented in [37–39]. This issue was considered in more detail elsewhere [33, 39]. Computational relationships based on which two values of S_f that ensure the same value of Q_P at a given value of D in a real technology are determined (i.e., there are two technological processes) were presented in [33]. Algorithms for calculating the characteristics of the process under the conditions of multiplicity were given. An example of the results of numerical calculation for two steady states was presented.

A more intricate problem was solved in [37], where S_f was taken as the initial value and the values of D that ensure the same value of Q_P were calculated. In this variant, the range of allowable values [37] is divided into three sections, for each of which based on a given value of S_f its own computational relationship is used. However, as was the case in [33], two values of D are obtained for each value of S_f; i.e., there are two steady states for the same value of Q_P. Examples of numerical calculations for each of the sections were given.

It was shown in [40] that taking into account inhibition by the concentration of biomass and the concentration of the product in a relationship for the specific growth rate can be written in the more general form as follows:

$$\mu = {{\mu }_{{\text{m}}}}\frac{S}{{{{K}_{S}} + S}}{{\left( {1 - \frac{X}{{{{X}_{{\text{m}}}}}}} \right)}^{f}}{{\left( {1 - \frac{P}{{{{P}_{{\text{m}}}}}}} \right)}^{h}}.$$

(15)

Estimates for f and h in the processing of six experiments with different concentrations of the lactose of a strain of Lactobacillus casei were also obtained in the same study. The values of f and h for all of the experiments were 0.5. Only one experiment showed f = 0.7 at h = 0.5.

These data were subsequently used in the modeling of processes with other strains of microorganisms.

In the modeling of steady states, the authors of [41, 42] considered the possibility of using raw materials that produce the main substrate during synthesis [41] and strains of microorganisms that form a by-product in sufficiently large amounts [42].

A process for producing lactic acid from wheat flour was considered and modeled in [41]. Maltose, during the hydrolysis of which the main substrate (glucose) was formed, was used as a component that produces the main substrate. Computational relationships for the characteristics of the steady-state process X, P, S, and M₀ were presented based on the solution to the following equations of the model:

$$\mu X - DX = 0;$$

(16)

$$\frac{{{{Y}_{P}}}}{{{{Y}_{X}}}}\mu X - DP = 0;$$

(17)

$$ - \frac{1}{{{{Y}_{X}}}}\mu X + {{k}_{M}}M + D\left( {{{S}_{0}} - S} \right) = 0;$$

(18)

$$ - {{k}_{M}}M + D\left( {{{M}_{0}} - M} \right) = 0,$$

(19)

where M₀ is the concentration of maltose in the inlet stream, g/L, and S₀ is the concentration of glucose in the inlet stream, g/L.

The specific rate of microorganism growth μ was used in the following form:

$$\mu = {{\mu }_{{\text{m}}}}\frac{S}{{{{K}_{S}} + S}}{{\left( {1 - \frac{P}{{{{P}_{{\text{m}}}}}}} \right)}^{h}},$$

(20)

i.e., inhibition by the substrate and product was taken into account.

Experimental studies were conducted in two variants: (1) S₀ = 125 g/L and M₀ = 60 g/L and (2) S₀ = 115 g/L and M₀ = 70 g/L.

The estimates of constants for (16)–(20), the values of which are given in Table 4, were obtained [41].

Table 4.   Identified values for the parameters of the model

The numerical values of the characteristics of steady-state processes, including the optimal one (maxQ_P), were given.

Relationships for calculating the characteristics of a process for lactic acid production using a strain of Lactococcus lactis ssp. lactis ATCC 19435 were presented in [42]. The specific feature of the process is that, in contrast to standard conditions, a by-product is formed at a temperature of above 30°C. Thus, the specific growth rate was used in the following form:

$${{r}_{X}} = \frac{{{{\mu }_{{\text{m}}}}{{S}_{g}}X}}{{{{S}_{g}} + {{K}_{S}} + {{S_{g}^{2}} \mathord{\left/ {\vphantom {{S_{g}^{2}} {{{K}_{{\text{i}}}}}}} \right. \kern-0em} {{{K}_{{\text{i}}}}}}}}{{\left( {1 - {{K}_{P}}P{\text{*}}} \right)}^{n}}.$$

(21)

The rate of the formation of the product r_P was as follows:

$${{r}_{P}} = \alpha {{r}_{X}} + \beta X.$$

(22)

The rate of the formation of the by-product ${{r}_{{{{P}_{2}}}}}$ was written in the following form:

$${{r}_{{{{P}_{2}}}}} = {{\alpha }_{a}}{{r}_{X}} + {{\beta }_{a}}X.$$

(23)

Under standard conditions (pH 6.0 and 30°C), a by-product does not form. For these conditions, we have n = 2.06, α = 13.2, and β = 6.45 × 10^–2.

The dependence of process parameters on temperature was written in the following form:

$${\text{Parameter}} = {{A}_{1}}{{e}^{{ - \frac{{{{E}_{1}}}}{{RT}}}}} + {{A}_{2}}{{e}^{{ - \frac{{{{E}_{2}}}}{{RT}}}}}.$$

(24)

The values for α_a were as follows: A₁ = 2.88 and E₁ = 53.9. The values for β_a were as follows: A₁ = 2.97 × 10^–2 and E₁ = 543; A₂ and E₂ were not specified.

The temperature dependence was studied in the temperature range from 30 to 37°C.

A more complex mathematical model for the description of a steady state in a fermenter using a strain of Lactococcus lactis NZ133 was developed in [43].

The complexity of the mathematical model is that it includes a large number of constants. The equations of the model were as follows:

$$\begin{gathered} {{\mu }_{m}}\left( {\frac{S}{{{{K}_{{SX}}} + S}}} \right)\left( {1 - \frac{{P - {{P}_{{iX}}}}}{{{{P}_{{mX}}} - {{P}_{{iX}}}}}} \right) \\ \times \,\,\left( {\frac{{{{K}_{{iX}}}}}{{{{K}_{{iX}}} + S}}} \right)X - DX = 0; \\ \end{gathered} $$

(25)

$$\begin{gathered} {{q}_{{P{\text{max}}}}}\left( {\frac{S}{{{{K}_{{SP}}} + S}}} \right)\left( {1 - \frac{{P - {{P}_{{iP}}}}}{{{{P}_{{mP}}} - {{P}_{{iP}}}}}} \right) \\ \times \,\,\left( {\frac{{{{K}_{{iP}}}}}{{{{K}_{{iP}}} + S}}} \right)X - DP = 0; \\ \end{gathered} $$

(26)

$$\begin{gathered} D\left( {{{S}_{0}} - S} \right) - {{q}_{{S{\text{max}}}}}\left( {\frac{S}{{{{K}_{{SS}}} + S}}} \right) \\ \times \,\,\left( {1 - \frac{{P - {{P}_{{iS}}}}}{{{{P}_{{mS}}} - {{P}_{{iS}}}}}} \right)\left( {\frac{{{{K}_{{iS}}}}}{{{{K}_{{iS}}} + S}}} \right)X = 0. \\ \end{gathered} $$

(27)

The values of constants were determined using experimental data under the conditions of batch cultivation.

An algorithm for calculating the characteristics of the process X, S, P, and Q_P for different values of the inlet characteristics S_f and D was developed and numerically implemented in [44] using the mathematical model presented in [43].

The numerical implementation of the algorithm was performed using constants from [43]. One important characteristic is the presence of the extremal dependence of productivity Q_P on D at values of S_f = 40 g/L and S_f = 60 g/L. The extremal dependence emphasizes that there is the multiplicity of steady states for the technology with this strain.

Relationships for optimal conditions and computational relationships for estimating the multiplicity of characteristics for steady-state processes based on a given value of the dilution rate D and the value of the substrate concentration S_f were presented using (25)–(27) in [45–47].

It was shown [45] that the value of productivity is determined by two characteristics, namely, the concentration of the substrate S and the dilution rate D; i.e., Q_P = Q_P(S, D).

The extremum condition was written using two relationships

$$\frac{{\partial {{Q}_{P}}}}{{\partial S}} = 0\,\,\,\,{\text{and}}\,\,\,\,\frac{{\partial {{Q}_{P}}}}{{\partial D}} = 0$$

(28)

with constraints on the inlet characteristics S_f and D.

The following relationship for the maximum productivity was derived:

$${\text{max}}{{Q}_{P}} = {{\mu }_{m}}\frac{{P_{{mX}}^{2}}}{{4\left( {{{P}_{{mX}}} - {{P}_{{iX}}}} \right)}}\frac{{{{K}_{{iX}}}}}{{{{{\left( {K_{{SX}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} - K_{{iX}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \right)}}^{2}}}}.$$

(29)

Three algorithms were described and numerically implemented. The main algorithm solves the problem of determining the values of S_f and D that ensure maхQ_P.

The sequence of estimating the characteristic S_f based on a given value of D under the condition that Q_P < maxQ_P was presented in [46]. The range of possible values of D that does not contradict material balance equations (25)–(27) is determined beforehand. The value of D is specified, and two values of S_f are calculated. Thus, two steady states at one value of D are determined. An algorithm of computations and numerical calculation using constants from [43] were presented.

A more complex variant of estimating a set of steady states based on a given value of S_f at Q_P < maxQ_P was described in [47]. The value of S_f can be specified using material balance equations in three different variants:

variant 1: S_f1 ≤ S_f < maxS_f;

variant 2: S_f2 < S_f < S_f1;

variant 3: minS_f < S_f ≤ S_f2.

Relationships for calculating the value of D for each of the variants are different. Since the values of D are limited for the conditions of practical implementation of the technology D₁ < D < D₂, we have ${{S}_{{f1}}} = {{S}_{f}}$ at D₁ and ${{S}_{{f2}}}$ at D₂; maxS_f and minS_f are the limiting values of S_f for a given strain of microorganisms.

The sequence of calculating the value of D when S_f is specified for each of the variants was presented. For the same variants, two values of D for each value of S_f were numerically calculated; i.e., two steady states were determined. Numerical calculations were performed using constants from [43].

A more general mathematical model that takes into account the formation of the by-product B (a set of all by-products) and the use of the components of raw materials that produce the main substrate during synthesis M₀ was constructed in [48].

The mathematical model has the following form:

$$ - DX + \mu X = 0;$$

(30)

$$\left( {\alpha \mu + \beta } \right)X - DP = 0;$$

(31)

$$\left( {{{\alpha }_{B}}\mu + {{\beta }_{B}}} \right)X - DB = 0;$$

(32)

$$D\left( {{{S}_{0}} - S} \right) - \frac{1}{{{{Y}_{X}}}}\mu X + {{k}_{M}}M = 0;$$

(33)

$$D\left( {{{M}_{0}} - M} \right) - {{k}_{M}}M = 0;$$

(34)

$$\mu = {{\mu }_{{{\text{max}}}}}{{\left( {1 - \frac{X}{{{{X}_{{{\text{max}}}}}}}} \right)}^{{{{n}_{1}}}}}{{\left( {1 - \frac{P}{{{{P}_{{{\text{max}}}}}}}} \right)}^{{{{n}_{2}}}}}\frac{S}{{{{K}_{{\text{m}}}} + S + {{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{{\text{i}}}}}}} \right. \kern-0em} {{{K}_{{\text{i}}}}}}}}.$$

(35)

The mathematical model contains elements that take into account the possibility of inhibition, which are included into a relationship for kinetics: inhibition by biomass (X_max, n₁), a product (P_max, n₂), and a substrate (K_i).

The results of the transformation of system of equations (30)–(35) are given in the appendix (formulas (A.1)–(A.11)), which are necessary for solving the formulated problem.

The sequence of solving the optimization problem at maxQ_P was presented in [48]. The specific feature of solving it is that it is possible to obtain a set of values for the characteristics of the process $S_{0}^{{{\text{opt}}}}$ and $M_{0}^{{{\text{opt}}}}$ for the same value of maxQ_P. The results of numerical calculations using constants from literature sources were given.

A detailed analysis of the generalized mathematical model from the standpoint of the assessment of steady states was presented in [49].

Computational relationships were given for three variants of the formulation of the problem. The most interesting variant is the third, which is the most general.

For all of the variants, formulas for calculating the maximum value of D^lim (when there is no feed, i.e., M₀ = 0) were presented. The range of values for D is formed using the following equation:

$$0 < {{D}^{{{\text{lim}}}}} < \frac{{{{\mu }_{{\text{m}}}}}}{{1 + 2{{{\left( {\frac{{{{K}_{{\text{m}}}}}}{{{{K}_{{\text{i}}}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}.$$

(36)

In variant 3, the value of S was given using the mathematical model

$$S = {{S}_{0}} + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}} - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{P}{{\left( {\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}} \right)}}.$$

(37)

An algorithm for solving the problem of estimating X, S, P, B, M, and Q_P with the numerical values of constants in equations was presented in [49].

In [50], computational relationships were given for estimating the characteristics of a steady state under the conditions of specifying the value of the dilution rate D, which are determined as the extreme values D₁ and D₂; i.e., D can be specified according to the following condition:

$${{D}_{1}} < D < {{D}_{2}}.$$

(38)

Computational relationships for D₁ and D₂ were presented.

Multiplicity is formed under the conditions of specifying D according to (37) and calculated using formulas for $S_{1}^{'}\left( D \right)$ and $S_{2}^{'}\left( D \right)$ (formulas (A.2), (A.6), and (A.7) in the appendix).

Relationships for constructing a set of steady states that, in fact, ensure lactic acid production were derived using the equations of the mathematical model (30)–(35) in [51, 52].

In [51], the characteristics of multiplicity were estimated based on the condition of specifying S₀ within the permissible limits, and M₀ and D were determined at a given value of productivity subject to the condition that Q_P < maxQ_P.

The region of the possible assignment of S₀ was marked. The determination of the region was performed by simultaneously solving Eqs. (A.6) and (A.7) using (A.2). In (A.6) and (A.7), we have $S_{1}^{'} = {{S}_{0}}$ and $S_{2}^{'} = {{S}_{0}}$ at M₀ = 0. The region is bounded by the coordinates of singular points. Singular points 1 and 2 were obtained based on the solution to (A.8) with the subsequent estimation of S₀ for D₁ and D₂. Two more singular points 3 and 4 were determined as the maximum value of S₀ using (A.6) (singular point 3) and the minimum value of S₀ using (A.7) (singular point 4), and point 5 is the extremum point.

In the assignment of S₀ for each of the singular points, a steady state is always unique; i.e., there is no set.

The entire region of the possible assignment of S₀ is divided into three sections. This is due to the fact that it is necessary to calculate the characteristics of multiplicity using different relationships for each of the sections:

$${\text{section}}\,\,{\text{I}}{\kern 1pt} :{{S}_{1}}\left( {{{D}_{1}}} \right) < {{S}_{0}} < {{S}_{3}}\left( {{{D}_{3}}} \right);$$

(39)

$${\text{section}}\,\,{\text{II}}{\kern 1pt} :{{S}_{2}}\left( {{{D}_{2}}} \right) < {{S}_{0}} < {{S}_{1}}\left( {{{D}_{1}}} \right);$$

(40)

$${\text{section}}\,\,{\text{III}}{\kern 1pt} :{{S}_{4}}\left( {{{D}_{4}}} \right) < {{S}_{0}} < {{S}_{2}}\left( {{{D}_{2}}} \right),$$

(41)

where ${{S}_{3}} = S_{1}^{'}\left( {{{D}_{3}}} \right)$, ${{S}_{2}} = S_{1}^{'}\left( {{{D}_{2}}} \right)$, ${{S}_{1}} = S_{1}^{'}\left( {{{D}_{1}}} \right)$, and ${{S}_{4}} = S_{2}^{'}\left( {{{D}_{4}}} \right)$.

It was shown that $S_{1}^{'} > S_{2}^{'}$. The construction of sets of steady states for the assumed value of Q_P was considered separately for each of the sections.

A table with formulas for calculating M₀ and D for a given value of S₀ for each of the sections was obtained and presented. The results of numerical calculations for each of the sections were given; i.e., the coordinates of singular points using constants given in the publication for the assumed value of Q_P were determined and the characteristics of the sets Set1*, Set2*, and Set3* for each of the sections, respectively, were formed.

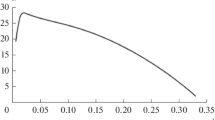
Figure 1 presents a portrait of the dependence of S₀ on D for Q_P = 6.0 g/(L h) with the boundaries of the sections of calculation.

Fig. 1.

Portrait for the dependence of S₀ on D at Q_P = 6 g/(L h): points 1–4 indicate the positions of singular points; point 5 indicates the position of the extremum point.

The characteristics of the estimation of multiplicity for a given concentration of the component that produces the main substrate during synthesis M₀ were presented in [52]. As was the case in [51], the region of the assignment of M₀ within the permissible limits and the corresponding values of S₀ and D at a given value of Q_P < maxQ_P was determined.

The region of the possible assignment of M₀ was determined by simultaneously solving Eqs. (A.6) and (A.7) using (A.2). Here, in (A.6) and (A.7), the value of $S{\kern 1pt} '$ is according to (A.4) at S₀ = 0.

Thus, we obtain the following two equations:

using (A.6):

$$\begin{gathered} {{M}_{0}} = \left[ {\frac{{D + {{k}_{M}}}}{{{{k}_{M}}}}} \right]\left[ {\frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{{Q}_{P}}}}{{\left( {\alpha D + \beta } \right)}} + \frac{{{{K}_{i}}}}{2}\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right]} \right. \\ \left. { + \,\,\sqrt {{{{\left( {\frac{{{{K}_{{\text{i}}}}}}{2}} \right)}}^{2}}{{{\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right]}}^{2}} - {{K}_{{\text{m}}}}{{K}_{{\text{i}}}}} } \right]; \\ \end{gathered} $$

(42)

using (A.7):

$$\begin{gathered} {{M}_{0}} = \left[ {\frac{{D + {{k}_{M}}}}{{{{k}_{M}}}}} \right]\left[ {\frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{{Q}_{P}}}}{{\left( {\alpha D + \beta } \right)}} + \frac{{{{K}_{i}}}}{2}\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right]} \right. \\ \left. { - \,\,\sqrt {{{{\left( {\frac{{{{K}_{{\text{i}}}}}}{2}} \right)}}^{2}}{{{\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right]}}^{2}} - {{K}_{{\text{m}}}}{{K}_{{\text{i}}}}} } \right]. \\ \end{gathered} $$

(43)

The region is bounded by the coordinates of singular points. Singular points 1 and 2 are calculated based on the solution to (A.8), from which we obtain D₁ and D₂. For D₁ and D₂, the values of M₀ are calculated:

$$\begin{gathered} {\text{for}}\,\,{{D}_{1}}{\kern 1pt} :{{M}_{0}}\left( {{{D}_{1}}} \right) \\ = \frac{{{{D}_{1}} + {{k}_{M}}}}{{{{k}_{M}}}}\left[ {\frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{{Q}_{P}}}}{{\left( {\alpha {{D}_{1}} + \beta } \right)}} + {{{\left( {{{K}_{{\text{m}}}}{{K}_{{\text{i}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right]; \\ \end{gathered} $$

(44)

$$\begin{gathered} {\text{for}}\,\,{{D}_{2}}{\kern 1pt} :{{M}_{0}}\left( {{{D}_{2}}} \right) \\ = \frac{{{{D}_{1}} + {{k}_{M}}}}{{{{k}_{M}}}}\left[ {\frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{{Q}_{P}}}}{{\left( {\alpha {{D}_{2}} + \beta } \right)}} + {{{\left( {{{K}_{{\text{m}}}}{{K}_{{\text{i}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right]. \\ \end{gathered} $$

(45)

Two more singular points 3 and 4 are calculated as the maximum value of M₀ using (42) (singular point 3) and the minimum value of M₀ using (43) (singular point 4). The value of М₀ for singular point 3 is calculated using (42) at D = D₃; the value of М₀ for singular point 4 is calculated using (43) at D = D₄.

As a result, the region of values for M₀ was divided into the following three sections:

$${\text{section}}\,\,{\text{I}}\,:{{M}_{0}}\left( {{{D}_{2}}} \right) < {{M}_{0}} < {{M}_{0}}\left( {{{D}_{3}}} \right);$$

(46)

$${\text{section}}\,\,{\text{II}}\,:\,{{M}_{0}}\left( {{{D}_{1}}} \right) < {{M}_{0}} < {{M}_{0}}\left( {{{D}_{2}}} \right);$$

(47)

$${\text{section}}\,\,{\text{III}}\,:\,{{M}_{0}}\left( {{{D}_{4}}} \right) < {{M}_{0}} < {{M}_{0}}\left( {{{D}_{1}}} \right),$$

(48)

where ${{M}_{0}}\left( {{{D}_{2}}} \right) > {{M}_{0}}\left( D \right)$.

The construction of sets of steady states for the assumed value of Q_P was considered separately for each of the sections.

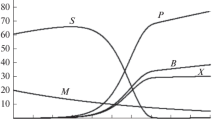
A table with formulas for calculating S₀ and D for a given value of M₀ for each of the sections was obtained and presented. The results of numerical calculations for each of the sections were given, and the characteristics of the sets Set1**, Set2**, and Set3** were formed. Figure 2 presents a portrait of the dependence of M₀ on D with the indication of the positions of singular points and the boundaries of sections I, II, and III. The portrait was constructed for Q_P = 6.0 g/(L h) using table constants [52]; point 5 is the extremum point.

Fig. 2.

Portrait for the dependence of M₀ on D at Q_P = 6 g/(L h): points 1–4 indicate the positions of singular points; point 5 indicates the position of the extremum point.

Concluding this part of the review, we cite one more study [53], which falls out of the general scheme of the review, since it describes a special apparatus for lactic acid production. The apparatus is a tube with a diameter of 10 mm and a length of 400 mm with a biofilm. The modeling (experimental) of a continuous process was described and the results of experiments were presented. There are no quantitative estimates (the equations of the material balances) in the cited study; however, based on conclusions, the apparatus is promising for use.

CONCLUSIONS

In conclusion, we cite two studies [54, 55] in which there are no calculations of the characteristics of steady states for lactic acid production; moreover, these publications themselves are review articles. The study [54] contains 63 references, and the study [55] has 35 references.

The publication [54] is a review of current developments in the continuous fermentation of lactic acid and a detailed study of the recycling of inexpensive raw materials. A list of microorganisms with the main characteristics of their cultivation in continuous fermentation, including that with cell recycle, was presented. The possibilities of using alternative substrates were described, and the general economic estimates for continuous fermentation processes were given. It should be noted that most references in the cited review pertain to 2016 or earlier.

Interest in the study [55] is due to the fact that, to a certain extent, this review broadens the review presented in [3] in the field of the food industry. In particular, the role of fermentation in food supply was pointed out; i.e., it was emphasized that the following properties of food are improved by lactic acid bacteria (LAB): aroma, the preservation of properties, poison prevention, and antibiotic properties.

A list of LAB for the food industry was presented: the preparation of cottage cheese, yoghurts, bread products, etc. It should be noted that there are no quantitative characteristics in the cited publication; thus, we have a purely literature review with the substantiation of conclusions from references to publications.

NOTATION

B	concentration of the total number of by-products, g/L
D	dilution rate, h–1
K i	inhibition constant, g/L
K m	substrate saturation constant, g/L
k M	constant that determines the amount of produced substrate, h–1
M	concentration of raw materials that additionally produce the substrate, g/L
P	concentration of the product, g/L
Q P	productivity, g/(L h)
S	concentration of the substrate, g/L
X	concentration of biomass, g/L
Y X/S	stoichiometric coefficient, g/g
α, αB, β, βB	constants
µ	specific rate of microorganism growth, h–1

SUBSCRIPTS AND SUPERSCRIPTS

0	initial value
max	maximum value
opt	optimum value

APPENDIX

$$\frac{D}{{{{\mu }_{{{\text{max}}}}}}} = A\left( D \right)\frac{{{{K}_{{\text{i}}}}S}}{{{{K}_{{\text{m}}}}{{K}_{{\text{i}}}} + {{K}_{{\text{i}}}}S + {{S}^{2}}}},$$

(A.1)

$$\begin{gathered} A\left( D \right) = {{\left( {1 - \frac{{{{Q}_{P}}}}{{{{X}_{{\max }}}\left( {\alpha D + \beta } \right)}}} \right)}^{{{{n}_{1}}}}} \\ \times \,\,{{\left( {1 - \frac{{{{Q}_{P}}}}{{{{P}_{{\max }}}\left( {\alpha D + \beta } \right)}}} \right)}^{{{{n}_{2}}}}}, \\ \end{gathered} $$

(A.2)

$$S = S{\kern 1pt} '\,\, - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{{Q}_{P}}}}{{\left( {\alpha D + \beta } \right)}},$$

(A.3)

$$S{\kern 1pt} ' = {{S}_{0}} + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}},$$

(A.4)

$$\begin{gathered} S = \frac{{{{K}_{{\text{i}}}}}}{2}\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right] \\ \pm \,\,\sqrt {{{{\left( {\frac{{{{K}_{{\text{i}}}}}}{2}} \right)}}^{2}}{{{\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right]}}^{2}} - {{K}_{{\text{m}}}}{{K}_{{\text{i}}}}} , \\ \end{gathered} $$

(A.5)

$$\begin{gathered} {{{S'}}_{1}} = \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{{Q}_{P}}}}{{\left( {\alpha D + \beta } \right)}} + \frac{{{{K}_{i}}}}{2}\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right] \hfill \\ + \,\,\sqrt {{{{\left( {\frac{{{{K}_{{\text{i}}}}}}{2}} \right)}}^{2}}{{{\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right]}}^{2}} - {{K}_{{\text{m}}}}{{K}_{{\text{i}}}}} {\kern 1pt} , \hfill \\ \end{gathered} $$

(A.6)

$$\begin{gathered} {{{S'}}_{2}} = \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{{Q}_{P}}}}{{\left( {\alpha D + \beta } \right)}} + \frac{{{{K}_{i}}}}{2}\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right] \\ - \,\,\sqrt {{{{\left( {\frac{{{{K}_{{\text{i}}}}}}{2}} \right)}}^{2}}{{{\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right]}}^{2}} - {{K}_{{\text{m}}}}{{K}_{{\text{i}}}}} . \\ \end{gathered} $$

(A.7)

The equations for calculating maxQ_P (the maximum value of Q_P) and the corresponding value of the dilution rate D^opt have the following form:

$${{\left( {\frac{{{{K}_{{\text{i}}}}}}{2}} \right)}^{2}}{{\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right]}^{2}} - {{K}_{{\text{m}}}}{{K}_{{\text{i}}}} = 0,$$

(A.8)

$$S_{{{\text{opt}}}}^{'} = \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{\max {{Q}_{P}}}}{{\left( {\alpha {{D}^{{{\text{opt}}}}} + \beta } \right)}} + {{({{K}_{{\text{m}}}}{{K}_{{\text{i}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$$

(A.9)

$$S_{{{\text{opt}}}}^{'} = S_{0}^{{{\text{opt}}}} + \frac{{{{k}_{M}}M_{0}^{{{\text{opt}}}}}}{{{{D}^{{{\text{opt}}}}} + {{k}_{M}}}},$$

(A.10)

$$\left\{ \begin{gathered} P = \frac{{{{Q}_{P}}}}{D};\,\,X = \frac{P}{{\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}}};\,\,B = \left( {{{\alpha }_{B}} + {{{{\beta }_{B}}} \mathord{\left/ {\vphantom {{{{\beta }_{B}}} D}} \right. \kern-0em} D}} \right)\frac{P}{{\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}}} \hfill \\ S = {{S}_{0}} + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}} - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{P}{{\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}}};\,\,M = \frac{{D{{M}_{0}}}}{{D + {{k}_{M}}}} \hfill \\ \end{gathered} \right..$$

(A.11)