INTRODUCTION

As is known, hydrodynamic equations in a generic form cannot be accurately solved. In connection with this, the search for and study of the most important case when the equations of motion of a fluid have accurate analytical solutions appear to be of utmost interest. Some such accurate solutions of hydrodynamic equations have been obtained and studied in detail in [1–4].

The situation is similar for equations of motion of viscous fluids through porous media; thus, these equations in a generic form cannot be accurately solved either.

The theory of motion of fluids through porous media has been recently intensively developing in connection with various applications in the modeling of technology processes, as well as when studying natural phenomena. Many technological processes in the chemical industry and in engineering are closely related to the motion of fluids through porous media. The motion of fluids inside and outside porous bodies is determined by hydrodynamic equations. Hydrodynamic regularities determine the character of occurrence of the processes of heat and mass transport taking into account chemical reactions in scaled industrial apparatuses. Multiple applications stimulate the study of the flows of a fluid inside and outside porous bodies limited by various surfaces, the simplest among which are a plane, spherical, and cylindrical surfaces. For them, analytical solutions of the corresponding boundary problems can be found under special assumptions.

Work [5] presents a review of the practical applications of hydrodynamics at small Reynolds numbers for studying natural phenomena and technology processes.

Works [6, 7] present solutions to the problems of motion of continuous (impermeable) solid bodies in a viscous fluid. In particular, work [6] considers the internal transverse waves that appear during the motion of a continuous solid sphere immersed into a fluid which makes oscillatory and translational motions. In [8], the problem of the flow of a viscous fluid around a porous sphere located in another porous medium has been solved using the Brinkman filtration model. In [9, 10], problems of the flow around a porous spherical surface limited by two concentric spherical shells have been solved using the Darcy filtration equation. In [11], the motion of a viscous fluid induced by the rotational oscillatory motion of a porous sphere immersed into it has been determined upon using the non-steady-state Brinkman equation.

In [12], a problem of the translational oscillatory motion of a porous sphere in a viscous fluid within the Brinkman filtration model has been solved.

In [13], the flows of a viscous fluid induced by the oscillatory motions of a porous spherical shell immersed into it have been determined. Analytical solutions of the non-steady-state Brinkman equation in the region inside a porous shell and the Navier–Stokes equation outside the shell have been obtained in the Stokes approximation. The moment of friction forces acting on the control spherical surface around the porous body has been determined.

In [14], the problem of oscillatory motions of a viscous fluid in contact with a flat layer of a porous medium has been solved.

Works [15–19] present the derivation of the motion equations of a fluid in a porous medium and an analysis of the limits to applicability of these equations. Works [16, 20, 21] present the derivation and analysis of the boundary conditions on a flat immobile interface of a porous medium and a free fluid. In this work, these boundary conditions are generalized for a mobile spherical interface of a porous medium and a fluid.

The aim of this work is to study the effect of the translational oscillatory motion of a porous spherical shell with a solid impermeable core in a viscous fluid on the flow of the fluid inside and outside this shell.

PROBLEM SETTING, EQUATIONS, AND BOUNDARY CONDITIONS

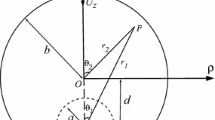
The flows of a viscous fluid upon the translational oscillatory motion of a spherical shell immersed into it with the internal and external radii equal to a and b (a < b), respectively, are considered. The radius of the solid impermeable core that is permanently bound to the porous shell is equal to a. The porous medium is supposed to be nondeformable, uniform, and isotropic. It is supposed that the porous medium has quite high porosity Γ close to unity and high permeability K. Under such conditions, the velocity of the fluid in the porous matrix can noticeably differ from the velocity of the matrix.

Let us write the velocity of the shell together with the core as a harmonic function of time t* of the form υ* = υ0exp (−iωt*), where υ0 is the real vector and ω is the oscillation frequency. Let us denote the dimensional variables (but not parameters) using * to distinguish them from the dimensionless variables denoted by the same symbols. Since all the mathematical operations under consideration in this work are linear, the drawing of the real parts from the corresponding complex expressions can be executed in the final results. The quantities referring to the regions occupied by the porous shell and free fluid outside the shell are denoted by indices 1 and 2, respectively.

The motion of a fluid immobile at infinity is considered in an Ox*y*z* fixed system of coordinates, the origin O of which coincides with the geometric center of the spherical shell at this time point. The z* axis and vector υ0 = υ0e (υ0 > 0, |e| = 1) are parallel.

Let us write the equations of the non-steady-state motion of the fluid in regions 1 and 2 in the Stokes approximation in the form [6, 15–18]

$$\begin{gathered} \frac{\rho }{\Gamma }\frac{{\partial {\mathbf{u}}_{1}^{*}}}{{\partial t{\text{*}}}} = - \nabla {\text{*}}p_{1}^{*} + \eta {\kern 1pt} '\Delta {\text{*}}{\mathbf{u}}_{1}^{*} - \frac{\eta }{K}\left( {{\mathbf{u}}_{1}^{*} - {\mathbf{u}}{\text{*}}} \right),\,\,\,\,\nabla {\text{*}}{\mathbf{u}}_{1}^{*} = 0, \\ \rho \frac{{\partial {\mathbf{u}}_{2}^{*}}}{{\partial t{\text{*}}}} = - \nabla {\text{*}}p_{2}^{*} + \eta \Delta {\text{*}}{\mathbf{u}}_{2}^{*},\,\,\,\,\nabla {\text{*}}{\mathbf{u}}_{2}^{*} = 0. \\ \end{gathered} $$
(1)

Here, \({\mathbf{u}}_{1}^{*}\) is the filtration rate, Γ is the porosity, \(p_{1}^{*}\) is the pressure in the porous medium, ρ is the density of the fluid, η' is a quantity with the dimensionality of viscosity, η is the viscosity of the free (outside the porous body) fluid, K is the permeability coefficient of the porous medium, u* = Γυ*, and \({\mathbf{u}}_{2}^{*}\) and \(p_{2}^{*}\) are the velocity and pressure of the free fluid. Assuming that the porosity is close to unity, let us further set η' = η [15, 18].

In connection with the symmetry of the problem, it is more convenient to consider its solution in a r*, θ, φ spherical system of coordinates, the polar axis of which is brought into coincidence with the z* axis, from which angle θ is counted off. Because of the assumed axial symmetry, the quantities do not depend on angle φ.

The boundary conditions are as follows [16, 20, 21]:

on the surface of the solid core at r* = a:

$$\begin{gathered} u_{{1r}}^{*} - \Gamma \upsilon {\text{*}}\cos \theta = 0\,\,\,\,(\upsilon * = {{\upsilon }_{0}}{\text{exp}}(-i\omega t*)), \\ u_{{1{{\theta }}}}^{*} + \Gamma \upsilon {\text{*}}\sin \theta = B\left( {\frac{{\partial u_{{{\text{1}{\theta }}}}^{*}}}{{\partial r{\text{*}}}} - \frac{{u_{{{\text{1}{\theta }}}}^{*}}}{a} - \frac{{\Gamma \upsilon {\text{*}}\sin \theta }}{a}} \right), \\ \end{gathered} $$
(2)

on the external surface of the spherical shell at r* = b:

$$\begin{gathered} u_{{1r}}^{*} - \Gamma \upsilon {\text{*}}\cos \theta = u_{{2r}}^{*} - \upsilon {\text{*}}\cos \theta , \\ u_{{{\text{1}{\theta }}}}^{*} + \Gamma \upsilon {\text{*}}\sin \theta = u_{{{\text{2}{\theta }}}}^{*} + \upsilon {\text{*}}\sin \theta ,\,\,\,\,p_{1}^{*} = p_{2}^{*}, \\ \Lambda \left( {\frac{{\partial u_{{{\text{1}{\theta }}}}^{*}}}{{\partial r{\text{*}}}} - \frac{{\partial u_{{{\text{2}{\theta }}}}^{*}}}{{\partial r{\text{*}}}}} \right) = u_{{{\text{1}{\theta }}}}^{*} + \Gamma \upsilon {\text{*}}\sin \theta . \\ \end{gathered} $$
(3)

The conditions at infinity at r* → ∞ are as follows: \(u_{{2r}}^{*} = 0,\) \(u_{{{\text{2}{\theta }}}}^{*} = 0.\) The conditions of finiteness of the quantities everywhere in the regions of their determination should be added to these boundary conditions.

First boundary condition (2) expresses the condition of impermeability of the fluid on the immobile solid surface of the core. The second condition is a condition of sliding of the fluid in the porous medium along the solid surface of the core [5]. Quantity B is called a coefficient of sliding friction. The sliding of the fluid is absent at B = 0. At B → ∞, we have the absence of tangential stresses (a gas bubble instead of a solid core).

The first two conditions (3) express the conditions of continuity of the velocity at the interface of the porous medium and free fluid. The third condition expresses the continuity of pressure at the interface. Constant Λ in the fourth condition (3) is determined by the equality \(\Lambda = {{\sqrt K } \mathord{\left/ {\vphantom {{\sqrt K } \tau }} \right. \kern-0em} \tau },\) where τ is a dimensionless parameter depending on the properties of the porous matrix [16, 21]. At Λ = 0 (which is tantamount to K = 0, i.e., the porous medium is impermeable for the fluid), the fourth condition (3) acquires the form \(u_{{{\text{1}{\theta }}}}^{*} + \Gamma \upsilon {\text{*}}\sin \theta = 0.\) At Λ → ∞ (τ → 0), the fourth condition acquires a form formally similar to the condition of continuity of the tangential stresses at the interface of two viscous fluids with the same viscosity.

PROBLEM SOLVING

Let us introduce dimensionless variables \({\mathbf{r}} = {{{\mathbf{r}}{\text{*}}} \mathord{\left/ {\vphantom {{{\mathbf{r}}{\text{*}}} b}} \right. \kern-0em} b},\) \(t = \omega t*,\) \({\mathbf{u}} = {{{\mathbf{u}}{\text{*}}} \mathord{\left/ {\vphantom {{{\mathbf{u}}{\text{*}}} {{{\upsilon }_{0}}}}} \right. \kern-0em} {{{\upsilon }_{0}}}}\) = \({\mathbf{e}}\Gamma \exp ( - it),\) \({{{\mathbf{u}}}_{j}} = {{{\mathbf{u}}_{j}^{*}} \mathord{\left/ {\vphantom {{{\mathbf{u}}_{j}^{*}} {{{\upsilon }_{0}}}}} \right. \kern-0em} {{{\upsilon }_{0}}}},\) and \({{p}_{j}} = p_{j}^{*}\left( {{b \mathord{\left/ {\vphantom {b {\eta {{\upsilon }_{0}}}}} \right. \kern-0em} {\eta {{\upsilon }_{0}}}}} \right)\) (j = 1, 2).

Equations of motion of the fluid (1) in the dimensionless form

$$\begin{gathered} \frac{{K\omega }}{{\nu \Gamma }}\frac{{\partial {{{\mathbf{u}}}_{1}}}}{{\partial t}} = - \frac{K}{{{{b}^{2}}}}\left( {\nabla {{p}_{1}} - \Delta {{{\mathbf{u}}}_{1}}} \right) - \left( {{{{\mathbf{u}}}_{1}} - {\mathbf{u}}} \right), \\ \nabla {{{\mathbf{u}}}_{{\text{1}}}} = 0,\,\,\,\,(\alpha < r < {\text{1}}); \\ \frac{{\omega {{b}^{2}}}}{\nu }\frac{{\partial {{{\mathbf{u}}}_{2}}}}{{\partial t}} = - \nabla {{p}_{2}} + \Delta {{{\mathbf{u}}}_{2}},\,\,\,\,\nabla {{{\mathbf{u}}}_{{\text{2}}}} = 0,\,\,\,\,(r > {\text{1}}). \\ \end{gathered} $$
(4)

Here, \(\alpha = {a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}\) (α < 1) and \(\nu = {\eta \mathord{\left/ {\vphantom {\eta \rho }} \right. \kern-0em} \rho }.\)

The dimensionless boundary conditions are as follows:

at r = α: u1r − Γe–itcos θ = 0,

$$\begin{gathered} {\text{at}}\,\,\,r = \alpha {\kern 1pt} :\,\,{{u}_{{1r}}}-\Gamma {{e}^{{-it}}}\cos \theta = {\text{ }}0, \\ {{u}_{{{\text{1}{\theta }}}}} + \Gamma {{e}^{{ - it}}}\sin \theta = \beta \left( {\frac{{\partial {{u}_{{{\text{1}{\theta }}}}}}}{{\partial r}} - \frac{{{{u}_{{{\text{1}{\theta }}}}}}}{\alpha } - \frac{{\Gamma {{e}^{{ - it}}}\sin \theta }}{\alpha }} \right); \\ {\text{at}}\,\,\,r = 1{\kern 1pt} :\,\,{{u}_{{1r}}}-\Gamma {{e}^{{-it}}}\cos \theta = {{u}_{{2r}}}-{{e}^{{-it}}}\cos \theta , \\ {{u}_{{1\theta }}} + \Gamma {{e}^{{-it}}}\sin \theta = {{u}_{{2\theta }}} + {{e}^{{-it}}}\sin \theta ,\,\,\,{{p}_{1}} = {{p}_{2}}, \\ \lambda \left( {\frac{{\partial {{u}_{{{\text{1}{\theta }}}}}}}{{\partial r}} - \frac{{\partial {{u}_{{{\text{2}{\theta }}}}}}}{{\partial r}}} \right) = {{u}_{{{\text{1}{\theta }}}}} + \Gamma {{e}^{{ - it}}}\sin \theta ; \\ {\text{at}}\,\,\,r \to \infty \,:\,\,{{u}_{{2r}}} \to 0,\,\,\,{{u}_{{2\theta }}} \to 0. \\ \end{gathered} $$
(5)

Here, \(\beta = {B \mathord{\left/ {\vphantom {B b}} \right. \kern-0em} b}\) and \(\lambda = {\Lambda \mathord{\left/ {\vphantom {\Lambda b}} \right. \kern-0em} b}.\) Also, conditions of finiteness of all quantities everywhere in the regions of their determination should be added to these boundary conditions. In connection with the axial symmetry, we adopt u1φ ≡ 0 and u2φ ≡ 0.

Let us search for the velocities of the fluid in a form proportionate to e−it, because of which \({{\partial {{{\mathbf{u}}}_{j}}} \mathord{\left/ {\vphantom {{\partial {{{\mathbf{u}}}_{j}}} {\partial t}}} \right. \kern-0em} {\partial t}} = - i{{{\mathbf{u}}}_{j}}\) (j = 1, 2).

It follows from the continuity equations that the components of the velocities of fluid u1 and u2 can be expressed through the flow functions ψ1 and ψ2 for an axisymmetrical flow, to which, in particular, the flow around a porous spherical shell with a solid impermeable core belongs. The expressions of the velocity components through the flow functions in spherical coordinates have the form [6]

$$\begin{gathered} {{u}_{{jr}}} = \frac{1}{{{{r}^{2}}\sin \theta }}\frac{{\partial {{\psi }_{j}}}}{{\partial \theta }},\,\,\,\,{{u}_{{j{{\theta }}}}} = - \frac{1}{{r\sin \theta }}\frac{{\partial {{\psi }_{j}}}}{{\partial r}}, \\ {{u}_{{j{{\varphi }}}}} \equiv 0\,\,\,\,(j = {\text{1}},{\text{2}}). \\ \end{gathered} $$
(6)

Dimensionless equations of motion (4) in a spherical system of coordinates are as follows:

in region 1 (α < r < 1):

$$\begin{gathered} - \frac{{iK\omega }}{{\nu \Gamma }}{{u}_{{1r}}} = - \frac{K}{{{{b}^{2}}}}\frac{{\partial {{p}_{1}}}}{{\partial r}} + \frac{K}{{{{b}^{2}}}}\left[ {\Delta {{u}_{{1r}}} - \frac{{2{{u}_{{1r}}}}}{{{{r}^{2}}}}} \right.\left. { - \,\,\frac{2}{{{{r}^{2}}\sin \theta }}\frac{\partial }{{\partial \theta }}\left( {{{u}_{{1\theta }}}\sin \theta } \right)} \right] - \left( {{{u}_{{1r}}} - {{u}_{r}}} \right), \\ - \frac{{iK\omega }}{{\nu \Gamma }}{{u}_{{{\text{1}{\theta }}}}} = - \frac{K}{{{{b}^{2}}r}}\frac{{\partial {{p}_{1}}}}{{\partial \theta }} + \frac{K}{{{{b}^{2}}}}\left[ {\Delta {{u}_{{{\text{1}{\theta }}}}} + \frac{2}{{{{r}^{2}}}}\frac{{\partial {{u}_{{1r}}}}}{{\partial \theta }}} \right.\left. { - \,\,\frac{{{{u}_{{{\text{1}{\theta }}}}}}}{{{{r}^{2}}{{{\sin }}^{2}}\theta }}} \right] - \left( {{{u}_{{{\text{1}{\theta }}}}} - {{u}_{{{\theta }}}}} \right); \\ \end{gathered} $$
(7)

in region 2 (r > 1):

$$\begin{gathered} - \frac{{i\omega {{b}^{2}}}}{\nu }{{u}_{{2r}}} = - \frac{{\partial {{p}_{2}}}}{{\partial r}} + \Delta {{u}_{{2r}}} - \frac{{2{{u}_{{2r}}}}}{{{{r}^{2}}}} - \frac{2}{{{{r}^{2}}\sin \theta }}\frac{\partial }{{\partial \theta }}\left( {{{u}_{{{\text{2}{\theta }}}}}\sin \theta } \right), \\ - \frac{{i\omega {{b}^{2}}}}{\nu }{{u}_{{{\text{2}{\theta }}}}} = - \frac{1}{r}\frac{{\partial {{p}_{2}}}}{{\partial \theta }} + \Delta {{u}_{{{\text{2}{\theta }}}}} + \frac{2}{{{{r}^{2}}}}\frac{{\partial {{u}_{{2r}}}}}{{\partial \theta }} - \frac{{{{u}_{{2\theta }}}}}{{{{r}^{2}}{{{\sin }}^{2}}\theta }}. \\ \end{gathered} $$
(8)

Here, \(\Delta f = \frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}\left( {{{r}^{2}}\frac{{\partial f}}{{\partial r}}} \right)\) + \(\frac{1}{{{{r}^{2}}\sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta \frac{{\partial f}}{{\partial \theta }}} \right).\)

Excluding pressures p1 and p2 from Eqs. (7) and (8), respectively, and using (6), we find the differential equations for determining flow functions ψ1 and ψ2:

$$\left[ {{{E}^{2}}\left( {{{E}^{2}} + m_{j}^{2}} \right)} \right]{{\psi }_{j}} = 0\,\,\,\,(j = {\text{1}},{\text{2}}).$$
(9)

Here, \(m_{1}^{2} = \frac{2}{\Gamma }\left[ {i{{{\left( {\frac{b}{{{{\delta }_{2}}}}} \right)}}^{2}} - {{{\left( {\frac{b}{{{{\delta }_{1}}}}} \right)}}^{2}}} \right],\) \(m_{2}^{2} = 2i{{\left( {\frac{b}{{{{\delta }_{2}}}}} \right)}^{2}},\) \({{\delta }_{1}} = \sqrt {\frac{{2K}}{\Gamma }} ,\) \({{\delta }_{2}} = \sqrt {\frac{{2\nu }}{\omega }} ,\) \({{m}_{1}} = \frac{b}{{\sqrt \Gamma }}\left( {\frac{1}{\delta } + \frac{{i\delta }}{{\delta _{2}^{2}}}} \right),\) \(\frac{1}{{{{\delta }^{2}}}} = - \frac{1}{{\delta _{1}^{2}}} + \sqrt {\frac{1}{{\delta _{1}^{4}}} + \frac{1}{{\delta _{2}^{4}}}} ,\) \({{m}_{2}} = \frac{b}{{{{\delta }_{2}}}}\left( {1 + i} \right),\)

\({{E}^{2}} = \frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + \frac{{\sin \theta }}{{{{r}^{2}}}}\frac{\partial }{{\partial \theta }}\left( {\frac{1}{{\sin \theta }}\frac{\partial }{{\partial \theta }}} \right)\) is the differential operator [5].

To satisfy boundary conditions (5), we will search for the flow functions in the form ψj(r, θ, t) = e−itfj(r)sin2 θ (j = 1, 2).

Substituting the expressions for ψ1 and ψ2 into Eqs. (9), we will obtain ordinary differential equations for the determination of the functions f1(r) and f2(r).

The boundary conditions to these differential equations are as follows:

$$\begin{gathered} {\text{at}}\,\,r = \alpha {\text{:}}\,\,\frac{2}{{{{\alpha }^{2}}}}{{f}_{1}}(r) - \Gamma = 0, \\ - \frac{1}{\alpha }f_{1}^{'}(r) + \Gamma = \beta \left( {\frac{2}{{{{\alpha }^{2}}}}f_{1}^{'}(r) - \frac{1}{\alpha }f_{1}^{{"}}(r) - \frac{\Gamma }{\alpha }} \right); \\ {\text{at}}\,\,r = {\text{1:}}\,\,2{{f}_{1}}(r) - \Gamma = 2{{f}_{2}}(r) - 1, \\ - f_{1}^{'}(r) + \Gamma = - f_{2}^{'}(r) + 1, \\ f_{1}^{{{{'''}}}}(r) + f_{1}^{{{'}}}(r)\left( {m_{1}^{2} - 2} \right) + 4{{f}_{1}}(r) + m_{2}^{2} - m_{1}^{2}\Gamma \\ = f_{2}^{{{{'''}}}}(r) + f_{2}^{'}(r)\left( {m_{2}^{2} - 2} \right) + 4{{f}_{2}}(r), \\ \lambda \left( {f_{1}^{'}(r) - f_{1}^{{''}}(r) - f_{2}^{'}(r) + f_{2}^{{''}}(r)} \right) = - f_{1}^{'}(r) + \Gamma . \\ \end{gathered} $$
(10)

The condition of finiteness of the solutions in the regions of their determination is also added here.

The equation for f1(r) is as follows:

$$\begin{gathered} f_{1}^{{IV}}(r) - \frac{4}{{{{r}^{2}}}}f_{1}^{{"}}(r) + \frac{8}{{{{r}^{3}}}}f_{1}^{'}(r) - \frac{8}{{{{r}^{4}}}}{{f}_{1}}(r) + m_{1}^{2} \\ \times \,\,\left( {f_{1}^{{"}}(r) - \frac{2}{{{{r}^{2}}}}{{f}_{1}}(r)} \right) = 0. \\ \end{gathered} $$
(11)

Using the substitution \(f_{1}^{{"}}(r) - \frac{2}{{{{r}^{2}}}}{{f}_{1}}(r)\) = \(\sqrt r {{g}_{1}}(r)\), fourth-order ordinary differential equation (11) is reduced to the second-order differential equation

$${{r}^{2}}g_{1}^{{"}}(r) + rg_{1}^{'}(r) + \left[ {m_{1}^{2}{{r}^{2}} - {{{\left( {\frac{3}{2}} \right)}}^{2}}} \right]{{g}_{1}}(r) = 0,$$
(12)

the general solution of which is as follows:

$${{g}_{1}}(r) = {{A}_{1}}{{J}_{{3/2}}}({{m}_{1}}r) + {{B}_{1}}{{Y}_{{3/2}}}({{m}_{1}}r).$$

Here, \({{J}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\) is the Bessel function of the first kind, \({{Y}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\) is the Bessel function of the second kind [22], and A1 and B1 are indefinite coefficients.

Therefore, we obtain a second-order linear inhomogeneous differential equation for determining the function f1(r):

$$f_{1}^{{"}}(r) - \frac{2}{{{{r}^{2}}}}{{f}_{1}}(r) = \sqrt r \left[ {{{A}_{1}}{{J}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}({{m}_{1}}r) + {{B}_{1}}{{Y}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}({{m}_{1}}r)} \right].$$
(13)

The general solution of Eq. (13) is

$${{f}_{1}}(r) = {{C}_{1}}{{r}^{2}} + \frac{{{{D}_{1}}}}{r} - \frac{{\sqrt r }}{{m_{1}^{2}}}\left[ {{{A}_{1}}{{J}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}({{m}_{1}}r) + {{B}_{1}}{{Y}_{{3/2}}}({{m}_{1}}r)} \right],$$

where C1 and D1 are indefinite coefficients.

According to [22], Bessel functions \({{J}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\) and \({{Y}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\) can be written as

$$\begin{gathered} {{J}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}(x) = \sqrt {\frac{{2x}}{\pi }} \left( {\frac{{\sin x}}{{{{x}^{2}}}} - \frac{{\cos x}}{x}} \right), \\ {{Y}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} = \sqrt {\frac{{2x}}{\pi }} \left( { - \frac{{\cos x}}{{{{x}^{2}}}} - \frac{{\sin x}}{x}} \right). \\ \end{gathered} $$
(14)

Taking into account equalities (14), the general solution of Eq. (13) will acquire the following form:

$$\begin{gathered} {{f}_{1}}(r) = {{C}_{1}}{{r}^{2}} + \frac{{{{D}_{1}}}}{r} - \frac{1}{{m_{1}^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2}}}r}}\sqrt {\frac{2}{\pi }} \\ \times \,\,\left[ {{{A}_{1}}(\sin {{m}_{1}}r - {{m}_{1}}r\cos {{m}_{1}}r) - {{B}_{1}}(\cos {{m}_{1}}r + {{m}_{1}}r\sin {{m}_{1}}r)} \right]. \\ \end{gathered} $$
(15)

The equation for f2(r) is as follows:

$$\begin{gathered} f_{2}^{{IV}}(r) - \frac{4}{{{{r}^{2}}}}f_{2}^{{"}}(r) + \frac{8}{{{{r}^{3}}}}f_{2}^{'}(r) - \frac{8}{{{{r}^{4}}}}{{f}_{2}}(r) + m_{2}^{2} \\ \times \,\,\left( {f_{2}^{{"}}(r) - \frac{2}{{{{r}^{2}}}}{{f}_{2}}(r)} \right) = 0. \\ \end{gathered} $$
(16)

Similarly, the general solution of Eq. (16) is

$${{f}_{2}}(r) = {{C}_{2}}{{r}^{2}} + \frac{{{{D}_{2}}}}{r} - \frac{{\sqrt r }}{{m_{2}^{2}}}\left[ {{{A}_{2}}{{J}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}({{m}_{2}}r) + {{B}_{2}}{{Y}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}({{m}_{2}}r)} \right].$$

Here, A2, B2, C2, and D2 are indefinite coefficients.

The solution of Eq. (16) is finite at r → ∞ and, taking into account equalities (14),

$${{f}_{2}}(r) = \frac{{{{D}_{2}}}}{r} + \frac{1}{{m_{2}^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2}}}r}}\sqrt {\frac{2}{\pi }} {{A}_{2}}{{e}^{{i{{m}_{2}}r}}}(i + {{m}_{2}}r).$$
(17)

Substituting Eqs. (15) and (17) into boundary conditions (10), we will obtain a system of six algebraic equations for determining coefficients A1, B1, C1, D1, A2, and D2. In view of the cumbersomeness of these coefficients, we do not present them in this work.

The components of the filtration rate and velocity of the free fluid outside the porous medium are as follows:

$$\begin{gathered} {{u}_{{1r}}} = \frac{{2{{e}^{{ - it}}}\cos \theta }}{{{{r}^{2}}}}\left( {{{C}_{1}}{{r}^{2}} + \frac{{{{D}_{1}}}}{r} - \frac{1}{{m_{1}^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2}}}r}}\sqrt {\frac{2}{\pi }} } \right. \\ \times \,\,\left[ {{{{\text{A}}}_{1}}(\sin {{m}_{1}}r - {{m}_{1}}r\cos {{m}_{1}}r)} \right. \\ \left. { - \,\,\left. {{{B}_{1}}(\cos {{m}_{1}}r + {{m}_{1}}r\sin {{m}_{1}}r)} \right]} \right),\,\,\,\,{{u}_{{{\text{1}{\theta }}}}} = - \frac{{{{e}^{{ - it}}}\sin \theta }}{r} \\ \times \,\,\left( {2{{C}_{1}}r - \frac{{{{D}_{1}}}}{{{{r}^{2}}}} + \frac{1}{{m_{1}^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2}}}{{r}^{2}}}}\sqrt {\frac{2}{\pi }} } \right. \\ \times \,\,\left[ {{{{\text{A}}}_{1}}\left( {\sin {{m}_{1}}r - {{m}_{1}}r\cos {{m}_{1}}r - m_{1}^{2}{{r}^{2}}\sin {{m}_{1}}r} \right)} \right. \\ \left. {\left. { - \,\,{{B}_{1}}\left( {\cos {{m}_{1}}r + {{m}_{1}}r\sin {{m}_{1}}r - m_{1}^{2}{{r}^{2}}\cos {{m}_{1}}r} \right)} \right]} \right), \\ {{u}_{{2r}}} = \frac{{2{{e}^{{ - it}}}\cos \theta }}{{{{r}^{2}}}}\left[ {\frac{{{{D}_{2}}}}{r} + \frac{1}{{m_{2}^{{7/2}}r}}\sqrt {\frac{2}{\pi }} {{A}_{2}}{{e}^{{i{{m}_{2}}r}}}(i + {{m}_{2}}r)} \right], \\ {{u}_{{{\text{2}{\theta }}}}} = - \frac{{{{e}^{{ - it}}}\sin \theta }}{r} \\ \times \,\,\left[ { - \frac{{{{D}_{2}}}}{{{{r}^{2}}}} - \frac{1}{{m_{2}^{{7/2}}{{r}^{2}}}}\sqrt {\frac{2}{\pi }} {{A}_{2}}{{e}^{{i{{m}_{2}}r}}}\left( {i + {{m}_{2}}r - im_{2}^{2}{{r}^{2}}} \right)} \right]. \\ \end{gathered} $$

In a particular case at α \( \to \) 0, a solution of the problem of the flow of a viscous fluid induced by the translational oscillatory motion of a porous sphere is received from the results [12]. In turn, a solution to the problem of the flow of a viscous fluid induced by the translational oscillatory motion of a solid impermeable sphere follows from this solution (at K → 0, λ → 0) [6, §24].

The motion of the fluid is non-steady-state. In connection with this, the fields of the filtration rates and velocities of the free fluid in the internal and external regions of a porous spherical shell with a solid impermeable core continuously change with time. Figure 1 shows the profiles of the filtration rates and velocities of the free fluid in regions 1 and 2 at a time point t = 0.

Fig. 1.
figure 1

Dependence of Re ur (the dashed lines) and Re uθ (the solid lines) on r: t = 0; α = 0.3; β = 0; λ = 1; Γ = 0.95; b/δ1 = 10; b/δ2 = 10; and θ = (1) π/8, (2) π/4, and (3) 3π/8.

Full size image

Figure 1 presents graphs of the dependence of Re ujr and Re ujθ (j = 1, 2) on r for three values of the angle θ (π/8, π/4, 3π/8) at α = 0.3, β = 0, λ = 1, Γ = 0.95, b/δ1 = 10, and b/δ2 = 10.

It is seen from Fig. 1 that Re ujr > 0 (j = 1, 2). The values of Re u1r and Re u2r monotonically decrease in regions 1 and 2. The values of Re u1θ < 0 and Re u2θ > 0 are nonmonotone in the regions inside and outside the porous spherical shell. With the increase in the values of the angle θ, the velocities Re ujr (j = 1, 2) and Re u1θ decrease at each set value of r; here, the velocities Re u2θ increase.

Figures 2 and 3 present the patterns of the flow lines at time point t = 0. The flow lines in the internal and external regions of a porous spherical shell with a solid impermeable core are a family of curves: ψ1 = const and ψ2 = const.

Fig. 2.
figure 2

Flow lines: t = 0; α = 0.3; β = 0; λ = 1; Γ = 0.95; b/δ1 = 10; b/δ2 = 10; and const = (1) 0.001, (2) 0.01, (3) 0.03, (4) 0.05, (5) 0.07, (6) 0.1, (7) 0.13, and (8) 0.15.

Full size image
Fig. 3.
figure 3

Flow lines: t = 0; α = 0.5; β = 0; λ = 1; Γ = 0.95; b/δ1 = 50; b/δ2 = 20; and const = (1) 0.001, (2) 0.01, (3) 0.03, (4) 0.05, (5) 0.1, (6) 0.15, (7) 0.2, (8) 0.25, (9) 0.3, (10) 0.35, and (11) 0.4.

Full size image

The equations of the flow lines in regions 1 and 2 (at t = 0) are as follows:

$$\begin{gathered} \operatorname{Re} {{\psi }_{j}}(r,\theta ) = \operatorname{Re} {{f}_{j}}(r){{\sin }^{2}}\theta = {\text{const}} \\ (j = {\text{1}},{\text{2}};\,\,0 < \theta < \pi ). \\ \end{gathered} $$

Figure 2 presents the flow lines constructed at α = 0.3; β = 0; λ = 1; Γ = 0.95; b/δ1 = 10; b/δ2 = 10; and const = (1–8) 0.001, 0.01, 0.03, 0.05, 0.07, 0.1, 0.13, and 0.15.

In Fig. 3, the flow lines are constructed at α = 0.5; β = 0; λ = 1; Γ = 0.95; b/δ1 = 50; b/δ2 = 20; and const = (1–11) 0.001, 0.01, 0.03, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, and 0.4.

The presence of discontinuities of the graphs at the interface of the porous medium and free fluid is associated with the fact that the filtration rate is not the velocity of the fluid particles. These discontinuities disappear at Γ → 1.

THE FORCE ACTING ON THE CONTROL SURFACE

The dimensionless force acting from the side of the free fluid on the control spherical surface enveloping the external surface of a porous shell with a solid impermeable core, which makes a translational oscillatory motion in a viscous fluid, is determined by the equality

$$\begin{gathered} {{F}_{z}} = \iint {\left( { - {{p}_{2}}\cos \theta + \sigma _{{2rr}}^{'}\cos \theta - \sigma _{{2r{{\theta }}}}^{'}\sin \theta } \right)}dS, \\ \sigma _{{2rr}}^{'} = 2\frac{{\partial {{u}_{{2r}}}}}{{\partial r}},\,\,\,\,\sigma _{{2r{{\theta }}}}^{'} = \frac{1}{r}\frac{{\partial {{u}_{{2r}}}}}{{\partial \theta }} + \frac{{\partial {{u}_{{{\text{2}{\theta }}}}}}}{{\partial r}} - \frac{{{{u}_{{{\text{2}{\theta }}}}}}}{r}. \\ \end{gathered} $$

Here, dS = 2π sinθ dθ is the area element, the integration is performed over the entire surface of the sphere r = 1 (\(0 \leqslant \theta \leqslant \pi \)), and \(\sigma _{{2rr}}^{'}\) and \(\sigma _{{2r{{\theta }}}}^{'}\) are the dimensionless viscous stress tensors in the external area. Quantity Fz is the force acting on the porous shell with the fluid present in it.

The expression for Fz acquires the form

$${{F}_{z}} = \frac{{8\pi }}{3}{{e}^{{ - it}}}\left[ {\frac{{m_{2}^{2}{{D}_{2}}}}{2} - \sqrt {\frac{2}{\pi }} \frac{{{{A}_{2}}{{e}^{{i{{m}_{2}}}}}(i + {{m}_{2}})}}{{m_{2}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}} \right]$$

or

$$\begin{gathered} {{F}_{z}} = \frac{{2\pi {{e}^{{ - it}}}}}{3} \\ \times \,\,\left[ {\frac{{{{Q}_{1}} + {{Q}_{2}}{{m}_{1}}\cos ({{m}_{1}} - \alpha {{m}_{1}}) + {{Q}_{3}}\sin ({{m}_{1}} - \alpha {{m}_{1}})}}{{{{Q}_{4}} + {{Q}_{5}}{{m}_{1}}\cos ({{m}_{1}} - \alpha {{m}_{1}}) + {{Q}_{6}}\sin ({{m}_{1}} - \alpha {{m}_{1}})}}} \right], \\ \end{gathered} $$
(18)

where

$$\begin{gathered} {{Q}_{1}} = 6\alpha {{m}_{1}}m_{2}^{2}\left( {2 - 2i{{m}_{2}} - 2m_{2}^{2} + \lambda \left( { - 5m_{1}^{2} + 5im_{1}^{2}{{m}_{2}} } \right.} \right.\left. {\left. { + \,\,2m_{2}^{2} - 2im_{2}^{3}} \right)} \right),\,\,\,\, \\ {{Q}_{2}} = {{Q}_{7}} + 3{{\alpha }^{2}}{{Q}_{8}} - 2m_{1}^{2}m_{2}^{2} + \,\,3\alpha m_{2}^{2} + 27{{\alpha }^{2}} - 27i{{\alpha }^{2}}{{m}_{2}} - {{\alpha }^{3}}m_{1}^{2}m_{2}^{2} \\ + \,\,\lambda \left( {{{Q}_{9}} + {{Q}_{{10}}} + {{Q}_{{11}}} + 3i{{\alpha }^{2}}m_{1}^{2}m_{2}^{3} + 6i{{\alpha }^{2}}m_{2}^{5}} \right), \\ {{Q}_{3}} = - {{Q}_{7}} + 3\alpha {{Q}_{8}} + m_{1}^{4}({{\alpha }^{3}} + 2)\left( {9 - 9i{{m}_{2}} - m_{2}^{2}} \right) + \,\,2m_{1}^{2}m_{2}^{3}(1 - {{\alpha }^{3}})(i + {{m}_{2}}) + 3\alpha m_{1}^{2}\left( { - 9 + 9i{{m}_{2}} - \alpha m_{2}^{2}} \right) \\ + \,\,\lambda \left( { - {{Q}_{9}} - i{{m}_{2}}{{Q}_{{10}}} + m_{1}^{2}{{Q}_{{11}}} + 3{{\alpha }^{2}}m_{1}^{4}m_{2}^{2} + 6{{\alpha }^{2}}m_{1}^{2}m_{2}^{4}} \right), \\ {{Q}_{4}} = 6\alpha {{m}_{1}}\left( { - 1 + i{{m}_{2}} + m_{2}^{2} + \lambda \left( {m_{1}^{2} - im_{1}^{2}{{m}_{2}} - m_{2}^{2} + im_{2}^{3}} \right)} \right), \\ {{Q}_{5}} = {{Q}_{{12}}} - 2m_{1}^{2} + 3\alpha - 3i{{\alpha }^{2}}{{m}_{2}} - 3{{\alpha }^{2}}m_{2}^{2} - {{\alpha }^{3}}m_{1}^{2} + \,\,\lambda \left( {{{Q}_{{13}}} + {{Q}_{{14}}} + 3i{{\alpha }^{2}}m_{1}^{2}{{m}_{2}} - 3i{{\alpha }^{2}}m_{2}^{3} + {{\alpha }^{3}}m_{1}^{4} - {{\alpha }^{3}}m_{1}^{2}m_{2}^{2}} \right), \\ \end{gathered} $$
$$\begin{gathered} {{Q}_{6}} = - {{Q}_{{12}}} + 3m_{1}^{2} - 2m_{1}^{4} - im_{1}^{2}{{m}_{2}} - m_{1}^{2}m_{2}^{2} + 3\alpha m_{1}^{2} - \,\,3i\alpha {{m}_{2}} - 3\alpha m_{2}^{2} - {{\alpha }^{3}}m_{1}^{4} + i{{\alpha }^{3}}m_{1}^{2}{{m}_{2}} + {{\alpha }^{3}}m_{1}^{2}m_{2}^{2} \\ + \,\,\lambda ( - {{Q}_{{13}}} - i{{m}_{2}}{{Q}_{{14}}} + 3{{\alpha }^{2}}m_{1}^{4} - 3{{\alpha }^{2}}m_{1}^{2}m_{2}^{2} - \,\,i{{\alpha }^{3}}m_{1}^{4}{{m}_{2}} + i{{\alpha }^{3}}m_{1}^{2}m_{2}^{3}),\,\,\,\, \\ {{Q}_{7}} = 18m_{1}^{2} - 18im_{1}^{2}{{m}_{2}} - \,\,6m_{2}^{2} + 6im_{2}^{3} + 6m_{2}^{4} - 27\alpha + 27i\alpha {{m}_{2}} - 27{{\alpha }^{2}}m_{1}^{2} \\ + \,\,27i{{\alpha }^{2}}m_{1}^{2}{{m}_{2}} + 9{{\alpha }^{3}}m_{1}^{2} - 9i{{\alpha }^{3}}m_{1}^{2}{{m}_{2}}, \\ {{Q}_{8}} = m_{2}^{2}( - 3 + m_{1}^{2} + 2i{{m}_{2}} + 2m_{2}^{2}), \\ {{Q}_{9}} = - 18m_{1}^{4} + 18im_{1}^{4}{{m}_{2}} + 24m_{1}^{2}m_{2}^{2} - 24im_{1}^{2}m_{2}^{3} - \,\,6m_{2}^{4} + 6im_{2}^{5} + 27\alpha m_{1}^{2} - 27i\alpha m_{1}^{2}{{m}_{2}} - 27\alpha m_{2}^{2} \\ + \,\,27i\alpha m_{2}^{3} - 9{{\alpha }^{3}}m_{1}^{4} + 9i{{\alpha }^{3}}m_{1}^{4}{{m}_{2}} + 9{{\alpha }^{3}}m_{1}^{2}m_{2}^{2} - 9i{{\alpha }^{3}}m_{1}^{2}m_{2}^{3}, \\ \end{gathered} $$
$$\begin{gathered} {{Q}_{{10}}} = 2m_{1}^{4}m_{2}^{2} - 2m_{1}^{2}m_{2}^{4} - 3\alpha m_{1}^{2}m_{2}^{2} - 6\alpha m_{2}^{4} + \,\,\alpha m_{1}^{4}m_{2}^{2} + 2{{\alpha }^{3}}m_{1}^{2}m_{2}^{4},\,\,\,\, \\ {{Q}_{{11}}} = - 27{{\alpha }^{2}}m_{1}^{2} + \,\,27i{{\alpha }^{2}}m_{1}^{2}{{m}_{2}} + 27{{\alpha }^{2}}m_{2}^{2} - 27i{{\alpha }^{2}}m_{2}^{3}, \\ {{Q}_{{12}}} = 3 - 3i{{m}_{2}} - 3m_{2}^{2} + 3\alpha m_{1}^{2}, \\ {{Q}_{{13}}} = - 3m_{1}^{2} + 3im_{1}^{2}{{m}_{2}} + 3m_{2}^{2} - 3im_{2}^{3}, \\ {{Q}_{{14}}} = 2m_{1}^{4} + m_{1}^{2}m_{2}^{2} - 3\alpha m_{1}^{2} + 3\alpha m_{2}^{2}. \\ \end{gathered} $$

Coefficients Q1, …, Q14 are definite at β = 0.

The dimensional force is \(F_{z}^{*} = \eta {{\upsilon }_{0}}b{{F}_{z}}.\)

Having proceeded to the limit λ → 0 (K → 0), α → 0, m1 → ∞ (any m2) in expression (18) for Fz, we will obtain the force acting on a continuous solid sphere (without pores), which makes a translational oscillatory motion in a viscous fluid:

$${{F}_{z}} = \frac{{2\pi }}{3}{{e}^{{ - it}}}\left( {m_{2}^{2} + 9i{{m}_{2}} - 9} \right).$$

In the dimensional form, this expression coincides with that presented in [6, §24].

At m2 = 0 (ω = 0), formula (18) (without the factor e−it) gives the expression for the force acting on the control surface of a porous spherical shell with a solid impermeable core, which moves uniformly and rectilinearly:

$${{F}_{z}} = - 6\pi \times \,\,\left[ {\frac{{{{T}_{1}}{{m}_{1}}\cos ({{m}_{1}} - \alpha {{m}_{1}}) - {{T}_{2}}\sin ({{m}_{1}} - \alpha {{m}_{1}})}}{{6\alpha {{m}_{1}}\left( { - 1 + \lambda m_{1}^{2}} \right) + {{T}_{3}}{{m}_{1}}\cos ({{m}_{1}} - \alpha {{m}_{1}}) + {{T}_{4}}\sin ({{m}_{1}} - \alpha {{m}_{1}})}}} \right],$$
(19)

where

$$\begin{gathered} {{T}_{1}} = {{T}_{5}} - 3{{\alpha }^{2}} + \lambda \left( {{{T}_{6}} + 3{{\alpha }^{2}}m_{1}^{2}} \right),\,\,\,\,{{T}_{2}} = {{T}_{5}} + 2m_{1}^{4} - \,\,3\alpha m_{1}^{2} + {{\alpha }^{3}}m_{1}^{4} + \lambda \left( {{{T}_{6}} - 3{{\alpha }^{2}}m_{1}^{4}} \right), \\ {{T}_{3}} = 3 - 2m_{1}^{2} + 3\alpha + 3{{\alpha }^{2}}m_{1}^{2} - {{\alpha }^{3}}m_{1}^{2} + \,\,\lambda \left( { - 3m_{1}^{2} + 2m_{1}^{4} - 3\alpha m_{1}^{2} + {{\alpha }^{3}}m_{1}^{4}} \right), \\ {{T}_{4}} = - 3 + 3m_{1}^{2} - 2m_{1}^{4} + 3\alpha m_{1}^{2} - 3{{\alpha }^{2}}m_{1}^{2} - {{\alpha }^{3}}m_{1}^{4} + \,\,\lambda \left( {3m_{1}^{2} + 3{{\alpha }^{2}}m_{1}^{4}} \right),\,\,\, \\ \,{{T}_{5}} = - 2m_{1}^{2} + 3\alpha + \,\,3{{\alpha }^{2}}m_{1}^{2} - {{\alpha }^{3}}m_{1}^{2},\,\,\,\,{{T}_{6}} = 2m_{1}^{4} - 3\alpha m_{1}^{2} + {{\alpha }^{3}}m_{1}^{4}. \\ \end{gathered} $$

At α = 0, expression (19) acquires the form of the dimensionless force acting on a porous sphere that uniformly and rectilinearly moves in a viscous fluid:

$${{F}_{z}} = - 12\pi \,\left[ {\frac{{m_{1}^{3}\left( { - 1 + \lambda m_{1}^{2}} \right)\cos {{m}_{1}} + m_{1}^{2}\left( {1 - m_{1}^{2} - \lambda m_{1}^{2}} \right)\sin {{m}_{1}}}}{{{{m}_{1}}\left( {3 - 2m_{1}^{2} + 2\lambda m_{1}^{4} - 3\lambda m_{1}^{2}} \right)\cos {{m}_{1}} + \left( {3m_{1}^{2} - 3 - 2m_{1}^{4} + 3\lambda m_{1}^{2}} \right)\sin {{m}_{1}}}}} \right].$$

CONCLUSIONS

The effect of the translational oscillatory motion of a porous spherical shell with a solid impermeable core immersed into a viscous fluid on the motion of this fluid inside and outside the porous body has been studied. The analytical solutions of the non-steady-state Brinkman equation describing the motion of a fluid in a porous medium and the Navier–Stokes equation describing the motion of a fluid outside a porous medium in a fixed spherical system of coordinates have been found. An analysis of the solutions of the obtained equations is presented. The fields of the filtration rates and velocities of the free fluid inside and outside the porous body have been determined. The graphs of the profiles of the filtration rates and velocities of the free fluid, as well as the flow lines at different values of the parameters, have been constructed. The force acting on the control spherical surface enveloping the external surface of a porous shell with a solid impermeable core which makes a translational oscillatory motion has been determined.

NOTATION

a, b

radii of the porous shell, m

K

permeability, m2

p*

pressure, Pa

r*, θ, φ

spherical coordinates

t*

time, s

u*

velocity of the fluid, m/s

\(u_{{1r}}^{*},\) \(u_{{2r}}^{*},\) \(u_{{{\text{1}{\theta }}}}^{*},\) \(u_{{{\text{2}{\theta }}}}^{*}\)

velocity components

x*, y*, z*

Cartesian coordinates, m

Γ

porosity

\(\eta \)

viscosity, kg m−1 s−1

η'

quantity with the dimensionality of viscosity

Λ

parameter with the dimensionality of length

ρ

density of the fluid, kg/m3

υ*

velocity of the shell, m/s

υ 0

amplitude of the velocity of the shell, m/s

ω

oscillation frequency, s−1

SUBSCRIPTS AND SUPERSCRIPTS

*

dimensional quantities

1

quantities referring to the porous medium

2

quantities referring to the free fluid

r, θ

vector and tensor components in spherical coordinates

j

number of the region (inside and outside the shell, 1 and 2, respectively)