Method for Producing Fine Liquid-Drop Systems in Ultrasound Fields

Abstract

This study is devoted to theoretical research on two-stage fine spraying of liquids that consists of the primary formation of large drops under the effect of ultrasound on a thin liquid film and the secondary breakup of generated drops under the influence of a high-frequency acoustic field in an air-drop medium. A physical mechanism is revealed and a physicomathematical model is proposed for the breakup of drops, which makes it possible to determine the threshold levels of acoustic pressure for various drop sizes, properties of a sprayed liquid, and types of action. It is found that the most effective method of acoustic action is the sequence of different-frequency pulses at a high aerosol concentration (greater than 10 vol %), which creates conditions for intermode dispersion. It is shown that, under the effect of continuous single-frequency vibrations, the radiator power necessary for drop disintegration can exceed 550 kW. Under pulsed action, the required power decreases to 2 kW at a radiating surface area of 800 cm².

INTRODUCTION

The application of heterogeneous systems with a finely dispersed liquid phase is promising in the decontamination of housings, neutralization of hazardous aerosols, creation of new and increasing energy indicators for existing fuels, drying various materials, etc.

The effectiveness of using heterogeneous systems with a finely dispersed liquid phase for solving various problems is mainly due to a large specific interfacial area per unit mass as compared to that in systems having a film or foamy structure [1–4].

Spraying 2 mL of detergent aerosol containing 0.16 vol % of polyhexamethyleneguanidine hydrochloride and 0.03 vol % of didecyldimethylammonium chloride (“Aeron”) can decontaminate 1 m³ of air. Dispersion of 1% water [3] in hydrocarbon fuel (gasoline, diesel oil, residual fuel, etc.) can increase efficiency in internal combustion engines and nozzle burners by more than 5% (for emulsion drops of 2–3 μm).

The main applied methods in creating the disperse phase in liquids or gases are based either on injection of surface-active agents (SAAs) or emulsifiers, or hydrodynamic phenomena: mechanical, hydrodynamic (nozzles), rotor-impulse [4], etc., which have already been elaborated at the turn of the 19th and 20th centuries. However, the most widespread contemporary methods allow effective creation of only coarsely dispersed systems with drop sizes greater than 100 μm. Attempts to create finely dispersed systems (with drop sizes smaller than 10 μm) using traditional methods led to nonproportional growth of energy consumption (the efficiency of the dispersion process was less than 0.1%) or secondary coagulation of drops.

One of the most promising approaches to the formation of the liquid disperse phase is low-frequency ultrasonic (US) impact (at 22–250 kHz), which allows dispersing liquid in either the carrying gas phase (spraying) or in another liquid (emulsification).

US dispersion has advantages such as eliminating the use of auxiliary substances (emulsifiers, SAA or spraying agents), the possibility of dispersing highly viscous liquids, small variation of sizes of formed drops with reference to average value, and high efficiency.

The mentioned method of forming liquid disperse drops is supported by numerous studies [5–17] devoted to establishing dependences of the disperse characteristics of formed drops in the liquid (emulsion) and gas phase (aerosol) via ultrasonic impact.

Despite the advantages and considerable attention of researchers [1–3, 5–17], ultrasonic dispersion has not been widespread in industry. This is connected with solving two mutually exclusive problems: simultaneously providing high productivity and the high dispersity of the formed dropping liquid. According to theoretical and experimental results in [5–17], productivity is inversely proportional to the size of the drops and is insufficient for industrial application when forming finely dispersed drops.

At present, the maximum productivity achieved for drops of 60–100 μm is 1 t/h due to the use of ultrasonic radiators with an increased surface area (up to 800 cm²) [18, 19], and, for drops smaller than 10 μm, it is not greater than 4 L/h.

This low productivity of the formation of finely dispersed drops is mainly attributed to US irradiation via cavitation, when the effect of cavitation causes the detachment of drops from the surface of a free liquid adjacent to the gas phase (spraying) or another liquid (emulsification).

Little oscillation energy (less than 1%) is used when transitioning from a liquid to a disperse state during the appearance of cavitation in the liquid phase. Most of the energy is spent on heating the liquid due to local temperature growth up to 5000 K (at the moment of collapse) in microscopic nuclei of cavitation bubbles [2, 3].

Finding and scientifically substantiating new ways of forming a finely dispersed liquid phase with increased performance in US fields is tangible.

The aim of this work is to develop a high-capacity method for producing fine liquid-drop systems based on theoretical studies of drop formation in high-intensity ultrasonic fields.

THE METHOD OF FORMING FINELY DISPERSED LIQUID PHASE IN ULTRASONIC FIELDS

Insufficient performance of US dispersing during formation of finely dispersed drops is connected to dispersing consisting of a single stage, which is the detachment of a drop from the phase boundary of a layer of the dispersed liquid phase and carrying medium.

Known approaches to formation of finely dispersed liquid drops require oscillation frequencies up to 5 MHz [5, 7, 8, 20]. However, high-frequency oscillations restrict the area of radiating surface, rapidly attenuate in dispersible liquid, and are intensively absorbed in the ultrasonic radiator material. High dispersing performance in case of high dispersiveness is principally unreachable using US impact within a single stage.

Therefore, the multistage method of ultrasonic dispersion of liquids is suggested. At the first stage large drops are formed from the interphase surface of the dispersed liquid layer and carrying phase under the influence of low-frequency US oscillations (20–30 kHz). Diameter of formed drops is defined via the profile of capillary waves formed in the surface of a liquid layer under the impact of cavitation created via low-frequency US influence. The influence of US impact on the profile of capillary waves and, consequently, on the diameter of drops is thoroughly studied by R.J. Lange, Yu.Ya. Boguslavskii, and O.K. Eknadiosyants [21, 22]. These authors formulated the following expression for diameter of drop formed from the surface of a liquid layer and dispersion performance via mass of liquid detached from a unit surface per unit time:

$${{D}_{1}} = 0.34\lambda = 0.34\sqrt[3]{{\frac{{8\pi \sigma }}{{\rho {{f}^{2}}}}}},$$

((1))

$${{\Pi }_{1}} = 2\frac{f}{{{{\lambda }^{2}}}}\pi \frac{{D_{1}^{3}}}{6},$$

((2))

where λ is the length of a capillary wave, m; f is the frequency of US oscillations, Hz; σ is the surface tension of dispersed liquid at the interface with the gas phase or another liquid, N/m; ρ is the density of liquid, kg/m³; D₁ is the diameter of drops, m; Π₁ is the specific capacity of dispersion, m³/(m s).

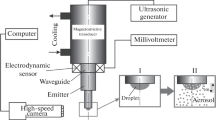
The disperse phase formed during the first stage and in a suspended state during the carrying phase is subjected to the influence of US field from the carrying phase. Thus, drops are deformed and broken up, and the dispersity of drops undergoes further evolution. The process is multiply repeated for each newly formed drop (Fig. 1).

Fig. 1.

Method for high-capacity formation of finely dispersed drops in US fields.

During deformation of a drop under the impact of a carrying medium, the shape of a drop wall is subjected to cylindrically symmetrical change with respect to the axis, the direction of which coincides with that of US oscillations. In turn, the changing of a drop shape is connected with formation of capillary waves on its surface. Formation of capillary waves on the interface between gas and liquid or two nonmixing liquids is widely investigated by J.W. Strutt (Lord Rayleigh), Yu.Ya. Bogusavskii, O.K. Eknadiosyants, etc., and is caused by the alternating of maximums and minimums of surface tension forces due to the mass conservation law of liquid, which comprises drop volume. Difference of forces between neighbor points of maximum F₁ and minimum of surface tension F₂ leads to flowing of liquid from zones of the largest surface curvature to zones of the least curvature. As a result, maximums and minimums of surface tension forces change places. The process is periodically repeated.

Since, initially, a drop is spherical, excitation of drop walls behaves like radial capillary waves with profile R(θ), where R is the length of radius-vector r of point on drop wall, equal $\sqrt {{{r}^{2}} + {{z}^{2}},}$ θ is the polar angle, the angle between radius-vector r and axis z.

For angles θ = 0; θ = π due to deformation symmetry $\frac{{\partial R}}{{\partial \theta }} = 0,$ which is similar to wave reflection conditions. Thus, radial capillary waves of the surface of drop are standing waves. A whole number of waves must fit within the half length of drop circumference. According to research in [20], the wave with the largest amplitude is the one with length equal the half length of drop circumference.

Thus, a drop deforms into a dumb-bell shape. When deformation of drop $\mathop {\max }\limits_{{\theta } \notin \left[ {0;{\pi }} \right]} \left| {R\left( \theta \right) - \frac{D}{2}} \right|$ exceeds critical value

$$\mathop {\max }\limits_{{\theta } \notin \left[ {0;{\pi }} \right]} \left| {R\left( \theta \right) - \frac{D}{2}} \right| \geqslant \frac{D}{4},$$

((3))

where D is the diameter of the initial drop, m, further avalanchelike decrement of thickness begins on the central region of the “dumb-bell” 1 (Fig. 2). Then, the next stage of drop breakup begins.

Fig. 2.

Schematic representation of the deformation and breakup of a drop in a US field.

Since the length of the capillary wave on a drop surface coincides with the half length of the drop circumference, breakup of one drop with diameter D and mass m leads to formation of two identical drops with diameter $\frac{D}{{\sqrt[3]{2}}}$ and mass $\frac{m}{2}.$

The deformation–breakup cycle is repeated for newly formed drops.

The proposed dispersion method makes it possible to increase the rate of the formation of a finely dispersed liquid phase by several times as compared to single-stage dispersion in the cavitation mode due to the following:

(1) the possibility of the required size of small drops (smaller than 10 μm) from large drops (40–80 μm) during primary dispersion. According to research in [5–17], dispersion of large drops is characterized by up to 200 times higher capacity compared to small drops. The breaking of large drops into small drops will take no more than a few dozen periods of US oscillations (not longer than 0.2 s).

(2) conservation of dispersion rate during the breakup of large drops into small drops at the second stage due to the law of conservation of mass that holds true for each elementary act of the breakup of drops:

$$\begin{gathered} \sum\limits_{i \in {{D}_{2}}} {{{m}_{{2i}}}} = \sum\limits_{i \in {{D}_{1}}} {{{m}_{{2i}}}} + \sum\limits_{i \in D_{1}^{'}} {{{m}_{{2i}}}} = \sum\limits_{i \in {{D}_{1}}} {\frac{{{{m}_{{1i}}}}}{2}} \\ + \,\,\sum\limits_{i \in D_{1}^{'}} {\frac{{{{m}_{{1\left( {i - {{N}_{{before}}}} \right)}}}}}{2}} = \sum\limits_{i \in {{D}_{1}}} {\frac{{{{m}_{{1i}}}}}{2}} + \sum\limits_{i \in {{D}_{1}}} {\frac{{{{m}_{{1i}}}}}{2}} = \sum\limits_{i \in {{D}_{1}}} {{{m}_{{1i}}}} , \\ \end{gathered} $$

((4))

where D₁ = N∩[1; N_before] is the multitude of numbers of drops before the breaking moment; ${{D}_{2}} = {{D}_{1}} \cup D_{1}^{'},$$D_{1}^{'} = \left\{ {\left. j \right|\exists i \in {{D}_{1}};\,\,j = i + {{N}_{{before}}}} \right\}$ is the multitude of numbers of drops after the breaking moment; m_1i is the mass of drop with number i before breaking, kg; ${{m}_{{2i}}} = \frac{{{{m}_{{1\left( {\left( {i - 1} \right)\bmod {{N}_{{before}}} + 1} \right)}}}}}{2}$ is the mass of drop formed after breaking with number i, kg; N_before is the amount of initial drops subjected to breaking.

In addition, the two-stage method will require less energy consumption on disperse phase formation in comparison with the single-stage method due to little energy required for primary generation of coarsely dispersed drops and cavitationless impact of US oscillations at the second stage of dispersing.

This was verified via comparative estimates of energy consumption of drops formation using single-stage and two-stage methods according to the following expression:

$$\begin{gathered} \varepsilon = \frac{{{{E}_{2}}}}{{{{E}_{1}}}} = \frac{{\frac{{\sigma \frac{{3V}}{{{{d}_{1}}}}}}{{{{K}_{1}}\left( {f_{1}^{'}} \right)}} + \frac{{3\sigma V\left( {\frac{1}{{{{d}_{2}}}} - \frac{1}{{{{d}_{1}}}}} \right)}}{{{{K}_{2}}\left( {f_{2}^{'}} \right)}}}}{{\frac{{\sigma \frac{{3V}}{{{{d}_{2}}}}}}{{{{K}_{1}}\left( {{{f}_{1}}} \right)}}}} \\ = \frac{{{{d}_{2}}}}{{{{d}_{1}}}}\frac{{{{K}_{1}}\left( {{{f}_{1}}} \right)}}{{{{K}_{1}}\left( {f_{1}^{'}} \right)}} + \frac{{{{K}_{1}}\left( {{{f}_{1}}} \right)}}{{{{K}_{2}}\left( {f_{2}^{'}} \right)}}\left( {1 - \frac{{{{d}_{2}}}}{{{{d}_{1}}}}} \right), \\ \end{gathered} $$

((5))

where E₂ is the energy required for two-stage spraying of liquid of a given volume V (m³) for drops with diameter d₂, J; E₁ is the energy required for single-stage spraying (in a layer) of liquid of a given volume V for drops with diameter d₂, J; σ is the surface tension of sprayed liquid, N/m; K₁(f) is the coefficient of transformation of ultrasonic oscillation energy into the detachment of drops from the liquid layer; K₂(f) is the coefficient of transformation of ultrasound oscillation energy into secondary breakup of drops suspended in air; f₁ is the oscillation frequency of the spraying surface, which is required for detachment of drops with diameter d₂ from the liquid layer, Hz; $f_{1}^{'}$ is the oscillation frequency of the spraying surface, which is required for detachment of drops with diameter d₁ from the liquid layer, Hz; f₂ is the frequency of oscillations in air medium, which is required for breakup of drops with diameter d₁ to drops with diameter d₂, Hz.

Coefficient of transformation K₁ of ultrasonic oscillation energy into detachment drops from dispersed liquid (dispersing efficiency) does not exceed 0.003 in [23] and decreases with decrement of drops diameter, which requires the increasing of impact frequency, i.e., K₁(f₁) < K₁($f_{1}^{'}$).

The coefficient of transformation K₂ of ultrasonic oscillation energy into the secondary breakup of already formed drops is close to 1, since no energy is required on creation of cavitation and since losses on viscous friction are negligibly small as viscosity of dispersed liquids used in practice does not exceed 50 MPa s.

Relative energy consumption required for the formation of drops during the two-stage dispersion method is shown as

$$\varepsilon < \frac{{{{d}_{2}}}}{{{{d}_{1}}}} + \frac{{{{K}_{1}}\left( {{{f}_{1}}} \right)}}{{{{K}_{2}}\left( {f_{2}^{'}} \right)}} = \frac{{10\;\mu {\text{m}}}}{{80\;\mu {\text{m}}}} + \frac{{0.003}}{1} = 0.128,$$

i.e., the energy required for a liquid-drop system with a given diameter of drops and performance using the two-stage dispersion method is more than seven times less than in the single-stage method.

To provide maximal efficiency in the suggested two-stage method, we must discover optimal excitation regimens of US impact based on complex theoretical research on the excitation processes of drop walls oscillations and the evolution of the disperse phase in US fields.

The next chapter describes the suggested physical-mathematical model of the oscillation of drop walls excited under the influence of highly intensive US fields.

PHYSICAL-MATHEMATICAL MODEL OF THE EXCITATION OF DROP WALLS OSCILLATIONS IN ULTRASONIC FIELDS

The model is based on computation of liquid motion in drop volume under the influence of the following forces (Fig. 3) in [20]: pressure difference in oscillating flux of the carrying phase (F_p), difference of surface tension forces during wavelike perturbations of a drop wall (F_s.t), forces of viscous stresses during wall motion with nonzero velocity (F_v).

Fig. 3.

Schematic representation of the deformation of a drop in a US field: n—vector of normal to drop wall; S—surface of wall; r, z—axes of cylindrical coordinates.

Computation of drop shape change was performed using a numeric method to solving Boltzmann lattice equations in [24], considering liquid flow as motion of an assembly of pseudo-particles having some function of distribution via discrete velocities N_k(x, t). N_k(x, t)dx is the number of pseudo-particles with velocity c_k and located within volume dx. Velocities c_k are selected in a way that particles would move to neighbor nodes of spatial lattice per time step Δt, where vectors fulfill condition e_k = c_kΔt.

Here, concentrations of liquid pseudo-particles are computed at each time step according to expression

$$\begin{gathered} {{N}_{k}}\left( {\left( {r + {{c}_{{kr}}}\Delta t} \right){{\cos\theta }},\left( {r + {{c}_{{kr}}}\Delta t} \right){{\sin\theta }},z} \right. \\ \left. { + \,\,{{c}_{{kz}}}\Delta t,t + \Delta t} \right) = {{N}_{k}}\left( {r{{\cos\theta }},r{{\sin\theta }},z,t} \right) \\ + \,\,\Omega \left( {{{N}_{k}}} \right) + \Delta {{N}_{k}}, \\ \end{gathered} $$

((6))

where Ω is the operator of collisions; ΔN_k is the change of particles concentration due to volumetric forces, m^–3; r; z, θ are the cylindrical coordinates of a point on the surface of deformed drop.

Analysis of a numeric model of drops breakup allows defining their maximal deformation via formula

$$x = \mathop {{\text{max}}}\limits_{{{\theta }} \in \left[ {0;{{\pi }}} \right]} \sqrt {{{{\left( {\frac{d}{2}{{\sin\theta }} - r\left( {{\theta }} \right)} \right)}}^{2}} + {{{\left( {\frac{d}{2}{{\cos\theta }} - z\left( {{\theta }} \right)} \right)}}^{2}}} ,$$

((7))

where d is the initial diameter of drop, m.

Maximal deformation determines the possibility of drop breakup. Breakup criterion is the condition x > d/4, when the Weber number exceeds critical value We > We_cr = 6 (forces of surface tension in the central region of drop 1 exceed that in peripheral region 2 (Fig. 3) due to local thinning of the drop) [20].

Maximal drop deformation is proportional to the introduced energy of oscillations. Therefore, to break up a drop, the energy of oscillations must exceed some threshold value, for which x = d/4.

Figures 4 and 5 present dependences of minimal energy of US field (ratio between intensity of oscillations and sonic speed in carrying phase E_min = I/c), required for realization of elementary breakup of drops under the impact of sine oscillations of one frequency.

Fig. 4.

Dependences of US field energy on drop diameter for various viscosities of liquid (frequency is 22 kHz): (1) 1 mPa s; (2) 2; (3) 3; (4) 5; (5) 7; (6) 10, (7) 15, (8) 20, (9) 30 mPa s (a)—20 mN/m; (b)—40 mN/m.

Fig. 5.

Dependences of the US field energy on drop diameter for various viscosities of liquid (with frequency at 44 kHz): (1) 1 mPa s; (2) 2; (3) 3; (4) 5; (5) 7; (6) 10, (7) 15, (8) 20, (9) 30 mPa s; (a)—20 mN/m; (b)—40 mN/m.

The dependences (Figs. 4, 5) imply that there are diameters, for which oscillation energy required for drop breakup reaches local minimum (lower than 10 kJ/m³). These are resonant diameters for given properties of liquid. However, it is impossible to continuously impact frequencies corresponding to resonant drop diameters, since the diameter is constantly changing due to breaking and evaporation. The US radiator is capable of creating a maximal level of sonic pressure for a finite set of frequencies conditioned via resonant properties of the radiator.

In addition, growth of viscosity leads to smoothing resonant minimums of the threshold level of US field energy, even though its influence on the value of the resonant diameter is weak. Minimums of oscillation energy completely disappear, beginning from a viscosity of 30 MPa s. Thus, we must consider the behavior of the dependency of oscillation energy outside of resonances. Beyond resonances, oscillation energy is 20–160 kJ/m³ higher than in the resonance region. Diagrams in Fig. 5 imply that the threshold energy of oscillations increases with decreasing drop diameter. This is connected with the growth of capillary forces, which impede drop deformation.

It was established that characteristics of US field must fulfill the following conditions for dispersion of liquid phase:

(1) partial energy of the formed field must constitute more than 20 kJ/m³ for acoustic power of radiator not greater than 2 kW, which is defined as P= EcS (E—partial energy of oscillations, J/m³; c—sonic speed in carrying phase, m/s; S—area of radiating surface), and a radiating surface from 800 cm²;

(2) formed US field must exclude the appearance of cavitation in dispersed liquid, since this will significantly decrease the fraction of oscillation energy spent on the transferring of liquid to a disperse state.

However, these are some physical restrictions, which impede creation of US fields with these high characteristics.

(1) Cavitation appearing in dispersed liquid for oscillation energy required for elementary breakup of drop, which exceeds 20 kJ/m³ for large drops (80–100 μm) and is greater than 80 kJ/m³ for small drops (5–15 μm), will lead to spending over 99% of energy on heating liquid due to local temperature growths, in nuclei of cavitation bubbles, up to 5000 K in [2, 3].

(2) During dispersing in the carrying gas phase given partial power is not achievable using existing radiators, since maximal oscillation energy created via available radiators of US impact for gas and gas-disperse media does not exceed 1 kJ/m³ (for acoustic radiator power, no greater than 2 kW in [18, 19, 25–27] with a radiating surface from 800 cm²), even in conditions of resonant reflection and propagation of US field. It is impossible to form a field of high intensity using small radiator power through impact via sine oscillations consisting of a single harmonic.

We suggested a further described method based on the formation of a sequence of wave packets of different frequencies.

METHOD OF FORMATION OF ULTRASONIC FIELD FOR LIQUID PHASE DISPERSION

Formation of highly intensive US field with characteristics sufficient for dispersion of drops at relatively little power from the radiator requires concentration of energy in space and/or time.

The suggested method of energy concentration is the radiation of a sequence of wave packets of a finite duration (not longer than 10 ms) at multiple frequencies (ultrasonic pulses). Due to intermode dispersion conditioned by the presence of heterogeneous impurities (liquid drops) in multiphase medium, these packets will have different propagation velocities and will comprise a superposition at some distance from the radiator.

To create conditions for the formation of highly intensive US field, we must analyze the propagation of wave packets in a gas medium via the influence of liquid drops. The analysis was based on the wave equation from general equations of dynamics of gas-drop media in [28]. The wave equation includes the nonzero right part, which accounts the influence of liquid drops and represents a double integral of the prehistory of changing sonic pressure with exponentially decreasing weight coefficients:

$$\begin{gathered} \Delta {{p}_{{11}}} - \frac{{{{{\alpha }}_{{10}}}}}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}{{p}_{{11}}}}}{{\partial {{t}^{2}}}} = - \frac{{9\mu {{{\alpha }}_{{20}}}}}{{2{{a}^{2}}}} \\ \times \,\,\frac{1}{{{{{\tau }}_{{21}}}}}\int\limits_0^t {\left[ {\int\limits_0^{{{t}_{{11}}}} {\frac{{{{e}^{{\frac{{{{{\alpha }}_{{20}}}}}{{{{{\alpha }}_{{10}}}{{{\tau }}_{{21}}}}}\left( {{{t}_{{21}}} - t} \right)}}}}}{{{{{\rho }}_{{10}}}{{c}^{2}}}}\frac{{{{\partial }^{2}}{{p}_{{11}}}}}{{\partial {{t}^{2}}}}\partial {{t}_{{21}}}} } \right]\partial {{t}_{{11}}}} , \\ \end{gathered} $$

((8))

where α₁₀ is the equilibrium volume content of air, %; α₂₀ is the equilibrium volume content of liquid, %; с is the sonic speed in air, m/s; ρ₁₀ is the density of air, kg/m³; μ is the viscosity of air, Pa s; a is the radius of a liquid drop, m; p₁ is the pressure of air, Pa; τ is the relaxation time, s.

Computations of sonic speed in medium with disperse liquid phase based on equation (8) establish that, for concentration of aerosol in air not less than 10 vol %, sonic speed increases up to 1.5 times with growth of frequency from 22 to 66 kHz (Fig. 6).

Fig. 6.

Dependence of sonic speed on US wave frequency for various volume contents of water aerosol (the drop diameter is 20 μm): (1) 5%; (2) 10; (3) 15; (4) 20; (5) 25; (6) 30, (7) 35, (8) 40%.

At this difference of speed, wave packets will be superimposed on each other at a distance not greater than 400 cm from the surface of the radiator (Fig. 7).

Fig. 7.

Distributions of partial energies of wave packet oscillations in a channel length of 900 mm (a US radiator with a diameter of 20 mm is located on the left end of the channel): (a)—22 kHz; (b)—44; (c)—22 + 44 kHz.

We have the possibility of concentrating US energy using the suggested method of impact (via a sequence of wave packets with providing of high concentration of disperse phase over 10 vol %) to realize the second stage of dispersing (breaking of preliminarily formed coarsely dispersed drops).

Further optimal impact systems via wave packets were discovered to provide maximal efficiency of secondary dispersion based on a previously described drop breaking model.

OPTIMAL CHARACTERISTICS OF ULTRASONIC FIELD FOR LIQUID PHASE DISPERSION

Figure 8 presents dependences of minimal energy of a separate wave packet required for breakup of drops under the impact of two alternating packets with frequencies of 22 and 44 kHz, which are created by the same radiator.

Fig. 8.

Energy dependences of a separate wave packet on the drop diameter for various viscosities of liquid (with frequency at 22 + 44 kHz): (1) 1 mPa s; (2) 2; (3) 3; (4) 5; (5) 7; (6) 10, (7) 15, (8) 20, (9) 30 mPa s; (a)—20 mH/m; (b)—40 mН/m.

The dependences highlight the decreasing of wave packet energy required for breakup of drops by more than 20 kJ/m³ even under impact from two packets with different frequencies. According to the results, an energy of 60 kJ/m³ is enough for breakup of drops to sizes smaller than 5 μm.

In addition, impact from wave packets with different frequencies is characterized by a quadratic increasing of the amount of drop resonant diameters with growth in number of packets in the sequence, since the force applied to a drop from the gas flux side is proportional to squared gas speed. This means that impact from wave packets on two frequencies will lead to the appearance of four resonant diameters, since drop oscillations include four time harmonics with the highest amplitudes on frequencies of 22, 44, 66, and 88 kHz. From the last statement, the force from the gas flux side applied to a drop is proportional to squared speed of flow with respect to the drop. Impact on several frequencies covers the whole range of change in resonant frequency of a drop during its breaking and evaporation, providing additional decrement of oscillation energy, which must be created via the radiator in a disperse system.

The presented dependences imply that, within the suggested impact method for secondary dispersing, it would be enough to have a radiator capable of creating oscillation energy of 1–10 kJ/m³ in continuous air medium (acoustic power not greater than 2 kW for radiating surface of 800 cm²). The manufacturing of this radiator (in contrast to that radiating oscillations at 20–160 kJ/m³) represents a technically realizable problem [29].

Efficiency of dispersion for discovered US field systems was defined based on comparative analysis of drop breakup time and time required for the appearance of coagulation, which impedes dispersion.

For this purpose, the evolution of drop diameter was computed. Breakup of a single drop was analyzed during computation of the evolution of the liquid disperse phase under the influence of US oscillations (each time, one drop was selected among two newly formed as a result of elementary breakup).

Assume that elementary breakup acts are realized at discrete moments of time t₁, t₂, …, t_n, where t_i ≤ t_{i+ 1}.

In the assumption that, during each breakup act, a drop is split into two identical drops, the following difference equation, conditioned by the fact that diameter of new drops is 2^1/3 times smaller than that of the original drop, will be true for the drop diameter:

$$\frac{{d\left( {{{t}_{{n + 1}}}} \right) - d\left( {{{t}_{n}}} \right)}}{{{{t}_{{n + {\text{1}}}}} - {{t}_{n}}}} = - \frac{{d\left( {{{t}_{n}}} \right)}}{{{{t}_{{n + 1}}} - {{t}_{n}}}}\left( {1 - \frac{1}{{\sqrt[3]{2}}}} \right).$$

((9))

For a large enough number of elementary breakup acts and after applying the averaging of random variables representing moment of times of acts t_i, we have the following differential equation:

$$\frac{{\partial \left\langle d \right\rangle }}{{\partial t}} = - \frac{{\left\langle d \right\rangle }}{{\left\langle {\tau } \right\rangle }}\left( {1 - \frac{1}{{\sqrt[3]{2}}}} \right),$$

where $\left\langle {\tau } \right\rangle$ is the average interval of time between elementary breakup acts, which is defined via the comparison of the absolute value of drop deformation with threshold deformation $\frac{{\left\langle d \right\rangle }}{4},$ which will cause breakup, s.

The presented equation allows the computing time required for drop breakup to the required size depending on the parameters of the US field.

Figure 9 shows dependences of drop breakup time on energy of a separate wave packet for various finite diameters of dispersed liquid drops and viscosities. The dependences were constructed for impact of wave packets superposition with two frequencies 22 + 44 kHz.

Fig. 9.

Diameter dependences of drops on time for various energies of separate wave packets and viscosities of dispersed liquid (with frequency at 22 + 44 kHz): (1) 20 μm; (2) 10; (3) 5 μm; (a)—1 mPa s; (b)—10 mPa s.

As it appears from the presented dependences (Fig. 9) for discovered parameters of formed US field drops, breakup duration is shorter than 0.015 s, i.e., shorter than required for secondary coagulation of particles (more than 100 s for coagulation of over 50% of initial particles in [30]). The impact during a certain time of drop breakup of less than 0.015 s allows increasing the maximum permissible energy up to three times, at which precavitation will be maintained during dispersion in the carrying liquid phase [25, 31].

This confirms the efficiency of the suggested method of formation of the finely dispersed phase.

CONCLUSIONS

A method of US dispersion providing increased performance of finely dispersed liquid phase formation (aerosol in the carrying gas phase or emulsion in the carrying liquid phase) with a drop size of 10 μm and consisting of two stages was suggested: primary formation of coarsely dispersed drops from the free surface of a dispersed liquid and breaking of primarily formed drops into finer drops under the impact of a highly intensive US field, which excites oscillations of drop walls.

A comprehensive identification of the optimal modes of high-intensity ultrasound field formation in the second stage of the process was carried out based on developed models of the propagation of ultrasonic oscillations and the evolution of drop sizes in a dispersed medium to provide maximal efficiency of dispersion to the required diameter of drops (smaller than 10 μm).

From model analysis, we established that the minimal energy of US field required for drop breakup under the impact of single-response sine oscillations is over 20 kJ/m³ for coarsely dispersed drops (80–100 μm) and over 160 kJ/m³ for finely dispersed drops (1–15 μm). Modern radiators cannot technically provide these high energies, since power must be greater than 550 kW for a radiating surface of 800 cm² (round, flat radiator with a diameter of 320 mm).

A method of field formation based on radiation of a wave packet sequence of finite duration having multiple frequencies was suggested to decrease the required power from a radiator. The suggested impact method allowed a decrease in power requirements for the US radiator to realize drops dispersion (acoustic power lower than 2 kW for a radiating surface of 800 cm²).

Under the influence of a sequence of wave packets, the duration of drop breakup to the required size (smaller than 10 μm) is shorter than 0.015 s, i.e., short compared to the time required for secondary coagulation of drops (longer than 100 s for coagulation of 50% of drops). The impact during a computed time period of drops breakup will allow an increase, of up to three times, in maximum permissible energy without undesirable cavitation during dispersion in the carrying liquid phase.

The suggested method of drop dispersion and the formation of the US field will provide higher performance of finely dispersed liquid phase formation compared with single-stage US dispersion.

FUNDING

This study was supported by the Russian Foundation for Basic Research, project no. 16-38-60082 mol_a_dk.

NOTATION

А	amplitude of oscillations, m
a	radius, m
c	speed of particle, m/s
c	sonic speed, m/s
d	diameter, m
d x	elementary volume, m3
E	partial energy, J/m3
e	trajectory of particle, m
F	force, N
f	frequency of oscillations, Hz
I	intensity of oscillations, W/m2
N	concentration, vol %
ΔN	change of concentration, vol %
P	acoustic power, W
p	pressure, Pa
r	polar radius of point, m
S	area, m2
t	time, s
Δt	time step, s
x	magnitude of drop deformation, m
z	applicate of point, m
α	equilibrium content, vol %
θ	polar angle, rad
μ	dynamic viscosity, Pa s
ρ	density, kg/m3
τ	relaxation time, s
Ω	dimensionless collision operator
We	Weber number

SUBSCRIPTS AND SUPERSCRIPTS

10, 20	gas and liquid phases withoutan ultrasonic field, respectively
11, 21	gas and liquid phases in the presence of an ultrasonic field, respectively
1, 2, n, i	numbers of components
cr	critical value
k	number of particle motion direction
kr	projection of vector of kth direction to axis r
kz	projection of vector of kth direction to axis z
min	minimal value
p	for forces of pressure difference
s.t	for forces of surface tension
v	for forces of viscous stresses