1. Introduction

Irreversibility is ubiquitous in nature and emerges frequently in many physical processes. The second law of thermodynamics, stating that the total entropy of a system either increases or remains constant in any spontaneous process, characterizes some fundamentally irreversible aspects of natural phenomena [1]–[4].

In the quantum world, irreversibility arises naturally from the system–environment interaction and quantum measurements, which lead to information leakage into the environment that cannot be recovered due to the uncontrollability of the environment. This causes decoherence and dissipation of open system dynamics [5]–[10].

In this paper, we are concerned with the irreversibility of quantum channels in the context of superoperators, i.e., maps sending quantum states (described by density operators) to quantum states [11]–[13]. In a rather broad and widely used setup, general quantum processes are often described by quantum channels (i.e., linear trace-preserving completely positive maps of quantum states, henceforth abbreviated as channels). These physical processes are usually divided into two categories: unitary evolutions (which are reversible) and open system dynamics (which are irreversible). While irreversible aspects of channels have been widely studied with the main focus on qualitative perspectives such as quantum error correction and quantum control, they are relatively less studied from a quantitative perspective. This calls for quantitative investigations of the irreversibility of channels.

To proceed in a rigorous way, we recall that a quantum process described by a channel \(\mathcal E\) is (physically) reversible if there exists a channel \(\mathcal D\) such that the composition \(\mathcal D \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E=\mathcal I\) is the identity channel in the system. Otherwise, it is termed irreversible. Evidently, any unitary channel \(\mathcal E_U(\rho)=U\rho U^\dagger\) (with \(U\) a unitary operator) is reversible, and the corresponding reverse is \(\mathcal D(\rho)=\mathcal E_{U^\dagger}(\rho)=U^\dagger\rho U\). Indeed, \((\mathcal E_{U^\dagger} \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E_{U})(\rho)=U^\dagger(U\rho U^\dagger) U=\rho\) for any state \(\rho\). On the other extreme, for a \(d\)-dimensional system, it is intuitively clear that the completely depolarizing channel \(\mathcal E_{\mathrm{cde}}(\rho)=\mathbf 1/d\) (for any state \(\rho\)) is among the most irreversible channels. Here, \(\mathbf 1\) denotes the identity operator on the system Hilbert space. Intermediate between these two extremes are many irreversible channels, the random unitary channels being prominent and important examples.

Many features of irreversibility have been studied in the literature from various aspects. For example, decoherence and dissipation have been extensively investigated in quantum measurements and the quantum-to-classical transition [5]–[10]. Entanglement fidelity has been introduced to characterize the quality of channels and quantum gates in preserving states [14]–[20]. Information and entropy change has been discussed for the coupling of systems to environments [21], [22]. Markovian/non-Markovian properties of open system dynamics have attracted great interest with the emergence of quantum information theory [23]–[27]. Entropy production has been extensively investigated in quantum dynamical semigroups and irreversible processes [28]–[41].

In view of the channel–state duality, for any channel, there is a corresponding Jamiołkowski–Choi state [42]–[44]. Because irreversibility is intimately related to a change in entropy, it is desirable to study the entropy of Jamiołkowski–Choi states and to see to what extent this entropy can be used to quantify the irreversibility of the corresponding channel. Inspired by this general idea, in this paper, by using the channel–state duality [42]–[45], we quantify the irreversibility of channels in terms of entropy of the associated Jamiołkowski–Choi states, which is connected to the entropy produced by the channels. We remark that the general idea of relating a change in entropy to irreversibility is well known. To pursue further quantitative and specific links between them, it is crucial to find appropriate entropic quantities of channels. Our key point here is to use the entropy of the Jamiołkowski–Choi states determined by the channels. We relate the measure of irreversibility to the notions of entanglement fidelity, entropy exchange, nonunitality, and decorrelating power [14]–[20], and illustrate the results by several important channels.

The remainder of this paper is organized as follows. In Sec. 2, we discuss irreversibility from an axiomatic standpoint and postulate some basic requirements for a reasonable measure of irreversibility. Somewhat complementary to irreversibility, we also discuss entanglement fidelity, which quantifies the capability of a channel to preserve states and is thus intimately related to the degree of reversibility. In Sec. 3, we propose to use the entropy of the Jamiołkowski–Choi states of channels as a measure of irreversibility and clarify its basic properties. In Sec. 4, we make a comparative study of irreversibility and entanglement fidelity. In Sec. 5, we relate irreversibility to the degree of nonunitality (deviation from the unital map). In Sec. 6, we establish an intuitive and succinct relation connecting irreversibility and decorrelating power. In Sec. 7, we evaluate the irreversibility of some widely used channels, and shed light on these channels from the perspective of irreversibility. In particular, as a simple illustrative application, we apply the results to the scenario of teleportation. We conclude with a summary and discussion in Sec. 8. In the appendix, we present a detailed proof of the main results, discuss an alternative measure of irreversibility in terms of the Tsallis entropy, which is easier to compute, and summarize the results in a table for comparison. For simplicity, we only work with finite-dimensional systems.

2. Basic features of irreversibility

We consider a channel

$$ \mathcal E(\rho)=\sum_k E_k\rho E_k^\dagger$$
(1)

on a quantum system described by a \(d\)-dimensional complex Hilbert space \(H\), where \(E_k\) are the Kraus operators of \(\mathcal E\) satisfying \(\sum_k E_k^\dagger E_k=\mathbf 1\) to ensure the trace-preserving property of \(\mathcal E\). If, moreover, \(\sum_k E_kE_k^\dagger=\mathbf 1\), then the channel is unital (i.e., leaving the maximally mixed state invariant, \(\mathcal E(\mathbf 1/d)=\mathbf 1/d\)). Clearly, the map \(\mathcal E\) defined by Eq. (1) actually makes sense for any operator \(X\) on \(H\colon \mathcal E(X)=\sum_k E_k X E_k^\dagger\).

We want to quantify the degree of irreversibility of the channel \(\mathcal E\). For this, we proceed from an axiomatic consideration motivated by physical intuition. We postulate the following simple and mandatory conditions for a reasonable measure \(S(\mathcal E)\) of irreversibility of the channel \(\mathcal E\).

  1. 1.

    \(S(\mathcal E)\ge 0\), which becomes an equality if and only if \(\mathcal E\) is a unitary channel in the sense that \(\mathcal E(\rho)=U\rho U^\dagger\) for some unitary operator \(U\) on the system Hilbert space \(H\). This is motivated by the fact that unitary channels are reversible and generate no irreversibility because there is no information leakage to the environment: the system is closed under unitary evolution. On the other extreme, for a fixed \(d\)-dimensional system, \(S(\mathcal E)\) attains its maximum value for the completely depolarizing channel \(\mathcal E_{\mathrm{cde}}(\rho)=\mathbf 1/d\) (for any state \(\rho\)). This channel completely loses the original information of the state \(\rho\) and should be considered among the maximally irreversible.

  2. 2.

    \(S(\,{\cdot}\,)\) is concave in the sense that

    $$S(p_1\mathcal E_1+p_2\mathcal E_2)\ge p_1 S(\mathcal E_1)+p_2 S(\mathcal E_2)$$

    for any \(p_1,p_2\ge 0\), \(p_1+p_2=1\), and any channels \(\mathcal E_1\) and \(\mathcal E_2\) on the system Hilbert space \(H\). This is motivated by the intuition that the mixing of channels loses information and generates more irreversibility on average.

  3. 3.

    \(S(\,{\cdot}\,)\) is invariant under composition with unitary channels in the sense that

    $$S(\mathcal E_U \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E)=S(\mathcal E \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E_U)=S(\mathcal E)$$

    for any channel \(\mathcal E_U(\rho)=U\rho U^\dagger\) with \(U\) any unitary operator on the system Hilbert space \(H\).

  4. 4.

    \(S(\,{\cdot}\,)\) is ancilla-independent in the sense that

    $$S(\mathcal I^a\otimes\mathcal E)=S(\mathcal E),$$

    where \(\mathcal I^a\) is the identity channel on any ancilla system \(a\).

  5. 5.

    \(S(\,{\cdot}\,)\) is monotonic in the sense that

    $$S(\mathcal F \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E)\ge S(\mathcal E)$$

    for any unital channel \(\mathcal F\).

It is conceivable that there may exist many quantities satisfying the above requirements, and it is desirable to seek those that are easy to compute and at the same time have intuitive physical significance. Taking these points into account, we provide some entropic quantifiers of the irreversibility of channels.

Complementary to the irreversibility in some sense, it is also desirable to investigate the capability of a channel to preserve states. This leads to the celebrated notion of entanglement fidelity [14], and is somewhat related to the reversibility of channels. Among all channels on a system, it is straightforward and intuitive to regard the identity channel \(\mathcal I\) as the channel with the maximal fidelity. Thus, the deviation of a channel \(\mathcal E\) from \(\mathcal I\) can be used to quantify the fidelity of \(\mathcal E\). We elaborate on the relations between irreversibility and entanglement fidelity in Sec. 4.

3. Irreversibility via entropy of Jamiołkowski–Choi states

In this section, we quantify the irreversibility of a channel via the entropy of the Jamiołkowski–Choi state determined by the channel, for which the Jamiołkowski–Choi isomorphism plays a key role [42]–[45]. Any channel \(\mathcal E\) on a system Hilbert space \(H\) is isomorphic to the bipartite state

$$ J_\mathcal E=(\mathcal I\otimes\mathcal E)(|\Phi^{+}\rangle\langle\Phi^{+}|),$$
(2)

where \(\mathcal I\) is the identity channel on an ancilla system \(H^a=H\) and

$$ |\Phi^{+}\rangle=\frac{1}{\sqrt{d}}\sum_i|i\rangle\otimes|i\rangle$$
(3)

is a maximally entangled state on \(H^a\otimes H=H\otimes H\) associated with an orthonormal basis \(\{|i\rangle\colon i=1,2,\ldots,d\}\) of \(H\). Thus, studying the channel \(\mathcal E\) is formally equivalent to studying the Jamiołkowski–Choi state \(J_\mathcal E\). In particular, we can connect the entropy of the latter to the irreversibility of the former, as is discussed in what follows.

For any state \(\rho\), its von Neumann entropy

$$S(\rho)=- \operatorname{tr} \rho\ln\rho$$

is a key quantity in quantum information theory [11]. Despite its alternative name of quantum entropy, it actually quantifies the mixedness (statistical uncertainty) of a state \(\rho\). If we take \(\rho\) to be the Jamiołkowski–Choi state \(J_\mathcal E\) (defined in Eq. (2)) of the channel \(\mathcal E\), we obtain the entropy

$$S(J_\mathcal E)=- \operatorname{tr} J_\mathcal E\ln J_\mathcal E.$$

It is obvious that \(S(J_\mathcal E)\) can be regarded as the entropy exchange of the channel \(\mathcal E\) in the maximally mixed state \(\mathbf 1/d\) [14]. We emphasize that this quantity is quite different from the entropy production, which is widely studied in both classical and quantum thermodynamics [40].

As a basic feature of a channel \(\mathcal E\), it is desirable to show that \(S(J_{\mathcal E})\) is independent of the choice of the orthonormal basis \(\{|i\rangle\colon i=1,2,\ldots,d\}\) of \(H\). To prove this, we let \(\mathcal E\) be a channel with Kraus operators \(\{E_k\colon k=1,2,\ldots,n\}\); then \(J_{\mathcal E}\) can be written as

$$ J_{\mathcal E}=\sum_{k=1}^n|\xi_k\rangle\langle\xi_k|=(|\xi_1\rangle,|\xi_2\rangle,\ldots,|\xi_n\rangle) \begin{pmatrix} \langle\xi_1| \\ \langle\xi_2| \\ \vdots \\ \langle\xi_n|\end{pmatrix},$$
(4)

where \(|\xi_k\rangle=(\mathbf 1\otimes E_k)|\Phi^{+}\rangle\in H\otimes H\). Let \(W=(w_{kl})\) be the Gram matrix with entries defined as \(w_{kl}=\langle\xi_k|\xi_l\rangle=\frac{1}{d} \operatorname{tr} (E_k^\dagger E_l)\); then \(W\) is apparently independent of the choice of the orthonormal basis \(\{|i\rangle\colon i=1,2,\ldots,d\}\), and can be further written as

$$ W=\begin{pmatrix} \langle\xi_1| \\ \langle\xi_2| \\ \vdots \\ \langle\xi_n|\end{pmatrix} (|\xi_1\rangle,|\xi_2\rangle,\ldots,|\xi_n\rangle).$$
(5)

By Eqs. (4) and (5), we have \(S(J_{\mathcal E})=S(W)\), which implies that \(S(J_{\mathcal E})\) is independent of the choice of the orthonormal basis.

After the above preparations, we introduce the quantity

$$ S(\mathcal E)=\frac{1}{2} S(J_\mathcal E)$$
(6)

as a quantifier of the irreversibility of a channel \(\mathcal E\). The factor \(1/2\) is for later convenience and for ensuring the upper bound \(\ln d\) for a \(d\)-dimensional system (see Eq. (7)), and originates from the fact that \(J_\mathcal E\) is a composite “system\({}+{}\)ancilla” state, which doubles the dimension of the system. The same symbol \(S\) used for both the von Neumann entropy and the irreversibility of channels should not cause confusion because their arguments respectively refer to states and channels.

The measure of irreversibility \(S(\mathcal E)\) has the following properties consistent with requirements 1–5 in Sec. 2.

Proposition 1.

Let \(\mathcal E\) be a channel on a \(d\)-dimensional quantum system with a Hilbert space \(H\).

  1. 1.

    We have

    $$ 0\le S(\mathcal E)\le\ln d.$$
    (7)

    Moreover, \(S(\mathcal E)=0\) if and only if \(\mathcal E\) is a unitary channel, and \(S(\mathcal E)\) attains the maximal value \(\ln d\) if and only if \(\mathcal E\) is the completely depolarizing channel \(\mathcal E_{\mathrm{cde}}(\rho)=\mathbf 1/d\) for any state \(\rho\).

  2. 2.

    \(S(\,{\cdot}\,)\) is concave in the sense that

    $$S(p_1\mathcal E_1+p_2\mathcal E_2)\ge p_1 S(\mathcal E_1)+p_2 S(\mathcal E_2)$$

    for \(p_1,p_2\ge 0\), \(p_1+p_2=1\), and any channels \(\mathcal E_1\) and \(\mathcal E_2\).

  3. 3.

    \(S(\,{\cdot}\,)\) is invariant under composition with unitary channels in the sense that

    $$S(\mathcal E_U \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E)=S(\mathcal E \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E_U)=S(\mathcal E),$$

    where \(\mathcal E_U(\rho)=U\rho U^\dagger\) with \(U\) any unitary operator on \(H\).

  4. 4.

    \(S(\,{\cdot}\,)\) is ancilla-independent in the sense that

    $$S(\mathcal I^a\otimes\mathcal E)=S(\mathcal E),$$

    where \(\mathcal I^a\) is the identity channel on any ancilla system Hilbert space \(H^a\).

  5. 5.

    \(S(\,{\cdot}\,)\) is monotonic in the sense that

    $$S(\mathcal F \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E)\ge S(\mathcal E)$$

    for any unital channel \(\mathcal F\).

  6. 6.

    \(S(\,{\cdot}\,)\) is additive under tensor product in the sense that

    $$S(\mathcal E^a\otimes\mathcal E^b)=S(\mathcal E^a)+S(\mathcal E^b),$$

    where \(\mathcal E^a\) and \(\mathcal E^b\) are channels on respective systems \(a\) and \(b\).

Proof is given in Appendix A.

Being simple and significant extensions of unitary channels, random unitary channels constitute an important class of channels and have many nice properties. Their degree of irreversibility has the following quantification.

Proposition 2.

For any random unitary channel

$$\mathcal E_{\mathrm{ru}}(\rho)=\sum_{k}p_k U_k\rho U_k^\dagger$$

with \(U_k\) being any unitary operators and \(p_k>0\), \(\sum_{k} p_k=1\), we have

$$0\le S(\mathcal E_{\mathrm{ru}})\le\min\biggl\{\frac{1}{2}H(\{p_k\}),\ln d\biggr\},$$

where \(H(\{p_k\})=-\sum_kp_k\ln p_k\) is the Shannon entropy of the probability distribution \(\{p_k\}\). Moreover,

  1. 1.

    \(S(\mathcal E_{\mathrm{ru}})=0\) if and only if \(\mathcal E_{\mathrm{ru}}\) is a unitary channel;

  2. 2.

    \(S(\mathcal E_{\mathrm{ru}})=\frac{1}{2}H(\{p_k\})\) if and only if the unitary operators \(U_k\) are pairwise orthogonal in the sense that \( \operatorname{tr} (U_k^\dagger U_l)=0\) for any \(k\neq l\);

  3. 3.

    \(S(\mathcal E_{\mathrm{ru}})=\ln d\) if and only if \(\mathcal E_{\mathrm{ru}}\) is the completely depolarizing channel, i.e., \(\mathcal E_{\mathrm{ru}}(\rho)=\mathcal E_{\mathrm{cde}}(\rho)=\mathbf 1/d\) for any state \(\rho\).

Proof is given in Appendix B.

To illustrate Proposition 2, we consider the generalized depolarizing channel

$$\mathcal E(\rho)=\sum_{k=0}^3p_k\sigma_k\rho\sigma_k$$

on a qubit system, where \(p_k\ge 0\), \(\sum_{k}p_k=1\), \(\sigma_0=\mathbf 1\), and \(\sigma_j\), \(j=1,2,3\), are the Pauli matrices. Direct calculation shows that

$$J_{\mathcal E}=\frac{1}{2}\begin{pmatrix} p_0+p_3& 0 & 0 & p_0-p_3 \\ 0 & p_1+p_2 & p_1-p_2 & 0 \\ 0 & p_1-p_2 & p_1+p_2 & 0 \\ p_0-p_3 & 0 & 0 & p_0+p_3 \\ \end{pmatrix}$$

with eigenvalues \(p_k\), \(k=0,1,2,3\). Thus,

$$S(\mathcal E)=-\frac{1}{2}\sum_k p_k\ln p_k.$$

In particular, the conventional depolarizing channel

$$\mathcal E_{\mathrm{de}}(\rho)=(1-3p)\rho+p\sum_{k=1}^3\sigma_k\rho\sigma_k,\qquad 0\le p\le\frac{1}{3},$$

corresponds to the generalized depolarizing channel with \(p_0=1-3p\), \(p_1=p_2=p_3=p\). In this case, we have

$$S(\mathcal E_{\mathrm{de}})=-\frac{1}{2}\bigl((1-3p)\ln (1-3p)+3p\ln p\bigr).$$

4. Comparison between irreversibility and entanglement fidelity

We consider a channel \(\mathcal E\), defined by Eq. (1), on a \(d\)-dimensional system with a Hilbert space \(H\). We take an ancilla system Hilbert space \(H^a=H\) and let \(|\Phi^{+}\rangle\) be any maximally entangled state defined by Eq. (3). Then the entanglement fidelity

$$F(\mathcal E)=F(|\Phi^{+}\rangle\langle\Phi^{+}|,(\mathcal I\otimes\mathcal E)(|\Phi^{+}\rangle\langle\Phi^{+}|)\big)= \langle\Phi^{+}|\mathcal I\otimes\mathcal E(|\Phi^{+}\rangle\langle\Phi^{+}|)|\Phi^{+}\rangle,$$

which was first introduced in [14], quantifies how well the entanglement (correlations) between the system of interest and the ancilla system is preserved by the (local) channel \(\mathcal E\) [14]–[20]. Here, \(F(\rho,\sigma)=( \operatorname{tr} (\rho^{1/2}\sigma\rho^{1/2})^{1/2})^2\) is the fidelity between the states \(\rho\) and \(\sigma\).

By the use of the channel–state duality, the entanglement fidelity can be represented as the fidelity between the Jamiołkowski–Choi states \(J_{\mathcal E}\) and \(J_{\mathcal I}\), i.e.,

$$F(\mathcal E)=F(J_{\mathcal E}, J_{\mathcal I}).$$

Direct calculation shows that [46]

$$F(\mathcal E)=\frac{1}{d^2}\sum_k| \operatorname{tr} E_k|^2,$$

which is intrinsically related to the average fidelity [47]

$$\begin{aligned} \, \kern1.6pt\overline{\vphantom{F}\kern5.6pt}\kern-7.4pt F\kern-0.2pt (\mathcal E)=\int F(|\phi\rangle\langle\phi|,\mathcal E(|\phi\rangle\langle\phi|))\,d\phi= \frac{1}{d+1}+\frac{1}{d(d+1)}\sum_k| \operatorname{tr} E_k|^2 \end{aligned}$$

as

$$F(\mathcal E)=\biggl(1+\frac{1}d\biggr) \kern1.6pt\overline{\vphantom{F}\kern5.6pt}\kern-7.4pt F\kern-0.2pt (\mathcal E)-\frac{1}{d}.$$

Here, \(d\phi\) is the normalized Haar measure on all pure states in the system Hilbert space \(H\).

Several nice properties of the entanglement fidelity are summarized as follows. Let \(\mathcal E\) be a channel on a \(d\)-dimensional quantum system with a Hilbert space \(H\).

  1. 1.

    \(0\le F(\mathcal E)\le 1\). Moreover, \(F(\mathcal E)=0\) if and only if all Kraus operators \(E_k\) of the channel \(\mathcal E\) have a vanishing trace, and \(F (\mathcal E)=1\) if and only if \(\mathcal E\) is the identity channel.

  2. 2.

    \(F(\mathcal E)\) is affine in the sense that

    $$F(p_1\mathcal E_1+p_2\mathcal E_2)= p_1 F(\mathcal E_1)+p_2 F(\mathcal E_2)$$

    for \(p_1,p_2\ge 0\), \(p_1+p_2=1\), and any channels \(\mathcal E_1\) and \(\mathcal E_2\).

  3. 3.

    \(F(\mathcal E)\) is unitarily covariant in the sense that

    $$F(\mathcal{U} \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal{U}^\dagger)=F(\mathcal E)$$

    for any unitary channel \(\mathcal{U}(\rho)=U\rho U^\dagger\), where \(\mathcal{U}^\dagger(\rho)=U^\dagger\rho U\) is its dual map and \( \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \) is the composition of maps. However, \(F(\mathcal E)\) is in general not invariant under composition with unitary channels in the sense that

    $$F(\mathcal E_U \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E)=F(\mathcal E \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E_U)\neq F(\mathcal E),$$

    where \(\mathcal E_U(\rho)=U\rho U^\dagger\) for any unitary operator \(U\) on the system Hilbert space.

  4. 4.

    \(F(\mathcal E)\) is multiplicative under tensor product in the sense that

    $$F(\mathcal E^a\otimes\mathcal E^b)=F(\mathcal E^a) F(\mathcal E^b),$$

    for the channels \(\mathcal E^a\), \(\mathcal E^b\), and \(\mathcal E^a\otimes\mathcal E^b\) on systems \(a\) and \(b\) and the composite system \(ab\). In particular, when \(\mathcal E^a=\mathcal I^a\), we have

    $$F(\mathcal I^a\otimes{\mathcal E}^b)=F(\mathcal E^b),$$

    which can be interpreted as the ancilla-independence of the entanglement fidelity.

The irreversibility \(S(\mathcal E)\) and the entanglement fidelity \(F(\mathcal E)\) have the following trade-off relation.

Proposition 3.

For any channel \(\mathcal E\) on a \(d\)-dimensional system, we have

$$ \sqrt{\ln d -S(\mathcal E)}+\sqrt{1-F(\mathcal E)}\ge 1-\frac{1}{d^2}.$$
(8)

A more transparent interpretation is to regard \(R(\mathcal E)=\ln d -S(\mathcal E)\) as a measure of reversibility, and \(G(\mathcal E)=1-F(\mathcal E)\) as a measure of infidelity; then (8) is equivalent to

$$\sqrt{R(\mathcal E)}+\sqrt{G(\mathcal E)}\ge 1-\frac{1}{d^2}.$$

This proposition establishes a constraint between these two quantities. The reversibility and infidelity cannot be simultaneously small, which is consistent with our physical intuition.

Proof is given in Appendix C.

5. Degree of nonunitality of channels

We recall that a channel \(\mathcal E\) is unital if \(\mathcal E(\mathbf 1/d)=\mathbf 1/d\). Nonunitality refers to the deviation of the state \(\mathcal E(\mathbf 1/d)\) from the maximally mixed state \(\mathbf 1/d\). In terms of the relative entropy \(S(\rho|\sigma)= \operatorname{tr} \rho (\ln\rho -\ln\sigma)\), a natural figure of merit for the nonunitality of \(\mathcal E\) can be defined as

$$ N(\mathcal E)=S(\mathcal E(\mathbf 1/d)|\mathbf 1/d)=\ln d-S(\mathcal E(\mathbf 1/d)).$$
(9)

This quantity has the following properties.

  1. 1.

    \(0\le N(\mathcal E)\le\ln d\). Moreover, \(N(\mathcal E)=0\) if and only if \(\mathcal E\) is a unital channel, and \(N(\mathcal E)=\ln d\) if and only if \(\mathcal E\) is a channel satisfying \(\mathcal E(\rho)=|\phi\rangle\langle\phi|\) for some pure state \(|\phi\rangle\).

  2. 2.

    \(N(\mathcal E)\) is convex in the sense that

    $$N(p_1\mathcal E_1+p_2\mathcal E_2)\le p_1 N(\mathcal E_1)+p_2 N(\mathcal E_2)$$

    for \(p_1,p_2\ge 0\), \(p_1+p_2=1\), and any channels \(\mathcal E_1\) and \(\mathcal E_2\).

  3. 3.

    \(N(\mathcal E)\) is unitary invariant in the sense that

    $$N(\mathcal E_U \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E)=N(\mathcal E \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E_U)=N(\mathcal E),$$

    where \(\mathcal E_U(\rho)=U\rho U^\dagger\) with \(U\) any unitary operator on \(H\).

  4. 4.

    \(N(\mathcal E)\) is nonincreasing in the sense that

    $$N(\mathcal F \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E)\le N(\mathcal E)$$

    for any unital channel \(\mathcal F\).

  5. 5.

    For any channels \(\mathcal E^a\) and \(\mathcal E^b\) on systems \(a\) and \(b\), we have

    $$N(\mathcal E^a\otimes\mathcal E^b)=N(\mathcal E^a)+N(\mathcal E^b).$$

    In particular, if \(\mathcal E^a=\mathcal I^a\) is an identity channel, we have

    $$N(\mathcal I^a\otimes\mathcal E^b)=N(\mathcal E^b).$$

The above properties readily follow from the properties of von Neumann entropy.

We recall the Araki–Lieb inequality

$$|S(\rho^a)-S(\rho^b)|\le S(\rho^{ab})$$

for any bipartite state \(\rho^{ab}\) on a composite system \(ab\) with reduced states \(\rho^a\) and \(\rho^b\) on respective parties \(a\) and \(b\). By taking \(\rho^{ab}=J_{\mathcal E}\), we derive a relation between irreversibility and nonunitality,

$$ N(\mathcal E)\le 2S(\mathcal E).$$
(10)

Thus, the degree of nonunitality is dominated by the degree of irreversibility, or, in other words, nonunitality accounts for part of the irreversibility.

6. Decorrelating power of channels

For a bipartite state \(\rho^{ab}\) on a composite system \(ab\), the total correlations in \(\rho^{ab}\) can be quantified by the quantum mutual information

$$ I(\rho^{ab})=S(\rho^{ab}|\rho^a\otimes\rho^b)=S(\rho^a)+S(\rho^b)-S(\rho^{ab}).$$
(11)

Among all channels, the identity channel \(\mathcal I\) is the channel that neither generates nor disturbs correlations. Thus, by the Jamiołkowski–Choi isomorphism, the difference of correlations between the Jamiołkowski–Choi states \(J_{\mathcal I}\) and \(J_\mathcal E\) associated with the channels \(\mathcal I\) and \(\mathcal E\) can be used to quantify the decorrelating power of the channel \(\mathcal E\). Thus, we introduce

$$\begin{aligned} \, D(\mathcal E)&=I(J_{\mathcal I})-I(J_{\mathcal E}) \end{aligned}$$
(12)

as a quantity characterizing the decorrelating power of \(\mathcal E\).

In [48], the total loss of correlations was decomposed into classical and quantum parts. Here, we obtain a new decomposition for the loss of correlations: nonunitality and irreversibility. We state the result as follows.

Proposition 4.

We have

$$ D(\mathcal E)=N(\mathcal E)+2S(\mathcal E),$$
(13)

which implies that the total correlations disturbed by \(\mathcal E\) can be divided into two parts: one part quantifies the nonunitality of \(\mathcal E\) and the other quantifies the irreversibility of \(\mathcal E\).

Proof is given in Appendix D.

The decorrelating power \(D(\mathcal E)\) has the following properties.

Proposition 5.

  1. 1.

    For any channel \(\mathcal E\) on a \(d\)-dimensional quantum system, we have

    $$ 0\le D(\mathcal E)\le 2\ln d.$$
    (14)

    Moreover, \(D(\mathcal E)=0\) if and only if \(\mathcal E\) is a unitary channel, and \(D(\mathcal E)\) attains the maximal value \(2\ln d\) if and only if \(\mathcal E\) is a replacement channel, i.e., \(\mathcal E(\rho)=\mathcal E(\mathbf 1/d)\) for any state \(\rho\).

  2. 2.

    \(D(\,{\cdot}\,)\) is concave in the sense that

    $$D(p_1\mathcal E_1+p_2\mathcal E_2)\ge p_1 D(\mathcal E_1)+p_2 D(\mathcal E_2)$$

    for \(p_1,p_2\ge 0\), \(p_1+p_2=1\), and any channels \(\mathcal E_1\) and \(\mathcal E_2\).

  3. 3.

    \(D(\,{\cdot}\,)\) is invariant under composition with unitary channels in the sense that

    $$D(\mathcal E_U \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E)=D(\mathcal E \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E_U)=D(\mathcal E),$$

    where \(\mathcal E_U(\rho)=U\rho U^\dagger\) with \(U\) any unitary operator on \(H\).

  4. 4.

    \(D(\,{\cdot}\,)\) is ancilla-independent in the sense that

    $$D(\mathcal I^a\otimes\mathcal E)=D(\mathcal E),$$

    where \(\mathcal I^a\) is the identity channel on any ancilla system \(a\).

  5. 5.

    \(D(\,{\cdot}\,)\) is monotonic in the sense that

    $$D(\mathcal F \mathbin{\stackrel{\scriptscriptstyle{\circ}}{{}_{\vphantom{.}}}} \mathcal E)\ge D(\mathcal E)$$

    for any channel \(\mathcal F\).

  6. 6.

    \(D(\,{\cdot}\,)\) is additive under tensor product in the sense that

    $$D(\mathcal E^a\otimes\mathcal E^b)=D(\mathcal E^a)+D(\mathcal E^b),$$

    where \(\mathcal E^a\), \(\mathcal E^b\) are channels on the respective systems \(a\) and \(b\).

Proof is given in Appendix E.

7. Evaluating the irreversibility of various channels

In this section, we evaluate the irreversibility of several basic and important channels and make some comparative studies. These quantitative results shed light on the structure of various channels from the perspective of irreversibility.

7.1. Unitary channel

For any unitary channel

$$\mathcal E_U(\rho)=U\rho U^{\dagger},$$

where \(U\) is any unitary operator on a \(d\)-dimensional quantum system, we have

$$J_{\mathcal E_U}=|\Phi^{+}_U\rangle\langle\Phi^{+}_U|$$

where \(|\Phi^{+}_U\rangle=\frac{1}{\sqrt d}\sum_i|i\rangle\otimes|i_U\rangle\) and \(|i_{U}\rangle=U|i\rangle\) for \(\{|i\rangle\colon i=1, 2,\ldots,d\}\) is an orthonormal basis of the system Hilbert space. Consequently, \(S(\mathcal E_U)=0\), as it should be.

7.2. Lüders channel

For the Lüders channel [49]

$$\Pi(\rho)=\sum_{k=1}^m\Pi_k\rho\Pi_k$$

on a \(d\)-dimensional system determined by a Lüders (projective) measurement

$$\Pi=\biggl\{\Pi_k=\sum_{j=n_{k-1}+1}^{n_k}|j\rangle\langle j|\colon k=1,2,\ldots,m\biggl\},\qquad \sum_k\Pi_k=\mathbf 1,$$

where

$$\Pi_k^\dagger=\Pi_k,\quad \Pi_k\Pi_l=\delta_{kl}\Pi_k,\qquad n_k=\sum_{j=1}^k \operatorname{tr} \Pi_j\;\,\text{for}\;\, k\ge 1,\quad n_0=0,$$

we have

$$J_{\Pi}=\frac{1}{d}\sum_{k=1\vphantom{n_{k-1}+1\le j,l\le n_k}}^m\sum_{n_{k-1}+1\le j,l\le n_k}^{}|jj\rangle\langle ll|.$$

It is obvious that \( \operatorname{tr} \Pi_k/d, k=1,2,\ldots,m\), are the nonzero eigenvalues of \(J_{\Pi}\) and

$$S(\Pi)=\frac{1}{2}\ln d-\frac{1}{2d}\sum_{k=1}^m( \operatorname{tr} \Pi_k)\ln ( \operatorname{tr} \Pi_k).$$

It is easy to verify that the Lüders channels with the maximal irreversibility are

$$\mathcal E_{\mathrm{vN}}(\rho)=\sum_k\Pi_k\rho\Pi_k$$

which are induced by any von Neumann measurement \(\{\Pi_k\colon k=1,2,\ldots,d\}\) (i.e., \( \operatorname{tr} \Pi_k=1\) for all \(k\)). In this case,

$$S(\mathcal E_{\mathrm{vN}})=\frac{1}{2}\ln d.$$

This reveals an interesting feature of von Neumann measurements: the irreversibility of any von Neumann measurement stands exactly half the way between the two extreme values of irreversibility (the minimum \(0\) and the maximum \(\ln d\)).

7.3. Channel induced by SIC-POVM

We recall that a SIC-POVM (symmetric informationally complete positive operator-valued measure) on a \(d\)-dimensional system is a set of \(d^2\) rank-one operators \(E_k=\frac{1}{d}|\phi_k\rangle\langle\phi_k|\), \(k=1,2,\ldots,d^2\), satisfying the relations [50]

$$\label{SIC} |\langle\phi_k|\phi_l\rangle|^2=\begin{cases} \quad\kern-0.5pt 1, & k=l, \\ \dfrac{1}{d+1}, & k\neq l. \end{cases}$$

Any SIC-POVM naturally induces a channel

$$\mathcal E_{\mathrm{sic}}(\rho)=\sum_{k}\sqrt {E_k}\rho\sqrt{E_k}.$$

By straightforward calculation, we obtain

$$J_{\mathcal E_{\mathrm{sic}}}=\frac{1}{d^2}\sum_k|\bar{\phi_k}\rangle\langle\bar{\phi_k}|\otimes|\phi_k\rangle\langle\phi_k|.$$

Here, \(|\bar{\phi}\rangle\) denotes the complex conjugate of the vector \(|\phi\rangle\) with respect to the basis \(\{|i\rangle\colon i=1,2,\ldots,d\}\) of \(H\). Let

$$|\psi_1\rangle=\frac{1}d\sum_k|\bar{\phi_k}\rangle\otimes|\phi_k\rangle,\qquad|\psi_l\rangle=\frac{1}{\sqrt{d^2+1}}(d|\bar{\phi_l}\rangle\otimes|\phi_l\rangle-|\psi_1\rangle),\quad l=2,3,\ldots,d^2.$$

It is then easy to verify that \(|\psi_1\rangle,|\psi_2\rangle,\ldots,|\psi_{d^2}\rangle\) are linearly independent and

$$J_{\mathcal E_{\mathrm{sic}}}|\psi_1\rangle=\frac{1}{d}|\psi_1\rangle,\quad J_{\mathcal E_{\mathrm{sic}}}|\psi_l\rangle= \frac{1}{d(d+1)}|\psi_l\rangle,\qquad l=2,3,\ldots,d^2.$$

Thus, \(J_{\mathcal E_{\mathrm{sic}}}\) has two different eigenvalues \(1/d\) and \(1/d(d+1)\) with the multiplicities respective \(1\) and \(d^2-1\), and the irreversibility of \(\mathcal E_{\mathrm{sic}}\) can be evaluated as

$$S(\mathcal E_{\mathrm{sic}})=\frac{1}{2}\ln d+\frac{d-1}{2d}\ln (d+1).$$

For large \(d\), this approximates the maximum \(\ln d\), which implies that the irreversibility of the channel induced by a SIC-POVM in higher dimensions is asymptotically maximal.

7.4. The Werner–Holevo channel

The Werner–Holevo channel [51]

$$\mathcal E_{\mathrm{WH}}(\rho)=\frac{1}{d-1}(\mathbf 1-\rho^{\mathrm T})$$

provides a counterexample to the additivity conjecture for the output purity of channels [51]. Here, \(\rho^{\mathrm T}\) is the transpose of \(\rho\) in an orthonormal basis \(\{|i\rangle\colon i=1,2,\ldots, d\}\) of \(H\). It is known that a Kraus representation of \(\mathcal E_{\mathrm{WH}}\) is

$$\mathcal E_{\mathrm{WH}}(\rho)=\frac{1}{2(d-1)}\sum_{i,j}(|i\rangle\langle j|-|j\rangle\langle i|)\rho(|i\rangle\langle j|-|j\rangle\langle i|)^\dagger.$$

Direct calculation shows that

$$J_{\mathcal E_{\mathrm{WH}}}=\frac{1}{d(d-1)}\biggl(\mathbf 1\otimes\mathbf 1-\sum_{i,j}|ij\rangle\langle ji|\biggr),$$

which is a Werner state and has two different eigenvalues \(0\) and \(2/(d^2-d)\) with the respective multiplicities \((d^2+d)/2\) and \((d^2-d)/2\). Thus, the irreversibility of \(\mathcal E_{\mathrm{WH}}\) can be directly evaluated as

$$S(\mathcal E_{\mathrm{WH}})=\frac{1}{2}\ln\frac{d^2-d}{2}.$$

In particular, if \(d=2\), the Werner–Holevo channel reduces to the unitary channel

$$\mathcal E_{\mathrm{WH}}(\rho)= \operatorname{tr} (\rho)\mathbf 1-\rho^{\mathrm T}=\sigma_2\rho\sigma_2$$

where \(\sigma_2\) is the second Pauli matrix. In this case, \(S(\mathcal E_{\mathrm{WH}})=0\).

7.5. Completely depolarizing channel

For the completely depolarizing channel

$$\mathcal E_{\mathrm{cde}} (\rho)=\frac{1}{d}\sum_kX_k\rho X_k=\frac{1}{d}\mathbf 1,$$

where \(\{X_k\colon k=1,2,\ldots,d^2\}\) is an orthonormal basis of \(L(H)\) consisting of all Hermitian operators on the system \(H\), we have

$$J_{\mathcal E_{\mathrm{cde}}}=\frac{1}{d^2}\mathbf 1\otimes\mathbf 1,$$

whence \(S(\mathcal E_{\mathrm{cde}})=\ln d\). Therefore, in view of Eq. (7), we see that the completely depolarizing channel attains the maximal value of irreversibility. This is reasonable, as is already suggested by the name of this channel.

7.6. Completely decoherent channel

We recall that a completely decoherent channel on a qubit system is defined as [52], [53], [48]

$$\mathcal E_{\mathrm{cd}}(\rho)=M*\rho,$$

where \(M\) is a nonnegative-definite matrix with all diagonal elements being 1 (i.e., a correlation matrix), and \(*\) denotes the Hadamard (entry-wise) product of matrices. For simplicity, we consider the \(2\times2\) matrix

$$M=\begin{pmatrix} 1 & \alpha \\ \alpha & 1 \end{pmatrix},\qquad -1\le\alpha\le 1.$$

It is easy to verify that the channel can be expressed as \(\mathcal E_{\mathrm{cd}}(\rho)=\sum_k E_k\rho E_k^\dagger\) with the Kraus operators

$$E_1=\begin{pmatrix} \sqrt{1-|\alpha|} & 0 \\ 0 & 0 \end{pmatrix},\qquad E_2=\begin{pmatrix} 0 & 0 \\ 0 & \sqrt{1-|\alpha|}\, \end{pmatrix},\qquad E_3=\sqrt{|\alpha|}\begin{pmatrix} 1 & 0 \\ 0 & \operatorname{sgn}\alpha\end{pmatrix}.$$

Direct calculation shows that

$$J_{\mathcal E_{\mathrm{cd}}}=\frac{1}{2}\begin{pmatrix} 1 & 0 & 0 & \alpha \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \alpha & 0 & 0 & 1 \end{pmatrix}.$$

The nonzero eigenvalues of \(J_{\mathcal E_{\mathrm{cd}}}\) are \((1+\alpha)/2\), \((1-\alpha)/2\) and the irreversibility of \(\mathcal E_{\mathrm{cd}}\) can be evaluated as

$$S(\mathcal E_{\mathrm{cd}})=-\frac{1+\alpha}{4}\ln\frac{1+\alpha}{2}-\frac{1-\alpha}{4}\ln\frac{1-\alpha}{2}.$$

7.7. Amplitude-damping channel

For the amplitude-damping channel

$$\mathcal E_{\mathrm{ad}}(\rho)=\sum_{k}E_k\rho E_k^{\dagger}$$

on a qubit system with the Kraus operators

$$E_1=\begin{pmatrix} 1 & 0 \\ 0 & \sqrt{1-p}\, \end{pmatrix},\qquad E_2=\begin{pmatrix} 0 & \sqrt{p} \\ 0 & 0 \end{pmatrix},\qquad 0\le p\le 1,$$

we have

$$J_{\mathcal E_{\mathrm{ad}}}=\frac{1}{2}\begin{pmatrix} 1 & 0 & 0 & \sqrt{1-p}\, \\ 0 & 0 & 0 & 0 \\ 0 & 0 & p & 0 \\ \sqrt{1-p} & 0 & 0 & 1-p \end{pmatrix}$$

which has the nonzero eigenvalues \(p/2\) and \(1-p/2\). Consequently,

$$S(\mathcal E_{\mathrm{ad}})=-\frac{p}{4}\ln\frac{p}{2}-\frac{2-p}{4}\ln\frac{2-p}{2}.$$

We see that \(S(\mathcal E_{\mathrm{ad}})\) is increasing with the parameter \(p\).

7.8. Phase-damping channel

For the phase-damping channel

$$\mathcal E_{\mathrm{pd}}(\rho)=\sum_{k}E_k\rho E_k^{\dagger}$$

on a qubit system with the Kraus operators

$$E_1=\begin{pmatrix} 1 & 0 \\ 0 &\sqrt{1-p\,} \end{pmatrix},\qquad E_2=\begin{pmatrix} 0 & 0 \\ 0 &\sqrt{p} \end{pmatrix},\qquad 0\le p\le 1,$$

we have

$$J_{\mathcal E_{\mathrm{pd}}}=\frac{1}{2}\begin{pmatrix} 1 & 0 & 0 & \sqrt{1-p}\, \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \sqrt{1-p} & 0 & 0 & 1 \end{pmatrix}$$

which has the nonzero eigenvalues \(p'=(1+\sqrt{1-p}\,)/2\) and \(1-p'\). Consequently,

$$S(\mathcal E_{\mathrm{pd}})=-\frac{1}{2}\bigl(p'\ln p'+(1-p')\ln(1-p')\bigr).$$

We see that \(S(\mathcal E_{\mathrm{pd}})\) is also an increasing function of the parameter \(p\).

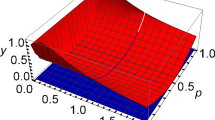
In this context, it is interesting to compare the amplitude-damping channel and the phase-damping channel for the same parameter \(p\): \(S(\mathcal E_{\mathrm{ad}})\ge S(\mathcal E_{\mathrm{pd}})\), which is illustrated in Fig. 1. We see that for the same parameter \(p\), the amplitude-damping channel is more irreversible than the phase-damping channel.

Fig. 1.
figure 1

Comparison between the degree of irreversibility of the amplitude-damping channel \(\mathcal E_{\mathrm{ad}}\) and the phase-damping channel \(\mathcal E_{\mathrm{pd}}\) for the parameter \(p\in[0,1]\). We see that except in the two extreme cases (\(p=0\) or \(p=1\)), the amplitude-damping channel \(\mathcal E_{\mathrm{ad}}\) is more irreversible than the phase-damping channel \(\mathcal E_{\mathrm{pd}}\).

Full size image

7.9. Channel induced by weak measurements

We consider the channel

$$\mathcal K(\rho)=E_x\rho E_x+E_{1-x}\rho E_{1-x},\qquad x\in[0,1/2),$$

associated with the weak measurement \(\{E_x,E_{1-x}\}\) with \(E_x=\sqrt {1-x}\,\Pi_0+\sqrt{x}\,\Pi_1\). Here, \(\{\Pi_0,\Pi_1\}\) is a Lüders measurement in a \(d\)-dimensional system. In particular, as \(x\to 0\), the weak measurement tends to the Lüders measurement \(\{\Pi_0,\Pi_1\}\). The corresponding Jamiołkowski–Choi state is

$$\begin{aligned} \, J_\mathcal K=\frac{1}d\biggl(&\,\sum_{1\le i,j\le \operatorname{tr} \Pi_0}|ii\rangle\langle jj|+\sum_{ \operatorname{tr} \Pi_0+1\le i,j\le d}|ii\rangle\langle jj|+2\sqrt{x(1-x)} \sum_{\substack{1\le i\le \operatorname{tr} \Pi_0,\\ \operatorname{tr} \Pi_0+1\le j\le d}}(|ii\rangle\langle jj|+|jj\rangle\langle ii|)\biggr) \end{aligned}$$

and the irreversibility of \(\mathcal K\) can be evaluated as

$$S(\mathcal K)=-\frac{1}{2} (\lambda_{+}\ln\lambda_{+}+\lambda_{-}\ln\lambda_{-}),$$

where

$$\lambda_{\pm}=\frac{1}{2}\biggl(1\pm\biggl(1-\frac {4(2x-1)^2}{d^2} \operatorname{tr} \Pi_0 \operatorname{tr} \Pi_1\biggr)^{\!1/2\,}\biggr)$$

are the nonzero eigenvalues of \(J_\mathcal K\). In particular, for a qubit weak measurement \(\mathcal E_{x}=\mathcal K\) with \({ \operatorname{tr} \Pi_0= \operatorname{tr} \Pi_1=1}\), \(d=2\), we further obtain

$$S(\mathcal E_{x})=-\frac{1}{2}\bigl(p_x\ln p_x+(1-p_x)\ln (1-p_x)\bigr)$$

with \(p_x=1/2+\sqrt{x(1-x)}\).

7.10. Measurement-preparation channel

We consider the measurement-preparation channel

$$\mathcal E_{\mathrm{mp}}(\rho)=\sum_k \operatorname{tr} (\rho M_k)\tau_k$$

with \(\tau_k\) quantum states and \(M=\{M_k\}\) a quantum measurement (POVM) such that \(\sum_k M_k=\mathbf 1\). The corresponding Jamiołkowski–Choi state is

$$J_{\mathcal E_{\mathrm{mp}}}=\frac{1}{d}\sum_k M_k^{\mathrm T}\otimes\tau_k,$$

where T denotes the transposition of a matrix (of an operator relative to a basis). Consequently,

$$S(\mathcal E_{\mathrm{mp}})=\frac{1}{2} S\biggl(\frac{1}{d}\sum_k M_k^{\mathrm T}\otimes\tau_k\biggr).$$

In particular, when \(M=\Pi=\{\Pi_k: k=1,2,\ldots,m\}\) is a Lüders measurement, we have

$$S(\mathcal E_{\mathrm{mp}})=\frac{1}{2}\ln d+\frac{1}{2d}\sum_k \operatorname{tr} (\Pi_k)S(\tau_k).$$

7.11. Teleportation channel

Let \(\rho^{ab}\) be a two-qubit state shared by Alice and Bob. The quantum teleportation via the resource state \(\rho^{ab}\) provides a way to transmit an unknown state \(\gamma\) from the sender Alice to the receiver Bob with fidelity better than the classical limit \(2/3\) via a classical channel [19], [54]–[58]. It has been shown that the standard teleportation can be described by a generalized depolarizing channel as [58]

$$\mathcal E_{\mathrm t}(\gamma)=\sum_{k=0}^3 p_k\sigma_k\gamma\sigma_k,$$

where \(\sigma_0=\mathbf 1\), \(\sigma_k\) are the Pauli matrices, and \(p_k= \operatorname{tr} (\rho^{ab}M_k)\) with the Bell measurement operators

$$M_k=(\sigma_k\otimes\mathbf 1)|\Phi^{+}\rangle\langle\Phi^{+}|(\sigma_k\otimes\mathbf 1),\qquad |\Phi^{+}\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle).$$

For the resource state

$$\rho^{ab}=\frac{1-p}{4}\mathbf 1\otimes\mathbf 1+p|\Phi^{+}\rangle\langle\Phi^{+}|,\qquad 0\le p\le 1,$$

the irreversibility of the teleportation channel \(\mathcal E_{\mathrm t}\) can be directly evaluated as

$$S(\mathcal E_{\mathrm t})=-\frac{1+3p}{8}\ln\frac{1+3p}{4}-\frac{3(1-p)}{8}\ln\frac{1-p}{4},$$

which is decreasing with the fraction parameter \(p\in[0,1]\). This is consistent with intuition because larger \(p\) correspond to greater entanglement and hence to greater fidelity (less irreversibility).

The entanglement fidelity and the average fidelity of the teleportation channel \(\mathcal E_{\mathrm t}\) can be directly evaluated as

$$F(\mathcal E_{\mathrm t})=\frac{1+3p}{4},\qquad \kern1.6pt\overline{\vphantom{F}\kern5.6pt}\kern-7.4pt F\kern-0.2pt (\mathcal E_{\mathrm t})=\frac{1+p}{2}.$$

Thus, the average fidelity of the teleportation protocol is greater than \(2/3\) (the best possible fidelity when Alice and Bob communicate only through a classical channel) if and only if \(p>1/3\). For a two-qubit state \(\rho^{ab}\), it has been shown that \(\rho^{ab}\) is entangled if and only if \(p>1/3\) [56], which implies that the entanglement of \(\rho^{ab}\) is a prerequisite for teleportation. In this case, \(p>1/3\) if and only if the irreversibility is \(S(\mathcal E_{\mathrm t})<(\ln 12)/4\). This sheds some light on the teleportation protocol from the perspective of irreversibility.

Fig. 2.
figure 2

Comparison between the irreversibility \(S(\mathcal E_{\mathrm t})\) and the average fidelity \( \kern1.6pt\overline{\vphantom{F}\kern5.6pt}\kern-7.4pt F\kern-0.2pt (\mathcal E_{\mathrm t})\) as functions of \(p\in[0,1]\).

Full size image

To visualize the difference between the irreversibility \(S(\mathcal E_{\mathrm t})\) and the average fidelity \( \kern1.6pt\overline{\vphantom{F}\kern5.6pt}\kern-7.4pt F\kern-0.2pt (\mathcal E_{\mathrm t})\) for the teleportation channel \(\mathcal E_{\mathrm t}\), we depict their behavior depending on the fraction parameter \(p\) in Fig. 2. To reflect the trade-off relation between them intuitively, we also depict the behavior of the sum \(S(\mathcal E_{\mathrm t})+ \kern1.6pt\overline{\vphantom{F}\kern5.6pt}\kern-7.4pt F\kern-0.2pt (\mathcal E_{\mathrm t})\), whence we find that the irreversibility \(S(\mathcal E_{\mathrm t})\) and the fidelity \( \kern1.6pt\overline{\vphantom{F}\kern5.6pt}\kern-7.4pt F\kern-0.2pt (\mathcal E_{\mathrm t})\) satisfy the trade-off relation

$$1\le S(\mathcal E_{\mathrm t})+ \kern1.6pt\overline{\vphantom{F}\kern5.6pt}\kern-7.4pt F\kern-0.2pt (\mathcal E_{\mathrm t})\le 1.3.$$

8. Summary

Motivated by intuitive and physical considerations, we have postulated some basic features for any reasonable measure of irreversibility, and have presented a concrete realization of the postulated requirements by quantifying the irreversibility of channels in terms of the entropy of the corresponding Jamiołkowski–Choi states. This is achieved by using the channel–state duality via the Jamiołkowski–Choi isomorphism between channels and states. We have further evaluated the irreversibility of several important channels, which highlights some basic features of channels from the perspective of irreversibility. We have also established several relations connecting irreversibility with entanglement fidelity, entropy exchange, nonunitality, and decorrelating power.

The measure of irreversibility has the apparent operational meaning as the entropy of the Jamiołkowski–Choi states of the channels, and thus may be used in characterizing information-theoretic aspects of quantum measurements and channels.

Irreversibility is a fundamental characteristic in information processing, and its quantitative characterization sheds light on the nature of channels and physical processes. It is desirable to find more applications of the measure of irreversibility, in particular, in the paradigm of quantum thermodynamics, where heat is usually related to irreversible processes.