A Generalized Multiscale Finite Element Method for Thermoelasticity Problems

Abstract

In this work, we consider the coupled systems of a partial differential equations, which arise in the modeling of thermoelasticity processes in heterogeneous domains. Heterogeneity of the properties requires a high resolution solve that adds many degrees of freedom that can be computationally costly. For the numerical solution, we use a Generalized Multiscale Finite Element Method (GMsFEM) that solves problem on a coarse grid by constructing local multiscale basis functions [1,2,3]. We construct multiscale basis functions for the temperature and for the displacements on the offline stage in each coarse block using local spectral problems [4,5,6,7]. On the online stage we construct coarse scale system using precalculated multiscale basis functions and solve problem with any forcing and boundary conditions. The numerical results are presented for heterogeneous and perforated domains.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Problem Formulation and Fine Scale Approximation

We consider linear thermoelasticity problem for temperature, T, and for displacement, u [8,9,10]

$$\begin{aligned} \begin{aligned} - \mathop {\text {div}}\nolimits \sigma ( u) + \beta \mathop {\text {grad}}\nolimits T&= 0 \text { in } \varOmega , \\ \beta \mathop {\text {div}}\nolimits \frac{\partial u}{\partial t} + c \frac{\partial T}{\partial t} - \mathop {\text {div}}\nolimits \left( k \mathop {\text {grad}}\nolimits T \right)&= f \text { in } \varOmega , \end{aligned} \end{aligned}$$

(1)

where f is a source term, c is a heat capacity, k is a thermal conductivity and $\beta$ is the coupling coefficient.

The stress and strain tensors are given by

$$ \sigma (u) = 2 \mu \varepsilon ( u) + \lambda \mathop {\text {div}}\nolimits (u) \, \mathcal {I}, \quad \varepsilon (u) = \frac{1}{2} \left( \mathop {\text {grad}}\nolimits u + \mathop {\text {grad}}\nolimits u^T \right) , $$

where $\mu$, $\lambda$ are Lame parameters, $\mathcal {I}$ is the identity tensor.

We consider (1) with initial condition $T( x, 0) = T_0$ and boundary conditions for displacement and for temperature

$$ \sigma n = 0, \quad x \in \varGamma ^u_N, \quad u = u_1, \quad x \in \varGamma ^u_D, $$

$$ - k \frac{\partial T}{\partial n}= 0, \quad x \in \varGamma ^T_N, \quad T = T_1, \quad x \in \varGamma ^T_D, $$

where n is the unit normal to the boundary.

For numerical solution on fine grid, we use a standard finite element method and implicit scheme for approximation by time [4, 5, 8]

$$\begin{aligned} \begin{aligned} a_{u} (u^{{n + 1}} ,v) + b(T^{{n + 1}} ,v)&= 0, \\ b(u^{{n + 1}} - u^{n} ,q) + m(T^{{n + 1}} - T^{n} ,q) + \tau a_{T} (T^{{n + 1}} ,q)&= \tau (f,q), \\ \end{aligned} \end{aligned}$$

(2)

for $(u, T) \in W = (V, Q)$ and $(v, q) \in \hat{W} = (\hat{V}, \hat{Q})$ where

$$\begin{aligned} \begin{array}{c} \displaystyle V = \{ v \in [H^1(\varOmega )]^d: v( x) = u_1, x \in \varGamma ^u_D \}, \quad Q = \{ q \in H^1(\varOmega ): q(x) = T_1, x \in \varGamma ^T_D \}, \\ \hat{V} = \{ v \in [H^1(\varOmega )]^d: v(x) = 0, x \in \varGamma ^u_D \}, \quad \hat{Q} = \{ q \in H^1(\varOmega ): q(x) = 0, x \in \varGamma ^T_D \}. \end{array} \end{aligned}$$

Here for bilinear and linear forms we have

$$\begin{aligned} \begin{array}{c} \displaystyle a_u( u, v) = \int _{\varOmega } (\sigma ( u), \varepsilon (v) ) dx, \quad a_T(T, q) = \int _{\varOmega } \left( k \mathop {\text {grad}}\nolimits T, \mathop {\text {grad}}\nolimits q \right) dx, \\ \displaystyle b(T, u) = \int _{\varOmega } \beta (\mathop {\text {grad}}\nolimits T, u) dx, \quad m(T, q) = \int _{\varOmega } c \, T \, q \, dx, \quad (f, q) = \int _{\varOmega } f \, q \, dx. \end{array} \end{aligned}$$

where as basis functions on fine grid we use standard linear basis functions for both temperature and displacement.

2 Coarse-Scale Approximaiton Using GMsFEM

Let $\mathcal {T}^H$ be a standard conforming partition of the computational domain $\varOmega$ into finite elements. We refer to this partition as the coarse-grid and assume that each coarse element is partitioned into a connected union of fine grid blocks. The fine grid partition will be denoted by $\mathcal {T}^h$. Let $\{x_i\}_{i=1}^{N}$ is the vertices of the coarse mesh $\mathcal {T}^H$, where N is the number of coarse nodes. We define the neighborhood (local) domain of the node $x_i$ by

$$ \omega _i= \bigcup _{j}\left\{ K_j\in \mathcal {T}^H \, | \, x_i\in \overline{K}_j\right\} , $$

where $K_j$ to denote a coarse element.

In the GMsFEM algorithm, we have three steps [1,2,3]:

• Step 1: Generate the coarse-grid, $\mathcal {T}^H$ and local domains $\omega _i$, $i = 1,2,\ldots ,N$;

• Step 2: The construction of the multiscale basis functions in local domains, $\omega _i$, $i = 1,2,\ldots ,N$ (offline space);

• Step 3: Use offline space to find the solution of a coarse-grid problem for any force term and/or boundary conditions.

We construct multiscale basis functions for temperature and displacements separately.

Multiscale Basis Functions for Pressure. To construct the offline space $Q_{\text {off}}$ for temperature, we solve following the eigenvalue problem in the local domain $\omega$:

$$\begin{aligned} \begin{array}{c} A_T \varPsi _k^{\text {off}} = \lambda _k^{\text {off}} S_T \varPsi _k^{\text {off}},\\ \displaystyle A_T = \left[ a_{ij} \right] , \quad a_{ij} = \int _{\varOmega } \left( k\mathop {\text {grad}}\nolimits \phi _i , \mathop {\text {grad}}\nolimits \phi _j \right) \, dx, \quad M_T = \left[ s_{ij} \right] , \quad s_{ij} = \int _{\varOmega } k \phi _i \phi _j \, dx, \end{array} \end{aligned}$$

(3)

and choose the eigenvectors $\psi _k^{\text {off}}$ that corresponds to the smallest $M^{\omega ,T}_{\text {off}}$ eigenvalues in Eq. (3) and denote the span of this reduced space as $Q_{\text {off}}^{\omega }$.

For construction of the offline space, to ensure the functions we construct form an conforming basis, we define multiscale partition of unity functions $\chi _i$

$$\begin{aligned} a_T(\chi _i , q) = 0 \quad \text { in } K, \quad \chi _i = g_i \quad \text { on } \partial K, \end{aligned}$$

(4)

for all $K \in \omega$. Here $g_i$ is a continuous on K and is linear on each edge of $\partial K$.

Finally, we multiply the partition of unity functions by the eigenfunctions in the offline space $Q_{\text {off}}^{\omega _i}$ to construct the resulting basis functions $\psi _{i,k} = \chi _i \psi _k^{\omega , \text {off}}$, for $1 \le i \le N$ and $\le k \le M_{\text {off}}^{\omega _i,T}$, where $M_{\text {off}}^{\omega _i,T}$ denotes the number of offline eigenvectors that are chosen for each coarse node i.

We define the multiscale space using a single index notation as

$$\begin{aligned} Q_{\text {off}} = \text {span} \{ \psi _{i} \}_{i=1}^{M^\text {off}_T}, \quad \text {and} \quad R_T = \left[ \psi _1 , \ldots , \psi _{M^\text {off}_T} \right] ^T, \end{aligned}$$

(5)

where $M^\text {off}_T =\sum _{i=1}^{N} M_{\text {off}}^{\omega _{i},T}$ denotes the total number of basis functions.

Multiscale Basis Functions for Displacement. For construction of multiscale basis functions for displacements we use similar algorithm that we used for the temperature. We solve the following eigenvalue problem in $V_h(\omega )$ [3,4,5]

$$\begin{aligned} \begin{array}{c} A_u \varPhi _k^{\text {off}} = \lambda _k^{\text {off}} S_u \varPhi _k^{\text {off}},\\ \displaystyle A_u = \left[ a_{ij} \right] , \quad a_{ij} = \int _{\varOmega } \Big ( 2\mu {\varepsilon }( \varphi _m^{\text {}}) : {\varepsilon }( \varphi _n^{\text {}}) + \lambda \mathop {\text {div}}\nolimits ({\varphi _m^{\text {}}}) \cdot \mathop {\text {div}}\nolimits ( \varphi _n^{\text {}} ) \Big ),\\ S_u = \left[ s_{ij} \right] , \quad s_{ij} = \int _{\varOmega } (\lambda + 2 \mu ) \varphi _m^{\text {}} \cdot \varphi _n^{\text {}}. \end{array} \end{aligned}$$

(6)

We then choose the eigenvectors that corresponds to the smallest $M^{\omega ,u}_{\text {off}}$ eigenvalues from Eq. (6) and denote the span of this reduced space as $V_{\text {off}}^{\omega }$.

For construction of multiscale partition of unity functions for the mechanics solve, we proceed as before and solve for all $K \in \omega$

$$\begin{aligned} a_u(\xi _i , v) = 0 \quad \text { in } K, \quad \xi _i = g_i \quad \text { on } \partial K, \end{aligned}$$

(7)

where $g_i$ is a continuous function on K and is linear on each edge of $\partial K$. Finally, we multiply the partition of unity functions by the eigenfunctions in the offline space $V_{\text {off}}^{\omega _i}$ to construct the resulting basis functions $\varphi _{i,k} = \xi _i \varphi _k^{\omega _i, \text {off}}$ for $1 \le i \le N$ and $1 \le k \le M_{\text {off}}^{\omega _i,u}$, where $M_{\text {off}}^{\omega _i,u}$ denotes the number of offline eigenvectors that are chosen for each coarse node i.

Next, we define the multiscale space as

$$\begin{aligned} V_{\text {off}} = \text {span} \{ \varphi _{i} \}_{i=1}^{M_u^{\text {off}}}, \quad \text {and} \quad R_u = \left[ \psi _1 , \ldots , \varphi _{M^\text {off}_u} \right] ^T, \end{aligned}$$

(8)

where $M_u^{\text {off}} =\sum _{i=1}^{N} M_{\text {off}}^{\omega _{i},u}$ denotes the total number of basis functions.

Coarse-Scale System. The variational form in (2) yields the following linear algebraic system

$$\begin{aligned} \begin{pmatrix} A^c_u &{} (B_c)^T \\ B^c &{} \left( M_c + \tau A^c_T \right) \end{pmatrix} \left( {\begin{array}{c}u_H^{n+1}\\ T_H^{n+1}\end{array}}\right) = \left( {\begin{array}{c}0\\ Q_c\end{array}}\right) , \end{aligned}$$

(9)

where

$$ A^c_u = R_u A_u R_u^T, \quad A^c_T = R_T A_T R_T^T \quad B_c = R_T B R_u^T, \quad M_c = R_T M R_T^T $$

and $Q_c = R_T \tau F + M_c T_H^n + B_c u_H^n$. Here $u_H$ and $T_H$ denotes the coarse-scale solutions that we can project into the fine-grid $u_h^{n+1} = R_u^T u_H^{n+1}$ and $T_h^{n+1} = R_T^T T_H^{n+1}$.

3 Numerical Examples

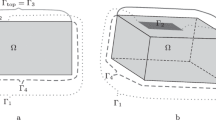
In this section, we present numerical examples to demonstrate the performance of the GMsFEM for computing the solution of the thermoelasticity problem in heterogeneous and perforated domains where the inclusions can have different size (see Figs. 1 and 2).

Fig. 1.

Coarse and fine computational grids (left) and heterogeneous backround (right). Blue color is the subdomain 2 and red is the subdomain 1. Fine grid contains 12426 vertices and 24124 cells. Coarse grid have 110 vertices and 180 cells. (Color figure online)

Fig. 2.

Coarse and fine computational grids (left) for domain with circle particles. Orange color is the subdomain 2 and blue is the subdomain 1. Fine grid contains 18378 vertices and 36254 cells. Coarse grid have 152 vertices and 252 cells. (Color figure online)

Table 1. Relative $L_2$ and $H_1$ errors for temperature and displacement in percentage

Fig. 3.

Fine-scale solution (top) and coarse-scale solution using 8 basis functions for temperature and 8 for displacement (bottom) for the Case 1a. Left: temperature. Middle: displacement $u_x$. Right: displacement $u_y$.

We present results for perforated and heterogeneous domains with random distribution of the inclusions (Fig. 1). For high-constrast domain, we consider case with one type of particles (Fig. 2). For numerical simulations we use following thermomechanical coefficients: $c_1 = 1000$, $c_2 = 100$, $k_1 = 1$, $k_2 = 100$, $E_1 = 100$, $E_2 = 10$, $\nu = 0.3$ and $\beta = 1.0$.

We consider three test cases:

• Case 1a. Perforated domain with homogeneous backround with source term $f = 100$ and zero Dirichlet boundary conditions for temperature and displacement on perforations;

• Case 1b. Perforated domain with heterogeneous backround with source term $f = 100$ and zero Dirichlet boundary conditions for temperature and displacement on perforations;

• Case 2. Heterogeneous domain with circle particles with zero source term $f = 0$ and boundary conditions: a fixed temperature $T = 1.0$ on cavity, a fixed displacements $u_x = 0$ for left boundary and $u_y = 0$ on top boundary.

Fig. 4.

Fine-scale solution (top) and coarse-scale solution using 8 basis functions for temperature and 8 for displacement (bottom) for the Case 1b. Left: temperature. Middle: displacement $u_x$. Right: displacement $u_y$.

Fig. 5.

Fine-scale solution (top) and coarse-scale solution using 8 basis functions for temperature and 8 for displacement (bottom) for the Case 2. Left: temperature. Middle: displacement $u_x$. Right: displacement $u_y$.

For numerical comparison, we calculate a weighted relative errors using $L^2$ norm and $H^1$ semi-norm for temperature

$$ ||\epsilon _T||_{L^2} = \left( \int _{\varOmega } k \epsilon _T^2 dx \right) ^{1/2}, \quad |\epsilon _T|_{H^1} = \left( \int _{\varOmega } \left( k \mathop {\text {grad}}\nolimits \epsilon _T, \mathop {\text {grad}}\nolimits \epsilon _T \right) dx \right) ^{1/2}, $$

and for displacement

$$ ||\epsilon _u||_{L^2} = \left( \int _{\varOmega } (\lambda + 2 \mu ) (\epsilon _u, \epsilon _u) dx \right) ^{1/2}, \quad |\epsilon _u|_{H^1} = \left( \int _{\varOmega } \left( \sigma (\epsilon _u), \varepsilon (\epsilon _u) \right) dx \right) ^{1/2}, $$

where $\epsilon _T = T_f - T_{ms}$, $\epsilon _u = u_f - u_{ms}$. Here $(u_f, T_f)$ and $(u_{ms}, T_{ms})$ are fine-scale and coarse-scale (multiscale) solutions, respectively for displacement and temperature.

In Fig. 3, we show the fine-scale and coarse-scale solutions for the Case 1a and in Fig. 4 for the Case 1b. For multiscale solution we used 8 multiscale basis functions for temperature and 8 multiscale basis functions for displacement. Comparing the fine-scale and coarse-scale solutions in Figs. 3 and 4, we can observe a good accuracy of the proposed multiscale method for both homogeneous and heterogeneous backround coefficients for perforated domain. In Fig. 5 we show solutions for the Case 2 for heterogeneous domain with circle particles. In Table 1 we present relative errors for the coarse-scale solutions with different number of the multiscale basis functions. We observe a good accuracy for all cases for multiscale solution using only $\approx 0.2 \%$ of fine-scale system size.