INTRODUCTION

The study of oxide film oxidation and formation is a challenging problem for the determination of laws for the corrosion stability of steels, including investigations of liquid-metallic corrosion [1]. A theory of diffusion growth of layers was developed for carbon steels [2]. The theory provides good correspondence with experiment. The thermodynamic prerequisites of internal oxidation zone formation in multicomponent alloys (metal–solvent + alloying element + insertion element (oxygen, nitrogen, and carbon)) were presented [3]. The kinetics of changing the component concentrations upon the formation of one- and two-phase oxide layers in alloyed steels was shown. The general laws (continuity equation) and the influence of boundary factors on the diffusion equation for the internal oxidation zones in multicomponent alloys were presented [4].

Only an internal oxidation zone can be formed and no external oxide layer is formed on the alloy surface under certain high-temperature oxidation conditions. This situation appears, for example, when the thermodynamic activity of oxygen is lower than or equal to the activity equilibrium with alloying-element oxide [5].

KINETICS OF INTERNAL OXIDATION ZONE FORMATION

The kinetics of formation of the internal oxidation zone (solid solution–particles of alloying-element oxide (Bω2Oω1) in binary alloy A–B) will be considered using a system of equations.

Since an external oxide layer is absent, this system is simplified and consists of the following equations:

diffusion in a solid solution in the two-phase region,

$$\begin{gathered} \frac{{\partial {{C}_{i}}}}{t} = {{D}_{{ii}}}\frac{{{{\partial }^{2}}{{C}_{i}}}}{{\partial {{x}^{2}}}} + {{D}_{{ij}}}\frac{{{{\partial }^{2}}{{C}_{j}}}}{{\partial {{x}^{2}}}} \\ + \,\,{{D}_{{ii}}}\frac{{\partial D}}{{\partial x}}\frac{{\partial {{C}_{i}}}}{{\partial x}} + {{D}_{{ij}}}\frac{{\partial Q}}{{\partial x}}\frac{{\partial {{C}_{i}}}}{{\partial x}} + C_{i}^{{{\text{ph}}}}\frac{{\partial Q}}{{\partial t}} \\ \end{gathered} $$
(1)

(Ci and Cj are the component concentrations, Dii and Dij are the diffusion coefficients, and Q = ln(1 – V), where V is the phase volume, 0 ≤ x ≤ y(t); i, j = 1, 2; i ≠ j);

diffusion in the one-phase region,

$$\begin{gathered} \frac{{\partial {{C}_{i}}}}{{\partial t}} = {{D}_{{ii}}}\frac{{{{\partial }^{2}}{{C}_{i}}}}{{\partial {{x}^{2}}}} + {{D}_{{ij}}}\frac{{{{\partial }^{2}}{{C}_{j}}}}{{\partial {{x}^{2}}}} \\ (x \geqslant y(t);\,\,i,j = 1,\,\,2;\,\,\,i \ne j); \\ \end{gathered} $$
(2)

mass balance at the two-phase region–solid solution interface

$$\begin{gathered} {{J}_{{ix = y - 0}}} = {{J}_{{ix = y + 0}}}\,\,(i = 1,\,\,2); \\ {{J}_{{ix = y - 0}}} = {{J}_{{ix = y + 0}}}\,\,(i = 1,\,\,2); \\ {{\left. {{{J}_{i}}} \right|}_{{x = y - 0}}} = {{\left. {{{J}_{i}}} \right|}_{{x = y + 0}}}\,\,(i = 1,\,\,2); \\ \end{gathered} $$
(3)

discontinuity for the function of the particle size distribution in the two-phase region,

$$\frac{{\partial f}}{{\partial {{t}_{1}}}} + \frac{{\partial {{v}_{R}}f}}{{\partial R}} = {{\mu }_{0}}\exp ( - \aleph R_{K}^{2})[R - {{R}_{K}}({{t}_{1}})],$$
(4)

where RK is the critical nucleus radius, μ0 and \(\aleph \) are constants, vR is the growth (dissolution) rate of the new phase particles, f is the function of the particle size distribution, and δ(x) is the delta function; and the corresponding initial and boundary conditions.

The following two main cases can be distinguished from the whole diversity of oxidation conditions leading to internal oxidation zone formation:

(1) alloying element is removed from a sample through its external surfaces, and equilibrium concentrations of oxygen and alloying element are maintained on them,

(2) no removal of an alloying element to the gas phase occurs.

In the first case, boundary conditions (boundary conditions of the first kind) has the form

$$\begin{gathered} {{C}_{i}}(0,t) = {{C}_{i}}(l,t) = C_{i}^{{{\text{eq}}}}, \\ {{\left. {\frac{{\partial {{C}_{i}}}}{{\partial x}}} \right|}_{{x = {l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}}}} = 0\,\,(i = 1,\,\,2), \\ \end{gathered} $$
(5)

where l is the plate thickness, \(C_{i}^{{{\text{eq}}}}\) is the equilibrium concentration of the ith component.

In the second case (boundary conditions of the second kind for an alloying element and boundary conditions of the first kind for oxygen), they are

$$\begin{gathered} {{\left. {{{J}_{2}}} \right|}_{{x = 0}}} = {{\left. {{{J}_{2}}} \right|}_{{x = l}}} = 0,\,\,\,{{C}_{1}}(0,t) = {{C}_{i}}(l,t) = c_{1}^{1}, \\ {{\left. {\frac{{\partial {{C}_{i}}}}{{\partial x}}} \right|}_{{x = {l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}}}} = 0\,\,\,(i = 1,\,\,2). \\ \end{gathered} $$
(6)

The kinetics of internal oxidation zone formation in the first case will be considered first. A numerical solution of the system of Eqs. (1)–(5) was performed using an implicit difference scheme. For every new step in time, nonlinear Eqs. (1) and (4) were solved by the iteration method until convergence with a high accuracy was achieved. As a result of the numerical solution, the distributions of the supersaturation of a solid solution L(x, t), the number of disperse particles N(x, t), average size \(\bar {R}\)(x, t), and total volume Vph(x, t) were obtained.

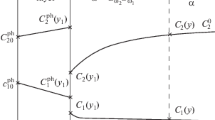
The distributions of the supersaturation L(x, t) in the diffusion zone of a plate with thickness l for various oxidation times are shown in Fig. 1 [5].

Fig. 1.
figure 1

Theoretical distribution of supersaturation L in the diffusion zone of the plate at various internal oxidation times: \(C_{1}^{0}\) = 0.0, \(C_{2}^{0}\) = 0.12, and \(C_{1}^{{{\text{eq}}}}\) = 0.01; D11 = 1 × 10–8 cm2/s, D12 = –0.5 × 10–9 cm2/s, and D22 = 1 × 10–12 cm2/s; 2γVm/kT = 7 × 10–8 cm; α = 1 × 10–18 cm3/s; μ0 = 1 × 1015 s–1; and \(\aleph \) = 3.5 × 101.3 cm–2; for oxide Bω2Oω1, ω1 = 3 and ω2 = 2.

Full size image

Since the component concentrations on the surface are equilibrium, L(0, t). For the second time L(x, t) vanishes at the point x = y(t), which is the coordinate of the internal oxidation zone boundary. Thus, the L(x, t) function has a maximum, which shifts deep into the plate. In this case, the supersaturation in the range x < xmax decreases in time due to both substance removal to the growing particles of alloying-element oxide and diffusional removal beyond the boundaries x = 0 and x = l (metal thickness). The removal of the substance to wastes similarly affects the maximum L(xmax, t), which also decreases in time.

The distributions of the particle number N(x, t), their average radius \(\bar {R}\)(x, t), and total phase volume Vph(x, t) presented in Fig. 2 show that the \(\bar {R}\)(x, t) and Vph(x, t) dependences repeat, on the whole, the L(x, t) distribution. At the same time, the maximum on the N(x, t) curve lies near the surface and does not shift with time to the plate center. As shown by an analysis of the obtained data, the nucleation rate (number of particles in this cross section of the diffusion zone) depends strongly on the maximum of the degree of supersaturation L(xmax, t). It is this circumstance which results in the situation where the main portion of particles is formed in the near-surface layer when L(xmax, t) is still fairly high. The probability of nucleation decreases sharply with a decrease in L(xmax, t), which corresponds to deeper layers of the diffusion zone, and the number of formed particles is low.

Fig. 2.
figure 2

Theoretical distributions of the number of disperse particles N, their average size \(\bar {R}\), and total volume Vph in the internal oxidation zone of the plate at various times of the process.

Full size image

The theoretical studies of the kinetics of L(x, t) changes in different cross sections of the diffusion zone showed that the character of supersaturation changing is similar (with shifting in time) for all presented cross sections: after the boundary reaches the y(t) zone of a certain cross section, the supersaturation of a solid solution increases rapidly, passes through a maximum, decreases with a sufficiently high rate, and, finally, asymptotically approaches zero. The modeling results show that certain stages of internal oxidation zone formation correspond to the time dependence of the L(x, t) change: the active nucleation of particles of alloying-element oxide occurs at a fast increase in supersaturation; the stage of a fast decrease in L(x, t) corresponds to the fast particle growth, and the nucleation frequency decreases sharply with an increase in the process time; no nucleation of new particles occurs at the asymptotic stage, and the main mechanism of their growth is coalescence.

The calculated curve of the \(\bar {R}\)(t) dependence for one of the cross sections of the plate is shown in Fig. 3. As a rule, the experimental kinetic \(\bar {R}\)(t) dependences have the form

$${{\bar {R}}^{n}} = kt.$$
(7)
Fig. 3.
figure 3

Kinetics of changing the average radius of the particles in the cross section of the internal oxidation zone.

Full size image

The corresponding processing of the curve in Fig. 3 shows that the whole curve cannot be described using Eq. (7) but its particular regions satisfy this dependence at certain (for each region) n value. As the internal oxidation time increases, n takes the following values: 1, 2, 3, and ~200. For low times and at the asymptotic stage, n corresponds to the particle growth mechanism known from the theory of solid solution supersaturation: at n = 1 the kinetics is determined by particle nucleation, at n = 2 the kinetics is determined by their diffusional growth due to the substance of a solid solution, and at n = 3 coalescence is determining.

The slow stage of the process (n ≈ 200) at which the average particle radius is nearly completely stabilized is not observed for the decomposition of an supersaturated solid solution in an isolated system. This stage is experimentally observed for the internal oxidation of a Ni–1 wt % Cr alloy. We will show that in a system with an supersaturated solid solution and growing particles of the second phase the stage of average radius stabilization is related to a diffusion flow of an alloying element to the plate surfaces x = 0 and x = l on which the supersaturation is zero.

In the case of a small volume of particles of alloying-element oxide Vph(x, t) and long oxidation times, when the whole alloy volume is internally oxidized (y = l/2), Eqs. (1) can be written as follows: (component 1 is oxygen, component 2 is alloying element, D21 = 0) [5]:

$$\begin{gathered} \frac{{\partial {{\Delta }_{1}}}}{{\partial t}} = {{D}_{{11}}}\frac{{{{\partial }^{2}}{{\Delta }_{1}}}}{{\partial {{x}^{2}}}} + {{D}_{{12}}}\frac{{{{\partial }^{2}}{{\Delta }_{2}}}}{{\partial {{x}^{2}}}} - C_{1}^{{{\text{ph}}}}\frac{{\partial {{V}_{{{\text{ph}}}}}}}{{\partial t}}, \\ \frac{{\partial {{\Delta }_{2}}}}{{\partial t}} = {{D}_{{22}}}\frac{{{{\partial }^{2}}{{\Delta }_{1}}}}{{\partial {{x}^{2}}}} - C_{2}^{{{\text{ph}}}}\frac{{\partial {{V}_{{{\text{ph}}}}}}}{{\partial t}}, \\ \end{gathered} $$
(8)
$$\begin{gathered} {{\Delta }_{i}}(0,t) = {{\Delta }_{i}}(l,t) = 0,\,\,\,{{\Delta }_{i}}(x,0) = \Delta _{i}^{0}(x) \\ (i = 1,\,\,2), \\ \end{gathered} $$
(9)

where Δi = Ci(x, t) – \(C_{i}^{{{\text{eq}}}}\).

The solution of the system of Eqs. (8) with the boundary and initial conditions (9) has the form

$$\begin{gathered} {{\Delta }_{1}} = \sum\limits_{m = 1}^\infty {\left( {{{a}_{{1m}}} - p{{a}_{{2m}}} + \frac{1}{{{{\lambda }_{{1m}}}}}\frac{{C_{1}^{{{\text{ph}}}}}}{{C_{2}^{{{\text{ph}}}}}}{{{\left. {\frac{{d{{b}_{{2m}}}}}{{dt}}} \right|}}_{0}}} \right){{e}^{{ - {{\lambda }_{{1{{m}^{t}}}}}}}}} \\ \times \,\,\sin \frac{{m\pi }}{l} + p{{\Delta }_{2}} + \frac{{C_{1}^{{{\text{ph}}}}}}{{{{D}_{{11}}}}}\int\limits_0^x {\int\limits_0^x {\frac{{{{V}_{{{\text{ph}}}}}}}{{\partial t}}} } dxdx, \\ \end{gathered} $$
(10)

where m is the oxide weight.

$$\begin{gathered} {{\Delta }_{2}} = \sum\limits_{m = 1}^\infty {\left( {{{a}_{{2m}}} + \frac{1}{{{{\lambda }_{{2m}}}}}{{{\left. {\frac{{d{{b}_{{2m}}}}}{{dt}}} \right|}}_{0}}} \right){{e}^{{ - {{\lambda }_{{2{{m}^{t}}}}}}}}} \\ \times \,\,\sin \frac{{m\pi }}{l}x + \frac{{C_{2}^{{{\text{ph}}}}}}{{{{D}_{{22}}}}}\int\limits_0^x {\int\limits_0^x {\frac{{\partial {{V}_{{{\text{ph}}}}}}}{{\partial t}}} } dxdx. \\ \end{gathered} $$

Here, we have

$${{a}_{{1m}}} = \frac{2}{l}\int\limits_0^l {\Delta _{1}^{0}\sin \frac{{m\pi }}{l}} xdx,$$
$${{a}_{{2m}}} = \frac{2}{l}\int\limits_0^l {\Delta _{2}^{0}\sin \frac{{m\pi }}{l}} xdx,$$
$${{b}_{{2m}}} - C_{2}^{{{\text{ph}}}}\frac{2}{l}\int\limits_0^l {{{V}_{{{\text{ph}}}}}(x,t)\sin \frac{{m\pi }}{l}xdx,} $$
$$p = - \frac{{{{D}_{{12}}}}}{{{{D}_{{11}}}}},\,\,\,{{\lambda }_{{1m}}} = {{D}_{{11}}}{{\left( {\frac{{m\pi }}{l}} \right)}^{2}},\,\,\,{{\lambda }_{{2m}}} = {{D}_{{22}}}{{\left( {\frac{{m\pi }}{l}} \right)}^{2}}.$$

The following approximation was made when solving Eq. (8):

$$\begin{gathered} {{\int\limits_0^t {\frac{{d{{b}_{{2m}}}}}{d}{{e}^{{ - {{\lambda }_{{im}}}(t - \tau )}}}d\tau \cong \frac{1}{{{{\lambda }_{{im}}}}}\frac{{d{{b}_{{2m}}}}}{{dt}} - \frac{1}{{{{\lambda }_{{im}}}}}\left. {\frac{{d{{b}_{{2m}}}}}{{dt}}} \right|} }_{0}}{{e}^{{ - {{\lambda }_{{im}}}t}}} \\ (i = 1,\,\,2), \\ \end{gathered} $$

which corresponds to a low phase growth rate.

The supersaturation of a three-component alloy is determined, according to Eq. (2), as follows:

$$L = \frac{\alpha }{{{{R}_{k}}}} = {{\gamma }_{1}}{{\Delta }_{1}} + {{\gamma }_{2}}{{\Delta }_{2}},$$
(11)

where α, γ1, and γ2 are constants. Introducing Eqs. (10) simplified for the case of long t into Eq. (11) and differentiating, we obtain

$$\begin{gathered} \frac{{{{\partial }^{2}}L}}{{\partial {{x}^{2}}}} = {{\beta }_{1}}\frac{{\partial {{V}_{{{\text{ph}}}}}}}{{\partial t}} - {{\left( {\frac{\pi }{l}} \right)}^{2}}{{\beta }_{2}}{{e}^{{ - {{\lambda }_{{12}}}t}}}\sin \frac{\pi }{l}x, \\ {{\beta }_{2}} = ({{\gamma }_{1}}p + {{\gamma }_{2}})\left( {{{a}_{{21}}} + {{{\left. {\frac{1}{{{{\lambda }_{{21}}}}}\frac{{d{{b}_{{21}}}}}{{dt}}} \right|}}_{0}}} \right), \\ {{\beta }_{1}} = \frac{{C_{2}^{{{\text{ph}}}}}}{{{{D}_{{22}}}}}\left[ {({{\gamma }_{1}}p + {{\gamma }_{2}}) + {{\gamma }_{1}}\frac{{{{D}_{{22}}}}}{{{{D}_{{11}}}}}\frac{{C_{1}^{{{\text{ph}}}}}}{{C_{2}^{{{\text{ph}}}}}}} \right]. \\ \end{gathered} $$
(12)

The first term in the right-hand part of Eq. (12) characterizes the decrease in the supersaturation due to the presence of internal drainages (particles of the second phase), and the second term is due to external drainages (plate surfaces x = 0 and x = 1). Equation (12) shows that these terms have opposite signs. If the power of the internal drainages is higher than that of the external drainages, then \({{{{\partial }^{2}}L} \mathord{\left/ {\vphantom {{{{\partial }^{2}}L} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}}\) > 0. In the opposite case, \({{{{\partial }^{2}}L} \mathord{\left/ {\vphantom {{{{\partial }^{2}}L} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}}\) < 0. Since on the plate surface L(0, t) = L(l, t) = 0 and, correspondingly, \({{{{\partial }^{2}}L} \mathord{\left/ {\vphantom {{{{\partial }^{2}}L} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}}\) ≥ 0, there is the maximum power of the internal drainages at which the second derivative of the supersaturation is zero. Based on this fact, from Eq. (12) we find

$$\begin{gathered} \frac{{\partial {{V}_{m}}}}{{\partial t}} = {{\left( {\frac{\pi }{l}} \right)}^{2}}\frac{{{{\beta }_{2}}}}{{{{\beta }_{1}}}}{{e}^{{ - {{\lambda }_{{21}}}t}}}\sin \frac{\pi }{l}x, \\ {{V}_{m}} = \frac{{{{\beta }_{2}}}}{{{{\beta }_{1}}}}\frac{1}{{{{D}_{{22}}}}}\sin \frac{\pi }{l}x(1 - {{e}^{{ - {{\lambda }_{{21}}}t}}}). \\ \end{gathered} $$
(13)

It follows from Eq. (13) that at long times the dependences of the volume of a molecule of the formed oxide Vm(t) and, correspondingly, \(\bar {R}\)(t) (at N = const) are weak functions of time and can be described by equations of the (7) type only very approximately. For this approximation, exponent n would depend on dVm/dt: the lower dVm/dt, the higher n. An analysis of Eq. (13) also shows that the maximum growth rate of the total phase volume depends on the diagonal diffusion coefficient of alloying element D22, plate thickness l, and remoteness of cross section x in which the process is considered from the plate surface: dVm/dt increases with a decrease in D22 and an increase in l and x. For dVph/dt < dVm/dt, Vph(t) is a weaker time function than function (13), but the drawn conclusions remain qualitatively valid for these cases as well. This is confirmed by the results of the numerical solution of the system of Eqs. (1)–(6).

The case analyzed by Wagner [3] will be emphasized to consider the kinetics of internal oxidation zone formation when the boundaries x = 0 and x = l are “closed” for an alloying element. The Wagner model is widely used for the description of the internal oxidation of the alloys containing alloying elements with a high oxygen affinity. These alloys do most frequently undergo internal oxidation in practice.

On the one hand, the kinetics of movement of the boundary of the internal oxidation zone and volume of the alloying-element oxide particles in the zone can theoretically be determined using the Wagner model, which is fairly simple and appropriate for analytical calculations. On the other hand, no information about the medium-size particle distribution in the zone and their number cannot be obtained from the Wagner model. This information can be obtained using the solution of the system of Eqs. (1)–(4) and (6). In addition, the solution of a more complete problem than that considered by Wagner makes it possible to reveal the applicability range of the model.

An analysis of the system of Eqs. (1)–(4) and (6) shows that Wagner’s case is accomplished when two main conditions are fulfilled: fast relaxation of an supersaturated solid solution in the diffusion zone and a high \({{dC_{1}^{{{\text{eq}}}}} \mathord{\left/ {\vphantom {{dC_{1}^{{{\text{eq}}}}} {dC_{2}^{{{\text{eq}}}}}}} \right. \kern-0em} {dC_{2}^{{{\text{eq}}}}}}\) derivative. The fulfillment of the first condition is related to the rate of disperse oxide particle formation and growth, amount of the formed phase, and maximum supersaturation of a solid solution. The fulfillment of the second condition is related to the energy of formation of alloying-element oxide.

The calculation results are given in Fig. 4, indicating that the supersaturation distribution L(x, t) is a curve with a maximum shifting deep inside the sample with time, which is accompanied by a decrease in the maximum value of L(xmax, t). This, in turn, induces a decrease in the number of formed particles in peripheral cross sections of the zone. Each point on the descending branch of the L(x, t) curve moves according to a parabolic law, and deeper cross sections of the diffusion zone exist in the supersaturated state for a longer time; i.e., particles in these cross sections have time to grow to the sizes exceeding sizes of excretions that are arranged closer to the surface. The particle number distribution corresponds to the dependences N(x) ~ x–1 for low x and N(x) ~ x–3 for high x, which confirms the earlier theoretical conclusions [6, 7].

Fig. 4.
figure 4

Theoretical distributions of the concentrations of oxygen C1 and alloying element C2, supersaturation L, number of particles N, average size \(\bar {R}\), and phase volume Vph in the internal oxidation zone of the plate: \(C_{1}^{0}\) = 0.0, \(C_{2}^{0}\) = 4.5 × 10–3, and \(C_{1}^{{{\text{eq}}}}\) = 6 × 10–4; D11 = 1 × 10–6 cm2/s, D12 = –5 × 10–8 cm2/s, and D22 = 1 × 1011 cm2/s; 2γVm/kT = 7 × 10–8 cm; α = 1 × 10–18 cm3/s; μ0 = 1 × 1015 s–1; and \(\aleph \) = 3.5 × 101.3 cm–2; for oxide Bω2Oω1, ω1 = 3 and ω2 = 2.

Full size image

The character of the distribution of the phase volume Vph over the diffusion zone depth (see Fig. 4) is close to the stepped one. Near the sample surface, Vph remains almost unchanged; i.e., the Vph distribution corresponds to the form that follows from the Wagner model. According to the Wagner scheme, the distinction between the numerical and analytical calculations is that the excretion region is not localized near the line representing the internal oxidation front but is somewhat blurred. In spite of the fact that the blurring is relatively weak, it still affects the parabolic constant of the rate of internal oxidation zone growth β0. This parameter calculated from the Wagner equation [3] (applied to the case illustrated in Fig. 4) is approximately by a factor of two lower than the value obtained by the numerical calculation. As shown by an analysis of the numerical solutions, the degree of blurring of the distribution of Vph is mainly determined by the relaxation rate of supersaturation of a solid solution near the internal oxidation front: the higher the rate, the better the fulfillment of the Wagner scheme. Of course, the cases important in the practical respect are not exhausted by the examples presented above.

CONCLUSIONS

The analyzed variants of the internal oxidation illustrate possibilities of the proposed quantitative model, which allows one to calculate the kinetics of this process and obtain information about the zone structure (number of particles, phase volume, and average particle size). This approach makes it possible to reveal the general laws of internal oxidation and, therefore, provides a possibility of controlling the process. This is important for the considered phenomenon, since the internal oxidation kinetics depends on many parameters, but only in a few cases one can predict what effect is exerted on the process occurrence by a change in each parameter. The conclusions presented in the article are consistent with the results of other researchers dealing with internal oxidation [8].