Model for the Inelastic Deformation of Shape Memory Alloys

Abstract

A version of the model of phase-structural deformation of shape-memory alloys is proposed. An isotropic hardening parameter for the deformation according to a structural mechanism is the intrinsic phase-structural strain intensity of the martensitic part of the representative material volume. The problem of the inverse thermoelastic phase transformation in a constrained rod with a preliminarily specified tensile or compressive strain is solved. The influence of the translational hardening parameter on the solution is investigated.

1 INTRODUCTION

The representative volume of a polycrystalline shape memory alloy (SMA) can consist of two types of structures, namely, austenitic and martensitic [1–4]. The transition from an austenitic crystal cell to a martensitic one is related to the crystallographic deformation of the direct phase transformation, the intensity of which in titanium nickelide $\varepsilon _{i}^{{crys}}$ can reach 8–9%. The phase deformation intensity averaged over the representative SMA volume changes from zero (in the case of chaotic, or fully twinned, martensite) to the value correlating with $\varepsilon _{i}^{{crys}}$ (for fully oriented martensite) [5, 6]. In [7], we experimentally found that strain hardening is uncharacteristic for the phase mechanism of SMA deformation.

When the representative volume of SMA (which is in the state of chaotic (fully twinned) martensite) is loaded by increasing stress, low-symmetric martensitic cells are reoriented and detwinned and the degree of misorientation of these cells decreases [8, 9]. As a result, the second, structural, mechanism of SMA deformation becomes operative. This mechanism is characterized by all manifestations of strain hardening effects, both isotropic [8, 9] and translational [10–13].

The authors of [14–16] experimentally found that SMA deformation according to the phase mechanism affects the manifestation of the structural mechanism. Thus, a problem arose to describe the deformation process that occurs according to two mechanisms, which are fundamentally different in phenomenological manifestations, with the first mechanism obviously affecting the second. These fundamental features were not taken into account in the well-known models of SMA deformation, which were reviewed in [17] and described in [18–20]. In this paper, we propose a model for SMA deformation, which is free of these disadvantages. This model is then used to solve the problem of the reverse phase transformation of an SMA rod in the constrained state.

2 FORMULATION OF THE MODEL

2.1 Loading Surface Equation

The authors of [21] proposed a model for the deformation of SMA in a fully martensitic phase state when only a structural transition (martensitic inelasticity) is operative; this model is an analog of the model adopted in the theory of plastic flow. They showed that, due to the specific shape of a martensitic inelasticity diagram, the use of such integral parameters of isotropic hardening as the work of stresses at inelastic strains or the Odqvist parameter leads to contradictions with the experimental data. Therefore, we proposed to use the maximum (over the entire history of the existence of the given martensitic volume) structural strain intensity as a parameter of isotropic hardening. It was found [22–24] that, in terms of such a model, one cannot limit oneself only to the consideration of isotropic hardening—it is also necessary to take into account translational hardening. From these considerations, a loading surface equation for the structural deformation of SMA was proposed in the form [21]

$${{\rho }_{{D2}}}{{\varphi }_{2}}(S^*) = \max (\varepsilon _{i}^{{st}}),$$

where ρ_D2 is a material parameter that determines the maximum strain intensity of martensitic inelasticity, φ₂(S) is the material function such that the ratio $\varepsilon _{i}^{{st}}$ = ρ_D2φ₂(S_i) is the martensitic inelasticity diagram equation, and S* is the loading surface radius in the active stress deviator space S_ij [23].

A necessary condition for active loading is the equality

$${{S}_{i}} = S^*,$$

where S_i = $\sqrt {3{{{{S}_{{ij}}}{{S}_{{ij}}}} \mathord{\left/ {\vphantom {{{{S}_{{ij}}}{{S}_{{ij}}}} 2}} \right. \kern-0em} 2}}$ is the active stress tensor intensity.

Function φ₂ is nonnegative, increases monotonically, and satisfies the conditions

$${{\varphi }_{2}}(0) = 0,\,\,\,\mathop {\lim }\limits_{x \to \infty } {{\varphi }_{2}}(x) = 1.$$

(1)

The model proposed in [21] only describes the structural mechanism of SMA deformation. Attempts to describe both mechanisms were made in [25–27], taking into account only isotropic [25, 26] or both isotropic and translational [27] hardening. However, integral parameter χ such that dχ = ${{{{S}_{{ij}}}d\varepsilon _{{ij}}^{{phst'}}} \mathord{\left/ {\vphantom {{{{S}_{{ij}}}d\varepsilon _{{ij}}^{{phst'}}} {{{S}_{i}}}}} \right. \kern-0em} {{{S}_{i}}}}$ as an isotropic hardening parameter and the loading surface equation [27]

$${{\rho }_{{D2}}}q{{\varphi }_{2}}(S^*) = \int {d\chi } $$

(2)

were used in those works.

A factor in the form of the volume fraction of martensitic phase q is added to the left-hand side of Eq. (2) to take into account the possibility of phase transitions.

It is easy to show that, for proportional (in general, nonmonotonic) loading, the right-hand side of Eq. (2) changes into an analog of the Odquist parameter [25, 27], which leads to contradictions with the experimental data for nonmonotonic loading [13]. To overcome this disadvantage, we [28] proposed to use the loading surface equation

$${{\rho }_{{D2}}}q{{\varphi }_{2}}S^* = \max (\varepsilon _{i}^{{phst}}).$$

(3)

The right-hand side of Eq. (3) represents the maximum intensity of the averaged phase-structural strain of the considered representative volume of SMA over the entire history of the existence of the martensitic part of this representative volume. There is no justification for the presence of factor q in the left-hand side of Eq. (3) or (2) in [25–28].

In this paper, we propose an alternative (Eq. (2) or (3)) formulation of the loading surface equation for the structural deformation of SMA; it is based on the assumption that isotropic hardening is determined by the maximum intensity of the intrinsic phase-structural strain of the martensitic part of the representative volume rather than by the strain intensity averaged over the entire representative volume.

$\varepsilon _{{ij}}^{{phst'}}$ is the phase-structural strain deviator averaged over the representative volume of SMA, which generally consists ${\text{of}}$ two parts, namely, martensitic and austenitic. In this case, inelastic strain is only observed in the martensitic part of the representative volume. Using the mixture rule, we can find that the deviator $\varepsilon _{{ij}}^{M}$ of the intrinsic phase-structural strain of the martensitic part of the representative volume and the intensity of this intrinsic strain $\varepsilon _{i}^{M}$ satisfy the relations

$$q\varepsilon _{{ij}}^{M} = \varepsilon _{{ij}}^{{phst'}},\,\,\,q\varepsilon _{i}^{M} = \varepsilon _{i}^{{phst}}.$$

It is natural to assume that the isotropic hardening of SMA, which is caused by structural strains and characterizes the state of the martensitic part of the representative volume, is determined by the maximum intensity of the intrinsic phase-structural strain of the martensitic part of the representative volume $\varepsilon _{i}^{M}$ over the entire history of the process. Therefore, the relation for the radius of the loading surface taking into account both the phase and structural transition is written as

$${{\rho }_{{D2}}}{{\varphi }_{2}}(S^*) = \max \left( {\frac{{\varepsilon _{i}^{{phst}}}}{q}} \right).$$

(4)

In contrast to Eq. (3) [28], changes in both $\varepsilon _{i}^{{phst}}$ and q are taken into account during the maximization of the right-hand side of Eq. (4).

2.2 Relations for the Phase and Structural Deformation Mechanisms

The strain increment induced by a structural transition is considered to be described by the associated law

$$d\varepsilon _{{ij}}^{{st}} = d\lambda {{S}_{{ij}}}.$$

(5)

Equation (5) is fulfilled only at S_i = S*, where S* fulfills Eq. (4) and the condition

$$d\lambda > 0;$$

(6)

otherwise, we have d$\varepsilon _{{ij}}^{{st}}$ = 0.

The displacement of the center of the loading surface r_ij, which determines the translational hardening, should also be related to the change in the intrinsic strain of the martensitic part of the representative volume. If we accept the hypothesis that the change in r_ij is proportional to the change in the intrinsic strain of martensite according to both the structural and phase mechanisms, we can write

$${{q}^{2}}d{{r}_{{ij}}} = g(qd\varepsilon _{{ij}}^{{phst'}} - \varepsilon _{{ij}}^{{phst'}}dq).$$

(7)

In Eq. (7), g has the meaning of the tangent modulus of translational hardening.

Stress deviator $\sigma _{{ij}}^{'}$ is connected to tensors S_ij and r_ij by the usual relation

$$\sigma _{{ij}}^{'} = {{S}_{{ij}}} + {{r}_{{ij}}},$$

(8)

which is accepted in the theory of plastic flow with translational or combined hardening [22–24]. The strain increment in SMA induced by a phase transition is determined by the relationships [7]

$$d\varepsilon _{{ij}}^{{ph}} = {{\varepsilon }^{0}}{{\delta }_{{ij}}}dq + \omega _{{ij}}^{ \pm }dq,$$

(9)

$$\omega _{{ij}}^{ + } = \frac{3}{2}{{\rho }_{{D1}}}\frac{{{{S}_{{ij}}}}}{{{{S}_{i}}}}{{\varphi }_{1}}({{S}_{i}})(1 - qf(q)) + f(q)\varepsilon _{{ij}}^{{phst'}},$$

$$\omega _{{ij}}^{ - } = \frac{{\varepsilon _{{ij}}^{{phst'}}}}{q}.$$

(10)

Here, ε⁰ is the linear strain of the volume effect of the phase transition; ρ_D1 is a material parameter correlating with the crystallographic strain intensity of the phase transformation; φ₁(S_i) and f(q) are the material functions, where φ₁ has the properties similar to Eq. (1) and the inequality ρ_D1φ₁(x) > ρ_D2φ₂(x) is valid for any x > 0 [25]; and signs “+” and “–” in the superscript correspond to the direct (dq > 0) and reverse (dq < 0) phase transformation, respectively.

The substitution of Eq. (10) into Eqs. (9) and (7) for the direct transformation gives

$$qd{{r}_{{ij}}} = g\left. {\left\{ {d\varepsilon _{{ij}}^{{st}} + \left[ {\frac{3}{2}{{\rho }_{{D1}}}\frac{{{{S}_{{ij}}}}}{{{{S}_{i}}}}{{\varphi }_{1}}({{S}_{i}}) - \frac{{\varepsilon _{{ij}}^{{phst'}}}}{q}} \right]} \right.(1 - qf(q))dq} \right\}.$$

For the reverse transformation and the structural transition, the equation for the motion of the center of the loading surface is significantly simplified,

$$qd{{r}_{{ij}}} = gd\varepsilon _{{ij}}^{{st}} = gd\lambda {{S}_{{ij}}}.$$

(11)

According to Eq. (11), in the case of the reverse transformation occurring together with the structural transition, the center of the loading surface is shifted only if the strain increment due to the structural transition is different from zero. The presence or absence and the magnitude or direction of strain increment induced by the phase transition does not affect dr_ij during the reverse transformation.

We can a priori accept the hypothesis that a change in the position of the center of the loading surface, which determines the deformation process according to a structural mechanism, occurs only when the inelastic strain changes according to the structural mechanism. Under this assumption, Eq. (11) is valid not only for the reverse, but also for the direct transformation accompanied by a structural transition. This equation is then used for both the direct and reverse transformations.

To formulate a flow law according to the structural mechanism, it is necessary to obtain an expression for factor dλ (Eq. (5)). For this purpose, using the formalism of the theory of plastic flow, it is necessary to consider the active process in which the point representing a state of stress is located on the loading surface; that is, Eq. (4) is satisfied for the current values of the quantities included in it,

$${{\rho }_{{D2}}}{{\varphi }_{2}}({{S}_{i}}) = \max \left( {\frac{{\varepsilon _{i}^{{phst}}}}{q}} \right).$$

(12)

Differentiating Eq. (12) and taking into account Eqs. (5) and (8)–(10), we can derive an expression for dλ. However, the presence of the maximization sign in Eq. (12) makes the right-hand side of this equation nonanalytical and makes it difficult to implement this algorithm.

If the maximum value of the ratio ${{\varepsilon _{i}^{{phst}}} \mathord{\left/ {\vphantom {{\varepsilon _{i}^{{phst}}} q}} \right. \kern-0em} q}$ is reached at an intermediate rather than current point of the process under consideration, the differential of the right-hand side of Eq. (12) is zero. A similar result is obtained if d(${{\varepsilon _{i}^{{phst}}} \mathord{\left/ {\vphantom {{\varepsilon _{i}^{{phst}}} q}} \right. \kern-0em} q}$) < 0 at the current point of the process. In both cases, dS_i = 0 according to Eq. (12); i.e., a purely translational hardening mode takes place. If the condition

$$\max \left\{ {\frac{{\varepsilon _{i}^{{phst}}}}{q}} \right\} = \frac{{\varepsilon _{i}^{{phst}}}}{q}$$

(13)

is met at the starting point of some stage of the process and, at the same time, d(${{\varepsilon _{i}^{{phst}}} \mathord{\left/ {\vphantom {{\varepsilon _{i}^{{phst}}} q}} \right. \kern-0em} q}$) > 0 at all points of the considered stage, then condition (13) is met and the notation max can be removed from Eq. (12) not only at the initial, but also at all points of the stage. This ratio is easily differentiated, and combined hardening (increase in S_i) occurs. Therefore, for the future consideration, it is important to determine the sign of d(${{\varepsilon _{i}^{{phst}}} \mathord{\left/ {\vphantom {{\varepsilon _{i}^{{phst}}} q}} \right. \kern-0em} q}$) for the reverse and direct transformations, which occur along with the structural transition.

For the reverse transformation, we have

$$d\left( {\frac{{\varepsilon _{i}^{{phst}}}}{q}} \right) = \frac{2}{3}\frac{{d\lambda }}{q}\frac{{{{S}_{{ij}}}\varepsilon _{{ij}}^{{phst'}}}}{{\varepsilon _{i}^{{phst}}}}.$$

(14)

According to Eq. (14), for the reverse phase transformation occurring together with the structural transition, the inequality d(${{\varepsilon _{i}^{{phst}}} \mathord{\left/ {\vphantom {{\varepsilon _{i}^{{phst}}} q}} \right. \kern-0em} q}$) > 0 is satisfied under the condition

$${{S}_{{ij}}}\varepsilon _{{ij}}^{{phst'}} > 0.$$

(15)

In the cases of fulfilling the inequality that is opposite to inequality (15) and the reverse transformation, the active process can occur only in the form of purely translational hardening.

A similar analysis for the direct transformation occurring simultaneously with the structural transition gives an equality, which is not presented here because of its cumbersomeness. According to this equality, we can state that, in the case of the direct transformation occurring along with the structural transition, the inequality ${{S}_{{ij}}}\varepsilon _{{ij}}^{{phst'}}$ ≤ 0 is a sufficient condition for the fulfillment of the inequality d(${{\varepsilon _{i}^{{phst}}} \mathord{\left/ {\vphantom {{\varepsilon _{i}^{{phst}}} q}} \right. \kern-0em} q}$) < 0, i.e., purely translational hardening, although this hardening can also occur when inequality (15) is fulfilled.

2.3 Flow Law for Purely Translational Hardening

First, we derive the laws of inelastic SMA deformation for the purely translational hardening mode, where

$$d{{S}_{i}} = 0.$$

(16)

Expressing active stress tensor intensity differential dS_i through the differentials of the tensor components and using Eqs. (5), (8), and (11), we can obtain expressions for dλ and d$\varepsilon _{{ij}}^{{st}}$,

$$d\lambda = \frac{3}{2}q\frac{{{{S}_{{ij}}}d\sigma _{{ij}}^{'}}}{{gS_{i}^{2}}},\,\,\,d\varepsilon _{{ij}}^{{st}} = \frac{3}{2}q\frac{{{{S}_{{mn}}}d\sigma _{{mn}}^{'}}}{{gS_{i}^{2}}}{{S}_{{ij}}},$$

(17)

which are valid for the structural transition occurring along with the direct or reverse phase transformation. The differential condition of active loading dλ > 0 in this case is equivalent to the inequality

$${{S}_{{ij}}}d\sigma _{{ij}}^{'} > 0.$$

(18)

In Eqs. (17) and (18), $\sigma _{{ij}}^{'}$ is the stress deviator.

As follows from Eqs. (17) and (18), in the purely translational hardening mode, neither the flow law for the structural mechanism nor the differential condition of active loading depend on either the magnitude or the sign of increment dq, which determines the phase transition, and they are only characterized by the stress deviator increment. It should be noted that, when Eqs. (3) from [28] rather than Eqs. (4) are used as a loading surface equation, Eqs. (17) and (18) become more complicated and contain terms proportional to dq in addition to the terms proportional to d$\sigma _{{ij}}^{'}$.

2.4 Flow Law for Combined Hardening

We now derive an expression for the law of deformation change as a result of the structural transition in the combined hardening mode, when the maximum value of ${{\varepsilon _{i}^{{phst}}} \mathord{\left/ {\vphantom {{\varepsilon _{i}^{{phst}}} q}} \right. \kern-0em} q}$ is reached at a current point of the process where d(${{\varepsilon _{i}^{{phst}}} \mathord{\left/ {\vphantom {{\varepsilon _{i}^{{phst}}} q}} \right. \kern-0em} q}$) > 0. In this case, loading surface equation (12) can be rewritten in the form

$${{\rho }_{{D2}}}q{{\varphi }_{2}}({{S}_{i}}) = \varepsilon _{i}^{{phst}}.$$

(19)

After differentiating Eq. (19) using Eqs. (11) and (5), we obtain a linear equation for dλ, the solution of which for the case of the inverse transformation has the form

$$d\lambda = \frac{{[{{\rho }_{{D2}}}q{{\varphi }_{2}}({{S}_{i}}) - \varepsilon _{i}^{{phst}}]{{dq} \mathord{\left/ {\vphantom {{dq} q}} \right. \kern-0em} q} + d{{R}_{1}}}}{{{{R}_{2}}}},$$

(20)

$$d{{R}_{1}} = \frac{3}{2}{{\rho }_{{D2}}}q\varphi _{2}^{'}({{S}_{i}})\frac{{{{S}_{{ij}}}d\sigma _{{ij}}^{'}}}{{{{S}_{i}}}},$$

$${{R}_{2}} = {{\rho }_{{D2}}}g\varphi _{2}^{'}({{S}_{i}}){{S}_{i}} + \frac{2}{3}\frac{{\varepsilon _{{ij}}^{{phst'}}{{S}_{{ij}}}}}{{\varepsilon _{i}^{{phst}}}}.$$

Taking into account that the process is active and Eq. (19) is fulfilled at each point, the expressions for dλ (Eq. (20)), d$\varepsilon _{{ij}}^{{st}}$, and d$\varepsilon _{{ij}}^{{phst'}}$ are simplified,

$$d\lambda = \frac{{d{{R}_{1}}}}{{{{R}_{2}}}},\,\,\,d\varepsilon _{{ij}}^{{st}} = {{S}_{{ij}}}\frac{{d{{R}_{1}}}}{{{{R}_{2}}}},$$

$$d\varepsilon _{{ij}}^{{phst'}} = {{S}_{{ij}}}\frac{{d{{R}_{1}}}}{{{{R}_{2}}}} + \frac{{\varepsilon _{{ij}}^{{phst'}}}}{q}dq.$$

(21)

Since combined hardening can occur during the reverse phase transition and the structural transformation only under the condition S_ij$\varepsilon _{{ij}}^{{phst'}}$ > 0, it follows from Eq. (21) that R₂ > 0 and the differential condition of active loading in this case is again reduced to Eq. (18).

According to Eq. (21), when the reverse transformation and the structural transition occur together, parameter dλ and, hence, the strain increment according to the structural mechanism do not depend on dq; that is, the deformation according to the phase mechanism affects the deformation according to the structural mechanism only through the loading surface radius.

Similar calculations for the structural transition occurring simultaneously with the direct phase transformation in the combined hardening mode for the simplified model (10), in which f(q) = 0 is assumed, give

$$\begin{gathered} d\lambda = \frac{{d{{R}_{1}} + {{R}_{3}}dq}}{{{{R}_{2}}}},\,\,\,d\varepsilon _{{ij}}^{{st}} = {{S}_{{ij}}}\frac{{d{{R}_{1}} + {{R}_{3}}dq}}{{{{R}_{2}}}}, \\ d\varepsilon _{{ij}}^{{phst'}} = {{S}_{{ij}}}\frac{{d{{R}_{1}} + {{R}_{4}}dq}}{{{{R}_{2}}}}, \\ \end{gathered} $$

$${{R}_{3}} = {{\rho }_{{D2}}}{{\varphi }_{2}}({{S}_{i}}) - {{\rho }_{{D1}}}{{\varphi }_{1}}({{S}_{i}})\frac{{\varepsilon _{{ij}}^{{phst'}}{{S}_{{ij}}}}}{{\varepsilon _{i}^{{phst}}{{S}_{i}}}},$$

$${{R}_{4}} = \left( {\frac{3}{2}{{\rho }_{{D1}}}g{{\varphi }_{1}}({{S}_{i}})\varphi _{2}^{'}({{S}_{i}}) + {{\varphi }_{2}}({{S}_{i}})} \right){{\rho }_{{D2}}}.$$

As was shown in [28], strain accumulates at intensity $\varepsilon _{i}^{{phst}}$ = ρ_D1qφ₁(σ_i) during the direct transformation under a constant stress at intensity σ_i, so that the ratio ${{\varepsilon _{i}^{{phst}}} \mathord{\left/ {\vphantom {{\varepsilon _{i}^{{phst}}} q}} \right. \kern-0em} q}$ = ρ_D1φ₁(σ_i) retains a constant value. Therefore, for any q (including the complete direct transformation (q = 1)), the condition max{${{\varepsilon _{i}^{{phst}}} \mathord{\left/ {\vphantom {{\varepsilon _{i}^{{phst}}} q}} \right. \kern-0em} q}$} = ρ_D1φ₁(σ_i) is met. Substituting this relation in the right-hand side of Eq. (4) we can determine the constant loading surface radius in this process,

$$S^* = \varphi _{2}^{{ - 1}}({{{{\rho }_{{D1}}}{{\varphi }_{1}}({{\sigma }_{i}})} \mathord{\left/ {\vphantom {{{{\rho }_{{D1}}}{{\varphi }_{1}}({{\sigma }_{i}})} {{{\rho }_{{D2}}}}}} \right. \kern-0em} {{{\rho }_{{D2}}}}}) > {{\sigma }_{i}}.$$

(22)

According to inequality (22), the structural transition does not occur during the direct transformation under a constant stress.

3 REVERSE TRANSFORMATION AFTER DIRECT TRANSFORMATION UNDER CONSTANT STRESS AND CONSTRAINT

3.1 Process Stages not Accompanied by Structural Transition

Let complete direct transformation occur at the first stage of the process under a constant tensile or compressive stress σ₁ (uniaxial state of stress). The parameters, namely, stress σ and phase strain deviator ε that accumulates during the direct transformation, are taken to be positive for both compression and tension. Under these conditions, σ and ε coincide with the intensities σ_i and ε_i of the corresponding tensors. As a result of the direct transformation, the following phase-structural strain is accumulated:

$${{\varepsilon }_{0}} = {{\varepsilon }_{1}} \pm {{\varepsilon }^{0}} = {{\rho }_{{D1}}}{{\varphi }_{1}}({{\sigma }_{1}}) \pm {{\varepsilon }^{0}},$$

where ε₁ > 0 is the deviatoric component of the accumulated phase strain parameter (hereafter, a sign in a superscript is used for tension and a sign in a subscript, for compression).

We now assume that the deviatoric component of the complete direct transformation strain exceeds the linear strain of the volume effect of this transformation, ε₁ > ε⁰. In this case, the inequality

$${{\varepsilon }_{0}} > 0$$

(23)

is valid.

The loading surface radius at the end of the direct transformation (Eq. (22)) is

$${{S}_{1}} = \varphi _{2}^{{ - 1}}({{{{\rho }_{{D1}}}{{\varphi }_{1}}({{\sigma }_{1}})} \mathord{\left/ {\vphantom {{{{\rho }_{{D1}}}{{\varphi }_{1}}({{\sigma }_{1}})} {{{\rho }_{{D2}}}}}} \right. \kern-0em} {{{\rho }_{{D2}}}}}) = \varphi _{2}^{{ - 1}}({{{{\varepsilon }_{1}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{1}}} {{{\rho }_{{D2}}}}}} \right. \kern-0em} {{{\rho }_{{D2}}}}}).$$

(24)

The center of the loading surface is located at the origin of coordinates, r = 0, S = σ. Then, complete elastic unloading to σ = 0 takes place. Then, the complete strain is fixed (constraint is performed), and the reverse thermoelastic phase transformation occurs under these conditions as a result of heating. In heating, we have

$${{\varepsilon }^{e}} + {{\varepsilon }^{{phst'}}} \pm q{{\varepsilon }^{0}} = {{\varepsilon }_{1}} \pm {{\varepsilon }^{0}} = {{\varepsilon }_{0}} = {\text{const}}{\text{.}}$$

(25)

Differentiating Eq. (25), we obtain

$$\frac{{d\sigma }}{{E(q)}} + \sigma \frac{{\Delta E}}{{{{E}_{A}}{{E}_{M}}}}dq + \left( { \pm {{\varepsilon }^{0}} + \frac{{{{\varepsilon }^{{phst'}}}}}{q}} \right)dq + \frac{2}{3}Sd\lambda = 0.$$

(26)

In Eq. (26), we take into account that ε^e = σ/E(q) for elastic deformation, where the dependence of Young’s modulus of SMA on q is taken into account using the formula

$${1 \mathord{\left/ {\vphantom {1 {E(q) = {q \mathord{\left/ {\vphantom {q {{{E}_{M}}}}} \right. \kern-0em} {{{E}_{M}}}} + {{(1 - q)} \mathord{\left/ {\vphantom {{(1 - q)} {{{E}_{A}}}}} \right. \kern-0em} {{{E}_{A}}}},}}} \right. \kern-0em} {E(q) = {q \mathord{\left/ {\vphantom {q {{{E}_{M}}}}} \right. \kern-0em} {{{E}_{M}}}} + {{(1 - q)} \mathord{\left/ {\vphantom {{(1 - q)} {{{E}_{A}}}}} \right. \kern-0em} {{{E}_{A}}}},}}$$

where E_M and E_A are Young’s moduli for the martensitic and austenitic states, respectively.

From Eq. (25), we obtain

$${{\varepsilon }^{{phst'}}} = {{\varepsilon }_{1}} \pm {{\varepsilon }^{0}} - {\sigma \mathord{\left/ {\vphantom {\sigma {E(q) \mp q{{\varepsilon }^{0}}}}} \right. \kern-0em} {E(q) \mp q{{\varepsilon }^{0}}}};$$

substituting this result into Eq. (26), we have

$$\frac{{d\sigma }}{{E(q)}} + \sigma \frac{{\Delta E}}{{{{E}_{A}}{{E}_{M}}}}dq + \left( {\frac{{{{\varepsilon }_{0}} - {\sigma \mathord{\left/ {\vphantom {\sigma {E(q)}}} \right. \kern-0em} {E(q)}}}}{q}} \right)dq + \frac{2}{3}Sd\lambda = 0.$$

Obviously, stresses appear during a phase transition and their parameter increases monotonically, σ > 0. Until σ reaches S₁ (Eq. (24)), the structural transmission does not occur, dλ = 0, and the process is determined by the equation

$$\frac{{d\sigma }}{{\sigma - {{E}_{A}}{{\varepsilon }_{0}}}} = \left( {\frac{1}{q} - \frac{1}{{{1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0em} \mu } + q}}} \right)dq,\,\,\,\mu = {{({{E}_{A}} - {{E}_{M}})} \mathord{\left/ {\vphantom {{({{E}_{A}} - {{E}_{M}})} {{{E}_{M}}}}} \right. \kern-0em} {{{E}_{M}}}},$$

the solution of which under the initial condition σ(1) = 0 gives

$$\sigma = \frac{{{{E}_{A}}{{\varepsilon }_{0}}(1 - q)}}{{\mu q + 1}}.$$

(27)

Since dε^st = 0 at the two process stages under study, we have dr = 0, r = 0 and S = σ > 0. This inequality is valid for q < 1 according to Eq. (23).

According to Eq. (27), σ increases with decreasing q until σ reaches S₁ (Eq. (24)) at some q = q_s. At the stage of decreasing q from 1 to q_s, no structural transition takes place, and only the reverse phase transformation occurs. Integrating the equation for changing the strains due to the reverse phase transition dε^phst' = ${{\varepsilon _{{}}^{{phst'}}dq} \mathord{\left/ {\vphantom {{\varepsilon _{{}}^{{phst'}}dq} q}} \right. \kern-0em} q}$ under the initial condition ε^phst'(1) = ε₁, for q ∈ [q_s, 1] we obtain

$${{\varepsilon }^{{phst'}}}(q) = q{{\varepsilon }_{1}}.$$

(28)

According to Eq. (28), the phase-structural strain deviator parameter in the considered part of the process decreases in magnitude monotonically and in proportion to q. At the same time, the loading surface radius is determined by the equation ρ_D2φ₂(S) = ε₁ and retains a constant value (24) in terms of the model under study with loading surface equation (4) and taking into account the fact that max{${{\varepsilon _{i}^{{phst}}} \mathord{\left/ {\vphantom {{\varepsilon _{i}^{{phst}}} q}} \right. \kern-0em} q}$} = ε₁ according to Eq. (28) during the reverse transformation in the absence of the structural transition. It should be noted that S* tends to increase sharply toward $\infty$ in terms of model (3) [28] under the same conditions. The condition for the point representing the state of stress to reach the loading surface is S₁ = σ or, according to (27),

$${{S}_{1}} = \frac{{{{E}_{A}}{{\varepsilon }_{0}}(1 - q)}}{{\mu q + 1}}.$$

(29)

From Eq. (29), we find the value of q_s at which the structural transition can join the reverse phase transformation if the corresponding differential condition is met. Solution (29) has the form

$${{q}_{s}} = {{({{E}_{A}}{{\varepsilon }_{0}} - {{S}_{1}})} \mathord{\left/ {\vphantom {{({{E}_{A}}{{\varepsilon }_{0}} - {{S}_{1}})} {({{E}_{A}}{{\varepsilon }_{0}} + \mu {{S}_{1}}).}}} \right. \kern-0em} {({{E}_{A}}{{\varepsilon }_{0}} + \mu {{S}_{1}}).}}$$

The considered stage ends at σ(q_s) = S(q_s) = S₁ and ε^phst'(q_s) = q_sε₁.

3.2 Process Stage Accompanied by Structural Transition

We now consider the reverse transformation for q ≤ q_s. It is interesting to establish whether (and if so, for how long) the structural transition occurs during further heating and in which version, combined or purely translational hardening?

At the initial moment q = q_s, the point representing the state of stress is located on the loading surface. Therefore, if the condition dλ > 0, which in this case is equivalent to dσ > 0 for both combined and translational hardening, is met at each point in a certain fragment of the further process, an active process occurs and the point is retained on the loading surface. Therefore, the active process stops only at the point where dσ ≤ 0.

At the initial point q = q_s, the condition Sε > 0 is met, which indicates that combined hardening place in the case of active loading (dσ > 0). Therefore, as long as the conditions dσ > 0 and Sε > 0 are met, an active combined hardening mode occurs and is described by a one-dimensional analog of Eq. (19),

$${{\rho }_{{D2}}}{{\varphi }_{2}}(S) = \frac{\varepsilon }{q},\,\,\,q \leqslant {{q}_{s}}.$$

(30)

At q = q_s, we find ε = ε₁q_s and ε/q = ε₁, and Eq. (30) has the form ρ_D2φ₂(S) = ε₁.

We now derive relations that would allow us to find the dependences of S, σ, and ε on q. For the active process of the reverse transformation and structural transition under combined hardening, the one-dimensional analogs of Eqs. (21) and(11) are as follows:

$$\begin{gathered} d{{\varepsilon }^{{st}}} = \frac{{{{\rho }_{{D2}}}q\varphi _{2}^{'}(\left| S \right|)d\sigma }}{{[3{{\rho }_{{D2}}}g\varphi _{2}^{'}{{(\left| S \right|)} \mathord{\left/ {\vphantom {{(\left| S \right|)} {2 + 1}}} \right. \kern-0em} {2 + 1}}]}}, \\ dr = \frac{3}{2}g\frac{{{{\rho }_{{D2}}}\varphi _{2}^{'}(\left| S \right|)(dr + dS)}}{{[3{{\rho }_{{D2}}}g\varphi _{2}^{'}{{(\left| S \right|)} \mathord{\left/ {\vphantom {{(\left| S \right|)} {2 + 1}}} \right. \kern-0em} {2 + 1}}]}}. \\ \end{gathered} $$

Solving the last equation for dr, we have

$$dr = \frac{3}{2}g{{\rho }_{{D2}}}\varphi _{2}^{'}(S)dS.$$

(31)

Integrating Eq. (31) under the initial condition r(S₁) = 0, we obtain

$$\begin{gathered} r = \frac{3}{2}g{{\rho }_{{D2}}}[{{\varphi }_{2}}(S) - {{\varphi }_{2}}({{S}_{1}})], \\ \sigma = S + \frac{3}{2}g{{\rho }_{{D2}}}[{{\varphi }_{2}}(S) - {{\varphi }_{2}}({{S}_{1}})]. \\ \end{gathered} $$

(32)

According to Eq. (32), when S increases from S₁, σ increases monotonically from S₁ and tends toward ∞ at S → ∞.

Constant strain condition (25) for q ≤ q_s, for an active combined hardening process, when Eq. (30) is fulfilled, is written as

$${{\rho }_{{D2}}}q{{\varphi }_{2}}(S) \pm {{\varepsilon }^{0}}q + {\sigma \mathord{\left/ {\vphantom {\sigma {E(q) = {{\varepsilon }_{0}}}}} \right. \kern-0em} {E(q) = {{\varepsilon }_{0}}}}.$$

Taking into account that

$${\sigma \mathord{\left/ {\vphantom {\sigma {E(q) = (\mu q + 1){\sigma \mathord{\left/ {\vphantom {\sigma {{{E}_{A}}}}} \right. \kern-0em} {{{E}_{A}}}},}}} \right. \kern-0em} {E(q) = (\mu q + 1){\sigma \mathord{\left/ {\vphantom {\sigma {{{E}_{A}}}}} \right. \kern-0em} {{{E}_{A}}}},}}$$

we obtain a linear equation for q, the solution of which has the form

$$q = \frac{{{{E}_{A}}{{\varepsilon }_{0}} - \sigma }}{{{{E}_{A}}[{{\rho }_{{D2}}}{{\varphi }_{2}}(S) \pm {{\varepsilon }^{0}}] + \mu \sigma }}.$$

(33)

According to Eq. (33), when S and σ increase, q decreases monotonically, tending toward zero at σ → E_Aε₀. Since the changes in functions S, σ, and q are monotonic, we can state that, when q decreases from q_s to zero, quantities S and ε = qρ_D2φ₂(S) are positive and dσ > 0; i.e., the conditions of active process (Sdσ > 0) and combined hardening (Sε > 0) are fulfilled. Therefore, the assumptions formulated on obtaining this solution about the presence of a structural transition and a combined character of hardening are correct at the considered stage of the process.

The second relation in Eq. (32), Eq. (33), and the relation ε^phst'(q) = qρ_D2qφ₂(S) (which is one of the active loading conditions) represent an explicit parametric representation of the solution to the problem for all the desired functions with parameter S ∈ [S₁, +∞]. In this case, parameter σ expressed in terms of S (the second relation in Eq. (32)) should be substituted into Eq. (33).

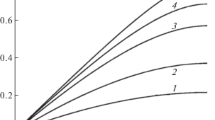
The calculations are then carried out using the following dimensionless variables: e = ε^phst'/ρ_D2, e₁ = ε₁/ρ_D2, e⁰ = ε⁰/ρ_D2, e⁰ = ε⁰/ρ_D2, c = S/σ₂₀, c₁ = S₁/σ₂₀, C = σ/σ₂₀, G = ρ_D2g/σ₂₀, e_A = ρ_D2E_A/σ₂₀, φ₂(σ) = Φ₂(σ/σ₂₀), Φ₂(C) = 1 – exp(–C^α), and φ₂(s) = Φ₂(S/σ₂₀) = Φ₂(c) = 1 – exp(–c^α). The calculations were performed for the following values of the parameters: g = 3000 MPa or g = 750 MPa, E_A = 84 000 MPa, E_M = 28 000 MPa, μ = 2, and ε⁰ = 0.001. For the case of tension (TiNi, flattened billets [29]), we have σ₂₀ = 180 MPa, ρ_D2 = 0.0572, and α₂ = 2.96. For the case of compression (rods 8 mm in diameter [29]), we have σ₂₀ = 305 MPa, ρ_D2 = 0.019, and α₂ = 4.9. Figures 1–3 show the dependences of phase-structural strain e on phase composition parameter q.

Fig. 1.

Dimensionless strain vs. q and the initial tensile strain.

The data shown in Fig. 1 correspond to the tension. Curves 1–5 were obtained for e₁ = 0.5, 0.4, 0.3, 0.2, and 0.1, respectively. Three characteristic segments can be distinguished in the curves. The first segment on the right corresponds to the reverse phase transformation without a structural transition, and this segment begins at the point q = 1, e = e₁ and ends at the point (q_s, e₁q_s) corresponding to the beginning of the structural transition. The continuation of all these segments passes through the origin of coordinates. The third segment represents the general linear asymptotics of all curves, ending at the origin of coordinates, and the equation of this asymptotic is e = q.

A transitional middle segment is between the first and third segments, and it starts from the point of break of the tangent, which is related to the operation of a structural deformation mechanism. Only in this transitional segment, the curve depends on translational hardening parameter g. The thin lines here correspond to g = 3000 MPa and the thick lines, to g = 750 MPa. When g decreases, the strains in this segment grow at the same values of q. For sufficiently low values of g at the beginning of the intermediate segment, the strain during the reverse transformation can not decrease, but even increase slightly.

In Fig. 2, similar curves are plotted with allowance for the properties of the material corresponding to compression for e₁ = 0.1–0.9. The curves are arranged from top to bottom from e₁ = 0.9 and to e₁ = 0.1 at a step of 0.1. Note that, during the transition from tension to compression (see Fig. 1), the first segment lengthens significantly and the intermediate one shortens. For low values of e₁, the second and third segments are absent at all, and the structural transition is not observed until the completion of the reverse transformation. The curves in Fig. 2 are plotted for g = 750 MPa and their shapes at g = 3000 MPa are almost the same.

Fig. 2.

Dimensionless strain vs. q and the initial compressive strain.

In Fig. 3, we compare the dependences of e on q for e₁ = 0.5 (1, 1' ) and e₁ = 0.1 (2, 2 ') in the case of tension (1, 2) and compression (1', 2 '). For a low initial strain e₁ = 0.1, structural deformation does not occur at all during compression, and a structural transition occurs in the major part of the q range during tension.

Fig. 3.

e vs. q for (1, 1') high and (2, 2') low initial strains for (1, 2) tension and (1', 2') compression.

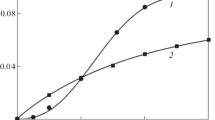
Figure 4 shows the q dependences of the dimensionless coordinates of the center of the loading surface r (curve 1), the dimensionless parameter of active stresses c (curve 2), and the dimensionless parameter of stress deviator C (curve 3). The solutions are obtained for compression, e₁ = 0.5 and g = 3000. The dependence of r on q reaches a horizontal asymptote when q approaches zero due to properties of (1) function φ₂. Curves 2 and 3 coincide with each other for q ∈ [q_s, 1] and become equidistant for q close to 0.

Fig. 4.

Effect of q on (1) microstresses, (2) active stresses, and (3) total stresses for compression.

In Fig. 5, similar curves are shown for the case of tension at an initial strain e₁ = 0.1. The lower group of thick and thin lines determines the changes of r with q, the middle group, the values of c, and the upper group, the values of C. When g increases, all other things being equal, the values of r and C in the segment q ∈ [0, q_s) decrease and c increases (thin lines, as before, correspond to g = 3000 MPa, thick lines, to g = 750 MPa). At q → 0, the dependences C(q) for various values of g have the same asymptotics. As g increases, the segment of the “horizontal” asymptotics of the dependence r(q) adjacent to the ordinate axis shortens and completely disappears.

Fig. 5.

Effect of q on (1) microstresses r, (2) active stresses c, and (3) total stresses C for tension.

Figure 6 shows the dependences of dimensionless stress C on dimensionless strain e for the process under consideration in the case of tension. The curves from right to left correspond to e₁ = 0.2, 0.15, 0.1, 0.05. As can be seen, for sufficiently low values of g (thick lines), the stresses are not a monotonic and single-valued function of strain. Immediately after the beginning of the structural transformation with an increase in stress, the deformation parameter passes from decreasing to increasing, reaching a local maximum, and then monotonically decreases to zero. This nonmonotonicity and nonuniqueness effect at fixed g increases with decreasing initial strain e₁.

Fig. 6.

Dimensionless stress vs. dimensionless strain for tension.

4 CONCLUSIONS

(1) The assumption that the intensity of the intrinsic phase-structural strain of the representative SMA volume should be used as a parameter of isotropic hardening for the structural deformation of SMA was substantiated. This assumption makes it possible to significantly simplify an SMA deformation model for the case of simultaneous structural and reverse phase transformations.

(2) Taking into account the structural transformation during the reverse transition in an SMA rod, which is in a constrained state, significantly changes the solution of the problem, leading to a nonmonotonic (in some cases, ambiguous) strain dependence of stresses.