Crystallographic Analysis and Mechanism of the Martensitic Transformation in the Heusler Alloy Ni₄₇Mn₄₂In₁₁

Abstract

The lattice parameters of the matrix of the modulated martensite crystal of the Ni₄₇Mn₄₂In₁₁ alloy have been determined. Based on the phenomenological crystallographic theory of martensitic transformations, orientational relationships between the crystal lattices of the martensite matrix and the initial phase have been calculated, and the magnitude and the direction of the macroscopic shear, the habit plane, and the angle and the axis of rotation of the martensite plate have been determined. The mechanism of deformation upon the martensitic transformation has been established.

INTRODUCTION

Studies of ferromagnetic alloys have attracted the attention of researchers due to the specific features of their phase transformations, structure formation, and new approaches in studies to such materials. The Ni–Mn–In-based alloys can be separated into a specific group of the so-called Heusler alloys due to the sequence of structural phase transformations occurring in them [1–6] and their potential use in various technological devices. Great attention has been paid in recent years to researching Ni–Mn–In Heusler alloys of nonstoichiometric compositions, in which magnetic-field-controlled shape-memory effects [4, 7] are realized. The investigation of structural and crystallographic peculiarities of martensitic transformations is of interest for determining the influence of structural and magnetic ordering on the functional characteristics of Ni–Mn–In Heusler alloys.

The phenomenological theory of martensitic transformations (PTMTs) describes the formation of a martensite crystal in terms of the product of three matrices: matrix of a Bain deformation (B); deformation (by twinning or slip) with an invariant lattice (P); and rotation (R) [8, 9]. The Bain deformation, which is a pure deformation, transforms the crystal lattice of austenite into the lattice of martensite and is therefore called the lattice deformation. The deformation with an invariant lattice is necessary to obtain the habit plane of the martensite crystal. The matrix of rotation of the martensite plate describes the rotation that mainly occurs when the austenite lattice is transformed into the martensite lattice. If we consider the real mechanism of deformation of the lattice of the initial phase to the lattice parameters of the martensite, which occurs mainly via shear, then the R matrix will describe only a small rotation that occurs when the martensite is deformed upon an invariant lattice. This was shown in [10–13].

To calculate crystallographic characteristics using the PTMTs it is necessary to know the parameters of the unit cells of the austenite and of the matrix of the martensite. Figure 1a shows a schematic representation of a martensite plate of an iron–nickel alloy with a twinned martensite. Figure 1b shows the unit cell of the modulated structure of 6M martensite of the Ni₄₇Mn₄₂In₁₁ alloy [14] (as we see, the six-layer structure consists of four layers of the matrix and of two layers in the twinned position). If we make a schematic image of the martensite plate of this alloy, we obtain the same image as in Fig. 1a. However, the thickness of the portions of the matrix and of the twins in the twinned martensite of the iron–nickel alloy is approximately 100–1000 times greater than in the modulated martensite. In the twinned martensite, the twins and the regions of the martensite matrix located between the twins scatter X-rays independently of each other, and the experimentally determined unit cell of the martensite lattice is the unit cell of the martensite matrix. In the case of the modulated martensite, the volume of a coherent-scattering region (CSR) involves a large number of alternating regions of the matrix and twins. The diffraction pattern obtained from such a CSR corresponds to a crystal lattice with a new unit cell (the unit cell of the modulated structure of martensite), including at least one region of the matrix and one twin. If we exclude the satellites present in the XRD patterns, we obtain a diffraction pattern corresponding to an “averaged” structure. The unit cell of such an averaged structure (basic unit cell) differs significantly from the unit cell of the matrix of the martensite, as can be seen in Fig. 1b. Based on the known parameters of the unit cell of the modulated structure of martensite, or on the parameters of the basic unit cell, it is possible to find the crystallographic characteristics of martensite using the PTMTs, as was done in [15] for the modulated 63.0 Ni–37.0 Al (at %) alloy, but the mechanism of deformation of the lattice upon the martensitic transformation cannot be determined. To determine this mechanism using the PTMTs, it is necessary to know the parameters of the unit cell of the martensite matrix, which cannot be obtained directly from XRD measurements, but can be calculated based on the known parameters of the unit cell of the modulated structure.

Fig. 1.

(a) A schematic representation of a martensite plate of an Fe–Ni alloy and (b) the unit cell of the 6M martensite lattice of the alloy Ni₄₇Mn₄₂In₁₁. AB₂F₂D is the unit cell of the martensite matrix; AB₁F₁D is the unit cell of the averaged martensite structure (basic cell); B₁, the point of intersection of lines AB and B₂F₂; F₁, the point of intersection of lines DF and of the straight line B₂F₂; ABFD, the unit cell of the modulated structure of the 6M martensite.

The aim of this work is to determine the unit cell of the martensite matrix and the mechanism of lattice deformation upon the martensitic transformation in the Ni₄₇Mn₄₂In₁₁ alloy, as well as to determine the crystallographic characteristics of the martensite using the PTMTs.

DETERMINATION OF PARAMETERS OF THE UNIT CELL OF MARTENSITE MATRIX

We determined in [14] the parameters of the unit cell of the modulated monoclinic structure of the Ni₄₇Mn₄₂In₁₁ alloy as a = 0.4406 nm, b = 0.5601 nm, c = 1.3024 nm, and β = 93.51°. As can be seen from Fig. 1b, the cell contains six layers, with four layers of atoms belonging to the matrix and two layers belonging to the twin. Figure 2 provides an auxiliary drawing for determining the parameters of the unit cell of the martensite matrix. The rectangular OLK and OAB triangles can be used to do this. From the OLK triangle, we find OK = c cos δ, LK = c sin δ. Taking into account that AB = LK and OB = OK/3, we find c₁ and δ₁: and ${{\delta }_{1}} = {\text{arctan}}\left( {3\,{\text{tan}}\delta } \right)$. As a result of calculations, we obtain: a₁ = a = 0.44053 nm, b₁ = b = 0.56013 nm, c₁ = 0.44064 nm, β₁ = 90° + δ₁ = 100.43°. Thus, we find the parameters of the monoclinic cell of the martensite matrix: a₁ = c₁ = 0.4406 ± 0.0001 nm, b₁ = 0.5601 ± 0.0001 nm, β₁ = 100.43° ± 0.01°. As can be seen, a₁ = c₁. This indicates that the lattice of the martensite matrix is orthorhombic. Therefore, we pass to the orthorhombic axes, as shown in Fig. 2, and find the unit cell of the martensite matrix: a₂ = 0.5601 ± 0.0001 nm, b₂ = 0.5639 ± 0.0001 nm, c₂ = 0.6771 ± 0.0001 nm. It could be expected that the unit cell of the martensite matrix should be more symmetrical than the unit cell of the modulated martensite structure, since the latter includes a structural defect in the form of a twin. Indeed, we obtained a more symmetrical (orthorhombic) cell close to a tetragonal cell.

Fig. 2.

Scheme for the determination of the lattice parameters of the martensite matrix. The scheme is given in a plane perpendicular to the unit vector $\overline b$; $\overline a$, $\overline b$,$\overline c$, and β = 90° + δ are the parameters of the unit cell of  the modulated structure of martensite; $\overline {{{a}_{1}}}$, $\overline {{{b}_{1}}}$, $\overline {{{c}_{1}}}$, β₁ = 90° + δ₁, the parameters of the monoclinic unit cell of the martensite matrix; $\overline {{{a}_{2}}}$, $\overline {{{b}_{2}}}$, $\overline {{{c}_{2}}}$, the parameters of the orthorhombic unit cell of the martensite matrix; $\overline b = \overline {{{b}_{1}}} = - \overline {{{a}_{2}}}$, $\overline a = \overline {{{a}_{1}}}$.

CALCULATION OF CRYSTALLOGRAPHIC PARAMETERS OF MARTENSITE USING THE PTMTs

For calculations, we take the lattice parameter of the initial cubic phase a₀ = 0.5998 nm, and the parameters of the lattice of the final orthorhombic phase a = 0.5601 nm, b = 0.5639 nm, and c = 0.6771 nm. The pure deformation of the cubic lattice to obtain this orthorhombic lattice is chosen from the equivalent variants as follows:

$${{B}_{0}} = \left( {\begin{array}{*{20}{c}} {\frac{{0.5601}}{{0.5998}}}&0&0 \\ 0&{\frac{{0.5639}}{{0.5998}}}&0 \\ 0&0&{\frac{{0.6771}}{{0.5998}}} \end{array}} \right)$$

((1))

This pure deformation of the lattice can be obtained by shear along the plane (112) in the direction [$\overline 1$$\overline 1$1] by 0.18503 and then by stretching along the direction [$\overline 1$$\overline 1$1] by 0.5%, compression along [1$\overline 1$0] by 6.4%, and stretching along [112] by 5.3%. The matrix that describes the shear Γ in this case is as follows:

((2))

where

$$T = \left( {\begin{array}{*{20}{c}} {\frac{{ - 1}}{{\sqrt 3 }}}&{\frac{{ - 1}}{{\sqrt 3 }}}&{\frac{1}{{\sqrt 3 }}} \\ {\frac{1}{{\sqrt 2 }}}&{\frac{{ - 1}}{{\sqrt 2 }}}&0 \\ {\frac{1}{{\sqrt 6 }}}&{\frac{1}{{\sqrt 6 }}}&{\frac{2}{{\sqrt 6 }}} \end{array}} \right)$$

is the matrix of rotation of the coordinate axes, and is the inverse matrix.

The matrix of the additional strain B₁ has the following form:

$${{B}_{1}} = {{T}^{{ - 1}}} \cdot \left( {\begin{array}{*{20}{c}} {1.00505}&0&0 \\ 0&{0.93700}&0 \\ 0&0&{1.05247} \end{array}} \right)\,\, \cdot \,\,T.$$

Thus, the deformation of the lattice can be calculated as follows:

((3))

Here, ${{B}_{2}} = \left( {\begin{array}{*{20}{c}} {0.99668}&0&{ - 0.00021} \\ 0&{1.00333}&{0.00021} \\ { - 0.00021}&{0.00021}&1 \end{array}} \right)$ is a correction related to the orthorhombic distortions of the lattice.

To obtain the habit plane, we introduce into the calculations the invariant-lattice deformation P by twinning of the martensite, as is done in the FTPMs. A system should be chosen from the twinning systems that results in a minimum deformation of the shape (P₁) of the martensite plate. Figure 3 shows that for the chosen deformation of the lattice upon the martensite transformation by shear along the plane (112)L2₁ in the direction [$\overline 1$$\overline 1$1]L2₁ there are two equivalent twinning systems: (101)[10$\overline 1$] and (011)[01$\overline 1$]. Thus, for each of the 12 variants of the lattice deformation, we have two variants of invariant-lattice deformation of martensite; as a result, we have 24 martensite orientations, as shown in Table 1.

Fig. 3.

Stereographic projection of the twinning systems in the orthorhombic lattice of the martensite matrix for the shear variant, in which the orientation relationships [111]L2₁ || [111]R and ($\overline 1$$\overline 1$2) L21 || ($\overline 1$$\overline 1$2)R are fulfilled.

Table 1.   Orientations and corresponding shear systems in the initial phase and the twinning systems in martensite

The crystallographic analysis is carried out for the case of the orientation no. 5, since the calculations for this orientation are simpler. The matrix P of the martensite deformation is as follows:

$$P = {{S}^{{ - 1}}} \cdot \left( {\begin{array}{*{20}{c}} 1&0&g \\ 0&1&0 \\ 0&0&1 \end{array}} \right) \cdot S.$$

((4))

Choose the twinning in the system (011)[01$\overline 1$]; in this case,

$$S = \left( {\begin{array}{*{20}{c}} {0.04761}&{0.68754}&{ - 0.72458} \\ { - 0.99797}&{0.00203}&{ - 0.06365} \\ { - 0.04229}&{0.72614}&{0.68624} \end{array}} \right)$$

is the matrix of rotation of the coordinate axes from the initial coordinates of the austenite lattice to the orthogonal coordinates chosen in the orthorhombic lattice of martensite in such a way that the X axis be coincident with the shear direction [01$\overline 1$ ]R, the Z axis be coincident with the normal to the plane (011)R, and the Y axis be perpendicular to them.

As was mentioned above, the XRD structural studies allow one to directly find the basic cell in the modulated martensite crystal. Figure 2 shows that the basic cell does not coincide with the unit cell of the martensite matrix. This gives two orientation relationships relative to the initial phase: one for the lattice of the martensite matrix, and the second one for the lattice of the averaged structure of the modulated martensite crystal. The first matrix (θ₁) to determine the indices of the direction [uvw] in the L2₁ lattice, which is parallel to the direction [UVW] in the orthorhombic lattice of the martensite matrix, is calculated as follows: θ₁ = RB. The second matrix (θ₂) for the determination of the indices of the direction [uvw] in the L2₁ lattice that is parallel to the direction [UVW] in the averaged martensite lattice is calculated as θ₂ = RDB, where

$$D = {{S}^{{ - 1}}} \cdot \left( {\begin{array}{*{20}{c}} 1&0&{{{g}_{1}}} \\ 0&1&0 \\ 0&0&1 \end{array}} \right) \cdot S$$

The value of g₁ is determined from Fig. 2:

$${{g}_{1}} = {\text{tan}}\left( {{{\delta }_{1}}} \right)-{\text{tan}}\left( \delta \right) = 0.12268.$$

((5))

The matrix D describes the invariant-lattice deformation of martensite within a CSR. Further calculations of the crystallographic characteristics of the martensite were made in full agreement with the PTMTs [1, 2].

The results for the three variants of calculations of the crystallographic characteristics of martensite transformation are presented in Table 2.

Table 2. Calculated crystallographic parameters of the martensitic transformation

ANALYSIS OF THE RESULTS

The PTMTs makes it possible to find various crystallographic parameters of the transformation, e.g., the habit plane, orientation relationships, shape deformation, etc. To do this, it is sufficient to know the parameters of the unit cell of the initial phase, the lattice parameters of the final phase, and the mechanism of invariant-lattice deformation of the martensite. In the first and second variants of the calculation, the unit cell of the martensite matrix is selected as the unit cell of the final phase. In the third variant, the unit cell of the modulated structure of martensite is chosen as such a cell, which, in addition to the matrix, includes a twin. Such a choice of the unit cell of the final phase was used in [15] for the crystallographic analysis of the martensitic transformation B2 → 7R in the Ni–37.0 at % Al.

In the first variant, the uniform deformation of the lattice is described by Eq. (3). In the second variant, as the mechanism of a homogeneous deformation of the lattice, the Bain deformation is used, containing only a pure lattice deformation without rotation elements. This makes it possible to obtain crystallographic characteristics of the martensitic transformation, but does not allow us to find the real mechanism of martensitic transformation, unlike the first variant. When choosing a realistic mechanism of martensitic transformation, the angle φ should be small. In the first variant, the angle φ is only 0.36°. In the second and third variants, unrealistic large values of the angle φ are obtained. Therefore, only the first variant corresponds to a real mechanism of the lattice deformation. This mechanism, as can be seen from calculations, consists in a shear in the plane (112) in the direction [$\overline 1$$\overline 1$1] by 0.185 and in an additional pure deformation, which consists in a stretching by 5.3% in the direction of the normal to the shear plane, stretching by 0.5% in the shear direction, and compression by 6.4% in the third direction [01$\overline 1$] perpendicular to the first two. As is known, the shear systems of the {112}〈$\overline 1$ $\overline 1$1〉 family are typical of bcc crystals. There are 12 such equivalent shear systems.

Taking into account Eq. (5), we find for the first variant g₂ = g – g₁ = 0.00374. Since g₁ is the invariant-lattice shear deformation of the martensite matrix within a CSR, the g₂ is a displacement of the CSRs relative to each other. For the third variant, we obtain g = g₂, which is equal to only 3% of the magnitude of g for the first variant.

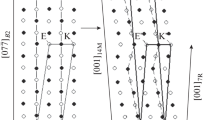
In [14], we experimentally determined the orientation relationships for the basic lattice of the martensite relative to the initial phase: (110)L2₁ || (12$\overline 1$)6M and [$\overline 1$10]L2₁ || [$\overline 1$11]6M (with an error of 0.5°). These orientation relationships refer to orientation no. 2 in Table 1. For this orientation, the calculated plane (12$\overline 1$)6M deviates from the plane (110)L2₁ by 0.13° and the calculated direction [$\overline 1$11]6M deviates from the direction [$\overline 1$10]L2₁ by 0.08°. Thus, the calculated orientation relationships of the basic lattice completely correspond to those found experimentally. A similar conclusion can also be drawn from the comparison of the calculated and experimental pictures in Fig. 4.

Fig. 4.

(a) Fragment of the stereographic projection showing the poles of the crystallographic planes of martensite that originate from the plane (110)L2₁ upon the martensitic transformation; and (b) the XRD pattern of texture maxima obtained in the vicinity of the pole (110)L2₁. The numbers 1 to 24 correspond to the order numbers of orientations.

CONCLUSIONS

(1) The parameters of the unit cell of the matrix of the modulated martensite crystal in the Heusler alloy Ni₄₇Mn₄₂In₁₁ have been determined to be a = 0.5601 nm, b = 0.5639 nm, c = 0.6771 nm, α = 90°, β = 90°, and γ = 90°.

(2) Based on the phenomenological crystallographic theory of martensitic transformations, the orientation relationships between the crystal lattices of the martensite matrix and the initial phase L2₁, as well as between the lattice of the averaged martensite structure and that of the initial phase, have been calculated. The magnitude and the direction of the macroscopic shear, the habit plane, the angle and the axis of rotation of the martensite plate have been determined.

(3) The mechanism of deformation upon martensitic transformation has been established to be as follows: a shear in the plane (112) in the direction [$\overline 1$$\overline 1$1] by 0.185% in the initial L2₁ phase and an additional stretching by 5.3% in the direction of the normal to the shear plane, stretching by 0.5% in the shear direction, and a compression by 6.4% in the transverse direction.

Thus, the shear mechanism we used, just as the Bain deformation, make it possible to obtain the lattice of the martensite. The advantage of the shear mechanism is that it not only deforms the lattice, but also rotates it by an angle that corresponds to the angle of the lattice rotation upon the martensitic transformation.