Assessment of Thermodynamic Properties of Lead-Free Soldering Co–Sb–Sn, Ag–In–Pd–Sn, and Ni–Cr–Co–Al–Mo–Ti–Cu Alloys

Abstract

In the present study, the Chou’s general solution model (GSM) has been used to predict the excess Gibbs enthalpy of the liquid Co–Sb–Sn ternary alloys with three selected sections x_Sb/x_Sn = 1/3, x_Co/x_Sb = 1/5, and x_Co/x_Sn = 1/4, of Ag₁₀–In₈₀–Pd–Sn₁₀, Ag₂₀–In₆₀–Pd–Sn₂₀, and Ag–In₄₀–Pd₂₀–Sn₄₀ quaternary alloys and the excess Gibbs energy of Ni–Cr–Co–Al–Mo–Ti–Cu with seven component alloys with selected sections, namely, x_Ni = x_Cu, x_Cr = x_Ti, x_Co = x_Ti, x_Al = x_Ti, x_Mo = rx_Ti, x_Ti = (1 – x_Cu)/(r + 5), and r = 0.1 at temperatures 1273, 1173, and 2000 K, respectively. However, any information in the literature regarding the application of GSM to the alloys mentioned above could not be found, the other geometric models such as Kohler, Muggianu, and Toop are also included in present calculations. Using standard deviation formula, it is seen that some reasonable agreements exist between the results of the geometric models and those of related experiments.

INTRODUCTION

At the first of July 2006, the European Union Waste Electrical and Electronic Equipment (WEEE) Directive and Restriction of Hazardous Substances (RoHS) Directive came into effect, prohibiting the inclusion of significant quantities of lead in most consumer electronics produced in the EU. Manufacturers may receive tax benefits reducing the use of lead-based solder in the USA. It is expected that similar regulations are active or impending in various other parts of the world. Lead-free solders are recommended in the drinking water—whether rain water in the soil or outdoor—applications. The most typical lead-free solder alloys of tin-silver and tin-copper—compounds being melted around the 523 K depending on their constituents as used to meet the requirements of specific applications,—they become more common in lead-free solders due to environmental pollution concerns. Lead-free solders in commercial use may contain elements such as tin, copper, silver, bismuth, indium, zinc, antimony, and traces of other metals. Suitable materials for low-temperature soft soldering have been found, such as Sn–Ag–Cu and Sn–Cu–Ni, whereas no convenient alloy has so far been found for high-temperature soft soldering because of melting temperature (higher than 503 K). Recently, several investigators have determined mixing enthalpies in the Co‒Sn and Sb–Sn systems [1‒4]. To the best knowledge of the authors, no data for the enthalpy of mixing of liquid alloys in the Co–Sb–Sn ternary system are available. On the other hand, Luef et al. [5] were the first to measure it at 1173 K in the liquid ternary Ag‒In–Sn and quaternary Ag–In–Pd–Sn alloys. The enthalpies of mixing of the five binary subsystems relevant to the Ag–In–Pd–Sn alloy systems, such as Ag–Pd [6], Ag‒Sn [7], In–Pd [8], In–Sn [8], and Pd–Sn [8] have recently been re-measured and assessed. When the melting temperature is greater than 503 K, the alloys such as Sn–Zn, Sn–Sb, and Sn–Au containing solders are promising candidates, while Cu and Ni may be used as additions and as contact materials as well. The systems consisting of the type solder and substrate are characterized general by huge differences in the melting points of the pure components. The high melting areas cannot be investigated experimentally at the temperatures relevant for soldering, i.e. 473–573 K, because diffusion is slow and thermodynamic equilibrium will not be reached in reasonable time. Therefore, it will be significant to study multicomponent systems of four or more metals, for instance, a Pb-free, seven-component Ni–Cr–Co–Al–Mo–Ti–Cu alloy. The excess Gibbs energy of mixing has been investigated in some ternary alloy systems, such as Cr—Co–Al [9], Cr–Co–Mo [9] for some sections using GSM (it can not only generalize various kinds of situations, break down the boundary between symmetrical and asymmetrical models, but can also thoroughly rule out any human interference in the calculation process for ternary systems), Kohler (symmetric), Toop (asymmetric) models. In another study, thermodynamic properties of the six-component systems Ni–Cr–Co–Al–Mo–Ti are discussed analytically [10]. Recently, the excess Gibbs energy of mixing has been investigated in quinary alloy system, Ni–Cr–Co–Al–Mo [11] at a temperature of 2000 K for some sections using GSM, Kohler, and Mugiannu (symmetric) models. Recently, the calculation of thermodynamic quantities of the subsystems in the quaternary Ni–Cr–Co–Al [12], ternary Ni–Cr–Co [13] and Ni–Cr–Al [14] alloys were carried out using some traditional and GSM models.

Table 1.   Redlich–Kister coefficients associated with the liquid phase of Co–Sb–Sn alloy used for the calculation of the excess Gibbs enthalpy of mixing at 1273 K

This study aims to calculate the excess Gibbs energy and activity coefficient for multicomponent systems, such as seven-component Ni–Cr–Co–Al–Mo–Ti–Cu, quaternary Pb-free Ag–In–Pd–Sn, and ternary Co–Sb–Sn alloys. In the system of seven components, such as quaternary Ag–In–Pd–Sn and ternary Co–Sb–Sn alloys, the excess Gibbs energy of mixing calculation has not been reported in literature up to now using GSM model. This study has proposed a calculation of the thermodynamic quantities such as the excess Gibbs energy and enthalpy of mixing to avoid the high cost of the experiments using all the model mentioned above.

Table 2.   Deviation sum of squares η(ij, ik) and similarity coefficients ξ associated with Co–Sb–Sn system at 1273 K

EQUATIONS OF TRADITIONAL GEOMETRIC MODELS

The main equations describing models just mentioned above are summarized as follows. One of them is Kohler model that uses the general expression as follows, so that i and j indices represent the first and second components in binary alloys:

$$\begin{gathered} {{G}^{{{\text{exc}}}}} = \sum\limits_i^{n - 1} {\sum\limits_{j = i + 1}^n {{{{({{x}_{i}} + {{x}_{j}})}}^{2}}} } \\ \times \,\,{{G}^{{{\text{exc}}}}}\left( {\frac{{{{x}_{i}}}}{{{{x}_{i}} + {{x}_{j}}}};\frac{{{{x}_{j}}}}{{{{x}_{i}} + {{x}_{j}}}}} \right). \\ \end{gathered} $$

((1))

Muggianu model is predominantly used by researchers in the optimization of ternary and higher order systems. In this model, the excess Gibbs energy of a phase in n-component system is estimated by the following equation:

$$\begin{gathered} {{G}^{{{\text{exc}}}}} = \sum\limits_i^{n - 1} {\sum\limits_{j = i + 1}^n {\frac{{4{{x}_{i}}{{x}_{j}}}}{{(1 + {{x}_{i}} - {{x}_{j}})(1 + {{x}_{j}} - {{x}_{i}})}}} } \\ \times \,\,{{G}^{{{\text{exc}}}}}\left( {(1 + {{x}_{i}} - {{x}_{j}});\,\,(1 + {{x}_{j}} - {{x}_{i}})} \right). \\ \end{gathered} $$

((2))

Unlike the other methods, the Toop extrapolation method is an asymmetric model and its equation is given generally as:

$$\begin{gathered} {{G}^{{{\text{Exc}}}}} = \sum\limits_{i = 2}^7 {\sum\limits_{j = i + 1}^7 {{{{({{x}_{i}} + {{x}_{j}})}}^{2}}} } \\ \times \,\,G_{{ij}}^{{{\text{exc}}}}\left( {\frac{{{{x}_{i}}}}{{{{x}_{i}} + {{x}_{j}}}};\frac{{{{x}_{j}}}}{{{{x}_{i}} + {{x}_{j}}}}} \right) + \sum\limits_{i = 2}^7 {\frac{{{{x}_{i}}}}{{(1 - {{x}_{1}})}}} G_{{1i}}^{{{\text{exc}}}}\left( {{{x}_{1}};(1 - {{x}_{1}})} \right). \\ \end{gathered} $$

((3))

The basic equation of GSM for seven-component alloys is given as follows, so that the probability weight W_ij of the ij binary system can be expressed as W_ij = x_ix_j/X_i(ij)X_j(ij), (i, j = 1–7, i ≠ j):

$${{G}^{{{\text{exc}}}}} = \sum\limits_{i,j = 1,i \ne j}^7 {{{W}_{{ij}}}} G_{{ij}}^{{{\text{exc}}}}.$$

((4))

Here, G^exc is the excess Gibbs energy of mixing for seven-component systems; and x₁, x₂, x₃, x₄, x₅, x₆, and x₇ are the mole fractions of the alloy systems in question. First of all, it is necessary to calculate the similarity coefficients $\xi _{{i(ij)}}^{{(k)}}$ for twenty one binaries which are defined by η(ij, ik) called the deviation sum of squares when GSM is applied to the alloy system and their definitions are given as follows, respectively:

$$\xi _{{i(ij)}}^{{(k)}} = \frac{{\eta \left( {ij,ik} \right)}}{{\eta \left( {ij,ik} \right) + \eta \left( {ji,ik} \right)}},$$

((5))

$$\eta \left( {ij,ik} \right) = \int\limits_0^1 {{{{\left( {\Delta G_{{ij}}^{{{\text{Exc}}}} - \Delta G_{{jk}}^{{{\text{Exc}}}}} \right)}}^{2}}} d{{X}_{i}}.$$

((6))

Equation (6) can be written analytically as

$$\begin{gathered} \eta \left( {ij,ik} \right) \\ = \sum\limits_{{\text{l}} = {\text{0}}}^{\text{n}} {\frac{{\text{1}}}{{2\left( {{\text{2}}l + 1} \right)\left( {{\text{2}}l + {\text{3}}} \right)\left( {{\text{2}}l + 5} \right)}}} {{\left( {A_{{ij}}^{l} - A_{{ik}}^{l}} \right)}^{2}} \\ + \,\,\sum\limits_{{\text{l}} = {\text{0}}}^{\text{n}} {\sum\limits_{m > l}^n {\frac{{\text{1}}}{{\left( {l + m + {\text{1}}} \right)\left( {l + m + 3} \right)\left( {l + m + 5} \right)}}} } \\ \times \,\,\left( {A_{{ij}}^{l} - A_{{ik}}^{l}} \right)\left( {A_{{ij}}^{m} - A_{{ik}}^{m}} \right). \\ \end{gathered} $$

((7))

$A_{{ij}}^{k}$ are the parameters for binary ij systems independent of composition, only relying on temperature.

The correctness of calculated similarity coefficients can be checked using Eq. (8) as follows:

$$\begin{gathered} \left( {1 - \xi _{{i(ij)}}^{{(k)}}} \right)\left( {1 - \xi _{{k(ki)}}^{{({\text{j}})}}} \right)\left( {1 - \xi _{{j(jk)}}^{{(i)}}} \right) \\ = \xi _{{i(ij)}}^{{(k)}}\xi _{{k(ki)}}^{{({\text{j}})}}\xi _{{j(jk)}}^{{(i)}}. \\ \end{gathered} $$

((8))

We prove that this higher order model can be reduced to a lower order model if two components in a multicomponent system are identical. The expression for the excess Gibbs energy of mixing for a six-component system—which is another form of Eq. (4)—is as follows:

$$\begin{gathered} {{G}^{{{\text{exc}}}}}{\text{ = }}\frac{{{{x}_{1}}{{x}_{2}}}}{{{{X}_{{1(12)}}}X{}_{{2(12)}}}}G_{{12}}^{{{\text{exc}}}} + \frac{{{{x}_{1}}{{x}_{3}}}}{{{{X}_{{1(13)}}}{{X}_{{3(13)}}}}}G_{{13}}^{{{\text{exc}}}} \\ + \,\,\frac{{{{x}_{1}}{{x}_{4}}}}{{{{X}_{{1(14)}}}{{X}_{{4(14)}}}}}G_{{14}}^{{{\text{exc}}}} + \frac{{{{x}_{1}}{{x}_{5}}}}{{{{X}_{{1(15)}}}X{}_{{5(15)}}}}G_{{15}}^{{{\text{exc}}}} \\ + \,\,\frac{{{{x}_{1}}{{x}_{6}}}}{{{{X}_{{1(16)}}}{{X}_{{6(16)}}}}}G_{{16}}^{{{\text{exc}}}} + \frac{{{{x}_{2}}{{x}_{3}}}}{{{{X}_{{2(23)}}}{{X}_{{3(23)}}}}}G_{{23}}^{{{\text{exc}}}} \\ + \,\,\frac{{{{x}_{2}}{{x}_{4}}}}{{{{X}_{{2(24)}}}X{}_{{4(24)}}}}G_{{24}}^{{{\text{exc}}}} + \frac{{{{x}_{2}}{{x}_{5}}}}{{{{X}_{{2(25)}}}{{X}_{{5(25)}}}}}G_{{25}}^{{{\text{exc}}}} \\ + \,\,\frac{{{{x}_{2}}{{x}_{6}}}}{{{{X}_{{2(26)}}}{{X}_{{6(26)}}}}}G_{{26}}^{{{\text{exc}}}} + \frac{{{{x}_{3}}{{x}_{4}}}}{{{{X}_{{3(34)}}}X{}_{{4(34)}}}}G_{{34}}^{{{\text{exc}}}} \\ + \,\,\frac{{{{x}_{3}}{{x}_{5}}}}{{{{X}_{{3(35)}}}{{X}_{{5(35)}}}}}G_{{35}}^{{{\text{exc}}}} + \frac{{{{x}_{3}}{{x}_{6}}}}{{{{X}_{{3(36)}}}{{X}_{{6(36)}}}}}G_{{36}}^{{{\text{exc}}}} \\ + \,\,\,\frac{{{{x}_{4}}{{x}_{5}}}}{{{{X}_{{4(45)}}}{{X}_{{5(45)}}}}}G_{{45}}^{{{\text{exc}}}} + \frac{{{{x}_{4}}{{x}_{6}}}}{{{{X}_{{4(46)}}}{{X}_{{6(46)}}}}}G_{{46}}^{{{\text{exc}}}} \\ + \,\,\frac{{{{x}_{5}}{{x}_{6}}}}{{{{X}_{{5(56)}}}{{X}_{{6(56)}}}}}G_{{56}}^{{{\text{exc}}}}. \\ \end{gathered} $$

((9))

One may obtain the following, when the fourth component is identical to the third one and using definition of deviation sum of squares:

$$G_{{56}}^{{{\text{Exc}}}} = 0,$$

((10))

$$\eta \left( {16,\,12} \right) = \eta \left( {15,\,12} \right),$$

((11))

$$\eta \left( {61,\,62} \right) = \eta \left( {51,\,52} \right),$$

((12))

$$\eta \left( {16,\,14} \right) = \eta \left( {15,\,14} \right),$$

((13))

$$\eta \left( {61,\,64} \right) = \eta \left( {51,\,54} \right),$$

((14))

$$\eta \left( {16,15} \right) = 0,$$

((15))

$$\eta \left( {61,\,65} \right) = \eta \left( {51,\,55} \right),$$

((16))

$$\eta \left( {16,\,13} \right) = \eta \left( {15,\,13} \right),$$

((17))

$$\eta \left( {61,\,63} \right) = \eta \left( {51,\,53} \right).$$

((18))

Substituting Eq. from (11) to (18) into Eq. (5), we have the following:

$$\xi _{{1\left( {16} \right)}}^{{\left( 2 \right)}} = \xi _{{1\left( {15} \right)}}^{{\left( 2 \right)}},$$

((19))

$$\xi _{{1\left( {16} \right)}}^{{\left( 4 \right)}} = \xi _{{1\left( {15} \right)}}^{{\left( 4 \right)}},$$

((20))

$$\xi _{{1\left( {16} \right)}}^{{\left( 5 \right)}} = \xi _{{1\left( {15} \right)}}^{{\left( 6 \right)}},$$

((21))

$$\xi _{{1\left( {16} \right)}}^{{\left( 3 \right)}} = \xi _{{1\left( {15} \right)}}^{{\left( 3 \right)}}.$$

((22))

So,

$${{X}_{{{\text{1}}\left( {{\text{16}}} \right)}}} = {{X}_{{{\text{1}}\left( {{\text{15}}} \right)}}}.$$

((23))

Taking into account the Eqs. (19)–(23), arranging the coefficients of terms having $G_{{15}}^{{{\text{exc}}}}$ and $G_{{16}}^{{{\text{exc}}}}$ in Eq. (9), the terms in question are written as:

$$\begin{gathered} \frac{{{{x}_{1}}{{x}_{5}}}}{{{{X}_{{1(15)}}}X{}_{{5(15)}}}}G_{{15}}^{{{\text{exc}}}} + \frac{{{{x}_{1}}{{x}_{6}}}}{{{{X}_{{1(16)}}}{{X}_{{6(16)}}}}}G_{{16}}^{{{\text{exc}}}} \\ = \,\,\frac{{{{x}_{1}}\left( {{{x}_{5}} + {{x}_{6}}} \right)}}{{{{X}_{{1(15)}}}{{X}_{{5(15)}}}}}G_{{15}}^{{{\text{exc}}}}. \\ \end{gathered} $$

((24))

For expressions of η(ij, ik) in X₂₍₂₆₎ one can obtain:

$$\eta \left( {26,\,21} \right) = \eta \left( {25,\,21} \right),$$

((25))

$$\eta \left( {62,\,61} \right) = \eta \left( {52,\,51} \right),$$

((26))

$$\eta \left( {26,\,23} \right) = \eta \left( {25,\,23} \right),$$

((27))

$$\eta \left( {62,\,63} \right) = \eta \left( {52,\,53} \right),$$

((28))

$$\eta \left( {25,\,26} \right) = 0,$$

((29))

$$\eta \left( {26,\,24} \right) = \eta \left( {25,\,24} \right),$$

((30))

$$\eta \left( {62,\,65} \right) = \eta \left( {52,\,55} \right).$$

((31))

Substituting Eq. from (25) to (31) into Eq. (5), we have the following:

$$\xi _{{2\left( {26} \right)}}^{{\left( 1 \right)}} = \xi _{{2\left( {25} \right)}}^{{\left( 1 \right)}},$$

((32))

$$\xi _{{2\left( {26} \right)}}^{{\left( 3 \right)}} = \xi _{{2\left( {25} \right)}}^{{\left( 3 \right)}},$$

((33))

$$\xi _{{2\left( {26} \right)}}^{{\left( 4 \right)}} = \xi _{{2\left( {25} \right)}}^{{\left( 4 \right)}},$$

((34))

$$\xi _{{2\left( {26} \right)}}^{{\left( 5 \right)}} = \xi _{{2\left( {25} \right)}}^{{\left( 6 \right)}} = 0.$$

((35))

According to these equations, it is:

$${{X}_{{{\text{2}}\left( {{\text{26}}} \right)}}} = {{X}_{{{\text{2}}\left( {{\text{25}}} \right)}}}.$$

((36))

Taking into account the Eqs. (32)–(36), arranging the coefficients of terms having $G_{{25}}^{{{\text{exc}}}}$ and $G_{{26}}^{{{\text{exc}}}}$ in Eq. (9), the terms in question are written as:

$$\begin{gathered} \frac{{{{x}_{2}}{{x}_{5}}}}{{{{X}_{{2(25)}}}X{}_{{5(25)}}}}G_{{25}}^{{{\text{exc}}}} + \frac{{{{x}_{2}}{{x}_{6}}}}{{{{X}_{{2(25)}}}{{X}_{{6(26)}}}}}G_{{26}}^{{{\text{exc}}}} \\ = \frac{{{{x}_{2}}\left( {{{x}_{5}} + {{x}_{6}}} \right)}}{{{{X}_{{1(25)}}}{{X}_{{5(25)}}}}}G_{{25}}^{{{\text{exc}}}}. \\ \end{gathered} $$

((37))

For expressions of $\eta (ij,ik)$ in X₃₍₃₆₎ one can obtain:

$$\eta \left( {36,\,31} \right) = \eta \left( {35,\,31} \right),$$

((38))

$$\eta \left( {63,\,61} \right) = \eta \left( {53,\,51} \right),$$

((39))

$$\eta \left( {36,\,32} \right) = \eta \left( {35,\,32} \right),$$

((40))

$$\eta \left( {63,\,62} \right) = \eta \left( {53,\,52} \right),$$

((41))

$$\eta \left( {36,\,35} \right) = 0,$$

((42))

$$\eta \left( {53,\,56} \right) = \eta \left( {53,\,55} \right),$$

((43))

$$\eta \left( {62,\,65} \right) = \eta \left( {52,\,55} \right).$$

((44))

Substituting Eqs. from (38) to (44) into Eq. (5), we have the following:

$$\xi _{{3\left( {36} \right)}}^{{\left( 1 \right)}} = \xi _{{3\left( {35} \right)}}^{{\left( 1 \right)}},$$

((45))

$$\xi _{{3\left( {36} \right)}}^{{\left( 2 \right)}} = \xi _{{3\left( {35} \right)}}^{{\left( 2 \right)}},$$

((46))

$$\xi _{{3\left( {36} \right)}}^{{\left( 4 \right)}} = \xi _{{3\left( {35} \right)}}^{{\left( 4 \right)}},$$

((47))

$$\xi _{{3\left( {36} \right)}}^{{\left( 5 \right)}} = \xi _{{3\left( {35} \right)}}^{{\left( 6 \right)}} = 0.$$

((48))

According to these equations, it is:

$${{X}_{{{\text{3}}\left( {{\text{36}}} \right)}}} = {{X}_{{{\text{3}}\left( {{\text{35}}} \right)}}}.$$

((49))

Taking into account the Eqs. (45)–(49), arranging the coefficients of terms having $G_{{35}}^{{{\text{exc}}}}$ and $G_{{36}}^{{{\text{exc}}}}$ in Eq. (9), the terms in question are written as:

$$\begin{gathered} \frac{{{{x}_{3}}{{x}_{5}}}}{{{{X}_{{3(35)}}}X{}_{{5(35)}}}}G_{{35}}^{{{\text{exc}}}} + \frac{{{{x}_{3}}{{x}_{6}}}}{{{{X}_{{3(36)}}}{{X}_{{6(36)}}}}}G_{{36}}^{{{\text{exc}}}} \\ = \frac{{{{x}_{3}}\left( {{{x}_{5}} + {{x}_{6}}} \right)}}{{{{X}_{{3(35)}}}{{X}_{{5(35)}}}}}G_{{35}}^{{{\text{exc}}}}. \\ \end{gathered} $$

((50))

Similarly, for expressions of $\eta (ij,ik)$ in X₄₍₄₆₎ one can obtain:

$$\eta \left( {46,\,41} \right) = \eta \left( {45,\,41} \right),$$

((51))

$$\eta \left( {64,\,62} \right) = \eta \left( {54,\,52} \right),$$

((52))

$$\eta \left( {46,\,43} \right) = \eta \left( {45,\,43} \right),$$

((53))

$$\eta \left( {64,\,63} \right) = \eta \left( {54,\,53} \right),$$

((54))

$$\eta \left( {46,\,45} \right) = 0,$$

((55))

$$\eta \left( {64,\,65} \right) = \eta \left( {54,\,55} \right),$$

((56))

$$\eta \left( {46,\,45} \right) = \eta \left( {45,\,45} \right).$$

((57))

Substituting Eq. from (51) to (57) into Eq. (5), we have the following:

$$\xi _{{4\left( {46} \right)}}^{{\left( 1 \right)}} = \xi _{{4\left( {45} \right)}}^{{\left( 1 \right)}},$$

((58))

$$\xi _{{4\left( {46} \right)}}^{{\left( 2 \right)}} = \xi _{{4\left( {45} \right)}}^{{\left( 2 \right)}},$$

((59))

$$\xi _{{4\left( {46} \right)}}^{{\left( 3 \right)}} = \xi _{{4\left( {45} \right)}}^{{\left( 3 \right)}},$$

((60))

$$\xi _{{4\left( {46} \right)}}^{{\left( 6 \right)}} = \xi _{{4\left( {45} \right)}}^{{\left( 6 \right)}} = 0.$$

((61))

According to these equations, it is:

$${{X}_{{{\text{4}}({\text{46}})}}} = {{X}_{{{\text{4}}\left( {{\text{45}}} \right)}}}.$$

((62))

Taking into account the Eqs. (58)–(62), arranging the coefficients of terms having $G_{{45}}^{{{\text{exc}}}}$ and $G_{{46}}^{{{\text{exc}}}}$ in Eq. (9), the terms in question are written as:

$$\begin{gathered} \frac{{{{x}_{4}}{{x}_{5}}}}{{{{X}_{{4(45)}}}X{}_{{5(45)}}}}G_{{45}}^{{{\text{exc}}}} + \frac{{{{x}_{4}}{{x}_{6}}}}{{{{X}_{{4(46)}}}{{X}_{{6(46)}}}}}G_{{16}}^{{{\text{exc}}}} \\ = \frac{{{{x}_{4}}\left( {{{x}_{5}} + {{x}_{6}}} \right)}}{{{{X}_{{4(45)}}}{{X}_{{5(45)}}}}}G_{{45}}^{{{\text{exc}}}}. \\ \end{gathered} $$

((63))

So, substituting Eqs. (24), (37), (50), and (63) into Eq. (9) and considering G₁₅ = G₁₆, G₂₅ = G₂₆, G₃₅ = G₃₆, G₄₅ = G₄₆, thus, Eq. (9) becomes

$$\begin{gathered} {{G}^{{{\text{exc}}}}} = \frac{{{{x}_{1}}{{x}_{2}}}}{{{{X}_{{1(12)}}}X{}_{{2(12)}}}}G_{{12}}^{{{\text{exc}}}}{\text{ + }}\frac{{{{x}_{1}}{{x}_{3}}}}{{{{X}_{{1(13)}}}{{X}_{{3(13)}}}}}G_{{13}}^{{{\text{exc}}}} \\ + \,\,\frac{{{{x}_{1}}{{x}_{4}}}}{{{{X}_{{1(14)}}}{{X}_{{4(14)}}}}}G_{{14}}^{{{\text{exc}}}} + \frac{{{{x}_{1}}x_{5}^{{\text{l}}}}}{{{{X}_{{1(15)}}}X{}_{{5(15)}}}}G_{{15}}^{{{\text{exc}}}} \\ + \,\,\frac{{{{x}_{2}}{{x}_{3}}}}{{{{X}_{{2(23)}}}{{X}_{{3(23)}}}}}G_{{23}}^{{{\text{exc}}}} + \frac{{{{x}_{2}}{{x}_{4}}}}{{{{X}_{{2(24)}}}X{}_{{4(24)}}}}G_{{24}}^{{{\text{exc}}}} \\ + \,\,\frac{{{{x}_{2}}x_{5}^{l}}}{{{{X}_{{2(25)}}}{{X}_{{5(25)}}}}}G_{{25}}^{{{\text{exc}}}} + \frac{{{{x}_{3}}{{x}_{4}}}}{{{{X}_{{3(34)}}}X{}_{{4(34)}}}}G_{{34}}^{{{\text{exc}}}} \\ + \,\,\frac{{{{x}_{3}}x_{5}^{l}}}{{{{X}_{{3(35)}}}{{X}_{{5(35)}}}}}G_{{35}}^{{{\text{exc}}}} + \frac{{{{x}_{4}}x_{5}^{l}}}{{{{X}_{{4(45)}}}{{X}_{{5(45)}}}}}G_{{45}}^{{{\text{exc}}}}, \\ \end{gathered} $$

((64))

where $x_{5}^{l} = {{x}_{5}} + {{x}_{6}}.$ We also prove that this higher order model can be reduced to a lower order model if two components for example x₅ and x₆ in a multicomponent system are identical [10].

RESULTS AND DISCUSSION

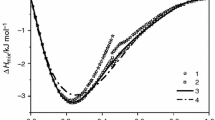
In order to discuss the application of GSM and practical applicability, experimental results of the excess Gibbs enthalpy of mixing associated with liquid Co_x–Sb_y–Sn_z ternary alloys are compared with GSM model, Muggianu, Kohler, and Toop models. The investigated cross-sections of ternary Co_x–Sb_y–Sn_z alloys (three sections are selected Sb_y/Sn_z = 1/3, Co_x/Sb_y = 1/5, and Co_x/Sn_z = 1/4 , see Fig. 1) used in this work are shown in Figs. 2–4. For this purpose, using the Eq. (6) via Eq. (7), similarity coefficients were calculated according to the procedure of the GSM and their values and deviation sum of squares were tabulated in Tables 1, 2. It is seen from Fig. 2 that the values quickly become more negative by adding Co as it was expected regarding the constituent binary Co-systems and are good in agreement the values obtained from all model treated in the present study. The measured excess Gibbs enthalpy of mixing becomes slightly more exothermic starting from the binary Co–Sn and passes a minimum of approx. –4500 J/mol at nearly 40 at % Sb and is good in agreement the values obtained from all model treated in the present study (Fig. 3). Comparing these experimental values [15] with those of the excess Gibbs enthalpy of mixing obtained by the geometric models in Co–Sb–Sn system at 1273 K, the best agreement was found for the data calculated by Kohler and GSM for section x_Sb/x_Sn = 1 : 3, while the higher differences were obtained in the case of the other two models. Whereas, Muggianu, Kohler and Toop, Kohler models were the most appropriate ones among the geometric models applied for sections x_Co/x_Sn = 1 : 4 and x_Co/x_Sb = 1 : 5, respectively (Table 3). The values of Redlich–Kister parameters are not calculated from the experimental binary excess energy functions, instead of this, the parameters are collected from the reliable studies on this topic in literature.

The similarity coefficients are given in Tables 2, 5 and 6 for the alloys Co–Sb–Sn, Ag–In–Pd–Sn and Ni–Cr–Co–Al–Mo–Ti–Cu, respectively. The similarity coefficients have been proposed in order to determine the asymmetric component in the multi component alloys. A thermodynamic criterion for identifying the symmetry of ternary systems from asymmetry can be explicitly proposed as follows. If the excess thermodynamic properties of the three sub binary systems are similar to each other, the ternary system is symmetric. Otherwise, if the deviations of the binary systems A–B and A–C from the ideal solution are similar but differ markedly from that of the binary system B–C, the A–B–C ternary system is an asymmetric one. In the asymmetric system, the common component A in two sub binary systems with thermodynamic similarity should be chosen as the thermodynamic asymmetric component. Therefore, the GSM including the similarity coefficients to the calculations gets rid of this problem. The GSM had no errors arising from symmetry and asymmetry properties.

Fig. 1.

Measured sections (A, B, C, D, E) and alloy compositions in the ternary Co–Sb–Sn system, the liquidus limit is marked by the dashed line. The investigated cross- sections for C, D and E are taken from [15].

The values of calculated similarity coefficients of the three binary systems Co–Sb, Co‒Sn, and Sb–Sn mentioned in the GSM are found as 0.30156, 0.893313, and 0.21701, respectively (Table 2). For the asymmetric model, i.e., Toop model, it is of vital importance to determine the asymmetric component i. However, none of the three similarity coefficients mentioned above is approximately equivalent to one. This case means that the asymmetric component in the ternary alloys is not easy to find. Here, = 0.893313, means that Co is relatively similar to Sb, indicating that we have no alternative option but to select Sn as the asymmetric component. According to the above mentioned analysis, an important conclusion can be made that the Co–Sb–Sn ternary alloy system is not exactly the symmetric system such as Muggianu, Kohler models or asymmetric such as Toop model. Therefore, is obvious that both the symmetric and asymmetric systems used in the present models cannot help obtain the accurate predicted values. So, in this work, the GSM should be included to the excess Gibbs energy calculations.

Fig. 2.

The excess Gibbs enthalpy H^exc of mixing of liquid Co–Sb–Sn alloys for all models along the section x_Sb/x_Sn = 1 : 3 at 1273 K. The experimental values are taken from [15].

Fig. 3.

The excess Gibbs enthalpy H^exc of mixing of liquid Co–Sb–Sn alloys for all models along the section x_Co/x_Sn = 1 : 4 at 1273 K. The experimental values are taken from [15].

Table 3.   Comparison among the calculated results of root mean square deviation corresponding to each geometric model for the selected ternary Co–Sb–Sn liquid alloy systems

Fig. 4.

The excess Gibbs enthalpy H^exc of mixing of liquid Co–Sb–Sn alloys for all models along the section x_Co/x_Sb = 1 : 5 at 1273 K. The experimental values are taken from [15].

Moreover, in this study, the excess Gibbs enthalpy of mixing in the liquid Ag–In–Pd–Sn quaternary alloys have been estimated at 1173 K along three compositions Ag₁₀–In₈₀–Pd–Sn₁₀, Ag₂₀–In₆₀–Pd–Sn₂₀ and Ag–In₄₀–Pd₂₀–Sn₄₀ with taking into account the consideration of the experimental data by dropping mole of Pd and Ag. Considering descriptions of the three binary subsystems (Tables 4), the excess Gibbs enthalpy of liquid Ag–In–Pd–Sn systems have been calculated at T = 1173 K by GSM model as well as by the three geometric models using Tables 5 and 6. The results of the calculations together with the experimental values [5] are given in Figs. 5–7. In order to analyze the model results, for the sake of simplicity, the root mean square deviation corresponding to experimental results are carried out, since a large number of points on the Figs. 5–7 result in overlapping of these points. Glancing at Table 7, it is seen that the results obtained by the Muggianu model show the best agreement with the experimental results.

Table 4. Binary interaction parameters dealing with the excess Gibbs enthalpy of mixing associated with Ag–In–Pd–Sn alloy system

Table 5.   Deviation sum of squares associated with Ag–In–Pd–Sn system at 1173 K

Table 6.   Similarity coefficients associated with Ag–In–Pd–Sn system at 1173 K

Fig. 5.

The excess Gibbs enthalpies H^exc of liquid Ag₁₀–In₈₀–Pd–Sn₁₀ alloys for all models at 1173 K. The experimental values are taken from [5].

Fig. 6.

The excess Gibbs enthalpies H^exc of liquid Ag₂₀–In₆₀–Pd–Sn₂₀ alloys for all models. The experimental values are taken from [5] at 1173 K.

Fig. 7.

The excess Gibbs enthalpies H^exc of liquid Ag–In₄₀–Pd₂₀–Sn₄₀ alloys for all models at 1173 K. The experimental values are taken from [5].

Table 7.   Comparison among the calculated results of root mean square deviation corresponding to each geometric model for the selected quaternary Ag–In–Pd–Sn liquid alloy systems

It is impossible now for multi-component alloys (of more than four components) to carry out experimental measurements due to not only technological difficulties but also the expenses and time consume. The method including the semi-empirical model that predicts ternary and multicomponent thermodynamic properties based on the binary ones is the most attractive approach with respect to their simple, effective, and employing more reliable binary sources experimentally and theoretically. All of these are basic requirements for a good model. Therefore, trying a calculation of Gibbs free energy associated with Ni–Cr–Co–Al–Mo–Ti–Cu seven-component alloys with some selected sections (any information concerning this has been reported in literature up to now using GSM model) is another goal in the present study. The indices of concentration 1, 2, 3, 4, 5, 6, and 7 have been used to denote Ni, Cr, Co, Al, Mo, Ti and Cu, respectively. Binary interaction parameters concerning the alloys Ni–Cr–Co–Al–Mo–Ti–Cu are given in Table 8. The similarity coefficients were calculated according to the procedure of the GSM and their values and deviation sum of squares were tabulated in Table 9 using total twenty-one Redlich–Kister parameters associated with binary systems given in Table 8. The correctness of these calculated similarity coefficients can be checked using the Eq. (65).

$$\begin{gathered} \left( {1 - \xi _{{7\left( {71} \right)}}^{{\left( 6 \right)}}} \right)\left( {1 - \xi _{{6\left( {67} \right)}}^{{\left( 1 \right)}}} \right)\left( {1 - \xi _{{1\left( {16} \right)}}^{{\left( 7 \right)}}} \right) \\ = 0.{\text{020007}} = \xi _{{7\left( {71} \right)}}^{{\left( 6 \right)}}\xi _{{6\left( {67} \right)}}^{{\left( 1 \right)}}\xi _{{1\left( {16} \right)}}^{{\left( 7 \right)}}, \\ \left( {1 - \xi _{{2\left( {24} \right)}}^{{\left( 1 \right)}}} \right)\left( {1 - \xi _{{4\left( {41} \right)}}^{{\left( 2 \right)}}} \right)\left( {1 - \xi _{{1\left( {12} \right)}}^{{\left( 4 \right)}}} \right) \\ = 0.{\text{085199}} = \xi _{{2\left( {24} \right)}}^{{\left( 1 \right)}}\xi _{{4\left( {41} \right)}}^{{\left( 2 \right)}}\xi _{{1\left( {12} \right)}}^{{\left( 4 \right)}}. \\ \end{gathered} $$

((65))

The values of similarity coefficients listed in Table 9, the simple relation between the selected binary compositions and the composition of the multicomponent system are calculated. A new model is established more realistic in computerization for estimating the excess Gibbs energies of liquid Ni–Cr–Co–Al–Mo–Ti–Cu alloys. Using these coefficients, it is possible to determine the phase diagrams of a multicomponent alloy system in question.

Table 8.   Binary interaction parameters dealing with the excess Gibbs energy of mixing associated with Ni–Cr–Co–Al–Mo–Ti–Cu alloy system at 2000 K

Table 9.   Deviation sum of squares η(ij, ik) and similarity coefficients ξ associated with Ni–Cr–Co–Al–Mo–Ti–Cu system at 2000 K

The excess Gibbs energy of mixing in the liquid phase is shown in Fig. 8. It is seen from Fig. 8 that values of the excess Gibbs energy of mixing of GSM model are in agreement with those of the Muggianu and Kohler which are symmetrical models.

Fig. 8.

The excess Gibbs energies H^exc of liquid Ni–Cr–Co–Al–Mo–Ti–Cu alloys for all models along the section x_Ni = x_Cu, x_Cr = x_Ti, x_Co = x_Ti, x_Al = x_Ti, x_Mo = rx_Ti, x_Ti = (1 – x_Cu)/(r + 5), and r = 0.1 at 2000 K as a function of Cu composition.

Recently, some papers related to GSM model, which are utilized at calculation stage of the excess Gibbs enthalpy of mixing via GSM, can be found in [16–18] and particularly some of studies dealing with the thermodynamic properties of the steel multi-component systems are appeared in literature [19–24].

CONCLUSIONS

GSM has been used for assessing the excess Gibbs enthalpy of mixing with three selected sections x_Sb/x_Sn = 1/3, x_Co/x_Sb = 1/5, and x_Co/x_Sn = 1/4, Ag₁₀–In₈₀–Pd–Sn₁₀, Ag₂₀–In₆₀–Pd–Sn₂₀, and Ag–In₄₀–Pd₂₀–Sn₄₀ quaternary alloys and the excess Gibbs energy of Ni–Cr–Co–Al–Mo–Ti–Cu with seven-component alloys with selected sections, x_Ni = x_Cu, x_Cr = x_Ti, x_Co = x_Ti, x_Al = x_Ti, x_Mo = rx_Ti, x_Ti = (1 – x_Cu)/(r + 5), and r = 0.1 at temperatures 1273, 1173, and 2000 K, respectively. Three traditional geometric models (Muggianu, Kohler, and Toop) are also included in calculations for comparison. Some important results are given as follows:

(1) The excess Gibbs enthalpy of liquid Co–Sb–Sn alloys for all models along the section x_Sb/x_Sn = 1 : 3 at 1273 K were decreasing as the compositions Co and Sb were increasing in the experimental interval. Whereas the calculated excess Gibbs enthalpy of mixing were also increasing as the composition Sn was increasing in the experimental interval. The best agreement was found for the data calculated by Kohler and GSM for section x_Sb/x_Sn = 1 : 3, while the higher differences were obtained in the case of the other two models. Whereas Muggianu, Kohler and Toop, and Kohler models were the most appropriate ones among the geometric models applied for sections x_Co/x_Sn = 1 : 4 and x_Co/x_Sb = 1 : 5, respectively.

(2) The excess Gibbs enthalpies of liquid Ag₁₀–In₈₀–Pd–Sn₁₀, Ag₂₀–In₆₀–Pd–Sn₂₀, and Ag–In₄₀–Pd₂₀–Sn₄₀ systems for all models at 1173 K were decreasing as the composition Pd was increasing in the experimental interval. Whereas the calculated excess Gibbs enthalpy of mixing is also increasing as the content of Ag increases in the experimental interval. Moreover, it is found from an assessment of the root mean square deviation that the results obtained by the Muggianu model show the best agreement with the experimental results.

(3) It is determined that the excess Gibbs energy values obtained from GSM model related with liquid Ni–Cr–Co–Al–Mo–Ti–Cu alloys for all model along the section x_Ni = x_Cu, x_Cr = x_Ti, x_Co = x_Ti, x_Al = x_Ti, x_Mo = rx_Ti, x_Ti = (1 – x_Cu)/(r + 5), and r = 0.1 at 2000 K were in agreement with those of the Muggianu and Kohler which were symmetrical models. Moreover, it was proved successfully in the present study that the higher order model can be reduced to a lower order model if two components for example x₅ and x₆ in a multicomponent system are identical.