INTRODUCTION

A description of the polarization spectrum of a two-level atomic system in polychromatic fields was obtained in [1] as the result of an analytical solution of the density matrix equations in the rotating wave approximation. However, the resulting solution is poorly suited for direct calculation of the polarization spectrum, because it involves the summation of values determined using a grid of points in space, the dimension of which is proportional to the number of components of the driving field. As a result, when the number of field components is more than a dozen, calculations turn out to be challenging to implement.

In order to calculate the polarization spectra for a more significant number of components of the driving field, we considered [2] the decomposition [3] of the solution obtained in [1] in the small-amplitude limit. In the first linear approximation, the well-known Lorentzian contour appears in the polarization spectrum [4]. The quadratic correction, as are other even-order corrections, is absent in the asymptotic expansion in powers of amplitude due to the symmetry of the spectrum of the driving field with respect to the transition frequency. The third-order correction, also obtained in [2], helps to describe nonlinear effects and intermode interaction. However, the third-order correction allows one to describe the polarization spectrum correctly only in a limited range of small amplitudes of the driving field. In order to expand the boundaries of the range to the region of large amplitudes, it is necessary to consider corrections of a higher order, for example, the fifth, seventh, etc. orders.

This paper presents the decomposition for the polarization spectrum (both real and imaginary parts) of a two-level atomic system in polychromatic fields in the small-amplitude limit. This expansion is a generalization of the results obtained in [2] to the case of an arbitrary order of expansion in powers of amplitudes.

The polarization spectra calculated using asymptotic expansions of different orders were compared with similar spectra obtained by numerical methods [5, 6]. A comparison was also made with the results of calculations of the component of the population difference at the transition frequency given in [7].

DECOMPOSITION IN THE SMALL-AMPLITUDE LIMIT

Under the condition of equality of the constants of the longitudinal and transverse relaxations, the interaction of a two-level medium with a polychromatic field symmetric with respect to the transition frequency ω21,

$$E(t) = \left( {{{E}_{0}} + 2\sum\limits_{k = 1}^K \,{{E}_{k}}\cos(k\Delta t)} \right)\cos{{\omega }_{{21}}}t,$$

in the approximation of a rotating wave and a fixed atom, is described by the density matrix equation

$$\frac{{d\rho }}{{dt}} = - i[V(t),\rho ] - \gamma \rho + \left( {\begin{array}{*{20}{c}} {{{\lambda }_{1}}}&0 \\ 0&{{{\lambda }_{2}}} \end{array}} \right),$$
((1))

where Ek are the amplitudes of the field k component, and the only nondiagonal element of the interaction matrix V12 = V21 is

$${{V}_{{12}}} = \frac{{{{\Omega }_{0}}}}{2} + \sum\limits_{k = 1}^K \,{{\Omega }_{k}}\cos(k\Delta t).$$
((2))

The values \({{\Omega }_{k}} = {{d}_{{21}}}{{E}_{k}}{\text{/}}\hbar \), k = 0, …, K, are determined by the amplitudes of the equidistant driving field; d21 is the dipole moment of the transition; Δ is the intermode distance; γ is the relaxation constant, and λ12 = λ1 – λ2 is the difference between the pump levels. Polarization P(t) is proportional to the nondiagonal element of the density matrix \({{\rho }_{{12}}} = \rho _{{21}}^{{\text{*}}}\) and the dipole moment of the transition.

In [1], expressions for the polarization spectrum of a two-level atomic system in a polychromatic field are given; that is,

$${\text{Re}}{{(P)}_{j}} = \frac{{{{\lambda }_{{12}}}{{d}_{{21}}}}}{4}\sum\limits_{\mathbf{n}} \,\sum\limits_{\mathbf{l}} \,R({\mathbf{n}},{\mathbf{l}})(\delta _{j}^{{F({\mathbf{n}},{\mathbf{l}})}} - \delta _{j}^{{ - F({\mathbf{n}},{\mathbf{l}})}}),$$
((3))
$${\text{Im}}{{(P)}_{j}} = - \frac{{{{\lambda }_{{12}}}{{d}_{{21}}}}}{4}\sum\limits_{\mathbf{n}} \,\sum\limits_{\mathbf{l}} \,I({\mathbf{n}},{\mathbf{l}})(\delta _{j}^{{F({\mathbf{n}},{\mathbf{l}})}} + \delta _{j}^{{ - F({\mathbf{n}},{\mathbf{l}})}}),$$
((4))

where the summation is carried out over two multi-indices of length K: n = \(\{ {{n}_{1}},{{n}_{2}}, \ldots ,{{n}_{K}}\} \) and l = {l1, l2, ..., lK}. The expressions dependent on the multi-indices are

$$R({\mathbf{n}},{\mathbf{l}}) = \frac{\gamma }{{{{\gamma }^{2}} + f{{{({\mathbf{n}})}}^{2}}}}\prod\limits_{k = 1}^K \,{{J}_{{{{n}_{k}}}}}\left( { - \frac{{2{{\Omega }_{k}}}}{{k\Delta }}} \right){{J}_{{{{l}_{k}}}}}\left( {\frac{{2{{\Omega }_{k}}}}{{k\Delta }}} \right),$$
$$I({\mathbf{n}},{\mathbf{l}}) = \frac{{f({\mathbf{n}})}}{{{{\gamma }^{2}} + f{{{({\mathbf{n}})}}^{2}}}}\prod\limits_{k = 1}^K \,{{J}_{{{{n}_{k}}}}}\left( { - \frac{{2{{\Omega }_{k}}}}{{k\Delta }}} \right){{J}_{{{{l}_{k}}}}}\left( {\frac{{2{{\Omega }_{k}}}}{{k\Delta }}} \right),$$
$$f({\mathbf{n}}) = {{\Omega }_{0}} - \sum\limits_{k = 1}^K \,k{{n}_{k}}\Delta ,$$

\(\delta \) is the Kronecker symbol, and expressions F determining at which frequency the corresponding multi-index contributes are

$$F({\mathbf{n}},{\mathbf{l}}) = \sum\limits_{k = 1}^K \,k({{n}_{k}} + {{l}_{k}}).$$

The dimension of the space in which the summation is performed in Eqs. (3) and (4), that is, the total length of multi-indices n and l, is 2K. Therefore, the calculation of the spectra using Eqs. (3) and (4) directly becomes impracticable with a large number of harmonics of the driving field. To solve this problem, we proposed in [2] to perform an asymptotic expansion [3] in powers of the amplitudes of the field components in the limit of \({{\Omega }_{k}} \to 0\), \(k = 0, \ldots ,K\); that is,

$$\begin{array}{*{20}{c}} {\operatorname{Re} {{{(P)}}_{j}} = \frac{{{{\lambda }_{{12}}}{{d}_{{21}}}}}{4}(\operatorname{Re} P_{j}^{{(1)}} + \operatorname{Re} P_{j}^{{(3)}} + \operatorname{Re} P_{j}^{{(5)}} + \ldots ),} \\ {\operatorname{Im} {{{(P)}}_{j}} = - \frac{{{{\lambda }_{{12}}}{{d}_{{21}}}}}{4}(\operatorname{Im} P_{j}^{{(1)}} + \operatorname{Im} P_{j}^{{(3)}} + \operatorname{Im} P_{j}^{{(5)}} + \ldots ),} \end{array}$$
((5))

where \(\operatorname{Re} P_{j}^{{(N)}} = \underline O ({{\Omega }^{N}})\) and \(\operatorname{Im} P_{j}^{{(N)}} = \underline O ({{\Omega }^{N}})\) are the corrections of the Nth order of smallness in the limit of small amplitudes; N = 1, 3, 5, …. Even-order corrections in expansions (5) are absent due to the symmetry of the spectrum of the driving field (Eq. (2)) with respect to the transition frequency. Odd corrections \(\operatorname{Re} P_{j}^{{(N)}}\) and \(\operatorname{Im} P_{j}^{{(N)}}\) are linear combinations of products of nonnegative degrees of amplitudes of various components of a polychromatic field; the sum of the exponents is N. The field amplitudes are not necessarily equal to each other, but have the same order of smallness \({{\Omega }_{k}} = \underline O (\Omega )\), \(k = 0,1, \ldots ,K\). It follows that the specified linear combination of products really has order N in smallness parameter Ω.

Generalizing the results of [2] to the case of an asymptotic expansion of an arbitrary length, we have for the correction of the Nth order to the imaginary part of the polarization

$$\begin{gathered} \operatorname{Im} P_{j}^{{(N)}} = \sum\limits_{n = 0}^N \,\sum\limits_{{{k}^{{(n)}}}} \,\frac{{\Omega _{0}^{{N - n}}{{\Omega }_{{k_{1}^{{(n)}}}}} \ldots {{\Omega }_{{k_{n}^{{(n)}}}}}}}{{n!k_{1}^{{(n)}}k_{2}^{{(n)}} \ldots k_{n}^{{(n)}}{{\Delta }^{n}}}} \\ \times \;\sum\limits_{\nu = 0}^n \,\frac{{{{{( - 1)}}^{{n - \nu }}}\left( \begin{gathered} n \\ \nu \\ \end{gathered} \right)a_{\nu }^{{(N + 1 - n)}}}}{{\mathop {\left( {{{\gamma }^{2}} + {{{\left( {\Delta \sum\limits_{l = 1}^\nu {k_{l}^{{(n)}}} } \right)}}^{2}}} \right)}\nolimits^{N + 1 - n} }} \\ \times \;(\delta _{j}^{{k_{1}^{{(n)}} + \ldots + k_{n}^{{(n)}}}} + \delta _{j}^{{ - k_{1}^{{(n)}} - \ldots - k_{n}^{{(n)}}}}), \\ \end{gathered} $$
((6))

where summation over multi-index \({{{\mathbf{k}}}^{{(n)}}} = \{ k_{1}^{{(n)}},...,k_{n}^{{(n)}}\} \) is carried out in n-dimensional space, with each of the indices \(k_{l}^{{(n)}}\), \(l = 1, \ldots ,n\), varying from –K to K, excluding the value 0. Coefficients \(a_{\nu }^{{(l)}}\), \(\nu = 0, \ldots ,n\), \(l = 1\), ..., N + 1 appearing in Eq. (6) are polynomials of degrees l from γ and Δ; that is,

$$a_{\nu }^{{(1)}} = \Delta \sum\limits_{l = 1}^\nu \,k_{l}^{{(n)}},$$
$$a_{\nu }^{{(2)}} = {{\gamma }^{2}} - {{(a_{\nu }^{{(1)}})}^{2}},$$
$$a_{\nu }^{{(3)}} = ( - 3{{\gamma }^{2}} + {{(a_{\nu }^{{(1)}})}^{2}})a_{\nu }^{{(1)}},$$
$$a_{\nu }^{{(4)}} = - {{\gamma }^{4}} + 6{{\gamma }^{2}}{{(a_{\nu }^{{(1)}})}^{2}} - {{(a_{\nu }^{{(1)}})}^{4}},$$
$$a_{\nu }^{{(5)}} = (5{{\gamma }^{4}} - 10{{\gamma }^{2}}{{(a_{\nu }^{{(1)}})}^{2}} + {{(a_{\nu }^{{(1)}})}^{4}}){\kern 1pt} a_{\nu }^{{(1)}}.$$

Note that \(a_{0}^{{(l)}} = {{( - 1)}^{{l/2 + 1}}}{{\gamma }^{l}}\) for even l, while it becomes 0 for odd l.

The structure of Eq. (6) indicates the presence of the intermode interaction. The numerator contains the product of the amplitudes of the components of the driving field. Thus, each term under the sign of summation over multi-index k(n) corresponds to some combination of N interacting components. In the first approximation (N = 1), intermode interaction is absent; in the third approximation, the interaction of three modes is described; in the next, the fifth, approximation, five modes are described; etc. The multiplier, which is the product of amplitudes, determines the interaction force of the considered components. This factor is the sum of n + 1 terms with the denominators of the Lorentzian type with a different characteristic ratio of constant relaxation and intermode distance. The frequency at which the result of the interaction is observed is a combination of the frequencies of the interacting components, which is described by the last factor with two Kronecker symbols inside.

An expression similar to Eq. (6) can also be obtained for the Nth correction in the limit of small amplitudes in the asymptotic expansion of the real part of polarization; that is,

$$\begin{gathered} \operatorname{Re} P_{j}^{{(N)}} = \sum\limits_{n = 0}^N \,\sum\limits_{{{k}^{{(n)}}}} \,\frac{{\Omega _{0}^{{N - n}}{{\Omega }_{{k_{1}^{{(n)}}}}} \ldots {{\Omega }_{{k_{n}^{{(n)}}}}}\gamma }}{{n!k_{1}^{{(n)}}k_{2}^{{(n)}} \ldots k_{n}^{{(n)}}{{\Delta }^{n}}}} \\ \times \;\sum\limits_{\nu = 0}^n \,\frac{{{{{( - 1)}}^{{n - \nu }}}\left( \begin{gathered} n \\ \nu \\ \end{gathered} \right)a_{\nu }^{{(N + 1 - n)}}}}{{{{{\left( {{{\gamma }^{2}} + {{{\left( {\Delta \sum\limits_{l = 1}^\nu {k_{l}^{{(n)}}} } \right)}}^{2}}} \right)}}^{{N + 1 - n}}}}} \\ \times \;(\delta _{j}^{{k_{1}^{{(n)}} + \ldots + k_{n}^{{(n)}}}} - \delta _{j}^{{ - k_{1}^{{(n)}} - \ldots - k_{n}^{{(n)}}}}). \\ \end{gathered} $$
((7))

The terms in the asymptotic expansion of the real part of the polarization differ from those in the expansion of the imaginary part by the presence of factor γ in the numerator; polynomial coefficients \(b_{\nu }^{{(l)}}\) present in Eq. (7) have a degree of l – 1 rather than l, like in Eq. (6),

$$b_{\nu }^{{(1)}} = - 1,$$
$$b_{\nu }^{{(2)}} = 2a_{\nu }^{{(1)}},$$
$$b_{\nu }^{{(3)}} = {{\gamma }^{2}} - 3{{(a_{\nu }^{{(1)}})}^{2}},$$
$$b_{\nu }^{{(4)}} = ( - 4{{\gamma }^{2}} + 4{{(a_{\nu }^{{(1)}})}^{2}})a_{\nu }^{{(1)}},$$
$$b_{\nu }^{{(5)}} = - {{\gamma }^{4}} + 10{{\gamma }^{2}}{{(a_{\nu }^{{(1)}})}^{2}} - 5{{(a_{\nu }^{{(1)}})}^{4}}.$$

In the first linear approximation (N = 1), the term with n = 0 in Eq. (7) is zero, because \(b_{0}^{{(2)}} = 0\). In the term with n = 1, internal summation is performed by only one index, \(k \equiv k_{1}^{{(1)}}\), yielding

$$\operatorname{Re} P_{j}^{{(1)}} = \sum\limits_{\begin{array}{*{20}{c}} {k = - K} \\ {k \ne 0} \end{array}}^K \,\frac{{{{\Omega }_{k}}\gamma }}{{k\Delta }}\left( { - \frac{{b_{0}^{{(1)}}}}{{{{\gamma }^{2}}}} + \frac{{b_{1}^{{(1)}}}}{{{{\gamma }^{2}} + {{\Delta }^{2}}{{k}^{2}}}}} \right)(\delta _{j}^{k} - \delta _{j}^{{ - k}})$$
$$ = \sum\limits_{\begin{array}{*{20}{c}} {k = - K} \\ {k \ne 0} \end{array}}^K \,\frac{{{{\Omega }_{k}}\Delta k}}{{\gamma ({{\gamma }^{2}} + {{\Delta }^{2}}{{k}^{2}})}}(\delta _{j}^{k} - \delta _{j}^{{ - k}})$$
$$ = \left\{ \begin{gathered} \frac{{2{{\Omega }_{j}}\Delta j}}{{\gamma ({{\gamma }^{2}} + {{\Delta }^{2}}{{j}^{2}})}},\quad \left| j \right| \leqslant K, \hfill \\ 0,\quad \left| j \right| > K. \hfill \\ \end{gathered} \right.$$

In the imaginary part of the polarization, in the first approximation, the term with n = 0 is nonzero, but the term with n = 1 and \(\nu = 0\) vanishes,

$$\operatorname{Im} P_{j}^{{(1)}} = \frac{{{{\Omega }_{0}}a_{0}^{{(2)}}}}{{{{\gamma }^{2}}}}2\delta _{j}^{0} + \sum\limits_{\begin{array}{*{20}{c}} {k = - K} \\ {k \ne 0} \end{array}}^K \,\frac{{{{\Omega }_{k}}}}{{k\Delta }}\frac{{a_{1}^{{(1)}}}}{{{{\gamma }^{2}} + {{\Delta }^{2}}{{k}^{2}}}}(\delta _{j}^{k} + \delta _{j}^{{ - k}})$$
$$ = \left\{ \begin{gathered} \frac{{2{{\Omega }_{j}}}}{{{{\gamma }^{2}} + {{\Delta }^{2}}{{j}^{2}}}},\quad \left| j \right| \leqslant K, \hfill \\ 0,\quad \left| j \right| > K. \hfill \\ \end{gathered} \right.$$

Thus, in the first approximation, the Lorentzian circuit appears in the polarization spectrum, bounded by a set of frequencies of the driving field.

In the third approximation, we obtain the formulas presented in [2] from Eqs. (6) and (7) at N = 3.

CALCULATION RESULTS OF POLARIZATION SPECTRUM

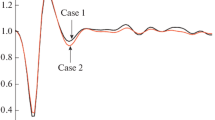
The results of calculations of the absorption and dispersion spectra performed using Eqs. (6) and (7) are shown in Figs. 1 and 2. Expansion (5) involves from one (linear approximation by Ω) to three (the fifth-order correction by Ω) terms. The polychromatic driving field consists of 101 equidistant components (K = 50), the amplitudes of which are Ω0 = Ω1 = ... = \({{\Omega }_{K}} = 0.1\gamma \); the distance between the components is Δ  = 0.3γ. The horizontal axis shows the component numbers; the transition frequency corresponds to the frequency of the component with index  j = 0.

Fig. 1.
figure 1

Spectrum of the imaginary part of polarization at Ω0 = …= ΩK = 0.1γ; K = 50; Δ = 0.3γ.

Full size image
Fig. 2.
figure 2

Spectrum of the real part of polarization at Ω0 = …= ΩK = 0.1γ; K = 50; Δ = 0.3γ.

Full size image

The solid curves in Figs. 1 and 2 show the results obtained numerically by directly solving density matrix equation (1) using the Runge–Kutta method followed by the Fourier transform of the obtained time dependence and by decomposing the solution in a harmonic basis, that is, by a method that is often described in publications as the “Floquet method” [8]. The accuracy of the numerical solution is rather high, which is confirmed by the difference in the results obtained by two completely different methods, which is less than 0.1%.

At a given value of the amplitude of the driving field of Ω = 0.1γ (Figs. 1, 2), the first, linear approximation gives a clearly unsatisfactory description of the polarization spectra. Namely, the value of the central, at the transition frequency pulse in the spectrum of the imaginary part turns out to be approximately twice as large as the value obtained numerically. Side pulses at the frequencies determined by the boundaries of the spectrum of the driving field are entirely absent in the first approximation.

A third-order approximation in amplitude gives a qualitatively correct description of the polarization spectrum, but quantitative estimates are not accurate enough. Thus, the amplitude of the central pulse of the imaginary part of the spectrum is underestimated by approximately 30%, while the amplitude of the side pulses is, on the contrary, overestimated by a third. The fifth-order correction gives a much more accurate description of the spectrum at Ω = 0.1γ with respect to the third-order correction: the values of the central and side pulses differ from the results of the numerical calculation by 3 and 5%, respectively.

To check the accuracy of the calculations, the result was compared with the dependences of the component of the difference between the level populations at the transition frequency and the amplitude of the polychromatic field obtained in [7]. For this purpose, the relation between polarization and population difference,

$$\left( {\frac{d}{{dt}} + \gamma } \right)P = i{{d}_{{21}}}{{V}_{{12}}}({{\rho }_{{11}}} - {{\rho }_{{22}}}),$$
((8))

resulting from equations of the density matrix (1), was used. Relation (8) written in the harmonic basis makes it possible to obtain the spectrum of the population difference from the polarization spectrum by inverting the Toeplitz ribbon matrix [9]. For comparison with the data of [7], we are only interested in the component of the spectrum with index 0, that is, at the transition frequency.

Figure 3 shows the dependence of the component of the difference in level populations \({\text{(}}{{\rho }_{{22}}} - {{\rho }_{{11}}}{\text{)/2}}\) at the transition frequency on the amplitude of the polychromatic driving field. The amplitudes of each of the 21 field components (K = 10) are the same; the distance between the components is Δ = 0.3γ. In the initial approximation, in which only one term of asymptotic series (5) is taken into account, the population difference is constant and does not depend on the amplitude of the driving field. In subsequent approximations, if the amplitudes of all field components are the same, the dependence of the components of the spectrum of the population difference on amplitude is an even-degree polynomial: second, fourth, etc. With an increase in the order of approximation, the amplitude range increases in which the asymptotic expansion gives an acceptable description of the population difference. If we assume that the deviation of the difference between the populations of levels at the transition frequency by 1% from the actual difference is admissible, then the first approximation leads to the correct value for Ω \( \lesssim \) 0.03γ; the third approximation, for Ω \( \lesssim \) 0.08γ; and the fifth approximation, for Ω \( \lesssim \) 0.12γ.

Fig. 3.
figure 3

Component of the population difference at the transition frequency depending on Ω; Ω = Ω0 = …= ΩK = 0.1γ; K = 10; Δ = 0.3γ.

Full size image

CONCLUSIONS

A method for calculating the polarization spectra in the range of small amplitudes of the driving field has been proposed. Compared to numerical calculation methods, the asymptotic expansion offers an analytical estimation of the contribution of each individual component of a polychromatic field and a description of the intermode interaction. However, with an increase in the intensity of the driving field, the computational efficiency of the method decreases, since, to achieve the required accuracy, it is necessary to increase the order of the asymptotic expansion.

This approach can be generalized to the case of systems with a large number of levels.