1 INTRODUCTION

The problem of evolution of light pulses in waveguides is currently the subject of thorough experimental and theoretical studies. It is well known that the solution to this problem in the approximation describing the dynamics of the electric-field envelope of the light-pulse without taking into account medium dispersion leads to wave breaking after it propagates a finite length in an optical waveguide. The derivatives of the pulse envelope with respect to either coordinate or time become infinite at the breaking point, while formal solution to the equations in the dispersionless approximation becomes multi-valued and loses its physical meaning beyond the breaking point. Taking dispersion into account eliminates such an unphysical behavior. However, this leads to the appearance of higher-order derivatives in the evolution equations for the envelopes, which greatly complicates their analytical interpretation. Nevertheless, numerical simulations reveal the following qualitative picture of the phenomenon. After wave breaking, instead of the multi-valuedness region, there appears a widening region of fast nonlinear oscillations in which parameters of the envelope change slowly relative to the characteristic oscillation frequency and their wavelength. This region of fast oscillations was referred to as the dispersive shock wave (DSW). Such structures were observed in nonlinear optics a long time ago [1, 2]. However, even before that, similar phenomena have been studied in the dynamics of waves on water surface [3] and in plasma physics [4]. R.Z. Sagdeev explained the general nature of these phenomena as being the result of combined action of nonlinear and dispersive effects in the presence of low viscosity, which makes DSWs stationary wave structures [5]. The general approach to theoretical description of DSWs when dissipative effects can be neglected was formulated by A.V. Gurevich and L.P. Pitaevskii [6] based on the Whitham theory of modulation of nonlinear waves [7, 8]. In this approximation, DSWs are presented in the form of evolving modulated nonlinear wave that represents periodic solution to the nonlinear wave equation under consideration in the form of a travelling wave. The theory and experimental studies of DSWs have experienced extensive development, expanding into other areas of nonlinear physics, including the dynamics of nonlinear waves in a Bose–Einstein condensate (see review [9] and references therein). In particular, the theory of DSWs applied to the nonlinear Schrödinger equation (NSE) for media exhibiting normal dispersion and Kerr nonlinearity [10, 11] is in excellent agreement with experimental studies of evolution of specially formed rectangular pulses in optical waveguides [12].

Although the theory of the NSE is one of the main approaches to description of waves in nonlinear optics and usually provides a good qualitative explanation of the main features of the phenomenon, it frequently turns out to be insufficient for quantitative interpretation of the appearing DSWs. Sometimes, even small corrections to the NSE taking into account small additional effects lead to radical deviations from predictions of the NSE when evolution continues for a sufficiently long time. However, exceeding the limits of the NSE creates considerable difficulties for the theory due to the fact that the NSE belongs to a special class of so-called “completely integrable equations,” which was demonstrated in [13], and falling outside the scope of this class makes the method of inverse scattering problem used in the NSE theory inapplicable. For example, optical shock waves were observed in high-intensity light beams propagating in photorefractive crystals exhibiting defocusing nonlinearity [14] with saturation, in which case the relative role played by the nonlinearity decreases with increase in the wave intensity. This situation is not taken into account by the NSE theory. In this case, the modulation Whitham equations turn out to be too complicated for their full-scale analytical interpretation. However, for a particular case of the initial condition in the form of an intensity jump, the method developed in [15] yields the main characteristics of the DSW [16]. A similar theory can be developed for optical DSWs in colloidal media [17]. A more general shape of the initial pulses can be analyzed by using the method recently developed in [18].

A change in the form of the nonlinearity can lead not only to quantitative deviations from the NSE theory, but also to qualitatively new effects. For example, a delay in the nonlinear response of the medium to the field of the wave transforms the NSE into the so-called “derivative nonlinear Schrödinger equation” containing, in addition to the Kerr nonlinearity, its time derivative. Such a modification of the NSE radically changes the DSW theory, enabling the appearance of new wave structures of combined type combining, e.g., the region of oscillations with the rarefaction waves, along with other wave configurations [19].

Small perturbations of the dissipative type result in qualitatively new effects. Over long time, they become comparable with small modulation of the wave packet, which can lead to DSW stabilization so that it acquires a stationary profile. It is this phenomenon that we are dealing with when taking into account the Raman effect under propagation of light pulses in an optical waveguide. It has been noted in [20] that, in the low-amplitude approximation, the NSE with an additional Raman term can be reduced to the Korteweg–de Vries–Burgers equation (KdV–B) for which the presence of the stationary DSWs was established in [21] by straightforward perturbation calculation and in [22, 23] by using the Whitham method (see also [24]). However, taking into account perturbation terms of this type in the NSE theory is substantially more complex [25, 26] and requires separate analysis. The present work aims at investigation of the influence of the Raman effect caused by delayed nonlinear response of the system on the dynamics of light pulses propagating in a single-mode optical fiber. First, in Section 3, we analyze how this effect influences the dynamics of linear waves propagating in the presence of a uniform background. Since some qualitative features of the behavior of the light-pulse envelope in a fiber can be analyzed using the low-amplitude limit of the evolution equations, we will calculate the main dispersive and nonlinear corrections to the dispersionless linear propagation of perturbations in Section 4. After that, we will proceed by description of several stages of DSW development after wave-pulse breaking. We will demonstrate that the Raman effect can be neglected at the first stage when the propagation length of the pulse along the fiber is relatively short. In this case, the system can be described by an ordinary NSE with Kerr nonlinearity the Whitham solution to which for some typical cases is well known. At the next stage, the Raman effect comes into play, and evolution of the DSW is described by the perturbed Whitham equations that will be derived in Section 5 within the framework of the theory developed in [25]. We will demonstrate that this effect influences the waves propagating in different directions differently. Finally, we will demonstrate that the shock wave propagating in the positive direction of the time axis \(t\) acquires a stationary character, while parameters of the DSW propagating in the opposite direction continue evolving with increase in the DSW amplitude and duration of the wave structure. The analytical results obtained in the present work are corroborated by numerical simulations.

2 BASIC EQUATIONS

Our analysis is based on a standard approach developed in [27] in which the dynamics of the envelope of the light-wave’s electric field \(E(x,t)\) is described by the NSE taking into account normal dispersion and defocusing Kerr nonlinearity, while damping is neglected:

$$\frac{{\partial E}}{{\partial X}} + {{\beta }_{1}}\frac{{\partial E}}{{\partial T}} + \frac{i}{2}{{\beta }_{2}}\frac{{{{\partial }^{2}}E}}{{\partial {{T}^{2}}}} - i\tilde {\gamma }{{\left| E \right|}^{2}}E = 0,$$
((1))

where \(X\) is the coordinate along the waveguide, \(T\) is time, \({{\beta }_{1}}\) is the reciprocal of the wave’s group velocity (\({{{v}}_{{gr}}}\) = \({\text{1/}}{{\beta }_{1}}\)), \({{\beta }_{2}}\) is the parameter determining pulse broadening, and \(\tilde {\gamma }\) is the nonlinear coefficient determined by the expression

$$\tilde {\gamma } = \frac{{{{n}_{2}}{{\omega }_{0}}}}{{{{c}_{l}}{{E}_{{{\text{eff}}}}}}},\quad {{E}_{{{\text{eff}}}}} = \pi {{w}^{2}}$$

for carrier frequency \({{\omega }_{0}}\). Here, \(w\) is the parameter of the Gaussian mode, \({{n}_{2}}\) is the refractive index, and \({{c}_{l}}\) is the speed of light in a vacuum. Hence, the second term in the evolution equation (1) describes propagation of the wave with group velocity, while the last term corresponds to Kerr nonlinearity. The term with coefficient \({{\beta }_{2}} > 0\) corresponds to quadratic dispersion. By using the substitution

$$x = - \tilde {\gamma }{{I}_{0}}X,\quad t = \sqrt {\frac{{\tilde {\gamma }{{I}_{0}}}}{{{{\beta }_{2}}}}} (T - {{\beta }_{1}}X),\quad q = \frac{E}{{\sqrt {{{I}_{0}}} }},$$

where \({{I}_{0}}\) is the characteristic intensity of the system, Eq. (1) can be reduced to a common dimensionless form

$$i{{q}_{x}} + \frac{1}{2}{{q}_{{tt}}} - {{\left| q \right|}^{2}}q = 0.$$
((2))

It was noted in the Introduction that small effects, such as higher-order dispersion, self-steepening, and the Raman effect, that are not taken into account in the NSE approximation can substantially influence propagation of pulses along sufficiently long fibers. The influence of self-steepening on DSW evolution was analyzed in detail in [19], where it was shown that it leads to formation of complex combination structures. In turn, the Raman effect describes frequency mixing of the stimulated Raman self-scattering. Taking it into account results in the appearance of an additional term in the evolution equation, so that the equation governing the envelope of the light pulse in dimensionless variables takes the form

$$i{{q}_{x}} + \frac{1}{2}{{q}_{{tt}}} - {{\left| q \right|}^{2}}q + \gamma q{{({{\left| q \right|}^{2}})}_{t}} = 0.$$
((3))

Constant \(\gamma \) that characterizes the tilt of the SRS gain curve is usually a small parameter of the system, which enables considering the last term in the equation as a perturbation when describing the DSW within the framework of the Whitham theory. It should be noted that the self-steepening and the Raman effect are of different character. Therefore, the influence of each of them on the system can be studied separately.

Let us begin our investigation of the influence of the Raman term by analyzing its effect on linear waves propagating in the presence of a uniform background.

3 LINEAR WAVES

Suppose that a light pulse propagates in the presence of a uniform wave background with an amplitude of \(\sqrt {{{I}_{0}}} \) = \(\left| {{{q}_{0}}} \right|\) = const. To find the role played by the Raman term, let us find the solution to the linearized NSE with a Raman term for a pulse in the linear approximation. In this case, it is convenient to transform to variable \(\tilde {q}\) determined by substitution \(q(x,t)\) = \(\tilde {q}(x,t)\exp( - i{{I}_{0}}x)\). Equation (3) takes the form

$$i\mathop {\tilde {q}}\nolimits_x + \frac{1}{2}\mathop {\tilde {q}}\nolimits_{tt} + ({{I}_{0}} - {{\left| {\tilde {q}} \right|}^{2}})\tilde {q} + \gamma \tilde {q}{{({{\left| {\tilde {q}} \right|}^{2}})}_{t}} = 0.$$
((4))

Such a substitution does not change the properties of the equation, because the wave phase is determined to within a constant factor. The evolution of small perturbation \(\delta q\) in the presence of a uniform background,

$$\tilde {q} = \sqrt {{{I}_{0}}} + \delta q,\quad \left| {\delta q} \right| \ll \sqrt {{{I}_{0}}} ,$$
((5))

can be described by the linearized equation

$$i\delta {{q}_{x}} + \frac{1}{2}\delta {{q}_{{tt}}} - {{I}_{0}}(\delta q + \delta q{\text{*}}) + \gamma {{I}_{0}}{{(\delta q + \delta q{\text{*}})}_{t}} = 0$$
((6))

with the initial condition \({{\left. {\delta q} \right|}_{{x = 0}}} = \delta {{q}_{0}}(t)\). Separating the real and imaginary parts,

$$\delta q = A + iB,$$
((7))

from (6), we have

$${{A}_{x}} + \frac{1}{2}{{B}_{{tt}}} = 0,\quad {{B}_{x}} - \frac{1}{2}{{A}_{{tt}}} + 2{{I}_{0}}A - 2\gamma {{I}_{0}}{{A}_{t}} = 0.$$
((8))

Function \(B\) can be excluded, and the latter system yields a linear equation for determining \(A\):

$${{A}_{{xx}}} - {{I}_{0}}{{A}_{{tt}}} + \gamma {{I}_{0}}{{A}_{{ttt}}} + \frac{1}{4}{{A}_{{tttt}}} = 0.$$
((9))

The latter equation can be solved by using the Fourier method. To this end, let us write the dispersion relation for the linear harmonic waves of the form \(A \propto \exp[i(kx - \omega t)]\):

$$k = \pm k(\omega ),\quad k(\omega ) = \omega \sqrt {\frac{{{{\omega }^{4}}}}{4} + {{I}_{0}}(1 + i\gamma \omega )} .$$
((10))

The imaginary unity in the dispersion relation means that the linear waves experience either decay or amplification at \(\gamma \ne 0\). The general solution to Eq. (9) can be written in the form

$$\begin{gathered} A(x,t) = \int\limits_{ - \infty }^{ + \infty } {{{W}_{1}}(\omega ){{e}^{{i(k(\omega )x - \omega t)}}}\frac{{d\omega }}{{2\pi }}} \\ + \;\int\limits_{ - \infty }^{ + \infty } {{{W}_{2}}(\omega ){{e}^{{i( - k(\omega )x - \omega t)}}}\frac{{d\omega }}{{2\pi }}} , \\ \end{gathered} $$
((11))

where functions \({{W}_{{1,2}}}(\omega )\) are determined from the initial conditions

$$\begin{gathered} A(0,t) = \int\limits_{ - \infty }^{ + \infty } {[{{W}_{1}}(\omega ) + {{W}_{2}}(\omega )]{{e}^{{ - i\omega t}}}\frac{{d\omega }}{{2\pi }}} , \\ {{A}_{x}}(0,t) = i\int\limits_{ - \infty }^{ + \infty } {k(\omega )[{{W}_{1}}(\omega ) - {{W}_{2}}(\omega )]{{e}^{{ - i\omega t}}}\frac{{d\omega }}{{2\pi }}} . \\ \end{gathered} $$
((12))

After simple calculations, we find functions \({{W}_{{1,2}}}(\omega )\) in terms of Fourier transforms \(\widehat {I_{0}^{'}}(\omega )\) and \(\widehat {\varphi _{0}^{'}}(\omega )\) of the initial (input) perturbation of intensity, \(I{\kern 1pt} '(x,t) = \)\(2\sqrt {{{I}_{0}}} A(x,t)\), and phase, \(\varphi '(x,t)\) = \(B(x,t){\text{/}}\sqrt {{{I}_{0}}} \), respectively:

$$\begin{gathered} {{W}_{1}}(\omega ) = \frac{1}{{4\sqrt {{{I}_{0}}} }}\left[ {\widehat {I_{0}^{'}}(\omega ) - i\frac{{{{\omega }^{2}}}}{{k(\omega )}}{{I}_{0}}\widehat {\varphi _{0}^{'}}(\omega )} \right], \\ {{W}_{1}}(\omega ) = \frac{1}{{4\sqrt {{{I}_{0}}} }}\left[ {\widehat {I_{0}^{'}}(\omega ) + i\frac{{{{\omega }^{2}}}}{{k(\omega )}}{{I}_{0}}\widehat {\varphi _{0}^{'}}(\omega )} \right]. \\ \end{gathered} $$
((13))

Suppose that the phase of the wave at the initial moment of time is constant, and there is a perturbation of only intensity; i.e., \(\varphi _{0}^{'} = 0\). Then, we have

$$I'(t,x) = \frac{1}{{4\pi }}\int\limits_{ - \infty }^{ + \infty } {\widehat {I_{0}^{'}}(\omega )[{{e}^{{ix{{f}_{1}}(\omega )}}} + {{e}^{{ix{{f}_{2}}(\omega )}}}]d\omega } ,$$
((14))

where

$${{f}_{1}}(\omega ) = k(\omega ) - \omega \frac{t}{x},\quad {{f}_{2}}(\omega ) = - k(\omega ) - \omega \frac{t}{x}.$$
((15))

For a long propagation distance \(x\), this integral can be estimated by using the standard saddle-point method, which yields

$$\delta I(t,x) \simeq \frac{{2\widehat {I_{0}^{'}}(\omega _{0}^{{(1)}})}}{{\sqrt {2x{{{\left| {\frac{{{{d}^{2}}{{f}_{1}}}}{{d{{\omega }^{2}}}}} \right|}}_{{\omega _{0}^{{(1)}}}}}} }}\cos\left( {x{{f}_{1}}(\omega _{0}^{{(1)}}) - \frac{\pi }{4}} \right)$$
((16))

for the wave propagating in the negative direction of the \(t\) axis and

$$\delta I(t,x) \simeq \frac{{2\widehat {I_{0}^{'}}(\omega _{0}^{{(2)}})}}{{\sqrt {2x{{{\left| {\frac{{{{d}^{2}}{{f}_{2}}}}{{d{{\omega }^{2}}}}} \right|}}_{{\omega _{0}^{{(2)}}}}}} }}\cos\left( {x{{f}_{2}}(\omega _{0}^{{(2)}}) - \frac{\pi }{4}} \right)$$
((17))

for the linear wave propagating to the right, where \(\omega _{0}^{{(1)}}\) and \(\omega _{0}^{{(2)}}\) are the values of \(\omega \) at the saddle points determined by the equations

$$\frac{{d{{f}_{1}}}}{{d\omega }} = 0,\quad \frac{{d{{f}_{2}}}}{{d\omega }} = 0.$$
((18))

Figure 1 presents a comparison of the result obtained by the numerical calculation of integral (14) and from the estimate given by (16) and (17) for initial perturbation

$$I_{0}^{'}(t) = \frac{1}{{\sqrt \pi a}}\exp\left( { - \frac{{{{t}^{2}}}}{{{{a}^{2}}}}} \right),\quad \widehat {I_{0}^{'}}(\omega ) = \exp\left( { - \frac{{{{\omega }^{2}}{{a}^{2}}}}{4}} \right).$$
((19))
Fig. 1.
figure 1

Pulse evolution in the linear approximation of the NSE with Raman term (3) at \(\gamma = 0.1\). The dashed grey line shows the initial perturbation, and the dashed blue line corresponds to the saddle-point method described by Eqs. (16) and (17), while the continuous red line corresponds to numerical calculation of integral (14) for \(x = 4\) with initial perturbation (19) at \(a = 1\). For comparison, the black solid line shows linear waves described by linearized equation (6) with \(\gamma = 0\).

Full size image

It can be seen that the pulse splits into two smaller pulses. However, in contrast to the case of an ordinary NSE, they do not represent symmetrical pulses propagating in the opposite directions. Instead, these two pulses have now different profiles. It can be seen that the pulse propagating in the positive direction of the \(t\) axis decays, while that propagating in the negative direction experiences gain. Obviously, this effect is a consequence of the action of the Raman term in Eq. (3). The approximate solution given by (16) and (17) shows that the amplitude of the packet of linear waves propagating to the left steadily grows. However, it should be remembered that this theory is valid for small deviations from the level of background intensity. It should also be noted that the asymptotic solution given by (16) and (17) describes the wave packet well even for short lengths \(x\) of the optical waveguide.

The time dependence of intensity of the linear waves is illustrated in Fig. 2 for the case in which a jump discontinuity modeled by the expression

$$I_{0}^{'}(t) = \frac{1}{2}\left\{ {{{I}^{R}} + {{I}^{L}} + ({{I}^{R}} - {{I}^{L}})\tanh\left( {\frac{t}{\Delta }} \right)} \right\}$$
((20))

was used as an initial perturbation. Here, jump discontinuity width \(\Delta \) should be chosen to be sufficiently small so that its influence was not be felt at rather long times. Constants \({{I}^{R}}\) and \({{I}^{L}}\) are responsible for the boundary values of the light intensity at the right and left sides of the jump discontinuity, respectively. The problem of initial-gap evolution represents one of the fundamental problems of the DSW theory. We will analyze it in detail below. Here, we will note only that the difference between the linear waves at \(\gamma = 0\) and \(\gamma \ne 0\) is noticeable even at small values of \(\gamma \), for the left wave in particular.

Fig. 2.
figure 2

Pulse evolution in the linear approximation of the NSE with Raman term (3) at \(\gamma = 0.02\). The dashed grey line shows the initial perturbation in the form of a jump discontinuity; the continuous red line corresponds to numerical calculation of integral (14) for \(x = 5\) with initial perturbation (20) at \({{I}^{L}} = 0.5\), \({{I}^{R}} = 0\), and \(\Delta = 0.3\). For comparison, the black solid line shows linear waves described by linearized equation (6) with \(\gamma = 0\).

Full size image

Let us investigate the influence of weak dispersion and nonlinearity on the evolution of a light pulse.

4 THE LIMIT OF LOW AMPLITUDE AND WEAK DISPERSION

Let us investigate the influence of the Raman effect on DSW evolution in the limit of low amplitudes and dispersion when they are taken into account in the main approximation, i.e., we are interested in the leading dispersion and nonlinear corrections to the dispersionless linear propagation of perturbations along a background pulse \({{I}_{0}}\) when the Raman term in (3) is taken into account. To this end, it is convenient to use functions of intensity \(I(x,t)\) and frequency modulation (chirp) \(u(x,t)\) as independent variables. To transform to equations for these variables, let us use the Madelung transform

$$q(x,t) = \sqrt {I(x,t)} \exp \left( {i\int\limits_{}^t {u(x,t')dt'} } \right).$$
((21))

Substituting the latter into (3), separating real and imaginary parts, and differentiating one of the equations, we obtain the following set of equations:

$$\begin{gathered} {{I}_{x}} + {{(uI)}_{t}} = 0, \\ {{u}_{x}} + u{{u}_{t}} + {{I}_{t}} + \mathop {\left( {\frac{{I_{t}^{2}}}{{8{{I}^{2}}}} - \frac{{{{I}_{{tt}}}}}{{4I}}} \right)}\nolimits_t = \gamma {{I}_{{tt}}}. \\ \end{gathered} $$
((22))

The last term in the left-hand side of the second equation describes the effects of dispersion, while the term in the right-hand side of this equation is reminiscent of the well-known Burgers viscosity in the theory of waves on the surface of water and other continuous media [8].

Using the latter set of equations and applying a standard perturbation theory approach with respect to the perturbation amplitude and the weak dispersion [28], we obtain a low-amplitude analog of Eq. (3). Let the wave be propagating in the positive direction of the \(t\) axis. An approximate equation for \(I' = I - {{I}_{0}}\) has the form

$$\begin{gathered} \frac{{\partial I'}}{{\partial x}} + \sqrt {{{I}_{0}}} \frac{{\partial I'}}{{\partial t}} + \frac{3}{{2\sqrt {{{I}_{0}}} }}I'\frac{{\partial I'}}{{\partial t}} - \frac{1}{{8\sqrt {{{I}_{0}}} }}\frac{{{{\partial }^{3}}I'}}{{\partial {{t}^{3}}}} \\ = \frac{1}{2}\gamma \sqrt {{{I}_{0}}} \frac{{{{\partial }^{2}}I'}}{{\partial {{t}^{2}}}}. \\ \end{gathered} $$
((23))

The latter is the KdV–B equation. It is well known [22, 24] that the evolution of the waves obeying this equation spits into three stages. At the first stage, when \(x \ll {{\gamma }^{{ - 1}}}\), the influence of the term characterizing low viscosity on the DSW evolution is small and can be neglected. At the second stage, when \(x\sim {{\gamma }^{{ - 1}}}\), the influence of viscosity becomes comparable with the DSW modulation. Obviously, viscosity cannot be neglected in this case and the perturbation theory approach is used for description of the DSW due to the small value of the viscosity coefficient. Finally, at the third stage, when \(x \gg {{\gamma }^{{ - 1}}}\), the DSW becomes stationary with respect to \(x\), i.e., the output-signal profile becomes independent of the optical-waveguide length. This kind of behavior of the DSW can also be expected in the case of approximation (23) for the wave propagating to the left.

However, the situation changes for the waves propagating in the opposite direction. The limiting equation for intensity perturbation \(I'\) can be written in the form

$$\begin{gathered} \frac{{\partial I'}}{{\partial x}} - \sqrt {{{I}_{0}}} \frac{{\partial I'}}{{\partial t}} + \frac{1}{{\sqrt {{{I}_{0}}} }}I'\frac{{\partial I'}}{{\partial t}} \\ + \;\frac{1}{{8\sqrt {{{I}_{0}}} }}\frac{{{{\partial }^{3}}I'}}{{\partial {{t}^{3}}}} = - \frac{1}{2}\gamma \sqrt {{{I}_{0}}} \frac{{{{\partial }^{2}}I'}}{{\partial {{t}^{2}}}}. \\ \end{gathered} $$
((24))

This is also a KdV–B equation. However, it should be noted that the signs before the terms describing dispersion and viscosity are different. This means that the character of the DSW changes, and the wave experiences amplification instead of standard decay.

Such a difference in the behavior of the waves propagating in opposite directions is caused by the lack of symmetry of Eq. (3) with respect to substitution \(t \to - t\). Obviously, this property will influence the pulse evolution described by full equation (3). Let us analyze formation of the DSW and derive equations describing their dynamics.

5 SHOCK-WAVE FORMATION

Let us discuss the dispersionless limit of the hydrodynamic equations that follow from the NSE when dispersion is neglected. In this limit, equations (22) without the term describing the influence of the Raman effect transform into a set of equation of the form

$$\begin{gathered} {{I}_{x}} + {{(uI)}_{t}} = 0, \\ {{u}_{x}} + u{{u}_{t}} + {{I}_{t}} = 0. \\ \end{gathered} $$
((25))

The first equation of the set can be interpreted as the continuity equation for intensity \(I(x,t)\), while the second equation can be interpreted as the Euler equation for the flow velocity \(u(x,t)\). Using standard technique, this set of equations can be reduced to the diagonal Riemann form:

$$\frac{{\partial {{r}_{ \pm }}}}{{\partial x}} + \frac{1}{{{{{v}}_{ \pm }}}}\frac{{\partial {{r}_{ \pm }}}}{{\partial t}} = 0$$
((26))

for the Riemann invariants

$${{r}_{ \pm }} = \frac{u}{2} \pm \sqrt I $$
((27))

and reciprocal velocities

$$\frac{1}{{{{{v}}_{ \pm }}}} = u \pm \sqrt I .$$
((28))

The functions introduced above will be used for choosing the initial state corresponding to a wave propagating in a certain direction.

Let the initial conditions at the input of the optical waveguide be formulated in the form of step functions:

$$\begin{gathered} I(x = 0) = \left\{ \begin{gathered} {{I}^{L}},\quad t < 0, \\ {{I}^{R}},\quad t > 0, \\ \end{gathered} \right. \hfill \\ u(x = 0) = \left\{ \begin{gathered} {{u}^{L}},\quad t < 0, \\ {{u}^{R}},\quad t > 0. \\ \end{gathered} \right. \hfill \\ \end{gathered} $$
((29))

For this choice of the initial conditions, wave breaking will take place at \(x = 0\). Had evolution of the light envelope \(q(x,t)\) be described by Eq. (2), two characteristic structures, namely, the rarefaction wave and the DSW, will be formed in the course of propagation. It is clear from the form of hydrodynamic equations (22) and the low-amplitude limit that the same structures will form in a general case. However, the Raman effect will influence only the evolution of the DSW, similar to viscosity in the case of wave dynamics on water described by the KdV–B equation. In this case, it makes sense limiting analysis of the shock-wave dynamics by the initial conditions the evolution of which will result in formation of the DSW without simultaneous formation of the rarefaction wave, which greatly simplifies the investigation. In terms of earlier introduced Riemann invariants, this would mean that the initial condition must be specified according to the conditions (a) \(r_{ + }^{L} = r_{ + }^{R}\), \(r_{ - }^{L} > r_{ - }^{R}\) or (b) \(r_{ + }^{L} > r_{ + }^{R}\), \(r_{ - }^{L}\) = \(r_{ - }^{R}\), where the upper index denotes the corresponding jump discontinuity boundary.

Having defined the initial condition in this way, let us proceed to the description of the three stages of DSW formation taking into account the Raman effect.

5.1 The First Stage: \(x \ll {{\gamma }^{{ - 1}}}\)

Since wave breaking occurs at \(x = 0\), dispersion must be taken into account at this stage when \(x \ll {{\gamma }^{{ - 1}}}\). However, modulation of the wave is relatively small, and the Raman effect can be neglected for the time being. In this case, the dynamics is described by an ordinary NSE (2) periodic solution of which is well known and can be expressed in the form [28]

$$\begin{gathered} I = \frac{1}{4}{{({{\lambda }_{4}} - {{\lambda }_{3}} - {{\lambda }_{2}} + {{\lambda }_{1}})}^{2}} \\ + \;({{\lambda }_{4}} - {{\lambda }_{3}})({{\lambda }_{2}} - {{\lambda }_{1}}){{\operatorname{sn} }^{2}}(\sqrt {({{\lambda }_{4}} - {{\lambda }_{2}})({{\lambda }_{3}} - {{\lambda }_{1}})} {\kern 1pt} {\kern 1pt} \theta ,m), \\ u = V - \frac{j}{I}, \\ \end{gathered} $$
((30))

where

$$\begin{gathered} \theta = t - \frac{x}{V},\quad \frac{1}{V} = \frac{1}{2}\sum\limits_{i = 1}^4 \,{{\lambda }_{i}}, \\ m = \frac{{({{\lambda }_{2}} - {{\lambda }_{1}})({{\lambda }_{4}} - {{\lambda }_{3}})}}{{({{\lambda }_{4}} - {{\lambda }_{2}})({{\lambda }_{3}} - {{\lambda }_{1}})}},\quad 0 \leqslant m \leqslant 1; \\ j = \frac{1}{8}( - {{\lambda }_{1}} - {{\lambda }_{2}} + {{\lambda }_{3}} + {{\lambda }_{4}}) \\ \times \;( - {{\lambda }_{1}} + {{\lambda }_{2}} - {{\lambda }_{3}} + {{\lambda }_{4}})({{\lambda }_{1}} - {{\lambda }_{2}} - {{\lambda }_{3}} + {{\lambda }_{4}}); \\ \end{gathered} $$
((31))

while real parameters \({{\lambda }_{i}}\) are zeros of the polynomial

$$P(\lambda ) = \prod\limits_{i = 1}^4 \,(\lambda - {{\lambda }_{i}}) = {{\lambda }^{4}} - {{s}_{1}}{{\lambda }^{3}} + {{s}_{2}}{{\lambda }^{2}} - {{s}_{3}}\lambda + {{s}_{4}},$$
((32))

where

$$\begin{gathered} {{s}_{1}} = \sum\limits_i \,{{\lambda }_{i}},\quad {{s}_{2}} = \sum\limits_{i < j} \,{{\lambda }_{i}}{{\lambda }_{j}},\quad {{s}_{3}} = \sum\limits_{i < j < k} \,{{\lambda }_{i}}{{\lambda }_{j}}{{\lambda }_{k}}, \\ {{s}_{4}} = {{\lambda }_{1}}{{\lambda }_{2}}{{\lambda }_{3}}{{\lambda }_{4}}, \\ \end{gathered} $$
((33))

and \({{\lambda }_{i}}\) are ordered according to inequalities

$${{\lambda }_{1}} \leqslant {{\lambda }_{2}} \leqslant {{\lambda }_{3}} \leqslant {{\lambda }_{4}}.$$

It can be seen that the reciprocal of the phase velocity of the wave \({{V}^{{ - 1}}}\), its amplitude a = (λ4 – \({{\lambda }_{3}})({{\lambda }_{2}} - {{\lambda }_{1}})\), background intensity \({{I}_{0}}\) = \(({{\lambda }_{4}} - {{\lambda }_{3}} - {{\lambda }_{2}}\) + \({{\lambda }_{1}}{{)}^{2}}{\text{/4}}\), and length

$$T = \frac{{2K(m)}}{{\sqrt {({{\lambda }_{1}} - {{\lambda }_{3}})({{\lambda }_{2}} - {{\lambda }_{4}})} }},$$
((34))

where \(K(m)\) is the complete elliptic integral of the first kind, are expressed in terms of these parameters. In a DSW, these parameters are slowly varying functions of \(x\) and \(t\). The advantage of writing the periodic solution in the form (30) is that parameters \({{\lambda }_{i}}\) represent Riemann invariants of the modulation equations and their evolution is determined by the Whitham equations in the diagonal form:

$$\frac{{\partial {{\lambda }_{i}}}}{{\partial x}} + \frac{1}{{{{{v}}_{i}}({{\lambda }_{1}},{{\lambda }_{2}},{{\lambda }_{3}},{{\lambda }_{4}})}}\frac{{\partial {{\lambda }_{i}}}}{{\partial t}} = 0,\quad i = 1,2,3,4.$$
((35))

Here, \({{{v}}_{i}}\) are the characteristic Whitham velocities:

$$\begin{gathered} \frac{1}{{{{{v}}_{1}}}} = \frac{1}{2}\sum\limits_{i = 1}^4 \,{{\lambda }_{i}} - \frac{{({{\lambda }_{4}} - {{\lambda }_{1}})({{\lambda }_{2}} - {{\lambda }_{1}})K}}{{({{\lambda }_{4}} - {{\lambda }_{1}})K - ({{\lambda }_{4}} - {{\lambda }_{2}})E}}, \\ \frac{1}{{{{{v}}_{2}}}} = \frac{1}{2}\sum\limits_{i = 1}^4 \,{{\lambda }_{i}} + \frac{{({{\lambda }_{3}} - {{\lambda }_{2}})({{\lambda }_{2}} - {{\lambda }_{1}})K}}{{({{\lambda }_{3}} - {{\lambda }_{2}})K - ({{\lambda }_{3}} - {{\lambda }_{1}})E}}, \\ \frac{1}{{{{{v}}_{3}}}} = \frac{1}{2}\sum\limits_{i = 1}^4 \,{{\lambda }_{i}} - \frac{{({{\lambda }_{4}} - {{\lambda }_{3}})({{\lambda }_{3}} - {{\lambda }_{2}})K}}{{({{\lambda }_{3}} - {{\lambda }_{2}})K - ({{\lambda }_{4}} - {{\lambda }_{2}})E}}, \\ \frac{1}{{{{{v}}_{4}}}} = \frac{1}{2}\sum\limits_{i = 1}^4 \,{{\lambda }_{i}} + \frac{{({{\lambda }_{4}} - {{\lambda }_{3}})({{\lambda }_{4}} - {{\lambda }_{1}})K}}{{({{\lambda }_{4}} - {{\lambda }_{1}})K - ({{\lambda }_{3}} - {{\lambda }_{1}})E}}, \\ \end{gathered} $$
((36))

where \(E = E(m)\) is an elliptic integral of the second kind.

In the limit \(m \to 1\) (\({{\lambda }_{3}} \to {{\lambda }_{2}}\)), the travelling wave transforms into a soliton solution in the presence of the constant-density background:

$$\begin{gathered} I = \frac{1}{4}{{({{\lambda }_{4}} - {{\lambda }_{1}})}^{2}} - \frac{{({{\lambda }_{4}} - {{\lambda }_{2}})({{\lambda }_{2}} - {{\lambda }_{1}})}}{{{{{\cosh }}^{2}}(\sqrt {({{\lambda }_{4}} - {{\lambda }_{2}})({{\lambda }_{2}} - {{\lambda }_{1}})} \theta )}}, \\ \theta = x - \frac{1}{2}({{\lambda }_{1}} + 2{{\lambda }_{2}} + {{\lambda }_{4}})t. \\ \end{gathered} $$
((37))

In the other (low-amplitude) limit in which \(m \to 0\) (\({{\lambda }_{3}} \to {{\lambda }_{4}}\) or \({{\lambda }_{2}} \to {{\lambda }_{1}}\)), the wave amplitude tends to zero, while the density attains the background value. It is essential that, in these limiting cases, the pair of the Whitham velocities transforms into the Riemann velocities of the dispersion limit. This means that the edges of the DSW are sewed together with the smooth solutions obtained in the hydrodynamic approximation of the dispersionless limit that is valid for description of the wave evolution outside of the DSW.

Since the initial condition does not contain parameters with a dimension of real time, the modulation parameters depend only on the self-similar variable \(\tau = t{\text{/}}x\). Therefore, the Whitham equations reduce to

$$\frac{{d{{\lambda }_{i}}}}{{d\tau }}(1{\text{/}}{{{v}}_{i}} - \tau ) = 0.$$
((38))

Hence, only one Riemann invariant is variable, while the other three must attain constant values. Knowing the initial conditions allows obtaining the form of a DSW for \(x \ll {{\gamma }^{{ - 1}}}\). Typical situations have been investigated in [10, 11], and we will not discuss the details here.

5.2 The Second Stage: \(x\sim {{\gamma }^{{ - 1}}}\)

At this stage, \(x\sim {{\gamma }^{{ - 1}}}\) and effects related to the Raman term start playing a substantial role, competing with the influence of the modulation. The DSW dynamics is regulated by a complete NSE with Raman term (3). The local form of the wave is still described by periodic solution (30). However, the Whitham equations become inhomogeneous in this case due to the appearance of the perturbation term. To derive these equations, we will use the method developed in [25]. The method can be formulated as follows. Let equations governing evolution of the wave variables \({{\varphi }_{m}}(x,t)\) have the form

$$\begin{gathered} \varepsilon \frac{{\partial {{\varphi }_{m}}}}{{\partial t}} = {{K}_{m}}\left( {{{\varphi }_{n}},\varepsilon \frac{{\partial {{\varphi }_{m}}}}{{\partial x}},{{\varepsilon }^{2}}\frac{{{{\partial }^{2}}{{\varphi }_{m}}}}{{\partial {{x}^{2}}}},...} \right) \\ + \;{{R}_{m}}\left( {{{\varphi }_{n}},\varepsilon \frac{{\partial {{\varphi }_{m}}}}{{\partial x}},{{\varepsilon }^{2}}\frac{{{{\partial }^{2}}{{\varphi }_{m}}}}{{\partial {{x}^{2}}}},...} \right), \\ m,n = 1,...,N, \\ \end{gathered} $$
((39))

where \(\varepsilon \ll 1\) is a small parameter describing the dispersion effects. Functions \({{K}_{m}}\) correspond to the core integrable part of the equations without taking into account perturbations, while functions \({{R}_{m}}\) represent the terms perturbing the system. It is assumed that the unperturbed system can be presented as a compatibility condition of two linear equations

$$\begin{gathered} {{\varepsilon }^{2}}{{\chi }_{{xx}}} = \mathcal{A}\chi , \\ {{\chi }_{t}} = - \frac{1}{2}{{\mathcal{B}}_{x}}\chi + \mathcal{B}{{\chi }_{x}}, \\ \end{gathered} $$
((40))

where \(\mathcal{A}\) and \(\mathcal{B}\) depend on functions \({{\varphi }_{n}}\), their spatial derivatives, and spectral parameter \(\lambda \). This condition holds for the NSE and allows using a powerful inverse scattering method for its investigation [28]. Linear second-order equations (40) have two basic solutions \({{\chi }_{ \pm }}\). Their product \(g = {{\chi }_{ + }}{{\chi }_{ - }}\) satisfies the third-order differential equation that can be integrated once thereby yielding the relation

$$\frac{{{{\varepsilon }^{2}}}}{2}g{{g}_{{xx}}} - \frac{{{{\varepsilon }^{2}}}}{4}g_{x}^{2} - \mathcal{A}{{g}^{2}} = \sigma P(\lambda ),$$
((41))

where coefficient \(\sigma \) is defined by the relation \({{\left. \mathcal{A} \right|}_{{\lambda \to \infty }}}\) → \( - \sigma {{\lambda }^{r}}\), while \(P(\lambda )\) is the polynomial of \(\lambda \) of degree \(M\) with zeros equal to \({{\lambda }_{i}}\).

In a modulated wave, parameters \({{\lambda }_{i}}\) become slow functions of \(x\) and \(t\), while their evolution is described by the perturbed Whitham equations that, in the case of Eq. (39), take the form

$$\begin{gathered} \frac{{\partial {{\lambda }_{i}}}}{{\partial t}} - \frac{{\left\langle {\mathcal{B}{\text{/}}g} \right\rangle }}{{\left\langle {1{\text{/}}g} \right\rangle }}\frac{{\partial {{\lambda }_{i}}}}{{\partial x}} \\ = \mathop {\lim}\limits_{\varepsilon \to 0} \left\{ {\frac{\sigma }{{\left\langle {1{\text{/}}g} \right\rangle \prod\limits_{j \ne k} {({{\lambda }_{k}} - {{\lambda }_{j}})} }}\sum\limits_{m = 1}^N \,\sum\limits_{l = 0}^{{{A}_{m}}} \,\left\langle {\frac{{\partial \mathcal{A}}}{{\partial \varphi _{m}^{{(l)}}}}\frac{{{{\partial }^{l}}{{R}_{m}}}}{{\partial {{x}^{l}}}}g} \right\rangle } \right\}, \\ i = 1,...,M, \\ \end{gathered} $$
((42))

where \({{A}_{m}}\) denotes the highest order of derivative of functions \({{\varphi }_{m}}\) appearing in \(\mathcal{A}\), while the angular brackets denote averaging over one wavelength \(L\). After averaging, all \(\lambda \) are taken equal to \({{\lambda }_{i}}\).

Let us apply this theory to the NSE with a Raman term:

$$i\varepsilon {{q}_{x}} + \frac{{{{\varepsilon }^{2}}}}{2}{{q}_{{tt}}} - {{\left| q \right|}^{2}}q = - \varepsilon \gamma q{{({{\left| q \right|}^{2}})}_{t}}.$$
((43))

A positive small parameter \(\varepsilon \ll 1\) introduced here explicitly reflects the smallness of the dispersion effects, which is assumed in the DSW theory, so that only the leading approximation with respect to this parameter should be retained after averaging. Equation (43) contains two variable functions \(q\) and \(q{\text{*}}\), along with two corresponding perturbation terms

$${{R}_{q}} = i\gamma q{{({{\left| q \right|}^{2}})}_{t}},\quad {{R}_{{q{\text{*}}}}} = - i\gamma q{\text{*}}{{({{\left| q \right|}^{2}})}_{t}}.$$
((44))

For an unperturbed NSE, functions \(\mathcal{A}\) and \(\mathcal{B}\) appearing in the linear equation (40) have the form

$$\begin{gathered} \mathcal{A} = - {{\lambda }^{2}} + i\varepsilon \lambda \frac{{{{q}_{t}}}}{q} + {{\left| q \right|}^{2}} - \frac{{{{\varepsilon }^{2}}}}{2}\frac{{{{q}_{{tt}}}}}{q} + \frac{{3{{\varepsilon }^{2}}}}{4}\frac{{q_{t}^{2}}}{{{{q}^{2}}}}, \\ \mathcal{B} = - \lambda + \frac{{i\varepsilon }}{2}\frac{{{{q}_{t}}}}{q}. \\ \end{gathered} $$
((45))

Averaging can be performed using equations known from the theory of periodic solutions to the NSE:

$$\begin{gathered} g = \lambda - \mu ,\quad \varepsilon \frac{{d\mu }}{{dt}} = 2\sqrt { - P(\mu )} , \\ \frac{1}{V} = \frac{{{{s}_{1}}}}{2},\quad T = \varepsilon \oint {\frac{{d\mu }}{{2\sqrt { - P(\mu )} }}} , \\ \end{gathered} $$
((46))

where \(P(\mu )\) and \({{s}_{1}}\) were defined in (32) and (33). To calculate the right-hand sides of the Whitham equations, we will also need an expression governing parameter \(\mu \) [28]:

$$\begin{gathered} \mu (I) = \frac{{{{s}_{1}}}}{4} + \frac{{ - j + i\sqrt {\mathcal{R}(I)} }}{{2I}},\quad \varepsilon \frac{{dI}}{{dt}} = 2\sqrt {\mathcal{R}(I)} , \\ \mathcal{R}(I) = (I - {{I}_{1}})(I - {{I}_{2}})(I - {{I}_{3}}), \\ \end{gathered} $$
((47))

where \({{I}_{i}}\) are zeros of function \(\mathcal{R}(I)\) related to the Riemann invariants \({{\lambda }_{i}}\) through expressions

$$\begin{gathered} {{I}_{1}} = \frac{1}{4}{{({{\lambda }_{1}} - {{\lambda }_{2}} - {{\lambda }_{3}} + {{\lambda }_{4}})}^{2}}, \\ {{I}_{2}} = \frac{1}{4}{{({{\lambda }_{1}} - {{\lambda }_{2}} + {{\lambda }_{3}} - {{\lambda }_{4}})}^{2}}, \\ {{I}_{3}} = \frac{1}{4}{{({{\lambda }_{1}} + {{\lambda }_{2}} - {{\lambda }_{3}} - {{\lambda }_{4}})}^{2}}, \\ \end{gathered} $$
((48))

while \(j\) was defined in (31). As a result, we obtain the Whitham equations for the Riemann invariants \({{\lambda }_{i}}\) in the form

$$\frac{{\partial {{\lambda }_{i}}}}{{\partial x}} + \frac{1}{{{{{v}}_{i}}}}\frac{{\partial {{\lambda }_{i}}}}{{\partial t}}$$
$$ = \frac{{\gamma j}}{{\partial T{\text{/}}\partial {{\lambda }_{i}}}}\frac{{{{\lambda }_{i}}}}{{\prod\limits_{j \ne i} {({{\lambda }_{i}} - {{\lambda }_{j}})} }}\int\limits_{{{I}_{1}}}^{{{I}_{2}}} {\frac{{\sqrt {\mathcal{R}(I)} }}{{{{I}^{2}}}}dI} ,$$
((49))
$$i = 1,2,3,4,$$

where wavelength \(T\) was defined in (34). The integral in the right-hand side can be expressed in terms of elliptic integrals. However, the resulting expression will be too complex, and it is easier to deal with its original form.

The solution to the perturbed Whitham equations (49) determines evolution of parameters \({{\lambda }_{i}}\) due to non-uniform modulation of the waves and a weak effect of the viscosity type caused by the Raman term. Based on the earlier analyzed low-amplitude limits of the KdV–B type, it is natural to expect that the DSW propagating in the positive direction will asymptotically approach the stationary waves, and some of their characteristics can be calculated analytically. The amplitudes of the DSW propagating to the left will continuously grow, and the corresponding solution can be found numerically from the obtained perturbed Whitham equations.

5.3 The Third Stage: \(x \gg {{\gamma }^{{ - 1}}}\).

At distances \(x \gg {{\gamma }^{{ - 1}}}\), the DSW propagating in the positive direction of the \(t\) axis becomes stationary, because the Raman effect compensates the influence of the wave modulation at such values of \(x\). This means that the DSW moves as a whole with constant velocity \(V\)and its profile remains unchanged. In this case, the DSW are described by the perturbed Whitham equations (49) with parameters \({{\lambda }_{i}}\) dependent on \(\theta = t - x{\text{/}}V\). Assuming that function \({{s}_{1}}\) is an integral of the Whitham equations, i.e., \({{s}_{1}} = {\text{const}}\) under the condition that \({\text{1/}}V\) = \({{s}_{1}}{\text{/2}}\), the Whitham equations can be recast in a simpler form:

$$\frac{{\partial {{\lambda }_{i}}}}{{\partial \theta }} = \frac{{{{\lambda }_{i}}Q}}{{\prod\limits_{j \ne i} {({{\lambda }_{i}} - {{\lambda }_{j}})} }},\quad i = 1,2,3,4,$$
((50))

where

$$Q = \frac{{2\gamma j}}{T}\int\limits_{{{I}_{1}}}^{{{I}_{2}}} {\frac{{\sqrt {\mathcal{R}(I)} }}{{{{I}^{2}}}}dI} .$$
((51))

Let us demonstrate that our assumption of \({{s}_{1}}\) being constant is valid and that the structure of these equations, in fact, ensures the existence of three integrals \({{s}_{1}}\), \({{s}_{2}}\), and \({{s}_{4}}\). This statement can be proved by using the Jacobi identities that follow from an obvious identity

$$\sum\limits_{i = 1}^M \,\frac{{\prod\limits_{j \ne i} {(\lambda - {{\lambda }_{j}})} }}{{\prod\limits_{j \ne i} {({{\lambda }_{i}} - {{\lambda }_{j}})} }} = 1,$$
((52))

where a polynomial of degree \(M - 1\) appears in the left-hand side. The polynomial is equal to unity at points \(\lambda = {{\lambda }_{i}}\), \(i = 1,...,M\) and is thus equal to unity identically. In our case, \(M = 4\), so that the latter identity yields

$$\sum\limits_{i = 1}^4 \,\frac{{\lambda _{i}^{n}}}{{\prod\limits_{j \ne i} {({{\lambda }_{i}} - {{\lambda }_{j}})} }} = \left\{ \begin{gathered} 0,\quad n = 0,1,2, \\ 1,\quad n = 3, \\ \end{gathered} \right.$$
$$\begin{gathered} \sum\limits_{i = 1}^4 {\frac{{\lambda _{i}^{n}\sum\limits_j {^{'}{{\lambda }_{j}}} }}{{\prod\limits_{j \ne i} {({{\lambda }_{i}} - {{\lambda }_{j}})} }}} = \left\{ \begin{gathered} 0,\quad n = 0,1,3, \\ - 1,\quad n = 2, \\ \end{gathered} \right. \\ \sum\limits_{i = 1}^4 {\frac{{\lambda _{i}^{n}\sum\limits_{j,k} {^{'}{{\lambda }_{j}}{{\lambda }_{k}}} }}{{\prod\limits_{j \ne i} {({{\lambda }_{i}} - {{\lambda }_{j}})} }}} = \left\{ \begin{gathered} 0,\quad n = 0,2,3, \\ 1,\quad n = 1, \\ \end{gathered} \right. \\ \end{gathered} $$
((53))
$$\sum\limits_{i = 1}^4 {\frac{{\lambda _{i}^{n}{{s}_{4}}}}{{\prod\limits_{j \ne i} {({{\lambda }_{i}} - {{\lambda }_{j}})} }}} = \left\{ \begin{gathered} 0,\quad n = 0,1,2, \\ - 1,\quad n = - 1, \\ \end{gathered} \right.$$

where the sum with a prime means that all terms with factor \({{\lambda }_{i}}\) in it are omitted. Hence, we have

$$\tfrac{{d{{s}_{1}}}}{{d\theta }} = 0,\quad \tfrac{{d{{s}_{2}}}}{{d\theta }} = 0,\quad \tfrac{{d{{s}_{3}}}}{{d\theta }} = Q,\quad \tfrac{{d{{s}_{4}}}}{{d\theta }} = 0,$$
((54))

which is to say that Eqs. (50) have three integrals of motion: \({{s}_{1}} = {\text{const}},\)\({{s}_{2}} = {\text{const}}\), and \({{s}_{4}} = {\text{const}}\). Set of equations (50) thus reduces to a single ordinary differential equation of the form

$$\frac{{d{{s}_{3}}}}{{d\theta }} = \tfrac{{2\gamma j}}{T}\int\limits_{{{I}_{1}}({{s}_{3}})}^{{{I}_{2}}({{s}_{3}})} {\frac{{\sqrt {\mathcal{R}(I)} }}{{{{I}^{2}}}}dI} $$
((55))

with the initial condition \({{s}_{3}}({{\theta }_{0}}) = s_{3}^{0}\) that can be conveniently chosen on the soliton edge of the DSW. It follows from the matching conditions at the DSW edges that

$$\lambda _{1}^{L} = r_{ - }^{L},\quad \lambda _{4}^{L} = r_{ - }^{L}\quad {\text{at}}\quad \lambda _{3}^{L} = \lambda _{2}^{L}$$
((56))

at the soliton edge and

$$\lambda _{1}^{R} = r_{ - }^{R},\quad \lambda _{2}^{R} = r_{ + }^{R}\quad {\text{at}}\quad \lambda _{3}^{R} = \lambda _{4}^{R}$$
((57))

at the low-amplitude edge.

The diagram of the Riemann invariants is illustrated in Fig. 3. Since we analyze here the wave propagating in the positive direction, we have \(r_{ + }^{L} > r_{ + }^{R}\) and \(r_{ - }^{L} = r_{ - }^{R}\). This means that \(\lambda _{4}^{L} > \lambda _{2}^{R}\) and \(\lambda _{1}^{L} = \lambda _{1}^{R}\). Hence, it follows from the fact that functions \({{s}_{1}}\) and \({{s}_{2}}\) are constant that

$$\begin{gathered} \lambda _{2}^{L} = \frac{1}{2}(\lambda _{2}^{R} + \sqrt {\lambda _{2}^{R}\lambda _{4}^{L}} ) \\ = \frac{1}{4}({{u}^{R}} + 2\sqrt {{{I}^{R}}} + \sqrt {({{u}^{L}} + 2\sqrt {{{I}^{L}}} )({{u}^{R}} + 2\sqrt {{{I}^{R}}} )} ) \\ \end{gathered} $$
((58))

and

$$\begin{gathered} \lambda _{4}^{R} = \frac{1}{2}(\lambda _{4}^{L} + \sqrt {\lambda _{2}^{R}\lambda _{4}^{L}} ) \\ = \frac{1}{4}({{u}^{L}} + 2\sqrt {{{I}^{L}}} + \sqrt {({{u}^{L}} + 2\sqrt {{{I}^{L}}} )({{u}^{R}} + 2\sqrt {{{I}^{R}}} )} ). \\ \end{gathered} $$
((59))
Fig. 3.
figure 3

Riemann invariants \({{\lambda }_{i}}\) as functions of \(\theta = t - x{\text{/}}V\).

Full size image

We thus found all Riemann invariants at both edges of the DSW, i.e., we know integrals \({{s}_{1}}\) and \({{s}_{4}}\) along entire shock wave. This allows finding the wave velocity and the amplitude of the leading soliton:

$$\begin{gathered} \frac{1}{V} = \frac{{{{s}_{1}}}}{2} = \frac{1}{2}(\lambda _{1}^{L} + \lambda _{4}^{L} + \lambda _{2}^{R} + \sqrt {\lambda _{2}^{R}\lambda _{4}^{L}} ) \\ = \frac{1}{4}(2{{u}^{L}} + {{u}^{R}} + 2\sqrt {{{I}^{R}}} + \sqrt {({{u}^{L}} + 2\sqrt {{{I}^{L}}} )({{u}^{R}} + 2\sqrt {{{I}^{R}}} )} ), \\ \end{gathered} $$
((60))
$$\begin{gathered} {{a}_{s}} = \frac{1}{4}(2\lambda _{4}^{L} - \lambda _{2}^{R} - \sqrt {\lambda _{2}^{R}\lambda _{4}^{L}} )(\lambda _{2}^{R} - 2\lambda _{1}^{L} + \sqrt {\lambda _{2}^{R}\lambda _{4}^{L}} ) \\ = {{I}^{L}} - \frac{1}{{16}}[2\sqrt {{{I}^{L}}} - 2{{u}^{L}} + {{u}^{R}} \\ + \;\sqrt {({{u}^{L}} + 2\sqrt {{{I}^{L}}} )({{u}^{R}} + 2\sqrt {{{I}^{R}}} )} {{]}^{2}}. \\ \end{gathered} $$
((61))

It is important noting that the speed of the DSW and the amplitude of the soliton depend only on the initial parameters and are independent of constant \(\gamma \) reflecting the Raman effect. The dependence of the soliton amplitude on coordinate \(x\) found by numerical simulation is presented in Fig. 4. It can be seen that there is some deviation of the theory from the results of the numerical simulation that is probably caused by the fact that the Whitham theory does not take into account the nonadiabatic effects that can play a substantial role in the DSW described by nonintegrable equations, such as the NSE with a Raman term. This kind of discrepancies has been noted in [16, 29] for other physical systems. Despite this discrepancy, in general, the DSW are described by the Whitham theory quite well, which can be seen from Fig. 5. We see that the agreement between the results of the Whitham theory and numerical simulations considerably improves with decrease in the wave amplitude.

Fig. 4.
figure 4

Dependences of the leading-soliton amplitude on propagation length \(x\) for several values of constant \(\gamma \) characterizing the Raman effect. The analytical result obtained by using the Whitham theory is illustrated by the black dashed line, while numerical results obtained by solving Eq. (3) are presented by the solid curves.

Full size image
Fig. 5.
figure 5

Stationary DSW. The Whitham theory (blue color) is compared with the numerical solution to Eq. (3) (red color) for \(\gamma = 0.05\) and boundary conditions \({{I}_{L}} = 0.5\), \({{I}_{R}} = 0.257\), \({{u}_{L}} = 0\), and \({{u}_{R}} = - 0.4\) at x = 200. The dashed lines illustrate the results obtained for the envelopes by using the Whitham theory.

Full size image

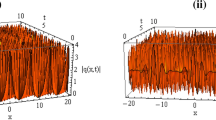
On the contrary, for the wave propagating in the opposite direction, the amplitude of oscillations in the wave and its duration continuously grow. It is difficult to construct an analytical theory of such a nonstationary nonlinear structure, prompting using numerical simulation instead. An example of such a wave obtained by numerical solution of Eq. (3) is illustrated in Fig. 6. It can be seen that the wave profile substantially changes with increase in distance \(x\). At sufficiently long waveguide distances \(x\), the amplitude of the wave packet separating from the DSW and described quite well by the linear theory discussed in Section 3 considerably increases.

Fig. 6.
figure 6

The DSW propagating in the negative direction of the \(t\) axis for \(\gamma = 0.1\) and boundary conditions \({{I}_{L}} = 0.257\), \({{I}_{R}} = 0.5\), \({{u}_{L}} = 0.4\), and \({{u}_{R}} = 0\).

Full size image

6 CONCLUSIONS

In the present work, we developed an analytical theory of propagation of relatively long light pulses in fibers described by the NSE modified by a small term characterizing the Raman effect. We analyzed the main stages of formation of a shock wave with an initial profile in the form of a step function and obtained analytical solutions for the initial and stable final stages of nonstationary shock-wave development by using the Whitham method for equations containing perturbation terms.

In principle, the results obtained in the present work can be experimentally observed in systems analogous to those used in recent experiment [12]. However, it should be kept in mind that the effect of self-steepening takes place in addition to the Raman effect in standard fibers. However, these two effects reveal themselves differently and, thus, can be distinguished. It was demonstrated in [19] that the main consequence of the effect of self-steepening is formation of combined shock waves due to the nonmonotonic dependence of the nonlinear term on the wave amplitude, whereas the Raman scattering leads to formation of stationary shock waves of final length. In the process, as a rule, the Raman effect is much stronger than the effect of self-steepening. The theory developed in the present work shows that the Whitham method provides a general and sufficiently efficient approach to description of the DSWs observed in light guides and other optical systems (see, e.g., [30]).