INTRODUCTION

Todate, most dynamic buckling investigations normally assume complete absence of any static pre-loading before impartation of any time-dependent load to the structure. Simitses [1, 2] was the first to consider a system, where a dynamic load was superposed on a structure that was statically pre-loaded. Subsequent researchers have tended to approach the subject matter by way of numerical analysis, principally, by way of the finite element technique [3–5]. As it is difficult to apply numerical solutions in engineering practice, it is of interest to consider analytical solutions. Static pre-loading systems have many applications. The approach adopted here is, in part, the technique used in [6], where the maximum displacement and static buckling of a circular cylindrical shell were determined. The same technique and procedure were adopted in [7].

The problem formulation in the present work contains two dimensionally unrelated parameters on which a two-timing multi-scaling perturbation procedure is initiated by using asymptotic expansions. The cubic nonlinear elastic structure under study was first considered in [8]; it describes the behavior of various mechanical structures, such as columns, beams, rods, plates, cylindrical and toroidal shells, etc.

Fig. 1
figure 1

Cubic model structure.

Full size image

1. FORMULATION OF THE CUBIC MODEL OF THE ELASTIC STRUCTURE

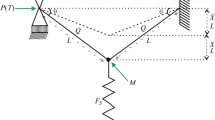
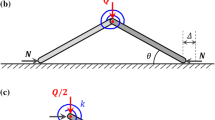
The structure consists of two rods, each of length \(L\)(Fig. 1). The rods are suddenly loaded by a horizontal force \(P(T)\) applied at the time \(T= 0\). The rods are assumed to be absolutely rigid and weightless. A mass \(M\) is attached to the rods at the point of their intersection. The mass motion in the vertical direction is limited by a spring whose rigidity follows a cubic law. From the side of the spring, the mass is affected by the reaction force

$$F_s=KL\Big(\frac{X}{L}-b\Big(\frac{X}{L}\Big)^3\Big),\qquad b>0,\quad K>0$$

(\(X\) is the additional displacement with respect to the equilibrium position).

Let \(Q\) be the force in each rod and \(\theta\) be the angle between the rod and the horizontal line (see Fig. 1). The angle \(\theta\) is assumed to be small; therefore, \(\cos\theta\approx 1\) and  \(\sin\theta\approx\theta\). Then we assume that \(\sin\theta = (\bar{X}+X)/L\) and \(\theta =(\bar{X}+X)/L\). The projection of the equilibrium equation for the rod onto the horizontal axis is written as

$$Q\cos\theta = P(T).$$
(1.1)

The equation of motion of the mass \(M\) in the vertical direction has the form

$$M\,\frac{d^2}{dT^2}\Big(\frac{X}{L}\Big) +KL\Big(\frac{X}{L}-b\Big(\frac{X}{L}\Big)^3\Big)=2Q\sin\theta.$$
(1.2)

Combining Eqs. (1.1) and (1.2), we obtain

$$M\,\frac{d^2}{dT^2}\Big(\frac{X}{L}\Big) +KL\Big(1-\frac{2P(T)}{KL}\Big)\frac{X}{L} -bKL\Big(\frac{X}{L}\Big)^3=2P(T)\,\frac{\bar{X}}{L}.$$
(1.3)

We introduce the dimensional variables

$$\xi =\frac{X}{L},\quad \bar{\xi }=\frac{\bar{X}}{L},\quad t=T\sqrt{\frac{KL}{M}}\,\qquad (0<\xi <1)$$
(1.4)

and assume that

$$2P(T)=\frac{2P(T)P(0)}{P(0)}=2f(t)P(0),\quad f(t)=\frac{P(T)}{P(0)},\quad \lambda =\frac{2P(0)}{KL},\quad P(0)\ne 0.$$
(1.5)

Substituting Eqs. (1.4) into Eq. (1.3) and taking into account Eqs. (1.5), we obtain

$$\frac{d^2\xi (t)}{dt^2}+(1-\lambda f(t))\xi -b\xi^3 =\lambda f(t)\bar{\xi },\qquad t>0.$$
(1.6)

The initial conditions are written in the form

$$t=0{:}\qquad \xi(t)=0,\quad \frac{d\xi(t)}{dt}=0.$$

Equation (1.6) is written with the damping element being ignored. On incorporating a small viscous damping term of the order of \(\delta\), Eq. (1.6) takes the form

$$\frac{d^2\xi (t)}{dt^2}+2\delta\,\frac{d\xi (t)}{dt} +(1-\ \lambda f(t))\xi -b\xi^3=\lambda f(t)\bar{\xi},\qquad t>0,$$

where \(0<\delta <1\).

According to [8], the equations of the cubic model (see Fig. 1), which describes the behavior of the elastic structure, are

$$\frac{d^2\xi (t)}{dt^2} + (1 - \lambda f(t))\xi - b\xi ^3 = \lambda \bar {\xi }f(t),\quad t > 0,\qquad \xi (t) =\frac{d\xi (t)}{dt} =0.$$
(1.7)

If a small viscous damping term of the order of \(\delta\) is taken into account in Eq. (1.7), this equation takes the form

$$\frac{d^2\xi (t)}{dt^2} + 2\delta\,\frac{d\xi (t)}{dt} + (1 - \lambda f(t))\xi - b\xi ^3 =\lambda \bar {\xi }f(t),\quad t >0,\qquad \xi (t) = \frac{d\xi (t)}{dt} = 0,$$
(1.8)

where \(0 < \delta < 1\) is the damping coefficient, \(b > 0\) is the imperfection sensitivity parameter, \(\bar{\xi}\) is the amplitude of imperfection, \(f(t)\) is the load function, and \(\lambda\) is the dimensionless magnitude of the dynamic step load (\(\lambda_0\)  corresponds to static pre-loading and \(\lambda\) corresponds to the dynamic load).

The step load \(f(t)\) satisfies the condition

$$f(t) = 0,\qquad t >0.$$

In our study, we are to determine a particular value \(\lambda _D\) of the parameter \(\lambda\) at which the structure buckles dynamically under the condition that the structure was pre-loaded at the level \(\lambda _0\). According to [8], the value of \(\lambda _D\) is defined as the greatest value of \(\lambda\) at which the displacement remains bounded.

2. STATIC DEFORMATION

According to Eq. (1.8), the static displacement \(\xi_0\)  corresponding to the load \(\lambda_0\) is the solution of the equation

$$(1 - \lambda _0 )\xi _0 - b\xi _0^3 = \lambda _0 \bar {\xi}.$$
(2.1)

Equation (2.1) is obtained from Eq. (1.8) by assuming that \(f(t)= 1\) and neglecting the terms corresponding to inertial and damping forces.

Let

$$\xi _0 = \sum\limits_{i = 1}^\infty \xi _0^{(i)}\bar {\xi}^i.$$
(2.2)

Substituting Eq. (2.2) into Eq. (2.1) and equating the coefficients at the terms \(\bar {\xi }^i\)(\(i = 1, 2, 3, \dots\)), we obtain the system of equations

$$(1 - \lambda _0 )\xi _0^{(1)} =0,\quad (1 - \lambda _0 )\xi _0^{(2)} = 0,\quad (1 - \lambda _0 )\xi _0^{(3)} = b(\xi _0^{(1)})^3,\quad\dots,$$
(2.3)

whose solution has the form

$$\xi _0^{(1)} = B_0 ,\quad \xi_0^{(2)} = 0,\quad \xi _0^{(3)} = bB_0^3/(1 - \lambda _0),\quad B_0 = \lambda _0/(1 - \lambda _0 ).$$
(2.4)

Therefore, the displacement \(\xi _0\) is written as

$$\xi _0 (\lambda _0 ) = \bar {\xi }B_0 + \bar {\xi}^3bB_0^3/(1 - \lambda _0 )+\dots\ .$$
(2.5)

To determine the static buckling load \(\lambda _S\), we use the notation \(\lambda\) instead of \(\lambda _0\).

The bifurcation condition for static buckling is

$$\frac{d\lambda }{d\xi _0 } =0.$$
(2.6)

Recasting Eq. (2.5) yields

$$\xi _0 (\lambda _0 ) = c_1 \bar {\xi } + c_3 \bar{\xi }^3 + \dots,\qquad c_1 = B_0,\quad c_3 = bB_0^3/(1 - \lambda _0 ).$$
(2.7)

Following [7, 9], Eq. (2.7) is reversed as

$$\bar {\xi } = d_1 \xi _0 + d_3 \xi _0^3 +\dots\ .$$
(2.8)

Substituting the expression for \(\xi _0\) from Eq. (2.7) into Eq. (2.8) and equating the coefficients at the powers of \(\bar {\xi }\), we obtain

$$d_1 = 1/c_1,\qquad d_3 = -c_3/c_1^4.$$
(2.9)

As \(d_1\) and \(d_3\) depend on \(\lambda\), Eq. (2.6) with allowance for Eq. (2.9) yields

$$\bar {\xi } = (2/(3\sqrt 3\,))\sqrt {c_1/c_3}\,.$$
(2.10)

Transforming Eq. (2.10) with allowance for Eqs. (2.4) and (2.9), we obtain

$$(1 - \lambda _S)^{3/2} = (3\sqrt 3/2)b^{1/2}\bar {\xi }\lambda _S.$$
(2.11)

3. DYNAMIC DEFORMATION

For a viscously damped structure that was not statically pre-loaded, its equation of motion under the action of a step load is

$$\frac{d^2\xi (t)}{dt^2} + 2\delta\,\frac{d\xi (t)}{dt} + (1 - \lambda f(t))\xi - b\xi ^3 =\lambda \bar {\xi }f(t),\quad t >0,\qquad \xi (t) = \frac{d\xi (t)}{dt} = 0,$$

where \(\xi (t)\) is the displacement produced explicitly by the step load (i.e., without static pre-loading).

If the structure was statically pre-loaded by the force \(\lambda_0\), the total displacement \(\eta (t)\) is presented as the sum

$$\eta (t) = \xi _0 + \xi (t)$$
(3.1)

and the equation of motion is written as

$$\frac{d^2\eta (t)}{dt^2} + 2\delta\,\frac{d\eta (t)}{dt} + (1 - \lambda _0 )\xi _0 + (1 - \lambda)\xi - b\eta ^3 = \lambda _0 \bar {\xi } + \lambda \bar {\xi},\qquad t > 0,$$
$$\xi (0) = \frac{d\xi (0)}{dt} = 0, \qquad \eta(0) = \xi _0,\qquad \frac{d\xi (0)}{dt} = 0.$$
(3.2)

Substituting Eq. (3.1) into Eq. (3.2), we obtain

$$\frac{d^2}{dt^2}\,(\xi _0 + \xi ) + 2\delta\,\frac{d}{dt}\,(\xi _0 + \xi ) + (1 - \lambda _0 )\xi _0 + (1- \lambda )\xi - b(\xi _0 + \xi )^3 = (\lambda _0 + \lambda )\bar {\xi },\qquad t >0,$$

whence it follows that

$$\frac{d^2\xi (t)}{dt^2} + 2\delta\,\frac{d\xi (t)}{dt} + (1 - \lambda )\xi - b[\xi ^3 + 3\xi _0\xi (\xi + \xi _0 )] = \lambda \bar {\xi},\qquad t > 0,$$
$$\xi (0) = \frac{d\xi (0)}{dt} = 0.$$
(3.3)

At \(\xi _0 = 0\), Eq. (3.3) is the equation of motion under the action of the step load without static pre-loading; at \(\xi _0 \ne 0\), it is the equation of motion of the statically pre-loaded system under the action of the step load.

4. PERTURBATION METHOD AND ASYMPTOTIC SOLUTION

Problem (3.3) contains two small independent parameters \(\delta\) and  \(\bar {\xi }\). Let

$$\tau = \delta t,\qquad \hat {t} = (1 - \lambda )^{1/2}t +\delta^{-1}[\mu _1(\tau)\bar {\xi } + \mu _2 (\tau)\bar {\xi}^2 + \mu _3 (\tau)\bar {\xi }^3+\dots\;],$$
$$\mu _i = \mu _i (\tau), \qquad \mu _i (0) = 0,\qquad i =1,2,3,\dots\ .$$

Then, we have

$$\frac{d\xi (t)}{dt} = \frac{\partial \xi }{\partial \hat {t}}\, \frac{\partial \hat {t}}{\partial t} + \frac{\partial \xi }{\partial \hat {t}}\, \frac{\partial \hat {t}}{\partial \tau }\,\frac{\partial \tau }{\partial t} + \frac{\partial\xi }{\partial \tau }\,\frac{\partial \tau }{\partial t}.$$
(4.1)

Therefore,

$$\frac{d\xi }{dt} = (1 - \lambda )^{1/2}\xi_{,\hat {t}} + [\mu'_1 (\tau)\bar {\xi } +\mu'_2 (\tau)\bar {\xi }^2 + \mu'_3 (\tau)\bar {\xi }^3+ \dots\;]\xi _{,\hat{t}} + \delta \xi _{,\tau },$$
$$\frac{d^2\xi}{dt^2} = (1 - \lambda )\xi_{,\hat {t}\hat{t}} [\mu'_1 (\tau)\bar {\xi } + \mu'_2(\tau)\bar {\xi }^2 +\mu'_3 (\tau)\bar {\xi }^3 + \dots\;]^2\xi_{,\hat{t}\hat {t}} + 2\delta (1 - \lambda )^{1/2}\xi _{,\hat {t}\tau } +\delta ^2\xi_{,\tau\tau}{}$$
(4.2)
$${}+2(1 - \lambda )^{1/2}[\mu'_1 (\tau)\bar {\xi} + \mu'_2 (\tau)\bar {\xi }^2 +\mu'_3(\tau)\bar {\xi }^3+ \dots] \xi _{,\hat {t}\tau } +2\delta[\mu'_1 (\tau)\bar {\xi } + \mu'_2 (\tau)\bar {\xi }^2 +\mu'_3 (\tau)\bar {\xi }^3 + \dots\;]\xi_{,\hat {t}\tau}{}$$
$${}+ \delta[\mu''_1 (\tau)\xi + \mu''_2(\tau)\varepsilon ^2 +\mu''_3 (\tau)\varepsilon ^3+ \dots\;]\xi_{,\hat {t}\hat {t}},$$

where the comma in the subscript means partial differentiation, and \(d\,(\,\cdot\,)/d\tau=(\,\cdot\,)'\). Now we assume that

$$\xi (\hat {t},\tau )= \sum\limits_{i = 1}^\infty \sum\limits_{j=0}^\infty \zeta^{(ij)} (\hat {t},\tau )\bar{\xi }^{i}\delta^{j},$$
(4.3)

where (\(ij\)) is the superscript rather than the power exponent.

Substituting Eq. (4.2) into Eq. (3.3), we divide the resultant equation by \(1 - \lambda\) and substitute presentation (4.3). In the resultant equation, we equate the coefficients at the powers \(\bar {\xi }^i\delta ^j\)(\(i =1,2,3,\dots\); \(j = 0,1,2,\dots\)). As a result, we obtain the following system of equations:

$$O(\bar {\xi}){:}\quad \zeta_{,\hat{t}\hat {t}}^{10} + \zeta ^{10} = \lambda/(1 - \lambda),$$
$$O(\bar {\xi}\delta){:}\quad \zeta _{,\hat {t}\hat {t}}^{11} + \zeta ^{11} = - 2(1 - \lambda )^{-1/2}\zeta_{,\hat {t}\tau }^{10} -2(1 - \lambda )^{-1/2}\zeta_{,\hat {t}}^{10},$$
(4.4)
$$O(\bar {\xi }\delta ^2){:}\quad \zeta_{,\hat {t}\hat {t}}^{12} + \zeta ^{12} = -(1 - \lambda )^{-1}\zeta _{,\tau\tau }^{10} -2(1 - \lambda )^{-1/2}\zeta _{,\hat {t}}^{10} -2(1 -\lambda )^{-1/2}\zeta_{,\hat {t}\tau}^{10} -2(1 - \lambda)^{-1};$$
$$O(\bar {\xi}^2){:}\quad \zeta _{,\hat {t}\hat {t}}^{20}+\zeta ^{20} = -(1 - \lambda )^{-1/2}\mu'_2 (\tau)\zeta _{,\hat{t}}^{20} - 2(1 - \lambda )^{-1}\mu'_1(\tau)\zeta _{,\tau }^{10}\zeta_{,\tau }^{11},$$
$$O(\bar {\xi }^2\delta ){:}\quad \zeta_{,\hat {t}\hat {t}}^{21} + \zeta ^{21} = -2(1 - \lambda )^{-1/2}\mu'_1(\tau)\zeta _{,\hat {t}}^{11} -2(1- \lambda )^{-1}\mu'_1(\tau)\zeta_{,\hat {t}}^{10} -2(1 - \lambda)^{-1}\zeta _{,\hat {t}}^{10}{}$$
$${}-2(1 - \lambda )^{-1/2}\zeta_{,\hat {t}\tau }^{10} -2(1 - \lambda )^{-1}\mu'_1(\tau)\zeta _{,\hat {t}}^{10} -(1 - \lambda )^{-1}\mu'_1(\tau)\zeta _{,\hat {t}}^{10},$$
(4.5)
$$O(\bar {\xi }^2\delta ^2){:}\quad \zeta _{,\hat {t}\hat{t}}^{22} + \zeta ^{22} =- (1 - \lambda )^{- 1}\zeta_{,\tau\tau }^{20} -2(1 - \lambda )^{-1/2}\mu'_1(\tau)\zeta _{,\hat{t}}^{12} -2(1 - \lambda )^{-1/2}\zeta _{,\hat {t}\tau }^{20}{}$$
$${}-(1 - \lambda )^{-1}\mu'_1(\tau)\zeta _{,\hat {t}}^{10} -2(1 - \lambda)^{-1/2}\zeta _{,\hat {t}}^{21} -2(1 - \lambda )^{-1}\mu'_1 (\tau)\zeta _{,\hat{t}}^{10} -2(1 - \lambda )^{-1}\zeta_{,\hat {t}}^{21};$$
$$O(\bar {\xi }^3){:}\quad \zeta_{,\hat {t}\hat {t}}^{30} + \zeta ^{30}= -(1 - \lambda )^{- 1}\mu'_1(\tau)\zeta_{,\hat {t}\tau }^{10} -2(1 -\lambda )^{-1/2}\mu'_1(\tau)\zeta_{,\hat {t}}^{10} -2(1 -\lambda )^{-1/2}\mu'_1(\tau)\zeta _{,\hat {t}}^{11}{}$$
$${}+(1 - \lambda)^{-1}b\{(\zeta ^{(10)})^3 +3[(\xi _0^{(1)})^2\zeta ^{(10)} + \xi _0^{(1)}(\zeta^{(10)})^2]\};$$
(4.6)

[3]

$$O(\bar {\xi }^3\delta ){:}\quad \zeta_{,\hat {t}\hat {t}}^{31} + \zeta ^{31}= -2(1 - \lambda )^{-1/2}\mu'_2(\tau)\zeta_{,\hat {t}\tau }^{11} - 2(1- \lambda )^{-1}\mu'_2(\tau)\zeta_{,\hat {t}}^{30} -(1 - \lambda )^{-1}\mu'_2(\tau)\zeta _{,\hat{t}}^{10}{}$$
$${}-2(1 - \lambda )^{-1}\mu'_2(\tau)\zeta_{,\hat {t}\tau }^{10} +(1 - \lambda )^{-1}3b\{(\zeta ^{(10)})^2 + \zeta ^{(11)} +[(\xi _0^{(1)} )^2\zeta ^{(11)} + 2\xi_0^{(1)} \zeta ^{(11)}\zeta ^{(11)}]\};$$
(4.7)
$$O(\bar {\xi }^3\delta ^2){:}\quad \zeta_{,\hat {t}\hat{t}}^{32} + \zeta ^{32} = -2(1 -\lambda )^{-1/2}\mu'_2 (\tau)\zeta_{,\hat {t}}^{12} -2(1 - \lambda)^{-1}\zeta_{,\tau\tau }^{30}{}$$
$${}+2(1 - \lambda )^{-1}\mu'_2(\tau)\zeta_{,\hat {t}\tau }^{11} -2(1 - \lambda )^{-1}\mu'_2(\tau)\zeta_{,\hat {t}\tau }^{11} -2(1 -\lambda )^{-1}\zeta _{,\hat {t}\tau }^{31} -(1 - \lambda )^{-1}\mu''_2(\tau)\zeta_{,\hat {t}}^{11}{}$$
$${}-2(1 - \lambda)^{-1}\mu'_2 (\tau)\zeta_{,\hat{t}}^{11} +2(1 - \lambda )^{-1}\zeta_{,\tau \tau }^{30} +(1 - \lambda )^{-1}3b\{(\zeta ^{(10)})^2+\zeta^{(12)} + (\zeta ^{(10)})^2 +\zeta ^{(10)} {}$$
$${}+[(\xi _0^{(1)})^2\zeta ^{(12)} + \xi _0^{(1)}] [(\zeta ^{(11)})^2 + 2\zeta^{(10)}\zeta ^{(12)}]\}$$
(4.8)

etc.

The initial conditions are obtained with the use of the first equation in system (4.2) at \(\hat {t} =\tau = 0\) and with allowance for Eq. (4.3):

$$O(\bar{\xi}){:}\quad \zeta ^{10}(0,0) = \zeta _{,\hat {t}\hat {t}}^{10} (0,0) = 0,\qquad O(\bar{\xi}\delta){:}\quad \zeta ^{11}(0,0) = \zeta _{,\hat {t}\hat {t}}^{11} (0,0) +\zeta_{,\tau }^{10} (0,0) =0,$$
$$O(\bar {\xi }\delta ^2){:}\quad \zeta^{12}(0,0) = \zeta_{,\hat {t}\hat{t}}^{12}(0,0) +\zeta _{,\tau }^{11} (0,0) = 0;$$
(4.9)
$$O(\bar {\xi }^2){:}\quad \zeta^{20}(0,0)=\zeta _{,\hat {t}\hat{t}}^{20} (0,0) + (1 - \lambda )^{-1/2}\mu'_1 (0) +\zeta_{,\hat{t}}^{22} (0,0) +(1 - \lambda )^{-1/2}\mu'_2 (0)=0,$$
$$O(\bar {\xi }^2\delta){:}\quad \zeta ^{21}(0,0) = \zeta_{,\hat {t}\hat {t}}^{21} (0,0) +(1 - \lambda)^{-1/2}\mu'_2 (0)\zeta_{,\hat {t}}^{11} (0,0) +\zeta_{,\tau }^{20}(0,0) = 0,$$
(4.10)
$$O(\bar {\xi}^2\delta ^2){:}\quad \zeta ^{22}(0,0) =\zeta _{,\hat {t}\hat {t}}^{22} (0,0) +(1 - \lambda )^{-1/2}\mu'_2 (0)\zeta _{,\hat {t}}^{21} (0,0) +(1 -\lambda )^{-1/2}\mu'_2 (0)\zeta_{,\hat {t}}^{20} (0,0)=0$$

etc.

The solution of the first equation in system (4.4) with allowance for the first initial condition in system (4.9) is written as

$$\zeta^{10}(\hat {t},\tau ) = a_1 (\tau)\cos \hat {t} + b_1 (\tau)\sin \hat {t}+B,$$
$$a_1 (0) = -B,\qquad b_1(0) = 0,\qquad B = \lambda/(1 - \lambda).$$
(4.11)

Substitution of this solution into the second equation of system (4.4) yields

$$\zeta _{,\hat {t}\hat {t}}^{11} + \zeta ^{11} = 2(1 - \lambda )^{-1/2}[(a_1 + a'_1)\sin \hat {t} +(b_1+ b'_1)\cos \hat{t}\;].$$
(4.12)

To ensure a uniformly valid asymptotic solution in the time scale \(\hat{t}\), we equate the coefficients at \(\cos \hat {t}\) and \(\sin \hat {t}\) in system (4.12) to zero. Thus, we obtain

$$b'_1 + b_1 = 0,\qquad a'_1 + a_1 =0.$$
(4.13)

Equations (4.13) and (4.11) yield

$$a_1 (\tau) = - B\mathrm{e}^{-\tau},\qquad b_1 (\tau) =0.$$
(4.14)

Therefore, we have

$$\zeta ^{10}(\hat {t},\tau) = a_1 (\tau)\cos \hat {t} + B.$$

Substituting Eq. (4.14) into the second equation of system (4.4), we obtain

$$\zeta^{11}(\hat {t},\tau ) = a_2 (\tau)\cos \hat {t} + b_2 (\tau)\sin \hat{t},\qquad a_{2} (0) =0,\qquad b_2 (0) = -B.$$
(4.15)

With the use of Eqs. (4.14) and (4.15), the third equation of system (4.4) yields

$$\zeta _{,\hat {t}\hat {t}}^{12} + \zeta ^{12} = -2(1-\lambda)^{-1/2}(-a_2 \sin \hat {t} + b_2\cos \hat {t}) -2(1-\lambda)^{-1/2}(-a'_2 \sin \hat {t} + b'_2 \cos \hat {t}){}$$
$${}-2(1 - \lambda )^{-1}a''_1 \cos\hat{t} -(1 - \lambda )^{-1}a''_1 \cos\hat{t}.$$
(4.16)

To ensure a uniformly valid asymptotic solution in the time scale \(\hat{t}\), we equate the coefficients at \(\cos \hat {t}\) and \(\sin \hat {t}\) in the right side of equality (4.16) to zero. As a result, we have

$$b'_2 + b_2 = (1 - \lambda)^{-1/2}(2a_1 + a''_1 )/2,\qquad a'_2+ a_2 =0.$$
(4.17)

Solving system (4.17) with the initial conditions (4.15), we find

$$a_2 (\tau) = 0,\qquad b_2 (\tau) = \frac{1}{2}\mathrm{e}^{- \tau}(1 - \lambda )^{-1/2} \Big(\int\limits_0^\tau (2a_1 +a''_1)\mathrm{e}^{s}\,ds + b_2 (0)\Big).$$

Therefore, we have

$$\zeta ^{11}(\hat {t},\tau )= b_2 (\tau)\sin \hat {t}.$$
(4.18)

Substituting Eq. (4.18) into the third equation of system (4.4), we obtain

$$\zeta ^{12}(\hat {t},\tau )=a_3 (\tau)\cos \hat {t} + b_3 (\tau)\sin \hat{t},\qquad a_3 (0) =0,\quad b_3 (0) =0.$$

The fourth equation of system (4.4) and Eq. (4.5) yield

$$\zeta ^{20} =\zeta ^{21} = \zeta ^{22} =0.$$

It should be noted that

$$(\zeta ^{10})^3 = (a_1 \cos \,\hat {t} + B)^3= \Big(B^3 + \frac{3}{2}\,Ba_1^2\Big) + \Big(3a_1 B^2 + \frac{3}{4}\,a_1^3\Big)\cos \hat {t} + \frac{3}{2}\,Ba_1^2\cos 2\hat {t} + \frac{1}{4}\,a_1^3 \cos 3\hat {t},$$
$$(\zeta ^{10})^2 = (a_1 \cos \hat {t} + B)^2 = \Big(B^2 + \frac{1}{2}\,a_1^2\Big) +2Ba_1 \cos \hat {t} + \frac{1}{2}\,a_1^2 \cos 2\hat {t}.$$
(4.19)

Taking into account Eq. (4.19), we write Eq. (4.6) in the form

$$\zeta_{,t\hat {t}}^{30} + \zeta ^{30} = \frac{2a_1\mu'_1}{1 - \lambda} \Big[\Big(B^3+ \frac{3}{2}\,Ba_1^2\Big) +\Big(3a_1 B^2 +\frac{3}{4}\,a_1^3\Big)\cos \hat {t} +\frac{3}{2}\,Ba_1^2 \cos 2\hat {t} + \frac{1}{4}\,a_1^3 \cos 3\hat{t}\Big]{}$$
$${}+ \frac{3b}{1 - \lambda}\Big\{\xi _0^{(1)} \Big[\Big(B^2 + \frac{1}{2}\,a_1^2\Big) + 2Ba_1 \cos \hat {t} + \frac{1}{2}\,a_1^2 \cos 2\hat {t}\Big] + (\xi _0^{(1)} )^2(a_1 \cos\hat {t} + B)\Big\}.$$
(4.20)

To ensure a uniformly valid asymptotic solution in the time scale \(\hat{t}\), we equate the coefficients at \(\cos \hat {t}\) in the right side of Eq. (4.20) to zero. Thus, we have

$$\mu'_2 (\tau) = - \frac{3}{2}\,b(1 -\lambda)^{-1/2} \Big[\Big(B^2 +\frac{1}{4}\,a_1^2\Big) +(2B\xi _0^{(1)} + (\xi _0^{(1)})^2)\Big],$$
$$\mu''_2 (\tau)= - \frac{3}{4}\,a_1 {a}'_1 b (1 - \lambda)^{-1/2},\qquad \mu'''_2 (\tau) = - \frac{3}{4}\,b(1 - \lambda )^{-1/2} (a_1^2 + a_1 a''),$$
$$\mu'_2 (0) = -\frac{15}{8}\,bB^2(1 - \lambda )^{-1/2}q_0,\qquad \mu'''_2 (0) = - \frac{3}{2}\,bB^2(1 - \lambda )^{-1/2}(a_1^2 + a_1 a''),$$
(4.21)
$$q_0= 1 + \frac{4}{15}\,\xi _0^{(1)} \Big(\frac{2}{B} + \frac{1}{B^2}\,\xi _0^{(1)}\Big).$$

Taking into account Eq. (4.21) similar to Eq. (4.20), we obtain the following expression from Eq. (4.6):

$$\zeta _{,\hat {t}\hat {t}}^{30} + \zeta ^{30} =a_4 (\tau)\cos \hat {t} + b_4 (\tau)\sin \hat{t}+ r_0 (t) - \frac{1}{3}\,r_1 (\tau)\cos 2\hat{t} - \frac{1}{8}\,r_2 (\tau)\cos 3\hat{t},$$
$$a_4(0) = - bB^3(1 - \lambda )^{ - 1}\Big(\frac{15}{32} + q_2\Big),\qquad q_2 = 3\xi _0^{(1)} \Big(\frac{3}{2B} + \frac{1}{B^2}\,\xi _0^{(1)} + \frac{1}{B}\Big),\qquad b_4 (0) =0,$$
$$r_0 (\tau) = b(1 - \lambda )^{ - 1}\Big[\Big(B^2 + \frac{3}{2}\,Ba_1^2\Big) + \Big(\frac{1}{2}\,B^2\,a_1^2 + B\xi _0^{(1)}\Big)\Big],$$
$$r_1 (\tau) = \frac{3}{2}\,ba_1(1- \lambda )^{ - 1}(B + \xi _0^{(1)}),\quad r_2 (\tau) = \frac{3}{4}\,ba_1^3 (1 - \lambda )^{ - 1},\quad r'_0 (\tau) = 3ba_1 a'_1 (1 - \lambda )^{ - 1}(B + \xi _0^{(1)}),$$
$$r''_0(\tau) = 3b(1 - \lambda )^{ - 1}(B + \xi _0^{(1)})(a_1 a''_1 + a_1^{\prime 2}),\quad r'_1(\tau) = 3ba_1a'_1(1 - \lambda )^{ - 1}(B + \xi _0^{(1)}),$$
$$r''_1(\tau) = 3b(1 - \lambda )^{ - 1}(B + \xi_0^{(1)})(a_1 a''_1 + a_1^{\prime2}),\quad r'_2 (\tau) =\frac{3}{4}\,ba'_1 a_1^2 (1 - \lambda )^{ - 1},$$
$$r''_2 (\tau) = \frac{3}{4}\,b(1 - \lambda )^{ - 1}(a_1^2 a''_1 + 2a_1 a_1^{\prime2}),\quad r_0 (0) = 3bB^3(1 -\lambda )^{ - 1}q_1,\quad r_1 (0) =\frac{3}{2}\,bB^3(1 - \lambda )^{ - 1}(1 + \xi _0^{(1)}),$$
$$r_2 (0) = -\frac{1}{4}\,bB^3(1 - \lambda )^{ -1},\quad r'_0(0) = 3bB^3(1 -\lambda )^{ - 1}\Big(1 + \frac{1}{4}\,\xi _0^{(1)}\Big),$$
$$r'_1(0) = - 3bB^3(1 - \lambda )^{ - 1}\Big(1 +\frac{1}{B}\,\xi_0^{(1)}\Big),\quad r'_2 (0) = - \frac{3}{4}\,bB^3(1 - \lambda )^{ -1},$$
$$r''_0(0) = 6bB^2(1 - \lambda)^{ - 1}(B + \xi _0^{(1)}),\qquad r''_1(\tau)=6bB^2(1 - \lambda )^{ - 1}(B + \xi _0^{(1)}),$$
$$r''_2 (0) = -\frac{9}{4}\,bB^3(1 - \lambda )^{ - 1}q_1,\quad q_1 = \frac{5}{2} + 3\xi _0^{(1)}\Big(\frac{3}{2B} + \frac{1}{B^3}\,\xi _0^{(1)}\Big).$$

It should be noted that

$$(\zeta ^{10})^2\zeta ^{11} = b_2 \Big(B^2 +\frac{1}{4}\,a_1^2\Big) \sin \hat {t} + a_1 b_2 B\sin 2\hat {t} +\frac{1}{4}\,b_2 a_1^2 \sin 3\hat {t}, \qquad \zeta^{10}\zeta ^{11} = \frac{1}{2}\,a_1 b_2 \,\sin 2\hat {t} + Bb_2 \sin\hat {t},$$
(4.22)
$$(\zeta ^{10})^2 = \Big(\frac{1}{2}\,a_1^2 + B^2\Big) +2Ba_1 \cos \hat {t} + \frac{1}{2}\,a_1^2 \cos 2\hat {t}.$$

With allowance for Eq. (4.22), Eq. (4.7) is written as

$$\zeta _{,t\hat {t}}^{31} + \zeta ^{31} = \frac{2b_4 \mu'_2 (\tau)}{\sqrt{1 - \lambda}}\sin \hat {t} + \frac{2a'_1\mu'_2 (\tau)}{1-\lambda}\,\sin \hat {t} +\frac{a'_1 \mu''_2 (\tau)}{1 - \lambda}\,\sin \hat {t}{}$$
$${} - \frac{2}{1 -\lambda}\sin \hat {t}\Big(-a'_4\sin \hat {t} + b'_4 \cos t + \frac{2}{3}\,r'_1 \sin 2\hat {t} + \frac{3}{8}\,r'_2\sin 3\hat{t}\Big){}$$
$${}+\frac{b}{1 - \lambda}\Big[3b_2\Big(B^2 + \frac{1}{2}\,a_1^2\Big)\sin \hat {t} +a_1 B\sin2\hat {t} + \frac{1}{4}\,a_1^2\sin 3\hat {t}\Big]{}$$
$${}+3\Big[b_2\xi _0^{(1)}\Big(\frac{1}{2}\,a_1 \sin 2\hat {t} +B\sin \hat {t}\Big)+ b_2(\xi _0^{(1)})^2\sin \hat {t}\Big]{}$$
$${}-\frac{2}{\sqrt{1 - \lambda}}\, \Big(-a_4 \sin \hat {t}+ b_4 \cos t+ \frac{2}{3}\,r_1 \sin 2\hat {t} +\frac{3}{8}\,r_2\sin 3\hat {t}\Big).$$
(4.23)

To ensure a uniformly valid asymptotic solution in the time scale \(\hat {t}\), we equate the coefficients at \(\cos \hat {t}\) in the right side of Eq. (4.23) to zero. Thus, we have

$$b'_4 + b_4 = 0,\qquad a'_2 + a_2 =q_3 (\tau),$$
$$q_3 (\tau) = - \frac{1}{2\sqrt{1 - \lambda}} \Big\{\mu'_2(\tau)\Big[2b_2(1 - \lambda ) +\frac{2}{1 - \lambda}\,(a_1+ a'_1)\Big]{} {}+\frac{3bb_2}{1 - \lambda}\Big[ \Big(B^2 +\frac{1}{4}\,a_2^2\Big) + 2B\xi _0^{(1)} + (\xi_0^{(1)})^2\Big] + \frac{a_1\mu'_2(\tau)}{1 - \lambda}\Big\},$$
$$q'_3(\tau)=-\frac{1}{2\sqrt{1 - \lambda}}\Big\{ \mu'_2(\tau)\Big[2b_2 (1 - \lambda )+ \frac{2}{1 - \lambda}\, (a'_1 + a_1)\Big] + \frac{1}{1 - \lambda}\,\mu''_2(\tau)(a_1 + a''_2){}$$
$${}+\frac{3bb_2}{1 - \lambda} \Big[\Big(B^2+\frac{1}{4}\,a_2^2\Big)+2B\xi _0^{(1)} + (\xi _0^{(1)})^2\Big]{} {}+ \frac{3}{2}\,\frac{a_1a'_1 bb_2}{1 - \lambda}\, \mu'_2(\tau)\Big(\frac{2b'_2}{\sqrt{1 - \lambda}} + \frac{2}{1 - \lambda}\,(a''_1 +a'_1)\Big)\Big\},$$
(4.24)
$$q_3(0)=-\frac{bB^3}{1 - \lambda}\,q_4,\qquad q'_3(0)=-\frac{bB^3}{(1 - \lambda )^{3/2}}\,q_5,$$
$$q_4 = \frac{15}{4}\,(q_0 - 1) - 3\xi _0^{(1)} \Big(\frac{2}{B} +\frac{1}{B^2}\,\xi _0^{(1)}\Big),$$
$$q_5= \frac{3}{2} + \Big(1 + \frac{1}{\sqrt{1 - \lambda}}\Big) \Big[\frac{15}{4}\,q_0 - 3\Big(\frac{5}{4} +\frac{2}{B}\,\xi _0^{(1)}\Big) + \frac{1}{B}\,(\xi_0^{(1)})^2\Big] - \frac{3}{\sqrt{1 - \lambda}}.$$

Solving system (4.24), we obtain

$$a_4 (\tau) = \mathrm{e}^{-\tau}\Big[-\frac{bB^3}{1 - \lambda}\, \Big(\frac{65}{32}+q_2\Big) \int\limits_0^\tau q_3(s)\mathrm{e}^s\,ds\Big],\qquad b_4(\tau) =0,$$
$$a_4'(0) =\frac{bB^3}{1 - \lambda}\,q_6,\quad a''_4(0) = - bB^3( 1-\lambda)^{3/2}\,q_7,\quad q_6 = q_1 + q_2,\quad q_7 = q_5 + \frac{q_6}{1 - \lambda}.$$

The solution of Eq. (4.7) with allowance for Eq. (4.23) is written as

$$\zeta ^{31}(\hat {t},\tau ) = a_5 (\tau)\cos \hat {t} + b_5 (\tau)\sin \hat {t} - \frac{1}{3}\,r_3(\tau)\sin 2\hat {t} - \frac{1}{8}\,r_4 (\tau)\sin3\hat {t},$$
$$a_5 (0) =0,\quad b_5 (0) =\frac{bB^3}{(1 - \lambda )^{3/2}}\,q_{11},\quad q_{11} = \frac{8}{3}\Big[\frac{1}{2} + \xi _0^{(1)} \Big(\frac{1}{B} + \frac{1}{2}\Big) + \frac{9}{64}\big(2(1 - \lambda)^{1/2} -1\big)\Big],$$
$$r_3 (\tau) = \frac{3bb_2}{1 - \lambda}\,(B + \xi _0^{(1)}) -\frac{4}{3\sqrt{1 - \lambda}}\,[r_1 (\tau) + r'_1 (\tau)],\quad r_4 (\tau) =\frac{3}{4}\Big[\frac{bb_2 a_1^2}{1 - \lambda} -\frac{r_2(\tau) + r'_2 (\tau)}{\sqrt{1 - \lambda}}\Big],$$
$$r'_3 (\tau) = \frac{3b}{1 - \lambda}\,(B + \xi _0^{(1)} ) (a_1 b'_2 + a'_1 ) - \frac{4}{3\sqrt{1 - \lambda}}\,[r'_1 (\tau) + r''_1 (\tau)],$$
$$r'_4 (\tau) = \frac{3b}{4(1 - \lambda)}\,(b'_2 a_1^2+ 2b_2 a_1 a''_1 ) -\frac{4}{3\sqrt{1 - \lambda}}\,[r'_2(\tau) + r''_2 (\tau)],$$
$$r_3 (0) = \frac{4bB}{\sqrt{1 - \lambda}}\, (B + \xi _0^{(1)})\Big[\frac{1}{3} + \xi _0^{(1)}\Big(\frac{1}{B} + \frac{1}{2}\Big)\Big],\qquad r_4 (0)= \frac{3}{4}\,\frac{bB^3}{\sqrt{1 - \lambda}}\,q_8,\quad q_8 = \frac{2}{\sqrt{1- \lambda}}-1,$$
$$r'_3 (0) = \frac{3B^3}{1- \lambda}\,(B + \xi _0^{(1)})(1 - \lambda )^{-1/2}\,q_9,\quad r'_4 (0) = \frac{3}{8}\,\frac{bB^3}{\sqrt{1 - \lambda}}\,q_{10},\quad q_{10} = \frac{4}{\sqrt{1 - \lambda}}- 1.$$

Let us calculate some terms in the right side of Eq. (4.8):

$$\zeta ^{10}(\zeta ^{11})^2 = \frac{1}{2}\,b_2^2 \Big(B + \frac{1}{2}\,a_1 \cos \hat {t} - B\cos 2\hat {t} - \frac{1}{2}\,a_1 \cos3\hat {t}\Big),\qquad (\zeta ^{11})^2 =\frac{1}{2}\,b_2^2 (1 - \cos 2\hat {t}),$$
$$\zeta ^{12}(\zeta ^{10})^2=\Big(B^2 + \frac{1}{2}\,a_1^2 \Big)a_2 \cos \hat {t} +a_1 a_2 B(1 + \cos 2\hat {t}) + \frac{1}{4}\,a_3 a_1^2(\cos 3\hat {t} + \cos \hat{t}){}$$
(4.25)
$${}+ \Big(B^2 + \frac{1}{4}\,a_1^2\Big)b_3 \sin \hat {t} + a_1 b_3 B\sin 2\hat {t} + \frac{1}{4}\,b_3 a_1^2 (\sin 3\hat {t} - \sin \hat{t}).$$

With allowance for Eq. (4.25), Eq. (4.8) is written as

$$\zeta_{,\hat {t}\hat {t}}^{32} + \zeta ^{32} = -\frac{2\mu'_2(\tau)}{\sqrt{1 - \lambda}} \Big(a''_4 \cos \hat {t} + r''_0 -\frac{1}{3}\,r''_1 \cos 2\hat {t} -\frac{1}{8}\,r''_2 \cos3\hat {t}\Big) -\frac{2\mu'_2(\tau)}{\sqrt{1 - \lambda}}\,(-a_3 \cos \hat {t}-b_3 \sin \hat {t}){}$$
$${}-\frac{2\mu'_2(\tau)}{\sqrt{1 -\lambda}}\,a'_2 \cos \hat {t} -\frac{1}{1 - \lambda}\,\mu''_2 (\tau)b_2 \cos \hat {t} -\frac{2}{\sqrt{1 - \lambda}}\Big(-a'_5\sin \hat {t} +b_5 \cos \hat {t} - \frac{2}{3}\,r'_3\cos 3\hat {t} - \frac{3}{8}\,r'_4 \cos 3\hat {t}\Big){}$$
$${}- \frac{2}{\sqrt{1 - \lambda}}\Big(- a_5 \sin \hat {t} + b_5 \cos \hat {t} + \frac{2}{3}\,r_3 \cos 2\hat {t} -\frac{3}{8}\,r_4 \cos 3\hat {t}\Big) - \frac{2\mu'_2(\tau)}{1 - \lambda}\,b_2\cos \hat {t}{}$$
$${}+\Big(a'_4 \cos \hat {t} +r_0 - \frac{1}{3}\,r'_1 \cos 2\hat {t} -\frac{1}{8}\,r'_2 \cos\hat {t}\Big){}$$
$${}+\frac{b}{1 - \lambda}\Bigg(3\Big\{\Big[\Big(\frac{1}{2}\,Bb_2^2 +\frac{1}{4}\,a_1 b_1^2 \sin \hat {t} -\frac{1}{2}\,Bb_2^2 \cos 2\hat {t} -\frac{1}{4}\,a_1 b_2^2 \cos 3\hat {t}\Big) + a_1 a_3{}$$
$${}+\Big[a_3 \Big(B^2 + \frac{1}{2}\,a_1^2\Big) +\frac{1}{4}\,a_3 a_1^2\Big]\cos \hat {t} +\Big[b_3\Big(B^2 +\frac{1}{2}\,a_1^2\Big) - \frac{1}{4}\,b_3 a_1^2\Big]\sin \hat {t} +a_1 a_3 \cos 2\hat {t}+ a_1 b_3 \sin 2\hat {t}{}$$
$${}+ \frac{1}{4}\,a_3a_1^2 \cos 3\hat {t} +\frac{1}{4}\,b_3 a_1^2 \sin 3\hat {t}\Big]\Big\} + 3\Big[\xi _0^{(1)}(a_1 a_3 +2a_3 \cos \hat {t} + 2b_3 \sin\hat {t} + a_1 a_3 \cos 2\hat {t}+ a_1 b_3\sin 2\hat {t}) {}$$
$${}+\frac{1}{2}\,b_2^2 \xi _0^{(1)} + (\xi _0^{(1)})^2(a_3 \cos \hat {t} + b_3 \sin \hat{t})\Big]\Bigg).$$
(4.26)

To ensure a uniformly valid asymptotic solution in the time scale \(\hat{t}\), we equate the coefficients at \(\cos \hat{t}\)  in the right side of Eq. (4.26) to zero. Thus, we obtain

$$b'_5 + b_5 = q_{12}(\tau),\qquad a'_5 + a_5 =q_{13}(\tau),$$
$$q_{12} (\tau) = \frac{1}{2\sqrt{1 - \lambda}}\, \Big\{\frac{a''_4}{1 - \lambda} - \frac{2a_3\mu'_2(\tau)}{\sqrt{1 - \lambda}} +\frac{2b'_2\mu'_2 (\tau)}{1 - \lambda} +\frac{b_2\mu''_2(\tau)}{1 - \lambda} +\frac{2}{1 - \lambda}\,(b_2\mu'_2(\tau) + a'_4 ){}$$
$${}-\frac{3b}{1 - \lambda}\Big[\frac{1}{4}\,a_1 b_2^2 +a_3\Big(B^2 +\frac{1}{2}\,a_1^2\Big) +\frac{1}{4}\,a_3 a_1^2 + 3a_3\xi _0^{(1)}(2 + \xi _0^{(1)})\Big]\Big\},$$
(4.27)
$$q_{13} (\tau) = -\frac{1}{2\sqrt{1 - \lambda}}\Big\{ \frac{2b_3\mu'_2 (\tau)}{\sqrt{1 - \lambda}} + \frac{3b}{1 - \lambda}\,\Big[b_3\Big(B^2 +\frac{1}{4}\,a_1^2\Big) - \frac{1}{4}\,b_3 a_1^2 + b_3 \xi _0^{(1)}(2 + \xi _0^{(1)})\Big]\Big\}.$$

It follows from Eqs. (4.27) that

$$a_5 (\tau) = \mathrm{e}^{ - \tau }\int\limits_0^\tau q_{13}(s)\mathrm{e}^s\,ds,\qquad b_5 (\tau)= \mathrm{e}^{ - \tau }\,\frac{bB^3}{(1 - \lambda )^{3/2}} +\mathrm{e}^{-\tau }\int\limits_0^\tau q_{12}(s)\mathrm{e}^s\,ds.$$

With allowance for Eq. (4.26), the solution of Eq. (4.8) is written as

$$\zeta ^{32}(\hat {t},\tau ) = a_6 (\tau)\cos \hat {t} + b_6 (\tau)\sin \hat {t} + r_5(\tau) - \frac{1}{3}\,r_6 (\tau)\cos 2\hat{t} - \frac{1}{3}\,r_7 \,(\tau)\sin 2\hat{t}{}$$
$${}-\frac{1}{8}\,r_8 (\tau)\cos 3\hat {t}- \frac{1}{8}\,r_9(\tau)\sin 3\hat {t},$$
$$a_6 (0) =\frac{bB^2}{(1 - \lambda )^{2}}\,q_{16},\qquad b_6(0) = 0,\qquad q_{16} = - \frac{15}{2}\,(B + \xi _0^{(1)} ) +\frac{1}{3}\,(q_{14} + Bq_{15}),$$
$$r_5(\tau) = \frac{r''_0(\tau)}{1 - \lambda} +\frac{3b}{1 - \lambda}\Big(\frac{1}{2}\,Bb_2^2 + a_1 a_3 +a_1 a_3 \xi _0^{(1)} + \frac{1}{2}\,b_2^2 \xi _0^{(1)}\Big),$$
$$r_6 (\tau)=\frac{1}{3}\,\frac{r''_1(\tau)}{1 - \lambda} +\frac{4}{3\sqrt{1 - \lambda}}\,[r_3(\tau) + r'_3 (\tau)] -\frac{3}{1 -\lambda}\Big(\frac{1}{2}\,Bbb_2^2-a_1 a_3 (1 - \xi_0^{(1)})\Big),$$
$$r_7 (\tau) =\frac{3ba_1b_3}{1 - \lambda}\,(1 + \xi_0^{(1)}),\quad r_8 (\tau) = \frac{1}{8}\,\frac{r''_2(\tau)}{1 - \lambda} +\frac{3}{4\,\sqrt{1 -\lambda}}\,[r_4(\tau)+r'_4 (\tau)] -\frac{3}{4}\,\frac{b}{1 -\lambda}\,(a_1 b_2^2 + a_3 a_1^2 ),$$
$$r_9 (\tau) =\frac{3}{4}\,bb_3 a_1^2 (1 - \lambda ),\quad r_5 (0) = \frac{15}{2}\,\frac{bB^2}{(1 - \lambda )^2}\, (B + \xi _0^{(1)}),\quad r_6(0) = \frac{bB^2}{(1 - \lambda )^2}\,q_{14},\quad r_7(0) = 0,$$
$$r_8(0) = \frac{1}{3}\,\frac{bB^3}{(1 - \lambda)^2}\,q_{15},\qquad r_9 (0) = -\frac{3}{4}\,\frac{B^3}{1 - \lambda},$$
$$q_{14} = \frac{1}{3}\,[6(B + \xi_0^{(1)}) + 4(B + \xi _0^{(1)} )q_9] + B\Big(\frac{16}{3}\,q_1-\frac{3}{2}\,(1 - \lambda )\Big),\quad q_{15} = q_{10} - 1 + 3(1 -\lambda ).$$

Continuing the calculations, we obtain the expression for the displacement \(\xi (\hat {t},\tau )\):

$$\xi (\hat {t},\tau ) = \bar {\xi }(\zeta ^{10} +\delta \zeta ^{11} + \delta ^2\zeta^{12} + \dots\;) + \bar {\xi}^3(\zeta ^{30} + \delta \zeta ^{31} + \delta^2\zeta ^{32}+ \dots\;) +\dots\;.$$
(4.28)

5. MAXIMUM DISPLACEMENT

The dynamic load \(\lambda _D\) is determined from the condition

$$\frac{d\lambda }{d\xi}\Big|_{\xi=\xi_a} =0,$$
(5.1)

where \(\xi_a\) is the value of \(\xi\) at which \(\lambda\)  reaches the maximum value.

Let \(\hat {t}_a\), \(t_{a}\), and \(\tau _a\) be the critical values of \(\hat {t}\), \(t\), and \(\tau\), respectively. The following asymptotic series are assumed to be valid:

$$\hat {t}_a = (\hat {t}_0 + \delta \hat {t}_{01} + \delta ^2\hat {t}_{02} + \dots\,) + \bar {\xi }(\hat {t}_{10} + \delta \hat {t}_{11} + \delta ^2\hat {t}_{12} + \dots\,) + \bar {\xi}^2(\hat {t}_{20}+ \delta \hat {t}_{21}+\delta ^2\hat {t}_{22} + \dots\,) +\dots\,,$$
$$t_a = (t_0 + \delta t_{01} + \delta ^2t_{02} + \dots\,) + \bar {\xi }(t_{10} + \delta t_{11} + \delta ^2t_{12} +\dots\,) + \bar {\xi }^2(t_{20} + \delta t_{21}+ \delta ^2t_{22} + \dots\,) + \dots\,,$$
$$\tau _a = \delta t_0 = \delta [(t_0 + \delta t_{01} + \delta ^2t_{02} + \dots\,) + \bar {\xi }(t_{10} + \delta t_{11}+ \delta ^2t_{12} +\dots \,){}$$
(5.2)
$${}+\bar {\xi }^2(t_{20} + \delta t_{21}+\delta ^2t_{22}+\dots\,)+ \dots\,].$$

For the maximum displacement, with allowance for Eq. (4.2), we have

$$\xi _{,\hat {t}} + (1 - \lambda )^{-1/2} \{\mu _1 (\tau)\bar {\xi } + \mu _2(\tau)\bar {\xi } + \mu'_3 (\tau)\bar {\xi}^2+ \dots\,\} \xi _{,\hat {t}} + \delta(1 - \lambda )^{-1/2}\xi _{,\tau } =0.$$
(5.3)

Substituting Eq. (4.28) into Eq. (5.3), using Eq. (5.2), and equating, after some transformations, the coefficients at \(\varepsilon ^i\delta ^j\)(\(i =1,2,3,\dots\), \(j = 1,2,3,\dots\)), we obtain the following system of equations:

$$O(\varepsilon){:}\quad \zeta _{,\hat{t}}^{10} = 0,\qquad O(\varepsilon \delta ){:}\quad \hat {t}_{01} \zeta _{,\hat {t}\hat{t}}^{10} + t_0 \zeta _{,\hat {t}\tau }^{10} + (1 -\lambda )^{-1/2}\zeta _{,\tau }^{10} +\zeta _{,\hat {t}}^{10} + \zeta _{,\hat {t}}^{11} =0,$$
$$O(\varepsilon \delta ^2){:}\quad \hat {t}_{02} \zeta _{,\hat {t}\hat{t}}^{10} + t_0 \zeta _{,\hat {t}\tau }^{11} + \hat{t}_{01}^2 \zeta _{,\hat {t}\hat {t}\hat {t}}^{10}/2 + \hat{t}_{01} t_0 \zeta _{,\hat {t}\hat {t}\tau }^{10} + \hat{t}_{01} \zeta _{,\hat {t}\hat {t}}^{11} + t_0 \zeta_{,\hat {t}\tau }^{11}+\zeta _{,\hat {t}}^{12}{} {}+ \hat {t}_{01}(1 - \lambda )^{-1/2}\zeta _{,\hat{t}\tau }^{10} + t_0(1 - \lambda )^{-1/2}\zeta _{,\tau \tau }^{10} = 0,$$
(5.4)
$$O(\varepsilon ^2){:}\quad \hat {t}_{01} \zeta_{,\hat {t}\hat {t}}^{10} =0;$$
$$O(\varepsilon ^3){:}\quad \hat {t}_{20}\zeta _{,\hat {t}\hat {t}}^{10} + \zeta _{,\hat{t}}^{30} + (1 - \lambda )^{-1}\mu'_2(\tau)\zeta _{,\hat {t}}^{10} + \hat {t}_0^2\zeta _{,\hat {t}\hat {t}\hat {t}}^{10}/2 =0,$$
$$O(\varepsilon ^3\delta ){:}\quad \hat {t}_{21} \zeta _{,\hat{t}\hat {t}}^{10} + t_{20} \zeta _{,\hat {t}\tau }^{10} + [(\hat {t}_{01} \hat {t}_{11} + 2\hat{t}_{20} \hat {t}_{01}) \zeta _{,\hat {t}\hat{t}\hat {t}}^{10} +(2\hat {t}_{20} t_0 +2\hat {t}_{20} t_{10} ) \zeta _{,\hat {t}\hat{t}\tau }^{10}]/2 +\hat {t}_{20} \zeta _{,\hat {t}\hat{t}}^{11}{}$$
(5.5)
$${}+\hat {t}_{01} \zeta _{,\hat {t}\hat {t}}^{30} +\zeta _{,\hat {t}}^{31} +(1 - \lambda )^{-1/2}\mu'_2(\tau)\hat {t}_{01} \zeta_{,\hat {t}\hat {t}}^{10} +(1 - \lambda )^{-1/2}\mu'_2(\tau)t_0\zeta _{,\hat{t}}^{10}{}$$
$${}+(1 - \lambda )^{-1/2}\mu'_2(\tau)\zeta _{,\hat {t}}^{11} +(1 - \lambda )^{-1/2}\hat {t}_{20} \zeta _{,\hat{t}\tau }^{10} +(1 - \lambda )^{-1/2}\zeta _{,\tau }^{30} =0.$$

Substituting \(\zeta _{,\hat {t}}^{10}\) from Eq. (4.14) into the first equation of system (5.4) and applying some simplifications, we obtain

$$\sin \hat {t}_0 = 0;$$

therefore,

$$\hat {t}_0 =\pi.$$
(5.6)

In Eq. (5.6), \(\hat {t}_0\) is the least nontrivial solution.

It follows from the second equation of system (5.4) that

$$\hat {t}_{01} = - \frac{1}{\zeta _{,\hat{t}\hat {t}}^{10} (\hat {t}_0 ,0)}\,\Big[ t_0\zeta _{,\hat {t}\tau }^{10} (\hat {t}_0 ,0) +\frac{1}{\sqrt{1 - \lambda}}\,\zeta_{,\tau }^{10} (\hat {t}_0 ,0) +\zeta_{,\hat {t}}^{11} (\hat {t}_0 ,0)\Big],$$
$$\zeta _{,\hat {t}\,\hat {t}}^{10} (\hat {t}_0 ,0) = -B,\quad \zeta _{,\hat {t}\,\tau }^{10} (\hat {t}_0 ,0) =0,\quad \zeta _{,\tau }^{11} (\hat {t}_0 ,0)=0,\quad \zeta _{,\tau }^{10}(\hat {t}_0 ,0) = -B;$$

therefore,

$$\hat {t}_{01} = 1 - (1 - \lambda)^{-1/2}.$$

Similarly, it follows from the third equation of system (5.4) that

$$\hat {t}_{02} = - \frac{1}{\zeta _{,\hat {t}\hat{t}}^{10} (\hat {t}_0 ,0)} \Big[t_0 \zeta_{,\hat {t}\tau }^{11} (\hat {t}_0 ,0) +\frac{t_{01}}{\sqrt{1 - \lambda}}\,\zeta_{,\hat {t}\tau }^{10} (\hat {t}_0 ,0) +\frac{t_0}{\sqrt{1 - \lambda}}\,\zeta _{,\tau \tau}^{011} (\hat {t}_0,0)\Big],$$
$$\zeta _{,\hat {t}\tau }^{10}(\hat {t}_0,0)= B,\quad \zeta _{,\hat {t}\tau }^{11}(\hat {t}_0,0)= -B[1 - 3/(2\sqrt{1- \lambda}\,)],\quad \zeta _{,\tau \tau }^{10} (\hat{t}_0 ,0) = B;$$

therefore,

$$\hat {t}_{02} =\Big(t_0 + \frac{\hat {t}_{01}}{\sqrt{1 - \lambda}}\Big) \Big[- B\Big(1 - \frac{3}{2\sqrt{1 - \lambda}}\Big)\Big] + t_0 \hat {t}_{01} - \frac{t_{01}}{\sqrt{1 - \lambda}}.$$

The first equation of system (5.5) yields

$$\hat {t}_{10} = \hat {t}_{20} =0.$$

Simplifying the second equation of system (5.5), we obtain

$$\hat {t}_{21} = - \frac{1}{\zeta_{,\hat {t}\hat {t}}^{10}(\hat {t}_0 ,0)}\, \Big[t_0 \zeta _{,\hat{t}\hat {t}}^{10} (\hat {t}_0 ,0) +\frac{t_{01}\mu'_2 (0)}{\sqrt{1 - \lambda}}\,\zeta _{,\hat {t}}^{10} (\hat {t}_0 ,0) +\zeta _{,\hat {t}}^{10} (\hat {t}_0 ,0) + \frac{1}{\sqrt{1 - \lambda}} +\zeta_{,\tau }^{30} (\hat {t}_0 ,0) +\zeta_{,\hat{t}}^{31} (\hat {t}_0 ,0)\Big],$$
$$\zeta _{,\hat {t}\hat {t}}^{10} (\hat {t}_0,0) = \frac{bB^3}{1 - \lambda}\,q_{17},\quad \zeta _{,\hat {t}\tau }^{31} (\hat {t}_0,0) = \frac{bB^3}{\sqrt{1 - \lambda}}\,q_{18},\quad \zeta _{,\hat {t}}^{30} (\hat {t}_0 ,0) = - \frac{B}{1-\lambda}\,q_{19},$$
$$\zeta _{,\tau }^{10} (\hat {t}_0 ,0) =\frac{bB^3}{1 -\lambda}\,q_{20},\quad q_{17} = - \frac{1}{B}\,q_2 + \frac{2}{3}\,(1 + \xi_0^{(1)}) + \frac{9}{8},$$
$$q_{18} = - q_{11} - \frac{8}{3}\,q_1 - \frac{9}{8}\Big(\frac{2}{\sqrt{1 - \lambda}} -1\Big),\quad q_{19} = q_2 +q_4,\quad q_{20} = q_{19} + 4\Big(1+ \frac{\xi _0^{(1)}}{B}\Big)-\frac{3}{8};$$

therefore,

$$\hat {t}_{21} = bB\Big[ \frac{B\hat {t}_{01}}{1 - \lambda}\,q_{17}\mu'_2 (0) \frac{1 - \hat {t}_{01}}{\sqrt{1 - \lambda}} + \frac{B}{\sqrt{1 - \lambda}}\,q_{18} + \frac{B}{\sqrt{1 -\lambda}}\,q_{20}\Big].$$

Now we determine the maximum displacement (critical value) \(\xi _a\). Taking into account Eq. (4.28), we obtain

$$\xi _a = \bar {\xi }(\zeta _a^{10} + \delta \zeta _a^{11} +\delta ^2\zeta _a^{12} + \dots\,) + \bar {\xi }^3(\zeta _a^{30} + \delta \zeta _a^{31} + \delta^2\zeta _a^{32} + \dots\,) + \dots\,,$$

where

$$\zeta _a^{(ij)} = \zeta ^{ij}(\hat {t}_a ,\tau _a ).$$
(5.7)

Expanding each term in Eq. (5.7) into the Taylor series and applying some transformations, we obtain

$$\xi _a = \bar {\xi }\{\zeta ^{10}(\hat {t}_0,0) + \delta[t_0 \zeta _{,\tau }^{10} (\hat{t},0) + \zeta ^{12}(\hat {t}_0 ,0)] + \delta ^2[t_{01} \zeta _{,\tau }^{10} (\hat{t}_0 ,0) +\hat {t}_{01} \zeta _{,\hat{t}\hat {t}}^{10} (\hat {t}_0 ,0)/2{}$$
$${}+t_0^2\zeta _{,\tau\tau }^{10} (\hat {t}_0 ,0)/2 + \hat{t}_{01}\zeta _{,\hat {t}}^{11} (\hat {t}_0 ,0) + \zeta ^{12}(\hat {t}_0 ,0)]\}{}$$
$$\qquad{}+ \bar {\xi }^3\{\zeta ^{30}(\hat {t}_0,0) +\delta[t_{20} \zeta _{,\tau }^{10} (\hat {t}_0 ,0) + t_0 \zeta _{,\tau }^{30} (\hat{t}_0 ,0) + \zeta ^{31}(\hat {t}_0 ,0)]{}$$
$${}+ \delta ^2[t_{21} \zeta _{,\tau }^{10} (\hat{t}_0 ,0) +\hat {t}_{01} \hat {t}_{21} \zeta_{,\hat {t}\hat {t}}^{10} (\hat {t}_0 ,0)/2 +\hat {t}_{21} \zeta _{,\hat {t}}^{10} (\hat {t}_0 ,0) +\hat {t}_{01}^2 \zeta _{,\hat {t}\hat {t}}^{10} (\hat {t}_0,0)/2{}$$
$${}+t_{01} \zeta _{,\tau }^{30} (\hat {t}_0 ,0) +t_0^2 \zeta _{,\tau \tau}^{31} (\hat {t}_0 ,0)/2 + \zeta ^{32}(\hat {t}_0 ,0)]\}+ \dots\,.$$
(5.8)

The expressions for the terms in Eq. (5.8) can be simplified:

$$\zeta ^{10}(\hat {t}_0 ,0) =2B,\quad \zeta_{,\tau }^{10} (\hat{t}_0,0) = - B,\quad \zeta^{10}(\hat {t}_0 ,0) = \frac{4bB^2}{1 - \lambda}\,q_{21},\quad \zeta _{,\hat {t}}^{30}(\hat {t}_0 ,0) = - \frac{19}{4}\,\frac{bB^3}{1 -\lambda}\,q_{23},$$
$$\zeta ^{31}(\hat {t}_0 ,0) =0,\quad \zeta _{,\hat {t}}^{11} (\hat{t}_0 ,0) = B,\quad \zeta ^{32}(\hat {t}_0 ,0) = \frac{bB^3}{1 - \lambda}\,q_{24},\quad \zeta_{,\tau\tau }^{30} (\hat{t}_0 ,0) = \frac{bB^3}{1 - \lambda}\,q_{25},$$
$$\zeta_{,\tau\tau }^{10} (\hat {t}_0,0)= 0,\quad \zeta_{,\tau}^{30}(\hat {t}_0 ,0)=\frac{bB^3}{1 -\lambda}\,q_{22},\quad \zeta_{,\hat {t}\tau }^{10} (\hat {t}_0 ,0) = - B,\quad \zeta ^{12}(\hat {t}_0 ,0) =0,$$
$$q_{21} = 1 + \frac{1}{8}\,\xi _0^{(1)}\Big[6\Big(\frac{3}{2B} + \frac{1}{B^2}\,\xi _0^{(1)}\Big)- 1\Big],\quad q_{22} = 6\Big(1 +\frac{1}{B}\,\xi _0^{(1)}\Big) + 3 - q_6,$$
(5.9)
$$q_{23} = \frac{1}{19}- 4\Big[\frac{5}{2} - 9\Big(\frac{3}{2B} + \frac{1}{B^2}\,\xi_0^{(1)}\Big)\Big],\quad q_{24} = 15\Big(1+ \frac{1}{B}\Big) - \frac{11}{24}\,\frac{1}{B}\,q_{14},$$
$$q_{25} = \frac{q_7}{\sqrt{1 - \lambda}} +4\Big(1 + \frac{1}{B}\,\xi _0^{(1)}\Big)-\frac{9}{32}.$$

Substituting Eq. (5.9) into Eq. (5.8) and applying some simplifications, we obtain

$$\xi _a = e_1 \bar {\xi } + e_3 \bar {\xi }^3 + \dots\,,$$
(5.10)

where

$$e_1 = 2B(1 + A_{11} \delta+ A_{12} \delta ^2),\quad e_3 = \frac{4bB^2}{1 - \lambda}\,q_{21}(1+ A_{31} \delta + A_{32}\delta ^2),$$
$$A_{11}= - \frac{1}{2}\,t_0 ,\quad A_{12} = - \frac{1}{2}\,t_{01} +\frac{3}{2}\,\hat {t}_{01} - \frac{1}{2}\,t_0^2,\quad A_{31} =\frac{1}{4B^2q_{21}}\,t_0(1 - \lambda)\,\Big( \frac{t_0}{1 - \lambda}\,q_{19} - q_{20}\Big),$$
$$A_{32} = \frac{1}{4q_{21}}\,(1 - \lambda ) \Big[\frac{1}{bB^2}\Big(\hat {t}_{21} -t_{21} - \frac{1}{2}\,\hat {t}_{01} \hat {t}_{02}\Big) +\frac{1}{1 -\lambda}\Big(t_{01}q_{19} - \frac{19}{2}\,t_{01}^2 q_{20} + \frac{q_{23}}{1 - \lambda} +\frac{1}{2}\,t_{20}^2 q_{25}\Big)\Big].$$

Equation (5.10) is similar to that from which we earlier derived Eq. (2.10); therefore, we expect the dynamic buckling load to be obtained as

$$\bar {\xi } = \frac{2}{3\sqrt 3 }\sqrt {\frac{e_1 }{e_3 }}\,.$$
(5.11)

It follows from Eq. (5.11) with allowance for Eq. (5.10) that

$$(1 - \lambda _D )^{3/2} = \frac{3\sqrt 6}{2\sqrt{q_{21}}}\,\sqrt{b}\, \lambda _D \bar {\xi }\,\Big(\frac{1 + A_{11} \delta + \delta ^2A_{12} } {1 + A_{31} \delta + \delta^2A_{32}}\Big)^{-1/2}.$$
(5.12)

Dividing Eq. (5.12) by Eq. (2.11), we obtain the relation between the dynamic buckling load \(\lambda _D\) and static buckling load  \(\lambda _S\):

$$\Big(\frac{1 - \lambda _D}{1 - \lambda _S}\Big)^{3/2} = \frac{\sqrt 2 }{\sqrt {q_{21}}}\,\frac{\lambda _D }{\lambda _S }\, \Big(\frac{1 + A_{11} \delta +A_{12} \delta ^2} {1 + A_{31} \delta + A_{32} \delta ^2}\Big)^{-1/2}.$$
(5.13)

Thus, if either \(\lambda _D\) or \(\lambda _S\) is known, one can determine the other load without the labor of repeating the arduous task all over. If the structure is undamped, but is stressed by a step load superposed on the static pre-load, the dynamic buckling load is calculated by Eqs. (5.12) and (5.13) as

$$(1 - \lambda _D )^{3/2} = \frac{3\sqrt 6}{2}\,\sqrt{b}\, \lambda _D \bar {\xi }\Big\{ 1 +\frac{1}{8}\,\xi _0^{(1)}\Big[6\Big(\frac{3}{2B} +\frac{1}{B^2}\,\xi _0^{(1)}\Big)-1\Big]\Big\}^{ -1/2},$$
$$\Big(\frac{1 - \lambda _D}{1 - \lambda _S}\Big)^{3/2} = \sqrt 2\,\frac{\lambda _D }{\lambda _S }\, \Big\{1 +\frac{1}{8}\,\xi _0^{(1)} \Big[6\Big(\frac{1}{2B} +\frac{1}{B^2}\,\xi _0^{(1)}\Big)-1\Big]\Big\}^{ -1/2}.$$
(5.14)

If there was no static pre-load, then \(\xi _0 =\xi _0^{(i)} = 0\)(\(i = 1,2,3,\dots\,\)), and Eq. (5.14) yields

$$(1 - \lambda _D )^{3/2} = \frac{3\sqrt 6 }{2}\,\sqrt{b}\,\lambda _D \bar {\xi },\qquad \Big(\frac{1 - \lambda _D}{1 - \lambda _S}\Big)^{3/2} = \sqrt 2\, \frac{\lambda _D }{\lambda _S }.$$
(5.15)

Formula (5.15) was first derived in [8] by using the phase plane analysis. Formulas (5.12) and (5.13) are valid for \(0 < \varepsilon \ll 1\) and \(0 < \delta \ll 1\).

Fig. 2
figure 2

Dynamic buckling load \(\lambda _D\) versus the imperfection parameter \(\bar {\xi }\) calculated by Eq. (5.12) for different values of \(\xi _0\) and \(\delta\): (1) \(\xi_0=0\) and  \(\delta=0\); (2) \(\xi_0=0\) and  \(\delta=0.02\); (3) \(\xi_0\neq 0\) and  \(\delta=0\); (4) \(\xi_0\neq 0\) and \(\delta=0.02\).

Full size image
Fig. 3
figure 3

Dynamic buckling load \(\lambda _D\) versus the static buckling load \(\lambda _S\) calculated by Eq. (5.13) for different values of \(\xi _0\) and \(\delta\)(notation the same as in Fig. 2).

Full size image
Fig. 4
figure 4

Dynamic buckling load \(\lambda _D\) versus the damping coefficient \(\delta\) for \(\bar {\xi } = 0.04\) and different values of \(\xi _0\) and \(\lambda _0\): (1) \(\xi_0=0\)  and \(\lambda_0=0\); (2) \(\xi_0=0\) and \(\lambda_0=0.02\); (3) \(\xi_0\neq 0\) and \(\lambda_0=0\); (4) \(\xi_0\neq 0\) and \(\lambda_0=0.02\).

Full size image

6. ANALYSIS OF RESULTS

The dynamic buckling load was calculated within the framework of the MATLAB software system. The relations between the dynamic buckling load \(\lambda _D\) and various parameters of the problem are shown in Figs. 2–4. In the case of static pre-loading, the dynamic buckling load\(\lambda _D\) is greater than that in the case without pre-loading. The value of \(\lambda _D\) increases with increasing damping and decreases with increasing initial imperfection \(\bar{\xi}\).

CONCLUSIONS

The problem of dynamic buckling of the structure is analyzed with the use of the perturbation procedures and asymptotic expansion in two small parameters. All the results are asymptotic in nature. Though the results are obtained for a nonlinear cubic model elastic structure, the proposed method can be extended to real-life elastic structures, such as toroidal, cylindrical, and spherical shells. Structures with nonlinear damping can be also investigated by using this perturbation procedure.