1 INTRODUCTION

To guarantee the security of quantum key distribution, it is fundamentally important to prevent the access of an eavesdropper to the transmitting and receiving devices. Bits of the key on the receiver side are obtained from photocounts of single-photon avalanche detectors, which should be inaccessible to the eavesdropper, which requires certain measures to protect detectors from information leakage at the detection of quantum states.

The eavesdropper (Eve) can know in which of the detectors a count occurs even without direct access to the detectors. Detecting back-flash emission from detectors to the communication channel, the eavesdropper can get information of the bits of the key, remaining undetected.

This particularly concerns quantum key distribution systems involving superconducting detectors. Because of the use of large “dry” cryostats, detectors are located beyond the main receiver device and are connected to it through a fiber and electric cables. For this reason, it is quite difficult to ensure their complete guaranteed isolation from the environment.

In this regard, there is a fundamental question: Can a quantum key distribution system where detectors are generally accessible and are even located beyond the main instrument and results are accessible to the eavesdropper guarantee the cryptography security of keys?  Footnote 1

The positive answer to this question is given in this work.

We consider below the BB84 protocol [1] in the standard point–point configuration involving phase encoding in optical fiber systems. Two bases, direct + and conjugate ×, and two states corresponding to 0 and 1 in each basis are used in the protocol.

Alice on the transmitter side randomly chooses a basis and a state in it by choosing the relative phase in two pulses of the states. Four phases are generally used. In the + basis, the logical bits 0+ and 1+ correspond to the phases φA = 0 and π, respectively. In the × basis, the bits 0× and 1× correspond to the phases φA = π/2 and 3π/2, respectively.

In the standard version of the protocol, Bob on the receiver side chooses only two phases φB = 0 and π/2 corresponding to the + and × bases, respectively.

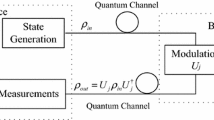
Alice and Bob hold only messages where their bases coincide. On the receiver side, states from the communication channel after passage through a Mach–Zehnder interferometer [2] reach the de-tectors. The probabilities of a count in detectors U and D are proportional to \({{\cos }^{2}}\left( {\frac{{{{\varphi }_{{\text{A}}}} - {{\varphi }_{{\text{B}}}}}}{2}} \right)\) and \({{\sin }^{2}}\left( {\frac{{{{\varphi }_{{\text{A}}}} - {{\varphi }_{{\text{B}}}}}}{2}} \right)\), respectively (Fig. 1). When the bases coincide, if Alice sends 0+, a count occurs only in the detector U because interference is constructive on the detector U and is destructive on the detector D. If Alice sends 1+, a count occurs in the detector D, whereas a count is absent in the detector U.

Fig. 1.
figure 1

Schemes of the quantum key distribution for (a) a modified protocol with untrusted detectors and (b) a twin-field protocol. The probabilities of a count in detectors U and D are proportional to \({{\cos }^{2}}\left( {\frac{{{{\varphi }_{{\text{A}}}} - {{\varphi }_{{\text{B}}}}}}{2}} \right)\) and \({{\sin }^{2}}\left( {\frac{{{{\varphi }_{{\text{A}}}} - {{\varphi }_{{\text{B}}}}}}{2}} \right)\), respectively.

Full size image

Similarly, in the × basis, the states 0× and 1× initiate a count in the detectors D and U, respectively.

Since bases (not states in a basis) are opened after the transfer of states, if the eavesdropper had access to detectors and knew which of the detectors recorded a count, the eavesdropper would know the entire transferred key. For this reason, detectors in the standard quantum key distribution systems should be protected; i.e., both the direct and indirect access of the eavesdropper should be excluded.

2 INFORMAL REASONS FOR THE SECURITY OF A MODIFIED PROTOCOL

Below, we describe a modified protocol with untrusted detectors and discuss informal reasons for the security of the new protocol.

The idea is a random choice of four rather than two phase values, two in each basis, on the receiver side. The phases and the corresponding detectors where a count occurs have the form

$${\kern 1pt} {\text{basis}} + \left\{ {\begin{array}{*{20}{l}} {{\kern 1pt} {\text{bit}}\;0\quad {{\varphi }_{{\text{A}}}} = 0}&{\left\{ {\begin{array}{*{20}{l}} {{{\varphi }_{{\text{B}}}} = 0 \to U} \\ {{{\varphi }_{{\text{B}}}} = \pi \to D} \end{array}} \right.} \\ {{\kern 1pt} {\text{bit}}\;1\quad {{\varphi }_{{\text{A}}}} = \pi }&{\left\{ {\begin{array}{*{20}{l}} {{{\varphi }_{{\text{B}}}} = 0 \to D} \\ {{{\varphi }_{{\text{B}}}} = \pi \to U} \end{array}} \right.} \end{array},} \right.$$
(1)
$${\kern 1pt} {\text{basis}} \times \left\{ {\begin{array}{*{20}{l}} {{\text{bit}}\;0\quad {{\varphi }_{{\text{A}}}} = \frac{\pi }{2}}&{\left\{ {\begin{array}{*{20}{l}} {{{\varphi }_{{\text{B}}}} = \frac{\pi }{2} \to U} \\ {{{\varphi }_{{\text{B}}}} = \frac{{3\pi }}{2} \to D} \end{array}} \right.} \\ {{\text{bit}}\;1\quad {{\varphi }_{{\text{A}}}} = \frac{{3\pi }}{2}}&{\left\{ {\begin{array}{*{20}{l}} {{{\varphi }_{{\text{B}}}} = \frac{{3\pi }}{2} \to U} \\ {{{\varphi }_{{\text{B}}}} = \frac{\pi }{2} \to D} \end{array}} \right.} \end{array}.} \right.$$
(2)

In each basis, e.g., in the + basis, if Alice sends 0 (φA = 0), depending on the random choice of phases by Bob (φB = 0 or π), which is unknown to Eve even after the opening of bases, Eve, who does not know Bob’s phase, will “see” a random count in one of the detectors U or D for each bit 0 or 1 (see Eqs. (1) and (2)). The procedures for other states are similar.

Thus, additional randomness introduced by Bob in each basis, which is unknown to Eve, makes it possible to open counts in detectors for Eve, but she will not know the transmitted key bit.

The possibility of access to detectors for Eve can be illustrated in terms of information theory.

In the standard protocol, Alice chooses a basis and a bit in this basis that are unknown to Eve. Bob chooses only a basis that is also unknown to Eve. Consequently, before the opening of the bases, Eve does not know three bits of information. When the bases are opened, Alice and Bob each open one bit of information. As a result, one of three bits remains unknown to Eve. This bit is a common secret of Alice and Bob. Knowing the basis, Bob obtains this bit through a count in a detector.

In the modified protocol, Alice has two bits of information unknown to Eve before opening of the bases. Bob also has two bits of information before opening of the bases. When the bases are opened, Alice and Bob each open one bit of information. Two bits remain unknown to Eve. If access to counts in detectors is allowed to Eve, she receives one bit of information after a count in a detector. As a result, one bit of information remains unknown to Eve and is present in a key. Bob also knows a detector where a count occurs, but Bob also knows his choice of the phase and, thus, can identify a bit sent by Alice. Eve does not know the phase chosen by Bob and knows only a count in a detector in a given basis. Observing only the count in the detector and knowing the basis, Eve cannot know the bit transmitted by Alice because she does not know the phase by Bob.

It is interesting to compare our protocol with the actively developed twin-field protocol [3, 4],Footnote 2 where the detectors are also untrusted and accessible (open) to Eve.

In the twin-field protocol (see Fig. 1), Alice and Bob independently and equiprobably choose two phases in each of the two bases, e.g., in the + basis, 0 → φA = 0 and 1 → φA = π for Alice and 0 → φB = 0 and 1 → φB = π for Bob. Since the interference signals on the detectors U and D are proportional to \({{\cos }^{2}}\left( {\frac{{{{\varphi }_{{\text{A}}}} - {{\varphi }_{{\text{B}}}}}}{2}} \right)\) and \({{\sin }^{2}}\left( {\frac{{{{\varphi }_{{\text{A}}}} - {{\varphi }_{{\text{B}}}}}}{2}} \right)\), respectively, the count occurs in the detectors U and D at the identical and different phases, respectively. The detectors are accessible to the eavesdropper.

Alice generates two bits of information unknown to the eavesdropper: one bit for the choice of the basis and the second bit for a logical 0 or 1 in the basis. Bob also generates two bits of information unknown to Eve. When the bases are opened, Alice and Bob each open one bit of information. Two of four bits remain unknown to Eve. After the count in the detector U or D, Eve gets one bit of information. One bit of information remains unknown to Eve and is a common secret of Alice and Bob.

Unlike Eve, knowing the count of the detector and which bit they send, Alice and Bob obtain a common bit. For example, if both Alice and Bob send 0, the count occurs in detector U. Such an event takes place if Alice and Bob send identical bits (each of them knows the sent bits). Consequently, preliminarily making an agreement, Alice and Bob will have the common bit 0. If both Alice and Bob send 1, the count also occurs in detector U, and Alice and Bob will have the common bit 1. Eve observes only the count in the detector U and does not know the common bit because the count in the detector U can occur from both bits 0 and 1 sent by Alice and Bob.

This is an informal information-theory reason for obtaining the common secret bit by Alice and Bob.

3 FORMAL PROOF OF SECURITY

The main idea in the formalization of untrusted detectors accessible to Eve is to reduce the new protocol to an equivalent protocol involving the standard BB84 protocol with the delivery of additional quantum states carrying information on the count in one of the two detectors to Eve.

We consider the standard BB84 protocol. Obtaining a count, 0 or 1 correct or incorrect, in detectors in each basis, which are inaccessible to Eve, Bob reports this result to Eve, randomly and equiprobably interchanging the detectors U and D. In particular, if the count occurs in the detector U, Bob randomly and equiprobably chooses the detector U or D and reports his choice to Eve.

This procedure is equivalent to the modified protocol where Bob randomly chooses one of two phases in each basis leading to the random permutation (for Eve) of counts in the detectors U and D.

Further, we consider a single-photon case with the identical quantum efficiencies of the detectors to avoid excess technical details. The nonequal quantum efficiencies of detectors can be taken into account by the method presented in [6, 7].

Thus, it is sufficient to consider the BB84 protocol supplemented by information for Eve concerning the random permutation of the detector where the count occurs. Because the situation is symmetric in the bases, it is sufficient to consider the situation in one basis, e.g., in the + basis. The results in the × basis are obtained by the unitary transformation of information states.

We use the EPR version of the protocol (see details in, e.g., [6]). Alice prepares the EPR state, i.e., her subsystem X, and stores it on her side as a reference subsystem and sends the subsystem Y to Bob. The subsystem Y in the quantum communication channel is attacked by Eve. Alice carries out measurements in the basis X; in this process, a state corresponding to 0 or 1 appears randomly and equiprobably. After the measurement, Bob’s subsystem Y is transformed to a state corresponding to 0 or 1 because of the structure of the EPR state. The EPR state has the standard form

$${\text{|}}{{\Phi }^{ + }}{{\rangle }_{{XY}}} = \frac{1}{{\sqrt 2 }}\left( {{\text{|}}0{{\rangle }_{X}}\; \otimes \;{\text{|}}0{{\rangle }_{Y}} + \;{\text{|}}1{{\rangle }_{X}} \otimes \;{\text{|}}1{{\rangle }_{Y}}} \right).$$
(3)

Since the EPR state has the same structure in both + and × bases, the index of the basis is omitted.

Any transformation of the input quantum state to the output state is described by the action of a superoperator, which is a completely positive map [8]. Any superoperator is representable unitarily (see details in [9]). This means that any superoperator is implemented by entangling the input state with an auxiliary state \({\text{|}}E{{\rangle }_{{\text{E}}}}\) by means of the unitary operator UBE, which is determined by Eve.

Eve’s attack described by the unitary operator UBE gives

$${{U}_{{{\text{BE}}}}}\left( {{\text{|}}{{\Phi }^{ + }}{{\rangle }_{{XY}}} \otimes \;{\text{|}}E{{\rangle }_{{\text{E}}}}} \right)$$
$$ = \frac{1}{{\sqrt 2 }}{\text{|}}0{{\rangle }_{X}} \otimes \left\{ {\sqrt {1 - Q} {\text{|}}0{{\rangle }_{Y}} \otimes \;{\text{|}}{{\Phi }_{0}}{{\rangle }_{{\text{E}}}} + \sqrt Q {\text{|}}1{{\rangle }_{Y}} \otimes \;{\text{|}}{{\Theta }_{0}}{{\rangle }_{{\text{E}}}}} \right\}$$
(4)
$$ + \;\frac{1}{{\sqrt 2 }}{\text{|}}1{{\rangle }_{X}} \otimes \left\{ {\sqrt {1 - Q} {\text{|}}1{{\rangle }_{Y}} \otimes \;{\text{|}}{{\Phi }_{1}}{{\rangle }_{{\text{E}}}} + \sqrt Q {\text{|}}0{{\rangle }_{Y}} \otimes \;{\text{|}}{{\Theta }_{1}}{{\rangle }_{{\text{E}}}}} \right\}.$$

States of Eve are normalized; for this reason, the coefficients are taken in the form \(1 - Q\) and Q to preserve normalization. As shown below, Q is the error probability on the receiver side.

Alice and Bob perform measurements in the identical bases \({{\{ {\text{|}}0\rangle }_{X}},{\text{|}}1{{\rangle }_{X}}\} \)and \({{\{ {\text{|}}0\rangle }_{Y}},{\text{|}}1{{\rangle }_{Y}}\} \), respectively. Taking into account Eqs. (3) and (4), the resulting Alice–Bob–Eve state is described by the density matrix

$${{\rho }_{{XY{\text{E}}}}} = \frac{1}{2}{\text{|}}0{{\rangle }_{XX}}\langle 0{\text{|}} \otimes \left\{ {(1 - Q){\text{|}}0{{\rangle }_{YY}}{{{\langle 0{\text{|}} \otimes \;{\text{|}}{{\Phi }_{0}}\rangle }}_{{\text{EE}}}}\langle {{\Phi }_{0}}{\text{|}}} \right.$$
$$\begin{gathered} \left. { + \;Q{\text{|}}1{{\rangle }_{YY}}{{{\langle 1{\text{|}} \otimes \;{\text{|}}{{\Theta }_{0}}\rangle }}_{{\text{EE}}}}\langle {{\Theta }_{0}}{\text{|}}} \right\} \\ + \;\frac{1}{2}{\text{|}}1{{\rangle }_{XX}}\langle 1{\text{|}} \otimes \left\{ {(1 - Q){\text{|}}1{{\rangle }_{YY}}{{{\langle 1{\text{|}} \otimes \;{\text{|}}{{\Phi }_{1}}\rangle }}_{{\text{EE}}}}\langle {{\Phi }_{1}}{\text{|}}} \right. \\ \end{gathered} $$
(5)
$$\left. { + \;Q{\text{|}}0{{\rangle }_{YY}}{{{\langle 0{\text{|}} \otimes \;{\text{|}}{{\Theta }_{1}}\rangle }}_{{\text{EE}}}}\langle {{\Theta }_{1}}{\text{|}}} \right\}.$$

As previously shown (see, e.g., [6]), the states \({{\{ {\kern 1pt} {\text{|}}{{\Phi }_{0}}\rangle }_{{\text{E}}}},{\text{|}}{{\Phi }_{1}}{{\rangle }_{{\text{E}}}}\} \) and \({{\{ {\kern 1pt} {\text{|}}{{\Theta }_{0}}\rangle }_{{\text{E}}}},{\text{|}}{{\Theta }_{1}}{{\rangle }_{{\text{E}}}}\} \) for Eve’s optimal attack lie in orthogonal subspaces and \(_{{\text{E}}}{{\langle {{\Theta }_{0}}{\text{|}}{{\Theta }_{1}}\rangle }_{{\text{E}}}} = {{\;}_{{\text{E}}}}{\kern 1pt} {{\langle {{\Phi }_{0}}{\text{|}}{{\Phi }_{1}}\rangle }_{{\text{E}}}} = 1 - 2Q\). Optimality means that Eve obtains maximum information on the transmitted key at the observed error Q on the receiver side.

Formula (5) has a simple interpretation. Alice sends 0 or 1 with a probability of 1/2. Bob obtains a correct count with a probability of \(1 - Q\) and Eve has the state \({\text{|}}{{\Phi }_{0}}{{\rangle }_{{\text{E}}}}\). Bob obtains an erroneous count with a probability of Q and Eve has the state \({\text{|}}{{\Theta }_{0}}{{\rangle }_{{\text{E}}}}\), similar to the case where Alice sends 1.

4 MODIFICATION OF THE PROTOCOL

Let Bob obtain 0 (correct or erroneous), i.e., observe the count in the detector U. Bob reports randomly and equiprobably one of the orthogonal states \({\text{|}}U{{\rangle }_{D}}\) and \({\text{|}}D{{\rangle }_{D}}\) to Eve; i.e., Eve receive the density matrix

$${{\rho }_{D}} = \frac{1}{2}\left( {{\text{|}}U{{\rangle }_{D}}_{D}{{{\langle U{\text{|}} + \;{\text{|}}D\rangle }}_{D}}_{D}\langle D{\text{|}}} \right).$$
(6)

Thus, when Bob records count 0 (count in the upper detector), state (6) is delivered to Eve. Measuring state (6), Eve identifies the detector U or D equiprobably according to Eqs. (1) and (2).

Similarly, if Bob observe count 1 in the detector D (correct or erroneous), measuring state (6), Eve observes the state U or D equiprobably.

As a result, the density matrix \({{\rho }_{{XY{\text{E}}}}}\) is replaced by

$${{\rho }_{{XY{\text{E}}D}}}$$
$$ = \frac{1}{2}{\text{|}}0{{\rangle }_{XX}}\langle 0{\text{|}} \otimes \left\{ {(1 - Q){\text{|}}0{{\rangle }_{YY}}{{{\langle 0{\text{|}} \otimes \;{\text{|}}{{\Phi }_{0}}\rangle }}_{{\text{EE}}}}\langle {{\Phi }_{0}}{\text{|}} \otimes {{\rho }_{D}}} \right.$$
$$\left. { + \;Q{\text{|}}1{{\rangle }_{YY}}{{{\langle 1{\text{|}} \otimes \;{\text{|}}{{\Theta }_{0}}\rangle }}_{{\text{EE}}}}\langle {{\Theta }_{0}}{\text{|}} \otimes {{\rho }_{D}}} \right\}$$
(7)
$$ + \;\frac{1}{2}{\text{|}}1{{\rangle }_{XX}}\langle 1{\text{|}} \otimes \left\{ {(1 - Q){\text{|}}1{{\rangle }_{YY}}{{{\langle 1{\text{|}} \otimes \;{\text{|}}{{\Phi }_{1}}\rangle }}_{{\text{EE}}}}\langle {{\Phi }_{1}}{\text{|}} \otimes {{\rho }_{D}}} \right.$$
$$\left. { + \;Q{\text{|}}0{{\rangle }_{YY}}{{{\langle 0{\text{|}} \otimes \;{\text{|}}{{\Theta }_{1}}\rangle }}_{{\text{EE}}}}\langle {{\Theta }_{1}}{\text{|}} \otimes {{\rho }_{D}}} \right\}.$$

5 KEY LENGTH, UNTRUSTED DETECTORS

According to [10], the length of the secret key in the asymptotic limit of a long sequence (this limit is considered to avoid lengthy technical details; a finite length of transmitted sequence can be taken into account in the way proposed in [7]) is given by the expression

$$\ell \geqslant H({{\rho }_{{X{\text{E}}D}}}{\text{|}}{{\rho }_{{ED}}}) - H({{\rho }_{{XY}}}{\text{|}}{{\rho }_{Y}}).$$
(8)

Here, \(H({{\rho }_{{X{\text{E}}D}}}{\text{|}}{{\rho }_{{ED}}})\) is the lack of information in bits on Alice’s reference bit string X to Eve under the condition that Eve has quantum systems \(ED\), and \(H({{\rho }_{{XY}}}{\text{|}}{{\rho }_{Y}})\) is the lack of information on Alice’s string to Bob under the condition that Bob has the bit string Y with errors. The difference between the deficits of information of Alice’s bit string X to Eve and Bob is the common secret of Alice and Bob.

The corresponding partial density matrices in Eq. (8) have the form

$${{\rho }_{{X{\text{E}}D}}} = {\text{Tr}}{{{\kern 1pt} }_{Y}}\{ {{\rho }_{{XY{\text{E}}D}}}\} $$
$$ = \frac{1}{2}{\text{|}}0{{\rangle }_{XX}}\langle 0{\text{|}} \otimes \left\{ {(1 - Q){\text{|}}{{\Phi }_{0}}{{\rangle }_{{\text{EE}}}}\langle {{\Phi }_{0}}{\text{|}} \otimes {{\rho }_{D}}} \right.$$
$$\left. { + \;Q{\text{|}}{{\Theta }_{0}}{{\rangle }_{{\text{EE}}}}\langle {{\Theta }_{0}}{\text{|}} \otimes {{\rho }_{D}}} \right\}$$
(9)
$$ + \;\frac{1}{2}{\text{|}}1{{\rangle }_{XX}}\langle 1{\text{|}} \otimes \left\{ {(1 - Q){\text{|}}{{\Phi }_{1}}{{\rangle }_{{\text{EE}}}}\langle {{\Phi }_{1}}{\text{|}} \otimes {{\rho }_{D}}} \right.$$
$$\left. { + \;Q{\text{|}}{{\Theta }_{1}}{{\rangle }_{{\text{EE}}}}\langle {{\Theta }_{1}}{\text{|}} \otimes {{\rho }_{D}}} \right\};$$
$${{\rho }_{{{\text{E}}D}}} = {\text{Tr}}{{{\kern 1pt} }_{{XY}}}\{ {{\rho }_{{XY{\text{E}}D}}}\} $$
$$ = \frac{1}{2}\left\{ {(1 - Q){\text{|}}{{\Phi }_{0}}{{\rangle }_{{\text{EE}}}}{{{\langle {{\Phi }_{0}}{\text{|}} \otimes {{\rho }_{D}} + Q{\text{|}}{{\Theta }_{0}}\rangle }}_{{\text{EE}}}}\langle {{\Theta }_{0}}{\text{|}} \otimes {{\rho }_{D}}} \right\}$$
(10)
$$ + \;\frac{1}{2}\left\{ {(1 - Q){\text{|}}{{\Phi }_{1}}{{\rangle }_{{\text{EE}}}}{{{\langle {{\Phi }_{1}}{\text{|}} \otimes {{\rho }_{D}} + Q{\text{|}}{{\Theta }_{1}}\rangle }}_{{\text{EE}}}}\langle {{\Theta }_{1}}{\text{|}} \otimes {{\rho }_{D}}} \right\}.$$

Further,

$${{\rho }_{{XY}}} = {\text{Tr}}{{{\kern 1pt} }_{{{\text{E}}D}}}\{ {{\rho }_{{XY{\text{E}}D}}}\} $$
$$ = \frac{1}{2}{\text{|}}0{{\rangle }_{XX}}\langle 0{\text{|}}\left\{ {(1 - Q){\text{|}}0{{\rangle }_{YY}}{{{\langle 0{\text{|}} + Q{\text{|}}1\rangle }}_{YY}}\langle 1{\text{|}}} \right\}$$
(11)
$$ + \;\frac{1}{2}{\text{|}}1{{\rangle }_{XX}}\langle 1{\text{|}}\left\{ {(1 - Q){\text{|}}1{{\rangle }_{YY}}{{{\langle 1{\text{|}} + Q{\text{|}}0\rangle }}_{YY}}\langle 0{\text{|}}} \right\};$$
$${{\rho }_{Y}} = {\text{Tr}}{{{\kern 1pt} }_{{X{\text{E}}D}}}\{ {{\rho }_{{XY{\text{E}}D}}}\} \frac{1}{2}\left\{ {{\text{|}}0{{\rangle }_{YY}}{{{\langle 0{\text{|}} + \;{\text{|}}1\rangle }}_{YY}}\langle 1{\text{|}}} \right\}.$$
(12)

Calculating the eigenvalues of the matrices (9)–(12), we obtain the following relations for the conditional von Neumann entropies:

$$H({{\rho }_{{X{\text{E}}D}}}{\text{|}}{{\rho }_{{{\text{E}}D}}}) = H({{\rho }_{{X{\text{E}}D}}}) - H({{\rho }_{{{\text{E}}D}}})$$
$$ = H({{\rho }_{{X{\text{E}}}}} \otimes {{\rho }_{D}}) - H({{\rho }_{{\text{E}}}} \otimes {{\rho }_{D}})H({{\rho }_{{X{\text{E}}}}}) - H({{\rho }_{{\text{E}}}})$$
(13)
$$ = 1 + h(Q) - 2h(Q) = 1 - h(Q),$$
$$H({{\rho }_{{XY}}}{\text{|}}{{\rho }_{Y}}) = H({{\rho }_{{XY}}}) - H({{\rho }_{Y}})h(Q).$$
(14)

Finally, taking into account Eqs. (13) and (14), we determine the key length

$$\ell = 1 - 2h(Q).$$
(15)

Thus, the length of the secret key in the modified protocol is the same as in the standard BB84 protocol [1, 10]. The critical error at which the key length vanishes is determined from the relation 2h(Qc) = 1 as Qc ≈ 11%; i.e., the modification of the protocol does not “destroy” the cryptographic properties of the pr-otocol.

6 CONCLUSIONS

An effective solution has been proposed for systems where it is technically difficult to ensure the cryptographic protection of detectors. This solution is reduced to the modification of the protocol such that detectors become untrusted and even counts in them are completely accessible to the observation of the eavesdropper. The proposed modification does not require any significant changes in the protocol and in the quantum key distribution system. Analogy with the twin-field protocol provides a qualitative information-theory explanation reasons for the security of keys in the case of detectors accessible to the eavesdropper.

Furthermore, the accessibility of detectors ensures natural protection from the detector mismatch attack, making it completely inefficient.

To conclude, this modification is achieved without significant changes in the equipment of the quantum key distribution system and does not reduce the key distribution rate.