INTRODUCTION

Over several recent decades, ultrashort-pulse lasers that provide radiation intensities on the surface of irradiated targets that exceed the so-called relativistic intensity (\(I > {{I}_{{{\text{rel}}}}} = 1.38 \times {{10}^{{18}}}\) W/cm2 at a wavelength of 1 µm) have become widespread [1, 2]. At such intensities, the maximum energy of ions per their unit charge reaches tens of megaelectronvolts, while a typical ion energy spectrum is reasonably described by a function \(\exp ( - {{E}_{i}}{\text{/}}T)\) with a characteristic “temperature” T from units to tens of megaelectronvolts [3]. Such ion flows are used in the production of semiconductor materials, medicine (e.g., for therapy of cancer diseases [4]), as well as in nuclear physics for initiating various processes (excitation of nuclear levels [5], thermonuclear reactions [6], and fission reactions [7]) and obtaining fast neutrons through reactions with nucleon transfer [8] or a photonuclear reaction [9].

When studying mechanisms of laser-plasma acceleration of ions, it is often required to determine their charge composition or energy spectrum. Track detectors (e.g., CR-39) are often used to detect the fastest ions and thermonuclear neutrons [10]. The ion energy spectra can be measured using time-of-flight (TOF) spectrometers; in order to increase the measurement accuracy, particles are separated by an electric field (for slow particles, up to 100 keV/charge [11]) or a magnetic field [12].

Microchannel plates (MCPs), which can efficiently detect even individual ions, are used to detect ions in such spectrometers. A significant disadvantage of such spectrometers is the necessity of a large number of laser shots for acquiring a full spectrum; this considerably complicates studies of, viz., nano- and microstructured targets.

A Thomson mass spectrometer (MS) is a more universal instrument that is widely used to diagnose flows of fast ions from laser plasma. Its operating principle consists in the simultaneous ion separation in energy and charge-to-mass ratio \(Z{\text{/}}M\) using parallel electric and magnetic fields. At present, there are many variations of the design of such a MS that were developed specially for particular experiments: spectrometers with aligned [13] and separated [14] electric and magnetic fields and even spectrometers with a special shape of electrodes [15]. However, as a rule, stationary electric and magnetic fields, which are created by plane–parallel plates and permanent magnets, are used most frequently.

The use of permanent magnets and parallel metal plates in both Thomson and TOF spectrometers with particle separation by an electric/magnetic field requires an accurate consideration of edge effects in calculations of trajectories of particles for the correct interpretation of results or in an experimental calibration.

The edge effects are usually taken into account either through the equivalent magnetic field Beffl0 = \(\int_{ - \infty }^{ + \infty } {B(z)} dz\) [16], where \({{l}_{0}}\) is the magnet length and \({{B}_{{{\text{eff}}}}}\) is the “effective” magnetic-field amplitude, which is determined experimentally from the deflection of calibration particles or using special calculation packages (TOSCA 3D [17], SIMION and RADIA [18], and Geant [19]). As a rule, all such packages numerically solve the Laplace equation with specified boundary conditions.

This approach has substantial disadvantages: the equivalent field does not take nuances in the spatial distribution of fields near magnets or plates into account, while a sufficiently accurate numerical field calculation for simulation using special programs requires considerable resources and a long period of time. These factors significantly complicate the calculation and optimization of MSs and the interpretation of the data that is obtained.

This paper presents a numerical analysis of the equation of particle motion through electric and magnetic fields with analytical consideration of edge effects and shows the necessity of taking these effects into account for a TOF spectrometer with a magnetic particle separator and a Thomson MS. The experimental data were interpreted for both types of spectrometers. The use of analytical formulas for taking the edge effects into account made it possible to significantly reduce the simulation time and perform an efficient analysis of the obtained data.

THE EXPERIMENTAL FACILITY

Radiation of the Ti : Sa laser system of the International Laser Center (ILC) of Moscow State University was used in the experiments. The laser-radiation wavelength was 800 nm, the pulse repetition rate was 10 Hz, the duration of a single pulse was \(45 \pm 5\) fs, and the pulse energy was 10 mJ. A laser pulse was focused with an off-axis parabolic mirror (\(F \approx 75\) mm, \(F{\text{/}}D \approx 5\)) at an angle of \(45^\circ \) to the target surface; in this case, the peak intensity on the target was \(2 \times {{10}^{{18}}}\) W/cm2.

Ions were registered with the TOF magnetic spectrometer [12] and the Thomson MS. All experiments were performed at a residual pressure in the interaction chamber of at most \(4 \times {{10}^{{ - 5}}}\) Torr.

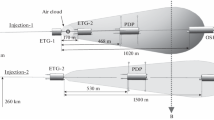
The TOF magnetic spectrometer (its schematic diagram is shown in Fig. 1) consists of a chamber in which ions are deflected by a magnetic field, a TOF tube, and a detection system. This system consists of a VEU-7М secondary electron multiplier based on a 50-mm-diameter MKP-25-10F chevron microchannel plate (MCP); the MCP gain exceeded \({{10}^{7}}\) at a nominal voltage of 2.4 kV.

Fig. 1.
figure 1

A diagram of the TOF magnetic spectrometer.

Full size image

A pair of NdFeB magnets in the form of rectangular parallelepipeds with dimensions of 30 × 8 × 4 mm was used to deflect ions; the maximum induction of the magnetic field on the axis created by two magnets (at a distance between the magnets of 2 cm) was 265 mT. After the diaphragm and paired magnets, ions enter a long pipe at the end of which the MCP is located. A metal anode for collecting electrons, the signal from which was fed to the computer, is positioned behind the MCP. The pipe length (together with the magnet) was l = 129 cm, while the distance from the target to the point at which the pipe was attached to the chamber (to the magnet) was d = 32 cm.

In order to avoid the re-reflection at the inner surface of the pipe, rings of black Teflon were installed on it. The pipe was attached to the chamber using movable corrugations, which allowed rotation of the ion spectrometer by small angles. Thus, knowledge of the ion time of flight to the MCP and the pipe angle of rotation, it is possible to calculate the ion charge-to-mass ratio \(Z{\text{/}}M\) and the ion energy; the information on the number of detected ions per unit time (i.e., the ion current) made it possible to obtain the energy spectrum for each \(Z{\text{/}}M\).

The Thomson MS uses both an electric and a magnetic field. The design and the 3D model of the Thomson MS, which will be discussed below, are shown in Fig. 2. The magnetic field is created by two magnets in the form of rectangular parallelepipeds 6 × 8 × 1.6 cm in size, the distance between them is 4 cm, and the maximum induction of the field on the axis is 65 mT. In this design, the magnets are outside the vacuum chamber; thus, they can be changed directly during the experiment, thereby changing the measured range of ion energies. The mass spectrometer is made of nonmagnetic stainless steel, thus eliminating the influence of its body on the magnetic-field distribution.

Fig. 2.
figure 2

(а) A diagram of the Thomson mass spectrometer (distances are given in millimeters) and (b) its 3D model.

Full size image

The electric field is created by a pair of plane–parallel plates, across which a voltage of 0.2–6 kV is set; the distance between them ranges from 1 to 3 cm, the length of the plates is Le = 25 cm, and their width is 12 cm. A collimating aperture with a diameter of 0.1 mm was in front of the magnets (at a distance of L1 = 21 cm). Ions were detected using the MCP with a K-67 luminophor screen (analogue of R-43). The MCP gain \({{k}_{{{\text{gain}}}}}\) was at least \({{10}^{7}}\) at a rated voltage at the MCP of 2.5 kV.

NUMERICAL SIMULATION

Magnetic Field

As was mentioned above, fields that are created by permanent magnets are commonly used in spectrometers. In a general case, a stationary magnetic field can be found by integrating the Maxwell equations (together with the material equations):

$$\left\{ \begin{gathered} (\nabla \cdot {\mathbf{B}}) = {{j}_{f}}, \hfill \\ [\nabla \times {\mathbf{H}}] = 0, \hfill \\ {\mathbf{B}} = {{\mu }_{0}}({\mathbf{H}} + {\mathbf{M}}), \hfill \\ \end{gathered} \right.$$
(1)

where B is the magnetic-field induction; H is the magnetic-field strength; and \({{j}_{f}}\) is the current of free charges.

In the case of a uniformly magnetized parallelepiped, these equations are easily integrated [20]:

$$\left\{ \begin{gathered} {{H}_{x}}(x,y,z) = \frac{{{{M}_{0}}}}{{4\pi }}\sum\limits_{k,l,m = 1}^2 {{{{( - 1)}}^{{k + l + m}}}\ln (\Delta {{y}_{l}} + \Delta {{r}_{{k,l,m}}})} , \hfill \\ {{H}_{y}}(x,y,z) = \frac{{{{M}_{0}}}}{{4\pi }}\sum\limits_{k,l,m = 1}^2 {{{{( - 1)}}^{{k + l + m}}}\ln (\Delta {{x}_{k}} + \Delta {{r}_{{k,l,m}}}),} \hfill \\ {{H}_{z}}(x,y,z) = \frac{{{{M}_{0}}}}{{4\pi }}\sum\limits_{k,l,m = 1}^2 {{{{( - 1)}}^{{k + l + m}}}\frac{{{\text{|}}\Delta {{z}_{m}}{\text{|}}}}{{\Delta {{z}_{m}}}}\arctan \left( {\frac{{\Delta {{x}_{k}}\Delta {{y}_{l}}}}{{{\text{|}}\Delta {{z}_{m}}{\text{|}}\Delta {{r}_{{k,l,m}}}}}} \right),} \hfill \\ \Delta {{x}_{k}} = x + {{( - 1)}^{k}}{{x}_{b}},\quad \Delta {{y}_{l}} = y + {{( - 1)}^{l}}{{y}_{b}},\quad \Delta {{z}_{m}} = y + {{( - 1)}^{m}}{{z}_{b}}, \hfill \\ \Delta {{r}_{{k,l,m}}} = \sqrt {\Delta {{x}_{k}}^{2} + \Delta {{y}_{l}}^{2} + \Delta {{z}_{m}}^{2}} . \hfill \\ \end{gathered} \right.$$
(2)

Here, \(a = 2{{x}_{b}}\), \(b = 2{{y}_{b}}\), and \(c = 2{{z}_{b}}\) are the linear dimensions of the parallelepiped, while \({{{\mathbf{M}}}_{0}}\) is the magnetization vector.

The line in Fig. 3 shows the change in the induction \({{B}_{z}}(x,0,h)\) on the x axis for y = 0 at a height of h = 5 mm above the magnet; points are the magnetic-field values measured with a calibrated Hall sensor. This dependence approximates well the actual magnetic field of a uniformly magnetized magnet. It should be noted that the results of a numerical calculation based on the summation of a large number of magnetic dipoles coincide well with the analytical dependence.

Fig. 3.
figure 3

The comparison of the experimental (dots) and theoretical (line) dependences of the magnetic-field induction \({{B}_{z}}(x,0,h)\), created by (а) one magnet, which is used in the Thomson mass spectrometer, at a height of h = 5 mm and (b) two magnets of the TOF magnetic spectrometer on the axis between the magnets, the distance between which is \(2h = 8\) mm.

Full size image

The negative “tail” of the magnetic field is a feature of such magnetic fields; it creates a perpendicular component of the particle velocity even before it enters the main magnetic field, deflecting this particle in the opposite direction relative to the direction of deflection by the main field. It should be noted that magnets with soft-iron yokes [18] can be used to eliminate the negative magnetic-field “tails,” while formulas (2) cannot be used.

Electric Field

A correct analysis of particle trajectories in the Thomson MS requires taking the edge effects of the electric field into account. Some of the simplest configurations of electrostatic fields can be found by the conformal mapping method. For fields created by two plane–parallel rectangular plates, there is an analytical solution [21] in special functions. It can be simplified in the case of wide and long plates that are often used in spectrometers, whose transverse dimensions of significantly exceed the distance between them. Thus, it is possible to be limited to considering a 2D profile and neglect the influence of one of the edges of the capacitor on the other.

The electric field of such a system is described by a so-called Rogowski profile [22]. To find the field near the edges of a semi-infinite capacitor with the potentials \( \pm U\) of the plates and the distance \(2h\) between them, it is necessary to find the complex potential w = f (z) = \(u + i{v},{\text{ }}z = x + iy\), that maps the appearance of two half-lines (i.e., the plane with two omitted half-lines) on the band \( - U < \operatorname{Im} (w) < U\). The inverse potential is known well:

$$z = \frac{h}{\pi }\left( {{{e}^{{\frac{\pi }{U}w}}} + \frac{\pi }{U}w + 1} \right).$$
(3)

The solution of this equation is expressed through the Lambert W-function [23]:

$$w = \frac{U}{\pi }\left( {\frac{{\pi z}}{h} - 1 - W\left[ {\exp \left[ {1 - \frac{{\pi z}}{h}} \right]} \right]} \right).$$
(4)

The electric-field strength is expressed as:

$$\begin{gathered} E = {{E}_{x}} + i{{E}_{y}} = \overline {if{\kern 1pt} '{\kern 1pt} (z)} = - i\frac{U}{h}\frac{1}{{1 + {{e}^{{\frac{\pi }{U}\bar {w}}}}}}, \\ {{E}_{x}} - i{{E}_{y}} = i\frac{U}{h}\frac{1}{{1 + {{W}_{k}}\left[ {\exp \left[ {1 - \frac{{\pi z}}{h}} \right]} \right]}}, \\ \end{gathered} $$
(5)

where the number of the complex branch of the solution is \(k = \left[ {\frac{{y - h}}{{2h}}} \right]\).

Because, in our case, the capacitor length significantly exceeds the distance between the plates, the obtained solution can be symmetrized: it is shifted by half the capacitor length and reflected relative to \(x = 0\). The final field distribution after the symmetrization is shown in Fig. 4.

Fig. 4.
figure 4

The theoretical dependences of the projections \({{E}_{x}}(x,z = 0)\) and \({{E}_{z}}(x,z = 0)\) of the electric field, which is described by the Rogowski profile, on the capacitor axis.

Full size image

Spectrometers

The correct interpretation of the results requires analysis of the particle motion in electric and magnetic fields. The motion of a nonrelativistic particle is generally described by the equation

$$\frac{{d{\mathbf{p}}(x,y,z)}}{{dt}} = Ze{\mathbf{E}}(x,y,z) + Ze[{\mathbf{v}}(x,y,z) \times {\mathbf{B}}(x,y,z)],$$
(6)

where p is the particle momentum, and \({\mathbf{E}},{\mathbf{B}}\) are the electric strength and magnetic-field induction, respectively. In the case of constant fields with given boundary conditions, the analytical solution of this equation is known well, which is often used in the interpretation of experimental results by introducing effective magnetic and electric fields. To solve this equation taking the edge effects into account on the basis of analytical dependencies for \({\mathbf{B}}(x,y,z)\) (2) and \({\mathbf{E}}(x,y,z)\) (5), we used the Wolfram Mathematica package.

Figure 5 shows the trajectories of protons \({{p}^{ + }}\) and carbon ions that were obtained as a result of the numerical simulation of the particle motion in the magnetic TOF spectrometer. The continuous curves correspond to the flight of particles through the field that is described by expression (2), while the dashed and dashed–dotted lines correspond to the flight through the field with sharp boundaries and the amplitude \(B = {{B}_{{{\text{eff}}}}} = \int_{ - \infty }^{ + \infty } {B(z)dz{\text{/}}(2{{x}_{b}})} \) and \(B = {{B}_{{\max }}}\), respectively. The numerical simulation shows a significant effect of the magnetic-field edge effects on the ion deflection angle. As noted above, the deflection angle decreases due to the presence of negative “tails” of the magnetic field, and the main contribution is made by the field before the magnets.

Fig. 5.
figure 5

The trajectories of protons \({{p}^{ + }}\) and  carbon ions that result from the numerical simulation of the particle motion in the TOF magnetic spectrometer. The continuous lines correspond to the flights of particles through the field described by formula (2); the dashed and dashed–dotted lines are the trajectories of particles that move through a field with sharp boundaries with the amplitudes \(B = {{B}_{{{\text{eff}}}}}\) and \(B = {{B}_{{\max }}}\), respectively.

Full size image

In the considered configuration of the TOF spectrometer, taking the edge effects into account is necessary in the estimation of the ion energy (due to changes in the effective flight length) and determination of the Z/M parameter. Even in calculations using the effective magnetic field, there is a significant error that depends on the TOF base of the spectrometer; when the maximum field on the axis of magnets is used in the calculation formulas, the data interpretation will be erroneous.

The numerical simulation shows that the replacement of the field taking the edge effects into account by a rectangular field with the amplitude \(B = {{B}_{{{\text{eff}}}}}\) is valid only for detectors with a large TOF base (in this case, \( > {\kern 1pt} 10\) cm) and is not applicable to compact detectors [13–15, 24].

The advantage of the magnetic-field model (6) is the pronounced dependence of the magnetic-field amplitude on the geometric parameters of the magnet: this allows accurate analysis and optimization of the spectrometer. An important optimization parameter is the minimization of the spectrometer length, since the smallest length provides a greater flow of detected particles. On the other hand, the field amplitude depends on the geometric dimensions of the magnets.

Figure 6 shows the dependence of the deflection of protons \({{p}^{ + }}\) on the thickness of the magnets (at a fixed distance between them). It can be seen that the deflection first rapidly increases and then saturates. We note that although the amplitude of the magnetic field also has a similar behavior, saturation occurs at another thickness of the magnets. In our example, the maximum deflection (and, therefore, the maximum energy recorded by the spectrometer) remains almost unchanged if the magnet thickness exceeds 2.67 cm.

Fig. 6.
figure 6

The dependences of the deflection of protons \({{p}^{ + }}\) with different initial energies on the thickness of the magnets at a fixed distance between them.

Full size image

The edge effects of the electric field must also be taken into account in the Thomson MS. In the configuration that is presented in Fig. 2, the electric plates and the ion-recording MCP are inside a metal vacuum chamber (see Fig. 2b), the electric field is shielded, and it does not go beyond the chamber. This configuration is almost equivalent to the sharp boundary of the electric field at one end of the capacitor and the presence of the edge effect at the other end.

In this case, taking the edge effects into account leads to an increase in the deflection by \( \approx {\kern 1pt} 0.1\) mm for protons with an initial energy of 300 keV, which causes an error of \( \approx {\kern 1pt} 30\) keV in determining the energy (see Fig. 7). However, in MSs with configurations where the electric field is not shielded [14, 16, 25], both edge effects of the electric field must be considered. For this MS configuration, the deflection along the z axis increases from 2.65 to 3.65 mm for ions, which is equivalent to an error of \( \approx {\kern 1pt} 300\) keV in determining the particle energy.

Fig. 7.
figure 7

The deflections of protons and carbon ions by electric and magnetic fields that were obtained as a result of the numerical simulation of the particle motion in the Thomson mass spectrometer for (1) an electric field with sharp boundaries, (2) an electric field with a sharp boundary at the input end and a “tail” at the capacitor output end, and (3) an electric field with edge effects at the both ends. Figures on the right of dots show the particle energy divided by 1 keV.

Full size image

In addition, it is necessary to take the changes in the amplitudes of the electric and magnetic fields for slow ions (with energies lower than 150 keV for the considered configuration) into account not only along the x axis but also on the z coordinate. In this case, the “tail” of the electric field “raises” an ion, and the latter enters the region of a stronger magnetic field, where it is deflected by the magnetic field to a higher degree (see Fig. 8).

Fig. 8.
figure 8

The trajectories of protons \({{p}^{ + }}\) that resulted from the numerical simulation of particle motion in the Thomson mass spectrometer with (1) an electric field with sharp boundaries, (2) an electric field with a sharp boundary at the input end and a “tail” at the capacitor output end, and (3) an electric field with edge effects at the both ends.

Full size image

THE MEASUREMENT RESULTS

Figure 9a shows the results of experiments on the interaction of ultrashort laser pulses with a carbon target using the TOF spectrometer, as well as calculations with and without consideration of the edge effects. The calculated curves for oxygen ions with different ionization multiplicity are presented for comparison. The analysis of this figure shows that disregarding edge effects may lead to erroneous conclusions on the ion composition of the target. Figure 9b shows a similar calculation for long magnets that are used in the Thomson spectrometer. It is seen that, in this case, the calculation in the effective average-field model with disregard of the edge effects leads to an erroneous identification of ions.

Fig. 9.
figure 9

The dependences of the ion detection time on the MCP displacement (carbon target) for (a) the TOF magnetic spectrometer and (b) for the magnets that are used in the Thomson mass spectrometer. The continuous curves correspond to the magnetic field with account for the edge effects, the dashed curves correspond to the magnetic field with sharp boundaries, and dots indicate the experimental results.

Full size image

We checked the correctness of the calculation model in a comparative experiment with \({\text{C}}{{{\text{H}}}_{2}}\) and \({\text{C}}{{{\text{D}}}_{2}}\) films as targets [9]. In the ion signal on the deuterated target, we observed an increase in the signal that corresponded, according to our calculations, to \(Z{\text{/}}M \sim 0.5\) by several times; this signal was due to deuterium ions or fully ionized carbon ions.

Figure 10 shows an image from the luminophor of the Thomson MS: dots indicate the theoretical positions of ions that are deflected in the electric and magnetic fields; the boundary that separates particles, which reach the plane where the MCP is positioned, from particles whose trajectories intersect the electrodes (i.e., such particles cannot be detected) is shown as well. The coincidence of the experimental and theoretical boundaries for С2+ ions, which cannot be detected because they hit the electrodes, confirms the correct operation of the theoretical model of the Thomson MS.

Fig. 10.
figure 10

An image from the luminophor of the Thomson mass spectrometer and the corresponding theoretical dependences of ion displacements in the electric and magnetic fields. The bright spot at the right lower corner is due to illumination with X-rays from plasma.

Full size image

CONCLUSIONS

Calculating the trajectories of particles in ion spectrometers with their electro- and magnetostatic separation within the model of the effective field with rectangular edges leads to erroneous conclusions about the mass and charge compositions of the ion current of plasma that is created by a relativistically intense laser pulse. Since the calculation of the energies of particles in the TOF spectrometer is based on time-of-flight measurements and the mass of a detected particle, this also leads to errors in determining the particle energies.

A substantial simplification of the calculation procedure is provided by the approach we proposed, in which the electric and magnetic fields are specified in an analytical form that takes the edge effects into account, while the trajectories of charged particles in these fields are calculated via a numerical solution of the equations of motion. The performed calculations for two configurations of ion spectrometers that are used in experiments (a TOF spectrometer with magnetic separation and a Thomson mass spectrometer with combined electro- and magnetostatic separation) and the comparison with the experimental data showed the efficiency of the offered approach and a good compliance with the experiment. Hence, the approach that is presented in this study considerably simplifies not only the initial design of ion spectrometers but also facilitates the analysis of the experimental data.