INTRODUCTION

To date, surface-tension isotherms of the binary alkali-metal systems Na–Cs, Na–Rb, Na–K, K–Rb, K–Cs, and Rb–Cs have been experimentally constructed. Table 1 shows the results of the study of the dependence of the surface tension σ(x) of melts of binary alkali-metal systems on composition according to the data from [1].

Table 1.   Concentration dependence of the surface tension of binary systems of alkali metal at T = 373 K [1]
Full size table

However, the literature does not contain sufficiently complete information about other thermodynamic properties of melt surfaces that could be extracted from the data in Table 1.

The reason for this state of the problem is the lack of a sufficiently convenient and accurate method of processing the experimental surface-tension isotherms [2]. When the isotherm equation of the surface tension of binary systems [3, 4] came into practice, it became possible to automate the calculations and to process more accurately the experimental surface-tension isotherms of binary systems:

$${\sigma }\left( x \right) = {\beta }\frac{{\left( {F - 1} \right)\left( {1 - x} \right)x}}{{1 + \left( {F - 1} \right)x}} + {{{\sigma }}_{A}}\left( {1 - x} \right) + {{{\sigma }}_{B}}x.$$
((1))

It was shown [3–5] that Eq. (1) works in the entire concentration range and describes the experimental surface-tension isotherms with high accuracy. It also makes it possible to calculate quite accurately the value \({{\left( {\partial {\sigma }/\partial x} \right)}_{{P,T}}},\) which is included in many calculations of other surface parameters. In addition, Eq. (1) for the first time provided a reliable method to determine an important surface parameter F, the exchange constant of particles of the surface layer of a melt with its volume [6]; this allows the use of the exact expressions known in the literature to calculate the adsorption and surface composition of the melt. Thus, it is of particular interest to process experimental surface-tension isotherms of alkali metals (Table 1) by the traditional method [2] and the method based on Eq. (1) [3–5] and to compare the results. First, one should consider the method to determine the parameters β and F of Eq. (1).

METHOD OF DETEMINATION OF β AND F PARAMETERS OF Eq. (1)

A method proposed earlier [5] was used to determine the β and F of Eq. (1) of the considered system A–B. Transform Eq. (1) to

$$\frac{{\left( {1 - x} \right)x}}{{\Delta \sigma \left( x \right)}} = \frac{1}{{\beta \left( {F - 1} \right)}} + \frac{1}{\beta }x,$$
((2))

in which Δσ (x) is determined by expression

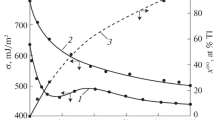
$$\Delta \sigma \left( x \right) = \sigma \left( x \right) - {{\sigma }_{A}}\left( {1 - x} \right){{\sigma }_{B}}x.$$
((3))

Eq. (3) expresses the deviation of the real isotherm (experimentally determined) from the additive. Here, σ(х) is the surface tension of a melt with composition x, where x is the content of the second component in the melt. Taking into account the experimental values of σ(х), σА, and σВ [1], lines were constructed according to Eq. (2) for six systems of alkali metals: Na–Cs, Na–Rb, K–Cs, Na–K, K–Rb, and Rb–Cs. As an example, Fig. 1 shows the experimental graphs of Eq. (2) for the systems Na–K (line 1) and Na–Cs (line 2).

Fig. 1.
figure 1

Experimental curves obtained according to Eq. (2) for Na–K (1) and Na–Cs (2) systems.

Full size image

We note here that the same lines are obtained for other systems (Na–Rb, K–Rb, K–Cs and Rb–Cs). This indicates the validity of Eq. (1) for systems of alkali metals and the validity of the assumptions made in [3, 4] in the derivation of Eq. (1).

Let us demonstrate the method to determine the parameters β and F of Eq. (1) on the example of the Na–K system (Fig. 1, line 1). Continuing the line (1) to the intersection with the y(x) axis, we determine у0, and we find the value tanα from the slope of line у(х) to the concentration axis. Using the values of у0 and tanα, as well as Eq. (2), we obtain

$${{y}_{0}} = \frac{1}{{{\beta }\left( {F - 1} \right)}},$$
((4))
$${{\tan\alpha }} = \frac{1}{{{\beta }}}.$$
((5))

Having solved the system of Eqs. (4) and (5) with respect to β and F, we find the values of these parameters for this system. Table 2 presents the calculated values of β and F for alkali-metal systems. The values of limiting surface activity of the second component of the binary system A–B according to Rebinder are also given: \({{A}_{{\sigma }}} = - \mathop {\lim }\limits_{x \to 0} \left( {\partial {\sigma }/\partial x} \right),\) which is calculated as

$${{A}_{{\sigma }}} = - {\beta }\left( {F - 1} \right) + \left( {{{{\sigma }}_{A}} - {{{\sigma }}_{B}}} \right).$$
Table 2.   Parameters β, F and σA of alkali-metal systems at Т = 373 K
Full size table

CALCULATION METHODS FOR THE ADSORPTION OF COMPONENTS OF BINARY ALKALI-METAL SYSTEMS

The adsorption of components of binary systems is calculated in two ways: in the approximation of ideal solutions (the traditional method) [2] and in the approximation of real solutions [5].

To calculate the adsorption of components of a binary solution of a system in the approximation of ideal solutions, we use the formula of the Guggenheim–Adam N variant [2, 7]

$${\Gamma }_{B}^{{\left( N \right)}}\left( x \right) = - \frac{{\left( {1 - x} \right)x}}{{RT}}\frac{{\partial {\sigma }}}{{\partial x}}.$$
((6))

Differentiating Eq. (1) and substituting the resulting expression into Eq. (6), we write the formula for calculating the adsorption of the second component B of the А–В system in the approximation of ideal solutions [3]:

$$\begin{gathered} {\Gamma }_{B}^{{\left( N \right)}}\left( x \right) = - \frac{{\left( {1 - x} \right)x}}{{RT}} \\ \times \,\,\left[ {{\beta }\left( {F - 1} \right)\frac{{1 - 2x - \left( {F - 1} \right){{x}^{2}}}}{{{{{[1 + \left( {F - 1} \right)x]}}^{2}}}} - \left( {{{{\sigma }}_{A}} - {{{\sigma }}_{B}}} \right)} \right]. \\ \end{gathered} $$
((7))

The ability to determine parameter F with Eq. (2) from the experimental dependence of surface tension on its composition [5] makes it possible to calculate the adsorption of a binary system component in the approximation of real solutions based on its determination in the Guggenheim–Adam N variant [6]:

$${\Gamma }_{B}^{{\left( N \right)}}\left( x \right) = \frac{{{{x}^{{\omega }}} - x}}{{{{{\omega }}_{m}}\left( x \right)}}.$$
((8))

Here, xω and x are the mole fraction of component B in surface and bulk solutions, and ωm(x) is the molar surface of a melt with composition х.

To calculate the adsorption according to Eq. (8) we use the value of the excessive concentration of component В in the form [7]

$$x_{i}^{{\omega }} - x = \frac{{\left( {F - 1} \right)\left( {1 - x} \right)x}}{{1 + \left( {F - 1} \right)x}}.$$

It should be noted here that parameter F in Eq. (1) takes into account the dependence of surface tension on the coefficients of activities \(f_{i}^{{\omega }}\) and \({{f}_{i}},\) as well as the chemical potentials \({\mu }_{i}^{{\omega }}\) and \({{{\mu }}_{i}}\)of components in the surface (ω) and bulk solutions [7, 8]. It is assumed that Eq. (1) describes the surface-tension isotherm of the real solution and makes it possible to obtain experimentally an F value that is close to the real value. Note that, at this determination of adsorption, \({\Gamma }_{A}^{N}\left( x \right) = - {\Gamma }_{B}^{N}\left( x \right).\)

We calculate the molar area of the melt ωm(x), required to calculate the adsorption according to Eq. (8) with respect to the concentration for systems that are close to ideal using the formula

$${{{\omega }}_{m}}\left( x \right) = {{{\omega }}_{{mA}}}\left( {1 - x} \right) + {{{\omega }}_{{mB}}}x,$$

where ωmA and ωmB are the molar areas of pure components А and В.

The values ωmi (i = A and B) are determined by the formula [6]

$${{{\omega }}_{{mi}}}\left( x \right) = \frac{\nu }{n}N_{{\text{A}}}^{{1/3}}{{\left( {{{V}_{{mi}}}\left( x \right)} \right)}^{{2/3}}},$$

where NА is Avogadro’s number.

The calculations were made in the approximation of a hard solution, i.e., with ν = 1 and n = 1 [9]. Experimental data for molar volumes Vm(х) of alkali metal melts [1], which are conveniently approximated by the function below, are used to calculate adsorption in the approximation of real solutions

$${{V}_{m}}\left( x \right) = {{V}_{{mA}}}\left( {1 - x} \right) + {{V}_{{mB}}}x + C\left( {1 - x} \right)x,$$
((9))

where С is a parameter characterizing degree of deviation of line Vm(x) from additive.

Table 3 presents the values of parameter С for systems of alkali metals.

Table 3.   Parameter С of Eq. (9) for alkali-metal systems
Full size table

RESULTS OF CALCULATIONS OF ADSORPTION OF COMPONENTS OF BINARY MELTS OF ALKALI-METAL SYSTEMS

Figure 2 presents the results of calculations of adsorption of the second components in binary alkali-metal systems in ideal approximations (curve 1, according to Eq. (7)) and real solutions (curve 2, according to (8)).

Fig. 2.
figure 2

Results of calculations of the adsorption of second components of binary melts of alkali metals: (1) in the approximation of ideal solutions (7); (2) in the approximation of real solutions (8).

Full size image

As one would expect, the results of calculations in approximations of ideal and real solutions differ significantly from each other. The data are primarily different for the Na–Cs, Na–Rb, K–Cs systems, which are far from being ideal. For the Na–K, K–Rb, and Rb–Cs systems, which are closer to ideal, the results are not very different from each other. However, in areas rich in components, the differences for these systems are more significant, which indicates that these solutions are not ideal.

Table 4 shows the ratio of the ionic radii of the added component B to the radius of solvent A (rB/rA).

Table 4.   Ratios of ionic radii of added component B to the radius of solvent A for alkali-metal systems
Full size table

Comparison of the data shown in Tables 2 and 4 shows that F decreases with a decrease in rB/rA, which indicates the significant role of the geometric factor in the adsorption processes in melts of alkali-metal systems.

CALCULATION METHODS FOR THE SURFACE COMPOSITION OF MELTS OF BINARY ALKALI-METAL SYSTEMS

The compositions of melt surfaces were also calculated in two ways: in approximations of ideal and real solutions.

Formula [8] is known for calculation of the surface concentration of the second component of the melt А–В in the approximation of ideal solutions:

$$x_{B}^{{\omega }} = \frac{{{{x}_{B}} + \frac{{\overline {{{{\omega }}_{A}}} }}{n}{\Gamma }_{B}^{{\left( N \right)}}}}{{1 + \frac{{\overline {{{{\omega }}_{A}}} - \overline {{{{\omega }}_{B}}} }}{n}{\Gamma }_{B}^{{\left( N \right)}}}}~.$$
((10))

If we bear in mind that the adsorption in Eq. (10) is determined in the approximation of an ideal solution (when the thermodynamic activities of the components are absent) according to Eq. (7), then it can be assumed that the surface concentrations of the second component according to Eq. (10) are also calculated in the approximation of an ideal solution.

In order to calculate the surface concentrations of a binary solution in the approximation of a real solution, we use the precise formula [7]

$${{x}^{{\omega }}} = \frac{{Fx}}{{1 + \left( {F - 1} \right)x}}.$$
((11))

Formula (11) was previously known [7]; however, it was not used due to the absence of a reliable method of F determination.

CALCULATION RESULTS FOR SURFACE CONCENTRATIONS OF COMPONENTS OF BINARY SOLUTIONS OF ALKALI METALS

Figure 3 presents the results of calculations of the surface concentrations of components of binary melts of alkali-metal systems.

Fig. 3.
figure 3

Compositions of surface solutions \(x_{i}^{{\omega }}\) of binary alkali metal systems (i—second component of system): (1) (10), (2) (11), (3) content of second component in the volume.

Full size image

When isotherms xω are determined with Eq. (10), the stability condition of the surface solution is taken into account; it is expressed by the inequality [9]:

$$\left( {\frac{{d{{x}^{\omega }}}}{{dx}}} \right) \geqslant 0.$$

It was found that n = 4 for the Na–Cs and Na–Rb systems, n = 2 for K–Cs and Na–K systems, and n = 1 for K–Rb and Rb–Cs systems. Comparing the obtained n values for systems of alkali metals, we note that, as parameter F decreases, the number of stable surface monolayers in alkali-metal systems decreases.

Comparison of the constructed isotherms \(x_{i}^{{\omega }}\) for alkali-metal systems shows that the results obtained from Eq. (11) are generally much higher than the data \(x_{i}^{\omega }\) obtained from Eq. (10), except for the first half of the data for the Rb–Cs system. If we compare \(x_{i}^{\omega }\) calculated by Eq. (11) with the volume content of x, then \(x_{i}^{{\omega }}\) > xi is significant. It can be noted that the values obtained by Eq. (10) are closer to хi.

CONCLUSIONS

It was shown that Eq. (1) describes the experimental isotherms of the surface tension of binary alkali-metal systems with high accuracy. In this case, the allowed error is about 1–2%. Expression (7) was obtained from Eqs. (1) and (6); this allows the construction of an adsorption isotherm for the surface-active component of an alkali-metal binary system in the approximation of an ideal solution without the use of an insufficiently accurate method of graphical differentiation of the experimental surface-tension isotherm.

It was established that one can use Eq. (1) to determine the exchange constant of the surface layer of a melt with its volume F using the experimental isotherm of the surface tension of a binary system. One of the most important results obtained in this work is the fact that, by defining constant F, we can use the well-known exact expressions (8) and (11) to calculate the component adsorption and the melt-surface composition.

The adsorption of components of binary melts of the alkali-metal systems Na–Cs, Na–Rb, Na–K, K–Cs, K–Rb, and Rb–Cs, as well as the composition of surface solutions in approximations of ideal and real solutions, were calculated. A significant difference was shown. When parameter F decreases, the number of stable surface monolayers in binary alkali-metal systems decreases. In the processes of component adsorption in alkali-metal systems, one of the determining factors is geometric: the differences in the ionic radii of the solution components. The closer the ratio of the ionic radii of system components is to unity, the closer the system itself is to the ideal.