INTRODUCTION

The wave heat transfer in solids is described by the wave heat conduction equation of a hyperbolic type, constructed on the basis of the Vernotte–Cattaneo–Lykov (VCL) law [1, 2]:

$${\mathbf{q}}\left( {{\mathbf{r}},t} \right) = - \Lambda \text{grad}T - {{\tau }_{p}}\frac{{\partial {\mathbf{q}}\left( {{\mathbf{r}},t} \right)}}{{\partial t}},$$
((1))

where q is the heat flux rate vector, r is the spatial position vector, Λ is the thermal conductivity tensor, T  is temperature, \({{\tau }_{p}}\) is the relaxation time—the heat flux delay time relative to the temperature gradient. Since for solids, \({{\tau }_{p}}\) has an order of \({{10}^{{ - 12}}} - {{10}^{{ - 14}}}\) s, the heat conduction law (1) is observed at very high heating rates \({{\partial {\mathbf{q}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{q}}} {\partial t}}} \right. \kern-0em} {\partial t}}.\)

The presence of such a small multiplier creates additional difficulties for the solution of wave heat transfer problems, since very large or very small numbers arise when one divides or multiplies by \({{\tau }_{p}},\) which results in inadequate results. Therefore, it is convenient to solve the wave heat transfer problems in dimensionless variables [3, 4].

Analytical methods for the solution of heat transfer problems are widely presented in the scientific literature (e.g., [1, 4–6] and others); however, there are many fewer publications concerning the wave heat transfer [2, 7]. Studies on the heat transfer in anisotropic nonlinear media are also very rare [8–12]. At the same time, the research on wave heat transfer is extremely important for the simulation of fast processes, for the study of the interaction between plasma and solids, and for relativistic mechanics, since the main errors in forming the temperature profile arise at small time intervals in the vicinity of the initial moment and the solid boundary. Therefore, the analytical solution of the wave heat conduction equation in the vicinity of the spatial-time boundary makes it possible to obtain an essentially nonstationary temperature field with no systematic errors. It should be noted that it is nearly impossible to do this experimentally.

In this work, a new analytical solution to the problem of heat transfer in a semi-infinite orthotropic solid under the action of a time-dependent point source of heat was obtained via the subsequent application of the Fourier transform with respect to the longitudinal variable and the Laplace transform with respect to time. With the help of this solution, the temperature fields are obtained at the time moments equal to several relaxation times. The temperature profiles show that, if the surface temperature exceeds the vaporization (sublimation) temperature, then the crater inside the solid must form with a shape similar to that of the temperature profile.

PROBLEM STATEMENT

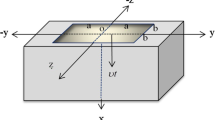
Let us consider the following problem of the wave heat transfer in an orthotropic half-space under the action of a time-dependent point heat source (Fig. 1):

$$\begin{gathered} c\rho \left( {{{\tau }_{p}}\frac{{{{\partial }^{2}}T}}{{\partial {{t}^{2}}}} + \frac{{\partial T}}{{\partial t}}} \right) = {{\lambda }_{{11}}}\frac{{{{\partial }^{2}}T}}{{\partial {{x}^{2}}}} + {{\lambda }_{{22}}}\frac{{{{\partial }^{2}}T}}{{\partial {{y}^{2}}}}, \\ - \infty < x < \infty ,\,\,\,\,0 < y < \infty ,\,\,\,\,t > 0; \\ \end{gathered} $$
((2))
$$\begin{gathered} - {{\lambda }_{{22}}}\frac{{\partial T}}{{\partial y}} = \left( {q\left( t \right) + {{\tau }_{p}}\frac{{\partial q}}{{\partial t}}} \right)\delta \left( {x - 0} \right), \\ - \infty < x < \infty ,\,\,\,\,y = 0,\,\,\,\,t > 0; \\ \end{gathered} $$
((3))
$$\begin{gathered} T\left( {x,y,0} \right) = {{T}_{0}} = {\text{const}}, \\ - \infty < x < \infty ,\,\,\,\,0 \leqslant y < \infty ,\,\,\,t = 0; \\ \end{gathered} $$
((4))
$$\begin{gathered} \frac{{\partial T\left( {x,y,0} \right)}}{{\partial t}} = 0,\,\,\,\, - \infty < x < \infty , \\ 0 \leqslant y < \infty ,\,\,\,\,t = 0. \\ \end{gathered} $$
((5))
Fig. 1.
figure 1

Calculation region.

Full size image

Here, \(\delta \left( {x - 0} \right)\) is the Dirac delta function.

The additional constraint conditions are as follows:

$$\begin{gathered} T\left( {x,y,t} \right) = {{T}_{0}},\,\,\,\,\left\{ {\frac{{\partial T\left( {x,y,t} \right)}}{{\partial x}},\,\,{ }\frac{{\partial T\left( {x,y,t} \right)}}{{\partial y}}} \right\} = 0, \\ x \to \pm \infty ,\,\,\,\,y \to \infty ,\,\,\,\,t > 0. \\ \end{gathered} $$
((6))

For the components of the thermal conductivity tensor

$$\begin{gathered} {{\lambda }_{{11}}} = {{\lambda }_{\xi }}{{\cos }^{2}}\varphi + {{\lambda }_{\eta }}{{\sin }^{2}}\varphi , \\ {{\lambda }_{{12}}} = {{\lambda }_{{21}}} = \left( {{{\lambda }_{\xi }} - {{\lambda }_{\eta }}} \right)\sin \varphi \cos \varphi , \\ {{\lambda }_{{22}}} = {{\lambda }_{\xi }}{{\sin }^{2}}\varphi + {{\lambda }_{\eta }}{{\cos }^{2}}\varphi , \\ \end{gathered} $$
((7))

in the orthotropic case, where the angle φ between the \(Ox\) axis and the principal axis \(O\xi \) is zero, we have

$${{\lambda }_{{11}}} = {{\lambda }_{\xi }},\,\,\,\,{{\lambda }_{{12}}} = 0,\,\,\,\,{{\lambda }_{{22}}} = {{\lambda }_{\eta }}.$$
((8))

In (7) and (8), \({{\lambda }_{\xi }},\)\({{\lambda }_{\eta }}\) are the principal components of the thermal conductivity tensor, which is diagonal.

Let us reduce the heat conduction equation (2) to a dimensionless form, dividing it by \(c\rho \) and introducing the new spatial variables:

$$\begin{gathered} {{x}_{1}} = x\sqrt {\frac{L}{{{{\lambda }_{\xi }}}}} ,\,\,\,\,{{x}_{2}} = y\sqrt {\frac{L}{{{{\lambda }_{\eta }}}}} , \\ \left( {{{\lambda }_{\xi }}\frac{{{{\partial }^{2}}T}}{{\partial {{x}^{2}}}} = L\frac{{{{\partial }^{2}}T}}{{\partial x_{1}^{2}}},\,\,{ }{{\lambda }_{\eta }}\frac{{{{\partial }^{2}}T}}{{\partial {{y}^{2}}}} = L\frac{{{{\partial }^{2}}T}}{{\partial x_{2}^{2}}}} \right), \\ \end{gathered} $$
((9))

where L is an arbitrary thermal conductivity. Then, multiplying the obtained equation by \({{\tau }_{p}}\) and introducing the dimensionless variables

$$\bar {t} = {t \mathord{\left/ {\vphantom {t {{{\tau }_{p}}}}} \right. \kern-0em} {{{\tau }_{p}}}},\,\,\,\,\bar {x} = {{{{x}_{1}}} \mathord{\left/ {\vphantom {{{{x}_{1}}} {\sqrt {\frac{{L{{\tau }_{p}}}}{{c\rho }}} }}} \right. \kern-0em} {\sqrt {\frac{{L{{\tau }_{p}}}}{{c\rho }}} }},\,\,\,\,\bar {y} = {{{{x}_{2}}} \mathord{\left/ {\vphantom {{{{x}_{2}}} {\sqrt {\frac{{L{{\tau }_{p}}}}{{c\rho }}} }}} \right. \kern-0em} {\sqrt {\frac{{L{{\tau }_{p}}}}{{c\rho }}} }},$$
((10))

where \(\left[ {\frac{{L{{\tau }_{p}}}}{{c\rho }}} \right] = {{{\text{m}}}^{2}},\) we obtain the equation

$$\begin{gathered} \frac{{{{\partial }^{2}}T}}{{\partial {{{\bar {t}}}^{2}}}} + \frac{{\partial T}}{{\partial \bar {t}}} = \frac{{{{\partial }^{2}}T}}{{\partial {{{\bar {x}}}^{2}}}} + \frac{{{{\partial }^{2}}T}}{{\partial {{{\bar {y}}}^{2}}}},\,\,\,\, - \infty < \bar {x} < \infty , \\ 0 < \bar {y} < \infty ,\,\,\,\,\bar {t} > 0. \\ \end{gathered} $$
((11))

Similarly, introducing variables (10) and taking into account boundary condition (3), we come to

$$\begin{gathered} - \frac{{\partial T}}{{\partial \bar {y}}} = \left( {q\left( t \right) + {{\tau }_{p}}\frac{{\partial q\left( t \right)}}{{\partial t}}} \right)\sqrt {\frac{{{{\tau }_{p}}}}{{{{\lambda }_{\eta }}c\rho }}} \delta \left( {\bar {x} - 0} \right), \\ - \infty < \bar {x} < \infty ,\,\,\,\,\bar {y} = 0,\,\,\,\,\bar {t} > 0. \\ \end{gathered} $$
((12))

If we take the function

$$q\left( t \right) = {{q}_{0}}\exp \left( {r\bar {t}} \right),$$
((13))

where \({{q}_{0}}\) is a constant, \(\left[ q \right]\) = W/m2, r is a dimensionless constant, then (12) takes the form

$$\begin{gathered} - \frac{{\partial T}}{{\partial \bar {y}}} = {{q}_{0}}\exp \left( {r\bar {t}} \right)\left( {1 + r} \right)\sqrt {\frac{{{{\tau }_{p}}}}{{{{\lambda }_{\eta }}c\rho }}} \delta \left( {\bar {x} - 0} \right), \\ - \infty < \bar {x} < \infty ,\,\,\,\,\bar {y} = 0,\,\,\,\,\bar {t} > 0. \\ \end{gathered} $$
((14))

Introducing the difference

$$T\left( {\bar {x},\bar {y},\bar {t}} \right) = {{T}_{1}}\left( {\bar {x},\bar {y},\bar {t}} \right) - {{T}_{0}},$$
((15))

we obtain relations (11) and (14) with respect to \({{T}_{1}}\left( {\bar {x},\bar {y},\bar {t}} \right)\), then, redesignating \({{T}_{1}}\left( {\bar {x},\bar {y},\bar {t}} \right)\) by \(T\left( {\bar {x},\bar {y},\bar {t}} \right)\), we come to the problem

$$\begin{gathered} \frac{{{{\partial }^{2}}T}}{{\partial {{{\bar {t}}}^{2}}}} + \frac{{\partial T}}{{\partial \bar {t}}} = \frac{{{{\partial }^{2}}T}}{{\partial {{{\bar {x}}}^{2}}}} + \frac{{{{\partial }^{2}}T}}{{\partial {{{\bar {y}}}^{2}}}},\,\,\,\, - \infty < \bar {x} < \infty , \\ 0 < \bar {y} < \infty ,\,\,\,\,\bar {t} > 0; \\ \end{gathered} $$
((16))
$$\begin{gathered} - \frac{{\partial T}}{{\partial \bar {y}}} = {{q}_{0}}\exp \left( {r\bar {t}} \right)\left( {1 + r} \right)\sqrt {\frac{{{{\tau }_{p}}}}{{{{\lambda }_{\eta }}c\rho }}} \delta \left( {\bar {x} - 0} \right), \\ - \infty < \bar {x} < \infty ,\,\,\,\,\bar {y} = 0,\,\,\,\,\bar {t} > 0; \\ \end{gathered} $$
((17))
$$\begin{gathered} T\left( {\bar {x},\bar {y},0} \right) = 0,\,\,\,\, - \infty < \bar {x} < \infty , \\ 0 \leqslant \bar {y} < \infty ,\,\,\,\,\bar {t} = 0; \\ \end{gathered} $$
((18))
$$\begin{gathered} \frac{{\partial T\left( {\bar {x},\bar {y},0} \right)}}{{\partial t}} = 0,\,\,\,\, - \infty < \bar {x} < \infty , \\ 0 \leqslant \bar {y} < \infty ,\,\,\,\,\bar {t} = 0; \\ \end{gathered} $$
((19))
$$\begin{gathered} T\left( {\bar {x},\bar {y},t} \right) = 0,\,\,\,\,\left\{ {\frac{{\partial T\left( {\bar {x},\bar {y},\bar {t}} \right)}}{{\partial \bar {x}}},{ }\,\,\frac{{\partial T\left( {\bar {x},\bar {y},\bar {t}} \right)}}{{\partial \bar {y}}}} \right\} = 0, \\ \bar {x} \to \pm \infty ,\,\,\,\,\bar {y} \to \infty ,\,\,\,\,t > 0. \\ \end{gathered} $$
((20))

METHOD OF SOLUTION

To solve problem (16)–(20), let us first apply the Fourier transform \({{T}_{\omega }}\left( {\bar {y},\bar {t}} \right)\) = \(\int_{ - \infty }^\infty {T\left( {\bar {x},\bar {y},\bar {t}} \right)\exp \left( {i\omega \bar {x}} \right)d\bar {x}} \) with respect to the variable \(\bar {x},\) and then the Laplace transform \({{T}_{{\omega ,p}}}\left( {\bar {y}} \right)\) = \(\int_0^\infty {{{T}_{\omega }}\left( {\bar {y},\bar {t}} \right)\exp \left( { - p\bar {t}} \right)d\bar {t}} \) with respect to variable \(\bar {t}.\) We will obtain the problem for an ordinary second-order differential equation in a semi-infinite bar with the second-type boundary condition:

$$\frac{{{{d}^{2}}{{T}_{{\omega ,p}}}\left( {\bar {y}} \right)}}{{d{{{\bar {y}}}^{2}}}} = \left( {{{p}^{2}} + p + {{\omega }^{2}}} \right){{T}_{{\omega ,p}}}\left( {\bar {y}} \right),\,\,\,\,0 < \bar {y} < \infty ;$$
((21))
$$\frac{{d{{T}_{{\omega ,p}}}\left( {\bar {y}} \right)}}{{d\bar {y}}} = - \frac{{{{q}_{0}}}}{{p - r}}\left( {1 + r} \right)\sqrt {\frac{{{{\tau }_{p}}}}{{{{\lambda }_{\eta }}c\rho }}} ,\,\,\,\,\bar {y} = 0;$$
((22))
$${{T}_{{\omega ,p}}}\left( {\bar {y}} \right) = 0\,\,\,\,{\text{at}}\,\,\,\,\bar {y} \to \infty .$$
((23))

Taking into account that the fundamental solution with a positive exponent is equal to zero, we get the following solution to problem (21)–(23)

$${{T}_{{\omega ,p}}}\left( {\bar {y}} \right) = \frac{Q}{{p - r}}\frac{{\exp \left( { - \bar {y}\sqrt {{{p}^{2}} + p + {{\omega }^{2}}} } \right)}}{{\sqrt {{{p}^{2}} + p + {{\omega }^{2}}} }},$$
((24))

where

$$Q = {{q}_{0}}\left( {1 + r} \right)\sqrt {\frac{{{{\tau }_{p}}}}{{{{\lambda }_{\eta }}{c}\rho }}} .$$

Let us execute the inverse Laplace transform using the Mellin transform [2]

$$\begin{gathered} {{T}_{\omega }}\left( {\bar {y},\bar {t}} \right) = \frac{Q}{{2\pi i}}\int\limits_{\sigma - i\infty }^{\sigma + i\infty } {\frac{1}{{p - r}}} \frac{{\exp \left( { - \bar {y}\sqrt {{{p}^{2}} + p + {{\omega }^{2}}} } \right)}}{{\sqrt {{{p}^{2}} + p + {{\omega }^{2}}} }} \\ \times \,\,\exp \left( {p\bar {t}} \right)dp = \frac{Q}{{2\pi i}}\int\limits_{{{\sigma }_{1}} - i\infty }^{{{\sigma }_{1}} + i\infty } {\frac{1}{{\left( {{{p}_{1}} - \left( {r + 0.5} \right)} \right)}}} \\ \times \,\,\frac{{\exp \left( { - \bar {y}\sqrt {p_{1}^{2} + \omega _{1}^{2}} } \right)}}{{\sqrt {p_{1}^{2} + \omega _{1}^{2}} }}\exp \left( {{{p}_{1}}\bar {t}} \right)\exp \left( {{{ - \bar {t}} \mathord{\left/ {\vphantom {{ - \bar {t}} 2}} \right. \kern-0em} 2}} \right)d{{p}_{1}} \\ = Q\exp \left( {\left( {r + 0.5} \right)\bar {t}} \right)\exp \left( {{{ - \bar {t}} \mathord{\left/ {\vphantom {{ - \bar {t}} 2}} \right. \kern-0em} 2}} \right) * {{J}_{0}}\left( {{{\omega }_{1}}\sqrt {{{{\bar {t}}}^{2}} - {{{\bar {y}}}^{2}}} } \right) \\ \times \,\,\eta \left( {\bar {t} - \bar {y}} \right), \\ \end{gathered} $$

where \({{p}_{1}} = p + 0.5,\)\(\omega _{1}^{2} = {{\omega }^{2}} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4},\)\(\eta \left( {\bar {t} - \bar {y}} \right)\) is the Heaviside function \(\left( {\eta \left( z \right) = 1} \right.\) at \(z > 0\) and \(\eta \left( z \right) = 0\) at \(z < 0),\)\({{J}_{0}}\) is the zero-order Bessel function of the first kind; the symbol * stands for the convolution operation.

Thus, the inverse Laplace transform of expression (24) results in the following expression

$$\begin{gathered} {{T}_{\omega }}\left( {\bar {y},\bar {t}} \right) = Q\exp \left( {r\bar {t}} \right) \\ \times \,\,\int\limits_0^{\bar {t}} {\exp [ - (r + {\text{ }}0.5\bar {\tau })]{{J}_{0}}\left( {\sqrt {{{\omega }^{2}} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \sqrt {{{{\bar {\tau }}}^{2}} - {{{\bar {y}}}^{2}}} } \right)} \\ \times \,\,\eta \left( {\bar {\tau } - \bar {y}} \right)d\bar {\tau }. \\ \end{gathered} $$
((25))

The inverse Fourier transform of (25), with the integrand parity with respect to \(\omega \) taken into account, gives

$$\begin{gathered} T\left( {\bar {x},\bar {y},\bar {t}} \right) = Q\exp \left( {r\bar {t}} \right)\frac{2}{{2\pi }} \\ \times \,\,\int\limits_0^{\bar {t}} {\exp [ - (r + {\text{ }}0.5\bar {\tau })]\int\limits_0^\infty {\cos \left( {\omega \bar {x}} \right)} } \\ \times \,\,{{J}_{0}}\left( {\sqrt {{{\omega }^{2}}{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 4}} \right. \kern-0em} 4}} \sqrt {{{{\bar {\tau }}}^{2}} - {{{\bar {y}}}^{2}}} } \right)\eta \left( {\bar {\tau } - \bar {y}} \right)d\bar {\tau }d\omega . \\ \end{gathered} $$
((26))

Expression (26) is the analytical solution to problem (16)–(20) of the wave heat transfer in the orthotropic half-space under the action of a nonstationary point source of thermal energy.

It is impossible to calculate the improper integral in (26) with respect to the variable ω from the Bessel function \({{J}_{0}}\left( \omega \right)\) for all values \(\omega \in \left( {0,\infty } \right)\) in radicals; however, we can use the asymptotic formulas for τ0(\(\omega \)) with small arguments, e.g., those less than 1, and with large arguments.

To extract these asymptotic formulas, let us consider the function \({{J}_{0}}\left( x \right)\) at \( - \infty < x < \infty \) and its approximations at \(x \leqslant 1\) and \(x > 1\) (Fig. 2). The zero-order Bessel function of the first kind is well approximated by the functions \(\exp \left( {{{ - {{x}^{2}}} \mathord{\left/ {\vphantom {{ - {{x}^{2}}} 4}} \right. \kern-0em} 4}} \right)\) at \(x \leqslant 1\) and \(\sqrt {\frac{2}{{\pi x}}} \cos \left( {x - \frac{\pi }{4}} \right)\) at \(x > 1:\)

$${{J}_{0}}\left( x \right) = \exp \left( {{{ - {{x}^{2}}} \mathord{\left/ {\vphantom {{ - {{x}^{2}}} 4}} \right. \kern-0em} 4}} \right) + O\left( {{{{{x}^{4}}} \mathord{\left/ {\vphantom {{{{x}^{4}}} {64}}} \right. \kern-0em} {64}}} \right),$$
((27))
$${{J}_{0}}\left( x \right) = \sqrt {\frac{2}{{\pi x}}} \cos \left( {x - \frac{\pi }{4}} \right) + O\left( {\frac{1}{{8x}}} \right).$$
((28))
Fig. 2.
figure 2

Comparison of functions: (1) \({{J}_{0}}\left( x \right),\) (2) \(\exp \left( {{{ - {{x}^{2}}} \mathord{\left/ {\vphantom {{ - {{x}^{2}}} 4}} \right. \kern-0em} 4}} \right),\) and (3) \(\sqrt {{2 \mathord{\left/ {\vphantom {2 {\pi x}}} \right. \kern-0em} {\pi x}}} \cos \left( {x - {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}} \right).\)

Full size image

Since we consider fast processes with a duration of nanoseconds, we will use the small limiting values \(x \leqslant 1,\) i.e., the asymptotics \({{J}_{0}}\left( x \right)\) ≈ \(\exp \left( {{{ - {{x}^{2}}} \mathord{\left/ {\vphantom {{ - {{x}^{2}}} 4}} \right. \kern-0em} 4}} \right),\) where \(x = \sqrt {{{\omega }^{2}} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \)\(\sqrt {{{{\bar {\tau }}}^{2}} - {{{\bar {y}}}^{2}}} ,\) when integral (26) is calculated with respect to the variable ω. In this case, expression (26) takes the form

$$\begin{gathered} T\left( {\bar {x},\bar {y},\bar {t}} \right) = \frac{Q}{\pi }\exp \left( {r\bar {t}} \right)\int\limits_0^{\bar {t}} {\exp \left( { - \left( {r + 0.5} \right)\bar {\tau }} \right)} \\ \times \,\,\int\limits_0^\infty {\left\{ {\cos \left( {\omega \bar {x}} \right)\exp \left[ { - \frac{1}{4}\left( {{{\omega }^{2}} - \frac{1}{4}} \right)\left( {{{{\bar {\tau }}}^{2}} - {{{\bar {y}}}^{2}}} \right)} \right]} \right.} \\ \left. {\frac{{}}{{}} \times \,\,d\omega } \right\}d\bar {\tau }\eta \left( {\bar {\tau } - \bar {y}} \right) = \frac{Q}{\pi }\exp \left( {r\bar {t}} \right) \\ \times \,\,\int\limits_0^{\bar {t}} {\exp \left( { - \left( {r + 0.5} \right)\bar {\tau } + \frac{{{{{\bar {\tau }}}^{2}} - {{{\bar {y}}}^{2}}}}{{16}}} \right)} \\ \times \,\,\int\limits_0^\infty {\left\{ {\exp \left. {\left( { - \frac{{{{{\bar {\tau }}}^{2}} - {{{\bar {y}}}^{2}}}}{4}{{\omega }^{2}}} \right)\cos \left( {\omega \bar {x}} \right)d\omega } \right\}} \right.d\bar {\tau }\eta \left( {\bar {\tau } - \bar {y}} \right)} \\ = \frac{Q}{\pi }\exp \left( {r\bar {t}} \right)\int\limits_0^{\bar {t}} {\exp \left( { - \left( {r + 0.5} \right)\bar {\tau } + \frac{{{{{\bar {\tau }}}^{2}} - {{{\bar {y}}}^{2}}}}{{16}}} \right)} \\ \times \,\,\frac{{\sqrt {\bar {\pi }} }}{{\sqrt {{{\tau }^{2}} - {{{\bar {y}}}^{2}}} }}\exp \left( { - \frac{{{{{\bar {x}}}^{2}}}}{{{{{\bar {\tau }}}^{2}} - {{{\bar {y}}}^{2}}}}} \right)d\bar {\tau }\eta \left( {\bar {\tau } - \bar {y}} \right). \\ \end{gathered} $$

The final solution to problem (16)–(20) for the arguments of the zero-order Bessel function of the first kind, which do not exceed 1, will be (29)

$$\begin{gathered} T\left( {\bar {x},\bar {y},\bar {t}} \right) = \frac{Q}{{\sqrt \pi }}\exp \left( {r\bar {t}} \right) \\ \times \,\,\int\limits_0^{\bar {t}} {\exp \left( { - \left( {r + 0.5} \right)\bar {\tau } + \frac{{{{{\bar {\tau }}}^{2}} - {{{\bar {y}}}^{2}}}}{{16}}} \right)\frac{1}{{\sqrt {{{{\bar {\tau }}}^{2}} - {{{\bar {y}}}^{2}}} }}} \\ \times \,\,\exp \left( { - \frac{{{{{\bar {x}}}^{2}}}}{{{{{\bar {\tau }}}^{2}} - {{{\bar {y}}}^{2}}}}} \right)d\bar {\tau }\eta \left( {\bar {\tau } - \bar {y}} \right), \\ \end{gathered} $$
((29))

where

$$\begin{gathered} Q = {{q}_{0}}\left( {1 + r} \right)\sqrt {\frac{{{{\tau }_{p}}}}{{{{\lambda }_{\eta }}c\rho }}} ,\,\,\,\,\bar {x} = x\sqrt {\frac{{c\rho }}{{{{\tau }_{p}}{{\lambda }_{\xi }}}}} , \\ \bar {y} = y\sqrt {\frac{{c\rho }}{{{{\tau }_{p}}{{\lambda }_{\eta }}}}} ,\,\,\,\,\bar {t} = {t \mathord{\left/ {\vphantom {t {{{\tau }_{p}}}}} \right. \kern-0em} {{{\tau }_{p}}}}. \\ \end{gathered} $$

ANALYSIS OF RESULTS

With expression (29), some results were obtained at very small time values, which have the same order of magnitude as the relaxation time. Figures 3 and 4 show the results for \(\bar {t} = {t \mathord{\left/ {\vphantom {t {{{\tau }_{p}}}}} \right. \kern-0em} {{{\tau }_{p}}}} = 1,2,3.\) The input data took the following values: \({{q}_{0}} = {{10}^{6}}\) W/m2, \({{\tau }_{p}} = {{10}^{{ - 12}}}\,\,{\text{s}},\)\(r = 2,\)\(c\rho = {{10}^{6}}\) J/(m3K), \({{\lambda }_{\xi }} = 0.04\) W/(m K); \({{\lambda }_{\eta }} = 0.06\) W/(m K), the initial temperature of the solid is zero.

Fig. 3.
figure 3

Dependence of the temperature on \(\bar {x}\) for three values of time: (1) \(\bar {t}\) = 1, (2) \(\bar {t}\) = 2, and (3) \(\bar {t}\) = 3.

Full size image
Fig. 4.
figure 4

Dependence of the temperature on \(\bar {y}\) for three values of time: (1) \(\bar {t}\) = 1, (2) \(\bar {t}\) = 2, (3) \(\bar {t}\) = 3.

Full size image

Figure 3 demonstrates the dependences of temperatures on \(\bar {x}\) for three values of time. By virtue of the high values of the heat flux rates \(q\left( {\bar {t}} \right)\), applied at the point \(\bar {x} = 0,\)\(\bar {y} = 0,\) the temperature at this point and in some its vicinity increases quickly and exceeds 1000 K already at \(t = 3{{\tau }_{p}};\) therefore, the phase transformations with formation of a crater can occur at \(\bar {x} = 0,\)\(\bar {y} = 0.\) Along the variable \(\bar {x},\) the temperature sharply decreases and becomes close to zero already at \(\bar {x} = 2.\) For the greater values of time \(\bar {t} > 3,\) the temperature profiles have the same behavior.

When \(\bar {x} \to 0,\) the temperature dependence converges to the ordinate axis (the temperature axis); therefore, a question arises as to whether the derivative \(\frac{{\partial T\left( {0,0,\bar {t}} \right)}}{{\partial \bar {x}}}\) is zero, i.e., if the temperature profiles are rounded or sharpened at the maximum point \(\left( {x = 0,} \right.\)\(T = 1100K).\) Differentiating expression (29) with respect to the variable \(\bar {x},\) we obtain the function equal to zero at \(\bar {x} = 0.\) This means that the tangents to the curves \(T\left( {\bar {x},\bar {y},{{{\bar {t}}}_{i}}} \right),\)\(i = 1,2,...\) at the point \(\bar {x} = 0,\)T = \({{T}_{{\max }}}\) are horizontal and, hence, the derivative \({{\left. {\frac{{\partial T}}{{\partial x}}} \right|}_{{\bar {x} = 0}}}\) at this point is continuous, \({{\left. {\frac{{\partial T}}{{\partial \bar {x}}}} \right|}_{{\bar {x} = 0 - 0}}}\) = \({{\left. {\frac{{\partial T}}{{\partial \bar {x}}}} \right|}_{{\bar {x} = 0 + 0}}}.\) Therefore, the graphs of temperatures at the point \(\bar {x} = 0,\)T = \({{T}_{{\max }}}\) are rounded.

Figure 4 shows the dependences of temperatures on \(\bar {y}.\) On the line \(\bar {x} = 0,\) the temperature profiles \(T\left( {0,0,t} \right)\) nearly coincide with the ordinate axis (the temperature axis); however, at \(\bar {y} = 0,\) the temperature profiles approach angularly the temperature axis, since the derivative \({{\left. {\frac{{\partial T}}{{\partial \bar {y}}}} \right|}_{{y = 0}}} \ne 0.\) At \(\bar {y} \to \infty \)\(T\left( {\bar {x},\bar {y},\bar {t}} \right) \to 0.\)

CONCLUSIONS

A new analytical solution to the problem of heat transfer in the orthotropic half-space under the action of a point source of thermal energy was obtained. This solution makes it possible to determine accurately the temperature field in the vicinity of the initial time moment, where, as a rule, the solutions have considerable errors. Since those are fast processes that were considered, the test results are obtained for the time moments proportional to the relaxation time \(\left( {{{\tau }_{p}} = {{{10}}^{{ - 12}}}-{{{10}}^{{ - 14}}}\,\,{\text{s}}} \right),\) and they showed that the temperature at the point of a lumped source of heat can quickly reach the temperature of phase transformations (for example, the sublimation temperature) with the formation of a crater.