1 INTRODUCTION

The main focus in research on the propagation of high-energy electrons appearing in solar plasma during solar flares is traditionally their Coulomb interaction with solar plasma particles (e.g., Nocera et al., 1985; Diakonov and Somov, 1988; Reznikova et al., 2009; Zharkova et al., 2010; Melnikov et al., 2013). In this case, both changes in the plasma concentration and changes in the magnetic field along the flare loop can be taken into account. This approach is explained primarily by the need to describe the parameters of hard X-ray emission of solar flares: the energy spectra, polarization, and directivity (Zharkova et al., 1995, Kudryavtsev and Charikov, 2012). Less attention is paid to the interaction of fast electrons with plasma waves in a flare plasma. It is known that fast electrons can excite Langmuir waves and that they quickly relax when interacting with them. In turn, these waves generate radio emission from the solar plasma (Zheleznyakov and Zaitsev, 1970; Kaplan and Tsytovich, 1972; Ratcliffe et al., 2014; Kudryavtsev and Kaltman, 2020, 2021), which carries information about physical processes on the Sun and is recorded during observations. This radio emission can be generated via the scattering of Langmuir waves by plasma particles and the coalescence of Langmuir waves (e.g., Tsytovich, 1971). Therefore, the study of the dynamics of fast electrons and Langmuir waves in a flare loop is of interest for the description of both the generation of hard X-ray radiation and the process of the generation of radio emission by Langmuir waves. However, the study of the evolution of the distribution function of fast electrons and the spectra of Langmuir waves in a flare plasma is limited either by time dynamics in a homogeneous plasma without allowance for the spatial change (Ivanov and Rudakov, 1967; Tsytovich, 1971; Grognard, 1975; Melrose, 1986; Kontar et al., 2012) or spatial evolution in the stationary approximation (Kudryavtsev et al., 2019). In addition to the interaction of fast electrons with Langmuir waves, the evolution of the electron distribution function can be influenced by their interaction with ion-acoustic waves (Kudryavtsev and Charikov, 1991; Charikov and Shabalin, 2016) and whistlers (Stepanov and Tsap, 2002; Melnikov and Filatov, 2020).

In this work, since the acceleration process in flares can have an impulse (millisecond) structure (Dmitriev et al., 2006), we will consider the evolution of the electron distribution function f and the spectral energy density of Langmuir turbulence Wk with a pulsed injection of electrons.

2 SPATIO-TEMPORAL DYNAMICS OF FAST ELECTRONS AND LANGMUIR WAVES UPON PULSE ACCELERATION IN FLARE PLASMA

Let us consider the problem of the evolution of the electron-distribution function f in plasma and the spectral energy density of Langmuir waves Wk in the pulse mode of acceleration. In this work, we will focus on the case of quasilinear relaxation, which will further allow us to analyze the role of nonlinear processes. This problem is described by the following equations (e.g., Zheleznyakov and Zaitsev, 1970; Tsytovich, 1971; Kontar et al., 2012)

$$\frac{{\partial f}}{{\partial t}} + {v}\frac{{\partial f}}{{\partial x}} = \frac{\partial }{{\partial {v}}}\left( {D\frac{{\partial f}}{{\partial {v}}} + {{\nu }_{e}}\left( {{v}f + {v}_{{{{T}_{e}}}}^{2}\frac{{\partial f}}{{\partial {v}}}} \right)} \right),$$
(1)
$$\frac{{\partial {{W}_{k}}}}{{\partial t}} + {{{v}}_{g}}\frac{{\partial {{W}_{k}}}}{{\partial x}} = ({{\gamma }_{k}} - {{\nu }_{{{\text{eff}}}}}){{W}_{k}} + {{Q}_{k}},$$
(2)
$$D = \frac{{\pi \omega _{e}^{2}}}{{{{m}_{e}}{{n}_{e}}{v}}}{{(W{}_{k})}_{{k{\kern 1pt} = {\kern 1pt} {{{{\omega }_{e}}} \mathord{\left/ {\vphantom {{{{\omega }_{e}}} {v}}} \right. \kern-0em} {v}}}}},\,\,\,\,{{\gamma }_{k}} = {{\left( {\frac{{\pi {{\omega }_{e}}}}{{{{n}_{e}}}}{{{v}}^{2}}\frac{{\partial f}}{{\partial {v}}}} \right)}_{{{v}{\kern 1pt} = {\kern 1pt} {{{{\omega }_{e}}} \mathord{\left/ {\vphantom {{{{\omega }_{e}}} k}} \right. \kern-0em} k}}}},$$
(3)

where t and x are the time and coordinate; v is the speed of electrons, k is the wave number of Langmuir waves; νe is the frequency of collisions of electrons with plasma particles; ωe is the electron plasma frequency; vTe is thermal speed of electrons; vg is the group velocity of Langmuir waves; γk is the increment of beam instability; νeff is the effective frequency of the damping of Langmuir waves due to collisions of plasma particles; ne is the concentration of plasma electrons; and Qk is the power of spontaneous emission of Langmuir waves.

In this work, like Kontar et al. (2012), we will use the following expression for the function Qk

$${{Q}_{k}}(t,x) = \frac{{\omega _{e}^{3}{{m}_{e}}}}{{4\pi {{n}_{e}}}}{{\left( {{v}\ln \left( {\frac{{v}}{{{{{v}}_{{Te}}}}}} \right)f} \right)}_{{{v}{\kern 1pt} = {\kern 1pt} {{{{\omega }_{e}}} \mathord{\left/ {\vphantom {{{{\omega }_{e}}} k}} \right. \kern-0em} k}}}}.$$
(4)

In the absence of fast electrons, Qk describes the spontaneous emission of Langmuir waves by thermal plasma electrons.

When simulating the process of electron propagation in a flare plasma, like Kudryavtsev et al. (2019), we will assume that electrons propagate downward from the top of the flare loop, and the change in the plasma concentration is described by the expression

$${{n}_{e}} = {{n}_{o}}(1 + {x \mathord{\left/ {\vphantom {x L}} \right. \kern-0em} L}).$$
(5)

Let us supplement the system of equations (1)–(3) with the initial condition. Let accelerated electrons with a beam distribution function appear at the boundary of the equilibrium plasma x = 0 at the initial time instant t = 0. In this case, we will assume that the distribution function of fast electrons at the initial moment of time rapidly decreases into the plasma depth. Then, at time t = 0, the electron-distribution function f is the sum of the Maxwellian distribution of thermal plasma electrons fM and the “beam” distribution of fast electrons fb:

$$\begin{gathered} f(t = 0,x,{v}) = {{f}_{M}} + {{f}_{b}}\exp ({{ - x} \mathord{\left/ {\vphantom {{ - x} {{{x}_{0}}}}} \right. \kern-0em} {{{x}_{0}}}}), \\ {{f}_{M}} = \frac{{{{n}_{e}}}}{{\sqrt {2\pi } {{{v}}_{{Te}}}}}\exp \left( { - \frac{{{{{v}}^{2}}}}{{2{v}_{{{{T}_{e}}}}^{2}}}} \right), \\ {{f}_{b}} = \frac{{{{n}_{b}}}}{{\sqrt {2\pi } \sigma }}\exp \left( { - \frac{{{{{({v} - {{{v}}_{o}})}}^{2}}}}{{2{{\sigma }^{2}}}}} \right), \\ \end{gathered} $$
(6)

where nb is the concentration of fast electrons at x = 0; x0 is the characteristic scale of the decrease in the concentration of fast electrons deep into the plasma; and σ is the root-mean-square deviation of the velocity distribution of fast electrons.

As a boundary condition on x, we take a condition that describes the time decay of the distribution function of fast electrons entering the plasma at the boundary x = 0, i.e.,

$$f(t,x = 0,{v}) = {{f}_{M}} + {{f}_{b}}\exp ({{ - t} \mathord{\left/ {\vphantom {{ - t} {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}}).$$
(7)

The parameter t0 sets the time decay of electrons injected into the plasma.

To agree with the previous conditions, we choose the following as the boundary conditions for the velocity v:

$$\begin{gathered} f(t,x,{v} = 0) = {{f}_{M}}({v} = 0) \\ + \,\,{{f}_{b}}({v} = 0)\exp ({{ - x} \mathord{\left/ {\vphantom {{ - x} {{{x}_{0}}}}} \right. \kern-0em} {{{x}_{0}}}})\exp ({{ - t} \mathord{\left/ {\vphantom {{ - t} {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}}), \\ f(t,x,{v} = {{{v}}_{{\max }}}) = {{f}_{M}}({v} = {{{v}}_{{\max }}}) \\ + \,\,{{f}_{b}}({v} = {{{v}}_{{\max }}})\exp ({{ - x} \mathord{\left/ {\vphantom {{ - x} {{{x}_{0}}}}} \right. \kern-0em} {{{x}_{0}}}})\exp ({{ - t} \mathord{\left/ {\vphantom {{ - t} {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}}). \\ \end{gathered} $$
(8)

As an initial condition for Wk, like Kontar et al. (2012), we will use the stationary spectrum of Langmuir waves in the absence of fast electrons, i.e., when the left side of equation (2) is zero:

$${{W}_{k}}(t = 0,x) = \frac{{{{Q}_{k}}}}{{({{\nu }_{{{\text{eff}}}}} - {{\gamma }_{k}})}} = {{\frac{{\omega _{e}^{3}{{m}_{e}}}}{{4\pi {{n}_{e}}}}{{{\left( {{v}\ln \left( {\frac{{v}}{{{{{v}}_{{Te}}}}}} \right){{f}_{M}}} \right)}}_{{{v}{\kern 1pt} = {\kern 1pt} {{{{\omega }_{e}}} \mathord{\left/ {\vphantom {{{{\omega }_{e}}} k}} \right. \kern-0em} k}}}}} \mathord{\left/ {\vphantom {{\frac{{\omega _{e}^{3}{{m}_{e}}}}{{4\pi {{n}_{e}}}}{{{\left( {{v}\ln \left( {\frac{{v}}{{{{{v}}_{{Te}}}}}} \right){{f}_{M}}} \right)}}_{{{v}{\kern 1pt} = {\kern 1pt} {{{{\omega }_{e}}} \mathord{\left/ {\vphantom {{{{\omega }_{e}}} k}} \right. \kern-0em} k}}}}} {\left( {{{\nu }_{{{\text{eff}}}}} - {{{\left( {\frac{{\pi {{\omega }_{e}}}}{{{{n}_{e}}}}{{{v}}^{2}}\frac{{\partial {\kern 1pt} {{f}_{M}}}}{{\partial {v}}}} \right)}}_{{{v}{\kern 1pt} = {\kern 1pt} {{{{\omega }_{e}}} \mathord{\left/ {\vphantom {{{{\omega }_{e}}} k}} \right. \kern-0em} k}}}}} \right)}}} \right. \kern-0em} {\left( {{{\nu }_{{{\text{eff}}}}} - {{{\left( {\frac{{\pi {{\omega }_{e}}}}{{{{n}_{e}}}}{{{v}}^{2}}\frac{{\partial {\kern 1pt} {{f}_{M}}}}{{\partial {v}}}} \right)}}_{{{v}{\kern 1pt} = {\kern 1pt} {{{{\omega }_{e}}} \mathord{\left/ {\vphantom {{{{\omega }_{e}}} k}} \right. \kern-0em} k}}}}} \right)}}.$$
(9)

In this formula, ne, ωe, νeff and fM are functions of x.

This expression describes the thermal background level of Langmuir oscillations in the plasma. As a boundary condition at the boundary x = 0, we also take the background level of oscillations:

$${{W}_{k}}(t,x = 0) = \frac{{{{Q}_{k}}}}{{({{\nu }_{{{\text{eff}}}}} - {{\gamma }_{k}})}} = {{\frac{{\omega _{e}^{3}{{m}_{e}}}}{{4\pi {{n}_{e}}}}{{{\left( {{v}\ln \left( {\frac{{v}}{{{{{v}}_{{Te}}}}}} \right){{f}_{M}}} \right)}}_{{{v}{\kern 1pt} = {\kern 1pt} {{{{\omega }_{e}}} \mathord{\left/ {\vphantom {{{{\omega }_{e}}} k}} \right. \kern-0em} k}}}}} \mathord{\left/ {\vphantom {{\frac{{\omega _{e}^{3}{{m}_{e}}}}{{4\pi {{n}_{e}}}}{{{\left( {{v}\ln \left( {\frac{{v}}{{{{{v}}_{{Te}}}}}} \right){{f}_{M}}} \right)}}_{{{v}{\kern 1pt} = {\kern 1pt} {{{{\omega }_{e}}} \mathord{\left/ {\vphantom {{{{\omega }_{e}}} k}} \right. \kern-0em} k}}}}} {\left( {{{\nu }_{{{\text{eff}}}}} - {{{\left( {\frac{{\pi {{\omega }_{e}}}}{{{{n}_{e}}}}{{{v}}^{2}}\frac{{\partial {\kern 1pt} {{f}_{M}}}}{{\partial {v}}}} \right)}}_{{{v}{\kern 1pt} = {\kern 1pt} {{{{\omega }_{e}}} \mathord{\left/ {\vphantom {{{{\omega }_{e}}} k}} \right. \kern-0em} k}}}}} \right)}}} \right. \kern-0em} {\left( {{{\nu }_{{{\text{eff}}}}} - {{{\left( {\frac{{\pi {{\omega }_{e}}}}{{{{n}_{e}}}}{{{v}}^{2}}\frac{{\partial {\kern 1pt} {{f}_{M}}}}{{\partial {v}}}} \right)}}_{{{v}{\kern 1pt} = {\kern 1pt} {{{{\omega }_{e}}} \mathord{\left/ {\vphantom {{{{\omega }_{e}}} k}} \right. \kern-0em} k}}}}} \right)}}.$$
(10)

This choice of the initial and boundary conditions ensures their agreement at t = 0 and x = 0. Moreover, like Hamilton and Petrosian (1987), we will assume that Wk = 0 for k > ωe/vTe as a result of Landau damping.

The system of equations (1)–(3) was solved with use of the method of summarized approximation (Samarskii, 1989).

Before proceeding to the description of the calculation results, it should be noted that expression (4) describes the spontaneous excitation of waves not only by thermal electrons, but also by fast electrons. Therefore, in the region of high phase velocities, the main contribution to the spontaneous generation of Langmuir waves is made by fast electrons.

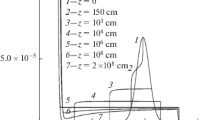
The results of the calculation of the electron-distribution function f and the spectral energy density of Langmuir waves Wk for different instants of time and at different distances from the place of acceleration of electrons in the flare plasma are presented in Figs. 1 and 2 at n0 = 1010 cm–3, nb = 104 cm–3, Te = 106 K, v0 = 1010 cm/s, σ = 0.07 v0, vmax = 1.5 v0, x0 = 102 cm, t0 = 10–3 s, L = 107 cm. In Figs. 1a–1c, it can be seen that the maximum f value remained practically unchanged up to x ~ 106 cm, and its relaxation at these distances occurs upon interaction with Langmuir waves. In this case, there is an increase in Langmuir waves (Figs. 2a–2c). As the electron-distribution function decreases with time, the spectral energy density of Langmuir waves also decreases (curves 6, 7 in Figs. 2b, 2c). With the propagation of electrons over long distances, there is a decrease f (Figs. 1d–1f) and the spectral energy density of the waves (Figs. 2d–2f). In this case, a faster penetration of high-energy electrons into the plasma is clearly seen (curves 1, 2 in Fig. 1d–1f). This separation of fast electrons from slower ones leads to the formation of a region with a positive derivative of the function f (Figs. 1d–1f) and the continued excitation of Langmuir waves (Figs. 2d–2f).

Fig. 1.
figure 1

Electron distribution function f at different distances x from the place of acceleration at different times t.

Full size image
Fig. 2.
figure 2

Spectral energy density of Langmuir waves Wk at different distances x from the place of acceleration at different times t.

Full size image

Figure 3 shows the energy density of Langmuir waves W at different distances from the place of electron injection into the flare plasma as a function of time. As can be seen in the figure, for the used parameters of the plasma and fast electrons, the duration of the existence of Langmuir turbulence in the flare plasma is ~ 10–2 s. Figure 4 shows the distribution of the energy density of Langmuir waves along the plasma.

Fig. 3.
figure 3

Time dependence of the energy density of Langmuir waves at various distances from the place of acceleration of electrons in a flare plasma.

Full size image
Fig. 4.
figure 4

Energy density distribution of Langmuir waves in flare plasma for different moments of time.

Full size image

As follows from Fig. 4, two spatial regions can be distinguished in the flare plasma. For x < 106 cm, Langmuir waves are generated as a result of the development of beam instability of fast electrons with an initial beam-type distribution function. This stage passes rather quickly, in a time t ~ 10–3 s (Fig. 1c). At distances exceeding x = 107 cm (Fig. 1d), faster electrons begin to penetrate the plasma. This leads to the formation of a portion of the distribution function with a positive derivative with respect to the velocity and the continuation of the excitation of plasma waves (Fig. 2d). As the electron velocity decreases and the plasma concentration increases (at x = 108 cm, the plasma concentration is ne = 1.1 × 1011 cm–3, and at x = 2 × 108 cm, ne = 2.1 × 1011 cm–3), Coulomb collisions begin to play their role. Figures 1f–1e clearly show the Maxwellization of electrons of lower energies (curves 5–7) at t > 2 × 10–2 s. In this case, the energy density of Langmuir waves approaches the background values (Fig. 4). The length of the region with an increased energy level of Langmuir waves is 107–108 cm. A similar size of the turbulent region was obtained by Kudryavtsev et al. (2019) when they considered the stationary problem. This region of the loop with Langmuir turbulence will generate radio emission (e.g., Zaitsev and Stepanov, 1983).

3 CONCLUSIONS

The spatio-temporal dynamics of fast electrons and Langmuir waves in a flare plasma under pulsed acceleration of fast electrons was considered. It was shown that the faster penetration of fast electrons and the effective deceleration of slow electrons lead to the continuation of the generation of Langmuir waves in the flare plasma outside the region of quasilinear relaxation of the distribution function. In this case, at a distance of ~106 cm from the place of fast-electron acceleration, the maximum of the distribution function changes little. The maximum energy density of Langmuir waves reaches 10–2 erg/cm3 at the selected parameters of plasma and fast electrons. The length of the region with an increased energy level of Langmuir waves is 107–108 cm, and the lifetime of a layer with Langmuir turbulence is about ~10–2 s.