1 Introduction

The standard solar-flare models (Priest, 2014; Tajima and Shibata, 2018) show that during a solar-flare event, the stored non-potential magnetic energy of the order of \(\approx 10^{32}\text{ erg}\) can be released within ≈ 10 – 100 seconds by the process of magnetic-reconnection (Parker, 1957). The released magnetic energy can later be converted into thermal, non-thermal, and kinetic energy of the plasma motions and turbulence (Emslie et al., 2012; Warmuth and Mann, 2016; Aschwanden et al., 2017). Recent observations show that in the top coronal loop of the flare, a significant portion of the released magnetic energy – of the order of 1% of the total energy (Kontar et al., 2017; Stores, Jeffrey, and Kontar, 2021) – ends up inducing magnetohydrodynamic (MHD) plasma turbulence (Alfvén, 1942; Iroshnikov, 1964; Gloaguen et al., 1985; Biskamp, 2003; Shibata and Magara, 2011; Beresnyak, 2019). The MHD plasma turbulence, which is a fluid model of turbulence (Priest, 2014), distributes energy in the full loop half-length of the flare and dissipates within a few seconds (Jeffrey et al., 2018; Stores, Jeffrey, and Kontar, 2021). The rapid dissipation causes sudden plasma heating over 10 MK and non-thermal acceleration of particles. The non-thermal acceleration of particles causes hard X-ray emission at the loop top as well as at the footpoint of the flare (Krucker et al., 2008; Kontar et al., 2013, 2017; Kong et al., 2019, 2022).

MHD plasma turbulence is a state of plasma where non-linear interactions and cascading of kinetic energy from larger to smaller scales produce a chaotic structure and stochastic and non-stochastic motions of the magnetized plasma. Fully developed MHD plasma turbulence consists of stochastic as well as non-stochastic accelerated plasma that may obey Maxwellian and non-Maxwellian velocity distributions. The stochastic and non-stochastic accelerated plasma may cause plasma heating to over 10 MK and energetic particles in the solar flare (LaRosa and Moore, 1993; Petrosian, 2012; Kontar et al., 2017; Vlahos and Isliker, 2018). The MHD plasma turbulence is believed to occur due to instabilities arising during the magnetic-reconnection process in the flare (Fang et al., 2016; Ruan, Xia, and Keppens, 2019; Shen et al., 2022; Ruan, Yan, and Keppens, 2023; Shibata, Takasao, and Reeves, 2023). As a result of an intricate non-linear interaction between the reconnection outflows and the chromosphere evaporation below the reconnection site, instabilities arise. However, what type of instability causes MHD turbulence is still an open question. An electron-beam-induced instability due to wave–particle interactions, producing anomalous resistivity, is thought to be a prevalent mechanism for turbulence generation in flares (Kontar et al., 2011). Anomalous resistivity will cause fast turbulence dissipation and heating (Xu, Chen, and Wu, 2013; Graham et al., 2022). The inertial-flow-driven Kelvin–Helmholtz instability (KHI) (Fang et al., 2016) could also generate turbulence-induced vortices. The KHI-induced turbulence is produced above the loop top of the flare, which later propagates to chromospheric footpoints with varying density along the magnetic field as Alfvénic perturbations. The KHI, however, takes a long time for turbulence to generate it (Ruan, Xia, and Keppens, 2018, 2019).

In solar flares, similar to hydrodynamic turbulence, the MHD plasma turbulence (Alfvén, 1942; Iroshnikov, 1964; Biskamp, 2003; Shibata and Magara, 2011; Beresnyak, 2019) transfers energy from the stressed magnetic field to the accelerated particles through the cascading of energy from larger to smaller scales (Miller et al., 1997; Krucker et al., 2008; Klein and Dalla, 2017). MHD turbulence impacts the thermal and electrical properties of the flare plasma (Bian, Kontar, and Emslie, 2016). The thermal conduction heat flux reduces to its classical value below the Spitzer (1962) limit and therefore accounts for a long cooling time (Jiang et al., 2006). Bian, Kontar, and Emslie (2016) observed that MHD turbulence is associated with the non-thermal electrons and the thermal electrons of low energy and cooled by the anomalous cooling effect. Krucker et al. (2008) and Fang et al. (2016) observed that during flares, it would be difficult to stop the energetic electrons of tens of keV energy because of the low electron density \(\approx 10^{10}\text{ cm}^{-3} \). However, if MHD turbulence is considered, the electrons can efficiently travel into the loops before leaving the flare-plasma environment and be trapped at the loop top (Simões and Kontar, 2013; Bian, Emslie, and Kontar, 2017; Effenberger and Petrosian, 2018).

Several theoretical and observational studies have been carried out to show the presence of turbulence in plasma (Jiang et al., 2006; Musset, Kontar, and Vilmer, 2018). High kinetic and magnetic Reynolds numbers and plasma motions during flares are the parameters that are used to reflect the presence of turbulence. Intensified cooling occurs at the top of flare loops. The cooling can be up to two times lower than expected from the classical theories of thermal conduction. In addition, it was noted that missing energy (additional energy input) could be larger than the energy input during the impulsive phase of a solar flare. These findings suggest that turbulence in a flare suppresses thermal conduction and leads to slower cooling (Jiang et al., 2006; Krucker et al., 2008; Bian, Kontar, and Emslie, 2016).

In the case of the high-energy electrons (≈ MeV) in a turbulent region, the charged particles can become trapped in the turbulent scattering of magnetic fluctuations, which is an observed phenomenon in solar flares (Kuznetsov and Kontar, 2015; Musset, Kontar, and Vilmer, 2018). Hinode/Euv Imaging Spectrometer measurements often show spectral-line broadening during flares (Kosugi et al., 2007; Culhane et al., 2007). It is believed that an increase in spectral-line widths results from superposed Doppler-shifted emissions of turbulent fluid motions or due to the superposition of electrons flows from different loops in the flare (Milligan, 2015; Del Zanna and Mason, 2018). The increase in spectral-line widths in excess is expected from the random thermal motions due to thermal broadening or velocity fluctuations (Kontar et al., 2017; Stores, Jeffrey, and Kontar, 2021). Kontar et al. (2017) observed that broad, soft X-ray spectral lines often formed near the top of a flaring loop. These observations suggest a significant level of turbulence in the bulk plasma flow near the electron-acceleration region. Hydrodynamic simulations of multi-thread flare loops show that the non-thermal broadening is produced mainly by turbulent motions (Polito, Testa, and De Pontieu, 2019). Using Interface Region Imaging Spectrograph (IRIS) spectral-modeling results, Jeffrey et al. (2018) observed the presence of turbulence in the lower solar plasma for 1.7 seconds. It was suggested that with the flare onset, the lower-atmospheric solar plasma is heated because of the dissipation of turbulence energy by the low-atmospheric turbulence (Jeffrey et al., 2018).

Although the above observations and modeling results show evidence for the existence of the MHD plasma turbulence (fluid model of turbulence) (Alfvén, 1942; Iroshnikov, 1964; Biskamp, 2003; Shibata and Magara, 2011; Beresnyak, 2019) and its crucial role in solar flares, a holistic view of its characteristics is still lacking. This is because of the challenges posed by the complexities in the MHD plasma turbulence itself. There are not many models and theories available that can characterize MHD plasma turbulence in its entire spectrum of evolution. The physics of MHD plasma turbulence becomes complex because of coupled velocity and magnetic-field vectors. The complexity is further increased by its dissipative characteristics such as viscosity and resistivity. It also has a mean magnetic field, which greatly increases the anisotropy of the process. Since the mean magnetic field cannot be removed in MHD models, turbulence becomes a trickier issue to comprehend (Verma, 2004; Beresnyak, 2019).

Turbulence in solar flares is characterized by stochastic motions of plasma particles and high Reynolds numbers (LaRosa and Moore, 1993; Petrosian, 2012; Kontar et al., 2017; Vlahos and Isliker, 2018). The presence of stochastic (random) motions and its many modes make turbulence in solar-flare plasma better dealt with in statistical ways (Taylor, 1935; Kolmogorov, 1941; Pope, 1991, 1994). The stochastic Lagrangian models of the turbulent velocity and dissipation developed by Pope (1991, 1994, 2011) are simple statistical models of the inhomogeneous hydrodynamic turbulence. These models have been extensively used for determining the characteristics of homogeneous and inhomogeneous turbulence in the fluid flow, but not so far for studying the turbulence observed in the solar-flare plasma (Kontar et al., 2017; Jeffrey et al., 2018; Stores, Jeffrey, and Kontar, 2021). It may be noted that hydrodynamic modeling of the impulsive and gradual phases of solar-flare plasma reflects a good correlation with the observations and numerical simulations. The thick-target and heat-conduction models can be described by hydrodynamic modeling in the solar-flare plasma (Gan, Zhang, and Fang, 1991). Warren (2006) presented multi-thread hydrodynamic modeling of a solar flare that is often consistent with the observations and numerical simulations. Solar-flare plasma can therefore be treated as a hydrodynamic/MHD fluid (Gan, Zhang, and Fang, 1991; Priest, 2014) and computed in an Eulerian or Lagrangian frame of reference (Pope and Pope, 2000; Mathieu and Scott, 2000).

In our analysis, we applied stochastic Lagrangian models of velocity and dissipation (relaxation rate/specific dissipation rate) to study the characteristics of inhomogeneous turbulence (assumed as an inhomogeneous MHD plasma turbulence) in the flare in a Lagrangian frame of reference (Pope and Pope, 2000; Mathieu and Scott, 2000). Monte Carlo experiments (Sacks, Schiller, and Welch, 1989; Paxton et al., 2001; Keller, 2003) are carried out to solve these models for a large number of realizations. Model parameters were approximated using the Euler–Maruyama method (Saito and Mitsui, 1993; Malham and Wiese, 2010; Bayram, Partal, and Buyukoz, 2018) and then Monte Carlo simulations were carried out for a large number of realizations. A detailed analysis is presented in the following sections. In Section 2, we present a brief description of stochastic Lagrangian models of velocity and dissipation of inhomogeneous hydrodynamics turbulence, simulation method, and estimation of initial parameters. The results, along with analysis, are presented in Section 3. The discussions are presented in Section 4. We finally present a summary of this analysis in Section 5.

2 Method

2.1 Model Description

Hydrodynamic turbulence involves the random motion of non-conducting fluid particles with low viscosity [\(\nu \)] and high kinetic Reynolds numbers > 4000 (Pope and Pope, 2000; Mathieu and Scott, 2000). This leads to energy transfer from larger to smaller scales, causing irregular velocity fluctuations (Kolmogorov, 1941). Instabilities in laminar flow give rise to turbulence, characterized by increased velocity gradients and energy dissipation. MHD plasma turbulence, seen in phenomena such as solar flares, arises from the chaotic motion of magnetized conducting fluid particles. The magnetic field’s interaction with the plasma creates a steady state where energy cascades from large to small scales, akin to hydrodynamic turbulence (Gloaguen et al., 1985; Biskamp, 2003; Schekochihin and Cowley, 2007; Shibata and Magara, 2011; Beresnyak, 2019). This energy-conversion process, however, is influenced significantly by magnetic-field lines (Ruan, Yan, and Keppens, 2023).

MHD plasma turbulence in solar flares is associated with magnetic-reconnection. Fluctuating magnetic-field lines release turbulent kinetic energy, leading to particle heating and non-thermal acceleration. This results in high-energy X-ray emissions at both the loop top and footpoints of the flare (Kontar et al., 2017; Jeffrey et al., 2018; Stores, Jeffrey, and Kontar, 2021). The turbulent magnetic field’s energy plays a crucial role in electron acceleration at the flare termination shock, explaining the looptop hard X-ray emissions. Turbulence intensity varies along flare loops due to density differences, with the highest intensity found at the loop top (Kontar et al., 2017; Stores, Jeffrey, and Kontar, 2021). These findings provide insights into the mechanisms behind energy conversion and particle acceleration in solar-flare turbulence.

For describing the fluid model, particularly the hydrodynamic model for solar-flare plasma turbulence, we employed simple stochastic Lagrangian models for velocity and dissipation. These models generate statistical Lagrangian trajectories for plasma particles within turbulence. The position [\(X^{+}(t)\)], velocity [\(U^{+}(t)\)], and dissipation rate [\(\epsilon ^{+}(t)\)] of fluid particles are time-dependent functions. When considering the Eulerian velocity field \(U(x, t)\), the corresponding Lagrangian velocity for fluid particles becomes \(U^{+}(t) = U(X^{+}(t), t)\).

In hydrodynamic turbulent flow, the estimation of dissipation rate [\(\epsilon \)] is carried out by the equation \(\epsilon \approx U^{3}/L \), here U and L are the mean turbulent velocity and integral length scale (Kolmogorov, 1941; Tennekes et al., 1972). The dissipation-rate equation, however, becomes independent of viscosity and resistivity [\(\rho \)] at high Reynolds numbers > 4000 and can be written in terms of turbulent kinetic energy (density) [k] as \(\epsilon \approx k/t\text{ erg}\,\text{g}^{-1}\,\text{s}^{-1} \) (Vassilicos, 2015; Pope and Pope, 2000). Pope (1991, 1994) proposed that for a homogeneous fluid that has Lagrangian fluid-particle parameters, namely, position \(x^{+} \), velocity \(U^{+} \), and dissipation rate \(\epsilon ^{+} \), the model of dissipation rate can be understood from the equation of relaxation rate/specific dissipation rate [\(\omega (x, t) \)]. The relaxation rate/specific dissipation rate can be defined as \(\omega (x, t) = \epsilon (x, t)/ k(x, t)\text{ s}^{-1} \). In this definition, \(\epsilon (x, t) \) is the dissipation rate that is random in nature and \(k(x, t) \) is the kinetic energy (density) of the turbulence and has a fixed value. For the case of a homogeneous fluid, the model of \(\omega (x, t)\) can be described in terms of \(\omega ^{+}(x, t)\) in the Lagrangian frame. The model of relaxation rate for a homogeneous turbulent flow evolves according to the Ito differential equation and is described in Equation 1. Using Equation 1, Pope (1991, 1994) derived an equation of \(\omega (x, t)\) for inhomogeneous turbulence that is described in Equation 2:

$$ \mathrm {d}\omega ^{*}(t) = -\omega ^{*}\omega \mathrm {d}t\{S + C[\operatorname {ln}( \omega ^{*}/ \omega ) -1/2\sigma ^{2}]\} +\omega ^{*}(2C\omega \sigma ^{2})^{1/2} \mathrm {d}W $$
(1)
$$ \mathrm {d}\omega ^{*}(t) = -\omega ^{*}\omega \mathrm {d}t\{S + C[\operatorname {ln}( \omega ^{*}/ \omega ) -1/2\sigma ^{2}] \} + \omega ^{2} h \mathrm {d}t +\omega ^{*}(2C\omega \sigma ^{2})^{1/2} \mathrm {d}W. $$
(2)

In Equations 1 and 2, \(\mathrm {d}W\) is the Weiner process, C and \(S = (C2-1) - (C1-1)P/{<}\epsilon{>}\) are constants. In the relation for \(S \), C1, and C2 are also constants and P is the rate of production of kinetic-energy density. In Equation 2 for inhomogeneous turbulence, the constant h is added, which is a function of both position and time. In these equations, the values of constants are taken as C = 6.2, C1 = 1.45, C2 = 1.90 (Pope, 1991, 1994). The values of \(\sigma =1 \), h = 1 are chosen arbitrarily. For very high Reynolds number, say above \(10^{6} \), the magnitude of C is chosen as 6.2 (Pope, 1991). For the case of solar-flare turbulence, which has also a very high Reynolds number, the value of C = 6.2 is an appropriate consideration.

The stochastic Lagrangian model of velocity of turbulence particles [\(U^{*}(t) \)] for inhomogeneous hydrodynamic turbulence at time t was derived from the Langevin equation of homogeneous isotropic turbulent flow (Pope, 1991, 1994). The Langevin equation for homogeneous velocity \(U^{*}(t) \) takes the form of a stochastic differential equation as given in Equation 3. For homogeneous turbulence, the mean turbulence velocity \({<}U{>} = 0 \), its variance \(k \approx {<}U{>}^{2} \), and dissipation rate \(\epsilon \approx \mathrm {d}k / \mathrm {d}t \) remain constant. For homogeneous turbulence, all three components of velocity are identical. Equation 3 can be extended for the flow of inhomogeneous turbulence by adding three drift terms in the equation. The first, second, and third drift terms are the mean pressure gradient [\(\triangledown{<}P{>} \)], local Eulerian mean of the velocity [\(U(x^{*}(t), t) \)], and addition of 1/2 in the coefficient (1/2 + 3/4 C). On applying these drift terms, the Langevin equation for inhomogeneous fluid flow takes the form described in Equation 4 (Pope, 1991, 1994). In Equations 3 and 4, C, \({<}\epsilon{>}\), and \(\mathrm {d}W(t)\) are the universal constant, dissipation rate, and Weiner process, respectively:

$$ \mathrm {d}U^{*}(t)=-\frac{3}{4}C\frac{{< }\epsilon{>}}{k}U^{*}(t) \mathrm{d}t+(C{< }\epsilon{>})^{1/2}\mathrm {d}W(t) $$
(3)
$$ \mathrm {d}U^{*}(t)=-\triangledown{< }p{>}\mathrm {d}t-(\frac{1}{2} + \frac{3}{4}C)\frac{{< }\epsilon{>}}{k}(U^{*}(t)- {< }U{>})\mathrm {d}t +(C{< }\epsilon{>})^{1/2}\mathrm {d}W(t). $$
(4)

2.2 Methods of Simulation

Monte Carlo simulations (Sacks, Schiller, and Welch, 1989; Paxton et al., 2001; Keller, 2003) were carried out using the Euler–Maruyama approximation (Saito and Mitsui, 1993; Malham and Wiese, 2010; Bayram, Partal, and Buyukoz, 2018) of the stochastic Lagrangian models for velocity and dissipation (relaxation rate) of the inhomogeneous hydrodynamic turbulence (Pope, 1991, 1994; Pope and Pope, 2000). In such simulations, 1, 10, 100, and 1000 possible paths of plasma particles, involved in the turbulence of the solar flares, were explored. The models, as described in Equations 2 and 4, were first approximated using the Euler–Maruyama method for the initial parameters of the MHD plasma turbulence in solar flares (Kontar et al., 2017; Jeffrey et al., 2018; Stores, Jeffrey, and Kontar, 2021) and further Monte Carlo simulations were carried out.

The Euler–Maruyama method is a numerical method and is widely used to approximate stochastic differential equations. It is based on the truncated Ito–Taylor expansion. This method provides a natural way of approximation of stochastic differential equations since it involves random numbers (Saito and Mitsui, 1993; Malham and Wiese, 2010; Bayram, Partal, and Buyukoz, 2018). The Euler–Maruyama approximations of Equations 2 and 4 are given in Equations 5 and 6, respectively. In these equations, \(\mathrm {d}W\) is a Weiner process and defined as \(\mathrm{d}W(t) =W(i + 1)(t) - W(i)(t)\). In Equation 5, d\(\omega \) is taken into account in spite of \({<}\omega{>} \) since it is variable in nature. The variable nature of d\(\omega \) is considered due to the inhomogeneous nature of MHD plasma turbulence in the solar-flare plasma. In order to simulate Equation 6 for the two components of velocities of turbulent particles, the equation was solved separately for the velocity components \(U_{x} (t)\), \(U_{y}(t) \), and the Brownian paths of the particles are presented. It allows us to understand the distribution of the statistical nature of turbulence particle’s velocity for a turbulent time scale of ten seconds:

$$ \begin{aligned} \omega _{i+1}(t) ={}& \omega _{i}(t) - \omega _{i} \mathrm {d}\omega \mathrm {d}t \lbrace S + C [\operatorname {ln}( \omega _{i}/ \mathrm {d}\omega ) -1/2 \sigma ^{2}] \rbrace + \mathrm {d}\omega ^{2} h \mathrm {d}t \\ &{}+\omega _{i}(2C \mathrm {d}\omega \sigma ^{2})^{1/2} W(t) \end{aligned} $$
(5)
$$ U_{i+1}(t)= U_{i}(t) - \mathrm {d}p \mathrm {d}t - (\frac{1}{2}+ \frac{3}{4}C)\frac{\mathrm {d}{< }\epsilon{>}}{k}(U_{i}(t) - {< }U{>}) \mathrm {d}t + (C\mathrm {d}{< }\epsilon{>})^{1/2}\mathrm {d}W(t). $$
(6)

2.3 Estimation of Initial and Final Parameters

In order to carry out Monte Carlo simulations, we first estimated initial parameters, namely mean turbulence velocity variance [\({<}U{>}\text{ cm}\,\text{s}^{-1} \)], mean pressure gradient [\(\triangledown{<}p{>} \text{ erg} \text{cm}^{-3} \)], turbulent kinetic energy (density) [k erg g−1], and dissipation rate [\(\epsilon \text{ erg}\,\text{g}^{-1}\,\text{s}^{-1} \)] for turbulence in large solar-flare plasma. We assumed the total injected turbulence kinetic energy [K] of \(K \approx 10^{30} \text{ erg}\) that can produce turbulence in the loop half-length of \(L \approx 10^{10}\text{ cm}\) (length scale) for the duration of ten seconds. Only 1% of the total released magnetic energy \(\approx 10^{32} \text{ erg}\) by the process of magnetic-reconnection (Parker, 1957) goes into turbulence kinetic energy in a large solar flare (Kontar et al., 2017; Stores, Jeffrey, and Kontar, 2021). Here, simulation consists of boundary conditions for turbulence duration (\(0 < t < \text{ten seconds}\)), in addition, we apply initial conditions of the parameters.

Mean values of turbulence velocity variance [\({<}U{>}\text{ cm}\,\text{s}^{-1}\)] and plasma pressure gradient [\(\triangledown{<}p{>}\text{ erg}\,\text{cm}^{-3}\)] were determined using the relations \(K = (3/2) m_{i} {<}U{>}^{2} n V \) and \(\triangledown{<}p{>} = 2 n \mathrm{k_{b}} T \). In these relations, \(m_{i} = 1.3~\mathrm{m_{p}} \) is the mean ion mass for the solar corona, and \(\mathrm{m}_{\mathrm{p}}\) is the mass of the proton, \(V \approx L^{3} \) and T are the flare volume and plasma temperature in MK, \(n = \sqrt{EM/V} \) is the number density of the ions, and \(\mathrm{k}_{ \mathrm{b}}\) is the Boltzmann constant. Since relations of \(n = \sqrt{EM/V} \) and \(P = 2 n \mathrm{k_{b}} T \) consist of values of emission measure [EM] and plasma temperature [T] of the solar flare, we first determined values of the emission measure EM and the plasma temperature T from spectral modeling of the thermal X-ray spectra using isothermal models. The X-ray spectra were from the X-class solar flares by the Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI) spacecraft (Schwartz et al., 2002; Lin et al., 2002). The X-ray spectral modeling allows us to find the mean values of emission measure of \(EM \approx 10^{49} \text{ cm}^{-3}\) and a plasma temperature of \(T \approx 29 \text{ MK}\) (Kumar et al., 2020; Kumar and Choudhary, 2021). Using \(L \approx 10^{10}\text{ cm}\), we obtained \(V = 10^{30} \text{ cm}^{3} \). Further, using the obtained parameters and the relations \(K = (3/2) m_{i} {<}U{>}^{2} n V \), \(P = 2 n \mathrm{k_{b}} T \), we observed the mean value of turbulence velocity of \({<}U{>} \approx 10^{7}\text{ cm}\,\text{s}^{-1} \) and pressure gradient of \(\triangledown{<}p{>} \approx 75 \text{ erg}\,\text{cm}^{-3}\).

The turbulent kinetic-energy density was estimated using the relation \(k \approx u^{2}\) and was observed to be \(k \approx 10^{14} \text{ erg}\, \text{g}^{-1} \). Since the turbulence is taken as inhomogeneous for the time scale of ten seconds, the dissipation rate (which is random in nature due to the inhomogeneous nature of turbulence) was estimated using the relation \(\epsilon \approx \mathrm {d}k/\mathrm {d}t \). Using the value of the kinetic-energy density of \(k \approx 10^{14}\text{ erg}\,\text{g}^{-1} \), and taking the initial parameters as zero, we found the dissipation rate (density) \(\epsilon \) to vary between \(\epsilon \approx (0\,\text{--}\,1) \times 10^{14}\text{ erg}\,\text{g}^{-1} \,\text{s}^{-1} \). Using the values of the dissipation rate (density) \(\epsilon \approx (0\,\text{--}\,1) \times 10^{14}\text{ erg}\,\text{g}^{-1}\,\text{s}^{-1} \) and the kinetic-energy density of \(k \approx 10^{14}\text{ erg}\,\text{g}^{-1} \), the value of the relaxation rate \(\omega (x, t) = \epsilon (x, t)/ k(x, t) \) was found to vary between \((0\,\text{--}\,1)\text{ s}^{-1} \). The mean value of the dissipation rate (density) and the relaxation rate was obtained of \({<}\epsilon{>} = 0.5 \times 10^{14}\text{ erg}\,\text{g}^{-1}\,\text{s}^{-1} \) and of \({<}\omega (x, t){>} \approx 0.5\text{ s}^{-1} \). Using the production rate of the turbulence kinetic energy \(P = 0.1 \times 10^{14}\text{ erg}\,\text{g}^{-1} \,\text{s}^{-1} \), C1 = 1.45, C2 = 1.90, the value of the constant \(S = (C2-1) - (C1-1)P/{<}\epsilon{>}\) in Equation 2 was estimated of \(S=1 \).

Since approximation of velocity and dissipation (Equations 5 and 6) through the Euler–Maruyama method requires estimated values of the number of steps [n] and time step size [dt], we estimated these parameters taking into account the size of the mean free path \(\lambda \) as a step length of the collisional particles in the turbulence of the solar flare. The mean free path \(\lambda \) or the step length was determined using a simple formula step length [\(\lambda \)] = velocity × time. Using the velocity \({<}U{>} \approx 10^{7}\text{ cm}\,\text{s}^{-1} \) and the time = ten seconds, we found a step length of \(\lambda = 10^{8}\text{ cm}\). The number of steps [n] of the turbulence particles (stochastic) was estimated using the formula n = total distance/step length. Taking full-loop half-lengths of \(L = 10^{10}\text{ cm}\) of the solar flare as a total distance (length scale of the turbulence), we found n = 200. The time step [dt] = total time / number of steps, and was found to be 0.05 seconds.

The dispersion time and range values of the relaxation rate \(\omega (x, t) \) and turbulent particle velocities \(U^{*}(t) \) in one and two dimensions obtained through Monte Carlo simulations were determined from the statistical/histogram analysis of the obtained data. It allows us to find the most probable range values of the parameters and probable value of the dispersion time. Further, the Monte Carlo mean values of these parameters were determined using a Gaussian distribution function drawing 10,000 random samples. 10,000 uniform random samples drawn between the range values of the parameters allowed us to find the Monte Carlo mean values of the parameters with an accuracy < 1% within a 95% confidence interval. The detailed results are presented and analyzed in Section 3.

3 Results and Analysis

We obtained results of velocity and dissipation characteristics in one and two dimensions of inhomogeneous turbulence in a large solar-flare plasma using Monte Carlo experiments (Sacks, Schiller, and Welch, 1989; Paxton et al., 2001; Keller, 2003). As described, we used stochastic Lagrangian models of velocity and dissipation of the inhomogeneous hydrodynamic turbulence (Pope, 1991, 1994). Initial parameters of inhomogeneous MHD plasma turbulence (as estimated in Section 3) of a large solar flare, namely, turbulent kinetic energy (density) of \(10^{14}\text{ erg}\,\text{g}^{-1} \), turbulence duration of ten seconds, and turbulence length scale of full loop half-length \(L = 10^{10}\text{ cm}\), etc., were utilized. The obtained results from the Monte Carlo experiment (Sacks, Schiller, and Welch, 1989; Paxton et al., 2001; Keller, 2003) for 1, 10, 100, and 1000 realizations of the sample paths of plasma particles in solar-flare turbulence are presented in one and two dimensions in Figures 1, 3, and 5, respectively.

Figure 1
figure 1

Upper-left, Upper-right, Lower-left, and Lower-right panels show the temporal evolution of relaxation rate [\(\omega (x, t) \)] for 1, 10, 100, and 1000 realizations, respectively, of the turbulent plasma particles in the solar flare. Here, positive values and the dispersive nature of \(\omega (x, t) \) after ≈ five seconds show the presence, energy cascading, and dissipation during the turbulence in the solar flare. Lower-right panel shows the range of \(\omega (x, t) \approx (1\,\text{--}\,8) \times 10^{-4} \text{ s}^{-1}\).

Full size image

The upper-left, right, and lower-left, right panels of Figure 1 show the results of the temporal evolution of relaxation rate [\(\omega (x, t) \)] (described in Equation 5) with respect to time for 1, 10, 100, and 1000 realizations of the particles present in the inhomogeneous turbulence of the solar flare. Here, the evolution of sample paths from lower to higher values clearly demonstrates the characteristic of energy transfer by turbulence (Kolmogorov, 1941). Figure 1 shows that after ≈ five seconds, the energy is suddenly dispersed, which suggests that the injected energy first cascaded from larger to smaller scales (during the first five seconds) and finally dissipated due to resistivity of the plasma to thermal and nonthermal energy. Kontar et al. (2017) also estimated a similar dissipation duration of ≈ five seconds for MHD plasma turbulence in a solar flare. It therefore partially confirms the presence of MHD plasma turbulence in a solar flare. The lower-right panel of Figure 1, which shows sample paths for 1000 realizations of the particles, highlights that \(\omega (x, t) \) lies between \(\omega (x, t) \approx (1\,\text{--}\,8) \times 10^{-4}\text{ s}^{-1} \). Taking this range, the estimated Monte Carlo mean of relaxation rate is found to be \(\omega (x, t) \approx 4.5 \times 10^{-4} \text{ s}^{-1} \) through drawing 10,000 uniform samples in the range of \(\omega (x, t) \). The Gaussian distribution of 10,000 samples and Monte Carlo mean of \(\omega (x, t) \) is shown in Figure 2.

Figure 2
figure 2

The Gaussian distribution (PDF) of the 10,000 samples of relaxation rate [\(\omega (x, t) \)] that were measured between \(\omega (x, t) \approx (1\,\text{--}\,8) \times 10^{-4}\text{ s}^{-1}\). Here, the Monte Carlo mean of \(\omega (x, t) \) is found of the order of \(\omega (x, t) \approx 4.5 \times 10^{-4}\text{ s}^{-1}\).

Full size image

It may be noted that \(\omega (x, t) \) provides the rate at which turbulence dissipates into heat per unit volume per unit time and raises the temperature of the flare corona above ≈ 10 MK. If we take \(\omega (x, t) \approx 4.5 \times 10^{-4} \text{ s}^{-1} \), the turbulence will dissipate heat of \(4.5 \times 10^{27}\text{ erg}\) in ten seconds in the loop half-length of \(L \approx 10^{10}\text{ cm}\) and volume of \(V = 10^{30} \text{ cm}^{3} \), respectively. This shows that fully injected kinetic energy does not convert into thermal energy. Only 0.5% of the energy goes into thermal energy and the rest may be converted into non-thermal energy/energetic particles and other processes of the solar flare. A significant portion of the injected energy is utilized for generating energetic particles and may produce hard X-ray emissions at the loop-top and footpoint of the flares (Krucker et al., 2008; Kontar et al., 2017; Vlahos and Isliker, 2018; Kong et al., 2019, 2022). However, if we consider, the \(10^{30} \text{ erg}\) energy to be converted into thermal energy in the volume of \(V=10^{30} \text{ cm}^{3} \) in ten seconds, the relaxation rate should increase to \(\omega (x, t) \approx 4.5 \times 10^{-2 }\text{ s}^{-1} \). Therefore, the estimated thermal energy in this analysis verifies particle dynamics (energy budget) into a standard solar-flare model (Priest, 2014; Tajima and Shibata, 2018).

Figures 3 and 5 show sample paths of velocities in one and two dimensions of the stochastic motions of plasma particles present in the turbulence of solar flares. From Figures 3 and 5, we may note that particles fluctuate chaotically and their velocity gradient increases from the lower to higher values during the time scale of the turbulence. The particles’ velocity dispersion occurs after ≈ five seconds that is readily visible in the velocity fields shown in Figures 3 and 5. In these figures, unsteady random paths demonstrate the presence of stochastic motions in the turbulence of solar-flare plasma. Therefore, the characteristics of the velocity field are evidence of stochastic motions in turbulence. It is known from the theory of turbulence that at higher velocities or during dissipation, greater plasma heating and particle acceleration occur. At this stage, the temperature becomes maximum in the solar-flare plasma (Gordovskyy, Kontar, and Browning, 2016). Therefore, the maximum velocities are related to the peak temperature of the solar-flare plasma.

Figure 3
figure 3

Upper-left, Upper-right, Lower-left, and Lower-right panels show the sample paths of the velocities of 1, 10, 100, and 1000 particles, respectively, in the turbulence of a solar flare in one dimension. The lower-right panel for the 1000 realizations of the turbulent plasma particles shows the velocity lies in the range \(U^{*}(t) \approx (0.5\,\text{--}\,3) \times 10^{6}\text{ cm}\,\text{s}^{-1} \).

Full size image

Here, it may be noted that plasma pressure is one of the parameters of the velocity Equation 6, therefore its effects cannot be neglected for turbulence in a solar flare. As plasma pressure is a function of electron density and temperature, it plays a vital role in governing the velocities of the particles in the solar-flare plasma. It is known that during magnetic reconnection, the fast flow of energy released towards the chromosphere causes an increase in temperature and pressure gradient of the chromosphere. Due to the pressure gradient, the plasma flows revert toward the corona and cause beam-plasma instability that produces turbulences in the solar-flare plasma (Yokoyama and Shibata, 2001; Shibata and Magara, 2011; Priest, 2014).

From the lower-right panel of Figure 3 that shows 1000 realizations of the plasma particles, we can see that velocities of plasma particles vary in the range \(U^{*}(t) \approx (0.5\,\text{--}\,3) \times 10^{6}\text{ cm}\,\text{s}^{-1} \). Here, the obtained range value of the velocity of the particles shows the presence of plasma motion that is evidence of MHD plasma turbulence in the solar flare (Ruan, Yan, and Keppens, 2023). Taking into account the obtained range value of the particles’ velocities, the Monte Carlo mean value of turbulent particles’ velocity for the 10,000 samples was obtained to be of the order of \(U^{*}(t) \approx 1.5 \times 10^{6}\text{ cm}\,\text{s}^{-1} \) (as shown in Figure 4). The velocity results obtained here are similar to the results of velocities for hotter and cooler ions (Fe XXIV, Fe XXIII, and Fe XXVI, Si IV) found in the solar-flare MHD plasma turbulence. Velocities of these ions were determined by Stores, Jeffrey, and Kontar (2021) and Jeffrey et al. (2018) in their analysis carried out from the observations of Hinode/Euv Imaging Spectrometer and IRIS, respectively.

Figure 4
figure 4

The Gaussian distribution (PDF) of 10,000 samples of the plasma particle velocities that lie in the range \(U^{*}(t) \approx (0.5\,\text{--}\,3) \times 10^{6}\text{ cm}\,\text{s}^{-1} \). Here, the Monte Carlo mean of the plasma particle velocities is found to be 1.5 \(\times 10^{6}\text{ cm}\,\text{s}^{-1} \).

Full size image

It is well known that during a flare, spectral lines of the ions often show wider line widths. It is expected from random thermal motions of the plasma particles and is termed thermal broadening or velocity. The excess broadening could be associated with the non-thermal broadening as well, which is believed to be the result of superposed Doppler-shifted emission of either turbulent fluid motions or the superposition of flows from different loops. Extracting the non-thermal broadening from the spectral profile analysis, Stores, Jeffrey, and Kontar (2021) found that the non-thermal velocity of the hotter ions Fe XXIII and Fe XXIV peaks at the beginning of the flare 60 – 65 km s−1, and later decreases to the velocities of 30 – 35 km s−1. Using the spectroscopy results from the spectral lines of IRIS taken from the plasma at a temperature of 0.8 MK, Jeffrey et al. (2018) observed that in lower-atmosphere turbulence, the velocities of the ions vary from the 30 – 10 km s−1. Jeffrey et al. (2018) concluded that the range velocity is due to the motion of the turbulent plasma in the loop half-lengths of the solar flare. The turbulence must exist in the low-temperature region (chromosphere) in the solar atmosphere.

The numerical analysis carried out by Ruan, Yan, and Keppens (2023) shows that KHI-induced turbulence consists of the velocities of the turbulent particles in the range 200 – 10 km s−1. The high values of turbulent velocities were found at the termination shock region where hard X-ray emissions originate, while the low velocities exist where the plasma density is around \(10^{11} \text{ cm}^{-3}\). This shows the presence of Maxwellian and non-Maxwellian distributions of turbulent plasma that primarily is non-Maxwellian in distribution (LaRosa and Moore, 1993; Petrosian, 2012; Kontar et al., 2017; Vlahos and Isliker, 2018). The range of values of the velocities of the turbulent particles demonstrate the motion of turbulence plasma from the loop top (hotter region) to footpoints (cooler region) by depositing its energy and heating the solar-flare full-loop half-lengths. It occurs due to interactions of nonthermal turbulent plasma (non-Maxwellian) to thermal (Maxwellian) background plasma of the solar flare (Ruan, Yan, and Keppens, 2023).

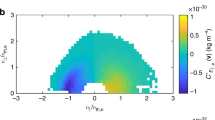
Figure 5 shows velocity profiles in two dimensions of the particles present in the turbulence of solar flares. The two-dimensional representation of the velocities shows the inhomogeneous chaotic velocity field of the turbulence in the solar flare. From Figure 5, we can note that the range of values of velocities are similar as estimated through the temporal evolution of velocities in one dimension as shown in Figure 3. Here, very few particles have negative velocities. The two-dimensional velocity field of the turbulent particles can be compared with the thermal images obtained from several observatories such as RHESSI, Hinode, GOES, etc. (Gallagher et al., 2002; Sui et al., 2003).

Figure 5
figure 5

Upper-left, Upper-right, Lower-left, and Lower-right panels show the sample paths of the velocities of 1, 10, 100 and 1000 particles, respectively, present in turbulence of the solar flare in two dimensions. Here, the panels also show the velocity field in two dimensions that is stochastic in nature.

Full size image

4 Discussion

An unresolved issue of solar flares is the question of how magnetic energy released through the magnetic-reconnection process leads to thermal and non-thermal particle acceleration so quickly and what causes loop-top and footpoint hard X-ray emissions (Krucker et al., 2008; Shibata and Magara, 2011). MHD plasma turbulence has been thought to facilitate the quick conversion of a significant portion of released magnetic energy to thermal and non-thermal particle energizing (acceleration) that leads to plasma heating (> 10 MK) and loop-top and footpoint hard X-ray emissions (Kontar et al., 2017; Kong et al., 2019, 2022). Therefore, the study of turbulence characteristics in solar flares becomes crucial in interpreting its type and processes occurring within it. Its existence in the solar flare proves the various processes of particle dynamics in the standard solar-flare model (Priest, 2014; Tajima and Shibata, 2018). The main aim of this article has been to study the velocity and dissipation characteristics of the particles having stochastic motions (very weakly collisional particles obeying a Gaussian velocity distribution) in inhomogeneous turbulence (Kontar et al., 2013) of the solar flare. We aim to understand the quick conversion of turbulent kinetic energy into thermal energy (> 10 MK) and other processes of a solar flare.

Our results of dissipation clearly demonstrate the existence of a very well-known inhomogeneous turbulence in the solar-flare plasma. The turbulence structure shows that ≈ 0.5% of the total injected turbulent kinetic energy converts into thermal energy within ten seconds, and the rest of the energy goes to creating energetic particles/non-thermal energy and other dynamical processes of the solar flares (Kontar et al., 2017; Kong et al., 2019, 2022). In this analysis, the estimated velocities of stochastic motions are in agreement with the results of the lower-atmospheric turbulence found using IRIS observations and Hinode/Euv Imaging Spectrometer observations, termed MHD plasma turbulence (Jeffrey et al., 2018; Stores, Jeffrey, and Kontar, 2021). Our results, therefore, directly show the existence of low-atmospheric MHD turbulence in a solar flare. We surmise that turbulence is most probably triggered by the beam–plasma instability that causes a weak collisional turbulent plasma. In order to obtain fast dissipation and heating, the anomalous resistivity must be taken into account (Kontar et al., 2011; Xu, Chen, and Wu, 2013; Graham et al., 2022). A detailed discussion is presented as follows.

The results of the relaxation rate shown in Figure 1 and 2 and their quantitative measurement show that the dissipation of the turbulent kinetic energy occurs in a similar manner as occurs in the hydrodynamic turbulence (Kolmogorov, 1941; Pope and Pope, 2000). We find that the rate at which relaxation occurs in our analysis could dissipate \(4.5 \times 10^{27}\text{ erg}\) in ten seconds. This means that a significant portion of the injected kinetic energy dissipates into thermal energy and the rest of the energy goes to non-thermal energetic particles. The estimated thermal energy of \(4.5 \times 10^{27}\text{ erg}\) for ten seconds is equivalent to the thermal energy of the microflares that mainly occur at the lower solar corona and is also believed to be responsible for the multi-million-degree temperature of the solar corona. In order to understand the fast dissipation, the concept of Spitzer resistivity for the collision plasma may be taken into account for the MHD turbulence in solar-flare plasma. We know that the dissipation-rate equation used in this analysis is based only on kinetic energy and time. It does not consist of resistivity or viscosity parameters that are responsible for turbulence. However, the kinetic energy is a function of plasma density, and therefore plasma resistivity depends on the electron density.

For MHD turbulence in solar plasma, which is weakly collisional, the Spitzer resistivity may not be always responsible for causing turbulence. Even in the case of space plasma, there is always a disparity between observations vis-a-vis the role of Spitzer resistivity. The anomalous resistivity is found to facilitate a fast energy dissipation process in the turbulence (Dum, 1971). The enhanced resistivity arises due to wave–particle interactions and nonlinear coupling between the electron wave and the turbulent plasma. Recent analysis carried out through the Magnetospheric Multiscale Spacecraft (MMS) also shows that anomalous resistivity is approximately balanced by anomalous viscosity in the wave–particle interaction system. These measurements show that although waves do not contribute to the reconnection electric field, the waves do produce an anomalous electron drift and diffusion across the current layer associated with magnetic-reconnection or turbulence (Graham et al., 2022).

The origin of anomalous resistivity in turbulence, however, is still an enigmatic question. To understand its origin in turbulence, we need to look at the types of instabilities responsible for the MHD plasma turbulence in the solar flare. We know from the standard solar-flare model that during the impulsive phase of the solar flare, magnetic-reconnection releases the stored magnetic energy in the nonpotential field. The fast flow of the evaporation from the footpoints causes instabilities in the plasma flow. This instability stretches and bends the magnetic-field lines of the flare loops, which are resisted by the Lorentz force of the plasma. The stretched and the back reactions develop on the magnetic-field lines of the solar flare, resulting in a statistically steady state of fully developed MHD turbulence. For the case of solar-flare turbulence, the beam plasma and KHI are supposed to play a key role (Kontar et al., 2011; Xu, Chen, and Wu, 2013; Fang et al., 2016; Ruan, Xia, and Keppens, 2018).

Recent studies show that the ion-acoustic wave turbulence excited by the beam return current consists of collisional and anomalous resistivity. In order to obtain a steady state during the ion-acoustic wave turbulence in a solar flare, the return current density, driven by the induced electric field according to Ohm’s law, must be equal to the beam current density. This analysis, therefore, shows that including anomalous resistivity can reasonably remove the discrepancy between observations and predictions (Xu, Chen, and Wu, 2013; Graham et al., 2022). The presence of anomalous resistivity in the KHI instability can also not be denied. However, the generation of KHI instability takes a longer time in comparison to the time scale of turbulence (Fang et al., 2016; Ruan, Xia, and Keppens, 2019). We will not discuss here much about the anomalous resistivity associated with KHI due to its being out of the scope of this analysis.

The velocities of the stochastic particles (Figures 3 and 4) found in our analysis are compatible with the velocities of hotter and cooler ions (Si IV, Fe XXIV, Fe XXIII, and Fe XVI) observed in the MHD plasma turbulence of the solar flare. These observations were carried out using IRIS, Hinode/Euv Imaging Spectrometer (Jeffrey et al., 2018; Stores, Jeffrey, and Kontar, 2021). This is a key finding of this analysis. The range of values of the stochastic particles’ velocities \(\approx (0.5\,\text{--}\,3) \times 10^{6}\text{ cm}\,\text{s}^{-1} \) observed in this analysis and their comparison with the observations demonstrates the presence of low-atmospheric chromosphere Gaussian turbulence in the solar flare. This turbulence might be onset at the loop top of the flare via the beam–plasma instability (Xu, Chen, and Wu, 2013; Graham et al., 2022). Our finding shows that dissipation from solar-flare turbulence will contribute to the heating of the chromosphere. These results are in agreement with the observations and simulations carried out by Jeffrey et al. (2018), Stores, Jeffrey, and Kontar (2021), and Ruan, Yan, and Keppens (2023), respectively, for the MHD plasma turbulence in the solar flare.

The turbulent plasma particles’ velocities in two dimensions (Figure 5) (Brownian motion of the particles in two dimensions) demonstrate the inhomogeneous nature of the turbulent plasma (Stores, Jeffrey, and Kontar, 2021) as well as the chaotic structure of the velocity field. These two features are the major characteristics of turbulent plasma. It can be inferred from the turbulent energy-release process that the released turbulent energy causes a stochastic structure of the velocity field. On the other hand, the density distribution of the plasma particles in the solar-flare plasma is absolutely not homogeneous and plays a key role in producing the inhomogeneity of the solar-flare plasma. Therefore, the observed high temperature of the solar-flare plasma > 10 MK is due to the stochastic acceleration of the particles (Kontar et al., 2011).

We should note that our dissipation model does not directly incorporate dissipative parameters such as resistivity and magnetic field. However, the input parameters used in our model simulations inherently account for magnetic-field fluctuations in solar flares. It is worth mentioning that our estimated dispersion time aligns well with the time of MHD turbulence observed by Kontar et al. (2017). The results of dissipation and particle velocities are of significant importance in understanding particle-acceleration models in solar flares. These velocities correspond to the velocities of energetic particles from the solar corona, providing valuable insights into their mechanics.

While we have obtained the desired results regarding turbulence velocity and dissipation in solar flares, our study does have limitations and further room for improvement. First, it does not directly consider physical parameters such as resistivity and magnetic-field fluctuations. Secondly, computational costs become prohibitively high for sample sizes above 1000, making it challenging to perform the Monte Carlo experiment on a standard computer with a normal processor. The high degree of freedom in MHD plasma turbulence in the solar-flare atmosphere also makes it difficult to accurately estimate input parameters, introducing the possibility of errors in our computer experiments using models. Moreover, the turbulent phenomenon’s complexity defies description by a single model, as a selected model can only explain certain aspects of the turbulent flow. Hence, the stochastic Lagrangian model should not be considered a complete statistical model for turbulence studies. There will always be a need to develop better models to comprehend MHD plasma turbulence in solar flares.

5 Summary

We have demonstrated the very well-known occurrence of lower-atmospheric turbulence in solar flares. This turbulence leads to the rapid conversion of 0.5% of the injected kinetic energy into thermal motions within ten seconds. The remaining energy is converted into non-thermal and particle energetics, resulting in loop-top and footpoint hard X-ray emissions, as well as other dynamic processes in solar flares (Kontar et al., 2017; Kong et al., 2019, 2022). Our results provide insight into the particle dynamics within the standard solar-flare model (Priest, 2014; Tajima and Shibata, 2018). The dissipation occurs approximately five seconds after the onset of turbulence, a time-frame similar to Kontar et al. (2017)’s findings on MHD plasma turbulence in solar flares.

From the mean values of the relaxation rate, we observed that Spitzer resistivity alone cannot account for the dissipation. To understand fast dissipation, the inclusion of anomalous resistivity is necessary (Xu, Chen, and Wu, 2013; Bian et al., 2016; Graham et al., 2022). Our particle-velocity field indicates the stochastic and inhomogeneous nature of the turbulence. The obtained range and mean values of plasma-particle velocities align with those of various ions forming in the lower-atmosphere MHD plasma turbulence of solar flares (Jeffrey et al., 2018; Stores, Jeffrey, and Kontar, 2021).

In conclusion, our analysis suggests that stochastic Lagrangian models of velocity and dissipation (relaxation rate) for inhomogeneous hydrodynamic turbulence could characterize the velocity and dissipation of MHD turbulence in solar flares. However, our approach has been purely statistical, and magnetic-field fluctuations are not considered in our model calculations. Since the magnetic-field plays a fundamental role in particle motion and energy dissipation in solar-flare plasmas, better modeling efforts are needed that include physical parameters such as magnetic field, plasma pressure, and resistivity for a more comprehensive representation of plasma turbulence in solar flares.