Formation of Three-Dimensional Internal Waves behind a Body in Motion in a Stratified Viscous Fluid

Abstract

A uniform motion of a disk in horizontal direction along its axis of symmetry in a stratified viscous fluid at rest is studied. The disk generates three-dimensional internal gravity waves occupying the entire volume between the disk and the location of its start. The waves are observed using two-color, beta-plus visualization of the vortex flow structure calculated within the framework of the system of Navier–Stokes equations in the Boussinesq approximation. The results of the study complete considerably the earlier-published mechanism of the formation of half-waves above the axis of symmetry of the disk, where emphasis was placed on the periodic process of generation of deformed vortex rings above the location of the disk start. Their generation is due to gravitation and shear instabilities, when the left semi-ring is transformed into a half-wave of depressions or crests, while the right one vanishes with time. In this paper it is established that the left parts of the right odd semi-rings are transformed into the axial parts of the crest half-waves.

The understanding of the process of formation of complicated three-dimensional (3D) vortex structures in fluids initiated by the motion of a body of finite dimensions throughout the fluid has always aroused a great interest. One of the ways of obtaining these complicated 3D structures was the visualization of the velocity vector fields calculated using the mathematical modeling of this process. If the case of a sphere, as the simplest 3D body of finite dimensions, in a homogeneous incompressible viscous fluid is considered, then the topology of the 3D vortex structure is fairly complicated. In 1987 the onset of the formation of a chain of vortex loops in the wake behind a sphere was visualized in [1] using several instantaneous 3D vorticity lines. This process is fairly laborious, since the initial point on any of this lines should be reasonably preassigned. Due to the appearance of new approaches to the visualization of vortex structures in liquids and gases in the years 1988–1995, as described in [2], it became possible to obtain the calculated 3D vortex structures in the wake behind a sphere [3, 4], whose topologies were in qualitative agreement with the experiment [5]. In 2006 the vortex formation mechanism (VFM) was first considered in detail in the wake of a sphere in uniform motion in a homogeneous incompressible fluid; it leads to the formation of a chain of vortex loops in the form of hairpins [6]. In this case, the VFM works in the recirculation region R of the wake located behind the sphere (Figs. 1g, 1h).

Fig. 1.

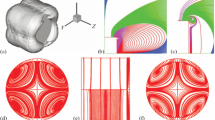
Flow over a disk at T = 1.5, Fr = 0.3, Re = 50, and T_b = 2π s; (a, b, i) are the isosurfaces ω+ = |curl v|+ = ±0.01, β+ = ±0.01, β = 0.2; (c, d, j) are the isolines ω_φ = (curl v)_φ with the step 0.02 (c) and β+ with the step 2 × 10^–3 (d) in the vertical x–z plane and β+ with the step 0.04 in the y–z plane (j); (e–h) are the instantaneous streamlines in CS3 (0, –0.01, 0) at 0 ≤ x ≤ d/2 and in the CS3 (0.973, 0.005, 0) at x > d/2, respectively (e), in CS2 (f) and in CS1 in the x–z (g) and y–z (h) planes.

In the case of an incompressible viscous fluid linearly stratified with respect to the density the field of fluid velocity vectors is symmetric about the horizontal plane passing through the geometric center О of a convex symmetric body. For this reason, for the sake of definiteness the dynamics of the variation of the stratified fluid flow structure is described only in the upper half-space, above point О. Let point F be above point О at the intersection of the body surface and the vertical upward X axis passing through point О. For example, for the sphere the point F is its upper pole. In [7] the sphere lies at rest on the neutral buoyancy level in a stratified viscous fluid at rest. In spite of the fact that the diffusion forces push the fluid to all directions and due to the fact that many parts of the spherical surface lie at an angle to the horizon, diffusion-initiated fluid flows directed to point F are initiated at X > 0 near these parts. This flow is very slow and axisymmetric about the X axis. In [7] it was shown that in the vicinity of the line X a new axisymmetric vortex ring is peridically generated above the uppermost ring due to gravity and shear instabilities. This ring reduces the vertical dimensions of the earlier-generated rings. Any pair of rings represents one interal gravity wave. The group velocities of these waves are perpendicular to their phase velocity and are directed along the radii-vectors from point F [7]. Further on only two vortex rings strongly flattened in the verical direction remain near point F; they could be observable in the experiment [7]. Thus, the brief formulation of the VFM in [7] is as follows: “rings fall on point F .”

If a sphere is replaced by a disk with the horizontal axis of symmetry Z, then diffusion induces a fluid flow only near the lateral surface of the disk [8]. For this reason, in [7] the singular point F is a node, whereas in [8] it is a saddle. In [8] it is deformed vortex rectangles rather than rings that fall at first on point F. Then the vortex structure of the flow becomes increasingly chaotic.

In this study, we consider the uniform right-to-left motion of a disk along the Z axis taken from paper [8]. Let Q be the location, where the center of the backward side of the disk starts its motion. In Figs. 1c–1f the point Q is at the intersection of the black vertical line and the Z axis coinciding with the lower boundary of the figures. It is known from the linear theory and experiments that the body start is accompanied by radiation of a bundle of time-dependent internal gravity waves propagating from point Q along the radii-vectors [9, 10]. The mathematical modeling makes it possible to investigate in detail this process of wave bundle radiation by studying in detail the dynamics of the 3D vortex structure of the fluid flow. The detailed description of this process was given in [11]. First, two vortex filaments  f₁ are formed between the disk and point Q; then they are transformed into the legs of the vortex loop –1, whose head end –1 is located to the right of Q (Fig. 2f). Then the deformed vortex rings k are periodically generated above Q; here, k = 2, 3, 4 …. Thus, the brief formulation of the VFM in [11] is as follows: “Deformed rings fall on point Q.” Thus, the brief formulations of the VFM in papers [7] and [11] are essentially the same.

Fig. 2.

Flow over a disk at Re = 50 and T_b = 2π s; (a, b) are the isosurfaces (β–) = 2 × 10^–3 and (λ₂–) = –3 × 10^–6 at x < 0, Fr = 0.8, and T = 1.51; (c–e) is the schematic representation of the β isosurfaces at x > 0, Fr ≤ 4, and 0.28 ≤ T ≤ 1.4: side view at the top and bottom view at the bottom;  (f) is the isosurface β = 0.003 at Fr = 4 and T = 0.28; (g) is the time dependence of the drag coefficient C_d of the disk at Fr = 0.3; the numbers k are associated with the time intervals [0.5T_b(k – 1), 0.5T_bk].

Here, an important difference that exists between the VFMs for homogeneous and stratified fluids should be emphasized. While in a homogeneous fluid vortex flow structures are formed directly behind a body [6], in a stratified fluid they appear above the location of the body start [11].

In [11] much attention was given to the explanation of the mechanism of vortex ring formation above point Q, which is due to gravity and shear instabilities. As shown in [11], the left semi-ring k transforms into a half-wave of depressions and crests, while the right semiring –k vanishes with time. The point is that the fluid whirlpool initiated by the disk start makes the left semi-rings to rotate more intensely than the right ones. As a result, the dimensions of the left semi-rings grow and the vorticity in these rings becomes an order greater than that in the right semi-rings (Figs. 1a, 1c). Thus, the internal half-waves (the former left semi-rings) occupy the entire volume between the disk and point Q.

The initial and subsequent VFM stages are considerably different in the above brief description. The wish to obtain a more universal VFM in a wide range of Froude numbers Fr and additional comprehensive studies of the dynamics of the 3D vortex structure of viscous stratified fluid flows led to the forthcoming of this paper. Here, the VFM is considerably advanced as compared with [11] and renamed as the internal wave formation mechanism (IWFM). This IWFM will be formulated after the formulation of this problem and the description of the methods of the numerical solution and visualization of 3D vortex fluid flow structures.

1 FORMULATION OF THE PROBLEM

A disk, d in diameter and h = 0.76d in thickness, is introduced into an incompressible viscous fluid at rest, linearly stratified in density, and starts immediately the uniform right-to-left motion along the horizontal axis of symmetry Z of the disk at a velocity U. Let the start point Q of the center of the back side of the disk be the origin of the Cartesian coordinate system at rest CS2 (z, x, y), where the x axis is vertical and the z axis coincides with the Z axis. Let the origin of the Cartesian coordinate system CS1 (Z, X, Y) in motion, where X is the vertical axis, be associated with the geometric center О of the disk. To solve the problem thus formulated we will formulate an auxiliary problem of uniform fluid flow past a disk at the velocity U in СS1. The fluid flow direction coincides with the positive direction of the Z axis.

Let T_b be the fluid buoyancy period and T be the time that has passed from the moment, when the disk was introduced into the fluid, non-dimensionalized by T_b. The fluid density ρ(Z, X, Y) = 1 – 0.5X/A + S(Z, X, Y) is non-dimensionalized by the density ρ₀ on the level of the disk center, while the coordinates Z, X, and Y are divided by d/2, where A = Λ/d is the scale ratio, N_b = 2π/T_b and Λ = g/$N_{{\text{b}}}^{2}$ are the fluid buoyancy frequency and scale, g is the gravity acceleration, and S(Z, X, Y) is the salinity disturbance non-dimensionlized by ρ₀, it is zero at T = 0.

To mathematically model the auxiliary problem of flow past the disk in CS1 we will solve the following dimensionless system of Navier–Stokes equations in the Boussinesq approximation [12]

$$\frac{{\partial S}}{{\partial t}} + ({\mathbf{v}} \cdot \nabla {\text{)}}S = \frac{2}{{{\text{Sc}} \cdot {\text{Re}}}}\Delta S + \frac{{{{v}_{X}}}}{{2{\text{A}}}},$$

(1.1)

$$\frac{{\partial {\mathbf{v}}}}{{\partial t}} + ({\mathbf{v}} \cdot \nabla {\text{)}}{\mathbf{v}} = - \nabla p + \frac{2}{{{\text{Re}}}}\Delta {\mathbf{v}} + \frac{{\text{A}}}{{2{\text{F}}{{{\text{r}}}^{2}}}}S\,\frac{{\mathbf{g}}}{g},$$

(1.2)

$$\nabla \cdot {\mathbf{v}} = 0.$$

(1.3)

It is written in the cylindrical coordinate system (Z, R, φ): Z = Z, X = Rcosφ, $Y = R\sin \varphi$, where ${\mathbf{v}} = \left( {{{{\text{v}}}_{Z}},{{{\text{v}}}_{X}},{{{\text{v}}}_{Y}}} \right)$ is the velocity vector normalized by U; p is the pressure disturbance non-dimensionalized by ρ₀U²; t is time non-dimensionalized by $f = d{\text{/}}\left( {2U} \right) = 1{\text{/}}\left( {2{\text{Fr}}{{N}_{{\text{b}}}}} \right)$; Re = U d/ν is the Reynolds number, Fr = U × T_b/(2πd) is the internal Froude number, Sc = ν/κ = 709.22 is the Schmidt number, ν = 0.01 cm²/s is the kinematic viscosity coefficient of water, κ = 4.1 × 10^–5 cm²/s is the salt diffusion coefficient, and ∇ and Δ are the Hamilton and Laplace operators.

In solving this problem we will use the numerical MERANZh method of splitting with respect to physical factors [13], which had been successfully used in modeling incompressible viscous flows past spheres, cylinders, and disks [4, 6–8, 11, 14–16] and for flows with free surfaces [13]. The details of the numerical method, the cylindrical computation grid, and the boundary conditions, together with the results of testing the program complex for mathematically modeling and visualizing the 3D flows of a viscous stratified fluid past a disk, were published in [11, 14]. The classification of viscous stratified flows past a disk, h = 0.76d in thickness, at 0.05 < Fr < 100 and 50 < Re < 500 presented in [14] is in good agreement with the three-dimensional calculations [15, 16] and the experimental data [17, 18].

The outer right boundary of the computation domain is at a distance of 25d from the center of the disk. At Fr ≥ 10 the internal wave length λ = 2πFrd ≥ 20πd ≈ 62.83d, that is, less than 40% of the first wave length can fit in the chosen computation grid. Moreover, the amplitude of this wave is small. For this reason, the nature of the flow past the disk will be equivalent to that of a homogeneous viscous fluid flow [6]. When Fr = 4 – λ = 8πd ≈ 25.13d, that is, only one wave is accessible for observations [11]. For this reason, in the case of the computation domain considered, exactly at Fr ≤ 4 it is possible to investigation the generation of the internal waves occupying the entire space of the computation grid to the left of point Q [11] (Fig. 1a). The calculations were carried out using the computation resources of the Joint Supercomputer Center of the Russian Academy of Sciences.

In CS2 the values of the dimensionless horizontal velocity components v_Z of the velocity vectors calculated in CS1 are reduced by unity (v_z = v_Z – 1), while the values of the variables v_x, v_y, S, and p in CS2 remain the same as in CS1. Thus, in CS2 the velocity of the flow incident on the disk is zero, while the dimensionless disk velocity is –1, that is, the disk travels uniformly, from right to left in the fluid at rest. For the time $T = \left[ {tf} \right]{\text{/}}{{T}_{b}} = \left[ {t{\text{/}}\left( {2{\text{Fr}}{{N}_{{\text{b}}}}} \right)} \right]\left[ {{{N}_{{\text{b}}}}{\text{/}}2\pi } \right] = t{\text{/}}\left( {4{{\pi Fr}}} \right)$ the center of the disk is displaced in CS2 at rest at the distance $L = U\left[ {tf} \right]{\text{/}}\left( {0.5d} \right) = t = 4{{\pi Fr}}T$ to the left from point Q (Fig. 1f).

2 VISUALIZATION OF THE VORTEX STRUCTURE OF THE FLOW

Due to fluid stratification, the slow velocity of the disk (Re = 50), and the disk symmetry about the x–z plane, the calculated 3D fields of the velocity vectors are at any time moment characterized by the horizontal y–z and vertical x–z planes of symmetry. Therefore, the pictures of the instantaneous streamlines in the x–z (Figs. 1f and 1g) and y–z (Fig. 1h) planes are meaningful. In Fig. 1f vortex cells 1, 2, and 3 in CS2 are visualized; they correspond to the internal half-waves 1, 2, and 3 generated at T = 1.5 for Fr = 0.3. In Figs. 1g and 1h the recirculation zone R formed as a result of the separation of the flow incident on the disk from its rear side is shown for CS1.

It is known that the construction of instantaneous 3D streamlines for the purpose of visualizing the 3D vortex structure of the flow is a difficult and thankless occupation. Many vortices can easily be lost. For this reason, in visualizing this 3D structures it would be natural to use the isosurfaces of the absolute value of vorticity ω = |ω| = |curl v| (Fig. 1a). We will first consider the isoline pictures of the φ-component of the vorticity ω_φ in the vertical plane x–z (Fig. 1c). From the definition of ω_φ it follows that in cells 1, 3, and –2 in Fig. 1c, where ω_φ > 0, the fluid rotates counterclockwise, which is confirmed by Fig. 1f. In cells 0, 2, –3, and –1 in Fig. 1c, where ω_φ < 0, the fluid rotates clockwise (see Fig. 1f). The isosurface ω = 0.01 in Fig. 1a visualizes the internal half-waves 1–3 (flow region with considerable rotation of the continuous medium) but it is not capable to illustrate the structures of weaker vortices occurring near the z axis [4]. In [2] it was proposed to use the isosurface λ₂ < 0 (Fig. 2b) to visualize the entire vortex structure of the 3D flow of an incompressible fluid. Here, λ₂ is the second eigenvalue of the symmetric tensor ${{{\mathbf{F}}}^{2}} + {{{\mathbf{B}}}^{2}}$, where ${\mathbf{F}} + {\mathbf{B}} = {\mathbf{G}}$ is the tensor of the velocity gradient with the elements ${{{\text{v}}}_{{i{\text{,}}j}}} = {{\partial {{{\text{v}}}_{i}}} \mathord{\left/ {\vphantom {{\partial {{{\text{v}}}_{i}}} {\partial {{x}_{j}}}}} \right. \kern-0em} {\partial {{x}_{j}}}}$, ${{F}_{{i,j}}} = 0.5\left( {{{{\text{v}}}_{{i,j}}} + {{{\text{v}}}_{{j,i}}}} \right)$, and ${{B}_{{i,j}}} = 0.5\left( {{{{\text{v}}}_{{i,j}}} - {{v}_{{j,i}}}} \right)$. In [2] the visualization of 3D flows using the isosurfaces of the imaginary parts β of two complex-conjugate eigenvalues of tensor G is also mentioned (Figs. 1b and 1i). It is interesting to note that in [2] this imaginary part is in no way designated. Because of this, it is denoted using different symbols in different papers, namely, Im(σ_1,2) [6, 15], β [8, 11, 14, 16], λ_ci [19], λ_cx [20], etc. First the λ₂-visualization was used in [4] and then it was the β-visualization [6, 8, 11, 14–16] having the following clear physical meaning. We will take in CS1 an arbitrary point М, where the fluid velocity is v_M. We will pass to the reference system CS3(v_M), which moves at the velocity v_M relative to CS1. Then at point M in CS3(v_M) the velocity becomes zero, while the velocities in a small vicinity of this point will obey the ordinary differential equation (ODE) v = dx/dt ≈ Gx. It is known that the occurrence of two complex-conjugate eigenvalues σ = α + iβ and $\bar {\sigma }$ = α – iβ of tensor G at point М leads to the following solution of this ODE [21]

$${\mathbf{x}} = C{\mathbf{h}}\exp (\sigma t) + \bar {C}{\mathbf{h}}\exp (\bar {\sigma }t) + {{C}_{3}}{{{\mathbf{\bar {h}}}}_{3}}\exp ({{\sigma }_{3}}t) = {{{\mathbf{x}}}_{1}} + {{{\mathbf{x}}}_{3}},$$

Here, the quantities С and С₃ are complex and real constants, respectively, σ₃ is the third (real) eigenvalue of tensor G, h₃ is the third (real) eigenvector, ${\mathbf{h}} = {{{\mathbf{h}}}_{1}} - i{{{\mathbf{h}}}_{2}}$ and ${\mathbf{\bar {h}}}$ are two complex-conjugate eigenvectors of tensor G, and h₁ and h₂ are two linearly-independent real vectors, which form the basis in the P plane. Let the complex number ζ = ξ₁ + iξ₂ = Сexp(σt); then x_I = ξ₁ ∙ h₁ + ξ₂ ∙ h₂. We will map affinnely the P plane onto an auxiliary plane P* of the complex variable ζ, so that vector h₁ passes to unity and vector h₂ passes to i. Then the vector x_I = ξ₁ ∙ h₁ + ξ₂ ∙ h₂ will be associated with the complex number ζ = ξ₁ + iξ₂. By virtue of this mapping, the trajectory in the P plane passes into a trajectory in the P* plane; it is described by the equation ζ = Сexp(σt). In the polar coordinates (r, θ) we have ζ = rexp(iθ), that is, ξ₁ = rcosθ and ξ₂ = rsinθ. Let С = С_realexp(iD), then r = С_realexp(αt) and θ = βt + D. Thus, if β ≠ 0, then we can speak of the vortex nature of the fluid motion in a small vicinity of point М in CS3 (v_M): the fluid molecules move along ovals (at α = 0) or oval spirals (at α ≠ 0), while β is the time-average angular velocity of the fluid molecule rotation about point М in CS3(v_M) [21]. For the sake of convenience, in plotting the monochromatic isosurface β = β₀ > 0 (Fig. 1i) illustrating the vortex structure of the fluid flow, the function β is redefined in the cells of the computation grid, where β = 0: β = –0.01 [6, 8, 11, 14–16].

The two-color β+-visualization introduced in [22] colors the half-waves of hollows 1, 3 and crests 2 in Fig. 1b to different colors according to the sign of ω_φ; this is very convenient in investigating the vortex structures of the internal waves (Figs. 3–5, IV). The function β+ is defined at β > 0: β+ = sgn(ω_φ)β, where the function sgn(ω_φ) = 1 at ω_φ ≥ 0 and sgn(ω_φ) = –1 at ω_φ < 0. We can introduce in the same fashion the two-color ω+-visualization: ω+ = sign(ω_φ)ω (Fig. 1a).

Fig. 3.

Flow over a disk at Fr = 0.3, Re = 50, and T_b = 2π s; (a–c) are the instantaneous streamlines in CS2 (I) and the isolines 10³ × β+ with the steps 500, 0.1, 1 (II) in the vertical x–z plane, the β+ isolines with the steps 0.5, 0.1, 0.1 in the plane φ = π/4 (III), and the isosurfaces 10³ × β = 0.5, 5 and 10³ × β+ = ±0.5 (IV) at T = 0.1, 0.2, and 0.24.

Fig. 4.

Flow over a disk at Fr = 0.3, Re = 50, and T_b = 2π s; (a–c) are the instantaneous streamlines in CS2 (I) and the isolines 10² × β+ with the steps 0.2, 5, 5 (II) in the x–z plane, the isolines β+ with the steps 0.1, 0.08, 0.04 in the φ = π/4 plane (III), and the isosurfaces β+ = ±0.0052, β = 0.15, β+ = ±0.05 (IV) at T = 0.28, 0.45, 0.68.

Fig. 5.

Flow over a disk at Fr = 0.3, Re = 50, and T_b = 2π s; (a–c) are the instantaneous streamlines in CS2 (I) and the β+ isolines with the step 10^–2 (II) in the x–z plane, the β+ isolines with the step 0.08 in the plane φ = π/4 (III), and the isosurfaces (β–) = 5 × 10^–3, β+ = ±10^–2, ±10^–2 (IV) at T = 0.8, 0.86, and 1.

Then it was noticed that throughout the most of Fig. 1c we have ω_φ < 0. For this reason, if the vortex structures, for which ω_φ ≥ 0, will be removed from Fig. 1c, then the flow structure becomes twice simpler, though the removed structures can be easily reconstructed mentally. For this reason, the one-color (β–)-visualization of the fluid flow was introduced in [22]. The function (β–) is defined at β > 0 and ω_φ < 0: (β–) = β (Fig. 2a). In the 3D case, in comparing the β+ isosurfaces in Fig. 1b and the β– isosurfaces in Fig. 2a it can be seen that in Fig. 2a all hollow half-waves, with exception of the first one, disappear without a trace. In Fig. 1b an approximate boundary between the regions (0 + S) and 1 is shown as a black line; here S is the head part of the lateral vortex loop (Fig. 2f) [11]. The removal of the region (S + 1) leaves a scratchy trace on the wake shell 0 (compare Figs. 4c, IV and 5a, IV).

Figures 1d and 1e illustrate the physical meaning of β for two points М₁ and М₂ with the velocities in CS1 (v_Z, v_R, v_φ) = (0.973, 0.005, 0) (at x > d/2) and (0, –0.01, 0), respectively; they are marked with black crosses. Figure 1e is bisected into the upper and lower parts by the black line x = d/2. The streamline patterns in the upper and lower parts of Fig. 1e are shown in CS3(0.973, 0.005, 0) and СS3(0, –0.01, 0), respectively, and illustrate fluid rotation in the vicinities of points М₁ and М₂. The streamline patterns in the upper and lower halves of Fig. 1e are similar with those in CS2 (Fig. 1f) and CS1 (Fig. 1g), respectively. Thus, the zone R is visible in Figs. 1e and 1g at 0 ≤ x ≤ d/2, while the half-waves of hollows and crests can be seen in Figs. 1e and 1f at x > d/2. For this reason, to approximately describe the variation in the kinematics of the internal waves and separation flows near the z axis in the vertical plane we can use the instantaneous streamlines in CS2 and CS1, respectively. Thus, in Figs. 1 and 3–6 in describing any isoline pattern β+ in the x–z plane we present the corresponding patterns of the instantaneous streamlines in CS2.

Fig. 6.

Flow over a disk at Fr = 0.3, Re = 50, and T_b = 2π s; (a–e) are the instantaneous streamlines in CS2 (I) and the isolines 10³ × β+ with the step 2 (II) in the x–z plane, and the β+ = ±10^–3 isosurfaces (III) at T = 1.25, 1.3, 1.4, 1.73, and 1.9.

By analogy with β+ and (β–)-visualizations we can define λ₂+ and (λ₂–)- visualizations (Fig. 2b). The function λ₂+ is defined at λ₂ < 0: λ₂+ = sign(ω_φ)|λ₂|, while the function (λ₂–) is defined at λ₂ < 0 and ω_φ < 0: (λ₂–) = λ₂. The comparison of Figs. 2a and 2b for T = 1.5 and Fr = 0.8 shows that the topologies of the vortex structures obtained using the (β–) and (λ₂–) visualizations are almost the same but the (β–) visualization presents the vortex structure of the fluid flow more harmonically. Thus, in Fig. 2a the filaments  f₁ are connected with the ring R, whereas in Fig. 2b they are disconnected. In Fig. 2a the vortex ring –1 is continuous, while in Fig. 2b it is broken into three parts.

3 INTERNAL WAVE FORMATION MECHANISM AT Fr ≤ 4

At T = 0 the disk is introduced in a viscous stratified fluid at rest and starts immediately a uniform right-left motion along the horizontal axis of symmetry z of the disk. The buoyancy force (the last term of Eq. (1.2)) starts to act on the disturbed fluid deviated from its initial position. On the other hand, as a result of fluid molecule adherence to the disk surface, the forces directed from right to left start to arise ahead of the disk and on either side of it. These forces lead to the generation of a vortex torus with the axis of symmetry z, which fills the entire space (Fig. 3a, I for T = 0.1), while the buoyancy forces generate internal gravity half-waves above Q (Fig. 3c, I at T = 0.24). Figures 3–5, IV present the dynamics of the 3D vortex flow structure at 0 < T < 1 determined by the gravity and shear instabilities. In turn, the gravity instability is due to the buoyancy forces in the fluid. Any 3D structure in Figs. 3–5 is supplemented with the β+ isolines in its sections at φ = 0 and φ = π/4 and with the instantaneous streamlines in CS2 in the vertical x–z plane (for φ = 0). In Fig. 3a, IV one quarter of the isosurface β = 5 × 10^–4 is cut out in order to show the disk surface.

At T ≤ 0.1 and Fr ≤ 4 two small vortex structures appear at x > 0 outside the axisymmetric vortex shell 0 of the disk, near the backward sharp edge of the disk (Fig. 3a, III–IV and Figs. 2a–2d, 2f, and 6a–6b from [11]); these are the embryos of two vortex filaments  f₁ (Figs. 3b and 3c, III–IV). The pattern of the isolines β+ in the section φ = π/4 illustrates the growth dynamics of the  f₁ filaments and the recirculation zone R. At 0.2 ≤ T ≤ 0.24 the gravity and shear instabilities lead to the situation in which the shape of instantaneous streamlines above point Q in CS2 at φ = 0 becomes wavy from rectilinear (Fig. 3c, I). The detailed description of the reason for which it passes was given in [11]. As a result, two vortex cascades are formed above Q: 1 (to the left) and –1 (to the right) (Fig. 3c, II). At T = 0.28 and Fr = 0.3 the hearts of cascades 1 and –1 form ring 1 (Fig. 4a, IV).

At Fr ≤ 1 and Fr ≥ 2 the details of the vortex formation process are somewhat different. While at 0.1 < T ≤ 0.28, Fr ≥ 2, and x > 0 the wake shell 0 does not almost change with time, and the two first filaments f₁ and the two second (lateral) filaments f_S are formed outside the shell 0 (Fig. 2f) [11], at 0.1 < T ≤ 0.28, Fr ≤ 1, and x > 0 the filaments f₁ and f_S are placed in the shell 0 itself. For this reason, at Fr ≤ 1 it makes sense to subdivide the shell 0 to the inner 0₁ and outer 0₂ parts using the β₀ isosurfaces. The absolute value of β₀ is presented in Figs. 3–5, III. The shell 0₁ varies with time only weakly, consisting of two rings r_I and r_II, which are generated by two sharp edges of the disk (Fig. 3a, IV). In Fig. 3b, III the cross-hatched filaments f₁ and the zone R near the backward disk side and other parts of 0₂ above the lateral side of the disk can be separated out in the shell section 0₂ at φ = π/4. At x > 0 and 0.2 ≤ T ≤ 1 two vortex filaments f₁ (the legs of the vortex loop –1) are the parts of cascade –1, while the loop –1 is the heart of cascade –1. The generation of two symmetric loops –1 at x > 0 and x < 0 is accompanied by the generation of the lateral loops S as the side parts of two symmetric cascades 1. At x > 0 and 0.24 ≤ T ≤ 0.32 four lateral filaments f_S are observable (Figs. 3c, 4a, IV) for Fr = 0.3 and two filaments f_S are observable for Fr = 4 (Fig. 2f). The apparition of the filaments S is due to the presence of the disk and is not mentioned in the internal wave formation mechanism (IWFM) discussed here, since this IWFM is devoted directly to the generation of internal waves.

Thus, at 0.1 ≤ T ≤ 0.32 two vortex loops are formed, namely, –1 with the legs f₁ and the side loops S. At T = 0.28 for Fr = 0.3 the hearts of cascades 1 and –1 form the ring 1 (Fig. 4a, IV) and for Fr = 4 the semi-ring 1, similar with an arc (as in Fig. 3b in paper [11]), whose radius is about five times as large as the radius of the semi-ring –1. For this reason, in formulating the IWFM the generation of two vortex cascades 1 and –1, whose hearts are the semi-rings 1 and –1, should be spoken of, rather than the formation of a single vortex ring 1.

At 0.28 < T ≤ 0.45 and Fr = 0.3 the diameter D(1) of the semi-ring 1 section by the x–z plane decreases by a factor of three and then vanishes. The fact that D(1) = 0 indicates that at x > 0 the semi-ring 1 has been split into two halves symmetric about the x–z plane. At x > 0 and 0.28 ≤ T ≤ 0.8 the disk is displaced to the left, while the cascade –1 remains near point Q; for this reason, the legs f₁ of loop –1 are extended in the horizontal direction (Figs. 4b, 4c, and 5а, IV); the semi-ring –1 is flattened in the vertical direction and transforms into the semicircle –1. In Figs. 4b and 4c, IV only the halves of the β isosurfaces are presented in order to show the disk. At 0.5 ≤ T ≤ 0.8 the vortex cascades 2 and –2 are generated above Q owing to the gravity and shear instabilities. The vortex cascade 2 becomes the half-wave of crests 2. The vortex filaments  f₂ encircled with black in Fig. 5a, IV for Fr = 0.3 or presented in the form of a semi-circular connection between filaments f₁ in Fig. 3a in [11] for Fr = 4 are the lower portions of the vortex cascade 2. Thus, at Fr = 4 the crest half-waves are formed from the even filaments near Q rather than from semi-rings above Q, as it is the case for Fr = 0.3.

Let β_max(k) be the value of the local maximum of the function β in the section of the semi-ring k by the x–z plane. At T = 0.8 and Fr = 0.3 the heart of cascade 2 approaches the z axis, β_max(2) = 0.025 and β_max(–1) = 0.142, that is, the semicircle –1 possesses the greatest β_max value in section φ = 0 outside the disk shell (Fig. 5a, II). At x > 0 and T = 0.86 cascade 2 sits on the left edge of the semicircle –1, β_max(2) increases to 0.088, and the values of β are redistributed between the left and right edges of the semicircle –1: β_max(–1, left) = 0.12 and β_max(–1, right) = 0.068 (Fig. 5b, II). Now in CS2 the fluid that arrived from both the semicircle –1 and the cascade 2 is pumped through the filaments f₁, which at T = 1 leads to the transformation of the semicircle –1 to the ring –1 (Fig. 5c, II, β_max(2) = 0.22, β_max(–1) = 0.038). In Figs. 5b and 5c, IV the β isosurfaces are presented at –π/2 ≤ φ ≤ π/10 in order to show the disk. Thus, as a result of the coalescence of the heart of cascade 2 and the left part of semicircle –1 at 0.86 ≤ T ≤ 1 cascade 2 now possesses the greatest β_max in the section φ = 0 outside the disk shell.

Thus, at T ≤ 1 the vortex cascades k and –k, where k = 1 and 2, are periodically formed above Q during any time interval ∆T = 0.5. The hearts of cascades –1 and 1 consist of the vortex loop –1 (with the legs f₁ and the semi-ring –1) and the semi-ring 1 with the lateral loops S, respectively. Primarily, the cascade 2 consisted of the filaments f₂ (near Q) and the semi-ring 2, which sits later on the left side of the semi-ring –1. As a result, there are formed a half-wave of depressions 1 (above the filaments f₁) and the half-wave of crests 2. At T = 1 the vortex structure of the first wave is based on the horizontal ring –1 formed from the half-ring –1.

The vortex formation process at T<1 described above is schematically presented in Figs. 2c and 2d. It can be generalized to include any other time interval (n – 1) < T ≤ n, where n = 2, 3, 4, … . In fact, at T > 0 the left (k) and right (–k) vortex cascades are periodically formed above Q during any time interval 0.5(k – 1) < T ≤ 0.5k. They consist of the filaments  f_k near Q and deformed semi-rings k and –k, where k = 1, 2, 3, … . For any odd k the vortex loop –k is formed near the z axis. It consists of the filaments  f_k and the lower semi-ring –k, onto which the even (k + 1) cascade sits in what follows. Then the lower semi-ring –k becomes a deformed ring. Thus, during any time interval (n – 1) < T ≤ n an internal wave n is formed; it consists of the half-waves of depressions k = (2n – 1) and crests (k + 1) = 2n. The left side of the ring –k becomes the axial part of the crest (k + 1). As a result, the axial parts of the crests turn out to be connected with each other by the odd filaments thus forming a chain. The IWFM for Fr ≤ 4 and ∆T = 1 can be formulated more briefly. It is formed by the odd cascades k and –k, the filaments f_k together with the lower vortex –k, the even cascades (k + 1) and –(k + 1), and the filaments (k + 1); the cascade (k + 1) sits on the lower vortex –k (Figs. 2c to 2e).

In Fig. 2g we have plotted the dependence of the disk drag coefficient C_d on time t at Fr = 0.3. The wavy form of the plot for T ≤ 1 is due to the fact that at T ≤ 1 point Q, above which the IWFM operates, is near the disk. The IWFM realization leads to disturbance of the velocity vector and pressure fields near the disk surface which determine C_d.

While at T ≤ 4 and Fr = 0.3 the IWFM realizations are somewhat different for different time intervals ∆T = 1, at T > 3 and Fr = 0.3 they are similar in appearance. Below we describe in detail the IWFM realization at 1 < T ≤ 3, Fr = 0.3, T_b = 2π s, and Re = 50 basing upon the data in Figs. 1, 6, and 7. The distinctive features of the IWFM at T > 3 are described without the help of figures.

Fig. 7.

Flow over a disk at Fr = 0.3, Re = 50, and T_b = 2π s; (a–d) are the isolines 10³ × β+ with the step 2 (I) in the x–z plane and the isosurfaces (β–) = 10^–3 (II) at T = 2.05, 2.6, 2.8, and 2.95.

4 DETALIZATION OF THE WAVE GENERATION PROCESS AT Fr = 0.3 AND T > 1

We will now consider the IWFM for 1 < T ≤ 2 (Fig. 6, 2e, 1) in more detail. Since at T = 1 and Fr = 4 point Q has got at the external boundary of the computation grid, the further investigation of the IWFM at Fr = 4 becomes impossible. At 1 < T ≤ 1.3 and Fr = 0.3 the vortex cascades 3 and –3 are generated above point Q (Figs. 6a and 6b). At 1 < T ≤ 1.3 β_max(2) increases to 0.33. At T > 1.3 β_max(2) no longer changes, which indicates that at T = 1.3 the crest 2 and the vortex structure to the left of it have been already more or less formed. In Figs. 6, III and 7, II the β isosurfaces are presented at π/2 ≤ φ ≤ π in order to show the disk and to understand better the 3D vortex structure of the fluid flow. At T = 1.25 in Fig. 6a, III a wide “amphitheater” of half-wave 2 stands ahead of the minor “stage” of the semi-ring –2, whose side parts are shown with the black circle. These side regions induce the appearance of filaments f₃ above point Q at T = 1.3. The filaments f₃ highlighted with the black rectangle in Figs. 6b and 6c, III, are the parts of cascade –3 in the stage of formation. At T = 1.4 the semi-ring –2 separates from the half-wave 2, β_max(3) = 0.021, β_max(–3) = 0.013, and the dimensions of the filaments f₃ increase (Fig. 6c, III). The filaments f₃ are located above the filaments f₁. The flow pattern at T = 1.5 presented in Figs. 1a–1h and 2a–2b has been already described in detail in Section 2 of this paper. Here, it remains only to add to this description the stable internal structure (“skeleton”) of the first wave in Fig. 1i, where the side filaments f_S are connected with the ring r_I, while the filaments f₁ are connected with the ring r_II. Here it can also be seen that at T = 1.5 the heart of two symmetrical half-waves 2 is the deformed ring 2 in a vertical plane parallel to the x-y plane (Fig. 1j). In Fig. 6d, III at T = 1.73 the filaments f₃ are connected with the ring 2. Thus, in a stratified fluid any vortex ring is connected with four filaments, whereas in a homogeneous fluid the vortex ring is connected with only two filaments [6].

At 1.5 < T ≤ 1.73 vortex cascades 4 and –4 are formed above point Q (Fig. 6d). At 1.3 < T ≤ 1.73 β_max(–2) decreases to 0.003. At 1.4 < T ≤ 1.73 β_max(3) and β_max(–3) increase to 0.027 and 0.052, respectively (Fig. 6d, II), the semi-ring –3 is transformed into the semicircle –3, the vortex loop –3 is formed from the filaments f₃ and the semicircle –3 (Fig. 6d, III); and D(3) decreases by a factor of about 1.5 (similarly to a decrease of D(1) at 0.28 < T ≤ 0.45) but the volume of the depression half-wave 3 considerably increases. At 1.73 < T ≤ 1.9 β_max(3) decrease to 0.023, while β_max(–3) increases to 0.057 (Fig. 6e, II). At T = 1.9 β_max(4) = 0.0124 and β_max(–4) = 0.0056.

At 1.9 < T ≤ 2.05 two half-waves 4 and –4 are developing. The vertical half-wave 4 sits on the left side of the extended horizontal semicircle –3 which transforms then to the deformed ring –3, shown in Fig. 7a, II by two black circles with a black broken line between them; β_max(–3) = 0.0046, β_max(4) and β_max(–4) increase to 0.08 and 0.0092, respectively. Thus, at 1 < T ≤ 2 the half-wave of depressions 3 is formed above the filaments  f₃, together with the half-wave of crests 4. At T = 2 the foundation of the vortex structure of the second wave is the horizontal ring –3. At 2.05 < T ≤ 2.95 the diameters of the deformed rings –1 and –3 increase gradually (Fig. 7, II).

At 2.05 < T ≤ 2.5 the vortex cascades 5 and –5 are generated above point Q. While at the moments of their generation, T = 0.28 and 1.3, respectively, the cascades –1 and –3 had the same clearly expressed heart, at 2.6 ≤ T ≤ 2.95 as many as three hearts of cascade –5 can be observable in Figs. 7b–7d in the shape of half-rings. At 2.1 ≤ T ≤ 2.5 the side parts of the semi-ring –4 form the filaments  f₅ (similarly to the formation of the filaments f₃), which link up with the lower semi-ring of cascade –5, which at T = 2.6 adjoins the upper part of the left inner portion –3* of the right part of ring –3 (Fig. 7b). Due to the fact that the portion –3* is located nearer to the z axis, β_max(–3) = 0.011 > 0.005 = β_max(–5). For this reason, at 2.6 < T ≤ 2.8 the piece –3* engulfs the semi-ring –5, that is, –3* := (–3*) + (–5). As a result, the filaments  f₅ become connected with the piece –3* (Fig. 7c). At 2.5 < T ≤ 2.95 the vortex cascades 6 and –6 are generated above point Q. At 2.8 < T ≤ 2.95 the piece –3* is separated from the right part of ring –3 and transforms into a strongly deformed ring –3* ≡ –5, whose side part is shown with a black rectangle in Fig. 7d, II. Then the vertical cascade 6 sits on the left half of ring –5, while the half-wave 1, that consisted earlier of two halves becomes again a full-featured half-ring, β_max(1) = 0.008 (Fig. 7d, I). Thus, the half-wave of depressions 5 are formed above the filaments f₅ and the half-wave of crests 6 at 2 < T ≤ 3. The foundation of the vortex structure of the third wave is the ring –5. At T ≥ 2.8 β_max(4) = 0.14 < 0.33 = β_max(2), that is, at T = 2.8 the crest 4 and the vortex structure to the left of it have been already approximately formed. For this reason, the widths of the half-waves 2 to 4 in Figs. 7c and 7d measured along the line perpendicular to them are approximately πFrd ≈ 0.94d. This is in good agreement with the linear theory of internal waves.

At T = 2.95 the vortex rings –1 and –3, together with the semi-rings –5 and –6 produce a vortex “nest” (Fig. 7d). Later, the vortex cascades 7 and –7 consisting of several cores, are generated in this nest; then the vortex loop –7 appears near the z axis, the vortex cascades 8 and –8 are formed, and the cascade 8 sits on the head part of loop –7. At T = 4 and π/2 ≤ φ ≤ π the lateral side of ring –5 becomes an additional filament connecting the axial parts of the crests –5 and –7, together with the filament  f₇. At the Froude number Fr = 0.3 all the IWFMs for T > 4 are similar with the IWFMs at 3 < T ≤ 4. As a result, the axial parts of the crests turn out to be chained with each other by the odd filaments of the vortex flow structure, similarly to the vertebrae of a skeleton (Fig. 7d, II). Two half-waves, those of hollows and crests, are fastened to any such “vertebra.” As Fr decreases, the horizontal distances between the centers of the “vertebrae,” which were equal to 2πFrd, are reduced.

SUMMARY

A uniform horizontal motion of a disk, d in diameter and h = 0.76d in thickness, along its axis of symmetry Z in a linearly density-stratified incompressible viscous fluid at rest is mathematically modeled at Re = 50 and T_b = 2π s in a wide range of the Froude number Fr. The disk generates three-dimensional (3D) internal gravity waves occupying the entire volume between the disk and the location Q of its start. The vortex formation mechanism (VFM) described in [11] that operates in forming internal gravity waves, revealed on the basis of an analysis of the dynamics of the 3D vortex flow structure visualized using isosurfaces of the imaginary parts β > 0 of the complex-conjugate eigenvalues of the velocity gradient tensor is considerably supplemented. For obtaining β the system of Navier–Stokes equations in the Boussinesq approximation written in the cylindrical coordinate system is solved for each cell of the computation grid using the numerical MERANZh method [13]. To make the image clearer the half-waves of crests and depressions are made varicolored depending on the sign of the angular vorticity component ω_φ. This visualization received the name of the β+ visualization [22].

In [11] emphasis was placed on the periodic process of the generation of deformed vortex rings above point Q which takes place due to the gravity and shear instabilities. In this case, the left semi-ring transforms into a half-wave of depressions or crests, while the right semi-ring vanishes with time. In this study, the important role played by the odd right semi-rings in the VFM is emphasized and the following universal IWFM behind a disk is formulated for Re = 50, T_b = 2π s, and Fr ≤ 4 in the upper half-space above the z axis. At T > 0 the left k and right –k vortex cascades are periodically formed above point Q during any time interval ∆T = 0.5; they consist of the filaments f_k near point Q and deformed semi-rings k and –k, where k = 1, 2, 3, … (cf. Figs. 3b to 4a, and 5a, 5b for k = 1 and 2, respectively). For any odd k a vortex loop –k is formed near the z axis; it consists of the f_k filaments and the lower semi-ring –k, onto which the even (k + 1) cascade sits. Then the head part of the loop –k becomes a deformed ring. Thus, during any ∆T = 1 interval a new internal wave consisting of the depression k and the crest (k + 1) is formed. The left half of the ring –k becomes the axial part of the (k + 1) crest. As a result, the axial parts of the crests turn out to be tied together into a chain by odd filaments. In order to catch a sight of this vortex chain it is necessary to visualize only that portion of the β = β₀ isosurface, on which ω_φ < 0. This visualization was named the (β–) visualization [22]. The IWFM has its own peculiar features for different time intervals ∆T = 1; in this study, they are described in detail. The IWFM depends slightly on Fr. For example, at 0.8 < Fr ≤ 4 the crest half-waves are formed of even filaments near Q, rather than of semi-rings above Q, as it is the case for Fr ≤ 0.5. At Fr = 0.8 and T ≥ 1 all the IWFMs for different time intervals ∆T = 1 are similar with the IWFM at Fr = 0.3 and T ≥ 3.

Thus, this study presents the detailed description and the results of a numerical and theoretical analysis of the dynamics of the formation of three-dimensional vortex structures in a linearly stratified viscous continuum created by a disk-shaped object moving in a horizontal direction.