On the Slender-Body Theory

Abstract

A review of fundamental theoretical studies concerning the theory and application of the nonsteady-state analogy to an incompressible fluid flowing around slender bodies is presented. Problems related to the application of nonsteady-state analogy to wings, to the wake behind an elliptically loaded wing, as well as methods for numerical calculation of the evolution of vortex sheets and for determining the positions of lines of low separation from solid surfaces are considered taking into account viscous-inviscid interactions. The issues of nonuniqueness and asymmetry of solutions for the problems of a separated flow moving around slender bodies are discussed.

INTRODUCTION

The main purpose of a wing consists in the creation of lift force. The lift force of a wing and the inductive part of the wing drag are associated with a vortex system formed near the wing, which in turn depends on the attached vortex-circulation distributed over the wing. The vortex system actively interacts with the gas flowing around the wing, casting it mainly downwards in the case of a positive lift force. Herewith the wing gains upward momentum.

If one limits oneself to studying the characteristics of a vortex flow near a wing in an inviscid fluid, then the solution to the problem is not unique. In order to select a specific solution from the whole range, it is necessary to set the lines of vortex-sheet vanishing from the wing surface. Such a choice cannot be determined based on the solution of the Euler equations, it should be set based on some other conditions, for example, empirical ones. One of these often used conditions is represented by the Chaplygin–Zhukovskii condition, i.e., the condition of the fact that vortex surfaces smoothly vanish into the flow from sharp wing edges. The Chaplygin–Zhukovskii condition is equivalent to the velocity-finiteness condition at sharp edges, since when it is satisfied, the flow does not have to go around corners greater than the unfolded corner.

In wing theory, there are two remarkable examples that demonstrate the mechanisms of transition from three-dimensional problems to flat ones. These are problems of flowing around high-aspect-ratio wings and low-aspect-ratio at low angles of attack. The flow near a high-aspect-ratio wing has been studied quite well. This paper is devoted to a steady-state flow around longitudinally elongated bodies. These can be represented by narrow 3D bodies without wings, by low-aspect-ratio wings, as well as by a combination of narrow 3D bodies with low-aspect-ratio wings. The foundations of the theory of flowing around such bodies were established by Munk [1] and Jones [2], and then substantially developed by Adams and Sears [3]. It turns out that in this case one can reduce a three-dimensional steady-state problem to a plane nonsteady-state one. Such a simplification of the problem is called a nonsteady-state analogy.

Numerical methods are presented which make it possible to calculate the vortex flow near elongated bodies using a nonsteady-state analogy. Of particular interest is description of the asymmetry of the solution to the problem of separated flow around elongated bodies, when in the course of a symmetrical flow oncoming to a symmetrical elongated body, an asymmetric vortex structure is generated, whereas a rather large lateral force affects the elongated body itself. Such asymmetry can be well realized both under the conditions of a wind tunnel and under flight conditions.

One of the main problems that arise when calculating a separated flow moving around elongated smooth bodies by a fluid flow at large Reynolds numbers consists in the problem of determining the positions of separation lines. This problem can be solved either by using empirical data or, as is done in this paper, via jointly solving equations describing the inviscid global separated flow (Euler equations) and boundary-layer equations.

1 FOUNDATIONS OF NONSTEADY-STATE ANALOGIES

Let us consider the steady-state flowing around a body with unit length along the x axis (linear sizes being nondimensionalized with respect to the length of the body) and the maximum size $\delta \ll 1$ along the y and z axes by an unbounded flow of an ideal fluid. Let us call such bodies elongated. The oncoming-flow velocity vector lies in the xy plane and is directed at an angle of α to the x axis. Let us also take the velocity modulo in the oncoming flow to be unity by nondimensionalizing the velocity with respect to the oncoming-flow velocity. Let us superpose the origin of the coordinate system with the apex of the body. Let $\alpha \ll 1$, and $\alpha = O(\delta )$. Then assume that vortex sheets can vanish into the flow from the lateral and rear sharp edges of the body, as well as from some lines on its smooth surface. The slope of these lines to the x axis does not exceed an order of magnitude of angle α. At $x\sim O\left( 1 \right)$ the transverse size of the body together with separation formations should be comparable in terms of order of magnitude with the transverse size of the body, i.e., should have a size on the order of O(δ).

The velocity potential φ in the domain beyond the vortex sheet should satisfy the Laplace equation

$$\frac{{{{\partial }^{2}}\varphi }}{{\partial \,{{x}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial \,{{y}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial \,{{z}^{2}}}} = 0.$$

(1.1)

It should also satisfy such necessary boundary conditions as impermeability on the body surface, the continuity of pressure and the normal velocity component upon crossing the discontinuity surface, the damping of perturbations at infinity, and the conditions on the separation lines.

The form of the asymptotic expansion for the velocity potential will depend on the scale in the domain in which the flow is under study. Let us introduce the following two asymptotic domains: an inner domain, Ω₁, with characteristic dimensions comparable to the body size $x\sim O\left( 1 \right),\;y\sim z\sim O\left( \delta \right)$, and an outer one, Ω₂ having a size of $x\sim y\sim z\sim O\left( 1 \right)$ [4].

In domain Ω₂, the streamlined body can be represented by a single segment of axis x, $0 \leqslant x \leqslant 1$. In the leading approximation, the velocity potential corresponds to the velocity potential of the oncoming flow:

$$\varphi \left( {x,y,z} \right) = x\cos \alpha + y\sin \alpha ,$$

or for small α

$$\varphi \left( {x{\text{,}}\,y{\text{,}}\,z} \right) = x + \alpha y - \frac{{{{\alpha }^{2}}}}{2}x.$$

(1.2)

Solution (1.2) does not satisfy the boundary conditions on a wing. Therefore, let us study the asymptotic behavior of flow characteristics in domain Ω₁. Instead of independent variables x, y, and z let us introduce new independent variables x^, ${{y}_{1}} = {y \mathord{\left/ {\vphantom {y \delta }} \right. \kern-0em} \delta }$ and ${{z}_{1}} = {z \mathord{\left/ {\vphantom {z \delta }} \right. \kern-0em} \delta }$, which have a size on the order of unity in the domain under consideration. According to the condition of fluid impermeability through body surfaces and the vortex sheet, the velocity vector on the surfaces themselves is directed tangentially with respect to the surfaces. Hence, the order of magnitude of the transverse velocity components amounts to ${v}\sim w\sim \delta$. The velocities ${v}$ and w are directed along the y and z axes, respectively. Since the size of the asymptotic domain under consideration is comparable with the body size, then the transverse velocity components should be an order of magnitude amounting to δ throughout the entire domain Ω₁.

$${v} = \delta {{{v}}_{1}} + o\left( \delta \right),\quad w = \delta \,{{w}_{1}} + o\left( \delta \right),$$

(1.3)

$${{{v}}_{1}}\sim {{w}_{1}}\sim O\left( 1 \right).$$

Relationship (1.3) defines the asymptotic expansion of the velocity potential, as follows

$$\varphi \left( {x,{{y}_{1}},{{z}_{1}}} \right) = x + {{\delta }^{2}}{{\varphi }_{1}}\left( {x,{{y}_{1}},{{z}_{1}}} \right) + \mu \left( \delta \right){{\varphi }_{2}}\left( x \right) + o({{\delta }^{2}}),$$

(1.4)

where φ₁ and φ₂ are on the order of unity in domain Ω₁.

The order of magnitude for the first two terms is determined. Only the longitudinal velocity component depends on term $\mu \left( \delta \right)\,{{\varphi }_{2}}\left( x \right)$. The order of function μ(δ) has not yet been determined, since only the order of the transverse velocities is known, but the following orders for the longitudinal velocity are unknown. Which of the terms (the second or the third one) is more important in the asymptotic representation of the longitudinal velocity depends on the order of μ(δ).

According to (1.1) and (1.4) in the leading approximation

$$\frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial \,y_{1}^{2}}} + \frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial \,z_{1}^{2}}} = 0,$$

(1.5)

i.e., potential ${{\varphi }_{1}}\left( {x,{{y}_{1}},{{z}_{1}}} \right)$ satisfies the two-dimensional Laplace equation.

Let us explore how the boundary conditions are transformed in the new variables. Two-dimensional Eqs. (1.5) should be solved in each section x = const. When moving along the x axis, the geometry of the body and vortex sheets exhibits a change. It is necessary to satisfy the condition of impermeability on these surfaces. Let us write this condition for the surface set by equation $F\left( {x,y,z} \right) = 0$:

$$\left( {{{\nabla }_{3}}\varphi ,{{\nabla }_{3}}F} \right) = 0.$$

By substituting into the latter relationship the expression for potential (1.4), in the leading approximation one can obtain

$$\frac{{\partial F}}{{\partial x}} + \left( {{{\nabla }_{2}}{{\varphi }_{1}},{{\nabla }_{2}}F} \right) = 0.$$

(1.6)

Differential operator ${{\nabla }_{3}}$ corresponds to the three-dimensional operator $\left( {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0em} {\partial x}}{\kern 1pt} ,\;{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0em} {\partial y}}{\kern 1pt} ,\;{\partial \mathord{\left/ {\vphantom {\partial {\partial z}}} \right. \kern-0em} {\partial z}}} \right)$, whereas ${{\nabla }_{2}}$ represents a two-dimensional operator, $\left( {\,{\partial \mathord{\left/ {\vphantom {\partial {\partial {{y}_{1}},}}} \right. \kern-0em} {\partial {{y}_{1}},}}\;{\partial \mathord{\left/ {\vphantom {\partial {\partial {{z}_{1}}}}} \right. \kern-0em} {\partial {{z}_{1}}}}} \right)$. Condition (1.6) means that in the case of moving along x the velocity of the fluid normal to the surface and the velocity of the surface itself (either the surface of the body or the surface of the vortex sheet) coincide.

The boundary condition of pressure continuity when crossing the discontinuity surface can be easily written in terms of the velocity potential using the Bernoulli integral:

$$\left\langle {\frac{{{{{\left( {{{\nabla }_{3}}\varphi } \right)}}^{2}}}}{2}} \right\rangle = 0,$$

or in the new variables:

$$\left\langle {\frac{{\partial {{\varphi }_{1}}}}{{\partial x}} + \frac{{{{{\left( {{{\nabla }_{2}}{{\varphi }_{1}}} \right)}}^{2}}}}{2}} \right\rangle = 0.$$

(1.7)

It should be noted that, since φ₂ depends only on x, then $\left\langle {{{\varphi }_{2}}} \right\rangle = 0$.

The conditions at the separation point determine the intensity of vortex-sheet vanishing into the flow. Let us determine the order of magnitude for this intensity. Since the characteristic size of the vortex sheet and the characteristic transverse velocity in any section with x = const are on the order of δ, then the total circulation of the vortex sheet should be on the order of δ².

Particular attention should be paid to the boundary conditions set at infinity. The velocity vector of the oncoming flow lies in the plane xy and has a unit length which is equivalent to the following conditions:

$${{{v}}_{{1\infty }}} = \bar {\alpha },\quad {{w}_{{1\infty }}} = 0$$

(1.8)

or

$$\frac{{\partial {{\varphi }_{1}}}}{{\partial {{y}_{1}}}} = \bar {\alpha },\quad \frac{{\partial {{\varphi }_{1}}}}{{\partial {{z}_{1}}}} = 0\quad {\text{at}}\quad y_{1}^{2} + z_{1}^{2} \to \infty .$$

The ${{\bar {\alpha } = \alpha } \mathord{\left/ {\vphantom {{\bar {\alpha } = \alpha } \delta }} \right. \kern-0em} \delta }$ ratio is called the relative angle of attack. As far as the perturbed solution φ₂ is concerned, one should not demand that it decay at infinity. There is no such requirement because going to infinity in the variables of domain Ω₁ and in physical variables is not equivalent. Instead of the requirement that perturbations decay at infinity, it is necessary to set a condition for splicing the solution in domains Ω₁ and Ω₂.

Let us consider now the two-dimensional nonsteady-state problem of separated flow around a body of variable geometry with given separation points. Let its geometry at the moment of time t correspond to the geometry of the cross section of a three-dimensional narrow body cut by plane x = t, and the location of the separation points on the two-dimensional body correspond to the separation lines on the three-dimensional body in this cross section. The oncoming flow has a velocity of $\bar {\alpha }$. In this case, to determine the characteristics of flow around a two-dimensional body, it is necessary to solve Eq. (1.5) with boundary conditions (1.6)–(1.7), wherein the role of time is played by coordinate x.

Indeed, condition (1.6), if the x coordinate is replaced by time t, means that the condition of impermeability through a body of variable geometry $F(t,{{y}_{1}},{{z}_{1}}) = 0$ is satisfied, whereas condition (1.7) means that potential ${{\varphi }_{1}}(t,{{y}_{1}},{{z}_{1}})$ satisfies the Cauchy–Lagrange integral. Thus, the three-dimensional steady-state problem of flow around a narrow body at a small angle of attack has been reduced to a two-dimensional nonsteady-state problem of flow around a flat body of variable geometry, corresponding to the geometry of the body’s cross section, with the use of conditions (1.8) at infinity. This correspondence is called a nonsteady-state analogy. In physical variables, the role of time in the nonsteady-state analogy is played by the ratio of $x{\text{/}}{{u}_{\infty }}$.

The velocity field corresponding to potential $\varphi (x,{{y}_{1}},{{z}_{1}})$ can be represented as the sum of velocities induced by the hydrodynamic singularities distributed on the body surface or inside the body and on the surface of the vortex sheet. Let us consider first the problem of finding this potential in the simplest case, when a flow around a body of zero volume is studied. Such bodies are called bearing surfaces. The velocity field around the body is simulated by a vortex surface attached to the body and free at a tangential velocity discontinuity.

Let us divide the vortex surface into elementary vortex filaments of variable intensity dΓ. The vortex filaments cannot end up on the body or in the flow. Hence, each vortex filament passes through the body and then leaves with its two free ends to infinity. Schematically, such vortex filaments are shown in Fig. 1. They simulate a velocity discontinuity on the upper and lower body surfaces and on the vortex sheet. The inclination angle of the vortex filaments is comparable in the order of magnitude with δ. Let us consider an elementary vortex filament having the circulation $d\,{{\Gamma }_{\ell }}$. The radius vector of a point on a vortex filament is

$${{{\mathbf{r}}}_{\ell }} = x \cdot {\mathbf{i}} + \delta {{g}_{{2,\ell }}}(x) \cdot {\mathbf{j}} + \delta {{g}_{{3,\ell }}}(x) \cdot {\mathbf{k}}{\text{.}}$$

(1.9)

Fig. 1.

Low-aspect-ratio wing (top view) and some vortex lines simulating the vortex surface of the wing.

The orths ${\mathbf{i}},{\mathbf{j}},{\mathbf{k}}$ are directed along axes $x,\,y,\,z$; index $\ell$ takes a value amounting to 1 for the left half of the vortex filament, and 2 for the right half of the filament; and functions g are comparable within an order of unity. By substituting relationship (1.9) into the Biot–Savart formula (1.12) for the velocity fields around the vortex filament with the intensity $d{{\Gamma }_{\ell }}$ one can obtain:

$$d{\mathbf{V}} = \frac{{d{{\Gamma }_{\ell }}}}{{4\pi }}\int\limits_L {\frac{{{\mathbf{d}}{{{\mathbf{r}}}_{\ell }} \times {\mathbf{s}}}}{{{{{\left| {\mathbf{s}} \right|}}^{3}}}}} ,$$

where s is the distance vector. One obtains that in the leading approximation the velocity along the x axis induced by the elementary vortex filament at the a point with coordinates $x,\,{{y}_{1}},\,{{z}_{1}}$ is (prime means the derivative with respect to x) as follows:

$$\begin{gathered} d\,u = - \frac{{d\,{{\Gamma }_{\ell }}}}{{2\pi }}\frac{{({{y}_{1}} - {{g}_{{2,1}}})\,g_{{3,1}}^{'} - ({{z}_{1}} - {{g}_{{3,1}}})\,g_{{2,1}}^{'}}}{{{{{({{y}_{1}} - {{g}_{{2,1}}})}}^{2}} + {{{({{z}_{1}} - {{g}_{{3,1}}})}}^{2}}}} \\ + \,\,\frac{{d\,{{\Gamma }_{\ell }}}}{{2\pi }}\frac{{({{y}_{1}} - {{g}_{{2,2}}})\,g_{{3,2}}^{'} - ({{z}_{1}} - {{g}_{{3,2}}})\,g_{{2,2}}^{'}}}{{{{{({{y}_{1}} - {{g}_{{2,2}}})}}^{2}} + {{{({{z}_{1}} - {{g}_{{3,2}}})}}^{2}}}}. \\ \end{gathered} $$

(1.10)

As it has been already mentioned above, the total circulation for all the vortex filaments is $\Gamma \sim {{\delta }^{2}}$. From this estimate and relationship (1.10) it follows that the longitudinal velocity induced by the entire vortex surface of the wing should be on the order of δ².

The velocity potential ${{\varphi }_{1}}(x,{{y}_{1}},{{z}_{1}})$ can be determined resulting from solving the plane problem concerning a nonsteady-state flow around a body corresponding to a plane section of the load-carrying surface. Let us consider an arbitrary cross section x. In this cross section, the flow can be simulated by rectilinear vortex filaments extending parallel to the x axis from $- \infty$ to $\infty$. The pre-image of a curvilinear vortex filament in the three-dimensional problem should represent two rectilinear vortex filaments in the two-dimensional problem: the left one having an intensity of $- d\,{{\Gamma }_{\ell }}$ and the right one having an intensity of $d\,{{\Gamma }_{\ell }}$. In cross section x, their coordinates are ${{y}_{{1,\ell }}} = {{g}_{{2,\ell }}}(x)$ and ${{z}_{{1,\ell }}} = {{g}_{{3,\ell }}}(x)$ The potential of two vortex filaments in cross section x is

$${{\varphi }_{1}} = \frac{{d\,{{\Gamma }_{\ell }}}}{{2\pi }}\arctan \frac{{{{z}_{1}} - {{g}_{{3,1}}}}}{{{{y}_{1}} - {{g}_{{2,1}}}}} - \frac{{d\,{{\Gamma }_{\ell }}}}{{2\pi }}\arctan \frac{{{{z}_{1}} - {{g}_{{3,2}}}}}{{{{y}_{1}} - {{g}_{{2,2}}}}}.$$

(1.11)

The velocity along the x axis is ${{\partial {{\varphi }_{1}}} \mathord{\left/ {\vphantom {{\partial {{\varphi }_{1}}} {\partial x}}} \right. \kern-0em} {\partial x}}$. By differentiating potential (1.11) one obtains relationship (1.10) again. This means that potentials potentials $\varphi (x,{{y}_{1}},{{z}_{1}})$ and ${{\varphi }_{1}}(x,{{y}_{1}},{{z}_{1}})$ in the leading approximation coincide for the bearing surface, whereas quantity ${{\varphi }_{2}}(x)$ is zero.

The expansions for the velocity potential (1.4) become invalid in the vicinity of the fore part of the wing. The solution in this domain, which has dimensions $x\sim y\sim z\sim O\left( \delta \right)$, as well as approximations of a higher order than those presented in (1.4), were obtained in [4].

In order to determine the forces affecting a thin low-aspect-ratio wing, let us represent pressure in the following form:

$$\frac{{p - {{p}_{\infty }}}}{{\frac{1}{2}\rho \,u_{\infty }^{2}}} = {{\delta }^{2}}{{p}_{1}}\left( {x,{{y}_{1}},{{z}_{1}}} \right).$$

The latter relationship follows from (1.4) and the Bernoulli integral. Let us determine the dimensionless pressure force coefficients ${{c}_{x}},{{c}_{y}},$ and c_z [5]:

$${{c}_{x}} = \frac{X}{{\frac{1}{2}\rho u_{\infty }^{2}S}} = \frac{{\iint {\left( {p - {{p}_{\infty }}} \right)}\,dy\,dz}}{{\frac{1}{2}\rho u_{\infty }^{2}S}} = \frac{{{{\delta }^{3}}}}{{{{S}_{1}}}}\iint\limits_S {{{p}_{1}}d{{y}_{1}}d{{z}_{1}}} = {{\delta }^{3}}{{C}_{1}},$$

$${{c}_{y}} = \frac{Y}{{\frac{1}{2}\rho u_{\infty }^{2}S}} = \frac{{\iint {\left( {p - {{p}_{\infty }}} \right)}\,dx\,dz}}{{\frac{1}{2}\rho u_{\infty }^{2}S}} = \frac{{{{\delta }^{2}}}}{{{{S}_{1}}}}\iint\limits_S {{{p}_{1}}dx\,d{{z}_{1}}} = {{\delta }^{2}}{{C}_{2}},$$

$${{c}_{z}}\, = \frac{Z}{{\frac{1}{2}\rho u_{\infty }^{2}S}} = \frac{{\iint {\left( {p - {{p}_{\infty }}} \right)}\,dx\,dy}}{{\frac{1}{2}\rho u_{\infty }^{2}S}} = \frac{{{{\delta }^{2}}}}{{{{S}_{1}}}}\iint {{{p}_{1}}dx\,d{{y}_{1}}} = {{\delta }^{2}}{{C}_{3}}.$$

Integration is performed over the surface of the wing; $S = \delta \,{{S}_{1}}$ is the area of the wing in plan view; and ${{C}_{1}},{{C}_{2}},$ and C₃ are the constants depending on the shape of the wing surface.

Let us now consider the flow around a narrow body having a nonzero thickness. The flow around such a body can be simulated by a vortex surface similar to that considered above. In addition to the vortex surface, along some line inside the bulk part of the body (or parts, if there are several), sources are placed. Let us determine the intensity of the sources q(x). Let the area of the body cross section changes according to the law of $\tilde {S}(x)$, $0 \leqslant x \leqslant 1$. If the body has a zero thickness, then $\tilde {S} = 0$. From the geometric conditions it follows that $\tilde {S}(x) = {{\delta }^{2}}\,{{\tilde {S}}_{1}}(x)$ and the order of magnitude for quantity ${{\tilde {S}}_{1}}(x)$ is comparable with unity. In addition, let us require for condition $\tilde {S}_{1}^{'}(x)\sim \tilde {S}_{1}^{{''}}(x)\sim O(1)$ to be satisfied. The increase in the cross-sectional area of a body in the two-dimensional nonsteady-state problem occurs due to an influx of fluid from a source, whereas a decrease in the area occurs due to outflow to a sink:

$$q(x) = \tilde {S}{\kern 1pt} ' = {{\delta }^{2}}\tilde {S}_{1}^{'}.$$

The potential of a two-dimensional source is

$${{\varphi }_{1}}(x,{{y}_{1}},{{z}_{1}}) = \frac{q}{{2\pi }}\ln \,(r) = \frac{q}{{2\pi }}\ln \,(\delta \,{{r}_{1}}),$$

(1.12)

where r is the distance from point ${{y}_{{1s}}}(x),\,\,{{z}_{{1s}}}(x)$, wherein the source is located

$$r = \delta \,\sqrt {{{{\left( {{{y}_{1}} - {{y}_{{1s}}}} \right)}}^{2}} + {{{\left( {{{z}_{1}} - {{z}_{{1s}}}} \right)}}^{2}}} .$$

When solving a 3D problem on the line corresponding to ${{y}_{1}} = {{y}_{{1s}}}(x)$, ${{z}_{1}} = {{z}_{{1s}}}(x)$,it is necessary to arrange 3D sources with the intensity of

$$d\,Q(x) = q(x)\,dx.$$

The velocity potential originating from such a source is

$$d\,\varphi = - \frac{{d\,Q}}{{4\,\pi \,r}}.$$

Only now, as the r distance, it is necessary to take the distance in three-dimensional space from point ${{x}_{{1s}}},\,{{y}_{{1s}}}({{x}_{{1s}}}),\,\,{{z}_{{1s}}}({{x}_{{1s}}})$:

$$r = \sqrt {{{{(x - {{x}_{{1s}}})}}^{2}} + {{\delta }^{2}}({{{\left( {{{y}_{1}} - {{y}_{{1s}}}} \right)}}^{2}} + {{{\left( {{{z}_{1}} - {{z}_{{1s}}}} \right)}}^{2}})} .$$

The contribution from the sources to the velocity potential $\varphi (x,{{y}_{1}},{{z}_{1}})$ is

$$\varphi (x,{{y}_{1}},{{z}_{1}}) = - \frac{1}{{4\,\pi }}\int\limits_0^1 {\frac{{d\,Q\,({{x}_{{1s}}})}}{r}} .$$

Since $\tilde {S}(x)\sim {{\delta }^{2}}$, then $\varphi (x,{{y}_{1}},{{z}_{1}})$ and ${{\varphi }_{1}}(x,{{y}_{1}},{{z}_{1}})$ should also be quantities on the order of δ², whereas their difference defines function ${{\varphi }_{2}}(x)$. In the leading approximation

$$\begin{gathered} \mu (\delta ) = {{\delta }^{2}}, \\ {{\varphi }_{2}}(x) = - \frac{1}{{4\pi }}\{ 2\,{{{\tilde {S'}}}_{1}}(x)\,\ln \,2 + \tilde {S}_{1}^{'}(0)\ln \,x + \tilde {S}_{1}^{'}(1)\,\ln \,(1 - x) \\ + \,\,\int\limits_0^x {\tilde {S}_{1}^{{''}}({{x}_{1}})\,\ln \,(x - {{x}_{1}})\,d\,{{x}_{1}} - \int\limits_x^1 {\tilde {S}_{1}^{{''}}({{x}_{1}})\,\ln \,({{x}_{1}} - x)\,d\,{{x}_{1}}} } \} . \\ \end{gathered} $$

(1.13)

From (1.12) and (1.13) it follows that at ${{r}_{1}} \to \infty$ the longitudinal velocity perturbations

$$u - 1 = {{\delta }^{2}}\left( {\frac{{\partial \,\left( {{{\varphi }_{1}} + {{\varphi }_{2}}} \right)}}{{\partial \,x}}} \right)\sim {{\delta }^{2}}\frac{{\tilde {S}_{1}^{{''}}(x)}}{{2\,\pi }}\,\ln \,(\delta \,{{r}_{1}})$$

do not decay at infinity [5]. The same feature at infinity should be exhibited by pressure. The fact that perturbations do not decay has already been discussed above. Decaying perturbation at infinity should be required for considering the solution in domain Ω₂.

2 APPLICATION OF THE NONSTEADY-STATE ANALOGY TO POWER-LAW WINGS

Let us consider the flow of an ideal fluid near a small-aspect-ratio wing formed by straight line segments parallel to axis z. The length of these segments changes according to the power law $\ell \left( x \right) = \varepsilon a{{x}^{n}}$, whereas the wing itself is curved according to a law corresponding to $y\left( x \right) = - \varepsilon b{{x}^{n}}$, where $0 \leqslant x < \infty$, a and b are some positive dimensional constants, ε is the dimensionless constant $\varepsilon \ll 1$ and $1{\text{/}}2 \leqslant n \leqslant 1$. The wing is symmetrical with respect to the plane z = 0 (Fig. 2) and has a zero thickness. The oncoming flow with velocity ${{u}_{\infty }}$ at infinity is directed along the x axis. Vortex sheets vanish into the flow from the sharp wing edges. The case of n = 1 corresponds to a delta-shaped wing.

Fig. 2.

Wing formed by straight segments parallel to the z axis. The wing is curved according to a power law and has a power-law shape in plan view.

At $x \gg {{\varepsilon }^{{1/\left( {1 - n} \right)}}}$, when n < 1, and at $x \geqslant 0$, when n = 1, the wing becomes elongated, and therefore the nonsteady-state analogy is valid. Replacing coordinate x by time t is the former: $t = x{\text{/}}{{u}_{\infty }}$. By applying it, one can obtain that the three-dimensional problem in the leading approximation is equivalent to a flow near a flat plate, the length of which varies over time according to the law $\ell \left( t \right) = \varepsilon au_{\infty }^{n}{{t}^{n}}$, $0 \leqslant t < \infty$. Herewith, the plate moves along the y axis with the velocity of ${v}\left( t \right) = {{dy\left( t \right)} \mathord{\left/ {\vphantom {{dy\left( t \right)} {dt = }}} \right. \kern-0em} {dt = }} - \varepsilon nbu_{\infty }^{n}{{t}^{{n - 1}}}$. The parameters of this flow should obey self-similar laws [6]. The circulation of vortex structures increases in proportion to ${{t}^{{2n - 1}}}$.

Paper [7] is devoted to the numerical calculation of an inviscid fluid flow around power-law wings using the nonsteady-state analogy. The method of discrete vortices was used. In this work it was shown that at $n \to 1{\text{/}}2$ the turns of the vortex sheet get free from the circulation that is concentrated in the core of the vortex structure.

If one returns to a three-dimensional steady-state flow again, then the circulation of vortex sheets in the leading approximation exhibits an increase in proportion to ${{x}^{{2n - 1}}}$.

Let us now turn at n < 1 to the fore part of the wing, where x ~ y ~ z. This scale corresponds to $x\sim {{\varepsilon }^{{1/\left( {1 - n} \right)}}}$. Here a sufficiently three-dimensional flow is realized. Thus, the flow does not become self-similar immediately, but only after the fluid passes through the fore part of the wing, which is a domain with a sufficiently three-dimensional flow. An interesting scenario consists in the potentialities of the fact that the flow attains a self-similar mode. It is especially interesting at n = 1/2, when the entire vorticity vanishing into the flow occurs from a very small domain of a three-dimensional flow $x\sim {{\varepsilon }^{2}}$ and then the evolution of the vortex structure occurs without feeding the vorticity from the sharp wing edges.

In contrast to a nonsteady-state plane flow, a three-dimensional flow can be readily reproduced in experimental studies. Such testing, in addition to the fact that they are themselves interesting, make it possible to find out how a vortex flow is formed in the vicinity of the wing apex.

The flow around a wing with a power-law shape in plan view $\ell (x) = 2\sqrt x$ and curved according to the power law $y(x) = - \sqrt x$, $0 \leqslant x \leqslant 20$,was experimentally studied in [8]. The linear dimensions are given in centimeters. Testing is carried out in a vertical wind tunnel with a working part of the square cross section measuring 150 × 150 mm in the range of Reynolds numbers Re = 2 × 10³–2 × 10⁴. The Reynolds number was calculated based on the wing length and on the oncoming-flow velocity. In order to visualize the flow, ink was supplied to the flow through a drainage hole in the fore part of the wing.

The experiment showed that the separated flow around the wing is steady state. In the fore part, “hanging” separated formations were found: two closed vortex recirculation zones neighboring the wing apex only. Vortex bundles separate from the recirculation zones, which in the theory of self-similar flow are idealized as vortex filaments. Ink, after supplying it to the fore part of the wing being stopped, remained therein for a time (about 10 min), much longer than the time it took for a fluid particle to travel the entire length of the wing (which is about 10 s). The closure of the circulation regions and further transition to a cylindrical flow occurred with no significant velocity fluctuations.

The laminar nature of the flow can be, it seems, caused by a favorable pressure gradient near the apex and by a small value of Reynolds number Re. Figure 3 shows the experimentally obtained flow patterns at an oncoming-flow velocity of ${{u}_{\infty }} = 2$ cm/s, whereas Fig. 3a shows a plan view of these zones, and Fig. 3b presents a side view 1 min after dye-supply stopped. Figure 4 shows the flow pattern. Thus, experimental studies performed using a wind tunnel have qualitatively confirmed the feasibility of a self-similar flow at n = 1/2.

Fig. 3.

Visualization of recirculation zones with the use of dye: (a) plan view, (b) side view.

Fig. 4.

Same as in Fig. 3. Flow pattern.

3 KADEN’S PROBLEM

Kaden [9] considered a steady-state problem of vortex-wake evolution behind an elliptically loaded wing under the assumption that the vortex sheet vanishes only from the trailing edge. In this case, the distribution diagram for circulation Γ along the wing span at $- \ell < z < \ell$ can be determined according to the following relationship:

$$\Gamma = {{\Gamma }_{m}}\sqrt {1 - \frac{{{{z}^{2}}}}{{{{\ell }^{2}}}}} .$$

In the case of an elliptically loaded wing, everywhere, except for the free ends, the downwash angle is the same [10]. Therefore, the cross section of the main part of the sheet at small x should represent a straight line segment. The free ends of the vortex sheet curl into spirals with an infinite number of turns.

If one assumes that curling the vortex sheet into a spiral occurs very slowly, as, for example, in the case of a high-aspect-ratio wing at a low angle of attack, then the vicinity of the curled part of the vortex sheet should represent an elongated formation (Fig. 5), for which the nonsteady-state analogy with the standard replacement of coordinate x by time $t = x{\text{/}}{{u}_{\infty }}$ is valid. Then, at short times, the transverse size of the curled part of the vortex sheet should be much smaller than the transverse size of the wake.

Fig. 5.

Vortex wake curling behind an elliptically loaded wing.

On the scale of the curled part of the vortex sheet, the size of the rectilinear part of the vortex sheet is infinite, the curled vortex at the second end of the sheet also goes to infinity, and its influence can be neglected (Fig. 6a). The problem of the evolution of the end part of a vortex sheet with an elliptical circulation-distribution law is equivalent to the problem of the evolution of a semiinfinite $(0 \leqslant {{z}_{1}} < \infty ,\,\,{{z}_{1}} = \ell - z)$ vortex sheet (Fig. 6b), whose circulation density at the initial moment of time t = 0 changes according to the following law:

$$\gamma = \frac{c}{{\sqrt {{{z}_{1}}} }}.$$

(3.1)

Fig. 6.

Evolution of the vortex wake behind an elliptically loaded wing; (a) plane section, (b) the vicinity of the right vortex, on its scale the left vortex is located at infinite distance from the right vortex.

Since there is no characteristic linear size at the initial moment of time t = 0, then it should be expected that the vortex-sheet evolution would be subject to a self-similar law. Let us mark on the vortex surface at t = 0 two points A and B, one of which is located at a k-fold longer distance from the free end than from the other, and let us consider the following two domains: from z₁ = 0 to the A point and from z₁ = 0 to the B point. At the similarly located points in these two domains, the initial velocities are proportional to each other. Hence, the motion of these points should also be similar. Only the duration of the corresponding process in a larger domain is longer.

The path traveled by a point in a larger domain should be k-fold longer, whereas the velocity should be ${1 \mathord{\left/ {\vphantom {1 {\sqrt k }}} \right. \kern-0em} {\sqrt k }}$-fold lower than the path and velocity of the corresponding point in the smaller domain. The time for achieving such a change is proportional to the traveled distance and inversely proportional to the motion velocity, i.e., this time should be different in the two areas by a factor of k^3/2. If r₁ and r₂ represent the scales of similar patterns at different points of time, then

$$\frac{{{{t}_{2}}}}{{{{t}_{1}}}} = {{\left( {\frac{{{{r}_{2}}}}{{{{r}_{1}}}}} \right)}^{{3/2}}}\quad {\text{or}}\quad \frac{{{{r}_{2}}}}{{{{r}_{1}}}} = {{\left( {\frac{{{{t}_{2}}}}{{{{t}_{1}}}}} \right)}^{{2/3}}}.$$

Thus, the problem of semi-infinite vortex-sheet evolution (3.1) is self-similar with a self-similarity index of n = 2/3.

In [11], the evolution of plain semi-infinite $- \infty < x \leqslant 0$ and infinite $- \infty < x \leqslant \infty$ vortex sheets is considered, the equation of which at the initial moment of time in the complex plane is determined according to relationship ${{\sigma }_{1}} = x + 0i$, whereas the initial circulation distribution depends on coordinate x in a power-law manner:

$$\left\{ \begin{gathered} \Gamma = 2\,{{a}^{{2 - p}}}{{\left| {{{x}_{1}}} \right|}^{p}},\quad - \infty < x \leqslant 0, \hfill \\ \Gamma = - 2\,{{a}^{{2 - p}}}\,\delta \,x_{1}^{p},\quad 0 \leqslant x < \infty . \hfill \\ \end{gathered} \right.$$

(3.2)

The solution to the problem depends on one dimensional constant a and on one dimensionless constant p ranging within $0 < p \leqslant 1$. For a semi-infinite vortex sheet δ = 0, whereas for an infinite one δ = 1. The circulation density has the following power-law form:

$$\gamma = \frac{{d\,\Gamma }}{{d\,{{x}_{1}}}}\sim {{\left| {{{x}_{1}}} \right|}^{{p - 1}}},$$

which at p = 1/2 coincides with relationship (3.1). The semi-infinite vortex sheet should be curled into a spiral in the vicinity of the free end. The infinite sheet should also be spiraled around point x = 0 due to the nonanalytic behavior of the circulation density at the initial moment of time.

Let the geometry of the vortex sheet obey a law corresponding ${{\sigma }_{1}} = {{\sigma }_{1}}(\Gamma ,t)$ at $\Gamma \geqslant 0$. If δ = 1, then the right part of the vortex sheet is symmetrical with respect to the left part relative to the point x = 0, and therefore its geometry obeys a law corresponding to ${{\sigma }_{1}} = - {{\sigma }_{1}}(\Gamma ,t)$. The evolution equation of the vortex sheet can be expressed in the following form:

$$\frac{{\partial \,{{{\bar {\sigma }}}_{1}}}}{{\partial \,t}} = \frac{1}{{2\,\pi \,i}}\int\limits_0^\infty {\frac{{d\,\Gamma '}}{{{{\sigma }_{1}}(\Gamma ,t) - {{\sigma }_{1}}(\Gamma ',t)}}} + \frac{\delta }{{2\,\pi \,i}}\int\limits_0^\infty {\frac{{d\,\Gamma '}}{{{{\sigma }_{1}}(\Gamma ,t) + {{\sigma }_{1}}(\Gamma ',t)}}} .$$

(3.3)

By direct verification, one can make sure that the evolution problem is self-similar with the following self-similarity index $n = {1 \mathord{\left/ {\vphantom {1 {\left( {2 - p} \right)}}} \right. \kern-0em} {\left( {2 - p} \right)}}$

$${{\sigma }_{1}}(\Gamma ,t) = a\,{{t}^{{1/(2 - p)}}}\sigma \left( G \right),$$

(3.4)

where

$$G = \frac{\Gamma }{{{{a}^{2}}\,{{t}^{{p/(2 - p)}}}}}.$$

(3.5)

Thus, problem [11] generalizes Kaden’s problem to the self-similarity parameters ranging from n = 1/2 at p = 0 to n = 1 at p = 1.

By substituting relationship (3.4) and (3.5) into integro-differential equation (3.3) one can obtain:

$$\frac{1}{{2 - p}}\left( {\bar {\sigma } - p\,G\,\frac{{d\,\bar {\sigma }}}{{d\,G}}} \right) = \frac{1}{{2\,\pi \,i}}\int\limits_0^\infty {\frac{{d\,G{\kern 1pt} {\kern 1pt} '}}{{\sigma (G) - \sigma (G{\kern 1pt} {\kern 1pt} ')}} + } \frac{\delta }{{2\,\pi \,i}}\int\limits_0^\infty {\frac{{d\,G{\kern 1pt} {\kern 1pt} '}}{{\sigma (G) + \sigma (G{\kern 1pt} {\kern 1pt} ')}}} .$$

(3.6)

Equation (3.6) and dependence (3.2) determine the behavior of function $\sigma (G) = \xi + i\eta$ at $G \to \infty$:

$$\sigma (G) = - {{\left( {\frac{G}{2}} \right)}^{{1/p}}} - i\,p\left[ {\frac{{\delta + \cos (p\,\pi )}}{{\sin (p\,\pi )}}} \right]{{\left( {\frac{G}{2}} \right)}^{{1 - 1/p}}} + o({{G}^{{1 - 1/p}}}).$$

The second term of the latter relationship is responsible for the downward motion of the vortex sheet. For a semi-infinite sheet, the downward motion velocity tends to infinity at $p \to 1$. Therefore, at δ = 0, to avoid the specific feature, let us study the vortex-sheet evolution in plane $\sigma {\kern 1pt} '(G) = \sigma (G) + i\,p\cot (p\,\pi )$ = ξ' + iη'. The geometry of vortex sheets can be determined based on the numerical solution of Eq. (3.6). Both for single-spiral and for double-spiral formations, such a geometry was obtained in [11]; it is given in Figs. 7 and 8. The result obtained for single-spiral structures is shown in the plane of $\sigma {\kern 1pt} ' = \xi {\kern 1pt} '\, + i\,\eta {\kern 1pt} '$ (see Fig. 7).

Fig. 7.

Geometry of single-spiral vortex sheets in the vicinity of the free end in the plane $\sigma ' = \xi '\, + i\,\eta '$: (a) p = 0.05, (b) p = 1.

Fig. 8.

Geometry of double-spiral vortex sheets in the vicinity of the center in the plane $\sigma = \xi + i\,\eta$, p = 0.05.

For infinite vortex sheets, there is no singularity in the expansion of function σ(G), the solution of Eq. (3.6) is shown in Fig. 8. It should be noted that the solution in the vicinity of the vortex-sheet center in [11] is obtained using an asymptotic solution for an infinite algebraic spiral. Figures 7 and 8 do not show the infinite spiral, only the center around which the spiral is curled is indicated.

4 COMPUTATIONAL STUDIES ON FLOWS AROUND BODIES OF SMALL ELONGATION

The calculation of elongated bodies using the nonsteady-state analogy can significantly simplify the problem. In general, a method is used that consists in replacing the vortex sheet with a set of discrete vortices (discrete-vortex method). As far as a solid surface is concerned, one can use methods, in the case of which attached vortices are located on the solid surface, and methods based on conformal mapping, in the case of which a streamlined contour is usually mapped onto a cylinder or a half-plane, followed by replacing the solid boundary with a system of mapped vortices. Let us present some results of calculations for elongated bodies. Let us especially dwell on two almost important cases such as flowing around a delta wing and flowing around a circular cone.

Delta-Shaped Wing. The flow around a delta wing of small elongation at relative angles of attack on the order of unity is accompanied by the vortex-sheet vanishing from the side and trailing edges. Intense vortex sheets radically change the flow topology near the wing. As compared to an unseparated flow, both pressure, and forces affecting the wing exhibit changes.

At the same time, alongside the main separated formations of vortex sheets depending on the angle of attack, secondary and tertiary vortex structures can also be observed, which already vanish from the smooth surface of the wing, rather than from the edges. All these vortex structures have a spiral shape, with a secondary vortex curled in the opposite direction with respect to the main vortex, whereas the tertiary vortex is curled in the opposite direction with respect to the secondary vortex. The authors of [12] experimentally studied the flow around a delta wing with the half-angle χ = 15° at the apex.

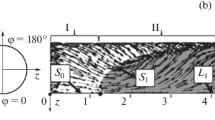
The wing edges are sharp. Figure 9 plotted on the basis of data taken from the above-mentioned paper shows the flow topology at angle of attack of α = 7.5°. Only the upper surface of the right half of the wing is shown. The flow velocity amounted to 40 m/s, the chord had a length of 1.45 m, which corresponded to the Reynolds number Re_c = 4 × 10⁶ calculated according to this chord. The designations in the figures are as follows: S₁, S₂ are the separation lines from a sharp edge and from a secondary vortex, respectively; and A₁, A₂ are the lines of flow attachment, the meaning of which is illustrated in Fig. 10.

Fig. 9.

Flow topology. Right half of the upper surface of the delta wing. χ = 15° and α = 7.5°.

Fig. 10.

Cross section of the right half of the wing.

Figure 10 shows an illustrative view of the main and secondary vortex sheet in the cross-section of the right half of the wing, as well as the projections of the streamlines (only the flow topology is shown with no quantitative data corresponding to a real flow). From Fig. 9 one can see that the lines A₁, A₂, and S₂ are conical for most of the length of the wing, with two conical lines observed, one being the fore part of the wing, the other starting at some distance from the fore part of the wing and continuing all the way to the trailing edge. These two conical lines are joined by a smooth curve. Such a curvature of the lines is associated with the state of the boundary layer near the wing surface. The fact is that only the main separation occurring at the sharp edges is fixed on the delta wing, whereas the position of flow separation from a smooth surface significantly depends on the characteristics of the boundary layer near the separation line.

In the initial part of the wing, the boundary layer is laminar, and the first conical line is observed, then a laminar—turbulent transition occurs, in the course of which the line is sufficiently curved, and then the transition of the boundary layer to a turbulent state occurs, and the second conical line is observed. In reality, the separation lines and attachment are only approximately conical, since as a figurative point moves along the wing, the transverse size of the wing linearly increases, whereas the boundary-layer thickness exhibits a nonlinear increase. However, this deviation from conicity is slight and insignificant in the case of a small wing. With increasing angles of attack, tertiary separated formations, as well as an attachment line caused by this separation appear on the wing surface.

As was already noted in Section 2, the separated flow around a small-aspect-ratio delta wing set at a low angle of attack can be studied in the framework of the nonsteady-state analogy. However, since studies concerning such a flow in the scope of the nonsteady-state analogy are carried out using inviscid equations, then all the separated formations are usually neglected in the consideration, except for the main one that vanishes from sharp wing edges. This simplification is connected, firstly, with the impossibility of determining the position of formations separated from a smooth surface using inviscid equations, and, secondly, with an insignificant effect of secondary vortex structures on the aerodynamic forces affecting the wing.

For the case of a zero-thickness wing, the three-dimensional steady-state problem turns out to be equivalent to a two-dimensional nonsteady-state problem of separated flow past a plate linearly expanding over time. Quite a lot of works are devoted to the calculation of such a flow, among which one could single out publications [13–16]. It is quite natural that this nonsteady-state problem is self-similar. In self-similar variables, when the linear sizes are nondimensionalized with respect to a local half-span of the wing, the geometry of spiral vortex sheets given in [16] for a small-aspect-ratio delta wing, λ = 0.698 at an angle of attack of α = 10° and at a zero slip angle, is shown in Fig. 11.

Fig. 11.

Vortex system inherent in a delta wing. Calculation according to the nonsteady-state analogy, $\lambda = 0.698$ and $\alpha = 10^\circ$.

It should be noted that to obtain the solution shown in Fig. 11, two numerical techniques have been developed. The first one is related to the fact that the vortex-sheet evolution is unstable. On account of the instability of the tangential discontinuity, the solution obtained using the discrete-vortex method will depend on how the continuous tangential discontinuity is approximated by discrete vortices and on the rule used for rounding numbers in the numerical calculations. Thus, the current problem is incorrect. In order to obtain a stable solution, it is necessary to regularize the equations of vortex-sheet evolution. The second technique is related to the fact that the vortex-sheet core represents a spiral with an infinite number of turns. The approximation of such a vortex formation by discrete vortices is impossible. Therefore, a model for the core of a spiral vortex sheet is needed.

Molchanov’s Regularizer. The velocity field induced by the vortex sheet can be described according to the following equation

$$\frac{{\partial \,\bar {\sigma }(\Gamma ,t)}}{{\partial \,t}} = \frac{1}{{2\pi i}}\int {\frac{{d\Gamma {\kern 1pt} '}}{{\sigma (\Gamma ,t) - \sigma (\Gamma {\kern 1pt} ',t)}}} .$$

In the case when a vortex sheet is not the only source that determines the motion of the fluid (for example, the oncoming flow, solid bodies in the flow, etc.), in studies on the local evolution of points on a vortex sheet, a potential part of the velocity should be added to the right side of the latter equation. In the case of numerical simulation, a flat vortex sheet is replaced by discrete vortices with a certain level of discretization in space. Following the work published by Molchanov [15], let us write out a finite difference scheme of the first order of accuracy for the numerical calculation based on the vortex-sheet evolution equation:

$$\begin{gathered} \frac{{x_{n}^{{m + 1}} - x_{n}^{m}}}{{\Delta \,t}} = - \frac{1}{{2\pi }}\sum\limits_{k \ne n} {\frac{{(y_{n}^{m} - y_{k}^{m}){{\Gamma }_{k}}}}{{{{{(x_{n}^{m} - x_{k}^{m})}}^{2}} + {{{(y_{n}^{m} - y_{k}^{m})}}^{2}}}}} + U, \\ \frac{{y_{n}^{{m + 1}} - y_{n}^{m}}}{{\Delta \,t}} = \frac{1}{{2\pi }}\sum\limits_{k \ne n} {\frac{{(x_{n}^{m} - x_{k}^{m}){{\Gamma }_{k}}}}{{{{{(x_{n}^{m} - x_{k}^{m})}}^{2}} + {{{(y_{n}^{m} - y_{k}^{m})}}^{2}}}}} + V. \\ \end{gathered} $$

(4.1)

Here $x_{n}^{m}$, $y_{n}^{m}$, and Γ_n are the coordinates $(\sigma _{n}^{m} = x_{n}^{m} + iy_{n}^{m})$ and circulation of the nth vortex at the moment of time $t = m\,\Delta t$ and U, V are the potential velocities.

Let us explore the stability of scheme (4.1) by an example whose exact solution is trivial. This is a discontinuity of constant intensity, coinciding with the x axis at $U = V = 0$. For the case where the discontinuity is represented by discrete vortices, the trivial solution should have the following form:

$$x_{n}^{m} = nh,\quad y_{n}^{m} = 0,\quad {{\Gamma }_{n}} = \gamma h,$$

where the number n takes both positive and negative values, h is the partition step, and γ is the circulation density. Let us check the stability of this scheme for the case of a set of solutions close to the trivial one:

$$x_{n}^{m} = nh + \xi _{n}^{m},\quad y_{n}^{m} = \eta _{n}^{m},\quad {{\Gamma }_{n}} = \gamma h.$$

Assuming the perturbations to be small, let us linearize scheme (4.1)

$$\begin{gathered} \frac{{\xi _{n}^{{m + 1}} - \xi _{n}^{m}}}{\tau } = - \frac{h}{\pi }\sum\limits_{k \ne n} {\frac{{(\eta _{n}^{m} - \eta _{k}^{m})}}{{{{{(\left( {n - k} \right)h + \xi _{n}^{m} - \xi _{k}^{m})}}^{2}} + {{{(\eta _{n}^{m} - \eta _{k}^{m})}}^{2}}}}} \approx - \frac{1}{{\pi h}}\sum\limits_{k \ne n} {\frac{{(\eta _{n}^{m} - \eta _{k}^{m})}}{{{{{\left( {n - k} \right)}}^{2}}}}} , \\ \frac{{\eta _{n}^{{m + 1}} - \eta _{n}^{m}}}{\tau } = \frac{h}{\pi }\sum\limits_{k \ne n} {\frac{{\left( {n - k} \right)h + \xi _{n}^{m} - \xi _{k}^{m}}}{{{{{(\left( {n - k} \right)h + \xi _{n}^{m} - \xi _{k}^{m})}}^{2}} + {{{(\eta _{n}^{m} - \eta _{k}^{m})}}^{2}}}}} \approx - \frac{1}{{\pi h}}\sum\limits_{k \ne n} {\frac{{(\xi _{n}^{m} - \xi _{k}^{m})}}{{{{{\left( {n - k} \right)}}^{2}}}}} , \\ \end{gathered} $$

(4.2)

where $\tau = \gamma \Delta t{\text{/}}2$.

System (4.2) has a solution that depends on parameter $\alpha ,0 \leqslant \alpha \leqslant \pi$

$$\xi _{n}^{m} = {{\lambda }^{m}}\,\cos \,n\alpha ,\quad \eta _{n}^{m} = \pm \xi _{n}^{m},\quad \lambda = 1 \mp \frac{\tau }{h}\left( {\alpha - \frac{{{{\alpha }^{2}}}}{{2\pi }}} \right).$$

It is obvious that some values of  λ are greater than unity, hence, the perturbations should increase, i.e., scheme (4.1) is unstable.

Thus, despite the fact that there exists an exact solution for a rectilinear discontinuity of constant intensity, it is impossible to obtain it numerically with the use of scheme (4.1).

For the correct solution of the vortex-sheet evolution equation, it was proposed in [15] to use a regularization method that makes it possible to smooth short-wavelength perturbations (on the order of h) without reducing the accuracy of the numerical scheme. In order to do this, instead of scheme (4.1), the author of [15] proposed the following calculation scheme:

$$\begin{gathered} \frac{{x_{n}^{{m + 1}} - x_{n}^{m}}}{{\Delta \,t}} = - \frac{1}{{2\pi }}\sum\limits_{k \ne n} {\frac{{(y_{n}^{m} - y_{k}^{m}){{\Gamma }_{k}}}}{{{{{(x_{n}^{m} - x_{k}^{m})}}^{2}} + {{{(y_{n}^{m} - y_{k}^{m})}}^{2}} + {{\theta }^{2}}}}} + \mu \frac{{x_{{n + 1}}^{m} - 2x_{n}^{m} + x_{{n - 1}}^{m}}}{{{{h}^{2}}}} + U, \\ \frac{{y_{n}^{{m + 1}} - y_{n}^{m}}}{{\Delta \,t}} = \frac{1}{{2\pi }}\sum\limits_{k \ne n} {\frac{{(x_{n}^{m} - x_{k}^{m}){{\Gamma }_{k}}}}{{{{{(x_{n}^{m} - x_{k}^{m})}}^{2}} + {{{(y_{n}^{m} - y_{k}^{m})}}^{2}} + {{\theta }^{2}}}}} + \mu \frac{{y_{{n + 1}}^{m} - 2y_{n}^{m} + y_{{n - 1}}^{m}}}{{{{h}^{2}}}} + V. \\ \end{gathered} $$

(4.3)

At $\theta \to 0$ and $\mu \to 0$ the numerical solution of system (4.3) should tend toward solution of the initial problem, only if scheme (4.3) is stable.

After the linearization of (4.3) one has

$$\begin{gathered} \frac{{\xi _{n}^{{m + 1}} - \xi _{n}^{m}}}{\tau } \approx - \frac{1}{\pi }\sum\limits_{k \ne n} {\frac{{(\eta _{n}^{m} - \eta _{k}^{m})h}}{{{{{\left( {n - k} \right)}}^{2}}{{h}^{2}} + {{\theta }^{2}}}}} \, + \mu \frac{{\xi _{{n + 1}}^{m} - 2\xi _{n}^{m} + \xi _{{n - 1}}^{m}}}{{{{h}^{2}}}}, \\ \frac{{\eta _{n}^{{m + 1}} - \eta _{n}^{m}}}{\tau }\,\, \approx - \frac{1}{\pi }\sum\limits_{k \ne n} {\frac{{(\xi _{n}^{m} - \xi _{k}^{m})h}}{{{{{\left( {n - k} \right)}}^{2}}{{h}^{2}} + {{\theta }^{2}}}}} + \mu \frac{{\eta _{{n + 1}}^{m} - 2\eta _{n}^{m} + \eta _{{n - 1}}^{m}}}{{{{h}^{2}}}}. \\ \end{gathered} $$

(4.4)

System (4.4) also has a solution that depends on parameter $\alpha ,\,\,\,0 \leqslant \alpha \leqslant \pi$

$$\begin{gathered} \xi _{n}^{m} = {{\lambda }^{m}}\,\cos \,n\alpha ,\quad \eta _{n}^{m} = \pm \xi _{n}^{m}, \\ \lambda = 1 \mp \frac{\tau }{\theta }\left( {\sinh \frac{{\alpha \theta }}{h} - \coth \,\frac{{\pi \theta }}{h}\left( {\cosh \frac{{\alpha \theta }}{h} - 1} \right)} \right) - 4\frac{{\mu \tau }}{{{{h}^{2}}}}{{\sin }^{2}}\frac{\alpha }{2}. \\ \end{gathered} $$

If one chooses such a θ, that $\theta \to 0$ and ${h \mathord{\left/ {\vphantom {h \theta }} \right. \kern-0em} \theta } \to 0$, it can be always done at $h \to 0$ and $\tau = ch$, where c is some constant, then

$$\mathop {\lim }\limits_{h \to 0} \,\lambda = 1 - 4\frac{{\mu \tau }}{{{{h}^{2}}}}{{\sin }^{2}}\frac{\alpha }{2} = 1 - 4\frac{{\mu c}}{h}{{\sin }^{2}}\frac{\alpha }{2}.$$

In the case of the right choice of μ $\left( {\mu \ll {h \mathord{\left/ {\vphantom {h {2c}}} \right. \kern-0em} {2c}}} \right)$, the value of  |λ| does not exceed unity, which means that scheme (4.3) becomes stable.

Figure 12 shows the results obtained for the vortex flow near the delta wing, calculated using the nonsteady-state analogy method. The quantitative data were taken from [15]. The angle of attack of the delta wing amounts to a half-angle at the apex, the linear sizes were nondimensionalized with respect to the local half-span, and the origin of coordinates are on the line of symmetry. Figures 12a and 12b show the results of calculations with the use of Molchanov’s regularizer at μ = 1/4 and θ = 0. Figure 12a corresponds to the moment of time t = 3.5; Fig. 12b corresponds to the moment of time t = 17. The vortices are drawn using round markers, the central vortex is drawn using a square marker. In the following calculation, the data presented in Fig. 12a are taken as the initial ones, but the calculation was carried out with no regularizer. The result obtained at t = 17.5 is shown in Fig. 12c. The calculation with no regularizer leads to a “blurring” of the vortex sheet.

Fig. 12.

Calculation of a flow around a delta wing at an angle of attack amounting to the half-angle at the wing apex with the use of the nonsteady-state analogy. (a) $t = 3.5$, (b) $17$, and (c) $17.5$; (a, b) calculation with the use of a regularizer [15] and (c) without a regularizer.

Model of the Vortex-Sheet Core. The replacement of the vortex sheet by discrete vortices with a certain discretization in space is correct beyond the vortex-sheet core. The core represents a spiral with an infinite number of turns and, if the step in space is regulated, i.e., no rediscretization of points on the vortex sheet is performed, then the distance between the vortices can become comparable to the distance between adjacent turns of the spiral, which is unacceptable for a correct numerical calculation scheme. Therefore, the vortex sheet core should be simulated differently than it is done for the rest of the sheet.

Let us limit ourselves to an algebraic vortex sheet most often used in aerodynamic problems. Despite the fact that one deals with a spiral with an infinite number of turns, the circulation of the vortex-sheet core is finite. Therefore, due to the fact that the geometry of the turns of the algebraic spiral is close to circular, the entire core can be replaced by one discrete vortex (Fig. 13a). However, over time, the size of the core should increase, since more and more vortices should fall into it (Fig. 13b), and we again arrive at the need to solve the problem mentioned above.

Fig. 13.

Replacing the vortex system in the vicinity of the center (core) of the spiral with a discrete vortex: (a) at the moment of time $t = {{t}_{1}}$, (b) at the moment of time $t = {{t}_{2}}$, where ${{t}_{2}} > {{t}_{1}}$.

A core model free of this shortcoming was proposed in [13]. It is assumed therein that the circulation of the vortex-sheet core can be time dependent ${{\Gamma }_{c}} = {{\Gamma }_{c}}{\kern 1pt} \left( t \right)$. This dependence is determined by the fact that at some moments of time the vortices approximating the vortex sheet, which are closest to the core, can be cast onto it (Fig. 14). Herewith the vortices cast from the sheet disappear from the flow, and the circulation of the core is increased by the circulation of these vortices. Such a model is called a vortex–cut system. The feeding cut connects the central vortex with the last vortex in the vortex sheet.

Fig. 14.

Vortex–cut model.

Let us find the velocity with which the central vortex moves. Let its coordinate be ${{\sigma }_{c}}\left( t \right)$, the coordinate of the last vortex on the sheet be ${{\sigma }_{e}}\left( t \right)$, its circulation be Γ_e, and the velocity of the flow at the central-vortex location point be ${{{v}}_{c}}\left( t \right)$. If at some moment of time there is no change in the circulation of the central vortex, i.e., ${{d{{\Gamma }_{c}}} \mathord{\left/ {\vphantom {{d{{\Gamma }_{c}}} {dt}}} \right. \kern-0em} {dt}} = 0$, then

$$\frac{{d{{\sigma }_{c}}}}{{dt}} = {{{v}}_{c}}.$$

If, however, vortex Γ_e is cast onto the central vortex, then the center of gravity of such a system as the central vortex plus vortex Γ_e is located at point can be expressed as

$${{\sigma }_{*}} = \frac{{{{\Gamma }_{c}}{{\sigma }_{c}} + {{\Gamma }_{e}}{{\sigma }_{e}}}}{{{{\Gamma }_{c}} + {{\Gamma }_{e}}}}.$$

The total displacement of the central vortex over time $\Delta t$, during which the vortex Γ_e is cast onto the central vortex amounts to its displacement with velocity ${{{v}}_{c}}$ and the displacement of its center of gravity by a value of ${{\sigma }_{*}} - {{\sigma }_{c}}$. Thus,

$$\Delta {{\sigma }_{c}} = {{{v}}_{c}}\Delta t + \left( {{{\sigma }_{*}} - {{\sigma }_{c}}} \right) = {{{v}}_{c}}\Delta t + \frac{{{{\Gamma }_{e}}\left( {{{\sigma }_{e}} - {{\sigma }_{c}}} \right)}}{{{{\Gamma }_{c}} + {{\Gamma }_{e}}}}.$$

Let the time step tend to zero. Then one can replace the step $\Delta t$ by a differential dt. Let us introduce the following designation:

$$\frac{{d{{\Gamma }_{c}}}}{{dt}} = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{{{\Gamma }_{e}}}}{{\Delta t}}.$$

Taking into account that ${{\Gamma }_{e}} \ll {{\Gamma }_{c}}$, finally one has

$$\frac{{d{{\sigma }_{c}}}}{{dt}} = {{{v}}_{c}} + \left( {{{\sigma }_{e}} - {{\sigma }_{c}}} \right)\frac{1}{{{{\Gamma }_{c}}}}\frac{{d{{\Gamma }_{c}}}}{{dt}}.$$

(4.5)

Based on other prerequisites, namely, on the condition of the absence of a force affecting the vortex–cut system, relationship (4.5) was obtained in [16].

Delta Wing with Blunted Edges. The authors of [17] studied a separated flow near a small-aspect-ratio delta wing with blunted leading edges. The cross section of the wing represented an ellipse with a small relative thickness (Fig. 15). The surface of the wing is smooth and vortex sheets can vanish from some lines of the surface. Since setting the position of the separation lines is possible in a rather wide range, then the solution to this problem is also not unique. Such nonuniqueness is usually inherent in the case when the separated flow around smooth bodies is studied in the scope of the Euler equations. The choice of a unique solution from the whole variety of solutions is possible only based on the equations of viscous fluid motion. Herewith the position of the separation lines should be dependent on the Reynolds number. Thus, different separation lines on the wing surface, and, correspondingly, different geometry and intensity of vortex sheets vanishing from these lines should correspond to different Reynolds-number values.

Fig. 15.

Separated flow around a delta wing having a small relative thickness.

For a delta wing with zero thickness, separation occurs from sharp edges, therefore, for a delta wing with a small relative thickness, the separation lines should lie in the vicinity of the wing edges. Since the wing geometry is conical, then it can be assumed that the geometry of the vortex sheets should be conical, too, and, hence, the separation line should represent a segment of a straight line going out of the wing apex, i.e., forming a cone. Let us also assume that the separated flow around the wing is symmetrical. In this case, one can construct a one-parameter family of solutions differing from each other in the position of the separation line.

From the standpoint of the nonsteady-state analogy, the three-dimensional steady-state problem is equivalent to a two-dimensional nonsteady-state problem of flowing around an expanding ellipse. The next two figures, Figs. 16 and 17 are based on data taken from [17]. Figure 16 shows the geometry of the vortex sheets at two different separation angles. It can be seen that a slight displacement of the separation point leads to a significant change in the vortex structure of the wing. The cases shown in Fig. 16 correspond to a flow moving over the wing at a relative angle of attack of $\bar {\alpha } = {\alpha \mathord{\left/ {\vphantom {\alpha {\chi = 1.5}}} \right. \kern-0em} {\chi = 1.5}}$, where χ is the half-angle at the wing apex. The ratio between the sizes of the minor b and the major a axes of the ellipse is $\varepsilon = {b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a} = 1{\text{/10}}$. The linear dimensions are nondimensionalized with respect to the local half-span.

Fig. 16.

Vortex-sheet geometry at two different separation angles.

Fig. 17.

Coefficient of normal force affecting a delta-shaped wing, depending on ε and z₁.

Let us denote by z₁ the distance from the wing edge (the end of the semimajor axis of the ellipse) to the point of separation in the section corresponding to x = const, nondimensionalized with respect to the local half-span. Let us consider this quantity positive when moving along the windward side, and negative when moving along the downwind side. The flow separation from the windward side can occur not from any position. In local variables n and τ in the vicinity of the separation point, the geometry of the vortex sheet in the leading approximation has the form of $n = \alpha \left( {{{z}_{1}}} \right){{\tau }^{{3/2}}}$ [6], whereas the radius of curvature of the vortex sheet is zero.

With increasing z₁ along the windward side, α exhibits a decrease, and finally, at some point $z_{1}^{*}$, quantity α vanishes. At this point, the radius of curvature of the vortex sheet amounts to the radius of curvature of the solid boundary, from which the separation occurs. This is the limiting separation point. In this case, the separated flow satisfies the Brillouin–Villat condition. At ${{z}_{1}} > z_{1}^{*}$ no flow separation is possible.

Figure 17 shows a ratio of the coefficient of normal force c_N affecting a delta wing to zero-thickness delta wing coefficient ${{c}_{{N0}}}$ at $\bar {\alpha } = 1.5$ for different ε. The curves reach points where the separated flow satisfies the Brillouin–Villat condition. It can be seen that at a decrease, the maximum value of the normal force approaches ${{c}_{{N0}}}$.

Circular Cone. The flow pattern around a circular cone depends on the angle of attack α, on the half-angle of the cone opening χ, on the Reynolds number, and on the laminar or turbulent state of the boundary layer. Just as it is in the case of fluid flowing around a delta wing, secondary separated formations flowing from the surface of the cone are quite possible. At the same time, even the lines of the main vortex structures cannot be fixed on the surface of the cone (in contrast to the delta wing). In terms of force action, the main separated formations play the main role; therefore, in the calculation of a separated flow around a circular cone in the framework of the ideal-fluid model, secondary vortex structures are usually neglected, whereas the position of the separation line of the main vortices is set based on a certain reasonable range of positions.

The calculation of a separated flow around a cone using the nonsteady-state analogy was performed in [18]. Below the results of calculations taken from this work are presented. This example is remarkable in the fact that in this case there is no need to use conformal mappings, since the three-dimensional steady-state problem of separated flow around a circular cone is equivalent to the two-dimensional nonsteady-state problem of flowing around an expanding circle. The velocity field near the circle can be represented as the superposition of an oncoming flow, a source and a dipole corresponding to an unseparated circulation-free flow around an expanding circle, two vortex sheets vanishing from given separation points, as well as two vortex sheets conjugated with them with respect to the circle. Just as in the previous paragraph, separation is possible only starting from a certain angle at which a separated formation satisfies the Brillouin–Villat condition, and at the same time this angle depends on the relative angle of attack $\bar {\alpha } = {\alpha \mathord{\left/ {\vphantom {\alpha \chi }} \right. \kern-0em} \chi }$.

Let us consider a symmetric incompressible inviscid-fluid flow with the velocity ${{u}_{\infty }}$ around a circular cone with the apex half-angle $\chi \ll 1$ at an angle of attack amounting to $\alpha \sim \chi$. Thus, the conditions for the applicability of the theory of elongated bodies are satisfied. As has been already shown above, according to this theory, the three-dimensional steady-state problem of separated flow around an elongated body can be reduced to a two-dimensional nonsteady-state problem concerning a separated flow around a flat contour expanding according to some law, having the shape of the body cross section via replacing the longitudinal coordinate x by time according to the relationship $t = {x \mathord{\left/ {\vphantom {x {{{u}_{\infty }}}}} \right. \kern-0em} {{{u}_{\infty }}}}$. In the case of a circular cone, this is the problem of a separated flow around a circle expanding with constant velocity.

Let us limit ourselves to a simplified mathematical model of separated flow around a cone with two symmetrical vortex sheets vanishing from the lines of a single primary separation. Thus, secondary separated formations are ignored. Let us assume that in the case of a separated flow around a circular cone the disturbed flow is conical, i.e., the separation line is assumed to be straight. Such a simplification is possible due to the fact that the location of the primary separation line slightly depends on the Reynolds number and the separation angle can be considered, in the first approximation, to be a constant that depends on the Reynolds number as a parameter.

In the case of the external inviscid plane problem, the radius of a streamlined circle varies according to the law of $r = {{u}_{\infty }}\chi \,t$. For the case of the plane problem, the oncoming-flow velocity amounts to a transverse velocity component at infinity ${{\hat {u}}_{\infty }} = \alpha \,{{u}_{\infty }}$. The problem of a separated inviscid flow around a circular cone is self-similar. Let us introduce self-similar variables: linear variables ${{\ell }_{*}} = {\ell \mathord{\left/ {\vphantom {\ell {{{u}_{\infty }}\,\chi \,t}}} \right. \kern-0em} {{{u}_{\infty }}\,\chi \,t}}$ and velocity variables ${{{\mathbf{u}}}_{*}} = {{\mathbf{u}} \mathord{\left/ {\vphantom {{\mathbf{u}} {{{u}_{\infty }}\chi }}} \right. \kern-0em} {{{u}_{\infty }}\chi }}$. In the self-similar variables, the circle has the radius ${{r}_{*}} = 1$, whereas the velocity of the transverse oncoming flow is determined by the relationship ${{\hat {u}}_{{*\infty }}} = {\alpha \mathord{\left/ {\vphantom {\alpha \chi }} \right. \kern-0em} \chi }$. Hence, in a symmetric system, in the external inviscid plane problem there is only one defining parameter represented by the relative angle of attack $\bar {\alpha } = {\alpha \mathord{\left/ {\vphantom {\alpha \chi }} \right. \kern-0em} \chi }$.

The structure of flow around a slender cone depends on this quantity [19]. At small $\bar {\alpha } \leqslant 0.6$ the flow around the cone is unseparated. For each value of the relative angle of attack $\bar {\alpha } > 1.1$, a one-parameter family of inviscid solutions exists depending on the angular separation-line coordinate η₀ measured from the lower (windward) generatrix of the cone. The value of η₀ can vary in the range from the angular coordinate of the separation line, on which the Brillouin–Villat condition $\eta _{0}^{*}(\bar {\alpha })$ is satisfied, to the angular coordinate of the upper generatrix of the cone $\eta _{0}^{*}(\bar {\alpha }) \leqslant {{\eta }_{0}} \leqslant \pi$.

Figure 18 shows the typical calculation result: the configuration of vortex sheets at $\bar {\alpha } = 3$ and η₀ = 100°.

5 CALCULATION OF SEPARATED FLOW TAKING INTO ACCOUNT STRONG VISCOUS-INVISCID INTERACTION

According to the method described in the previous section, one can obtain a one-parameter family of inviscid solutions for a symmetric separated flow around a thin circular cone. In this section, the problem of extracting a unique solution from this family for a given Reynolds number is solved, i.e., the problem of obtaining a calculated position of the separation lines on the cone depending on the Reynolds number Re [20].

Boundary-Layer Equations. In order to determine the characteristics of the boundary layer, let us choose a coordinate system on the surface of the cone in the following manner where: ξ is the distance along the generatrix of the cone, ζ is the distance along the normal to the surface, η is the angle measured from the lower generatrix of the cone, and $r\,(\xi )$ is the current radius of the cone. The velocity components in coordinate system $(\xi ,\zeta ,\eta )$ are denoted by $(u,{v},w)$. The boundary-layer equations can be written as follows:

$$\begin{gathered} u\frac{{\partial \,u}}{{\partial \,\xi }} + {v}\frac{{\partial \,u}}{{\partial \,\zeta }} + \frac{w}{r}\frac{{\partial \,u}}{{\partial \,\eta }} - \frac{{{{w}^{2}}}}{r}\sin \chi = \nu \frac{{{{\partial }^{2}}u}}{{\partial \,{{\zeta }^{2}}}}, \\ \frac{{\partial \,p}}{{\partial \,\zeta }} = 0, \\ u\frac{{\partial \,w}}{{\partial \,\xi }} + {v}\frac{{\partial \,w}}{{\partial \,\zeta }} + \frac{w}{r}\frac{{\partial \,w}}{{\partial \,\eta }} + \frac{{uw}}{r}\sin \chi = - \frac{1}{{\rho \,r}}\frac{{\partial \,p}}{{\partial \,\eta }} + \nu \frac{{{{\partial }^{2}}w}}{{\partial \,{{\zeta }^{2}}}}, \\ \frac{{\partial \,(ur)}}{{\partial \,\xi }} + r\frac{{\partial {v}}}{{\partial \,\zeta }} + \frac{{\partial \,w}}{{\partial \,\eta }} = 0. \\ \end{gathered} $$

(5.1)

The boundary conditions here represent no-slip conditions and the condition of switching to solving an external inviscid problem

$$u = {v} = w = 0\quad {\text{at}}\quad \zeta = 0,$$

(5.2)

$$u \to {{u}_{e}}(\eta ),\quad w \to {{w}_{e}}(\eta )\quad {\text{at}}\quad \zeta \to \infty .$$

(5.3)

The solution of Eq. (5.1) is sought in the following form [21]:

$$\begin{gathered} u = {{u}_{e}}(\eta )\,E(\eta ,\lambda ), \\ w = {{w}_{e}}(\eta )\,G(\eta ,\lambda ), \\ {v} = {{\left( {\frac{{{{u}_{e}}\nu }}{\xi }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left( {V(\eta ,\lambda ) + \frac{1}{2}\lambda E - \frac{{u_{e}^{'}{{w}_{e}}}}{{2u_{e}^{2}\sin \chi }}\lambda G} \right), \\ \end{gathered} $$

where $\lambda = {{\left( {{{{{u}_{e}}} \mathord{\left/ {\vphantom {{{{u}_{e}}} {\xi \,\nu }}} \right. \kern-0em} {\xi \,\nu }}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\zeta$.

Quantities E, G, and V can be determined based on (5.1)

$$\begin{gathered} \frac{{{{\partial }^{2}}E}}{{\partial \,{{\lambda }^{2}}}} = V\frac{{\partial \,E}}{{\partial \,\lambda }} + {{A}^{2}}{{\sin }^{2}}\chi (EG - {{G}^{2}}) + A\,G\frac{{\partial \,E}}{{\partial \,\eta }}, \\ \frac{{{{\partial }^{2}}G}}{{\partial \,{{\lambda }^{2}}}} = V\frac{{\partial \,G}}{{\partial \,\lambda }} + B({{G}^{2}} - 1) + E\,G - 1 + A\,G\frac{{\partial \,G}}{{\partial \,\eta }}, \\ \frac{{\partial \,V}}{{\partial \,\lambda }} = - \frac{3}{2}E - G\,\left( {B - \frac{{{{A}^{2}}{{{\sin }}^{2}}\chi }}{2}} \right) - A\,\frac{{\partial \,G}}{{\partial \,\eta }}, \\ \end{gathered} $$

(5.4)

where $A(\eta ) = {{{{w}_{e}}} \mathord{\left/ {\vphantom {{{{w}_{e}}} {\left( {{{u}_{e}}\sin \,\chi } \right)}}} \right. \kern-0em} {\left( {{{u}_{e}}\sin \,\chi } \right)}}\sim O(1)$ and $B(\eta ) = {{w_{e}^{'}} \mathord{\left/ {\vphantom {{w_{e}^{'}} {\left( {{{u}_{e}}\sin \chi } \right)}}} \right. \kern-0em} {\left( {{{u}_{e}}\sin \chi } \right)}}\sim O(1)$.

In the new variables, boundary conditions (5.2) and (5.3) are transformed, too:

$$E = V = G = 0\quad {\text{at}}\quad \lambda = 0,$$

(5.5)

$$E \to 1,\quad G \to 1\quad {\text{at}}\quad \lambda \to \infty .$$

(5.6)

Since one considers a cone with a small angle θ, i.e., the study is carried out under the assumption of the theory of elongated bodies, quantities $E,\;V,\;G,\;A$, and B can be represented in the form of asymptotic expansion in χ: $E = {{E}_{1}} + {{\chi }^{2}}{{E}_{2}} + ...$, etc. In the first approximation, Eq. (5.4) can be written in the following form

$$\begin{gathered} \frac{{{{\partial }^{2}}E}}{{\partial \,{{\lambda }^{2}}}} = V\frac{{\partial \,E}}{{\partial \,\lambda }} + A\,G\frac{{\partial \,E}}{{\partial \,\eta }}, \\ \frac{{{{\partial }^{2}}G}}{{\partial \,{{\lambda }^{2}}}} = V\frac{{\partial \,G}}{{\partial \,\lambda }} + B({{G}^{2}} - 1) + E\,G - 1 + A\,G\frac{{\partial \,G}}{{\partial \,\eta }}, \\ \frac{{\partial \,V}}{{\partial \,\lambda }} = - \frac{3}{2}E - B\,G\, - A\,\frac{{\partial \,G}}{{\partial \,\eta }}. \\ \end{gathered} $$

(5.7)

To simplify the expression, subscript 1 has been omitted. $A(\eta ) = {{{{w}_{e}}} \mathord{\left/ {\vphantom {{{{w}_{e}}} {({{u}_{\infty }}{\text{sin}}\chi )}}} \right. \kern-0em} {({{u}_{\infty }}{\text{sin}}\chi )}}$ and $B(\eta ) = {{w_{e}^{'}} \mathord{\left/ {\vphantom {{w_{e}^{'}} {\left( {{{u}_{\infty }}\sin \,\chi } \right)}}} \right. \kern-0em} {\left( {{{u}_{\infty }}\sin \,\chi } \right)}}$. In the symmetry plane, the parameter A vanishes. This makes it possible to obtain the following boundary condition at η = 0:

$$\begin{gathered} \frac{{{{\partial }^{2}}E}}{{\partial \,{{\lambda }^{2}}}} = V\frac{{\partial \,E}}{{\partial \,\lambda }}, \\ \frac{{{{\partial }^{2}}G}}{{\partial \,{{\lambda }^{2}}}} = V\frac{{\partial \,G}}{{\partial \,\lambda }} + B({{G}^{2}} - 1) + E\,G - 1, \\ \frac{{\partial \,V}}{{\partial \,\lambda }} = - \frac{3}{2}E - B\,G. \\ \end{gathered} $$

(5.8)

In the case of a fixed line of vortex-sheet vanishing, the calculation of the boundary-layer equations leads to an earlier location of the boundary-layer separation. A numerical experiment was carried out. At a given angle of vortex-sheet vanishing η₀, without taking into account the viscous-inviscid interaction, the point of boundary-layer separation ${{\tilde {\eta }}_{1}}$ was calculated. The dependence of these quantities is shown in Fig. 19. The calculation was performed at $\bar {\alpha } = 3$. The angle was $\eta _{0}^{*} = 76^\circ$. The dashed line in Fig. 19 corresponds to line ${{\tilde {\eta }}_{1}} = {{\eta }_{0}}$. As expected, the angular difference ${{\eta }_{0}} - {{\tilde {\eta }}_{1}}$ (solid line) decreases as the vanishing angle tends to the angle at which the Brillouin–Villat condition is satisfied. If the vortex sheet vanishes at large angles, then the angular difference ${{\eta }_{0}} - {{\tilde {\eta }}_{1}}$ is significant. This difference should decrease due to the strong viscous-inviscid interaction.

Fig. 18.

Separated flow around a cone at $\bar {\alpha } = 3$ and η₀ = 100°.

Fig. 19.

Boundary-layer separation angle depending on the angle of vortex-sheet vanishing. Calculation performed without taking into account the viscous-inviscid interaction.

Strong Viscous-Inviscid Interaction in Flows with Global Separation. Let us determine the Reynolds number $\operatorname{Re} = {{{{u}_{\infty }}\xi } \mathord{\left/ {\vphantom {{{{u}_{\infty }}\xi } \nu }} \right. \kern-0em} \nu }$. At a given angle of vortex-sheet vanishing, one can splice the solution of the external problem with the solution of the internal one only at a specific value of the Reynolds number Re₀. At greater Reynolds numbers, the boundary layer should be thinner than it is at Re₀ and it is not able to correct a large pressure gradient in the external inviscid flow. At smaller Reynolds numbers, the boundary layer should be, on the contrary, thicker than it is at Re₀, and such a boundary layer is able to overcome a pressure gradient greater than the set one.

The viscous-inviscid interaction is taken into account via setting appropriate boundary conditions at $\lambda \to \infty$. Let us represent ${{w}_{e}}(\eta )$ in the following form

$${{w}_{e}}(\eta ) = {{w}_{{e0}}}(\eta ) + {{w}_{{e\delta }}}(\eta ).$$

(5.9)

Dependence ${{w}_{{e0}}}(\eta )$ is a result obtained in solving the problem of an inviscid separated flow around an expanding circle, whereas ${{w}_{{e\delta }}}(\eta )$ is the correction for taking into account the displacing effect of the boundary layer exerted on the external flow. It should be noted that the coordinate of inviscid separation at a set Reynolds number Re is not a priori known, and therefore, in contrast to the case of taking into account the strong viscous-inviscid interaction for local separation, quantity ${{w}_{{e0}}}(\eta )$ should change in the course of solving the problem.

The displacement effect of the boundary layer from angle $\eta = 0$ to the coordinate of boundary-layer separation, taking into account strong viscous-inviscid interaction, $\eta = {{\eta }_{1}}$, can be simulated by sources distributed over the surface of the cone cross section. Owing to viscosity affecting at $\lambda \to \infty$, the velocity normal to the cone changes by a quantity of ${{{v}}_{{e\delta }}}(\eta )$. The source density is $q = 2{{{v}}_{{e\delta }}}$, or in the above-mentioned notation and in self-similar variables is

$${{q}_{*}} = 2\frac{{V(\eta ,\lambda ) + \lambda \left( {\frac{3}{2} + B} \right)}}{{\chi \,{\text{R}}{{{\text{e}}}^{{1/2}}}}}\quad {\text{at}}\quad \lambda \to \infty .$$

(5.10)

Let us consider now a domain that represents a small vicinity of the separation point. Let us superpose the origin of the local coordinate system $(\tau ,n)$ with the vortex-sheet vanishing point $\eta = {{\eta }_{0}}$, which, generally speaking, does not coincide with point ${{\eta }_{1}}$. The vortex-sheet equation in this domain according to [6] is

$$n = c({{\eta }_{0}})\,{{\tau }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} + O({{\tau }^{2}}).$$

With an increase in the vanishing angle of the vortex sheet, coefficient c in the latter relationship exhibits an increase, and, naturally, the pressure gradient in the vicinity of the vanishing point increases, too.

The velocity $\Delta w$ induced by a part of the vortex sheet corresponding to $0 \leqslant \tau \leqslant \Delta \tau$ at point τ₀ is determined with the use of a mapping method. Since the curvature of a streamlined circle is much less than the curvature of the tangential discontinuity surface, then it is in the first approximation:

$$\Delta w = \frac{1}{{2\pi i}}\int\limits_0^{\Delta \tau } {\frac{{\gamma \,d\,\tau }}{{\tau + i\,c\,{{\tau }^{{3/2}}} - {{\tau }_{0}}}}} - \frac{1}{{2\pi i}}\int\limits_0^{\Delta \tau } {\frac{{\gamma \,d\,\tau }}{{\tau - i\,c\,{{\tau }^{{3/2}}} - {{\tau }_{0}}}}} .$$

The vortex-sheet intensity γ amounts to the flow velocity ${{w}_{e}}({{\eta }_{0}})$ at point ${{\eta }_{0}}$. By expanding into a series at small τ one can obtain:

$$\Delta w = \frac{{\gamma \,c}}{\pi }\left( {\frac{{\Delta {{\tau }^{{3/2}}}}}{{\Delta \tau - {{\tau }_{0}}}} - \frac{3}{2}\int\limits_0^{\Delta \tau } {\frac{{\,{{\tau }^{{1/2}}}\,d\,\tau }}{{\tau - {{\tau }_{0}}}}} } \right).$$

From the latter relationship, it follows that the vortex sheet has a displacing effect with respect to the body surface, and in the leading approximation, the inductive effect of a part of the sheet corresponding to $0 \leqslant \tau \leqslant \Delta \tau$ can be expressed through sources with a density of

$$q = \frac{3}{2}\frac{{\gamma \,c}}{\pi }{{\tau }^{{1/2}}}$$

distributed over the surface from τ = 0 to $\tau = \Delta \tau$ and through an intensity sink of

$$Q = \frac{{\gamma \,c}}{\pi }\Delta {{\tau }^{{3/2}}},$$

located at point $\tau = \Delta \tau$. In self-similar variables

$${{q}_{*}} = \frac{3}{2}\frac{{\gamma \,c}}{{\pi {{u}_{\infty }}\chi }}{{\tau }^{{1/2}}},\quad {{Q}_{*}} = \frac{{\gamma \,c}}{{\pi {{u}_{\infty }}\chi }}\Delta {{\tau }^{{3/2}}}.$$

(5.11)

As is known, at distances much larger than the size of the interaction domain, the geometry of the vortex sheet and its contribution to the inductive velocities obey inviscid equations. In the vicinity of the separation point, on the contrary, viscosity plays a primary role. Therefore, it makes sense to divide the vortex surface behind the boundary-layer separation point into the following three parts:

1. For a domain extending from the boundary-layer separation point η₁ to a certain point $\eta = {{\eta }_{2}}$ chosen a priori and sufficiently distant from the separation point, it is assumed that the flow characteristics can be determined by viscous equations. In the domain, where $G(\lambda ) \geqslant 0$, the calculation is made based on Eqs. (5.7) with the use of boundary conditions (5.5), (5.6), (5.8), and (5.9). In the domain of reverse flows $G(\lambda ) < 0$ to solve the boundary-layer equations, it is necessary to set the boundary conditions at $\eta = {{\eta }_{2}}$. Determining these conditions represents a difficult problem. However, it is known that in the domain of reverse flows, the transverse velocities are small, $\left| G \right| \ll 1$. Limiting oneself in Eqs. (5.7) only to terms of the same order of smallness in G, one can obtain equations that do not require setting any boundary conditions at $\eta = {{\eta }_{2}}$ for their solution

$$\begin{gathered} \frac{{{{\partial }^{2}}E}}{{\partial \,{{\lambda }^{2}}}} = V\frac{{\partial \,E}}{{\partial \,\lambda }}, \\ \frac{{{{\partial }^{2}}G}}{{\partial \,{{\lambda }^{2}}}} = V\frac{{\partial \,G}}{{\partial \,\lambda }} - B\, + E\,G - 1, \\ \frac{{\partial \,V}}{{\partial \,\lambda }} = - \frac{3}{2}E. \\ \end{gathered} $$

For the boundary between domains $G \geqslant 0$ and G < 0 determined in the course of solving, it is assumed that the quantities E and V do not suffer discontinuity. In domain ${{\eta }_{1}} \leqslant \eta \leqslant {{\eta }_{2}}$ there are sources with a density, whose value is determined according to relationship (5.10).

2. For the case of the domain extending from point $\eta = {{\eta }_{2}}$ to point $\eta = {{\eta }_{3}}$, it is assumed that the flow characteristics can be determined by inviscid equations. Here, the sources are located, too, but their density is determined according to relationships (5.11). The role of this zone consists in the fact that the effect of sources on the boundary conditions in domain $\eta \leqslant {{\eta }_{2}}$ can be expressed through the principal value of the Cauchy-type integral. For correct calculation of the latter, it is necessary to set singularities equidistant both before the point wherein the inductive velocity is calculated, and after this point.

3. for the case of the domain extending from point $\eta = {{\eta }_{3}}$ and further, it is assumed that the flow characteristics and the shape of the zero streamline can be determined based on inviscid equations. The surface of the vortex sheet is divided into discrete vortices, based on which inductive velocities on the surface of the streamlined circle can be calculated.

At the center of the circle, there is a point sink with an intensity amounting to half the sum of the intensities of the sources distributed over the surface of the circle. This sink is necessary in order to satisfy the condition of equality between the source density and a twofold velocity normal to the surface, which occurs due to an increase in the thickness of the displaced boundary layer on the surface of the cone.

Thus, quantity ${{w}_{{e\delta }}}(\eta )$ represents the field of velocities that originate from sources located on a streamlined circle in domains $0 \leqslant \eta \leqslant {{\eta }_{1}}$ and ${{\eta }_{1}} \leqslant \eta \leqslant {{\eta }_{2}}$. The intensity of these sources can be determined according to relationship (5.10). Quantity ${{w}_{{e0}}}(\eta )$ represents a superposition of the velocity of unseparated flow around an expanding circle, the velocity originating from the sources located on the circle in domain ${{\eta }_{2}} < \eta \leqslant {{\eta }_{3}}$, whose intensity is determined according to relationships (5.11), and the velocity originating from a part of the vortex sheet located in domain $\eta > {{\eta }_{3}}$.

When the Prandtl equations are solved in domain $0 \leqslant \eta \leqslant {{\eta }_{2}}$, the unknown variables are represented by the source density q(η) and the boundary condition ${{w}_{e}}(\eta )$. Only the interrelations between quantities q(η) and ${{w}_{e}}(\eta )$ are known, the procedure for whose identification is described above. Joint solution of the Euler and Prandtl equations is performed by means of the iteration method. According to a set value of the Reynolds number Re, dependence $q(\eta )$ and the vortex-sheet vanishing point η₀ exhibit a change in the course of each iteration. The problem is considered solved if the source distribution calculated up to point η₂ according to relationship (5.10) can be smoothly spliced with the source distribution calculated according to relationship (5.11) up to this point, i.e., the source distribution given by the Prandtl equations smoothly converges to the inviscid-source distribution. Such numerical splicing is shown in Fig. 20. The case of $\bar {\alpha } = 3$ and ${{\chi }^{2}}{\text{Re}} = 1.2 \times {{10}^{4}}$ was calculated. Figure 21 shows the dependence of the angle of the boundary-layer separation on ${{\chi }^{2}}\operatorname{Re}$ at $\bar {\alpha } = 3$.

Fig. 20.

Distribution of sources along the surface of a cone. Curve 1 corresponds to an inviscid distribution of the sources; curve 2 corresponds to a viscous distribution of the sources.

Fig. 21.

Boundary-layer separation angle depending on ${{\chi }^{2}}\operatorname{Re}$ at $\bar {\alpha } = 3$. The solid line coresponds to the calculation taking into account the viscous-inviscid interaction, the dashed line corresponds the calculation according to asymptotic theory, the dotted line corresponds to $\eta _{0}^{*}(3)$, and the markers indicate experimental data taken from [22].

For comparison, the results of experimental studies and calculations based on asymptotic theory, taken from [22], are presented. The mathematical model of the separated flow around two symmetrical vortices in the calculations according to asymptotic theory correspond to the mathematical model in the calculations taking into account strong viscous-inviscid interaction. The existing discrepancies in the calculations taking into account strong viscous-inviscid interaction can be explained by the inadequacy of the chosen mathematical model with respect to a physical flow pattern, namely, with respect to calculations without taking into account secondary separated formations. Figure 22 shows the angle of the boundary-layer separation depending on the relative angle of attack $\bar {\alpha }$ for two values of ${{\chi }^{2}}\operatorname{Re}$: 10⁴ and 10⁵.

Fig. 22.

Boundary-layer separation angle depending on the relative angle of attack $\bar {\alpha }$ for two values of ${{\chi }^{2}}\operatorname{Re}$: 10⁴ and 10⁵.

6 NONUNIQUENESS AND ASYMMETRY OF SOLUTIONS TO THE PROBLEM OF A SEPARATED FLOW AROUND EXTENDED BODIES

Nonuniqueness. In the framework of the ideal-fluid model, the solution to the problem concerning separated flows around elongated bodies, even at fixed separation lines, could be nonunique. An example of such nonuniqueness can be found in [23, 24], where, using the nonsteady-state analogy, a flow around an elongated conical body consisting of a tapered fuselage with an axis coinciding with the x axis, and a delta-shaped wing lying in plane y = 0 and having a half-angle χ at the apex was considered. Such a system is in a flow with velocity ${{u}_{\infty }}$ oncoming at an angle of attack α at infinity. It is assumed that flow separation occurs only from the sharp wing edges (Fig. 23). As before, let us denote the relative angle of attack by $\bar {\alpha } = {\alpha \mathord{\left/ {\vphantom {\alpha \chi }} \right. \kern-0em} \chi }$ and the ratio of the fuselage diameter to the wing span for any cross section $x = \text{const}$ is denoted by m $\left( {m < 1} \right)$.

Fig. 23.

Separated flow around a conical body.

In order to solve the problem, a velocity potential is introduced that satisfies the Laplace equation both beyond the body surfaces and beyond the vortex sheet. The boundary conditions are standard consisting in impermeability through the body and the sheet surfaces and the absence of a pressure jump on different sides of the vortex sheet. The separation from sharp edges provides the Chaplygin–Zhukovskii condition on the edges. From the standpoint of the nonsteady-state analogy corresponding to $t = {x \mathord{\left/ {\vphantom {x {{{u}_{\infty }}}}} \right. \kern-0em} {{{u}_{\infty }}}}$, the problem can be reduced to studying the separated flow around a uniformly expanding body corresponding to the cross section of the wing–fuselage combination. The solution of such a problem is self-similar in time. An important factor consists in the fact that a symmetrical solution is sought, i.e., it is assumed that the circulation and geometry of the right and left vortex sheets are the same. As is seen from the next subsection, this is very important, since at high relative angles of attack, the separated flow could become asymmetric.

Let us introduce new dimensionless variables ${{y}_{*}} = {{y\cot \chi } \mathord{\left/ {\vphantom {{y\cot \chi } x}} \right. \kern-0em} x}$, ${{z}_{*}} = {{z\cot \chi } \mathord{\left/ {\vphantom {{z\cot \chi } x}} \right. \kern-0em} x}$. In these variables, the cross section of the wing has a span amounting to 2 and the fuselage diameter is 2m. In the space of parameters $\bar {\alpha }$ and m there are domains wherein the solution to the problem is not unique. The next two figures, Figc. 24 and 25 show the curves plotted according to data presented in [24]. Figure 24 shows two solutions: weak solution I and strong solution II. The calculation is carried out for the case of  $\bar {\alpha } = 4$, m = 0.9. The circulation of vortex formations Γ, i.e., the circulation around the contour located in plane x = const and completely enclosing one vanishing vortex sheet, is different in the case of a weak and a strong sheet. In the case of a strong vortex sheet, the circulation is much greater. Figure 25 shows a change in the dimensionless circulation

$$G = \frac{\Gamma }{{{{u}_{\infty }}x{\text{ta}}{{{\text{n}}}^{2}}\chi }}$$

with changing relative angle of attack for the solutions with weak and strong vortex sheets at different m. Figure 25 also shows the existence range for two solutions at m = 0.9.

Fig. 24.

Separated flow around the tapered fuselage–wing combination at $\bar {\alpha } = 4$ and m = 0.9. Separated formation geometry: (I) weak separated formation and (II) strong separated formation.

Fig. 25.

Dimensionless circulation depending on the relative angle of attack at different m. The dotted line marks the dependence at $m = 0.9$.

The question of choosing a solution should be postponed until the next section, wherein the symmetry condition is abandoned in the solution obtaining procedure.

Asymmetry. At large relative angles of attack, even in the case of a symmetrical oncoming flow, the separated flow around symmetrical elongated bodies has an asymmetric structure. As was shown in the previous subsection, the solution to the problem of a separated flow in the case of a symmetric solution could be nonunique. The presence of asymmetric solutions exacerbates the nonuniqueness of the problem solution. In practice, only those solutions that are stable with respect to external perturbations can be realized. Just in the same way, as is seen below, the selection of solutions that can be implemented in practice takes place.

The occurrence of asymmetric vortex formations leads to the emergence of a lateral force affecting an elongated body. Hence, the occurrence of asymmetry is possible only under flow around such bodies that have a nonzero cross section in the direction of lateral force. So, for example, on an infinitely slender delta-shaped wing in the case of a symmetrical oncoming flow, the occurrence of asymmetric vortex formations is impossible, since there is no cross section that could take the lateral force.

The characteristics of an asymmetric flow depend on the shape of an elongated body, on the Mach and Reynolds numbers, on the turbulence of the oncoming flow, as well as on the surface roughness. A review of experimental studies on determining the characteristics of an asymmetric flow and the effect of different parameters on them can be found in the collective monograph [25].

Let us consider the same problem that was explored in the previous paragraph, i.e., a flow around a low-aspect-ratio tapered wing–fuselage combination with fixed separation forms vanishing from the sharp wing edges. In the most simplified mathematical formulation, when the separation vortex sheet is replaced by a discrete vortex and by cut feeding connecting the vortex with the wing edge (Fig. 26), various solutions together with study of their the stability were obtained in [26, 27], the main results of which are presented in this section.

Fig. 26.

Separated flow around a conical body. The vortex sheet is replaced by the vortex–cut model.

Let us introduce the following notations: Γ₁ and Γ₂ are the circulation of the right and left vortices, respectively, and W is the complex flow potential.

As already noted, in this case, the nonsteady-state analogy reduces the three-dimensional steady-state problem to a plane problem self-similar in time. Let us nondimensionalize the linear quantities in section x with respect to the half-span of the wing in this section

$${{y}_{*}} = \frac{y}{{\varepsilon x}},\quad {{z}_{*}} = \frac{z}{{\varepsilon x}},$$

(6.1)

where $\varepsilon = \tan\chi$, whereas the circulation and complex potential are nondimensionalized as follows:

$$G = \frac{\Gamma }{{2\pi \alpha {{u}_{\infty }}\varepsilon x}},\quad {{W}_{*}} = \frac{W}{{\alpha {{u}_{\infty }}\varepsilon x}}.$$

The complex conjugate velocity at infinity has the only vertical component

$${{\left. {{{u}_{*}} - i{{{v}}_{*}}} \right|}_{{y_{*}^{2} + z_{*}^{2} \to \infty }}} = - i\alpha {{u}_{\infty }}.$$

We denote the coordinates of the vortices by σ₁ and σ₂ in the complex plane $\sigma = {{z}_{*}} + i{{y}_{*}}$ (Fig. 27a).

Fig. 27.

Complex planes σ, μ, and $\zeta$. Plane σ shows two vortices connected through a cut to the sharp edges of the wing.

Let us conformally map the exterior of the figure shown in Fig. 27a, at first onto the exterior of segment $[ - (1 + {{m}^{2}}){\text{/}}2,\,\,(1 + {{m}^{2}}){\text{/}}2]$ in complex domain μ (Fig. 27b)

$$\sigma = \mu + \sqrt {{{\mu }^{2}} - {{m}^{2}}} ,$$

and then onto the exterior of a unit circle (Fig. 27c) located in complex plane ζ, according to the following relationship:

$$\mu = \frac{{1 + {{m}^{2}}}}{4}\left( {\zeta + \frac{1}{\zeta }} \right).$$

The complex potential of a separated flow around a circle represents a superposition of the potentials of an expanding circle, right and left vortices and vortices reflected with respect to the circle

$${{W}_{*}}\left( \zeta \right) = - \frac{{1 + {{m}^{2}}}}{2}i\left( {\zeta - \frac{1}{\zeta }} \right) + \frac{{{{m}^{2}}}}{{\bar {\alpha }}}\ln \,\sigma \left( \zeta \right) - i{{G}_{1}}\ln \,\frac{{\zeta - {{\zeta }_{1}}}}{{\zeta - {1 \mathord{\left/ {\vphantom {1 {{{{\bar {\zeta }}}_{1}}}}} \right. \kern-0em} {{{{\bar {\zeta }}}_{1}}}}}} - i{{G}_{2}}\ln \,\frac{{\zeta - {{\zeta }_{2}}}}{{\zeta - {1 \mathord{\left/ {\vphantom {1 {{{{\bar {\zeta }}}_{2}}}}} \right. \kern-0em} {{{{\bar {\zeta }}}_{2}}}}}},$$

(6.2)

where ζ₁ and ζ₂ are the coordinates of the vortices in plane ζ, which are unknown. In addition to the coordinates, the circulations of the vortices G₁ and G₂ are also unknown.They can be determined based on the conditions of Chaplygin–Zhukovskii at sharp edges, as well as the condition of the absence of force affecting the vortex–cut system.

The Chaplygin–Zhukovskii condition on velocity finiteness should be satisfied on the sharp wing edges as follows

$${{\left. {\frac{{d{{W}_{*}}}}{{d\sigma }}} \right|}_{{\sigma = \pm 1}}} < \infty .$$

Since

$$\frac{{d{{W}_{*}}}}{{d\sigma }} = \frac{{d{{W}_{*}}}}{{d\zeta }}\frac{{d\zeta }}{{d\sigma }}$$

and at points $\sigma = \pm 1$ (which corresponds to points $\zeta = \pm 1$)

$$\frac{{d\sigma }}{{d\zeta }} = 0,$$

then

$${{\left. {\frac{{d{{W}_{*}}}}{{d\zeta }}} \right|}_{{\zeta = \pm 1}}} = 0.$$

(6.3)

The fact that the real part of relationship (6.3) is zero follows directly from (6.2). Hence, the Chaplygin–Zhukovskii condition can be finally written in the following form

$${{\left. {\operatorname{Im} \frac{{d{{W}_{*}}}}{{d\zeta }}} \right|}_{{\zeta = \pm 1}}} = 0.$$

The condition of the absence of force affecting the vortex–cut system predetermines the unknown equations relating the coordinates and circulations of vortices to each other. Taking into account the self-similarity of the solution, i.e., the fact that in self-similar variables (6.1) the coordinates of vortices should be fixed, let us transform (4.5) into the following relationship:

$${{\left. {\frac{{d{{W}_{*}}}}{{d\sigma }}} \right|}_{{\sigma = {{\sigma }_{1}}}}} = \frac{1}{{\bar {\alpha }}}\left( {2{{{\bar {\sigma }}}_{1}} + 1} \right),\quad {{\left. {\frac{{d{{W}_{*}}}}{{d\sigma }}} \right|}_{{\sigma = {{\sigma }_{2}}}}} = \frac{1}{{\bar {\alpha }}}\left( {2{{{\bar {\sigma }}}_{2}} - 1} \right).$$

(6.4)

The velocities involved in relationship (6.4) are the velocities of vortex motion. The calculation thereof is carried out according to the following already familiar relationship:

$${{\left. {\frac{{d{{W}_{*}}}}{{d\sigma }}} \right|}_{{\sigma = {{\sigma }_{j}}}}} = \mathop {\lim }\limits_{\sigma \to {{\sigma }_{j}}} \left( {\frac{{d{{W}_{*}}}}{{d\zeta }}\frac{{d\zeta }}{{d\sigma }} + \frac{{i{{G}_{j}}}}{{\sigma - {{\sigma }_{j}}}}} \right),\quad j = 1,2.$$

(6.5)

Relationships (6.3) determine an analytical dependence of circulations on the coordinates of vortices. By substituting this dependence into relationship (6.4) (taking into account (6.5)) and by extracting the real and imaginary parts therein, at given $\bar {\alpha }$ and m one can obtain four equations with four real unknown quantities, i.e., the coordinates of the vortices:

$${{F}_{i}}\left( {{{\xi }_{1}},{{\eta }_{1}},{{\xi }_{2}},{{\eta }_{2}};\bar {\alpha },m} \right) = 0,\quad i = 1,2,3,4.$$

(6.6)

Figure 28 shows the numerical solution of Eqs. (6.6) at m = 0.5 depending on a relative angle of attack ranging from $\bar {\alpha } = 2$ to $\bar {\alpha } = 10$. The numerals I mark symmetrical branches of the solution, the numerals II and III mark asymmetric ones. On branch II, the right vortex is located above the left one; on branch III, it is vice versa. At $\bar {\alpha } = {{\bar {\alpha }}_{*}} \approx 5.18$ a bifurcation of solutions is observed.

Fig. 28.

Position of vortices depending on $\bar {\alpha }$. (I) Symmetric branch of the solution, (II) and (III) asymmetric branches.

Replacing the vortex sheet by a single vortex is, of course, a rough model. However, this model gives a qualitatively correct bifurcation behavior of separated formations. In a more accurate model, wherein the vortex sheet is simulated by a set of discrete vortices, whereas the vortex–cut model is used only in the case of core simulation, the solution bifurcation is shifted by approximately 20–25% towards lower values of $\bar {\alpha }$. Figure 29 shows vortex structures at m = 0.5, corresponding to relative angles of attack of $\bar {\alpha } = 3$, at which the solution is still symmetrical, and that of $\bar {\alpha } = 4$, at which the symmetrical solution has already lost its stability.

Fig. 29.

Separated flow around a tapered combination, m = 0.5; (a) symmetrical one at $\bar {\alpha } = 3$, (b) asymmetric one at $\bar {\alpha } = 4$.

The instability of the solutions obtained in [26] was studied again using the example of a model of a discrete vortex connected with the wing edge by a cut as follows: nonsteady-state equations of motion were written for discrete vortices; further, the equations were linearized in the vicinity of the solutions of Eqs. (6.6). Then these equations were studied for stability. Depending on m and $\bar {\alpha }$ Fig. 30 shows a diagram wherein different domains correspond to different numbers of solutions. In domain 1, only one solution of Eqs. (6.6) exists, and it is stable. In domain 2 there are three solutions of Eqs. (6.6): a symmetric unstable one and two asymmetric (mirror) stable ones.

Fig. 30.

Bifurcation diagram of solutions.

There are seven solutions in domain 3: three symmetric solutions, one stable and two unstable; as well as four asymmetric solutions, two stable and two unstable. In domain 4, there are five solutions: one stable symmetric solution and four asymmetric solutions, two of which are stable and two are unstable. Which of the stable solutions could be implemented in practice depends on many factors: on the accuracy in manufacturing a symmetric body, on perturbing factors, and on the history of attaining a preset flow mode. So, for example, when a symmetrical body is arranged at a slip angle with respect the oncoming flow, then with changing slip-angle hysteresis dependences of the aerodynamic characteristics can occur [27, 28].