Development of a Numerical Model Designed to Calculate the Temperature Field and Thermal Stresses in Structural Elements of Aircrafts

Abstract

The algorithm for the numerical solution of the quasistatic thermoelasticity problem in the domains of simple spatial forms is briefly described. The initial validation and verification of the developed numerical technique was performed. Some results of the solution of the quasistatic thermoelasticity problem in the simplest structural elements of aircraft.

1. INTRODUCTION

One of the most difficult problems of aerothermodynamics is the problem of modeling conjugate heat exchange on the surface of a high-speed aircraft (AC), as well as calculating the resulting thermal stresses in its structure. In this case of AC motion, the boundary layer can be considered as a narrow spatial region adjacent to the surface of the streamlined body, in which an intense heat release occurs due to energy dissipation processes. The latter are accompanied by a strong change in thermophysical (density, pressure, temperature, viscosity, heat conductivity, etc.), dynamic properties of gas, heat fluxes directed towards the surface of the aircraft, construction of the material, and operating characteristics. However, carrying out real physical experiments in the considered area of motion of the AC is characterized by high cost and is associated with many technological and technical difficulties. Therefore, mathematical modeling of thermal stresses and thermophysical processes in an aircraft as well as near its surface is of great importance for optimizing operating characteristics and design of the AC.

The aim of this study is to develop an approximate method for estimating thermal stresses in an AC (or in the key elements: the edges of the hull and wings, the nose cone) of a simple spatial form, for example, a sphere conjugated with a cylinder. The mathematical model of estimates designed for calculation of thermal stresses in individual structural elements of an AC is based on the solution of the quasi-static problem of thermoelasticity [1–5]. It includes the equations of mechanical equilibrium of a linearly elastic medium, taking into account thermal stresses (however, this mathematical model does not allow a complete description of thermomechanical processes, since it lacks the main physical mechanisms that account for the plastic deformation of structural materials) and heat equation of a special type. As a rule, the physical domain (in which the solution is sought) has curvilinear boundaries, and their shape changes during the modeling process under the influence of thermal and mechanical loads. To solve a problem with such spatial boundaries, the computational domain is transformed into a domain in which it is possible to introduce a regular Cartesian (structured) grid.

The following simplifying assumptions are introduced when estimating thermal stresses:

• The structural material is an isotropic continuous medium.

• The geometry and heat-stressed state of a structural element of the AC is described in two-dimensional (2D) formulation.

• Initial external mechanical (forces, pressure fields) and thermal impacts (convective and radiational heat fluxes) are set.

• The velocity of acoustic waves in the structural elements of ACs is significantly greater than that of propagation of thermal waves in them.

2. MATHEMATICAL FORMULATION OF THE PROBLEM OF ESTIMATING THERMAL STRESSES IN STRUCTURAL ELEMENTS OF AIRCRAFT

Mathematical formulation of the problem under consideration is reduced to numerical solution of a set of two-dimensional equations of quasi-static thermoelasticity, which allow determining fields of temperatures T and displacements $\overrightarrow U$ and components of stress ${{\varepsilon }_{{ij}}}$ and strain ${{\sigma }_{{ij}}}$ tensors in structural elements of AC [2‒8]

$$\mu {\text{div}}({\text{grad}}(\overrightarrow U )) + \left( {\lambda + \mu } \right){\text{grad}}({\text{div}}\overrightarrow U ) - \left( {3\lambda + 2\mu } \right){{\alpha }_{T}}{\text{grad}}\left( \theta \right) = 0,$$

$$\rho {{c}_{{\varepsilon = 0}}}\frac{{\partial \theta }}{{\partial t}} + {{\alpha }_{T}}\left( {3\lambda + 2\mu } \right){{T}_{0}}{\text{div}}({{\partial \overrightarrow U } \mathord{\left/ {\vphantom {{\partial \overrightarrow U } {\partial t}}} \right. \kern-0em} {\partial t}}) = {\text{div}}\left( {{{\lambda }_{q}}{\text{grad}}\theta } \right),$$

(2.1)

where $t,{{x}_{j}}$ are the time and Cartesian coordinates; $\overrightarrow U$ is the vector describing displacement of a point of the body; T is the temperature of the body; ${{T}_{0}}$ is the initial temperature of the body; $\theta = T - {{T}_{0}}$ is excessive temperature; $\rho$ is the density in the body; ${{c}_{{\varepsilon = 0}}}$ is the heat capacity at zero strain; $\mu ,\lambda$ are Lame coefficients; and ${{\alpha }_{T}}$ is the thermal expansion coefficient.

Boundary conditions for temperature are formulated by setting the heat flux on the surface of a structural element of the AC

$${{\left. { - {{\lambda }_{q}}\frac{{\partial T}}{{\partial {{x}_{i}}}}} \right|}_{{{\Gamma}}}} = {{q}_{i}},$$

where ${{T}_{{0i}}}$, ${{q}_{i}}$ are given constants; and symbol Г indicates the surface of the AC. Mechanical boundary conditions in the form of stresses are set similarly to [3]. Initial conditions (for moment of time t = 0) are determined as initially set spatial distribution of temperature T and displacements $\overrightarrow U$.

Boundary conditions required for solving the quasi-static problem of thermoelasticity using the finite difference method are easily implemented, when the boundaries of computational domain $\Omega$ coincide with coordinate lines in some generalized coordinate system $\xi ,\eta$. At the same time, computational domain $\Omega$ goes into parametric domain ${{\Omega }_{p}}$ (for example, into a rectangle).

Let us introduce a coordinate transformation in form

$$r = r\left( {\xi ,\eta } \right),\quad z = z\left( {\xi ,\eta } \right).$$

At known coordinates of grid nodes $\xi ,{\text{ }}\eta$ in physical space, metric coefficients in general can be found by numerical differentiation using formulas

$$J = \frac{{\partial \left( {r,z} \right)}}{{\partial \left( {\xi ,\eta } \right)}} = \frac{{\partial r}}{{\partial \xi }}\frac{{\partial z}}{{\partial \eta }} - \frac{{\partial r}}{{\partial \eta }}\frac{{\partial z}}{{\partial \xi }},$$

$${{\xi }_{r}} = {{J}^{{ - 1}}}\frac{{\partial z}}{{\partial \eta }},\quad {{\eta }_{r}} = - {{J}^{{ - 1}}}\frac{{\partial z}}{{\partial \xi }},\quad {{\xi }_{z}} = - {{J}^{{ - 1}}}\frac{{\partial r}}{{\partial \eta }},\quad {{\eta }_{z}} = {{J}^{{ - 1}}}\frac{{\partial r}}{{\partial \xi }},$$

where $J = {{\partial \left( {r,z} \right)} \mathord{\left/ {\vphantom {{\partial \left( {r,z} \right)} {\partial \left( {\xi ,\eta } \right)}}} \right. \kern-0em} {\partial \left( {\xi ,\eta } \right)}}$ is the Jacobian of transition from cylindrical coordinate system r, z to curvilinear coordinate system $\xi ,\eta$.

The use of Euler coordinates in equations of linear elasticity theory and heat conductivity makes it possible to build economical (at the expense of simplification of spatial derivatives), which allow an end-to-end calculation of flows with strong spatial deformations.

Functions $r\left( {\xi ,\zeta } \right)$ and $z\left( {\xi ,\zeta } \right)$ can be searched using the equation set obtained in [9]. These equations guarantee that found functions $r = r\left( {\xi ,\eta } \right),z = z\left( {\xi ,\eta } \right)$ are smooth functions of coordinates $\xi ,\eta$. However, in some cases, the computational grid created in this way can be considered unsuccessful for one reason or another. In this situation (together with differential methods) it is expedient to use analytical algebraic transformations [10].

The equation set of thermoelasticity (1) in vector semi-divergent form in arbitrary curvilinear coordinate system $\xi ,{\text{ }}\eta$ is denoted as

$$A\vec {U} = B\frac{{\partial \vec {F}}}{{\partial \xi }} + B\frac{{\partial \vec {G}}}{{\partial \eta }} + {{C}_{\xi }}\frac{{\partial \vec {I}}}{{\partial \xi }} + {{C}_{\eta }}\frac{{\partial \vec {I}}}{{\partial \eta }} + {{D}_{\xi }}\frac{{\partial \vec {W}}}{{\partial \xi }} + {{D}_{\eta }}\frac{{\partial \vec {W}}}{{\partial \eta }} + \vec {S} = 0.$$

(2.2)

Vectors involved in this equation set are denoted as follows:

$$\vec {F} = \left\| {\begin{array}{*{20}{c}} {{{F}_{1}}} \\ {{{F}_{2}}} \end{array}} \right\|,\quad \vec {G} = \left\| {\begin{array}{*{20}{c}} {{{G}_{1}}} \\ {{{G}_{2}}} \end{array}} \right\|,\quad \overrightarrow I = \left\| {\begin{array}{*{20}{c}} I \\ I \end{array}} \right\|,\quad \overrightarrow W = \left\| {\begin{array}{*{20}{c}} \theta \\ \theta \end{array}} \right\|,$$

$$B = \left[ {\begin{array}{*{20}{c}} {\frac{\mu }{J}}&0 \\ 0&{\frac{\mu }{J}} \end{array}} \right],\quad {{C}_{\xi }} = \left[ {\begin{array}{*{20}{c}} {\left( {\lambda + \mu } \right){{\xi }_{r}}}&0 \\ 0&{\left( {\lambda + \mu } \right){{\xi }_{z}}} \end{array}} \right],\quad {{C}_{\eta }} = \left[ {\begin{array}{*{20}{c}} {\left( {\lambda + \mu } \right){{\eta }_{r}}}&0 \\ 0&{\left( {\lambda + \mu } \right){{\eta }_{z}}} \end{array}} \right],$$

$${{D}_{\xi }} = \left[ {\begin{array}{*{20}{c}} {{{\alpha }_{T}}\left( {3\lambda + 2\mu } \right){{\xi }_{r}}}&0 \\ 0&{{{\alpha }_{T}}\left( {3\lambda + 2\mu } \right){{\xi }_{z}}} \end{array}} \right],\quad {{D}_{\eta }} = \left[ {\begin{array}{*{20}{c}} {{{\alpha }_{T}}\left( {3\lambda + 2\mu } \right){{\eta }_{r}}}&0 \\ 0&{{{\alpha }_{T}}\left( {3\lambda + 2\mu } \right){{\eta }_{z}}} \end{array}} \right],$$

$$I = {\text{div}}\overrightarrow U = \left[ {\frac{1}{J}\frac{{\partial J\left( {{{U}_{\xi }}} \right)}}{{\partial \xi }} + \frac{1}{J}\frac{{\partial J\left( {{{U}_{\eta }}} \right)}}{{\partial \eta }}} \right],$$

$${{F}_{1}} = J(\xi _{r}^{2} + \xi _{z}^{2}){{u}_{\xi }},\quad {{F}_{2}} = J(\xi _{r}^{2} + \xi _{z}^{2}){{{v}}_{\xi }},\quad {{G}_{1}} = J(\eta _{r}^{2} + \eta _{z}^{2}){{u}_{\eta }},\quad {{G}_{2}} = J(\eta _{r}^{2} + \eta _{z}^{2}){{{v}}_{\eta }},$$

$$\overrightarrow S = \left\| {\begin{array}{*{20}{c}} {{{S}_{1}}} \\ {{{S}_{2}}} \end{array}} \right\| + \left\| {\begin{array}{*{20}{c}} {{{S}_{r}}} \\ {{{S}_{z}}} \end{array}} \right\|,$$

$${{S}_{1}} = \frac{1}{J}\frac{{\partial \left\{ {J\left( {{{\xi }_{r}}{{\eta }_{r}} + {{\xi }_{z}}{{\eta }_{z}}} \right){{u}_{\eta }}} \right\}}}{{\partial \xi }} + \frac{1}{J}\frac{{\partial \left\{ {J\left( {{{\eta }_{r}}{{\xi }_{r}} + {{\eta }_{z}}{{\xi }_{z}}} \right){{u}_{\xi }}} \right\}}}{{\partial \eta }} + \alpha \frac{1}{r}\left\{ {{{\xi }_{r}}\frac{{\partial u}}{{\partial \xi }} + {{\eta }_{r}}\frac{{\partial u}}{{\partial \eta }}} \right\},$$

$${{S}_{2}} = \frac{1}{J}\frac{{\partial \left\{ {J\left( {{{\xi }_{r}}{{\eta }_{r}} + {{\xi }_{z}}{{\eta }_{z}}} \right){{{v}}_{\eta }}} \right\}}}{{\partial \xi }} + \frac{1}{J}\frac{{\partial \left\{ {J\left( {{{\eta }_{r}}{{\xi }_{r}} + {{\eta }_{z}}{{\xi }_{z}}} \right){{{v}}_{\xi }}} \right\}}}{{\partial \eta }} + \alpha \frac{1}{r}\left\{ {{{\xi }_{r}}\frac{{\partial {v}}}{{\partial \xi }} + {{\eta }_{r}}\frac{{\partial {v}}}{{\partial \eta }}} \right\},$$

$${{S}_{r}} = \left( {\lambda + \mu } \right)\left[ {{{\xi }_{r}}\frac{{\partial \left( {\alpha \frac{u}{r}} \right)}}{{\partial \xi }} + {{\eta }_{r}}\frac{{\partial \left( {\alpha \frac{u}{r}} \right)}}{{\partial \eta }}} \right],\quad {{S}_{z}} = \left( {\lambda + \mu } \right)\left[ {{{\xi }_{z}}\frac{{\partial \left( {\alpha \frac{u}{r}} \right)}}{{\partial \xi }} + {{\eta }_{z}}\frac{{\partial \left( {\alpha \frac{u}{r}} \right)}}{{\partial \eta }}} \right],$$

where $u\left( {r,z,t} \right) = {{U}_{r}}$, ${v}\left( {r,z,t} \right) = {{U}_{z}}$ are projections of displacement vector $\overrightarrow U \left( {r,z,t} \right)$ on the r- and z-axis; ${{U}_{\xi }} = {{\xi }_{r}}u + {{\xi }_{z}}{v}$, ${{U}_{\eta }} = {{\eta }_{r}}u + {{\eta }_{z}}{v}$ are contravariant components of vector $\overrightarrow U$, which describes displacement of a point of the body in curvilinear coordinate system $\xi ,\eta$; and $\alpha = 0$ corresponds to flat and $\alpha = 1$ to axisymmetric cases of deformation.

Now, using transition to curvilinear coordinate system $\xi ,\eta$, let us transform the equation associated with transferring the internal energy by the process of heat conductivity

$$\rho {{c}_{{\varepsilon = 0}}}\frac{{\partial \theta }}{{\partial t}} = \frac{1}{J}\frac{{\partial (J{{\lambda }_{q}}(\xi _{r}^{2} + \xi _{z}^{2}){{\theta }_{\xi }})}}{{\partial \xi }} + \frac{1}{J}\frac{{\partial (J{{\lambda }_{q}}(\eta _{r}^{2} + \eta _{z}^{2}){{\theta }_{\eta }})}}{{\partial \eta }} + f,$$

$${{S}_{\lambda }} = \frac{1}{J}\frac{{\partial \left\{ {J{{\lambda }_{q}}\left( {{{\xi }_{r}}{{\eta }_{r}} + {{\xi }_{z}}{{\eta }_{z}}} \right){{\theta }_{\eta }}} \right\}}}{{\partial \xi }} + \frac{1}{J}\frac{{\partial \left\{ {J{{\lambda }_{q}}\left( {{{\eta }_{r}}{{\xi }_{r}} + {{\eta }_{z}}{{\xi }_{z}}} \right){{\theta }_{\xi }}} \right\}}}{{\partial \eta }} + \alpha \frac{{{{\lambda }_{q}}}}{r}\left\{ {{{\xi }_{r}}\frac{{\partial \theta }}{{\partial \xi }} + {{\eta }_{r}}\frac{{\partial \theta }}{{\partial \eta }}} \right\},$$

$${{D}_{\lambda }} = - {{\alpha }_{T}}\left( {3\lambda + 2\mu } \right){{T}_{0}}\left[ {\frac{1}{J}\frac{{\partial J\left( {{{\partial {{U}_{\xi }}} \mathord{\left/ {\vphantom {{\partial {{U}_{\xi }}} {\partial t}}} \right. \kern-0em} {\partial t}}} \right)}}{{\partial \xi }} + \frac{1}{J}\frac{{\partial J\left( {{{\partial {{U}_{\eta }}} \mathord{\left/ {\vphantom {{\partial {{U}_{\eta }}} {\partial t}}} \right. \kern-0em} {\partial t}}} \right)}}{{\partial \eta }}} \right] - \alpha \frac{{{{\alpha }_{T}}\left( {3\lambda + 2\mu } \right){{T}_{0}}u}}{r},$$

(2.3)

where $f = {{S}_{\lambda }} + {{D}_{\lambda }}$.

3. SEPARATE MATHEMATICAL DETAILS OF THE NUMERCAL CALCULATION METHOD

In numerical implementation of Eqs. (2) and (3), regular grid ${{\omega }_{h}} = \left\{ {{{\xi }_{j}},{{\eta }_{k}};j = \overline {0,J} ,k = \overline {0,K} } \right\}$, ${{\omega }_{h}} \in {{\Omega }_{h}}$ is introduced in parametric domain Ω_p. Here, ${{h}_{\xi }} = {{\xi }_{j}} - {{\xi }_{{j - 1}}}$, ${{\xi }_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{\xi }_{j}} + 0.5{{h}_{\xi }}$, ${{\xi }_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{\xi }_{j}} - 0.5{{h}_{\xi }}$, ${{h}_{\eta }} = {{\eta }_{k}} - {{\eta }_{{k - 1}}}$, ${{\eta }_{{k + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{\eta }_{k}} + 0.5{{h}_{\eta }}$, and ${{\eta }_{{k - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{\eta }_{k}} - 0.5{{h}_{\eta }}$.

Numerical solution of Eqs. (2) and (3) is implemented in two steps. At the first stage, the heat conductivity equation of special form (3) is implicitly solved. Then, at the second stage, solution of thermoelasticity equation (2) is found.

When solving the “thermal” part of two-dimensional equations of quasi-static thermoelasticity, which describe transfer of internal energy by the process of heat conductivity, the following two-step difference scheme is applied (using [11]):

$${{c}_{{j,k}}}\frac{{\theta _{{j,k}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} - \theta _{{j,k}}^{n}}}{{{\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}}} = \frac{{{{a}_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},k}}}(\theta _{{j + 1,k}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} - \theta _{{j,k}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}) - {{a}_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},k}}}(\theta _{{j,k}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} - \theta _{{j - 1,k}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}})}}{{h_{\xi }^{2}}} + F_{\xi }^{n} + O(h_{\xi }^{2},h_{\eta }^{2}),$$

$$\theta = \theta (\xi ,\eta ,t = {{t}^{n}}),\quad {{F}_{\xi }} = \frac{{\partial [J{{\lambda }_{q}}(\eta _{r}^{2} + \eta _{z}^{2}){{\theta }_{\eta }}]}}{{\partial \eta }} + Jf,$$

$${{c}_{{j,k}}}\frac{{\theta _{{j,k}}^{{n + 1}} - \theta _{{j,k}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}{{{\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}}} = \frac{{{{a}_{{j,k + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(\theta _{{j,k + 1}}^{{n + 1}} - \theta _{{j,k}}^{{n + 1}}) - {{a}_{{j,k - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(\theta _{{j,k}}^{{n + 1}} - \theta _{{j,k - 1}}^{{n + 1}})}}{{h_{\eta }^{2}}} + F_{\eta }^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} + O(h_{\xi }^{2},h_{\eta }^{2}),$$

$$\theta = \theta \left( {\xi ,\eta ,t = {{t}^{n}} + \frac{{\Delta t}}{2}} \right),\quad {{F}_{\eta }} = \frac{{\partial [J{{\lambda }_{q}}(\xi _{r}^{2} + \xi _{z}^{2}){{\theta }_{\xi }}]}}{{\partial \xi }} + Jf,$$

where n is the upper index related to the moment of “time” $t = n\Delta t$, $\Delta t$ is the time step; $c = \rho {{c}_{{\varepsilon = 0}}}J$; ${{a}_{\xi }} = J{{\lambda }_{q}}(\xi _{r}^{2} + \xi _{z}^{2})$; and ${{a}_{\eta }} = J{{\lambda }_{q}}(\eta _{r}^{2} + \eta _{z}^{2})$. This difference scheme (along spatial direction $\xi ,\;\eta$) is easily solved by scalar sweep.

Equations of thermoelasticity $A\vec {U} = 0$ are solved using the method of establishment [12]. At the same time, time step $\Delta t$ can be found using an iteration method of variation type. For this, we determine vector of residuals $\vec {R} = \left( {{{R}_{1}},{{R}_{2}}} \right)$

$$R_{{1,j,k}}^{n} = \left( {A{{U}_{{j,k}}}} \right)_{1}^{n} - b_{{1,j,k}}^{n},\quad R_{{2,j,k}}^{n} = \left( {A{{U}_{{j,k}}}} \right)_{2}^{n} - b_{{2,j,k}}^{n},\quad \vec {b}_{{j,m}}^{n} = \left\{ {b_{{1,j,k}}^{n},b_{{2,j,k}}^{n}} \right\} = \left\{ {0,0} \right\},$$

$$j = \overline {1,J} - 1,\quad k = \overline {1,K - 1} .$$

Let us introduce the scalar product as follows [11]:

$$\left( {\overrightarrow a ,\overrightarrow b } \right) = \sum\limits_{j = 1}^{J - 1} {\sum\limits_{k = 1}^{K - 1} {\left( {{{a}_{{1,j,k}}}{{b}_{{1,j,k}}}{{h}_{\xi }}{{h}_{\eta }}} \right)} } + \sum\limits_{j = 1}^{J - 1} {\sum\limits_{k = 1}^{K - 1} {\left( {{{a}_{{2,j,k}}}{{b}_{{2,j,k}}}{{h}_{\xi }}{{h}_{\eta }}} \right)} } ,$$

$${{\overrightarrow a }_{{j,k}}} = {{\left( {{{a}_{1}},{{a}_{2}}} \right)}_{{j,k}}},\quad {{\overrightarrow b }_{{j,k}}} = {{\left( {{{b}_{1}},{{b}_{2}}} \right)}_{{j,k}}}.$$

We will minimize the value of residual ${{\vec {R}}_{{j,k}}} = A{{\vec {U}}_{{j,k}}} - {{\vec {b}}_{{j,k}}}$ using the modified option of the iteration method of variation type, the least residual method [13]. In this case, the iterations should be carried out according to formulas

$$\vec {U}_{{j,k}}^{{n + 1}} = \vec {U}_{{j,k}}^{n} + c\Delta t\vec {R}_{{j,k}}^{n},\quad c \approx 0.9,\quad \Delta t = \frac{{(\vec {R},A\vec {R})}}{{(A\vec {R},A\vec {R})}}.$$

In numerical implementation of the method of least residual for approximating derivatives of vectors $\vec {F},\;\vec {G},\,\,\overrightarrow I ,\;\overrightarrow W$ and variables $u,{v},\theta$, we set the following finite difference representation of the derivatives on the grid ${{\omega }_{h}} \in {{\Omega }_{h}}$ introduced above [14]:

$$\frac{\partial }{{\partial \xi }}{{\left[ {a\frac{{\partial g}}{{\partial \xi }}} \right]}_{{j,k}}} = \frac{{{{a}_{{j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},k}}}\left( {{{g}_{{j + 1,k}}} - {{g}_{{j,k}}}} \right) - {{a}_{{j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},k}}}\left( {{{g}_{{j,k}}} - {{g}_{{j - 1,k}}}} \right)}}{{h_{\xi }^{2}}} + O(h_{\xi }^{2}),\quad {{a}_{{j \pm {1 \mathord{\left/ {\vphantom {1 {2,k}}} \right. \kern-0em} {2,k}}}}} = \frac{{{{a}_{{j,k}}} + {{a}_{{j \pm 1,k}}}}}{2},$$

$$\frac{\partial }{{\partial \xi }}{{\left[ {a\frac{{\partial g}}{{\partial \eta }}} \right]}_{{j,k}}} = \frac{{{{a}_{{j + 1,k}}}\left( {{{g}_{{j + 1,k + 1}}} - {{g}_{{j + 1,k - 1}}}} \right) - {{a}_{{j - 1,k}}}\left( {{{g}_{{j - 1,k + 1}}} - {{g}_{{j - 1,k - 1}}}} \right)}}{{4{{h}_{\xi }}{{h}_{\eta }}}} + O(h_{\xi }^{2},h_{\eta }^{2}).$$

Note that for correct operation of the described algorithm it is necessary:

• To rebuild the computational grid (for example, using the method in [9]) after each computation step (since there was a deformation of the boundaries of the computational domain.

• Then to perform interpolation (taking into account conservation law and the required degree of smoothness of the solution, see [15]) of magnitudes $\overrightarrow U (r,z,t)$ and $\theta (r,z,t),$ known on the computational grid at moment of time tⁿ to the grid obtained after its rebuilding.

4. SOME CALCULATION RESULTS

To test the performance of the formulated numerical technique, a group of test problems was solved. In all series of calculations, the system of equations of the linear theory of elasticity and the heat equation in Euler coordinates were used.

The first test (validation) problem is to find the equilibrium thermally deformed state of a steel beam, which is fixed on both sides with fixed hinges (Fig. 1) and is in a uniform temperature field $T\left( {x,y} \right) \equiv {{T}_{0}} + \Delta T$ (where ${{T}_{0}}$ is the initial value of temperature, $\Delta T$ is the value of uniform temperature heating). Only the problem of mechanics in the given uniformly distributed temperature field $T\left( {x,y} \right) \equiv {{T}_{0}} + \Delta T$ is solved. The exact solution of the two-dimensional problem of the elasticity theory for a rectangular band is denoted as follows [3]:

$${{U}_{y}}\left( x \right) = \frac{h}{2}\left[ {\frac{{\cos \left( {\lambda x} \right)}}{{\cos \left( {{{\lambda l} \mathord{\left/ {\vphantom {{\lambda l} 2}} \right. \kern-0em} 2}} \right)}} - 1} \right],\quad \lambda = \sqrt {\frac{P}{D}} ,\quad D = \frac{{E{{h}^{3}}}}{{12}}.$$

where h is the height of the beam; l is the length of the beam; and E is the elasticity modulus of the first kind. Support reaction force P is calculated from equation

$$\frac{{Pl}}{{hE}} + \frac{{{{h}^{2}}}}{2}\lambda \tan \left( {\frac{{\lambda l}}{2}} \right) + \frac{{{{h}^{2}}}}{8}\frac{P}{D}\frac{{\frac{l}{2} - \frac{{\sin \left( {\lambda l} \right)}}{{2\lambda }}}}{{{{{\cos }}^{2}}\left( {\frac{{\lambda l}}{2}} \right)}} - \alpha \Delta Tl = 0,$$

where α is the temperature expansion coefficient.

Fig. 1.

Scheme of the test problem on bending of a uniformly heated fixed beam under the action of temperature stresses.

Figure 2 presents the results (at h = 2.5 mm, l = 100 mm, E = 2 × 10¹¹ Pa, α = 1.2 × 10^‒5 C^‒1, ΔT = 36°C) of numerical computation of the first test problem on determination of deflection of uniformly heated fixed beam under the action of temperature stresses (the maximal value of relative error constituted 2%).

Fig. 2.

The results of numeric calculation of the test problem on determination of deflection of a uniformly heated fixed beam under the action of temperature stresses.

It is known from systematic calculations [16, 17], that convective heat flux q_w near the front critical point can be determined using formulas ($R$ is the blunt radius)

$${{q}_{w}} = 1.93 \times {{10}^{{ - 4}}}V_{\infty }^{{1.08}}\left( {{{H}_{0}} - {{H}_{w}}} \right)\sqrt {\frac{{{{\rho }_{\infty }}}}{R}} \,\,({\text{in laminar case}});$$

$${{q}_{w}} = 4.69 \times {{10}^{{ - 4}}}V_{\infty }^{{1.25}}\left( {{{H}_{0}} - {{H}_{w}}} \right){{\left( {1 + \frac{{{{T}_{w}}}}{{{{T}_{0}}}}} \right)}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}\frac{{\rho _{\infty }^{{0.8}}}}{{{{R}^{{0.2}}}}}\,\,({\text{in turbulent case}}),$$

where ${{H}_{w}}$ [J/kg], ${{T}_{w}}$ [K] is the enthalpy and temperature on the surface of the streamlined body; ${{H}_{0}}$ [J/kg], ${{T}_{0}}$ [K] is the enthalpy and temperature taken on the external boundary of the boundary layer; ${{\rho }_{{{\kern 1pt} \infty }}}$ [kg/m³], ${{V}_{\infty }}$ [m/s] is the density and velocity of unperturbed flow oncoming on the body; R [m] is the radius of the body at the front critical point; and q_w [W/m²] is the heat flux at the front critical point.

It follows from the formulas that heat transfer coefficient α at the front critical point can be estimated using relation

$${{\alpha \sim 1} \mathord{\left/ {\vphantom {{\alpha \sim 1} {\sqrt R }}} \right. \kern-0em} {\sqrt R }}\,\,({\text{in turbulent case}}\,\,{{\alpha \sim 1} \mathord{\left/ {\vphantom {{\alpha \sim 1} {{{R}^{{0.2}}}}}} \right. \kern-0em} {{{R}^{{0.2}}}}}).$$

Therefore, at high motion velocities (M > 6) and correspondingly higher stagnation temperatures, the values of convective and radiational fluxes sharply increase (if we do not take into account the reciprocal effect of growth of body temperature ${{T}_{w}}$ on convective heat flux q_w) with decreasing the blunt radius. These formulas also demonstrate a noticeable effect of body temperature ${{T}_{w}}$ of the AC element on convective heat flux q_w.

Calculations carried out in this study (Figs. 3‒10) allow estimating the effect of blunt radius R, geometric shape, structural material, and distribution of the surface temperature ${{T}_{w}}$ of the AC element on convective heat flux q_w.

Fig. 3.

Distribution of temperature Т [K] in a wedge-shaped shell (Inconel 617 alloy) blunted along the cylinder. The blunt radius of the cylinder R = 3.18 mm, Mach number in oncoming flow М = 5.25.

Fig. 4. 

Distribution of displacements U_x [mm] in direction of the X-axis in a wedge-shaped shell (Inconel 617 alloy) blunted along the cylinder. The blunt radius of the cylinder R = 3.18 mm, Mach number in oncoming flow М = 5.25. Solid lines indicate outlines of the initial undeformed body.

Fig. 5. 

Distribution of displacements U_y [mm] in direction of the Y-axis in a wedge-shaped shell (alloy Inconel 617) blunted along the cylinder. The blunt radius of the cylinder R = 3.18 mm, Mach number in oncoming flow М = 5.25. Solid lines indicate outlines of the initial undeformed body.

Fig. 6.

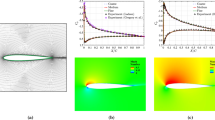
Distribution of convective heat flow density along the surface of a spherically blunted cylinder [20]. Blunt radius R = 1.27 cm.

Fig. 7.

Distribution of temperature Т [K] along the surface of a spherically blunted cylinder. Sphere blunt radius R = 1.27 cm, velocity of oncoming flow V_∞ = 4.17 km/s (Mach number М = 9.8, height h = 22 km).

Fig. 8.

Distribution of temperature Т [K] in a spherically blunted cylinder. Sphere blunt radius R = 1.27 cm, velocity of oncoming flow V_∞ = 4.17 km/s (Mach number М = 9.8, height h = 22 km).

Fig. 9.

Distribution of displacements ${{U}_{x}}$ [mm] in direction of the X-axis in a spherically blunted cylinder. Sphere blunt radius R = 1.27 cm, velocity of oncoming flow V_∞ = 4.17 km/s (Mach number М = 9.8, height h = 22 km).

Fig. 10.

Distribution of displacements ${{U}_{z}}$ [mm] in direction of the Z-axis in a spherically blunted cylinder. The sphere blunt radius R = 1.27 cm, velocity of oncoming flow V_∞ = 4.17 km/s (Mach number М = 9.8, height h = 22 km).

For validation and verification of the developed numerical technique, the data of [18, 19] were taken as the second test problem. The geometry (Figs. 3–5) of the testing problem is a 2D wedge-shaped shell (the shell material is Inconel 617 alloy, the wedge length is 7.62 mm, the shell thickness is constant and equal to 11 mm, and the wedge opening angle is 6°), blunted along the cylinder (bluntness radius R = 3.18 mm).

The convective heat flux entering the surface of the wedge-shaped shell, as well as the aerodynamic loads distributed along its surface, are taken from [18, 19]. The parameters of the air flow flowing onto the aircraft element (edges of the wings, nose cone) are determined by Mach number M = 5.25. It is assumed that the stabilization of the internal energy in the AC element, which is rigidly embedded, is carried out by thermal radiation.

The results of calculation of equilibrium thermally deformed state, corresponding to the test problem (Figs. 3‒5):

• The maximal value of relative error either by temperature distribution or by the values of displacements constitutes <3%.

• There is a noticeable change in distribution of temperature ${{T}_{w}}$ along the surface of AC element T_w = 1100–3100 K.

• Displacements U_x of the front part of the AC element along the x-axis is equal to 2 mm in the direction of body elongation.

• Displacements U_y of the front part of the AC element along the y-axis: 0.25 mm – in the lower part of the body, 0.5 mm – in the upper part of the body.

• Blunt radius R varies and reaches value R = 2.10 mm (leading to growth of convective heat flux q_w by 23%), which is 34% less than initial radius R = 3.18 mm.

The next problem was to find distributions of temperature $T$ and displacements $\overrightarrow U$ in the structural AC element, in a cylinder blunted on a sphere. When solving this problem, the following geometry of the AC element was specified (spherical blunt with a radius of 1.27 cm, cylinder length 10 cm), as well as the convective heat flux (Fig. 6) incident on the surface of the element under consideration.

For gas-dynamic calculated data in the oncoming external flow, the data of [20] were used: pressure: $P = 0.23 \times {{10}^{3}}$ Pa; density $\rho = 0.178 \times {{10}^{{ - 5}}}$ g/cm³; velocity $V = 4.167 \times {{10}^{5}}$ cm/s; and temperature T = 450 K. At the same time the temperature of the surface of the element was considered constant and equal to ${{T}_{w}} = 300$ K. Distribution of density of the convective heat flux along the streamlined non-catalytic surface is taken from [18] and shown in Fig. 6. Figure 7 presents distribution of the gas temperature along the surface of the cylinder blunted by the sphere [21‒32]. Note that the pointed aerothermophysical values correspond to hypersonic gas flow regime (М = 9.8).

When solving this problem, as before, it is assumed that the loss of internal energy by the AC element is carried out only due to thermal radiation. The AC element itself (Figs. 8–10) is made of tungsten and is rigidly embedded.

Figures 8‒10 present the results of calculations carried out using the above-described technique for the AC element under consideration.

This follows from the graphical dependences presented in Figs. 8‒10:

• Distribution of the surface temperature T_w = 1500–2200 K, streamlined by an external flow of the AC element (along the generatrix of the AC element), differs from the constant and significantly exceeds the temperature (${{T}_{w}} = 300$ K) of the element surface, taken as the boundary condition in calculation of aircraft aerothermodynamics.

• Blunt radius R changes by 4.6% (with R = 12.7 mm to values R = 12.12 mm). At the same time convective heat flux ${{q}_{w}}$ at the front critical point increases by 2.4% at the expense of the change in curvature radius R. However, if we take the significant growth of surface temperature ${{T}_{w}} = 2200$ K into account, then the change will be at the level q_w ≈ 10–20%.

• Displacements $\overrightarrow U$ of points of the considered solid AC element are small and mainly concentrated near the embedment.

• Convective heat flux (see Fig. 6), taken from [20] should be corrected by 70% along the generatrix of the cylinder if we take solutions of the equations of quasi-static thermoelasticity into account (due to significant increase in temperature of the body and on the surface of the AC element).

6. CONCLUSIONS

A 2D theoretical calculation technique is formulated, which makes it possible to find a solution to the system of thermoelasticity equations with boundary conditions of a general form. The initial validation and verification of the developed numerical technique based on the test problem was carried out. Numerical modeling of temperature fields and thermal stresses in the simplest structural elements of AC (a wedge-shaped shell blunted in a cylinder or a cylinder blunted in a sphere) was performed. It follows from the performed calculations that numerical modeling of physical processes occurring on the surface (and in the immediate vicinity) of high-speed AC should be carried out on the basis of complex, mutually consistent, conjugated mathematical models of aerothermodynamics, heat transfer, and thermal strength. We also note that it is expedient (in this case, the deformations will be minimal) to make the edges of the hull, wings and nose cone of the hull in the form of a single piece.