Nonstationary Flow of a Viscous Incompressible Electrically Conductive Fluid on a Rotating Plate

Abstract

In this work, the evolution of a flow of a viscous electrically conductive fluid on a rotating plate in the presence of a magnetic field is studied. The analytical solution of three-dimensional unsteady equations of magnetohydrodynamics is presented. The velocity field and the induced magnetic field in the flow of a viscous electrically conductive fluid filling a half-space bounded by a flat wall are determined. The fluid, together with the bounding plane, rotates as a whole with a constant angular velocity around a direction not perpendicular to the plane. An unsteady flux is induced by suddenly beginning vibrations of the wall and an applied magnetic field directed perpendicular to the plane. A number of special cases of the wall motion are considered. Based on the results obtained, the individual structures of the boundary layers near the wall are investigated.

1 INTRODUCTION

Magnetic hydrodynamics (MHD) began to develop intensely in the middle of the last century due to the rapid development of research in astrophysics and thermonuclear energy and the creation of new instruments and devices for power and propulsion systems.

A large series of papers exists dealing with the study of magnetohydrodynamic boundary layers. The interest in this subject is associated with the possibility of using an electromagnetic field as a control factor aiming at restructuring the entire flow, which is especially relevant in connection with the development of hypersonic aerodynamics and rocket technologies. A deep analogy has been found between the flowing of bodies and the flowing of local resistances.

This paper generalizes previous results [1–5]. We have investigated [1] the unsteady motion of a viscous fluid bounded by a moving flat wall. Unsteady boundary layers of a viscous incompressible fluid (Rayleigh–Stokes layers) on a rotating plate in the absence of a magnetic field have been considered [2]. The evolution of a viscous flow on a rotating plate, which was induced by longitudinal vibrations of a wall and injection (suction) of medium in the absence of a magnetic field, has been studied in [3]. The steady flow of an ideal electrically conductive fluid rotating between parallel walls in a constant magnetic field has been studied in [4]. The unsteady motion of a viscous electrically conductive fluid between rotating parallel walls in the presence of a magnetic field has been investigated in [5]. In the present paper, the unsteady flow of a viscous electrically conductive incompressible fluid on a rotating plate in the presence of a magnetic field is studied. The fluid occupies a half-space bounded by a flat wall and rotates together with the wall with a constant angular velocity around an axis. At time moment t > 0, the wall begins to vibrate longitudinally, and, at the same time, a homogeneous magnetic field with constant induction is switched on and directed normally to the wall. Next, we study the propagation of perturbations in a homogeneous conductive medium under the action of a homogeneous magnetic field and longitudinal vibrations of the wall. This paper is motivated by both fundamental and purely applied aspects of modern geophysical research. In particular, the problem of determining the parameters of artificial wave source using the electromagnetic effect of the agitation caused by it is very urgent. The relevance of the topic is stipulated by the need to study the World Ocean, which is playing an increasingly significant role in the life of humanity. This consideration has contributed to starting research of macroscopic motions of seawater (conductive fluid) exposed to the Earth’s magnetic field, which are accompanied by the appearance of electric currents and, consequently, an induced magnetic field. Therefore, the problem of determining the induced electromagnetic field is divided into two parts: determining the field of wave velocities and finding the electromagnetic disturbance velocity by the set velocity field. The velocity of the medium is found either from the results of in situ observations or by solving the hydrodynamic problem. The contents of the present paper can be considered as a mathematical model of seawater flows in the Earth’s magnetic field, as well as of other processes in astrophysical problems (planet magnetospheres, jets and accretion disks, etc.). The case of resonance (when the frequency of the wall longitudinal oscillations coincides with the doubled frequency of the projection of the angular velocity of the body–liquid system) is discussed in the paper. The resonance leads to a nontrivial physical effect: the amplitude of the oscillating velocity field does not vanish at infinity, but remains finite.

2 ANALYTICAL SOLUTION OF EQUATIONS OF MAGNETIC HYDRODYNAMICS

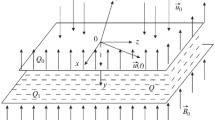
Let us consider the motion of a viscous electrically conductive incompressible fluid in a half-space bounded by a flat wall; the fluid rotates as a unit with the wall with angular velocity ${{\omega }_{0}} = {\text{const}}$, and vector ω₀ forms angle $\beta \left( {0 < \beta \leqslant \frac{\pi }{2}} \right)$ with this plane. Infinite plate H confines half-space Q filled with an incompressible fluid with density ρ, kinematic viscosity ν, and magnetic permeability $\mu$. The fluid is in a field of mass forces with potential U. The geometry is shown schematically in Fig. 1.

Fig. 1.

We associate with the plate the Cartesian coordinate system ${{Q}_{{xyz}}}$ with unit vectors ${{\vec {e}}_{x}}$, ${{\vec {e}}_{y}}$, ${{\vec {e}}_{z}}$, so that plane O_xz coincides with the plate and axis Q_y is directed perpendicularly to the plate inward the fluid.

At time moment t > 0, the plate begins to move in a longitudinal direction with velocity $\vec {u}(t)$; at the same moment, a homogeneous magnetic field with induction ${{\vec {B}}_{0}}$ normal to the plate—i.e., ${{\vec {B}}_{0}}$ = ${{B}_{0}}{{\vec {e}}_{y}}$—is switched on.

Before writing the equations of motion of a viscous electrically conductive fluid, let us specify some characteristics of the induction equation $\frac{{\partial \vec {B}}}{{\partial t}}$ = ${\text{curl}}\left( {{\vec {v}} \times \vec {B}} \right)$ + $\frac{1}{{\mu \sigma }}\Delta \vec {B}$. An important property of this equation is invariance with respect to the transition to the rotating coordinate system. This can be explained by the fact that field $\vec {B}$ has the above invariance in the magnetohydrodynamic approximation. Another important property of this equation is that, in the case of an infinitely conductive fluid, the flux of field $\vec {B}$ through any material surface inside the fluid is conserved (the field lines are frozen into the moving substance). We assume large Reynolds magnetic number ${{\operatorname{Re} }_{m}}$ = $\frac{{VL}}{{{{\nu }_{m}}}}$, which is the ratio by order of magnitude of the second term on the right-hand side of this equation to the first term. Here, V is the characteristic velocity in this problem, $L$ is the characteristic size, and ν_m is the magnetic viscosity. The case ${{\operatorname{Re} }_{m}} \ll 1$ is realized not only at a very high conductivity, but also in the case of large sizes and velocities of the system, which is typical for astrophysical problems. Since the presented problem can be a mathematical model of a seawater (conductive fluid) flow in the magnetic field of the rotating Earth, the case ${{\operatorname{Re} }_{m}} \gg 1$ takes place. In this case, only the first term should be left in the induction equation.

The equation of fluid motion in coordinate system Q_xyz that rotates with angular velocity ${{\vec {w}}_{0}}$ and the boundary and initial conditions can be written as

$${{\vec {\omega }}_{0}} \times \left( {{{{\vec {\omega }}}_{0}} \times \vec {r}} \right) + 2{{\vec {\omega }}_{0}} \times {\vec {v}} + \frac{{\partial {\vec {v}}}}{{\partial t}} + ({\vec {v}}\nabla ){\vec {v}} = - \frac{1}{\rho }\nabla P$$

$$ + \;\nabla U + \nu \Delta {\vec {v}} + \frac{1}{{\mu \rho }}{\text{curl}}\vec {B} \times \vec {B},$$

$$\operatorname{div} {\vec {v}} = 0\quad {\text{for}}\quad \vec {r} \in Q,$$

(2.1)

$$\frac{{\partial \vec {B}}}{{\partial t}} = {\text{curl}}\left( {{\vec {v}} \times \vec {B}} \right),$$

$$\operatorname{div} \vec {B} = 0\quad {\text{for}}\quad \vec {r} \in Q,$$

(2.1)

and the boundary and initial conditions are

$${\vec {v}}(\vec {r},t) = \vec {u}(t),\quad \vec {r} \in H,\quad t > 0,$$

$$\left| {{\vec {v}}(\vec {r},t)} \right| \to 0,\quad \left| {\vec {r}} \right| \to \infty ,\quad t > 0,$$

$${\vec {v}}(\vec {r},0) = 0,\quad \vec {r} \in Q,$$

$$\vec {B}(\vec {r},t) = {{\vec {B}}_{0}} = \operatorname{const} ,\quad \vec {r} \in H,\quad t > 0,$$

$$\vec {B}(\vec {r},0) = 0,\quad \vec {r} \in Q.$$

Here, t is time, $\vec {r}$ is radius vector with respect to pole O, ${\vec {v}}$ is fluid velocity, and P is pressure.

We look for the solution of system of equations (2.1) satisfying the initial and boundary conditions in the following form:

$$\begin{gathered} {\vec {v}} = {{{v}}_{x}}(y,t){{{\vec {e}}}_{x}} + {{{v}}_{z}}(y,t){{{\vec {e}}}_{z}}, \\ \vec {B} = {{B}_{x}}(y,t){{{\vec {e}}}_{x}} + {{B}_{0}}{{{\vec {e}}}_{y}} + {{B}_{z}}(y,t){{{\vec {e}}}_{z}}, \\ P = \frac{\rho }{2}{{({{{\vec {\omega }}}_{0}} \times \vec {r})}^{2}} + \rho U + \rho q(y,t). \\ \end{gathered} $$

(2.2)

System (2.1) can then be divided into subsystems:

$$\begin{gathered} \frac{{\partial {{{v}}_{x}}}}{{\partial t}} + 2{{{\vec {\omega }}}_{{0y}}}{{{\vec {e}}}_{y}} \cdot {{{v}}_{z}} = \nu \frac{{{{\partial }^{2}}{{{v}}_{x}}}}{{\partial {{y}^{2}}}} + \frac{1}{{\mu \rho }}{{B}_{0}}\frac{{\partial {{B}_{x}}}}{{\partial y}}, \\ \frac{{\partial {{{v}}_{z}}}}{{\partial t}} - 2{{{\vec {\omega }}}_{{0y}}}{{{\vec {e}}}_{y}} \cdot {{{v}}_{x}} = \nu \frac{{{{\partial }^{2}}{{{v}}_{z}}}}{{\partial {{y}^{2}}}} + \frac{1}{{\mu \rho }}{{B}_{0}}\frac{{\partial {{B}_{z}}}}{{\partial y}}, \\ \end{gathered} $$

(2.3)

$$\frac{{\partial q}}{{\partial y}} = 2{\vec {v}}({{\vec {\omega }}_{0}} \times {{\vec {e}}_{y}}) - \frac{1}{{\mu \rho }}\left( {{{B}_{z}}\frac{{\partial {{B}_{z}}}}{{\partial y}} + {{B}_{x}}\frac{{\partial {{B}_{x}}}}{{\partial y}}} \right),$$

(2.4)

$$\frac{{\partial {{B}_{x}}}}{{\partial t}} = {{B}_{0}}\frac{{\partial {{{v}}_{x}}}}{{\partial y}},\quad \frac{{\partial {{B}_{z}}}}{{\partial t}} = {{B}_{0}}\frac{{\partial {{{v}}_{z}}}}{{\partial y}}.$$

(2.5)

We denote ${{\omega }_{y}} = {{\vec {\omega }}_{0}}{{\vec {e}}_{y}} = \Omega$ and introduce the complex structure

$${\hat {v}} = {{{v}}_{x}}(y,t) + i{{{v}}_{z}}(y,t),\quad \hat {u} = {{u}_{x}} + i{{u}_{z}},\quad \hat {B} = {{B}_{x}}(y,t) + i{{B}_{z}}(y,t).$$

The system of equations can then be written as

$$\begin{gathered} \frac{{\partial {\hat {v}}}}{{\partial t}} - i2\Omega {\hat {v}} = \nu \frac{{{{\partial }^{2}}{\hat {v}}}}{{\partial {{y}^{2}}}} + \frac{{{{B}_{0}}}}{{\mu \rho }}\frac{\partial }{{\partial y}}\hat {B}, \\ \frac{{\partial \hat {B}}}{{\partial t}} = {{B}_{0}}\frac{{\partial {\hat {v}}}}{{\partial y}}, \\ \end{gathered} $$

(2.6)

with the boundary and initial conditions:

$$\begin{gathered} {\hat {v}}(y,t) = \hat {u}(t)\quad {\text{for}}\quad y = 0,\quad \hat {B}(y,t) = 0\quad {\text{for}}\quad y = 0,\quad t > 0, \\ \left| {{\hat {v}}(y,t)} \right| = 0\quad {\text{for}}\quad y \to \infty ,\quad \left| {\hat {B}(y,t)} \right| = 0\quad {\text{for}}\quad y \to \infty , \\ {\hat {v}}(y,0) = 0,\quad \hat {B}(y,0) = 0,\quad {\text{for}}\quad t = 0,\quad y > 0. \\ \end{gathered} $$

Excluding the magnetic induction from Eqs. (2.6), we obtain

$$\begin{gathered} \frac{{{{\partial }^{2}}{\hat {v}}}}{{\partial {{t}^{2}}}} - \left( {i2\Omega + \nu \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right)\frac{{\partial {\hat {v}}}}{{\partial t}} - \frac{{B_{0}^{2}}}{{\mu \rho }}\frac{{{{\partial }^{2}}{\hat {v}}}}{{\partial {{y}^{2}}}} = 0, \\ {\hat {v}}(0,t) = \hat {u}(t)\quad {\text{for}}\quad y = 0, \\ {\hat {v}}(0,t) = 0\quad {\text{for}}\quad y \to \infty , \\ {\hat {v}}(y,0) = 0. \\ \end{gathered} $$

(2.7)

We look for the solution of Eq. (2.7) using the Fourier sine transform that we introduce by the following formula [8]:

$$\tilde {V}(\lambda ,t) = \sqrt {\frac{2}{\pi }} \int\limits_0^\infty {\tilde {V}(y,t)\sin\lambda ydy} .$$

Differential equation (2.7) takes the form

$$\begin{gathered} \frac{{{{\partial }^{2}}\tilde {V}(\lambda ,t)}}{{\partial {{t}^{2}}}} + (\nu {{\lambda }^{2}} - i2\Omega )\frac{{\partial \tilde {V}(\lambda ,t)}}{{\partial t}} + \frac{{{{\lambda }^{2}}B_{0}^{2}}}{{\mu \rho }}\tilde {V}(\lambda ,t) = \lambda \sqrt {\frac{2}{\pi }} \left( {\nu \hat {u}_{t}^{'} + \frac{{B_{0}^{2}}}{{\mu \rho }}\hat {u}} \right) = \mu (\lambda ,t), \\ \begin{array}{*{20}{l}} {\tilde {V}(\lambda ,0) = 0,\quad \frac{{\partial \tilde {V}(\lambda ,0)}}{{\partial t}} = 0} \end{array}. \\ \end{gathered} $$

(2.8)

here, $\begin{array}{*{20}{l}} {\mu (\lambda ,t) = \lambda \sqrt {\frac{2}{\pi }} \left( {\nu \hat {u}_{t}^{'} + \frac{{B_{0}^{2}}}{{\mu \rho }}\hat {u}} \right)} \end{array}$.

Characteristic equation (2.8) and its roots can be written as follows:

$$\begin{array}{*{20}{l}} {{{q}^{2}} + (\nu {{\lambda }^{2}} - i2\Omega )q + \frac{{{{\lambda }^{2}}B_{0}^{2}}}{{\mu \rho }} = 0} \end{array},$$

$$\begin{array}{*{20}{l}} {{{q}_{{1,2}}} = - \frac{1}{2}(\nu {{\lambda }^{2}} - i2\Omega ) \pm \sqrt {\frac{1}{4}{{{(\nu {{\lambda }^{2}} - i2\Omega )}}^{2}} - \frac{{{{\lambda }^{2}}B_{0}^{2}}}{{\mu \rho }}} = \sigma \pm \omega ,} \end{array}$$

where

$$\begin{array}{*{20}{l}} {\sigma = - \frac{1}{2}(\nu {{\lambda }^{2}} - i2\Omega ),\quad {{\omega }^{2}} = \frac{1}{4}{{{(\nu {{\lambda }^{2}} - i2\Omega )}}^{2}} - \frac{{{{\lambda }^{2}}B_{0}^{2}}}{{\mu \rho }} = {{\sigma }^{2}} - \frac{{{{\lambda }^{2}}B_{0}^{2}}}{{\mu \rho }}} \end{array}.$$

The solution of inhomogeneous equation (2.8) is

$$\begin{array}{*{20}{l}} {\tilde {V}(\lambda ,t) = {{C}_{1}}{{e}^{{{{q}_{1}}t}}} + {{C}_{2}}{{e}^{{{{q}_{2}}t}}},} \end{array}$$

where c₁ and c₂ can be found by the Lagrange method of variations of arbitrary constants:

$$\begin{gathered} c_{1}^{'}{{e}^{{{{q}_{1}}t}}} + c_{2}^{'}{{e}^{{{{q}_{2}}t}}} = 0, \\ c_{1}^{'}{{q}_{1}}{{e}^{{{{q}_{1}}t}}} + c_{2}^{'}{{q}_{2}}{{e}^{{{{q}_{2}}t}}} = \mu (\lambda ,t). \\ \end{gathered} $$

From it follows

$${{c}_{1}}(t) = {{\tilde {c}}_{1}} + \int\limits_0^t {\frac{{\mu \left( {\lambda ,\tau } \right){{e}^{{ - {{q}_{1}}\tau }}}}}{{{{q}_{1}} - {{q}_{2}}}}d\tau } ,\quad {{c}_{2}}(t) = {{\tilde {c}}_{2}} - \int\limits_0^t {\frac{{\mu (\lambda ,\tau ){{e}^{{ - {{q}_{2}}\tau }}}}}{{{{q}_{1}} - {{q}_{2}}}}d\tau } .$$

Finally,

$$\tilde {V}(\lambda ,t) = {{\tilde {c}}_{1}}{{e}^{{{{q}_{1}}t}}} + {{\tilde {c}}_{2}}{{e}^{{{{q}_{2}}t}}} + \frac{1}{{{{q}_{1}} - {{q}_{2}}}}\int\limits_0^t {\mu (\lambda ,\tau )({{e}^{{{{q}_{1}}(t - \tau )}}} - {{e}^{{{{q}_{2}}(t - \tau )}}})d\tau } .$$

(2.9)

If the initial conditions are satisfied, we obtain

$$\tilde {V}(\lambda ,t) = \frac{1}{\omega }\int\limits_0^t {\mu (\lambda ,\tau ){{e}^{{\sigma (t - \tau )}}}{\text{sinh}}\omega (t - \tau )d\tau } .$$

(2.10)

To find $\hat {V}(y,t)$, we apply the inverse Fourier sine transform

$$\hat {V}(y,t) = \sqrt {\frac{2}{\pi }} \,\int\limits_0^\infty {\tilde {V}(\lambda ,t)\sin\lambda yd\lambda } ,$$

and then we have

$$\hat {V}(y,t) = \frac{2}{\pi }\int\limits_0^\infty {\frac{\lambda }{\omega }} \,\int\limits_0^t {\left[ {\nu \hat {u}_{t}^{'}(\tau ) + \frac{{B_{0}^{2}}}{{\mu \rho }}\hat {u}(\tau )} \right]{{e}^{{\sigma (t - \tau )}}}} \sinh \omega (t - \tau )d\tau \sin\lambda yd\lambda $$

or

$$\hat {V}(y,t) = \frac{2}{\pi }\int\limits_0^t {\left[ {\nu \hat {u}_{t}^{'}(\tau ) + \frac{{B_{0}^{2}}}{{\mu \rho }}\hat {u}(\tau )} \right]} \int\limits_0^\infty {\frac{{\lambda \sin\lambda y}}{\omega }{{e}^{{\sigma (t - \tau )}}}} \sinh \omega (t - \tau )d\lambda d\tau .$$

(2.11)

The vector of tangential stresses acting on the wall from the fluid side is determined by the expression [1]

$$\begin{array}{*{20}{l}} {\hat {F} = \rho \nu {{{\left. {\frac{{\partial \hat {V}}}{{\partial y}}} \right|}}_{{y = 0}}}} \end{array}.$$

Substituting velocity $\begin{array}{*{20}{l}} {\hat {V}(y,t)} \end{array}$ from (2.11), we obtain

$$\hat {F} = \rho \nu \frac{2}{\pi }\int\limits_0^t {\left[ {\nu \hat {u}_{t}^{'}(\tau ) + \frac{{B_{0}^{2}}}{{\mu \rho }}\hat {u}(\tau )} \right]} \int\limits_0^\infty {\frac{{{{\lambda }^{2}}}}{\omega }{{e}^{{\sigma (t - \tau )}}}} \sinh \omega (t - \tau )d\lambda d\tau .$$

(2.12)

The relations found solve the problem completely.

3 LONGITUDINAL QUASI-HARMONIC VIBRATIONS OF THE PLATE

We consider a quasi-harmonic mode; i.e., we assume that the time dependence of all temporal factors of the problem is expressed through the multiplier ${{e}^{{\lambda t}}}$: $\lambda = - \alpha + i\omega$.

System of equations (2.6) and (2.8) can be written as

$$\lambda {{{v}}_{x}} + 2\Omega {{{v}}_{z}} = \nu \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}{{{v}}_{x}} + \frac{1}{{\mu \rho }}{{B}_{0}}\frac{\partial }{{\partial y}}{{B}_{x}},$$

$$\lambda {{{v}}_{z}} - 2\Omega {{{v}}_{x}} = \nu \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}{{{v}}_{z}} + \frac{1}{{\mu \rho }}{{B}_{0}}\frac{\partial }{{\partial y}}{{B}_{z}},$$

$$\lambda {{B}_{x}} = {{B}_{0}}\frac{{\partial {{{v}}_{x}}}}{{\partial y}},$$

(3.1)

$$\lambda {{B}_{z}} = {{B}_{0}}\frac{{\partial {{{v}}_{z}}}}{{\partial y}},$$

$$\begin{array}{*{20}{l}} {\frac{{\partial q}}{{\partial y}} = 2{\vec {v}}({{{\vec {\omega }}}_{0}} \times {{{\vec {e}}}_{y}}) - \frac{1}{{\mu \rho }}\left( {{{B}_{z}}\frac{{\partial {{B}_{z}}}}{{\partial y}} + {{B}_{x}}\frac{{\partial {{B}_{x}}}}{{\partial y}}} \right)} \end{array}.$$

We exclude the magnetic induction from Eqs. (3.1). Then the system of equations can be written as

$$\begin{gathered} \lambda {{{v}}_{x}} + 2\Omega {{{v}}_{z}} = \left( {\nu + \frac{{B_{0}^{2}}}{{\mu \rho \lambda }}} \right)\frac{{{{\partial }^{2}}{{{v}}_{x}}}}{{\partial {{y}^{2}}}}, \\ \lambda {{{v}}_{z}} - 2\Omega {{{v}}_{x}} = \left( {\nu + \frac{{B_{0}^{2}}}{{\mu \rho \lambda }}} \right)\frac{{{{\partial }^{2}}{{{v}}_{z}}}}{{\partial {{y}^{2}}}}. \\ \end{gathered} $$

We multiply the second equation by i and add it to the first equation:

$$\lambda ({{{v}}_{x}} + i{{{v}}_{z}}) - 2\Omega i({{{v}}_{x}} + i{{{v}}_{z}}) = \left( {\nu + \frac{{B_{0}^{2}}}{{\mu \rho \lambda }}} \right)\frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}\left( {{{{v}}_{x}} + i{{{v}}_{z}}} \right).$$

(3.2)

We denote $\begin{array}{*{20}{l}} {{{{v}}_{x}} + i{{{v}}_{z}} = {{W}_{2}}} \end{array}$, ${{\left. {{{W}_{2}}} \right|}_{{y = 0}}} = {{u}_{x}}(0) + i{{u}_{z}}(0)$, and then

$$\begin{array}{*{20}{l}} {\frac{{{{\partial }^{2}}{{W}_{2}}}}{{\partial {{y}^{2}}}} = \frac{{\lambda - i2\Omega }}{{\nu + {{B_{0}^{2}} \mathord{\left/ {\vphantom {{B_{0}^{2}} {\mu \rho \lambda }}} \right. \kern-0em} {\mu \rho \lambda }}}}{{W}_{2}};\quad {{W}_{2}} \to 0\quad {\text{for}}\quad y \to \infty } \end{array}.$$

Next, by multiplying the second equation by i and subtracting from the first, we obtain

$$\begin{gathered} \frac{{{{\partial }^{2}}{{W}_{1}}}}{{\partial {{y}^{2}}}} = \frac{{\lambda + i2\Omega }}{{\nu + {{B_{0}^{2}} \mathord{\left/ {\vphantom {{B_{0}^{2}} {\mu \rho \lambda }}} \right. \kern-0em} {\mu \rho \lambda }}}}{{W}_{1}}, \\ \begin{array}{*{20}{l}} {{{W}_{1}} = {{{v}}_{x}} - i{{{v}}_{z}},\quad {{{\left. {{{W}_{1}}} \right|}}_{{y = 0}}} = {{u}_{x}}(0) - i{{u}_{z}}(0),\quad {{W}_{1}} \to 0\quad {\text{for}}\quad y \to \infty .} \end{array} \\ \end{gathered} $$

(3.3)

Here,

$$\begin{array}{*{20}{l}} {{{W}_{1}} = {{{v}}_{x}} - i{{{v}}_{z}};\quad {{{v}}_{x}} = \frac{1}{2}\left( {{{W}_{1}} + {{W}_{2}}} \right),} \\ {{{W}_{2}} = {{{v}}_{x}} + i{{{v}}_{z}};\quad {{{v}}_{z}} = \frac{i}{2}\left( {{{W}_{1}} - {{W}_{2}}} \right).} \end{array}$$

(3.4)

Equations (3.2)–(3.4) have a solution for $\lambda \ne \pm i2\Omega$.

$$\begin{gathered} {{W}_{1}} = \left[ {{{u}_{x}}(0) - i{{u}_{z}}(0)} \right]{{e}^{{{{\mu }_{1}}y}}},\quad {\text{where}}\quad {{\mu }_{1}} = \sqrt {\frac{{\lambda + i2\Omega }}{{\nu + {{B_{0}^{2}} \mathord{\left/ {\vphantom {{B_{0}^{2}} {\mu \rho \lambda }}} \right. \kern-0em} {\mu \rho \lambda }}}}} ,\quad \operatorname{Re} {{\mu }_{1}} < 0, \\ {{W}_{2}} = \left[ {{{u}_{x}}(0) + i{{u}_{z}}(0)} \right]{{e}^{{{{\mu }_{2}}y}}},\quad {\text{where}}\quad {{\mu }_{2}} = \sqrt {\frac{{\lambda - i2\Omega }}{{\nu + {{B_{0}^{2}} \mathord{\left/ {\vphantom {{B_{0}^{2}} {\mu \rho \lambda }}} \right. \kern-0em} {\mu \rho \lambda }}}}} ,\quad \operatorname{Re} {{\mu }_{2}} < 0. \\ \end{gathered} $$

(3.5)

Finally,

$$\begin{gathered} {{{v}}_{x}} = \frac{1}{2}(\left[ {{{u}_{x}}\left( 0 \right) - i{{u}_{z}}\left( 0 \right)} \right]{{e}^{{{{\mu }_{1}}y}}} + \left[ {{{u}_{x}}\left( 0 \right) + i{{u}_{z}}\left( 0 \right)} \right]{{e}^{{{{\mu }_{2}}y}}}){{e}^{{\lambda t}}}, \\ {{{v}}_{z}} = \frac{i}{2}(\left[ {{{u}_{x}}\left( 0 \right) - i{{u}_{z}}\left( 0 \right)} \right]{{e}^{{{{\mu }_{1}}y}}} - \left[ {{{u}_{x}}\left( 0 \right) + i{{u}_{z}}\left( 0 \right)} \right]{{e}^{{{{\mu }_{2}}y}}}){{e}^{{\lambda t}}}, \\ {{B}_{x}} = \frac{{{{B}_{0}}}}{\lambda }\frac{{\partial {{{v}}_{x}}}}{{\partial y}},\quad {{B}_{z}} = \frac{{{{B}_{0}}}}{\lambda }\frac{{\partial {{{v}}_{z}}}}{{\partial y}}, \\ q\left( {y,t} \right) = 2\int {{\vec {v}}({{{\vec {\omega }}}_{0}} \times {{{\vec {e}}}_{y}})dy} - \frac{1}{{2\mu \rho }}(B_{x}^{2} + B_{z}^{2}), \\ \end{gathered} $$

(3.6)

or, in vector form,

$${\vec {v}}(y,t) = {{e}^{{\lambda t}}}\left[ {\vec {u}(0)\frac{{{{E}_{1}} + {{E}_{2}}}}{2} + i\vec {u}(0) \times {{{\vec {e}}}_{y}}\frac{{{{E}_{1}} - {{E}_{2}}}}{2}} \right],$$

(3.7)

where $\begin{array}{*{20}{l}} {{{E}_{j}} = {{e}^{{{{\mu }_{j}}y}}}} \end{array}$, $j = 1,2$, $\begin{array}{*{20}{l}} {{{\mu }_{j}} = \sqrt {\frac{{\lambda \pm i2\Omega }}{{{v} + {{B_{0}^{2}} \mathord{\left/ {\vphantom {{B_{0}^{2}} {\mu \rho \lambda }}} \right. \kern-0em} {\mu \rho \lambda }}}}} } \end{array}$.

Consider the resonance case: $\begin{array}{*{20}{l}} {\lambda = \pm i2\Omega } \end{array}$. Then,

$$\begin{gathered} {\vec {v}}(y,t) = {{e}^{{\lambda t}}}\left[ {\vec {u}(0)\frac{{{{E}_{1}} + 1}}{2} + i\vec {u}(0) \times {{{\vec {e}}}_{y}}\frac{{{{E}_{1}} - 1}}{2}} \right]\quad {\text{for}}\quad \lambda = + i2\Omega , \\ {\vec {v}}(y,t) = {{e}^{{\lambda t}}}\left[ {\vec {u}(0)\frac{{1 + {{E}_{2}}}}{2} + i\vec {u}(0) \times {{{\vec {e}}}_{y}}\frac{{1 - {{E}_{2}}}}{2}} \right]\quad {\text{for}}\quad \lambda = - i2\Omega . \\ \end{gathered} $$

In both cases, for $\begin{array}{*{20}{l}} {y \to \infty } \end{array}$, the fluid velocity field

$$\begin{array}{*{20}{l}} {{\vec {v}}(y,t) = \frac{1}{2}{{e}^{{\lambda t}}}\left[ {\vec {u}\left( 0 \right) \mp i\vec {u}\left( 0 \right) \times {{{\vec {e}}}_{y}}} \right]} \end{array}$$

has an oscillatory character and, while remaining bounded, does not vanish. In this resonance case $\begin{array}{*{20}{l}} {\lambda = \pm i2\Omega } \end{array}$, the solution satisfies the conditions on plate H, but does not satisfy the conditions at infinity. This is the so-called “hydrodynamic paradox.”

From relations (3.7), we find the field $\vec {B} = ({{B}_{x}},{{B}_{z}})$,

$$\begin{array}{*{20}{l}} {\vec {B}(y,t) = \frac{{{{B}_{0}}}}{\lambda }{{e}^{{\lambda t}}}\left[ {\vec {u}\left( 0 \right)\frac{{{{\mu }_{1}}{{E}_{1}} + {{\mu }_{2}}{{E}_{2}}}}{2} + i\vec {u}\left( 0 \right) \times {{{\vec {e}}}_{y}}\frac{{{{\mu }_{1}}{{E}_{1}} - {{\mu }_{2}}{{E}_{2}}}}{2}} \right]} \end{array},$$

and the field of pressures

$$q(y,t) = \left[ {\left( {{{{\vec {\omega }}}_{0}} \times {{{\vec {e}}}_{y}}} \right)\left[ {\vec {u}(0)\left( {\frac{{{{E}_{1}}}}{{{{\mu }_{1}}}} + \frac{{{{E}_{2}}}}{{{{\mu }_{2}}}}} \right) + i(\vec {u}\left( 0 \right) \times {{{\vec {e}}}_{y}})\left( {\frac{{{{E}_{1}}}}{{{{\mu }_{1}}}} - \frac{{{{E}_{2}}}}{{{{\mu }_{2}}}}} \right)} \right]} \right]{{e}^{{\lambda t}}} - \frac{1}{2}\frac{1}{{\mu \rho }}{{\left| {\vec {B}(y,t)} \right|}^{2}}.$$

4 STRUCTURE OF THE BOUNDARY LAYERS

Let the plate move with velocity $\vec {u}\left( t \right)$ = $\vec {u}\left( 0 \right){{e}^{{\lambda t}}}$, $\lambda = - \alpha + i\omega$. The velocity field of a viscous electrically conductive fluid can be written in the form

$$\begin{array}{*{20}{l}} {{\vec {v}}\left( {y,t} \right) = {{e}^{{\left( { - \alpha + i\omega } \right)t}}}\left[ {\vec {u}\left( 0 \right)\frac{{{{E}_{1}} + {{E}_{2}}}}{2} + i\vec {u}\left( 0 \right) \times {{{\vec {e}}}_{y}}\frac{{{{E}_{1}} - {{E}_{2}}}}{2}} \right],} \end{array}$$

(4.1)

where $\begin{array}{*{20}{l}} {{{E}_{1}} = {{e}^{{{{\mu }_{1}}y}}}} \end{array}$, ${{E}_{2}} = {{e}^{{{{\mu }_{2}}y}}}$, ${{\mu }_{{1,2}}} = \sqrt {\frac{{\lambda \pm i2\Omega }}{{\nu + {{B_{0}^{2}} \mathord{\left/ {\vphantom {{B_{0}^{2}} {\mu \rho \lambda }}} \right. \kern-0em} {\mu \rho \lambda }}}}}$, $\operatorname{Re} {{\mu }_{{1,2}}} < 0$.

We consider

$$\frac{{\lambda \pm i2\Omega }}{{\nu + {{B_{0}^{2}} \mathord{\left/ {\vphantom {{B_{0}^{2}} {\mu \rho \lambda }}} \right. \kern-0em} {\mu \rho \lambda }}}} = \frac{{ - \alpha A + B\left( {\omega \pm 2\Omega } \right) + i\left( {\alpha B + A\left( {\omega \pm 2\Omega } \right)} \right)}}{{{{A}^{2}} + {{B}^{2}}}},$$

where $\begin{array}{*{20}{l}} {A = \nu - \frac{{\alpha B_{0}^{2}}}{{\mu \rho ({{\alpha }^{2}} + {{\omega }^{2}})}}} \end{array}$; $B = - \frac{{\omega B_{0}^{2}}}{{\mu \rho ({{\alpha }^{2}} + {{\omega }^{2}})}}$.

Then, $\begin{array}{*{20}{l}} {{{A}^{2}} + {{B}^{2}} = {{\nu }^{2}} + \frac{{B_{0}^{4} - 2\nu \alpha \mu \rho B_{0}^{2}}}{{{{\mu }^{2}}{{\rho }^{2}}({{\alpha }^{2}} + {{\omega }^{2}})}}} \end{array}$.

We denote

$$\begin{array}{*{20}{l}} {C = \frac{{ - \alpha A + B\left( {\omega \pm 2\Omega } \right)}}{{{{A}^{2}} + {{B}^{2}}}},\quad D = \frac{{\alpha B + A\left( {\omega \pm 2\Omega } \right)}}{{{{A}^{2}} + {{B}^{2}}}}} \end{array}$$

and consider $\begin{array}{*{20}{l}} {{{\mu }_{{1,2}}} = \sqrt {C + iD} } \end{array}$.

Let us introduce the notations $\sqrt {C + iD} = {{\mu }_{{1,2}}} = \frac{1}{{{{\delta }_{{1,2}}}}} + i{{k}_{{1,2}}}$, where subscript “1” corresponds to the “+” sign and subscript “2” corresponds to the “–” sign.

Here,

$$\begin{array}{*{20}{l}} {\frac{1}{{\delta _{{1,2}}^{2}}} = \frac{{\sqrt {{{C}^{2}} + {{D}^{2}}} + C}}{2},\quad k_{{1,2}}^{2} = \frac{{\sqrt {{{C}^{2}} + {{D}^{2}}} - C}}{2}} \end{array}.$$

Adjusted for the introduced notations, the velocity field takes the form

$${\vec {v}} = {{\hat {A}}_{1}}{{e}^{{i\left( {\omega t - {{k}_{1}}y} \right)}}} + {{\hat {A}}_{2}}{{e}^{{i\left( {\omega t + {{k}_{2}}y} \right)}}},$$

where

$${{\hat {A}}_{1}} = \frac{1}{2}\left[ {\vec {u}\left( 0 \right) + i\vec {u}\left( 0 \right) \times {{{\vec {e}}}_{y}}} \right]{{e}^{{ - \alpha t}}}{{e}^{{ - {y \mathord{\left/ {\vphantom {y {{{\delta }_{1}}}}} \right. \kern-0em} {{{\delta }_{1}}}}}}},\quad {{\hat {A}}_{2}} = \frac{1}{2}\left[ {\vec {u}\left( 0 \right) - i\vec {u}\left( 0 \right) \times {{{\vec {e}}}_{y}}} \right]{{e}^{{ - \alpha t}}}{{e}^{{ - {y \mathord{\left/ {\vphantom {y {{{\delta }_{2}}}}} \right. \kern-0em} {{{\delta }_{2}}}}}}}.$$

The obtained solution is a superposition of two waves with wavenumbers k_{1, 2} and frequency ω, which propagate along the Oy axis in the opposite direction and exponentially attenuate at distances about δ_{1, 2}, respectively. The size of the boundary layer is determined by the distance at which the wave amplitude decreases by a factor of e; i.e., δ_{1, 2} are the thicknesses of the boundary layers adjacent to the wall.

The plane waves are induced by the decaying harmonic oscillations of the plate. The phase velocities of these waves are different because wavenumbers k₁ and k₂ are different. In addition, the velocities depend on frequency. This means that the flow of a viscous electrically conductive fluid is a disperse medium.

Group velocities of these waves ${{{v}}_{{\operatorname{gr} }}} = \frac{{d\omega }}{{dk}}$ are also different. They depend on the attenuation and rotation coefficients of the system, magnetic induction, and fluid parameters. The amplitudes of these waves depend on the magnitude of the angular velocity projection on the y axis, wall-motion parameters, magnetic induction, and fluid parameters. Note that the wave emitted by the wall attenuates at depth δ₁ and the next wave coming from infinity to the wall attenuates at depth δ₂.

Choose the field induction $B_{0}^{2} = 2\nu \alpha \mu \rho$. Then, ${{A}^{2}} + {{B}^{2}} = {{\nu }^{2}}$, where $A$ = $\nu \frac{{{{\omega }^{2}} - {{\alpha }^{2}}}}{{{{\alpha }^{2}} + {{\omega }^{2}}}}$, $B$ = $- \nu \frac{{2\alpha \omega }}{{{{\alpha }^{2}} + {{\omega }^{2}}}}$.

In this case, the wavenumbers can be written in the form

$${{k}_{{1,2}}} = \sqrt {\frac{\alpha }{{2\nu }}} {{\left( {\sqrt {1 + \frac{{{{{(\omega \pm 2\Omega )}}^{2}}}}{{{{\alpha }^{2}}}}} + \frac{{2\omega (\omega \pm 2\Omega )}}{{{{\alpha }^{2}} + {{\omega }^{2}}}} + \frac{{{{\omega }^{2}} - {{\alpha }^{2}}}}{{{{\alpha }^{2}} + {{\omega }^{2}}}}} \right)}^{{\frac{1}{2}}}},$$

$${{\delta }_{{1,2}}} = \sqrt {\frac{{2\nu }}{\alpha }} {{\left( {\sqrt {1 + \frac{{{{{(\omega \pm 2\Omega )}}^{2}}}}{{{{\alpha }^{2}}}}} - \frac{{2\omega (\omega \pm 2\Omega )}}{{{{\alpha }^{2}} + {{\omega }^{2}}}} - \frac{{{{\omega }^{2}} - {{\alpha }^{2}}}}{{{{\alpha }^{2}} + {{\omega }^{2}}}}} \right)}^{{ - \frac{1}{2}}}}.$$

Wavenumbers k₁ and k₂ and boundary-layer values δ₁ and δ₂ do not depend on the magnetic permeability or electrical conductivity of the fluid, but are determined only by attenuation coefficient α and fluid viscosity ν.

In addition, the fluid rotation (the projection of the angular velocity of the system rotation onto the Oy axis) has a great influence on the wave-propagation pattern.

We introduce dimensionless variable $Y = \omega {\text{/}}\alpha$ and dimensionless parameter $S = 2\Omega {\text{/}}\alpha$. The expressions for the wavenumbers can then be written in the following form:

$${{k}_{{1,2}}} = \sqrt {\frac{\alpha }{{2\nu }}} {{\left( {\sqrt {1 + {{{(Y \pm S)}}^{2}}} + \frac{{2Y(Y \pm S)}}{{{{Y}^{2}} + 1}} + \frac{{{{Y}^{2}} - 1}}{{{{Y}^{2}} + 1}}} \right)}^{{\frac{1}{2}}}},$$

$${{\delta }_{{1,2}}} = \sqrt {\frac{{2\nu }}{\alpha }} {{\left( {\sqrt {1 + {{{(Y \pm S)}}^{2}}} - \frac{{2Y(Y \pm S)}}{{{{Y}^{2}} + 1}} - \frac{{{{Y}^{2}} - 1}}{{{{Y}^{2}} + 1}}} \right)}^{{ - \frac{1}{2}}}}.$$

In Fig. 2, wavenumbers k₁ and k₂ are presented as functions of Y (frequency ω at fixed s = 2).

Fig. 2.

In the case under consideration, $k(\omega )$ is generally a complex wavenumber. Its real part characterizes the frequency dependence of the wave phase velocity, and its imaginary part shows the frequency dependence of the attenuation coefficient of the wave amplitude. As a rule, dispersion is related to the internal properties of the material medium. There is a frequency (temporal) dispersion, which implies that the dispersing medium polarization depends on the field values at the preceding time moments (memory), and a spatial dispersion, meaning that the polarization at a given point depends on the field values in a certain area of the space (nonlocality). The curves show that wavenumber k₂ increases monotonously with the increase in frequency of the wall oscillations, while wavenumber k₁ displays a complex behavior and has a salient point.

The analysis of the dependence of wavenumbers δ₁ and δ₂ on Y (on frequency ω) for fixed s (s = 2) presented in Fig. 3 shows that there are singular points of the nonstationary problem, in the vicinity of which the wavenumbers become infinite. Derivatives ${{\partial {{\delta }_{1}}} \mathord{\left/ {\vphantom {{\partial {{\delta }_{1}}} {\partial Y}}} \right. \kern-0em} {\partial Y}}$ and ${{\partial {{\delta }_{2}}} \mathord{\left/ {\vphantom {{\partial {{\delta }_{2}}} {\partial Y}}} \right. \kern-0em} {\partial Y}}$ show a discontinuity of the first kind; therefore, the problem of the wave-packet propagation in the given medium should be investigated more thoroughly. For a wave emitted by an oscillating wall, Y = 2.81 is a singular point, near which wavenumber δ₁ has a discontinuity and vanishes with the increase in frequency. The wave packet velocity V_g1 shown in Fig. 4 also has a discontinuity at this point $(Y = 2.81)$. The wave incoming on the wall has singular point Y = 1.31, at which wavenumber δ₂ has an infinite discontinuity and vanishes with further increase in frequency.

Fig. 3.

Fig. 4.

Let us consider the case of resonance $\omega = 2\Omega$ (in dimensionless variables $Y = S$). The wavenumber and the boundary layer thickness for the wave emitted by the wall are

$${{k}_{1}} = \sqrt {\frac{\alpha }{{2\nu }}} {{\left\{ {\sqrt {1 + 4{{S}^{2}}} + \frac{{5{{S}^{2}} - 1}}{{{{S}^{2}} + 1}}} \right\}}^{{\frac{1}{2}}}},\quad \frac{1}{{{{\delta }_{1}}}} = \sqrt {\frac{{2\nu }}{\alpha }} {{\left\{ {\sqrt {1 + 4{{S}^{2}}} - \frac{{5{{S}^{2}} - 1}}{{{{S}^{2}} + 1}}} \right\}}^{{\frac{1}{2}}}}.$$

The wavenumber of the incoming wave is ${{k}_{2}}$ = $\sqrt {\frac{\alpha }{\nu }} \frac{S}{{\sqrt {1 + {{S}^{2}}} }}$, and the boundary layer thickness is ${{\delta }_{2}}$ = $\sqrt {\frac{\nu }{\alpha }} \sqrt {1 + {{S}^{2}}}$.

It is of interest to compare the obtained solution with the solution to the problem of a flat wall vibrations in a viscous incompressible fluid rotating in a half-space bounded by a wall considered in [6].

The structure of the solution can be written as follows:

$${\vec {v}} = {{\hat {A}}_{1}}{{e}^{{i\left( {\omega t - {{k}_{1}}y} \right)}}} + {{\hat {A}}_{2}}{{e}^{{i\left( {\omega t + {{k}_{2}}y} \right)}}},$$

where

$$\begin{gathered} {{{\hat {A}}}_{1}} = \frac{1}{2}\left[ {\vec {u}\left( 0 \right) + i\vec {u}\left( 0 \right) \times {{{\vec {e}}}_{y}}} \right]{{e}^{{ - \alpha t}}}{{e}^{{ - {y \mathord{\left/ {\vphantom {y {{{\delta }_{1}}}}} \right. \kern-0em} {{{\delta }_{1}}}}}}} \\ {{{\hat {A}}}_{2}} = \frac{1}{2}\left[ {\vec {u}\left( 0 \right) - i\vec {u}\left( 0 \right) \times {{{\vec {e}}}_{y}}} \right]{{e}^{{ - \alpha t}}}{{e}^{{ - {y \mathord{\left/ {\vphantom {y {{{\delta }_{2}}}}} \right. \kern-0em} {{{\delta }_{2}}}}}}}, \\ \end{gathered} $$

(4.2)

but the wave amplitudes and wavenumbers are different since the roots of the characteristic equation are quite different—namely, ${{\mu }_{j}} = \hat {\delta }_{{1,2}}^{{ - 1}}$ + $i{{\hat {k}}_{{1,2}}}$, and the branches of the root, for which $\operatorname{Re} {{\mu }_{j}} \leqslant 0$; $j = 1,2$, are chosen. The obtained solution is a superposition of two waves with wavenumbers ${{k}_{j}}$ $(j = 1,2)$ and frequency ω; the waves propagate along the Oy axis in the opposite direction and decay exponentially at distances about δ_j, respectively. Solution (4.2) is uniformly valid for the whole region, both in the nonresonance and resonance cases $(2\Omega = \omega )$. Indeed, when $\Omega = \omega$,

$${{k}_{1}} = \frac{{4\Omega }}{{\sqrt {2\nu } }}{{({{\alpha }^{2}} + 16{{\Omega }^{2}})}^{{ - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}},\quad {{\delta }_{1}} = \frac{{4\Omega }}{{{{k}_{1}}}}{{(2{{\alpha }^{2}} + 16{{\Omega }^{2}})}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\quad {{k}_{2}} = 0,\quad {{\delta }_{2}} = \sqrt {{\nu \mathord{\left/ {\vphantom {\nu \alpha }} \right. \kern-0em} \alpha }} ,$$

(4.3)

which means that, in the resonance case, there is no wave incoming on the plate; however, the solution is still decaying into the fluid. However, when α = 0, ${{\delta }_{2}} \to \infty$, and so the solution turns invalid for $y \to \infty$, since the thickness of one of the boundary layers increases infinitely. This effect of the absence of an oscillatory solution for $\omega = 2\Omega$ was discussed in [2]. An important conclusion from the above analysis is the fact that the attenuation removes the difficulties noted in [2]. In this sense, it plays a similar role to that of fluid suction from the surface of a porous plate considered in [3]. Let us find the connection between the wavenumbers of our problem and the wavenumbers of the problem of the wall oscillations in a viscous incompressible fluid. We denote the wavenumbers of this problem as ${{\tilde {k}}_{{1,2}}}$, ${{\tilde {\delta }}_{{1,2}}}$. Performing simple but cumbersome calculations, we obtain

$${{k}_{{1,2}}} = \left\{ {\frac{\alpha }{{{{{\tilde {\delta }}}_{{1,2}}}}} - \omega {{{\tilde {k}}}_{{1,2}}}} \right\}\frac{1}{{\sqrt {{{\omega }^{2}} + \alpha } }},\quad \frac{1}{{{{\delta }_{{1,2}}}}} = \left\{ {\frac{\omega }{{{{{\tilde {\delta }}}_{{1,2}}}}} - \alpha {{{\tilde {k}}}_{{1,2}}}} \right\}\frac{1}{{\sqrt {{{\omega }^{2}} + \alpha } }}.$$

Let us compare the wavenumbers for the resonance case $\omega = 2\Omega$ $(Y = S)$ ${{\tilde {k}}_{{1,2}}} = 0$, ${{\tilde {\delta }}_{{1,2}}} = \sqrt {\nu {\text{/}}\alpha }$. We obtain ${{k}_{2}}$ = $\frac{\alpha }{{{{{\tilde {\delta }}}_{{1,2}}}}}\frac{1}{{\sqrt {{{\omega }^{2}} + \alpha } }}$ = $\sqrt {\frac{\alpha }{\nu }} \frac{S}{{\sqrt {1 + {{S}^{2}}} }}$, ${{\delta }_{2}}$ = $\sqrt {\frac{\nu }{\alpha }} \sqrt {1 + {{S}^{2}}}$; i.e., in an electrically conductive fluid in a magnetic field, there is an incoming wave on the wall. The boundary layer thickness increases by the factor of $\sqrt {1 + {{S}^{2}}}$. Wavenumbers k₁ and ${{\hat {k}}_{1}}$ are also different. Comparing the results, we see how the magnetic field changes the velocity profile, the boundary-layer thickness, and the tangential stresses on the wall. It is interesting to compare the results obtained in [5] with the results of the present paper. Different boundary conditions in the problems of both papers lead to different solutions for the velocity field. In [5], the solution was presented as a superposition of two waves, one of which reflected from the stationary wall. These waves had equal wavenumbers and boundary-layer thicknesses, which differed from the corresponding values of the present problem. The velocities of the wave packets in [5] coincided, in contrast to the present paper, in which the velocities of the wave packets are different and differ from those in [5]. Only in the resonance case $\omega = 2\Omega$ do the wavenumbers from [5], which can be written in the form k = $\frac{{\sqrt {\alpha {\text{/}}\nu } }}{{\sqrt {1 + {{{{\alpha }^{2}}} \mathord{\left/ {\vphantom {{{{\alpha }^{2}}} {(4{{\Omega }^{2}})}}} \right. \kern-0em} {(4{{\Omega }^{2}})}}} }}$, $\delta$ = $\sqrt {\frac{\nu }{\alpha }} \sqrt {1 + \frac{{4{{\Omega }^{2}}}}{{{{\alpha }^{2}}}}}$, coincide with the values of k₂ and δ₂ obtained for the incoming wave in the present paper.

CONCLUSIONS

The problem of the unsteady flow of a viscous electrically conductive incompressible fluid in the parallel-plane configuration has been analyzed. The exact solutions of three-dimensional nonstationary equations of magnetic hydrodynamics have been found. No restrictions are imposed on the plate-motion pattern. The velocity field of the flow and the tangential stress vectors acting on the wall from the fluid are determined. For the case of “normal” oscillations of the plate, the resonance case is considered and the structure of boundary layers adjacent to the wall is studied. It is shown how the magnetic field changes the pattern of flow of the electrically conductive fluid by changing the fluid velocity field, the values of wavenumbers and of boundary layers. In addition, the tangential stresses acting on the wall from the fluid also change.

The mathematical procedure of integrating the system of differential equations of the considered problem can be used in the study of more complex problems. In addition, the obtained results can be used to consider the force effects of fluid motion in cavities of different shapes, as well as in filtration problems and in modeling various physical phenomena in a moving fluid.