Dynamic Modeling of Heated Oscillatory Layer of Non-Newtonian Liquid

Abstract—

In this work, we have effectively used the numerical inversion of the Laplace transform to study the time-dependent thin heated film flow of a viscoelastic fluid flowing on an infinitely long flat substrate. Exact and analytical solutions are obtained in some limiting cases. The model describing this problem is a system of equations, coupling the linearized Navier–Stokes equation of the viscoelastic fluid with regard for gravity as an external force and the temperature relation for the energy profile. By assuming that the fluids are incompressible, we first derive a new system of equations, by taking into account additional terms, due to the insoluble surfactants and the viscoelastic properties. The velocity and temperature profiles are shown and the influence of coupling constant, viscoelastic parameters and the interfacial surfactants on the liquid film are discussed in detail. The validity of our solutions is verified by the numerical results to show the effects of different parameters involved and to show how the fluid flow evolves with time.

The study of dynamical properties of a thin layer flow on a heated infinite long plate is still an important type for a large number of technological methods and has vast applications in industry. Moving liquid films have extensive use in various technological studies because of their applications to modern technology and industries. Such flows have implementations in microchips fabrication, condensers, heat exchangers, biomedical engineering, material processing, coating of paper or plastic, evaporators, food, and chemical industries and many other fields. Laplace transform is a very helpful tool for dealing with differential equations. However, to analytically evaluate the inverse Laplace transform of the solutions acquired by the utilization of the Laplace transform is a very significant but complicated step. To review some previous studies on this problem, a lot of algorithms for numerical inversion of the Laplace technique have been approached in the literature [1–7]. In [4] the Laplace transformation was applied to illustrate the problem of the unsteady and irrotational flow of a dipolar liquid set to motion by the acceleration of a flat plate from rest. Some significant new results concerning steady flows were given. The results obtained were compared with the relating case for a viscous Newtonian fluid, in which an exact general solution is obtained.

In [5] the Laplace transform method have been used to perform the exact solutions of two Couette flows of a second–grade fluid in a porous liquid layer in the case when the lower substrate moves unexpectedly and oscillates. In [6] the unsteady viscous flows and Stokes’s first problem have been investigated. In the unsteady motion, the relationship between Couette flow, Poiseuille flow, and boundary layer flow in the light of Stokes’ first problem are examined in that research. In a rectangular tank that is obeyed to a periodic oscillation, in [7] Durbin’s numerical inverse Laplace transform technique has been applied to illustrate the motion of a viscoelastic fluid layer in the presence of heat transfer.

Non-Newtonian fluids have been a very important problem of scientific research because of their various employ in considerable industrial processes. Several complex fluids like polymer melts, oils, distinct types of drilling muds and coatings of clay and many emulsions are involved in the category of non-Newtonian fluids. Flows of non-Newtonian fluids have been investigated by many authors [8–11]. Depending on a linear stability analysis in [8] the Bénard–Marangoni thermal instability has been investigated for Jeffreys’ fluid layer in a viscoelastic media bounded from the upper by a realistic free deformable surface and by a lower plane surface. It has been illustrated that the relaxation time, as well as surface deflection, have a destabilizing impact, unlike the retardation time.

In [9] the two-dimensional flow of a fluid represented by Walter’ B” model have been investigated in a viscoelastic domain running down an oblique heated substrate in the finite–amplitude regime, where a linear temperature variation is assumed. The analytical solutions relating to two modes of unidirectional flows of a generalized Oldroyd-B fluid with fractional derivative confined between two parallel planes in which the motion is unsteady are mentioned in [10]. In [11], the accelerated flows for fluid in terms of by the fractional Burgers’ model are considered, in which the fluid has viscoelastic properties. The problems of flow induced by a constantly accelerating plate and flow induced by changing accelerated substrate are solved exactly.

On the other hand, the presence of surfactants has an important impact on the shape and the motion of the interfaces. Surfactants also have an enormous range of implementation in the oil industry, for example in the cleanup of oil spills and for enhanced oil recovery. A number of studies have been devoted to the insoluble surfactant limit. In the limit of vanishing Reynolds number [12] the influence of surfactants has been illustrated on the gravity-driven flow of a liquid thin layer down an oblique wall with indentations or periodic undulations.

The subject of [13] is the study of a thin-film flow, in which the evolution relations for the surfactant concentration and the film thickness are discussed in the concept of the linear stability, where numerical calculations are done.

In [14] the longwave Marangoni convection in a liquid thin film with surfactant located on the surface has been examined in the linear approximation. The layer is subjected to a transverse temperature gradient, and a surfactant is governed by interfacial speed range and diffuses only over the free surface.

The motivation of the current study is to explore numerically and analytically the non-Newtonian impact in the presence of heat transfer and insoluble surfactants on the surface wave scheme formatted at the free interface of a liquid layer within a viscoelastic nature. The flow motion has happened on a horizontally oscillated infinite substrate. From this point of view, the present paper gives an extension to some published papers that recently used the Laplace transformation. Indeed, the Laplace method is very important for solving the problems and it is still used in recent research such as [15] that dealing with unsteady laminar boundary layer flow of a Maxwell liquid over an exponentially accelerated vertical flat wall subject to Newtonian and slip heating at the boundary. The authors obtained semi-analytical solutions of the dimensionless problem by employing the inverse Laplace transforms for temperature and speeds fields. In [16], the authors apply the Laplace transform to study the problem of free convection flow of a fractional viscous fluid over an infinite vertical plate with exponential heating, where the fluid motion is induced by the plate that involves arbitrary time-dependent shear stress to the liquid motion.

Overall, the fundamental differences in our work is to highlight the role of surfactants as well as the retardation and the relaxation times on the stability of the considered system, that is by applying the Laplace transform to obtain the numerical and semi analytical solutions in the original domain and to find the impacts of several fluid parameters. Exact and analytical outcomes are obtained in some limiting cases. In addition, in future studies, our work can be extended to include motion through porous media, porous substrate, wavy plane or imposed shear stress on the surface as well as a magnetic or electric field with surface charge. Further, the results presented here can find applications in modern technology and industries such as diesel and gas turbine engines, the production of plastics, oil burners, metal powders, liquid rocket engines, and lubricants.

1 MATHEMATICAL FORMULATION

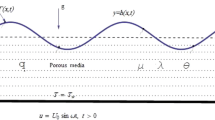
The problem under consideration is composed of a two-dimensional flow of a heated viscoelastic liquid film on an infinite long substrate. Away from the bulk of the fluid insoluble surfactants are assumed on the free surface. The phenomenon of the flow and the kind of boundary conditions are illustrated in Fig. 1. The substrate and the fluid are both initially motionless. Unexpectedly, the plate is shaken into motion at its own level with an oscillatory speed.

Fig. 1.

Schematic representation of the problem.

1.1 Equations of Motion

The constitutive relations depend on the conservation of mass (the continuity equation) and momentum equation for the motion of the liquid film and the heat equation for the temperature area [17–19].

$$\nabla \cdot {\mathbf{u}} = 0,$$

(1.1)

$$\rho \frac{{d{\mathbf{u}}}}{{dt}} = - \nabla p + \nabla \cdot \Pi + \rho {\mathbf{g}},$$

(1.2)

$$\rho {{c}_{p}}\frac{{dT}}{{dt}} = \kappa {{\nabla }^{2}}T,$$

(1.3)

where the notation u $= (u,{v})$ indicates the velocity vector, $\rho$ is the density of the fluid film, $d{\text{/}}dt \equiv \partial {\text{/}}\partial t + ({\mathbf{u}} \cdot \nabla )$ refers to the convective derivative, ${\mathbf{g}}$ is the gravity force, $\nabla \equiv (d{\text{/}}dx,d{\text{/}}dy)$ indicates the gradient operator, p is the pressure. Also, in Eq. (1.3)T identifies the temperature domain and $\kappa$ refers to thermal conductivity as well as c_p denotes the specific heat when the pressure is constant.

In this work we use the Oldroyd-B model, which classified a constitutive technique applied to the flow of viscoelastic fluids. The constitutive equation for the viscoelastic fluid is [8, 9]

$$\left( {1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}}} \right)\Pi = \mu \left( {1 + {{\lambda }_{2}}\frac{\partial }{{\partial t}}} \right)[\nabla {\mathbf{u}} + \nabla {{{\mathbf{u}}}^{{{{T}_{r}}}}}],$$

(1.4)

where λ₁ and λ₂ refer respectively to the characteristic relaxation time and the constant deformation retardation time and $\nabla {{{\mathbf{u}}}^{{{{T}_{r}}}}}$ characterizes the transpose of the gradient of the velocity vector.

1.2 Initial and Boundary Conditions

The corresponding boundary conditions on the limited surface and the interfacial constraints are mentioned to achieve the problem formulation (1.2)–(1.4). For time greater than zero, the substrate at zero vertical axis beginning unexpectedly to slide in its own level with an oscillatory speed. Under this circumstance, we formulate the following

$$u(y,t) = \left\{ \begin{gathered} 0\quad {\text{for}}\quad t = 0,\quad y > 0, \hfill \\ {{U}_{0}}{\text{sin}}\omega t\quad {\text{for}}\quad t > 0,\quad y = 0. \hfill \\ \end{gathered} \right.$$

(1.5)

The condition imposed for the temperature field reads as

$$T = {{T}_{w}}\quad {\text{at}}\quad y = 0.$$

(1.6)

Let the deformable free surface be $y = h(x,t)$ = $\ell + \,\eta (x,t)$. When the interface always has the same fluid particles, the kinematic condition is then imposed and therefore the function $y = h(x,t)$ whose graph defines the interface satisfies with each other:

$$\frac{{\partial h}}{{\partial t}} + {\mathbf{u}} \cdot \nabla (h - y) = 0.$$

(1.7)

The jump in the normal component of the surface–traction through the free surface is balanced by surface tension times curvature, which is expressed as

$${{p}_{{_{{{\text{air}}}}}}} - p + {\mathbf{n}} \cdot \Pi \cdot {\mathbf{n}} = 2H\sigma (\Gamma ,T),$$

(1.8)

where ${{p}_{{{\text{air}}}}}$ symbolizes the pressure afforded by the surrounding air, which is assumed to be constant. The perpendicular vector at any position on the surface signifies n = $\nabla (y - h(x,t))/{\text{|}}\nabla (y - h(x,t)){\text{|}}$, and H = $- \frac{1}{2}\nabla \cdot {\mathbf{n}}$ is the mean surface curvature.

The quantity $\sigma (\Gamma ,T)$ refers to the surface tension, which changes according to the linear law with the temperature range and the concentration of the surfactant domain, in which both Marangoni influences are taken into account, so that [9]

$$\sigma (\Gamma ,T) = {{\sigma }_{0}}({{\Gamma }_{0}},{{T}_{s}}) - {{\sigma }_{T}}(T - {{T}_{s}}) - {{\sigma }_{\Gamma }}(\Gamma - {{\Gamma }_{0}}),$$

(1.9)

where ${{\sigma }_{0}}$ is the reference parameter distinguish the surface tension, σ_T = $- \partial \sigma {\text{/}}\partial T{{{\text{|}}}_{{T = {{T}_{s}}}}}$ and σ_Γ = $- \partial \sigma {\text{/}}\partial \Gamma {{{\text{|}}}_{{\Gamma = {{\Gamma }_{0}}}}}$. Due to the presence of the Marangoni influences and air stress, the tangential component of the surface–traction is affected and reads as

$${\mathbf{n}} \cdot \Pi \cdot {\mathbf{t}} = \nabla \sigma (\Gamma ,T) \cdot {\mathbf{t}}.$$

(1.10)

Here, t refers to the unit vector over the tangential orientation at that point, where ${\mathbf{n}}$ · ${\mathbf{t}}$ = 0. Another thermal condition is Newton’s law of cooling that comes across the continuity of heat flux through the free surface:

$$\kappa \nabla T \cdot {\mathbf{n}} + {{h}_{{\text{g}}}}(T - {{T}_{s}}) = 0,$$

(1.11)

where ${{h}_{{\text{g}}}}$ represents the heat transfer parameter between the liquid and the air. On the free surface, the liquid layer contains insoluble surfactants with a concentration $\Gamma (x,t)$. The concentration allocation varies according to the transport equation [12–14]:

$$\frac{{\partial (N\Gamma )}}{{\partial t}} + \frac{{\partial (N\Gamma u)}}{{\partial x}} = {{D}_{s}}\frac{\partial }{{\partial x}}\left( {\frac{1}{N}\frac{{\partial \Gamma }}{{\partial x}}} \right).$$

(1.12)

Here, in the above equation $N = \sqrt {1 + {{{\left( {\frac{{\partial h}}{{\partial x}}} \right)}}^{2}}}$ and D_s characterizes the surface diffusion coefficient where the effect of buoyancy can be ignored, that it is assumed that the film is sufficiently thin.

1.3 Scalings and Non-Dimensionalization

Before solving the problem, it is usual to remove the units related to the above system utilizing the physical quantities, reference scales should be specified. Using the unperturbed film thickness l as the characteristic length, we can assign the following parameters to form dimensionless controlling equations and boundary conditions:

$$(x,y) = \,\ell (x{\text{*}},y{\text{*}}),\quad {\mathbf{u}} = \sqrt {\ell g} {\mathbf{u}}{\text{*}},\quad t = \sqrt {\frac{\ell }{g}} t{\text{*}},\quad {{\lambda }_{1}} = \sqrt {\frac{\ell }{g}} \,\lambda _{1}^{*},\quad {{\lambda }_{2}} = \sqrt {\frac{\ell }{g}} \,\lambda _{2}^{*},$$

$$p = \frac{{\mu \sqrt {\ell g} }}{\ell }p{\text{*}},\quad \Pi = \frac{{\mu \sqrt {\ell g} }}{\ell }\Pi {\text{*}},\quad T = ({{T}_{w}} - {{T}_{s}})T{\text{*}} + {{T}_{s}},\quad \Gamma = {{\Gamma }_{0}}\Gamma {\text{*}}.$$

(1.13)

The asterisk $*$ is omitted here for simplicity. Thus, by substituting these dimensionless variables into the previous governing equations and the related boundary conditions, we arrive at the following system of equations:

$${{R}_{e}}\left( {1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}}} \right)\frac{{du}}{{dt}} = - \left( {1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}}} \right)\frac{{\partial p}}{{\partial x}} + \left( {1 + {{\lambda }_{2}}\frac{\partial }{{\partial t}}} \right){{\nabla }^{2}}u,$$

(1.14)

$${{R}_{e}}\left( {1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}}} \right)\frac{{d{v}}}{{dt}} = - \left( {1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}}} \right)\frac{{\partial p}}{{\partial y}} + \left( {1 + {{\lambda }_{2}}\frac{\partial }{{\partial t}}} \right){{\nabla }^{2}}{v} - 1,$$

(1.15)

$${{P}_{e}}\frac{{dT}}{{dt}} = {{\nabla }^{2}}T,$$

(1.16)

where ${{R}_{e}} = \frac{{\rho \sqrt {{{\ell }^{3}}g} }}{\mu }$ refers to the Reynolds number, the notation ${{P}_{e}} = {{P}_{r}}{{R}_{e}}$ characterizes the Péclet number, whereas ${{P}_{r}} = \frac{{\mu {{c}_{p}}}}{\kappa }$ describes the Prandtl number. In terms of these non-dimensional quantities, the boundary conditions at the substrate y = 0 then read

$$u = {v} = 0,\quad T = 1.$$

(1.17)

The interfacial stress created by the surface tension gradient including the Marangoni influences and the connected modes of instability is known as the thermocapillary instability. Hence, the boundary conditions at the free surface $y = h(x,t)$ can be written in the form:

$$\left( {1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}}} \right)[{{p}_{{_{{{\text{air}}}}}}} - p] + \frac{{2\left( {1 + {{\lambda }_{2}}\frac{\partial }{{\partial t}}} \right)}}{{{{N}^{2}}}}\left\{ {\frac{{\partial {v}}}{{\partial y}} + \frac{{\partial u}}{{\partial x}}{{{\left( {\frac{{\partial h}}{{\partial x}}} \right)}}^{2}} - \left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial {v}}}{{\partial x}}} \right)\frac{{\partial h}}{{\partial x}}} \right\}$$

$$ = \frac{{(1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}})}}{{{{N}^{3}}}}\left\{ {\frac{1}{{{{C}_{a}}}} - {{M}_{a}}T - {{N}_{e}}(\Gamma - 1)} \right\}\frac{{{{\partial }^{2}}h}}{{\partial {{x}^{2}}}},$$

(1.18)

$$\left( {1 + {{\lambda }_{2}}\frac{\partial }{{\partial t}}} \right)\left\{ {\left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial {v}}}{{\partial x}}} \right)\left( {1 - {{{\left( {\frac{{\partial h}}{{\partial x}}} \right)}}^{2}}} \right) + 2\left( {\frac{{\partial {v}}}{{\partial y}} - \frac{{\partial u}}{{\partial x}}} \right)\frac{{\partial h}}{{\partial x}}} \right\}$$

$$ = - N\left( {1 + {{\lambda }_{1}}\frac{\partial }{{\partial t}}} \right)\left\{ {{{M}_{a}}\left( {\frac{{\partial T}}{{\partial x}} + \frac{{\partial T}}{{\partial y}}\frac{{\partial h}}{{\partial x}}} \right) + {{N}_{e}}\frac{{\partial \Gamma }}{{\partial x}}} \right\},$$

(1.19)

$${v} = \frac{{\partial h}}{{\partial t}} + u\frac{{\partial h}}{{\partial x}},$$

(1.20)

$$\frac{{\partial (N\Gamma )}}{{\partial t}} + \frac{{\partial (N\Gamma u)}}{{\partial x}} = \frac{1}{{{{P}_{{es}}}}}\frac{\partial }{{\partial x}}\left( {\frac{1}{N}\frac{{\partial \Gamma }}{{\partial x}}} \right),$$

(1.21)

$$\frac{{\partial T}}{{\partial y}} - \frac{{\partial h}}{{\partial x}}\frac{{\partial T}}{{\partial x}} + N{{B}_{i}}T = 0,$$

(1.22)

where ${{M}_{a}} = \frac{{{{\sigma }_{T}}({{T}_{w}} - {{T}_{s}})}}{{\mu \sqrt {\ell g} }}$ denotes the Marangoni number, ${{N}_{e}} = \frac{{{{\sigma }_{\Gamma }}{{\Gamma }_{0}}}}{{\mu \sqrt {\ell g} }}$ is the elasticity number that expresses the effect of surface surfactants, ${{C}_{a}} = \frac{{\mu \sqrt {\ell g} }}{{{{\sigma }_{0}}}}$ represents the capillary number expressing the effect of surface tension, ${{P}_{{es}}} = \frac{{\sqrt {{{\ell }^{3}}g} }}{{{{D}_{s}}}}$ is the surfactant surface Péclet number, which denotes the interfacial diffusivity of the surfactant and ${{B}_{i}} = \frac{{{{h}_{{\text{g}}}}\ell }}{\kappa }$ refers to the Biot number.

2 METHOD OF SOLVING

2.1 Solution for the Basic State

As the system is unperturbed, in base laminar state, the speed profile and the heat domain are separated from each other. Depending on this, the base state output of the speed and the energy relations are acquired by using the zero order of the controlling equations and the related constraints at the planar and the surface boundaries. By considering a motionless initial state, the solutions of the base state are gained, and hence the base velocity in the liquid film is zero in which the flow is independent of time and fully developed.

In the undisturbed case, the energy relation for the dimensionless temperature field is

$$\frac{{{{d}^{2}}{{T}_{b}}(y)}}{{d{{y}^{2}}}} = 0,$$

(2.1)

associated with the basic flow thermal boundary conditions

$${{T}_{b}}(y) = 1\quad {\text{at}}\quad y = 0,$$

(2.2)

$$\frac{{\partial {{T}_{b}}(y)}}{{\partial y}} + {{B}_{i}}{{T}_{b}}(y) = 0\quad {\text{at}}\quad y = 1.$$

(2.3)

Equation (2.1) together with Eqs. (2.2) and (2.3) give the basic temperature field

$${{T}_{b}}(y) = 1 - \frac{{{{B}_{i}}y}}{{1 + {{B}_{i}}}},$$

(2.4)

where the relation

$${{p}_{0}} = \mathop {\hat {p}}\nolimits_0 - y,$$

(2.5)

outlines the hydrostatic pressure, in which $\mathop {\hat {p}}\nolimits_0$ signifies the constant pressure due to the surrounding air.

2.2 Perturbed Flow

In order to perturb the velocities, the pressure, the temperature, the interfacial position and the concentration of surfactant magnitude, we introduce a small perturbation from its basic state:

$${\mathbf{u}} = 0 + (\tilde {u},{\tilde {v}}),\quad p = {{p}_{0}} + \tilde {p},\quad T = {{T}_{b}} + \tilde {T},\quad h = 1 + \eta ,\quad \Gamma = 1 + \tilde {\Gamma }.$$

(2.6)

For facilitating the solution of the above system of governing relations and related boundary conditions, we define the stream function $\psi (x,y,t)$:

$$\tilde {u} = \frac{{\partial \psi }}{{\partial y}},\quad {\tilde {v}} = - \frac{{\partial \psi }}{{\partial x}}.$$

(2.7)

The solution of the current problem depends on the Laplace transform. With respect to time, the Laplace transform has the general standard form

$$\bar {f}(x,y,s) = L(f(x,y,t)) = \int\limits_0^\infty {f(x,y,t){{e}^{{ - st}}}dt,} $$

(2.8)

where $s \geqslant 0$ being the transform parameter. With the aid of Eq. (2.8) and by taking the Laplace transform of Eqs. (1.15) and (1.16), we arrive at

$${{\nabla }^{4}}\bar {\psi }(x,y,s) - \frac{{s{{R}_{e}}}}{{F({{\lambda }_{1}},{{\lambda }_{2}},s)}}{{\nabla }^{2}}\bar {\psi }(x,y,s) = 0,$$

(2.9)

where $F({{\lambda }_{1}},{{\lambda }_{2}},s) = \frac{{1 + s{{\lambda }_{2}}}}{{1 + s{{\lambda }_{1}}}}$, and the heat equation becomes

$${{\nabla }^{2}}\bar {\tilde {T}}(x,y,s) - {{P}_{e}}\left( {s\bar {\tilde {T}}(x,y,s) - \frac{{d{{T}_{b}}}}{{dy}}\frac{{\partial \bar {\psi }}}{{\partial x}}} \right) = 0.$$

(2.10)

Also, the associated boundary conditions can be transformed into

$$\bar {\psi } = 0,\quad \frac{{\partial \bar {\psi }}}{{\partial y}} = \bar {U}(s)\quad {\text{at}}\quad y = 0,$$

(2.11)

$$\bar {\tilde {T}} = 0\quad {\text{at}}\quad y = 0,$$

(2.12)

$$\frac{{F({{\lambda }_{1}},{{\lambda }_{2}},s)}}{{{{R}_{e}}}}\left( {\frac{{{{\partial }^{3}}\bar {\psi }}}{{\partial {{y}^{3}}}} + 3\frac{{{{\partial }^{3}}\bar {\psi }}}{{\partial {{x}^{2}}\partial y}}} \right) - s\frac{{\partial \bar {\psi }}}{{\partial y}} - \frac{{\partial \bar {\eta }}}{{\partial x}} + \left( {\frac{1}{{{{C}_{a}}}} - {{M}_{a}}\frac{{d{{T}_{b}}}}{{dy}}} \right)\frac{{{{\partial }^{3}}\bar {\eta }}}{{\partial {{x}^{3}}}} = 0\quad {\text{at}}\quad y = 1,$$

(2.13)

$$F({{\lambda }_{1}},{{\lambda }_{2}},s)\left( {\frac{{{{\partial }^{2}}\bar {\psi }}}{{\partial {{y}^{2}}}} - \frac{{{{\partial }^{2}}\bar {\psi }}}{{\partial {{x}^{2}}}}} \right) + {{M}_{a}}\left( {\frac{{d{{T}_{b}}}}{{dy}}\frac{{\partial \bar {\eta }}}{{\partial x}} + \frac{{\partial \bar {\tilde {T}}}}{{\partial x}}} \right) + {{N}_{e}}\frac{{\partial \bar {\tilde {\Gamma }}}}{{\partial x}} = 0\quad {\text{at}}\quad y = 1,$$

(2.14)

$$s\bar {\eta } + \frac{{\partial \bar {\psi }}}{{\partial x}} = 0\quad {\text{at}}\quad y = 1,$$

(2.15)

$$\frac{{{{\partial }^{2}}\bar {\psi }}}{{\partial x\partial y}} + s\bar {\tilde {\Gamma }} - \frac{1}{{{{P}_{{es}}}}}\frac{{{{\partial }^{2}}\bar {\tilde {\Gamma }}}}{{\partial {{x}^{2}}}} = 0\quad {\text{at}}\quad y = 1,$$

(2.16)

$$\frac{{\partial \bar {\tilde {T}}}}{{\partial y}} + {{B}_{i}}\left( {\bar {\tilde {T}} + \frac{{d{{T}_{b}}}}{{dy}}\bar {\eta }} \right) = 0\quad {\text{at}}\quad y = 1.$$

(2.17)

The solutions of the above problem can be expressed as

$$\bar {\psi }(x,y,s) = \bar {U}(s)y + \bar {f}(y,s)\cos(kx),$$

(2.18)

$$\bar {\tilde {T}}(x,y,s) = {{\bar {g}}}(y,s)\sin(kx).$$

(2.19)

Consequently, the quantities $\bar {f}$ and ${{\bar {g}}}$ are defined by the next equations:

$$\frac{{{{d}^{4}}\bar {f}}}{{d{{y}^{4}}}} - \left( {2{{k}^{2}} + \frac{{s{{R}_{e}}}}{{F({{\lambda }_{1}},{{\lambda }_{2}},s)}}} \right)\frac{{{{d}^{2}}\bar {f}}}{{d{{y}^{2}}}} + {{k}^{2}}\left( {{{k}^{2}} + \frac{{s{{R}_{e}}}}{{F({{\lambda }_{1}},{{\lambda }_{2}},s)}}} \right)\bar {f} = 0,$$

(2.20)

$$\frac{{{{d}^{2}}{{\bar {g}}}}}{{d{{y}^{2}}}} - ({{k}^{2}} + s{{P}_{e}}){{\bar {g}}} + \frac{{k{{P}_{e}}{{B}_{i}}}}{{1 + {{B}_{i}}}}\bar {f} = 0.$$

(2.21)

With the aid of the boundary conditions (2.11)–(2.17), the functions $\bar {f}$ and ${{\bar {g}}}$ are governed by the relations

$$\bar {f} = {{c}_{1}}\cosh(\gamma y) + {{c}_{2}}\sinh(\gamma y) + {{c}_{3}}\cosh(ky) + {{c}_{4}}\sinh(ky),$$

(2.22)

$${{\bar {g}}} = \frac{{k{{P}_{e}}{{B}_{i}}{{{(1 + {{B}_{i}})}}^{{ - 1}}}}}{{({{k}^{2}} - {{\delta }^{2}})({{\delta }^{2}} - {{\gamma }^{2}})}}{\text{\{ }}({{k}^{2}} - {{\delta }^{2}})[{{c}_{1}}\cosh(\gamma y) + {{c}_{2}}\sinh(\gamma y)] - ({{\delta }^{2}} - {{\gamma }^{2}})$$

$$\, \times [{{c}_{3}}\cosh(ky) + {{c}_{4}}\sinh(ky)]{\text{\} }} + {{c}_{5}}\cosh(\delta y) + {{c}_{6}}\sinh(\delta y),$$

(2.23)

where $\gamma = \sqrt {{{k}^{2}} + \frac{{s{{R}_{e}}}}{{F({{\lambda }_{1}},{{\lambda }_{2}},s)}}}$, $\delta = \sqrt {{{k}^{2}} + s{{P}_{e}}}$.

Thereby, Eqs. (2.9) and (2.10) will take the following solutions

$$\bar {\psi }(x,y,s) = {\text{\{ }}{{c}_{1}}\cosh(\gamma y) + {{c}_{2}}\sinh(\gamma y) + {{c}_{3}}\cosh(ky) + {{c}_{4}}\sinh(ky){\text{\} }}\cos(kx) + \bar {U}(s)y,$$

(2.24)

$$\bar {T}(x,y,s) = 1 - \frac{{{{B}_{i}}y}}{{1 + {{B}_{i}}}} + \left\{ {\frac{{k{{P}_{e}}{{B}_{i}}{{{(1 + {{B}_{i}})}}^{{ - 1}}}}}{{({{k}^{2}} - {{\delta }^{2}})({{\delta }^{2}} - {{\gamma }^{2}})}}{\text{\{ }}({{k}^{2}} - {{\delta }^{2}})[{{c}_{1}}\cosh(\gamma y) + {{c}_{2}}\sinh(\gamma y)]} \right.$$

$$\left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}} - \,({{\delta }^{2}} - {{\gamma }^{2}})[{{c}_{3}}\cosh(ky) + {{c}_{4}}\sinh(ky)]} \right\} + {{c}_{5}}\cosh(\delta y) + {{c}_{6}}\sinh(\delta y){\text{\} }}\sin(kx),$$

(2.25)

$$\bar {\eta }(x,s) = \frac{k}{s}{\text{\{ }}{{c}_{1}}\cosh\gamma + {{c}_{2}}\sinh\gamma + {{c}_{3}}\cosh k + {{c}_{4}}\sinh k{\text{\} }}\sin(kx).$$

(2.26)

The mathematical formulas for the coefficients ${{c}_{1}},\;{{c}_{2}},\;...,\;{{c}_{6}}$ are given in Appendix. It is useful, at this point to define the flow rate (also known as volumetric flow rate or volume velocity). Depending on the zone of the channel and the speed of the liquid, the flow rate in the physical meaning can be defined as the volume of liquid which occurs per unit time. The rate of flow $Q(x,s)$ is ordinarily given by the relation:

$$Q = \int\limits_0^{h(x,s)} {\bar {u}dy} = \int\limits_0^{h(x,s)} {\frac{{\partial \bar {\psi }}}{{\partial y}}dy} $$

$$ = {\text{\{ }}{{c}_{1}}[\cosh(h\gamma ) - 1] + {{c}_{2}}\sinh(h\gamma ) + {{c}_{3}}[\cosh(hk) - 1] + {{c}_{4}}\sinh(hk){\text{\} }}\cos(kx) + h\bar {U}(s).$$

(2.27)

In addition, we can also evaluate the shear stress to obtain the skin friction $S$ on the lower boundary:

$$S = {{\left. {\frac{{\partial \bar {u}}}{{\partial y}}} \right|}_{{y = 0}}} = {{\left. {\frac{{{{\partial }^{2}}\bar {\psi }}}{{\partial {{y}^{2}}}}} \right|}_{{y = 0}}} = {\text{\{ }}{{c}_{1}}{{\gamma }^{2}} + {{c}_{3}}{{k}^{2}}{\text{\} }}\cos(kx).$$

(2.28)

The expressions (2.27) and (2.28) are in agreement with the results obtained previously (see [22–24]).

2.3 Inversion of the Laplace Transforms

In complex form, the inversion notation for Laplace transform $\bar {f}(x,y,s)$ of a domain $f(x,y,t)$ is specified by the next contour integral [1, 2]

$$f(x,y,t) = \frac{1}{{2\pi i}}\mathop {\lim}\limits_{\varrho \to \infty } \int\limits_{\upsilon - i\varrho }^{\upsilon + i\varrho } {\bar {f}(x,y,s){{e}^{{st}}}ds} .$$

(2.29)

Here, $\upsilon + i\varrho$ and $\upsilon$ is greater than the real part of any singularity in the transformed function $\bar {f}(x,y,s)$. The numerical inversion style of Durbin’s [25, 26] is adopted to obtain the unknown physical functions

$$f(x,y,t) = \frac{{{{e}^{{\upsilon t}}}}}{\tau }\left[ { - \frac{1}{2}{\text{Re}}\bar {f}(x,y,\upsilon ) + \sum\limits_{j = 0}^J \left\{ {{\text{Re}}\left\{ {\bar {f}\left( {x,y,\upsilon + i\frac{{j\pi }}{\tau }} \right)} \right\}\cos\frac{{j\pi }}{\tau }t} \right.} \right.$$

$$\left. {\left. { - \;{\text{Im}}\left\{ {\bar {f}\left( {x,y,\upsilon + i\frac{{j\pi }}{\tau }} \right)} \right\}\sin\frac{{j\pi }}{\tau }t} \right\}} \right],\quad 0 < t < 2\tau ,$$

(2.30)

where ${\text{Re\{ }}{\text{.\} }}$ denotes the real part of ${\text{\{ }}.{\text{\} }}$, whereas ${\text{Im\{ }}{\text{.\} }}$ stands for the imaginary part. The function f indicates $\psi$, T, or $\eta$. The parameter J is a sufficiently large integer symbolizing the number of terms in the truncated infinite Fourier series. The parameter J must be selected such that

$${{e}^{{\upsilon t}}}\left\{ {{\text{Re}}\left\{ {\bar {f}\left( {x,y,\upsilon + i\frac{{j\pi }}{\tau }} \right)} \right\}\cos\frac{{j\pi }}{\tau }t - {\text{Im}}\left\{ {\bar {f}\left( {x,y,\upsilon + i\frac{{j\pi }}{\tau }} \right)} \right\}\sin\frac{{j\pi }}{\tau }t} \right\} \leqslant \varepsilon ,$$

(2.31)

where $\varepsilon$ is a suggested small positive number that corresponds to the degree of accuracy to be performed. The optimal selection of $\upsilon$ was acquired according to the criteria given in [27]. The prescribed magnitude of $\upsilon \tau$ is through 5 and 10 for reaching the sufficient accuracy, with J extending from 50 to 5000 [25]. Also, the solution is generally valid for $\tau \geqslant 2{{t}_{{{\text{max}}}}}$ where t_max is the time up to which the results are to be achieved [28].

2.4 Limiting Cases

In the following, it is useful to examine some significant limiting situations:

(i) The case of isothermal fluid layer.

Here, we assume to investigate the case in which the sheet is considered to be isothermal and thus there is no heat transfer in the liquid film. In this case, the equations of motion are the same as Eq. (2.9), and the corresponding conditions are

$$\frac{{{{\partial }^{3}}\bar {\psi }}}{{\partial {{y}^{3}}}} + 3\frac{{{{\partial }^{3}}\bar {\psi }}}{{\partial {{x}^{2}}\partial y}} + \frac{{{{R}_{e}}}}{{F({{\lambda }_{1}},{{\lambda }_{2}},s)}}\left( {\frac{1}{s}\frac{{{{\partial }^{2}}\bar {\psi }}}{{\partial {{x}^{2}}}} - s\frac{{\partial \bar {\psi }}}{{\partial y}} - \frac{1}{{s{{C}_{a}}}}\frac{{{{\partial }^{4}}\bar {\psi }}}{{\partial {{x}^{4}}}}} \right) = 0\quad {\text{at}}\quad y = 1,$$

(2.32)

$$\frac{{{{\partial }^{2}}\bar {\psi }}}{{\partial {{y}^{2}}}} - \frac{{{{\partial }^{2}}\bar {\psi }}}{{\partial {{x}^{2}}}} + \frac{{{{N}_{e}}}}{{F({{\lambda }_{1}},{{\lambda }_{2}},s)}}\frac{{\partial \bar {\tilde {\Gamma }}}}{{\partial x}} = 0\quad {\text{at}}\quad y = 1,$$

(2.33)

with the same type of conditions (2.11) and (2.16), whereas we combine Eqs. (2.13) and (2.15) to give condition (2.31). Consequently, the solution for the stream function will be expressed as

$$\bar {\psi }(x,y,s) = {\text{\{ }}A[\cosh(\gamma y) + \cosh(ky)] + B[\gamma \sinh(ky) - k\sinh(\gamma y)]{\text{\} }}\cos(kx) + \bar {U}(s)y,$$

(2.34)

and the surface deflection becomes

$$\bar {\eta }(x,s) = \frac{k}{s}{\text{\{ }}A\,[\cosh\gamma + \cosh k] + B\,[\gamma \sinh k - k\sinh\gamma ]{\text{\} }}\sin(kx),$$

(2.35)

where the unknowns A and B are clear from the context. Furthermore, in dealing with clean liquid film, i.e., in the absence of the interfacial surfactants, we obtain the same type of Eq. (2.33), when we put ${{N}_{e}} \to 0$ in the coefficients A and B.

(ii) The case of small Reynolds number.

In this case we take the Newtonian viscous flow as well as the Reynolds parameter is much less than unity, that is, it vanishes to zero then $\gamma = k + \frac{s}{{2k}}{{R}_{e}} + O(R_{e}^{2})$ and ${{e}^{{\gamma y}}} = {{e}^{{ky}}}\left( {1 + \frac{{sy}}{{2k}}{{R}_{e}}} \right) + O(R_{e}^{2})$. In this limit, the stream function has the solution

$$\bar {\psi }(x,y,s) = \frac{{{{U}_{0}}\omega y}}{{{{s}^{2}} + {{\omega }^{2}}}} + \frac{{({{\varsigma }_{{11}}}{{s}^{2}} + k{{\varsigma }_{{12}}}s)\cos(kx)}}{{k({{\varsigma }_{{01}}}{{s}^{3}} + {{\varsigma }_{{02}}}{{s}^{2}} + {{\varsigma }_{{03}}}s + {{\varsigma }_{0}})}}.$$

(2.36)

In the light of the Laplace transformation in the inverse form, the stream function and the surface deviation will be given as functions of the time:

$$\psi (x,y,t) = [{{U}_{0}}y + {{L}_{1}}\cos(kx)]\sin(\omega t) + \cos(kx){\text{\{ }}{{L}_{2}}\cos(\omega t) + {{L}_{3}}{{e}^{{(\alpha + \sqrt \beta )t}}} + {{L}_{4}}{{e}^{{(\alpha - \sqrt \beta )t}}}{\text{\} }},$$

(2.37)

$$\bar {\eta }(x,s) = \frac{k}{s}{\text{\{ }}{{L}_{1}}\sin(\omega t) + {{L}_{2}}\cos(\omega t) + {{L}_{3}}{{e}^{{(\alpha + \sqrt \beta )t}}} + {{L}_{4}}{{e}^{{(\alpha - \sqrt \beta )t}}}{\text{\} }}\sin(kx).$$

(2.38)

The quantities $\varsigma$ and L, as well as α and β that given in the above relations are coefficients of the basic parameters of the issue under study. The values of these quantities are lengthy and not appeared here. In any case, they are available upon request from the authors. Such results are in good agreement with those mentioned in the researches [20, 21].

3 RESULTS AND DISCUSSIONS

In this section we choose the values $\upsilon t = 9$, $J = 700,$ $\tau = 2{{t}_{{{\text{max}}}}}$ = 200, where a number of numerical estimations was accomplished to select these values. Durbin inversion formula (2.30) supplies stable and convergent outcomes in all cases investigated The computations were performed based on a suitable personal computer, and the convergence of numerical estimations was established in a simple test and error technique, by increasing the number the truncation parameter J, while searching for stability in the numerical parameters of the computed solutions.

In all graphs, the numerical investigation is performed by fixing the quantity of all the physical parameters except for one parameter having various values for comparison. In the calculation given below, all the physical variables are sought in the dimensionless form as appointed previously. Figures 2a and 2b are plotted to show respectively the effect of the variations of the velocity U₀ and the angular frequency ω on the free surface time history, represented by Eq. (2.26). The graphs are shown in the plane (t, η) and the values of the other quantities are fixed, as given in the caption of Fig. 2. Figure 2a is plotted for three values of ${{U}_{0}}$ = 0.1, 0.4, and 0.7, corresponding to the continuous, dashed, and dotted lines respectively. The results are shown by the dashed, and dotted curves explain that there is no qualitative variation in the behavior of the surface waves with the evolution in time at the various values of the velocity U₀, a noticeable growth in values of $\eta$ is observed. As the curves displayed in Fig. 2b are compared to each another, it is noted that the frequency has a regular impact on the surface wave elevation, especially at the values of $t > 3$.

Fig. 2.

Free surface elevation as a function of time corresponding to (2.26), for a system having ${{B}_{i}} = 0.7$, ${{M}_{a}} = 1$, ${{P}_{e}} = 2$, ${{C}_{a}} = 0.05,$ ${{P}_{{{\text{es}}}}} = 0.5,$ ${{\lambda }_{1}} = 0.3,$ ${{\lambda }_{2}} = 0.1,$ ${{N}_{e}} = 0.5$, ${{R}_{e}} = 5,$ and x = 3; (a) $\omega$ = 2, (b) ${{U}_{0}}$ = 0.5. While (c) represents the variation of ${{\lambda }_{1}}$ = $0.01,0.4,0.9$ and (d) shows the changing in ${{\lambda }_{2}}$ = $0.01,0.5,0.8$.

The effects of both relaxation time ${{\lambda }_{1}}$ and the retardation time ${{\lambda }_{2}}$ on the surface waves profile are presented in Figs. 2c and 2d in which the elevation is plotted against the time. The relaxation and retardation times have some different values for the sake of comparison. In Fig. 2c we select the values ${{\lambda }_{1}}$ = 0.01, 0.4, and 0.9 correspond to the solid, dashed, and dotted curves respectively. From the inspection of Fig. 2c, the phenomenon of the dual (irregular) role is observed for increasing the relaxation time: one of the two roles is a slight influence in the range $0 < t < 50$ (a very slight decreasing on the surface wave motion), and the other is a significant increase in values of the surface waves elevation when $50 < t < 80$. The curves in Fig. 2d are plotted at ${{\lambda }_{2}}$ = 0.01, 0.5, and 0.8, a general trend shown by this graph is that the effect of retardation time on the surface waves elevation is contrary to that of relaxation time. It is obvious that the relaxation and retardation times have slight effects on the surface elevation at $t < 50$, but when the time value exceeds 50 we observe that both the relaxation and retardation time have a significant effect on the movement of the layer. Such conclusions are in a fully agreement with those reported in [10]. On the other hand, the modes presented in Fig. 3 through its partitions supply the graphical explanation of the impact of the increasing quantity of Marangoni number on the fluid free surface in the three-dimensional interface. It is observed from these partitions that the motion of the free surface diminishes gradually with the large values of the Marangoni number. Further, an oscillating motion is noted for growing Marangoni number, through the horizontal position in the liquid mode.

Fig. 3.

Three-dimensional spatial evolution of free-surface deformation for the system has ${{R}_{e}} = 1000$, ${{B}_{i}} = 0.7$, ${{P}_{e}} = 2$, ${{C}_{a}} = 30$, ${{P}_{{{\text{es}}}}} = 0.5$, ${{U}_{0}} = 0.3$, ${{\lambda }_{1}} = 0.3$, ${{\lambda }_{2}} = 0.1$, ${{N}_{e}} = 0.5$, and $\omega = 0.2$, whereas the values ${{M}_{a}} = 1$, 4, and 10 are taken for (a–c) respectively.

The aim of the numerical results investigated in Figs. 4a and 4b is to explore the effect of the Biot number B_i on the behavior of the temperature profile, when Biot number has values less or greater than unity. In these partitions, the dimensionless temperature is plotted against the horizontal position. In Fig. 4a the solid, dashed and dotted curves correspond to the values 0.1, 0.2, and 0.3 of the Biot number, respectively, while the magnitudes 1, 2, and 3 are selected to refer these curves in Fig. 4b. An inspection of Figs. 4a and 4b then shows that, broadly speaking, the fluid temperature distribution increases with the horizontal position until it reaches the maximum value and then decreases gradually with increasing position. On the other hand, by comparing the results displayed throughout Figs. 4a and 4b, it is remarkable that the effect of increasing the Biot number when it has values less than unity is to increase the fluid temperature. Whereas the converse is true for increasing the Biot number when it has values greater than or equal to unity in the range $0 < x < 2$, and so it is concluded that the Biot number strongly influences the temperature.

Fig. 4.

Variation of the temperature distribution with the horizontal position for the same system as investigated in Fig. 3, with ${{R}_{e}} = 800$, ${{M}_{a}} = 1$, corresponding to ${{B}_{i}}$ = 0.1, 0.2, 0.3 (a) and ${{B}_{i}}$ = 1, 2, 3 (b). with the time, with ${{B}_{i}}$ = 0.7: (c) at ${{C}_{a}} = 5$, where ${{P}_{e}}$ = 1, 2, 3, (d) at ${{P}_{e}} = 3$, where ${{C}_{a}}$ = 1, 5, and 9.

Figures 4c and 4d provide the graphical illustration of the fluid temperature field within the liquid layer with time for the variation of both Péclet and capillary numbers, respectively. In contrast to the results presented in these graphs, it is worthwhile to notice that the curves meet at the same point t = 95 for increasing Péclet number ${{P}_{e}}$ (it is increased stepwise from 1 to 3) in Fig. 4c while increasing the capillary number (it is increased stepwise from 1 to 9) leads to the curves intersecting t axis in three close points, as in Fig. 4d.

On the other hand, investigation of the numerical results demonstrated in these partitions, it is observed that growing both capillary and Péclet parameters lead to an increment in the maximum magnitudes of the liquid temperature.

To understand the flow behavior better, figure 5 illustrates the passing dimensionless streamline and the related temperature range. The streamlines are effective apparatus to visualize a qualitative impression of the flow behavior through the motion. A streamline is the curve formed by the velocity vectors of each fluid particle at a certain time such that the tangent at each point of this curve signalizes the direction of fluid movement at that point. Snapshots of instantaneous streamlines of the stream function are shown in Figs. 5a–5c, the streamlines picture is achieved by fixing the value of all the physical parameters except the Reynolds number ${{R}_{e}}$ equal to 1, 400, and 800 at t equal to 5. When the Reynolds number is increasing the dimensionless streamline value increases (the density of streamline cells increases), this is due to the fact that by increasing Reynolds number the viscous effect decreases.

Fig. 5.

Streamlines contours for a system having the same parameters considered in Fig. 4: (a)${{R}_{e}}$ = 1, (b)${{R}_{e}}$ = 400, (c) ${{R}_{e}}$ = 800, while Fig. (d–f) display the corresponding isothermal contours.

Changing Reynolds number in Figs. 5d–5f has an effect on dimensionless isothermal contours, where the contours are transformed gradually into two sets of cells (Figs. 5e and 5f). This is due to the effect of convection heat transfer which increases by increasing Reynolds number. A conclusion that may be made from the comparison among Figs. 5d and 5f is that higher Reynolds numbers increase the concentration of the isothermal curves in the movement of the fluids. Similar results were also found in [29–31].

In the limiting case of no heat transfer in the fluid layer, Figs. 6a and 6b exhibits the effects of both the Reynolds number and the angular frequency of the periodic horizontal velocity on the surface waves deflection. The other quantities are given in the caption to Fig. 6, so that, the plane is assigned ($\eta - x$) to Figs. 6a and 6b, where the values 100, 400, and 800 are chosen for the Reynolds number in Fig. 6a, whereas in Fig. 6b three different magnitude of the angular frequency (0.2, 0.5, and 0.8) are taken into account, for the aim of differentiation. It is obvious, from Fig. 6a that as the Reynolds number increases, the interfacial elevation enlarges; while the opposite is true due to growing the angular frequency in Fig. 6b. By comparing the outcomes established over Figs. 6a and 6b it is worth mentioning to remark that the impact of growing the Reynolds number on the liquid film flow is contrary to that of the angular frequency.

Fig. 6.

Isothermal case in the plane $(\eta - x)$, where ${{U}_{0}} = 0.7$, ${{C}_{a}} = 0.1$, ${{N}_{e}} = 0.1$, ${{P}_{{{\text{es}}}}} = 1$, ${{\lambda }_{1}} = 0.3$, and ${{\lambda }_{2}} = 0.1$: (a) at $\omega = 0.2$, where ${{R}_{e}}$ = 100, 400, and 800, (b) at ${{R}_{e}} = 500$, where $\omega$ = 0.2, 0.5, and 0.8. Effects of the velocity ${{U}_{0}}$ = 0.5, 1, 1.5 illustrated in (c) at t = 2, while (d) at x = 1.

As the Reynolds parameter vanishingly small, the numerical illustrations presented in Figs. 6c and 6d aim to investigate the influence of increasing the velocity parameter on the surface wave domain with the evolution in both the horizontal level and the time. For this purpose the two planes ($\eta - x$) and ($\eta - t$) are illustrated corresponding to Fig. 6c and Fig. 6d, respectively. Investigation of the numerical results shown in Figs. 6c and 6d reveals that the increase in the values of the velocity results in a significant increase in values of $\eta$ (Fig. 6c). Whereas the effect of the velocity on the motion of the free surface will slightly diminish gradually with the evolution in time, which occurs in Fig. 6d. On the other hand, it is noted that the surface evolution has small growth with time due to the increase of velocity. This means that the motion of the fluid layer is slightly unstable due to an increase in velocity. However, this behavior can be explained physically, as we study the special case of small Reynolds number which is sufficient for high viscosity and from here the system is more stable. Similar behavior is outlined in [32]. To demonstrate a more clear representation of the wave motion, the impact of the increasing value of velocity on the liquid free surface in the three–dimensional domain, corresponding to the cases of Figs. 6c and 6d is graphically illustrated, where Figs. 7a, 7b, and 7c are respectively corresponding to the continuous, dashed and dotted curves of Fig. 6.

Fig. 7.

Three dimensional spatial evolution of free-surface deformation for the same system as considered in Fig. 6.

SUMMARY

In this study, we have investigated a two-dimensional flow of a viscoelastic fluid film on an infinite long heated plate, in the presence of insoluble surfactants appearing in the free surface. The substrate and the fluid are both motionless at first. Unexpectedly, the plate is shaken into motion at its own level with an oscillatory speed. The solution to the governing relations is acquired depending on the usual Laplace transform. However, the numerical inversion of the Laplace transform is applied to transform the solutions from the Laplace area back to the original domain. At this end, time–domain solutions are investigated by involving Durbin’s numerical inverse Laplace transform technique. This shows that, in solving the boundary layer flow, the numerical inversion of the Laplace transform is a very useful and effective scheme.

Numerical results are presented graphically to elucidate the impacts of the several physical quantities on the behavior of the surface wave model, the alteration of the thermal distribution within the liquid film, the streamlines, and isothermals curves. The results of our study showed that the relaxation and retardation times have slight effects on the surface elevation when the value of the time less than 50 and their effect reflected at a time greater than this value. In three-dimensional space, an oscillating behavior is noted for growing Marangoni number, in which the free surface diminishes progressively. The increase in the Reynolds parameter reveals that a continuous increase in the values of the temperature of the fluid layer, where it approaches the center of the layer, after which the temperature will decrease to reach the end of the layer. A similar behavior is noticeable for the effect of Marangoni number. The effect of increase in the Biot number when it has values less than unity is to increase the liquid temperature distribution. While, we note that the opposite role is achieved, in the event that the Biot number takes values greater than or equal to unity. It is observed that increase in the capillary as well as Péclet numbers leads to an increment in the maximum quantities of the liquid temperature. When the Reynolds number is growing the dimensionless streamline value increases (the density of streamline cells enlarged), this is due to the fact that by increasing Reynolds number the viscous effect decreases.

In the limiting case of no heat transfer in the fluid layer, it is found that the Reynolds number increases motion of the surface waves, while the inverse behavior is true for growing the angular frequency. It is worthwhile to notice that the impact of increasing the Reynolds number on the isothermal fluid layer is contrary to that of the angular frequency. In the special case when the Reynolds parameter is very small (${{R}_{e}} \ll 1$), it was observed that the effect of increase in the capillary number is opposite to the effect of increase in the elasticity number.

APPENDIX

The quantities ${{c}_{1}},{{c}_{2}},...,{{c}_{6}}$ given in Eqs. (2.24)–(2.26) may be formulated as follows:

$${{c}_{1}} = \frac{{A\bar {U}(s)}}{{{{M}_{0}}}}((k{{M}_{2}} - \gamma {{M}_{4}}){{J}_{6}}{{\mathfrak{M}}_{0}} + {{M}_{6}}(\gamma {{J}_{4}}{{\mathfrak{M}}_{0}} - k{{J}_{2}}{{\mathfrak{M}}_{0}} + k{{N}_{e}}(k{{\mathfrak{M}}_{2}} - \gamma {{\mathfrak{M}}_{4}}))),$$

$${{M}_{0}} = A({{J}_{1}} - {{J}_{3}})((k{{M}_{2}} - \gamma {{M}_{4}}){{J}_{6}}{{\mathfrak{M}}_{0}} + {{M}_{6}}(\gamma {{J}_{4}}{{\mathfrak{M}}_{0}} - k{{J}_{2}}{{\mathfrak{M}}_{0}} + k{{N}_{e}}(k{{\mathfrak{M}}_{2}} - \gamma {{\mathfrak{M}}_{4}})))$$

$$ + \,\gamma {{J}_{4}}\left( {{{M}_{6}}\left( {A{{J}_{3}}{{\mathfrak{M}}_{0}} - A{{J}_{1}}{{\mathfrak{M}}_{0}} + k\left( {A{{N}_{e}}({{\mathfrak{M}}_{1}} - {{\mathfrak{M}}_{3}}) + {{A}_{1}}{{P}_{e}}{{J}_{5}}{{\mathfrak{M}}_{0}}\left( {{{\Lambda }_{K}} - \Lambda } \right)} \right)} \right)} \right.$$

$$\, + {{J}_{6}}{{\mathfrak{M}}_{0}}(A{{M}_{1}} - A{{M}_{3}} + k{{A}_{1}}{{P}_{e}}{{M}_{5}}(\Lambda - {{\Lambda }_{K}}))) + k{{J}_{2}}({{J}_{6}}{{\mathfrak{M}}_{0}}(A{{M}_{3}} - A{{M}_{1}}$$

$$\left. { + \,k{{A}_{1}}{{P}_{e}}{{M}_{5}}\left( {{{\Lambda }_{K}} - {{\Lambda }_{\gamma }}} \right)} \right) + {{M}_{6}}(A{{J}_{1}}{{\mathfrak{M}}_{0}} - A{{J}_{3}}{{\mathfrak{M}}_{0}} - k(A{{N}_{e}}({{\mathfrak{M}}_{1}} - {{\mathfrak{M}}_{3}})$$

$$\left. {\left. {\left. { + \,{{A}_{1}}{{P}_{e}}{{J}_{5}}{{\mathfrak{M}}_{0}}({{\Lambda }_{K}} - {{\Lambda }_{\gamma }})} \right)} \right)} \right),\quad A = ({{k}^{2}} - {{\delta }^{2}})({{\gamma }^{2}} - {{\delta }^{2}}),\quad {{A}_{1}} = - \frac{{{{B}_{i}}}}{{1 + {{B}_{i}}}},$$

$${{\Lambda }_{K}} = {{k}^{2}} - {{\delta }^{2}},\quad {{\Lambda }_{\gamma }} = {{\gamma }^{2}} - {{\delta }^{2}},$$

$${{J}_{1}} = \frac{1}{{2{{s}^{2}}{{C}_{a}}{{R}_{e}}}}({{k}^{4}}\cosh(\gamma ) - {{C}_{a}}({{k}^{2}}\cosh(\gamma ) + {{k}^{4}}\cosh(\gamma ){{A}_{1}}{{M}_{a}} - {{s}^{2}}\gamma \sinh(\gamma ){{R}_{e}}$$

$$\, - 3{{k}^{2}}s\gamma \sinh(\gamma )F\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right) + s{{\gamma }^{3}}\sinh(\gamma )F\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right))),$$

$${{J}_{2}} = \frac{1}{{2{{s}^{2}}{{C}_{a}}{{R}_{e}}}}({{k}^{4}}\sinh(\gamma ) - {{C}_{a}}({{k}^{2}}\sinh(\gamma ) + {{k}^{4}}\sinh(\gamma ){{A}_{1}}{{M}_{a}} - {{s}^{2}}\gamma \cosh(\gamma ){{R}_{e}}$$

$$ - \,3{{k}^{2}}s\gamma \cosh(\gamma )F\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right) + s{{\gamma }^{3}}\cosh(\gamma )F({{\lambda }_{1}},{{\lambda }_{2}},s))),$$

$${{J}_{3}} = \frac{{k({{k}^{3}}\cosh(k) + {{C}_{a}}({{s}^{2}}\sinh(k){{R}_{e}} + 2{{k}^{2}}s\sinh(k)F\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right) - k\cosh(k) - {{k}^{3}}\cosh(k){{A}_{1}}{{M}_{a}}))}}{{2{{s}^{2}}{{C}_{a}}{{R}_{e}}}},$$

$${{J}_{4}} = \frac{{k({{k}^{3}}\sinh(k) + {{C}_{a}}({{s}^{2}}\cosh(k){{R}_{e}} + 2{{k}^{2}}s\cosh(k)F\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right) - k\sinh(k) - {{k}^{3}}\sinh(k){{A}_{1}}{{M}_{a}}))}}{{2{{s}^{2}}{{C}_{a}}{{R}_{e}}}},$$

$${{J}_{1}} = \frac{{\cosh(\gamma )({{k}^{2}}{{A}_{1}}{{M}_{a}}(A + s{{P}_{e}}{{\Lambda }_{K}}) + sA({{k}^{2}} + {{\gamma }^{2}})F\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right))}}{{sA}},$$

$${{J}_{2}} = \frac{{\sinh(\gamma )({{k}^{2}}{{A}_{1}}{{M}_{a}}(A + s{{P}_{e}}{{\Lambda }_{K}}) + sA({{k}^{2}} + {{\gamma }^{2}})F\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right))}}{{sA}},$$

$${{J}_{3}} = \frac{{{{k}^{2}}\cosh(k)\left( {{{A}_{1}}{{M}_{a}}\left( {A + s{{P}_{e}}{{\Lambda }_{\gamma }}} \right) + 2sAF\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right)} \right)}}{{sA}},$$

$${{J}_{4}} = \frac{{{{k}^{2}}\sinh(k)\left( {{{A}_{1}}{{M}_{a}}\left( {A + s{{P}_{e}}{{\Lambda }_{\gamma }}} \right) + 2sAF\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right)} \right)}}{{sA}},\quad {{J}_{5}} = k\cosh(\delta ){{M}_{a}},\quad {{J}_{6}} = k\sinh(\delta ){{M}_{a}},$$

$${{\mathfrak{M}}_{0}} = s + \frac{{{{k}^{2}}}}{{{{P}_{{{\text{es}}}}}}},\quad {{\mathfrak{M}}_{1}} = - k\gamma \sinh(\gamma ),\quad {{\mathfrak{M}}_{2}} = - k\gamma \cosh(\gamma ),\quad {{\mathfrak{M}}_{3}} = - {{k}^{2}}\sinh(k),\quad {{\mathfrak{M}}_{4}} = - {{k}^{2}}\cosh(k),$$

$${{M}_{1}} = \frac{{k{{A}_{1}}(\gamma \sinh(\gamma ) + \cosh(\gamma ){{B}_{i}}){{P}_{e}}{{\Lambda }_{K}}}}{A},\quad {{M}_{2}} = \frac{{k{{A}_{1}}(\gamma \cosh(\gamma ) + \sinh(\gamma ){{B}_{i}}){{P}_{e}}{{\Lambda }_{K}}}}{A},$$

$${{M}_{3}} = \frac{{k{{A}_{1}}(k\sinh(k) + \cosh(k){{B}_{i}}){{P}_{e}}{{\Lambda }_{\gamma }}}}{A},\quad {{M}_{4}} = \frac{{k{{A}_{1}}(k\cosh(k) + \sinh(k){{B}_{i}}){{P}_{e}}{{\Lambda }_{\gamma }}}}{A},$$

$${{M}_{5}} = \delta \sinh(\delta ) + \cosh(\delta ){{B}_{i}},\quad {{M}_{6}} = \delta \cosh(\delta ) + \sinh(\delta ){{B}_{i}},$$

$${{c}_{2}} = \frac{{ - k\bar {U}(s)}}{{{{M}_{0}}}}({{M}_{6}}\left( {A{{J}_{3}}{{\mathfrak{M}}_{0}} - A{{J}_{1}}{{\mathfrak{M}}_{0}} + k\left( {A{{N}_{e}}({{\mathfrak{M}}_{1}} - {{\mathfrak{M}}_{3}}) + {{A}_{1}}{{P}_{e}}{{J}_{5}}{{\mathfrak{M}}_{0}}\left( {{{\Lambda }_{K}} - {{\Lambda }_{\gamma }}} \right)} \right)} \right)$$

$$ + \;{{J}_{6}}{{\mathfrak{M}}_{0}}(A{{M}_{1}} - A{{M}_{3}} + k{{A}_{1}}{{P}_{e}}{{M}_{5}}({{\Lambda }_{\gamma }} - {{\Lambda }_{K}}))),$$

$${{c}_{3}} = - {{c}_{1}},\quad {{c}_{4}} = - (\gamma {\text{/}}k){{c}_{2}},$$

$${{c}_{5}} = \frac{{k{{A}_{1}}{{P}_{e}}\bar {U}(s)({{\Lambda }_{\gamma }} - {{\Lambda }_{K}})}}{{{{M}_{0}}}}((k{{M}_{2}} - \gamma {{M}_{4}}){{J}_{6}}{{\mathfrak{M}}_{0}} + {{M}_{6}}(\gamma {{J}_{4}}{{\mathfrak{M}}_{0}} - k{{J}_{2}}{{\mathfrak{M}}_{0}} + k{{N}_{e}}(k{{\mathfrak{M}}_{2}} - \gamma {{\mathfrak{M}}_{4}}))),$$

$${{c}_{6}} = \frac{{\bar {U}(s)}}{{{{M}_{0}}}}(k{{M}_{2}}\left( {A{{J}_{3}}{{\mathfrak{M}}_{0}} - A{{J}_{1}}{{\mathfrak{M}}_{0}} + k\left( {A{{N}_{e}}({{\mathfrak{M}}_{1}} - {{\mathfrak{M}}_{3}}) + {{A}_{1}}{{P}_{e}}{{J}_{5}}{{\mathfrak{M}}_{0}}\left( {{{\Lambda }_{K}} - {{\Lambda }_{\gamma }}} \right)} \right)} \right)$$

$$ + \;(\gamma {{J}_{4}}{{\mathfrak{M}}_{0}} - k{{J}_{2}}{{\mathfrak{M}}_{0}} + k{{N}_{e}}(k{{\mathfrak{M}}_{2}} - \gamma {{\mathfrak{M}}_{4}}))\left( {A{{M}_{3}} - A{{M}_{1}} + k{{A}_{1}}{{P}_{e}}{{M}_{5}}\left( {{{\Lambda }_{K}} - {{\Lambda }_{\gamma }}} \right)} \right)$$

$$ + \;\gamma {{M}_{4}}(A{{J}_{1}}{{\mathfrak{M}}_{0}} - A{{J}_{3}}{{\mathfrak{M}}_{0}} + k(A{{N}_{e}}({{\mathfrak{M}}_{3}} - {{\mathfrak{M}}_{1}}) + {{A}_{1}}{{P}_{e}}{{J}_{5}}{{\mathfrak{M}}_{0}}({{\Lambda }_{\gamma }} - {{\Lambda }_{K}})))).$$