Vortex Formation and Separation from the Surface of a Charged Dielectric Microparticle in a Strong Electric Field

Abstract

—The motion of a charged dielectric microparticle in an electric field is first studied over a wide parameter range on the base of the numerical solution of the system of Nernst–Planck–Poisson–Stokes equations. As the most important result, the formation of microvortices on the rear side of the particle is revealed. The microvortices lose their steadiness with increase in the electric field strength and separate periodically from the particle surface. Separation becomes chaotic with further increase in the electric field strength. The phenomenon strongly resembles the formation of the Kármán street but it has another physical mechanism by virtue of almost zero Reynolds numbers of micro- and nanoparticle flow. The asymptotic analysis is carried out and the mechanism of microvortex formation and separation is theoretically substantiated at small Debye numbers.

Electrophoresis represents the basic problem of theoretical physics. Its theoretical study has started more than hundred years ago beginning from the classic Smoluchowski work [1] for dielectric particles. The practical interest in the problem has sharply aroused in the last twenty years in connection with the problems of charge particle control in microfluid devices, the problem of medical diagnostics, and the study of motion and separation of various DNA and proteins in accordance with their properties [2, 3]. Besides the above-mentioned applications to microfluidics, the possibility of fluid mixing by means of microvortex generation, in particular for removal of thermal stresses, is of great importance. The behavior of a particle, its velocity, potential, and ion density fields depend crucially on the type of the surface, namely, ion-selective, metal, dielectric, or more complex type (Janus-face particles with inhomogeneity of their surface or volume properties [4], proteins, DNA, etc.). The present study is completely focused on particles with the dielectric surfaces.

The linear Smoluchowski theory ceases to be valid for strong electric fields when the nonlinear effects become important. Recently, the theoretical description of certain such effects has appeared [5–7], only the asymptotic methods having been mainly proposed in certain particular cases. At the same time, the numerical analysis is bounded by small and moderate electric field strengths. Among the experimental studies we can mention only the latest investigation [8] which contains references to other earlier experimental works. In both experimental and theoretical works most attention has been concentrated on the dependence of the microparticle velocity on the external electric field strength, the Debye number, and the charge density on the particle surface. The theory and the experiment for the electrophoresis rate were compared only in [8], the comparison being restricted to the particle nano-dimensions.

Besides the electrophoresis rate, for applications to microfluidics it is of importance to know the distributions of the fluid velocity, the electric potential, and the ion concentration in the neighborhood of the particle surface; however, the experimental methods are poorly suited for measuring the details of unknown fields. For these purposes the direct numerical simulation carried out in the present study over a wide parameter range from nano- to micro-dimensions gives the best fit.

The most important result obtained is the detection of formation of microvortices on the rear side of the particle. As the electric field strength increases, the microvortices lose their steadiness and separate periodically from the surface. Separation becomes chaotic with further increase in the electric field strength. The phenomenon strongly resembles the formation of the Kármán street but it has another physical mechanism by virtue of the creeping flow approximation. As known from the experiments [9] and confirmed by the calculations [10, 11], the steady-state microvortices are formed near an ionoselective particle (particle whose surface transmits ions of a single sign) in the neighborhood of the surface point at which the ion flux changes sign. In the case of the dielectric particle there is no ion flow across its surface; nevertheless, microvortices are formed. The asymptotic analysis is carried out for small Debye numbers to explain the physical mechanism of microvortex formation and separation.

1 FORMULATION OF THE PROBLEM

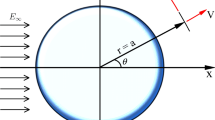
We will consider the motion of a spherical dielectric microparticle of radius $\tilde {a}$ located in an electrolyte solution under the action of an external electric field of strength ${{\tilde {E}}_{\infty }}$.

In the electrokinetics problems two approaches to description of the behavior of a charge in liquids are most widespread. The first of them supposes that the liquid is dielectric and the charge is formed in it as a result of injection from the electrodes [12]. In this case the charge can propagate into the liquid volume and lead to electrohydrodynamic effects. The second approach based on the electrokinetics principles supposes that the liquid is an electrolyte and the charge is formed due to the difference between the concentrations of ions of salts dissolved in liquid. In the present study we will use the second approach since it corresponds to the microhydrodynamics problems to the higher extent.

As the buffer electrolyte, we will consider a binary monovalent electrolyte solution. The cation and anion diffusion coefficients are assumed to be identical, i.e., ${{\tilde {D}}^{ + }} = {{\tilde {D}}^{ - }} = \tilde {D}$. The behavior of electrolyte can be described by the system of the Nernst–Planck equations for the ion concentrations ${{\tilde {c}}^{ \pm }}$. The system must be supplemented with the Poisson equations for the electric potential $\tilde {\Phi }$ and the Navier–Stokes equations for the velocity field ${\mathbf{\tilde {U}}} = (\tilde {U},\tilde {V})$. By virtue of the small scale and, as a result, of the low Reynolds number, the Stokes approximation for creeping flow is used to describe the fluid flow. The electric field inside the microparticle can be described by the Laplace equation for the potential $\tilde {\varphi }$; a surface charge is assumed to exist on the particle surface, the electric charge density $\tilde {\sigma }$ is homogeneous over the entire surface.

The problem is formulated in the spherical coordinate system that moves with the particle velocity and the origin of the coordinate system is at the center of particle (Fig. 1).

Fig. 1.

Flow diagram in the coordinate system moving with a microparticle.

To go over to the dimensionless formulation, we used the following characteristic quantities: the microparticle radius $\tilde {a}$, the thermal potential ${{\tilde {\Phi }}_{0}} = \tilde {R}\tilde {T}{\text{/}}\tilde {F}$, the equilibrium electrolyte concentration ${{\tilde {c}}_{\infty }}$, the dynamic fluid viscosity $\tilde {\mu }$, and the ion diffusion coefficient $\tilde {D}$. Here, $\tilde {R}$ is the universal gas constant, $\tilde {T}$ is the absolute temperature, and $\tilde {F}$ is the Faraday constant

The system is characterized by the following dimensionless parameter: the electric field strength ${{E}_{\infty }} = \tilde {a}{{\tilde {E}}_{\infty }}{\text{/}}{{\tilde {\Phi }}_{0}}$, the Debye number $\nu = {{\tilde {\lambda }}_{{\text{D}}}}{\text{/}}\tilde {a}$, where $\tilde {\lambda }_{{\text{D}}}^{2} = \tilde {\varepsilon }R\tilde {T}{\text{/}}{{\tilde {F}}^{2}}{{\tilde {c}}_{\infty }}$ is the thickness of the double electric layer, the coefficient of coupling between the hydrodynamic and electrostatic parts of the problem $\kappa = \tilde {\varepsilon }{{\tilde {\Phi }}_{0}}{\text{/}}\tilde {\mu }\tilde {D}$, and the permittivity ratio $\delta = {{\tilde {\varepsilon }}_{d}}{\text{/}}\tilde {\varepsilon }$, where ${{\tilde {\varepsilon }}_{d}}$ and $\tilde {\varepsilon }$ are the permittivities of the microparticle material and the liquid medium, respectively.

For the electrolyte the dimensionless system of equations takes the form:

$$\frac{{\partial {{c}^{ \pm }}}}{{\partial t}} + {\mathbf{U}} \times \nabla {{c}^{ \pm }} = \pm \nabla \times ({{c}^{ \pm }}\nabla \Phi ) + {{\nabla }^{2}}{{c}^{ \pm }},\quad {{\nu }^{2}}{{\nabla }^{2}}\Phi = {{c}^{ - }} - {{c}^{ + }},$$

(1.1)

$$ - \nabla P + {{\nabla }^{2}}{\mathbf{U}} = \frac{\kappa }{{{{\nu }^{2}}}}({{c}^{ + }} - {{c}^{ - }})\nabla \Phi ,\quad \nabla \times {\mathbf{U}} = 0.$$

(1.2)

Inside the microparticle the electric potential φ can be described by the Laplace equation

$${{\nabla }^{2}}\varphi = 0.$$

(1.3)

The electric potential is assumed to be continuous across the particle surface, whereas its derivative along the normal to the surface has a jump caused by the surface charge σ; on the particle surface the flux of positive and negative ions is equal to zero and the velocity components must satisfy the no-flow and no-slip conditions:

$$r = 1{\text{:}}\quad \Phi = \varphi ,\quad \nu \frac{{\partial \Phi }}{{\partial r}} = \delta \nu \frac{{\partial \varphi }}{{\partial r}} - \sigma ,\quad \pm {{c}^{ \pm }}\frac{{\partial \Phi }}{{\partial r}} + \frac{{\partial {{c}^{ \pm }}}}{{\partial r}} = 0,\quad U = V = 0.$$

(1.4)

Far from the microparticle, as $r \to \infty$, the ion concentration tends to the equilibrium one, the electric field strength to the external applied field, and the fluid velocity to the particle velocity:

$$r \to \infty {\text{:}}\quad {{c}^{ \pm }} \to 1;\quad \Phi \to - {{E}_{\infty }}r\cos\theta ;\quad U \to - {{U}_{\infty }}\sin\theta ;\quad V \to - {{U}_{\infty }}\cos\theta .$$

(1.5)

The condition of absence of the singularity at r = 0 must be imposed on the potential $\varphi$ inside the microparticle.

For closing the problem it must be supplemented with conditions for the concentrations ${{c}^{ \pm }}$; at the initial instant of time the concentrations are uniformly distributed over the space

$$t = 0{\text{:}}\quad {{c}^{ \pm }} = 1.$$

(1.6)

2 NUMERICAL SOLUTION

In the performed numerical simulation of the problem the values of the parameters κ and δ were specified for an aqueous NaCl solution and a dielectric glass microparticle for which $\kappa = 0.26$ and δ = 0.1. The calculations were carried out for several values of the parameter ν; however, by virtue of the fact that the results differ insignificantly, in the present study we will give the results only for $\nu = 0.0086$. This corresponds to the dimensional particle radius of 5 μm. The calculations at δ = 0, that demonstrated only slight difference from the calculations at δ = 0.1 (of the order of 3–5%) were performed separately. This corresponds to the Yariv results [6, 7] obtained analytically for moderate values of the external electric field strength ${{E}_{\infty }}$.

For solving the time-dependent problem (1.1)–(1.6) we used the direct numerical simulation method based on the finite-difference approach adapted from [13]. Time integration was carried out using the third-order semi-implicit Runge–Kutta method. The established solutions were found as $t \to \infty$. The problem was parallelized on the “Lomonosov” supercomputer to carry out the massive calculations and reveal new phenomena.

For nanoparticles, for which $\nu = O(1)$, the solutions rapidly tend to the steady-state regime with $\partial {\text{/}}\partial t = 0$ and coincide well with those obtained in [5–7]. The most interesting results were obtained for microparticles at small Debye numbers $\nu \ll 1$ and strong electric field strengths ${{E}_{\infty }}$. For a certain critical value $E_{\infty }^{ * }$, a system of steady-state toroidal-shaped microvortices developed on the rear side of the particle. It is convenient to characterize each of the vortices by the angle $a = {{\theta }_{T}}$, at which $\partial \Psi {\text{/}}\partial \theta = 0$ (see Fig. 2). In Fig. 3 we have reproduced the typical propagation of microvortices in the coordinate system of a stationary observer.

Fig. 2.

Maximum stream function $\Psi$ along the radius as a function of the angle $\theta$ for ${{E}_{\infty }} = 400$, $\nu = 0.0086$, and $\sigma = 20$. The value of r is in agreement with Fig. 3.

Fig. 3.

Propagation of unsteady separating vortex: ${{E}_{\infty }} = 320$, $\nu = 0.0086$, and $\sigma = 5$; instants of time $t = {{t}_{1}}$ (a), ${{t}_{2}}$ (b), ${{t}_{3}}$ (c), and ${{t}_{4}}$ (d); ${{t}_{1}} < {{t}_{2}} < {{t}_{3}} < {{t}_{4}}$.

From Fig. 3, in which we have reproduced the successive frames of propagation of a vortex, it can be seen that the vortex is generated in the equator at ${{\theta }_{T}} = 90^\circ$. When the distance from the particle surface increases, the vortices are stretched along the stream and end at the limiting value of the angle $\theta _{T}^{\infty } \approx 60^\circ$ at which the vortex collapses into a point. In all the calculations the angle $\theta _{T}^{\infty }$ varied only slightly and was on the range $\theta _{T}^{\infty } \approx 50^\circ {-} 60^\circ$.

With further increase in ${{E}_{\infty }}$ the microvortex losses steadiness, its periodic separation from the surface occurs, and the vortex is entrained by the stream (Fig. 3). For a fairly strong ${{E}_{\infty }}$, separation becomes chaotic. The phenomenon strongly resembles the formation of the Kármán street but it has another physical mechanism by virtue of the creeping flow approximation.

Earlier, a steady-state microvortex was revealed in the neighborhood of the ion-selective particle, initially experimentally [9] and then numerically [10, 11]. The existence of this vortex called Dukhin-Mishchuk vortex is usually related to nonequilibriumness of the processes in the neighborhood of the ion-selective surface. The vortex develops in the neighborhood of a point on the surface at which the ion flux changes sign. At the same time, the dielectric surface is impermeable for both types of ions and the processes have the equilibrium nature near the dielectric particle. Consequently, there must exist some another physical mechanism responsible for the development of microvortex in the neighborhood of the dielectric particle.

In order to understand the results of the numerical simulation we will consider the analytical solution of the complete problem as $\nu \to 0$. It breaks into the solution for the internal expansion in terms of ν at $r - 1 = O(\nu )$ and that for the outer expansion at $r - 1 = O(1)$. As $(r - 1){\text{/}}\nu \to \infty$ and $r - 1 \to 0$, two expansions are matched [14].

Usually, in the electrostatics problems it is assumed that the charge density $\rho = {{c}^{ + }} - {{c}^{ - }}$ is nonzero only in the neighborhood of the surface at distances of the order of the Debye number, $O(\nu )$, i.e., for the inner solution, while for the outer solution the solution (dilution) is electrically neutral (see, e.g., [15]). As a result, we have

$$\rho \ne 0{\text{:}}\quad \frac{{r - 1}}{\nu } = O(1);\quad \rho = 0{\text{:}}\quad r - 1 = O(1).$$

(2.1)

From the inner expansion as $(r - 1){\text{/}}\nu \to \infty$ we can found the slip velocity ${{U}_{m}}(\theta )$; the normal component of the velocity ${{V}_{m}}$ is equal to zero.

For the outer expansion, far from the surface, the right-hand side of the Stokes equations caused by the Coulomb forces vanishes. The fluid is put in motion by not the body forces but by the surface forces due to the slip velocity which gives the effective hydrodynamic boundary condition at r = 1. Just this assumption was made in the studies of Yariv team [5–7].

Eliminating the pressure from the system (1.2) by means of crossed differentiation and introduction of the stream function, in the axisymmetric formulation in the coordinates $r$ and $\theta$ the stream function $\Psi$ can be determined from the relations:

$$U = - \frac{1}{{\sin\theta }}\frac{1}{r}\frac{{\partial \Psi }}{{\partial r}},\quad V = \frac{1}{{\sin\theta }}\frac{1}{{{{r}^{2}}}}\frac{{\partial \Psi }}{{\partial \theta }}.$$

(2.2)

For the electrically neutral outer solution the equations of system (1.2) go over in the homogeneous biharmonic equation for the stream function $\Psi$ with the effective boundary conditions for the outer solution:

$$r = 1{\text{:}}\quad \Psi = 0,\quad \frac{{\partial \Psi }}{{\partial r}} = - \sin\theta {{U}_{m}}(\theta ),$$

$$r \to \infty {\text{:}}\quad \Psi \to \frac{{{{r}^{2}}}}{{2{{\sin}^{2}}\theta }}{{U}_{\infty }},\quad \frac{{\partial \Psi }}{{\partial r}} \to r{{U}_{\infty }}{{\sin}^{2}}\theta .$$

On the basis of the homogeneous Stokes equation in the spherical coordinate system with the slip velocity ${{U}_{m}}(\theta )$ and the velocity ${{U}_{\infty }}$ at infinity, the stream function $\Psi$ can be represented as the linear combination of the solution with zero slip velocity and the solution with zero velocity at infinity:

$$\Psi = {{\Psi }_{0}} + {{\Psi }_{1}}.$$

(2.3)

In the coordinate system moving with the particle the solution takes the form:

$${{\Psi }_{0}} = {{U}_{\infty }}\left( {\frac{3}{2}r - \frac{1}{{2r}}} \right){{Q}_{1}}(\cos\theta ),$$

(2.4)

$${{\Psi }_{1}} = \sum\limits_{i = 1}^\infty {{{C}_{i}}} {{Q}_{i}}(\cos\theta )({{r}^{{2 - i}}} - {{r}^{{ - i}}}),$$

(2.5)

where Q_i are the Gagenbauer polynomials [16] and ${{C}_{i}}$ are the coefficients of expansion of the slip velocity U_m in terms of the Gagenbauer polynomials:

$${{C}_{i}} = - \frac{{i(i + 1)(2i + 1)}}{4}\int\limits_0^\pi {{{U}_{m}}} (\theta ){{Q}_{i}}(\cos\theta )d\theta .$$

(2.6)

In accordance with the Gary Leal theorem (see [17], relation 4-180) we have: in order for the balance of the forces exerted on a spherical particle in infinite liquid volume in the absence of body forces to be fulfilled, it is necessary that the stream function be orthogonal to the Gagenbauer polynomial ${{Q}_{1}} = \cos\theta$. In our case this condition means that

$${{C}_{1}} = - \frac{3}{2}{{U}_{\infty }}.$$

(2.7)

Using this relation, we can write the formula for the stream function in the form:

$$\Psi = \frac{{{{U}_{\infty }}}}{r}{{Q}_{1}}(\cos\theta ) + {{C}_{2}}\left( {1 - \frac{1}{{{{r}^{2}}}}} \right){{Q}_{2}}(\cos\theta ) + \sum\limits_{i = 3}^\infty {{{C}_{i}}} {{Q}_{i}}(\cos\theta )({{r}^{{2 - i}}} - {{r}^{{ - i}}}).$$

(2.8)

Curve ${{\theta }_{T}} = {{\theta }_{T}}(r)$ is the curve on which the centers of vortex in the cross-section in the angle θ are located and which can be calculated as the extremum of the stream function in the angle:

$$\frac{{\partial \Psi }}{{\partial \theta }}({{\theta }_{T}}) = 0.$$

(2.9)

On the particle itself r = 1, from (2.8) this angle is equal to π/2, as the root of the first Legendre polynomial

$$\frac{{\partial {{Q}_{1}}}}{{\partial \theta }} = - \sin\theta {{P}_{1}}(\cos\theta ) = - \sin\theta \cos\theta ,$$

(2.10)

$$\frac{{\partial {{Q}_{2}}}}{{\partial \theta }} = - \sin\theta {{P}_{2}}(\cos\theta ) = - \frac{{\sin\theta }}{2}(3{{\cos}^{2}}\theta - 1).$$

(2.11)

As a result, we have $\theta _{T}^{\infty } \approx 54.7^\circ$, the value of this angle being independent of both the slip velocity ${{U}_{m}}$ and ${{U}_{\infty }}$. These quantities affect only the transition rate of ${{\theta }_{T}}$ from 90° on the particle to 54.7° at infinity. The numerical pattern shows that tending to the angle of 54.7° occurs fairly rapidly. In this case, in the numerical simulation in the complete formulation, separation of the space electric charge zone can be observed just in the neighborhood of 54.7° and this separation seems to be initiated namely by the convective influence of the Dukhin vortex. The fact that the separation angle is almost independent of the parameter also argues for this hypothesis.

Both angles ${{\left. {{{\theta }_{T}}} \right|}_{{r = 1}}}$ and ${{\left. {{{\theta }_{T}}} \right|}_{{r = \infty }}}$ correlate well with those obtained in the numerical experiment.

Thus, the existence of steady-state vortex is physically attributable to inhomogeneity of the charge distribution and, consequently, of the Coulomb force in the neighborhood of the particle surface. The question arises: why the microvortices begin to separate from the particle surface at a fairly strong electric field strength?

One of the reasons for the above asymptotic analysis is the assumption of the force balance in the outer solution. This is responsible for the use of the Gary Leal theorem [17]. Actually, it is assumed that for outer flow the right-hand side of the Stokes equations caused by the Coulomb forces vanishes. However, as shown by the numerical calculations, such an assumption is valid only for fairly small electric field strengths ${{E}_{\infty }}$. For fairly large ${{E}_{\infty }}$ an interesting phenomenon takes place, namely, the charge begins to be entrained by the fluid stream and enters out into the outer solution. One of the consequences: violation of the force balance that leads to vortex separation. In this case the typical charge distribution is given in Fig. 4: charge separation can take place in both the particle equator $\theta = 90^\circ$ and the particle pole $\theta = 0^\circ$.

Fig. 4.

Distribution of the charge density $\rho = {{c}^{ + }} - {{c}^{ - }}$ in the neighborhood of a microparticle, ${{E}_{\infty }} = 400$, $\nu = 0.0086$, and $\sigma = 20$.

SUMMARY

The formation of the Dukhin vortex initiated by a dielectric particle is revealed by means of the direct numerical simulation of the system of equations. The presence of both steady-state and unstable and unsteady vortices is shown. For small supercriticalities, the vortices are strictly periodically separated. As the electric field strength increases, vortex separation becomes chaotic. This resembles the well-known pattern of von Kármán street. As distinct from the von Kármán street, in which inertia is the mechanism of vortex formation, in our problem the inertia forces are negligibly small and the Coulomb force serves as the mechanism of generation of the Dukhin vortices.