Modeling of Continuous Spin Detonation of a Hydrogen–Air Mixture in an Annular Cylindrical Combustor

Abstract

A closed mathematical model of continuous spin detonation with the chemical kinetics equation correlated with the second law of thermodynamics is developed for a hydrogen–air mixture within the framework of the quasi-three-dimensional unsteady gas-dynamic formulation. The model takes into account the reverse influence of the oscillation processes in the combustor on the injection system of the mixture components. For comparisons with experimental data, the numerical simulations are performed for the geometric parameters of the flow-type annular combustor with an outer diameter of 306 mm used in the experiments. For the flow rates of the mixture varied in the interval 73.1–171.3 kg/(s$\, \cdot\,$m$^{2}$), the one-wave, two-wave, and three-wave regimes of continuous spin detonation are calculated, the flow structure is analyzed, the specific impulses are determined, and comparisons with experimental data are performed. It is shown that the use of a simplified single-stage kinetic scheme of hydrogen oxidation, which was used in some investigations, for simulating continuous spin detonation leads to results that differ from the experimental data by several times.

INTRODUCTION

A currently considered possible alternative to conventional combustion of fuels in the turbulent flame is the method of fuel burning in accordance with the scheme proposed by Voitsekhovskii [1] in the regime of continuous spin detonation (CSD) with transverse detonation waves (TDWs) [2, 3]. Continuous spin detonation in a flow-type annular cylindrical combustor 306 mm in diameter (DK-300) was obtained for the first time in an acetylene–air mixture in [4] and in a hydrogen–air mixture in [5, 6]. The first numerical studies of CSD in the rocket-type detonation combustor were performed for hydrogen as a fuel in [7, 8] and for some hydrocarbon fuels in [9]. The current status of two-dimensional and three-dimensional numerical investigations of CSD was reviewed in [10]. Three-dimensional numerical simulations of CSD in a stoichiometric hydrogen–air mixture were performed in [11, 12] with the use of a standard $k$–$\varepsilon$ turbulence model with simplified single-stage chemical kinetics. For comparisons with experimental data, the computational domain size was taken to be the same as that used in the experiments [5]; the specific flow rate of the mixture was $g_{\Sigma } \approx 170$ kg/(s$\, \cdot\,$m$^{2}$). To simplify the problem, the computations [11] were performed with injection of a premixed mixture into the combustor, and separate injection of the fuel and oxidizer were modeled in [12]. In both cases, only one-wave CSD regimes with the TDW rotation frequency $f$ = 1.7 kHz [11] and $f$ = 2$–$2.1 kHz [12] were obtained, whereas a regular three-wave CSD regime with the TDW frequency $f$ = 4.46 kHz was observed in the experiments in DK-300 [5] at $g_{\Sigma } \approx 135$ kg/(s$\, \cdot\,$m$^{2}$). The quantitative differences of the predictions [11, 12] from the experimental results [5] (three-fold underestimation of the number of TDWs) are apparently caused by using a simplified single-stage kinetic scheme of hydrogen oxidation used in the simulations. Therefore, further effort has to be applied for the development of mathematical models of CSD with more reliable kinetics equations for hydrogen oxidation in air.

Fig. 1

Schematic of the annular cylindrical combustor model.

Fig. 2

Domain of the numerical solution of the problem.

The goals of the present study are the development of a closed mathematical model of CSD in a flow-type combustor with the chemical kinetics equation [13] correlated with the second law of thermodynamics in a quasi-three-dimensional gas-dynamic approximation, numerical investigation of the CSD regime in the hydrogen–air mixture, and verification of the mathematical model on the basis of the experimental results [5].

MATHEMATICAL FORMULATION OF THE PROBLEM

System of Equations

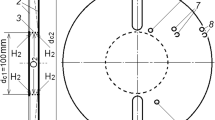
Let us consider the problem of mathematical modeling of detonation combustion of a hydrogen–air mixture in a flow-type annular cylindrical combustor with exhaustion of the mixture from a manifold. For subsequent comparisons of the predicted parameters with the experimental data [5], the scheme and geometric sizes of the annular combustor were taken as close as possible to the combustor parameters used in [5, Fig. 1]. Thus, we assume that the mixture is injected from a high-pressure receiver through injectors in the end face of the annular manifold (total length $L_{m}$, width $H_{m}$, and converging section length $L_{m}$/2), passes through an annular slot of width $\delta$, and enters the combustor (Fig. 1). The diameter of the annular combustor is $d_c$, its total length is $L_c$, and the diverging section length is $L_{\Delta }$(the combustor expands to a size $\Delta > \delta$).

As the inequalities $\delta < \Delta < H_{m}\ll d_c$ are valid for the experimental combustors with annular geometry [5], the problem can be considered in a quasi-three-dimensional approximation, similar to [3]. In the combustor space with the boundaries $\Gamma_0$ (end face of the annular manifold), $\Gamma_1$ (combustor entrance), and $\Gamma_2$ (open end of the combustor where detonation products leave the combustor), the annular domain can be cut and unfolded into a rectangular domain of the problem solution $\Omega =\Omega _{1}\, \cup\, \Omega _{2}$ shown in Fig. 2. Here $\Omega _{1}= (- L_{m} < x < 0$, $0 < y < l)$, $\Omega _{2}= (0< x < L_c$, $0 < y < l)$, $x$ and $y$ are the spatial variables of the orthogonal coordinate system, and $l$ is the period of the problem.

Let a certain amount of energy sufficient for detonation initiation be released in the computational domain area $\Omega _{3}$ at a certain time instant after the reacting mixture is supplied to the combustor entrance (boundary $\Gamma _{1}$). As a result of initiation, an unsteady detonation wave propagates in the domain $\Omega _{2}$. The goal is to determine its dynamics, structure, and also conditions of reaching a self-sustained CSD regime for various values of the governing parameters of the problem.

An unsteady gas-dynamic flow of a hydrogen–air mixture in the domain $\Omega$ is described by the following system of equations of unsteady gas dynamics with chemical transformations:

$${} \rho _t + S^{ - 1}(\rho uS)_x + (\rho v)_y = 0,$$

$${} (\rho u)_t + S^{ - 1}(\rho u^2S)_x + (\rho uv)_y + p_x = 0,$$

$$(\rho v)_t + S^{ - 1}(\rho uvS)_x + (\rho v^2)_y + p_y = 0,$$

(1)

$${} (\rho E)_t + S^{ - 1}[\rho u(E + {p}/{\rho })S]_x + [\rho v(E +{p}/{\rho })]_y = 0,$$

$${} (\rho Y)_t + S^{ - 1}(\rho uYS)_x + (\rho vY)_y = \rho f_5 ,$$

$${} (\rho \mu )_t + S^{ - 1}(\rho u\mu S)_x + (\rho v\mu )_y = \rho f_6 .$$

Here $t$ is the time, $\rho$ is the density, $u$ and $v$ are the velocity vector components, $p$ is the pressure, $E = U + (u^{2} + v^{2})/2$, $U(T,\mu )$ is the total internal energy of the gas, $T$ is the temperature, $\mu$ is the current molar mass of the mixture, and $Y$ is the fraction of the chemical induction period.

The cross-sectional area of the manifold and combustor channel $S = S(x)$ along the $x$ coordinate with smooth sinusoidal convergence ($-L_{m}/2 < x < 0$) to the width $\delta$ and subsequent smooth sinusoidal divergence ($0 < x < L_{\Delta })$ to the combustor channel width $\Delta$ is defined in the form

$$S(x) = \left\{\begin{array}{l} H_m l, \quad\quad\quad - L_m < x < - L_m / 2, \\[2mm] [ (H_m - \delta )\sin ( - \pi x / L_m ) + \delta ] l, \\[1mm] \quad\quad\quad\quad\quad\;\, - L_m / 2 < x < 0, \\[2mm] [(\Delta - \delta )\sin (\pi x / 2 L_\Delta ) + \delta] l, \\[1mm] \quad\quad\quad\quad\quad\;\; 0 < x < L_\Delta, \\[2mm] \Delta l, \quad\quad\quad\quad x \ge L_\Delta. \\[2mm] \end{array}\right.$$

(2)

The energy release is described within the framework of the two-stage kinetic model [14]: induction stage ($0 < Y \le 1$, $f_{5}= - 1/t_{\mathit ind}$, $f_{6}$ = 0) where the energy release is absent and chemical transformation stage ($Y = 0$, $f_{5}$ = 0, $f_{6} \ne 0$), where the energy release rate is determined by the chemical reaction rates.

According to the experiments [15], the chemical delay of ignition of the hydrogen–air mixture in the induction region ($0 < Y \le 1$) has the form

$$t_{\mathit ind}=\frac{K_a \mu_{O_2} }{\rho z}\,\exp\bigg(\frac{\varepsilon _a }{RT}\bigg),$$

(3)

where $\varepsilon _a$ = 17.15 kcal/mol is the activation energy, $K_{a}$ = 5.38$\, \cdot\,$10$^{ - 11}$ mol$\, \cdot\,$s/l is the pre-exponent, $R$ is the universal gas constant, $\mu_{O_2}$ is the molar mass of oxygen, $z = \mu_{O_2}$/($\mu_{O_2}$+ 2$\phi$$\mu_{H_2}+\alpha \mu _{in})$ is the mass fraction of oxygen in the hydrogen–air mixture, $\mu_{H_2}$ is the molar mass of hydrogen, $\phi$ is the fuel-to-oxidizer equivalence ratio, $\alpha$ = 3.772, and $\mu _{in}$ = 28.144 kg/kmol. The inert component of air included nitrogen (N$_{2}$) and argon (Ar). Then the structural formula for the hydrogen–air mixture can be presented as 2$\phi$H$_{2}$ + O$_{2}$ + 3.7275N $_{2}$ + 0.0445Ar, and $\mu _{in}$ = 0.988$\mu_{N_2}$ + 0.012$\mu_{Ar}$. Here $\mu_{N_2}$ and $\mu_{Ar}$ are the molar masses of nitrogen and argon.

System (1) is supplemented with the equations of state

$$p = \rho RT/\mu ,\;\;\; U = U_{th} + U_{ch},$$

(4)

where $U_{th}$ and $U_{ch}$ are the thermodynamic and chemical components of internal energy. The internal energy of the gas $U(T,\mu )$ is counted from the ultimately dissociated composition at zero temperature.

In the induction region ($Y > 0$), the molar fraction of the mixture is $\mu =\mu _{0}$ = const and energy release is absent; therefore, the following expressions are valid:

$$U_{th} = \frac{p}{(\gamma - 1)\rho },\;\;\; U_{ch}= - \frac{E_2^0 z}{\mu_{O_2} } - \frac{\phi E_1^0 z}{8 \mu _{H_2} }.$$

(5)

where $\gamma$ is the ratio of specific heats of the gas in the chemical induction region, $E_1^0$ and $E_2^0$ are the dissociation energies of the H$_{2}$ and O$_{2}$ molecules, respectively.

According to [13, 16], the thermodynamic and chemical components of the internal energy of the gas in the region of chemical transformations have the form

$${} U_{th} = A(\mu ,T)\frac{RT}{\mu },\quad U_{ch} = E_d \bigg( {\frac{1}{\mu } - \frac{1}{\mu _{\min } }} \bigg),$$

$${} A(\mu ,T) = \frac{\mu }{\mu _a } + \frac{1 - \sigma }{2} + \bigg( {\frac{\mu }{\mu _a } + \sigma - 1} \bigg) \frac{\theta / T}{\exp (\theta / T) - 1},$$

(6)

where $\sigma =\sigma _{\max}(\mu /\mu _{\min} - 1)/(\mu_{\max}/\mu _{\min } - 1)$, $\mu _{a}$, $\mu _{\min}$, and $\mu_{\max}$ are the molar masses of the gas in the atomic, ultimately dissociated, and ultimately recombined states, $\sigma _{\max}$ is the molar fraction of triatomic molecules in the ultimately recombined state, $\theta$ is the effective temperature of excitation of vibrational degrees of freedom of molecules, $E_d$ is the mean energy of dissociation of reaction products, and $\gamma = 1 + 1/A(\mu _{0},T)$. All parameters are uniquely determined by the atomic composition of the original mixture (mass fraction of oxygen $z$). For the hydrogen–air mixture, we have

$${} \mu _0^{ - 1} = \frac{z(1+ 2\phi )}{\mu _{O_2}}+ X_{in},$$

$${} \mu _{\min }^{ -1} = \frac{2z(1+ 2\phi )}{\mu _{O_2}} + X_{in},\quad E_{d} \approx E_1^0 \approx E_2^0 ;$$

in the case of oxygen deficit $z \le z_{st }$($\phi \ge 1)$,

$${} \mu _{\max }^{ - 1} = \frac{2\phi z}{\mu _{O_2}} + X_{in},\quad \sigma_{\max}= \frac{2z \mu _{\max}}{\mu _{O_2}},$$

$${} \theta = 3000 + 500 \sigma _{\max};$$

in the case of oxygen excess $z > z_{st }$($\phi < 1)$,

$${} \mu _{\max }^{ - 1} = \frac{(1 + \phi )z}{\mu _{O_2}} + X_{in},\quad \sigma _{\max}= \frac{2{\phi}z \mu _{\max}}{\mu _{O_2}},$$

$${} \theta = 1500 + (2000 + 750\, \cdot\, 3{.}7275 /\phi ) \sigma _{\max}.$$

Here $X_{in}= [1 - (1 + 2\phi \mu _{H_2}/\mu _{O_2})z]/\mu_{in}$, and $z_{st}=\mu _{O_2} / ( {\mu _{O_2} + 2\mu _{H_2} +\alpha \mu _{in} })$ is the mass fraction of oxygen in the hydrogen–air mixture with a stoichiometric ratio of the oxidizer and the fuel ($\phi$ = 1).

The composition (molar mass $\mu$) of the gas phase behind the ignition front changes in accordance with the chemical kinetics equation [13] correlated with the second law of thermodynamics; for the refined description of the thermodynamic part of the internal energy (6), it has the form

$${} f_6 = 4K_ + [W_1 (\mu )\rho ^2 - W_2 (T,\mu )\rho ],$$

$$W_1 (\mu ) = \frac{(1 - {\mu }/{\mu _{\max } })^2}{\mu },$$

(7)

$$W_2 (T,\mu ) = K_ - \bigg(\frac{\mu }{\mu _{\min } } - 1\bigg) \bigg( {\frac{T}{T_0 }} \bigg)^{{\beta }/{2}}$$

$${}\times\bigg[ {1 - \exp \bigg(\frac{ - \theta }{T}\bigg)}\bigg]^\beta \exp \bigg( - \frac{E_d }{RT}\bigg),$$

where $K_ +$ is the constant of the generalized recombination rate, $K_ -$ is the equilibrium constant, $T_0$ is the initial temperature of the mixture, and $\beta = 1+\sigma _{\max}/(\mu _{\max}/\mu _{\min } - 1)$.

System (1)–(7) is closed and completely defines the unsteady motion of the reacting hydrogen–air mixture with variable heat release in the reaction region of the detonation wave.

Boundary Conditions

Condition 1. On the boundary $\Gamma_0$($x = -L_{m}$, $0 \le y \le l)$, fuel and oxidizer injection into the manifold is modeled by the inflow of the combustible mixture through a system of the Laval micronozzles uniformly distributed along $\Gamma_0$. The ratio of the cross-sectional areas of the micronozzle throat and micronozzle exit is assumed to be equal to the ratio of the total cross-sectional area of the orifices $S_{*}$ to the total cross-sectional area of the manifold $S_{m}$. The gas-dynamic parameters at the micronozzle exit are determined by the initial parameters of the mixture in the receiver and by the pressure in the manifold $p(- L_{m},y,t)$ [7]. Then the following relations are valid on the boundary $\Gamma_0$:

$${} p = p(- L_{m},y,t)$$

$${}\mbox{if}\,\, p' \le p(- L_{m},y,t) <p_{r};$$

$$u = u_{\max}[1 - (p/p_{r})^{(\gamma - 1) / \gamma }]^{1 / 2},\;\; \rho =\rho _{r}(p/p_{r})^{1 / \gamma }$$

$$\mbox{if}\,\, p''\le p(- L_{m},y,t) < p_{r};\quad\quad$$

(8)

$$\rho uS_{m}=\rho _{ * }u_{ * }S_{ * },\;\; \gamma /(\gamma -1)p/\rho + u^{2}/2 = u_{\max}^{2}/2$$

$$\mbox{if}\,\, p(- L_{m},y,t) <p''.$$

Here $p_{r}$, $\rho _{r}$, and $T_{r}= p_{r}\mu _{0}/(\rho _{r}R)$ are the pressure, density, and temperature of the mixture in the receiver; $\rho_{ * }$, $u_{ * }$, and $u_{\max}$ are the critical density, critical velocity, and maximum possible velocity, which are known functions of $\gamma$, $p_{r}$, and $\rho _{r}$; $S_{m}$ and $S_{ * }$ are the cross-sectional areas of the micronozzle exit and throat; finally, $p'$ and $p''$ are the calculated pressures of the supersonic and subsonic exhaustion modes satisfying the equation

$$(p/p_{r})^{1 / \gamma }[1 - (p/p_{r})^{(\gamma - 1) / \gamma}]^{ 1 / 2}{}$$

$${}= [2/(\gamma +1)]^{1 / (\gamma - 1)}[(\gamma -1)/(\gamma +1)]^{ 1 / 2} S_{ * }/S_{m}.$$

Condition 2. The following condition is imposed on the boundary $\Gamma_1$ ($x = 0$, $0 \le y \le l$), where the transition from the manifold through the annular slot to the combustor occurs:

$$Y = 1,\;\;\mu =\mu _{0}.$$

(9)

This condition ensures the inert character of the gas flow in the manifold ($-L_{m} \le x \le 0$), because H$_{2}$ was injected at the combustor entrance in the experiments [5].

Condition 3. The left and right boundaries of the domain $\Omega$ are subjected to the condition of solution periodicity. By virtue of periodicity (with the period $l$) along the $x$ coordinate, all gas-dynamic functions $F(x,y,t)$ satisfy the condition

$$F(x, 0, t) = F(x, l, t),\;\; -L_{m} \le x \le L_c.$$

(10)

Condition 4. At the combustor exit (boundary $\Gamma_2$: $x = L_c$; $0 \le y \le l$) with exhaustion of the combustion products into the ambient state with the ambient pressure $p = p_{a}$, the combustor-exit values of the pressure $P_{ex}$, density $R_{ex}$, velocity vector component $u_{ex}$ and $v_{ex}$, and, correspondingly, the mass, momentum, and energy fluxes on the boundary $\Gamma_2$

$$M_{ex}= R_{ex} u_{ex},\;\; J_{ex}= P_{ex} + u_{ex} M_{ex},$$

(11)

$${} E_{ex}= (U + u^{2 }/2 + v^{2 }/2)_{ex} M_{ex} + P_{ex} u_{ex}$$

are determined by the method [17, § 15] of solving the Riemann problem with setting the ambient pressure$p_{a}$ in the finite difference grid cell outside the computational domain contour. The initial data in the combustor imply a motionless stoichiometric hydrogen–air mixture at $p = p_{a}$.

Initial Constants of the Model

For the numerical solution of the formulated problem (1)–(11), it is necessary to set all initial constants of the model and the basic thermodynamic properties of the mixture with the chosen composition and its combustion products, as well as the constant involved into the chemical kinetics equation (7). The basic constants are $\mu _{H_2 }$ = 2 kg/kmol, $\mu _{O_2}$ = 32 kg/kmol, $\mu _{in}$ = 28.144 kg/kmol, $\alpha$ = 3.772, $R$ = 8.3144$\, \cdot\,$10$^{3 }$ J/(kmol$\, \cdot\,$K), $E_1^0$ = 104.2 kcal/mol, $E_2^0$ = 117.9 kcal/mol, $E_{d}$ = 110 kcal/mol, $K_{ + }$ = 6$\, \cdot\,$10$^{8}$ m$^{6}$/(kmol$^{2}\, \cdot\,$s), $T_{0}$ = 300 K, and $p_{0 }$ = 1.013$\, \cdot\,$10$^{5}$ Pa.

For a specified value of the equivalence ratio $\phi$, we determine the mass fraction of oxygen in the mixture $z = \mu _{O_2}/(\mu _{O_2} + 2{\phi }\mu _{H_2} +\alpha \mu _{in})$, initial molar mass of the mixture $\mu_{0}(z)$, and other constants included into the description of the thermodynamic properties of the gas and its combustion products: $\mu _{\min}(z)$, $\mu _{\max}(z)$, $\sigma_{\max}(z)$, $\theta (z)$, $\beta (z)$, and $K_{ - }(z)$.

The values of these constants for the stoichiometric ($\phi$ = 1) hydrogen–air mixture are $z_{st}$ = 0.2251, $\mu _{0 }$ = 20.992 kg/kmol, $\mu_{\min}$ = 14.5483, $\mu _{\max}$ = 24.6304, $\sigma _{\max}$ = 0.3492, $\theta$ = 3175 K, $\beta$ = 1.5, and $K_{ - }$ = 3529 kmol/m$^{3}$.

It should be noted that the chemical equilibrium constant $K_{ - }$ is determined from the chemical kinetics equation (7) by substituting the parameters of the Chapman–Jouguet detonation at $f_{6}$ = 0 calculated in [18].

For comparisons with the experiments [5], the numerical simulations are performed for the same geometric parameters of the manifold and combustor channel:

$${} L_{m}= 7.5\:cm,\; H_{m}= 4.2\:cm,$$

$$L_{\delta }= L_{m} /2,\; \delta = 0.2\:cm,$$

(12)

$${} L_c= 66.5\:cm,\; L_{\Delta }= 4\:cm,\; \Delta = 2.3\:cm.$$

Governing Parameters of the Problem

For fixed geometric parameters of the manifold and combustor (12), the solution of the unsteady problem of CSD depends on the governing parameters

$$p_{r},\; T_{r},\; S_{ * },\; {\phi } ,\; p_{a} ,\; l .$$

(13)

The first four parameters are those in the injection system: the pressure $p_{r}$ and stagnation temperature $T_{r}$ in the receiver, the total cross-sectional area of the micronozzle throat $S_{ * }$ at the manifold entrance, and the equivalence ratio $\phi$, which define the initial flow rate of the mixture in the manifold and combustor:

$$G_{\Sigma 0 }=\bigg(\frac{2}{\gamma + 1}\bigg)^{{0.5(\gamma + 1)}/({\gamma -1})}p_r \sqrt {\frac{\gamma \mu _0}{RT_r}} S_\ast .$$

(14)

The parameter $p_{a}$ is the ambient pressure, and $l$ is the period of the problem along the $y$ axis.

COMPUTATION RESULTS

Problem (1)–(11) is solved numerically. The solution domains $\Omega _{1}$ (manifold) and $\Omega _{2}$ (combustor) are covered by a motionless grid with uniform cells in the $y$ direction and nonuniform cells in the $x$ direction. The number of cells is 50 $\times$ 400 in the domain $\Omega _{1 }$ and 200 $\times$ 400 in the domain $\Omega _{2 }$. Equations (1) are integrated by the Godunov–Kolgan second-order finite difference scheme [17, 19].

The dynamics of CSD formation in the stoichiometric hydrogen–air mixture was calculated for the geometric parameters of the manifold and combustor channel given in Eqs. (12) and for the parameters in the injection system and ambient pressure corresponding to the experimental data [5]:

$$\frac{p_{r}}{p_{0}}= 6{.}4,\;\; \frac{T_{r}}{T_{0}}= 0{.}757,\;\; \frac{S_{ * }}{S_{m}}= 0{.}027,$$

(15)

$${} \phi = 1,\;\;\; \frac{p_{a}}{p_{0}}= 1,$$

with the specific flow rate of the mixture $g_{\Sigma 0 }= G_{\Sigma 0}/S_{\Delta }$ = 73.1 kg/(s$\, \cdot\,$m$^{2}$). For finding the periodic solution with TDWs, there is only one free parameter left, i.e., the problem period $l$. For comparisons of the flow pattern with the one-wave ($n$ = 1) CSD regime [5], the parameter $l$ is assumed to be equal to the combustor perimeter calculated on the basis of the mean diameter of the annular gap: $\Pi=\pi (d_{c } - \Delta )$ = 88.907 cm.

A certain amount of energy sufficient for detonation initiation is instantaneously released at the initial time ($t$ = 0) in the domain $\Omega _{3}$(see Fig. 2) shaped as a quarter of an ellipse. As a result, a TDW propagates over the combustor.

The calculated dimensionless static pressure $P(t) = p(t)/p_{0}$ (solid curve) and the period-averaged static pressure $\langle P(t)\rangle = \langle p(t)\rangle/p_{0}$ (dashed curve) at the combustor point with the coordinates ($x$ = 1.5 cm, $y$ = 0) as functions of time $t$ are shown in Fig. 3. Here $\displaystyle\langle p(t)\rangle= \frac{1}{l}\int\limits_0^lp(x,y,t)dy$. It is seen that the pressure behaves nonmonotonically (fluctuates with time) as the TDW propagates over the combustor. The computations show that the pressure at the early stage of the process (within 5 ms) experiences irregular fluctuations with decreasing amplitude, and then the fluctuations become almost periodic (with the period $\Delta t$ $\approx$0.47 ms). The mean pressure reaches a constant value $\langle P\rangle$ $\approx$1.1 with time. It should be noted that the static pressure sensor mounted at a distance $x$ = 1.5 cm from the end face of the combustor showed $\langle P\rangle$ $\approx$ 1.2 in the experiments [5] at $\phi$ = 1 and $g_{\Sigma }$ = 73.1 kg/(s$\, \cdot\,$m$^{2}$).

Fig. 3

Current (solid curve) and period-averaged (dashed curve) static pressure versus time at the combustor point with the coordinates ($x$ = 1.5 cm, $y$ = 0).

Knowing the time period $\Delta t$, one can find the TDW rotation frequency $f = 1/\Delta t$ = 2.13 kHz, the period-averaged velocity $D = l/\Delta t$ $\approx$1.9 km/s, and the ratio $D/D_{CJ}$ = 0.96. Here $D_{CJ}$ = 1.966 km/s is the velocity of the ideal Chapman–Jouguet detonation in a stoichiometric hydrogen–air mixture [18]. Thus, a TDW propagates continuously over the layer of the hydrogen–air mixture injected from the manifold through the boundary $\Gamma$$_{1}$; this wave propagates with a velocity $D$ that is smaller than the Chapman–Jouguet detonation velocity.

To check whether the periodic solution reaches the quasi-steady detonation mode, the following quantities averaged over the period $l$ at the combustor exit are additionally calculated at each time instant:

$${} g_{\Sigma }(L_c,t) = \frac{1}{l}\int\limits_0^l {\rho udy} ;$$

$$\langle p_{0}(L_c,t)\rangle {}$$

(16)

$${}=\frac{1}{l}\int\limits_0^l {(p(L,y,t) + \rho u^2(L,y,t))dy};\qquad\qquad$$

$${} I_{sp}~= (\langle p_{0}\rangle - p_{a})\cdot S_{\Delta }/(G_{\!f} g).$$

Here $g_{\Sigma }(L_c,t)$ is the mean specific flow rate of the mixture, $\langle p_{0}(L_c,t)\rangle$ is the mean total pressure at the combustor exit, $I_{sp}$ is the mean specific impulse per unit mass of the fuel, $S_{\Delta }$ =$\pi (d_c \, - \, \Delta ) \Delta$ is the free cross-sectional area of the combustor, $G_{\!f}$ is the fuel flow rate, and $g$ is the acceleration due to gravity.

The computed results show that the parameters $g_{\Sigma }(L_c,t)$ and $I_{sp}$ reach constant values at $t > 8$ ms since the instant of CSD initiation; for the variant under consideration, these values are

$${} g_{\Sigma }(L_c,t) \approx g_{\Sigma 0}= 73.1\mbox{~kg/(s$\, \cdot\, $m$^{2}$)},\; I_{sp} \approx 2680\mbox{~s.}$$

Fig. 4

Calculated two-dimensional structure of CSD in the hydrogen–air mixture for $g_{\Sigma }$ = 73.1 kg/(s$\, \cdot\,$m$^{2}$), $\phi$ = 1, and $n$ = 1: (a) pressure contours $p/p_{0}$; (b) temperature contours $T/T_{0}$; (c) Mach number contours M$_{x}$ = $u/c$.

TDW Structure

Figure 4 shows the two-dimensional structure of the flow in the case of TDW propagation in the combustor with the geometric parameters (12) at $l$ = 88.91 cm at the time $t$ = 10.8 ms. The TDW front height for the injection parameters (15) is$h$ = 10 cm. The upper part of the figures ($x > 0$) shows the flow structure in the manifold ($\Omega _{1}$), and the lower part of the figures ($x< 0$) shows the flow structure in the combustor ($\Omega _{2}$). The TDW moves from left to right with the velocity $D$ = 1.9 km/s over the triangular low-temperature region of the original mixture injected through the upper boundary from the manifold. The pressure contours (Fig. 4a) display a rapid decrease in pressure behind the TDW front. When the pressure behind the TDW front becomes smaller than that in the manifold, the detonation products are displaced downstream by the new portions of the mixture from the manifold. It is seen that the TDW forms an oblique shock wave (SW) (Fig. 4a) penetrating upstream through the slot to the manifold; as a result, the mean pressure in the manifold increases with time and reaches the constant value $\langle P(-L_{m}, t)\rangle$ $\approx$4.34 (in the present computation). An oblique SW (tail) departs downstream from the TDW and moves over the hot detonation products ($T \approx 1600–1800$ K, Fig. 4b). The temperature behind the oblique SW front reaches the values $T \approx 2200–2800$ K in the upper part of the tail; the temperature and degree of inhomogeneity of this wave decrease at the combustor exit ($T$ = 1950$–$2350 K). The Mach number contours for the projection of the velocity vector onto the $x$ axis (Fig. 4c) show that the values of M$_{x}$ ahead of the SW front monotonically increase from 0.55 to 1.17 with distance from the combustor entrance (boundary $\Gamma$$_{1}$), whereas the velocity in the detonation products behind the TDW front is subsonic. The attempt to continue the computation for this variant with $g_{\Sigma }$ = 73.1 kg/(s$\, \cdot\,$m$^{2}$) by reducing the problem period to $l$ =$\Pi$/2 = 44.45 cm ($n$ = 2) resulted in TDW failure and decay. This means that the above-described numerical solution for one-wave CSD in the combustor with parameters (12) is the only possible solution.

Table 1. Calculated parameters of CSD in the hydrogen–air mixture in the combustor with parameters (12)

Fig. 5

Static pressure versus time at the combustor point with the coordinates ($x$ = 0, $y$ = 0) for $p_{r}/p_{0}$ = 10 at $l$ = 44.45 cm (solid curve) and $l$ = 29.63 cm (dashed curve).

Fig. 6

Temperature field $T/T_{0}$ in the combustor with CSD in the hydrogen–air mixture ($\phi$ = 1): (a) $g_{\Sigma }$ = 114.2 kg/(s$\, \cdot\,$m$^{2}$), $n$ = 2, and $D$ = 1.82 km/s; (b) $g_{\Sigma }$ = 171.3 kg/(s$\, \cdot\,$m$^{2}$), $n$ = 3, and $D$ = 1.77 km/s.

Increase in the Injection Pressure

For the geometric parameters of the manifold and combustor (12), the influence of the injection pressure of the mixture in the receiver $p_{r}$ on the parameters and flow structure with TDWs is considered. For fixed values $T_{r}/T_{0}$ = 0.757, $S_{ * }/S_{m}$ = 0.027, $\phi$ = 1, and $p_{a}/p_{0}$ = 1, CSD computations are performed with variations of the injection pressure in the interval $p_{r}/p_{0}$ = 6.4–15 and, correspondingly, specific flow rate of the mixture $g_{\Sigma 0 }$ = 73.1–171.3 kg/(s$\, \cdot\,$m$^{2}$). The computed data are summarized in Table 1, where $\langle p\rangle$ is the mean static pressure at the combustor entrance, $n$ is the number of TDWs accommodated over the combustor perimeter, and $h$ is the TDW height.

Figure 5 shows the calculated dimensionless static pressure as a function of time $P(t) = p(t)/p_{0}$ at the combustor point with the coordinates ($x$ = 0, $y$ = 0) for $p_{r}$/$p_{0}$ = 10 ($g_{\Sigma 0 }$ = 114.2 kg/(s$\, \cdot\,$m$^{2})$) for the problem periods $l$ =$\Pi$/2 (solid curve) and $l$ =$\Pi$/3 (dashed curve). It is seen that there are periodic oscillations of pressure with the period $\Delta t$ = 0.244 ms ($f$ = 4.1 kHz and $D$ = 1.82 km/s) at $l$ =$\Pi$/2 ($n$ = 2), i.e., the wave reaches the CSD regime. As the period decreases to $l$ = $\Pi$/3 ($n$ = 3), the pressure experiences two oscillations (dashed curve) with variable amplitude, followed by its monotonic decrease; finally, at $t$ $>$3.4 ms, the pressure reaches an almost constant value $P(t)$ $\approx$ 3.15. The analysis of the solution shows that the rotating TDW fails and the combustion front and combustion products are entrained downstream toward the combustor exit. After that, the flow of the non-reacting mixture entering the combustor through the upper boundary $\Gamma_1$ and leaving the combustor through the lower boundary $\Gamma_2$ is formed in the solution domain. According to the classification [3], the one-wave CSD regime in this case is a “parasitic" periodic solution, which is physically meaningless. Thus, as the injection pressure increases to $p_{r}/p_{0}$ = 10 ($g_{\Sigma }$ = 114.2 kg/(s$\, \cdot\,$m$^{2})$), the only periodic solution in the combustor with parameters (12) is the two-wave CSD regime. Its two-dimensional structure (temperature field) is shown in Fig. 6a.

The series of CSD computations performed for $p_{r}/p_{0}$ = 15 ($g_{\Sigma 0 }$ = 171.3 kg/(s$\, \cdot\,$m$^{2})$) with consecutive reduction of the problem period to $l$ =$\Pi$/4 = 22.2 cm and rejection, as was noted above, of parasitic solutions made it possible to obtain a unique solution for the combustor with parameters (12); three-wave ($n$ = 3) CSD regime propagating with the velocity $D$ = 1.77 km/s. Its two-dimensional structure (temperature field) is shown in Fig. 6b.

Table 2. Calculated CSD parameters ($p_{r}$/$p_{a} = 15$ and $l= 29{.}63$ cm) in combustors of different lengths

Fig. 7

Calculated two-dimensional TDW structure (temperature contours $T/T_{0}$) in combustors of different lengths: $L_c$ = 40 (a),  20 (b), and 10 cm (c).

According to the data of Table 1, an increase in the injection pressure $p_{r}$ leads to a monotonic increase in the mean static pressure $\langle p\rangle$ at the combustor entrance (from 2.5 to 6 atm), the mean total pressure $\langle p_{0}\rangle$ at the combustor exit (from 1.5 to 2.8 atm), the number of TDWs (from 1 to 3), and the specific impulse (from 2680 to 3860 s), whereas the TDW front height $h$ monotonically decreases (from 10 to 5.6 cm).

Reduction of the Combustor Length

The influence of the combustor length $L_c$ on the parameters and two-dimensional structure of the CSD gas-dynamic flow is considered for fixed values of the governing parameters (13) $\phi$ = 1, $p_{r}$/$p_{0}$ = 15, $T_{r}$/$T_{0}$ = 0.757, $S_{ * }$/$S_{m}$ = 0.027, $p_{a}$/$p_{0}$ = 1, and $l$ =$\Pi$/3 = 29.6 cm. The combustor length was gradually reduced in the computations as $L_c$ = 66.5 $\to$10 cm. Some results of these computations are listed in Table 2 ($p_{2}/p_{1}$ and $T_{2}/T_{1 }$ are the ratios of the pressures and temperatures on the oblique SW front at the combustor exit), and the two-dimensional CSD structures (temperature field) in combustors of different lengths are shown in Fig. 7.

It is seen that the flow structure in the vicinity of the TDW, the height of the TDW front ($h$ $\approx$5.6 cm), and the slope of the oblique SW adjacent to the TDW with respect to the abscissa axis ($\approx$65$^{\circ}$) remain almost unchanged as the combustor length decreases to$L_c$ = 10–20 cm. According to the data of Table 2, a decrease in the combustor length leads to minor changes in the problem parameters ($\langle p\rangle$, $\langle p_{0}\rangle$, and $D$), whereas the degree of inhomogeneity of the gas-dynamic parameters at the combustor exit monotonically increases. Thus, for $L_c$ = 66.5 cm, jumps of pressure $(p_{2 }- p_{1})/p_{1}$ $\approx$0.61 and temperature $(T_{2 }- T_{1})/T_{1 }$ $\approx$0.11 are obtained at the combustor exit. For $L_c$ = 10 cm, the jumps of these parameters increase by more than a factor of 4: $(p_{2 }-p_{1})/p_{1}$ $\approx$2.79 and $(T_{2 }- T_{1})/T_{1 }$ $\approx$ 0.47.

It is of interest to note (see Table 2) that the specific impulse of CSD $I_{sp}$ starts to increase with reduction of the combustor length at $L_c < 30$ cm ($h/L_c$ $>$ 0.2); it increases approximately by 6$\%$ at $L_c$ = 10 cm ($h/L_c$ $\approx$0.56). The analysis of the solution (see Fig. 7c) shows that only some part of the detonation products passes through the oblique SW front, which increases their entropy, in the combustor with the length $L_c$ = 10 cm, while the remaining part of the products immediately escapes from the combustor. As the combustor length increases, the fraction of the products passing through the oblique SW front gradually increases until this flow includes all the products (see Figs. 7a and 7b); correspondingly, the irreversible entropy losses in the products also increase. It is known [3] that the increase in entropy behind the TDW front in the CSD case is smaller than that in the case of combustion. Naturally, additional entropy losses behind the oblique SW front slightly decrease the detonation combustion efficiency.

The results of computations with variations of the parameter $L_c$ show (see Table 2) that the CSD regime persists as the combustor length decreases to $L_c$ = 10 cm. Moreover, the entropy losses in the detonation products become smaller, which leads to an increase in the specific impulse at $L_c$ = 10 cm ($h/L_c$ $\approx$ 0.56) approximately by 6$\%$ to $I_{sp} \approx 4160$ s.

ANALYSIS OF RESULTS

Numerical simulations of CSD in the flow-type annular combustor [5] in the range of the injection pressure of the hydrogen–air mixture $p_{r}$ = (6.4–15)$p_{a}$ show that an increase in the specific flow rate of the mixture $g_{\Sigma }$ leads to an increase in the number of TDWs and their rotation frequency, the mean static pressure at the combustor entrance $\langle p\rangle$, the mean total pressure at the combustor exit $\langle p_{0}\rangle$, and the specific impulse $I_{sp}$, whereas the CSD velocity decreases from $D$ = 1.9 to 1.77 km/s. The calculated velocities of CSD propagation (see Table 1) are greater by 20–30$\%$ than the experimental results [5], and the predicted TDW size is smaller by a factor of 1.5–2.5. This is explained by the condition of instantaneous mixing of the mixture components in the mathematical model, whereas this factor produced a significant effect in the experiments: on the one hand, it reduced the detonability of the mixture and the TDW propagation velocity; on the other hand, it increased the TDW front height.

A comparison of the number of TDWs accommodated over the DK-300 perimeter for identical specific flow rates in the computations and experiments reveals almost complete coincidence. Thus, one TDW is observed at $g_{\Sigma }$ = 73 kg/(s$\, \cdot\,$m$^{2}$), two TDWs are observed at $g_{\Sigma }$ = 97 kg/(s$\, \cdot\,$m$^{2}$), and three TDWs are observed at $g_{\Sigma }$ = 137 kg/(s$\, \cdot\,$m$^{2}$). An exception is the intermediate variant with $g_{\Sigma }$ = 114 kg/(s$\, \cdot\,$m$^{2}$) for which the computations predict two TDWs, whereas the experiments [5] reveal three TDWs.

Fig. 8

TDW rotation frequency versus the specific flow rate of the mixture: experimental data [5] (points 1), present computations (points 2), and computations [11, 12] (points 3).

The calculated TDW rotation frequency as a function of the specific flow rate of the mixture is shown in Fig. 8. The experimental data [5] and computations [11, 12] are presented for comparison. The experimental data [5] (points 1) and the present computations (points 2) show that the number of TDWs increases with an increase in the specific flow rate and that the TDW velocity and rotation frequency increase at a fixed number of TDWs. Our computations correlate with the experimental data, exceeding the latter in terms of frequency by 30$\%$. For comparison, the results of the three-dimensional computations [11, 12] (points 3) where only the one-wave CSD regime was obtained are also presented. It is seen that the computations [11, 12] for the hydrogen–air mixture differ from the experiments [5] and present computations (points 2) by a factor of 3 in terms of the number of TDWs and by a factor of 2 in terms of the TDW rotation frequency. As the computations [11] for the premixed mixture and the computations [12] for separate injection of the fuel and oxidizer yield identically wrong results (one-wave CSD regimes), the discrepancy with the experiments [5] can be attributed to the use of the simplified single-stage kinetic scheme of hydrogen oxidation in those studies. Thus, the reliability of the chemical kinetics equations is the governing factor in CSD modeling.

CONCLUSIONS

A closed mathematical model of continuous spin detonation for a hydrogen–air mixture in a flow-type annular combustor with the chemical kinetics equation [13] is formulated within the framework of quasi-three-dimensional unsteady gas-dynamic formulation. The TDW dynamics and its two-dimensional structure is numerically studied for the geometric parameters used in the experiments [5] and varied flow rates of the hydrogen–oxygen mixture. The one-wave, two-wave, and three-wave CSD regimes are calculated in the range of the flow rates of the mixture 73–171 kg/(s$\, \cdot\,$m$^{2}$), the flow structure is analyzed, and comparisons are performed with the experiments [5] and computations [11, 12]. As the combustor length decreases to $L_c$ = 10 cm, the CSD regime persists and the specific impulse increases owing to reduction of the entropy losses in the detonation products. It is demonstrated that the use of the simplified single-stage kinetic scheme of hydrogen oxidation, such as that used in [11], for CSD modeling in the hydrogen–air mixture leads to results that differ from the experimental data by several times.

This work was partly supported by the Russian Foundation for Basic Research (Grant No. 16-01-00102a).