Adaptive Control System with a Variable Adjustment Law Gain Based on the Recursive Least Squares Method

Abstract

The aim of the present paper is to synthesize an adaptive control system with variable adaptation-loop gain to compensate for the plant parametric uncertainty. In contrast to the existing ones, such a system simultaneously (1) includes an algorithm for the automatic calculation of the parameter adjustment law gain in the controller, which operates in proportion to the current regressor value, thus permitting one to obtain an adjustable upper bound for the rate of convergence of the plant output–controller parameter errors to zero (subject to the condition of persistent excitation of the regressor); (2) does not require knowing the signs or values of the entries of the plant gain matrix. The Lyapunov second method and the recursive least squares method are used to synthesize such a control system. For this system, the stability and the boundedness of the above-mentioned error values are proved, and estimates for the rate of their convergence to zero are obtained. The efficiency of our approach is demonstrated by mathematical modeling of an example of a plant corresponding to the statement of the research problem.

1. INTRODUCTION

The main purpose of operation of adaptive control systems with a reference model is to maintain the desired control performance in the presence of a substantial parametric uncertainty of the plant by adjusting the controller parameters. Nowadays, there are two classical approaches to designing such control systems, namely, indirect and direct adaptive control [1, 2]. This paper deals exclusively with the problem of direct adaptive control based on the complete vector of state coordinates.

The algorithm for adjusting the controller parameters in direct adaptive control schemes is usually based on a first-order optimization method (the gradient descent method and its variations) as well as on the Lyapunov second method [1, 3, 4]. So far, most adjustment laws involve the following unresolved problems: first, a persistent excitation of the regressor is necessary for the exponential decay of the parametric error between the adjusted and ideal controller parameters; second, the adaptation law contains a parameter—the adaptation gain—that must be chosen experimentally [4, 5]. The main techniques for solving the first problem can be found in [6]. In the present paper, we focus on the analysis and solution of the second problem.

The very presence of an experimentally selected parameter in the adjustment law causes difficulties, because it is not always possible to carry out experiments on its selection with a real plant, while the gain selected on the basis of a mathematical model is most often unsuitable for the real plant.

To analyze other problems that arise when using a constant value of the gain, we separately consider the cases of presence and absence of a persistent excitation of the regressor.

In the absence of persistent excitation, it is well known [1] that the use of large values of the adaptation-loop gain for a real plant can strongly amplify the high-frequency parasitic components in the plant dynamics and the measurement noise, which is unacceptable from the viewpoint of robust stability [7, 8]. Three types of instability of adaptive control systems caused by a high adjustment law gain and the presence of parasitic high-frequency dynamics in the plant are distinguished in the literature: instability due to fast adaptation, high-frequency instability, and instability due to large values of the controller parameters obtained as a result of adaptation [1, 7, 8, 9]. All these effects necessitate a trade-off in the choice of the gain: its values must be large enough to ensure a satisfactory performance of the adaptation process but not large enough to enhance the parasitic dynamics of the plant.

In addition, even if the gain is selected appropriately and the parasitic dynamics is absent, an adaptive system provides the desired performance of the adjustment algorithm and hence of the control only for a limited number of reference values for the plant under consideration. This is because the adaptive control system, even with a linear plant and a linear reference model, forms a nonlinear closed control loop, for which the superposition principle does not hold [10]. A gain scaling method was proposed in [11, 12] to solve this problem and ensure the desired performance for the widest range of tasks in the system. An approach using a similar idea can be found in [13]. These techniques allow the experimentally selected optimal rate to be scaled to different settings. The disadvantage of this method is the need for the experimental, manual selection of the initial gain value ensuring that the adaptation process has the desired convergence rate and of the scaling factor. Thus, the main disadvantages of using a constant adaptation law gain value in the absence of persistent excitation are the possible amplification of the high-frequency dynamics if the gain is too large and the limited number of tasks for which the desired adjustment rate of the controller parameters can be ensured.

In the presence of a persistent excitation, the above-described disadvantages associated with the use of large gain values are supplemented with yet another problem. In [6, 7, 14], the existence of an optimal gain value for the current regressor in the presence of persistent excitation was proved, and it was shown by example that the convergence rate of the adaptation process decreases rather than increases with the gain increasing beyond the optimal value. This means, on the one hand, that the rate of convergence of the adjusted parameters to the ideal values cannot be made arbitrarily large, and on the other hand, that for each new value of the regressor there exists a new optimal value of the gain for the adaptation process.

It follows from the analysis that the use of an experimentally selected constant adaptation gain in the presence as well as absence of persistent excitation leads to serious problems that significantly reduce the likelihood of success in the practical implementation of adaptive control systems.

Thus, the problem of developing a method for adjusting the gain in the adaptation loop is topical in the theory of adaptive systems and especially in their practical application.

Therefore, in this study we suggest to develop an adaptation loop that includes an algorithm for calculating the gain and hence is free from the above-described disadvantages related to its experimental selection. As a basis for the development of such a loop, we suggest to use the recursive least squares method with exponential forgetting factor [1, 8]. The advantages of this method are the presence of a gain adjustment law per se and the exponential decay of the parametric error with an adjustable convergence rate under the persistent excitation condition [1]. This approach is widely known in identification theory; however, the authors have not been able to find its efficient applications in direct adaptive control schemes.

In the present paper, when developing a parameter adaption loop for the controller with a variable adjustment rate, we restrict ourselves to the case of persistent excitation of the predictor.

2. STATEMENT OF THE PROBLEM

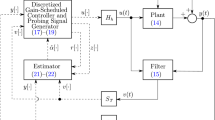
We consider the adaptive control problem for a class of linear plants that can be written in the space of state coordinates in the Frobenius form

$$ \dot x = Ax + Bu,$$

(2.1)

where $x\in R^n$ is the vector of plant state coordinates, $u\in R$ is the control, $A \in R^{n\times n}$ is the Frobenius matrix of system states, and $B=[0,0,\dots ,b]\in R^{n\times 1}$ is the gain matrix. The values of $A$ and $B$ are unknown, but the pair $(A,B)$ is controllable. It is assumed that the state coordinate vector $x$ and the vector $\dot x$ of its first derivatives are available for direct measurement. In practice, one can estimate the derivative of the state coordinate vector, in particular, by the methods in [15, 16]. The reference model determining the desired control performance for the plant (2.1) with unknown parameters is taken in the Frobenius form as well,

$$ {\dot x_\mathrm {ref\,}} = {A_\mathrm {ref\,}}{x_\mathrm {ref\,}} + {B_\mathrm {ref\,}}r,$$

(2.2)

where $x_\mathrm {ref\,}\in R^n$ is the state coordinate vector of the reference model, $r\in R$ is a bounded reference input signal, and $B_\mathrm {ref\,} =[0,0,\dots ,b_\mathrm {ref\,}]\in R^{n \times 1}$. The state matrix $A_\mathrm {ref\,} \in R^{n\times n}$ of the reference model is a Hurwitz matrix and is written in Frobenius form.

The equation for the errors between the plant equations (2.1) and the reference model equations (2.2) can be found in the form

$$ {\dot e_\mathrm {ref\,}} = {A_\mathrm {ref\,}}{e_\mathrm {ref\,}} + Bu - \left ( {{A_\mathrm {ref\,}} - A} \right )x - {B_\mathrm {ref\,}}r.$$

(2.3)

Since both the plant and the reference model are written in Frobenius form, it follows that the adaptability condition [4] is naturally satisfied,

$$ \mathrm {rank}\left \{ {B,{B_\mathrm {ref\,}}} \right \} = \mathrm {rank}\left \{ {B,A - {A_\mathrm {ref\,}}} \right \} = 1. $$

(2.4)

Assertion.

If the adaptability condition (2.4) is satisfied then so are the relations

$$ \begin {gathered} B{B^\dag } = \left [ {\begin {array}{*{20}{c}} {{Z_{n - 1,n}}}\\[.3em] {\begin {array}{*{20}{c}} 0&0& \ldots &1 \end {array}} \end {array}} \right ]; \\[.3em] B{B^\dag }\left ( {{A_\mathrm {ref\,}} - A} \right ) = {A_\mathrm {ref\,}} - A;\quad B{B^\dag }{B_\mathrm {ref\,}} = {B_\mathrm {ref\,}}, \end {gathered} $$

(2.5)

where $Z_{n-1,n}$ is the zero matrix. The assertion can be verified, for example, by a straightforward substitution of any matrices consistent with the statement of the problem into formulas (2.5).

Condition (2.4) and relations (2.5) permit one to rewrite Eq. (2.3) in the form

$$ {\dot e_\mathrm {ref\,}} = {A_\mathrm {ref\,}}{e_\mathrm {ref\,}} + B\left [ {u - {B^\dag }\left ( {{A_\mathrm {ref\,}} - A} \right )x - {B^\dag }{B_\mathrm {ref\,}}r} \right ],$$

(2.6)

where $B^\dag$ is the pseudoinverse of the matrix $B$.

Then the control law delivering the desired control performance for the plant (2.1) can be determined from the error equation (2.6),

$$ \begin {gathered} {u^*} = {B^\dag }\left [ {\left ( {{A_\mathrm {ref\,}} - A} \right )x + {B_\mathrm {ref\,}}r} \right ] = {k_r}{k_x}x + {k_r}r,\\ {k_r}{k_x} = {B^\dag }\left ( {{A_\mathrm {ref\,}} - A} \right );\quad {k_r} = {B^\dag }{B_\mathrm {ref\,}}, \end {gathered} $$

(2.7)

where $k_x \in R^{1 \times n}$ and $k_r \in R$ are the ideal control law parameters.

For the case of known, say, rated values of the entries of the matrices $A$ and $B$, one can calculate the ideal controller for the plant (2.1) by formulas (2.7).

For the case of unknown (quasistationary) parameters of the matrices $A$ and $B$, we introduce a control law with the current parameters

$$ u = {\hat k_r}{\hat k_x}x + {\hat k_r}r. $$

(2.8)

From the definition of the parameters $k_x$ and $k_r$ in the expression (2.7), one can derive analytical expressions for calculating the matrix $B$ and the difference $({A_\mathrm {ref\,}} - A)$,

$$ {A_\mathrm {ref\,}} - A = {B_\mathrm {ref\,}}{k_x}; \quad B = k_r^{ - 1}{B_\mathrm {ref\,}}.$$

(2.9)

Taking into account the expressions (2.9) when substituting the control law (2.8) into the error equation (2.6), we obtain

$$ \begin {aligned} {\dot e}_\mathrm {ref\,} &= A_\mathrm {ref\,}e_\mathrm {ref\,} + B\left [{\hat k}_r{\hat k}_x x + {\hat k}_r r\right ] - \left ( A_\mathrm {ref\,} - A\right )x - B_\mathrm {ref\,}r \\ &= A_\mathrm {ref\,}e_\mathrm {ref\,} + k_r^{-1}B_\mathrm {ref\,}\left [{\hat k}_r{\hat k}_x x + {\hat k}_r r \right ] - B_\mathrm {ref\,}k_x x -B_\mathrm {ref\,}r + \left (B_\mathrm {ref\,}{\hat k}_x x - B_\mathrm {ref\,}{\hat k}_x x\right ) \\ &= A_\mathrm {ref\,}e_\mathrm {ref\,} + B_\mathrm {ref\,} \left [\left ({\hat k}_x - k_x\right ) x + {\hat k}_x x \left (k_r^{-1}{\hat k}_r - I \right ) + r\left (k_r^{-1}{\hat k}_r - I\right )\right ] \\ &= A_\mathrm {ref\,}e_\mathrm {ref\,} + B_\mathrm {ref\,}\left [{\tilde k}_x x + \left (k_r^{-1}{\hat k}_r - I\right )\left ({\hat k}_x x + r\right )\right ] \\ &= A_\mathrm {ref\,}e_\mathrm {ref\,} + B_\mathrm {ref\,}\left [{\tilde k}_x x - {\tilde k}_r^{-1}{\hat k}_r\left ({\hat k}_x x + r\right )\right ]. \end {aligned}$$

(2.10)

Here ${\tilde k_x} = {\hat k_x} - {k_x}$, $\tilde k_r^{ - 1} = \hat k_r^{ - 1} - k_r^{ - 1}$. In Eq. (2.10), we introduce the notion of a generalized parameter error function $\varepsilon$,

$$ \varepsilon = {B_\mathrm {ref\,}}{{\tilde \theta }^\mathrm {T}}\omega ,\quad \omega = {\left [ {\begin {array}{*{20}{c}} {{x^\mathrm {T}}}&{ - {{\hat k}_r}\left ( {{{\hat k}_x}x + r} \right )} \end {array}} \right ]^\mathrm {T}};\quad {{\tilde \theta }^\mathrm {T}}= \left [ {\begin {array}{*{20}{c}} {{{\tilde k}_x}}&{\tilde k_r^{ - 1}} \end {array}} \right ] = {{\hat \theta }^\mathrm {T}} - {\theta ^\mathrm {T}}. $$

(2.11)

Here ${\hat \theta ^\mathrm {T}} \in {R^{n + 1}}$ are adjustable parameters via which one can calculate (by inverting the estimate $\hat k_r^{ - 1}$) the current parameters of the controller (2.8), ${\theta ^\mathrm {T}} \in {R^{n + 1}}$ are the ideal parameters via which one can calculate (by inverting $k_r^{ - 1}$) the parameters of the ideal controller (2.7), and ${\tilde \theta ^\mathrm {T}}\in {R^{n + 1}}$ is the difference between $\hat \theta ^\mathrm {T}$ and $\theta ^\mathrm {T}$. Then Eq. (2.10), in view of (2.11), can be rewritten in the form

$$ {\dot e_\mathrm {ref\,}} = {A_\mathrm {ref\,}}{e_\mathrm {ref\,}} + {B_\mathrm {ref\,}}{\tilde \theta ^\mathrm {T}}\omega . $$

(2.12)

Based on Eq. (2.12), one can derive an adaptation law for the controller (2.8). Since we can pass from $\hat \theta$ to the current parameters $\hat k_x$, $\hat k_r$ of the controller (2.8), its adaptation law will be understood to be the adjustment law $\hat \theta$. The parametrization (2.12) was for the first time proposed in [17] with the aim to construct an adaptation law that does not require knowledge of the plant gain matrix $B$.

For system (2.12), we need to construct a law for adjusting the parameters $\hat \theta$ not requiring an experimental, manual selection of the adjustment law gain and ensuring the exponential decay of the error $\xi =\big [\,e_\mathrm {ref\,}^\mathrm {T}\enspace {\tilde \theta }^\mathrm {T}\,\big ]^ \mathrm {T}$ under the persistent excitation condition for the regressor $\omega$.

Definition.

For a bounded signal $\omega$, the persistent excitation condition is satisfied if for all $t \geqslant 0$ there exists a $T > 0$ and an $\alpha > 0$ such that

$$ \displaystyle \int \limits _t^{t + T} {\omega \left ( \tau \right ){\omega ^\mathrm {T}}\left ( \tau \right )d} \tau \geqslant \alpha I, $$

(2.13)

where $I$ is the identity matrix and $\alpha$ is the excitation degree.

3. IDENTIFYING THE IDEAL PARAMETERS OF A CONTROLLER WITH VARIABLE GAIN IN THE ADAPTATION LOOP

To achieve our goal, we start by constructing an estimation law $\hat \theta$ that only ensures the exponential decay of the error $\tilde \theta ^\mathrm {T}$ rather than of the entire vector $\xi$ and does not involve manual gain selection.

To this end, we introduce the notion of desired behavior for the error equation (2.12), which we specify by the differential equation

$$ {\dot e_d} = {A_\mathrm {ref\,}}{e_\mathrm {ref\,}}. $$

(3.1)

Then the generalized parametric error (2.11) can be calculated via the difference between the error equation (2.12) and its desired behavior (3.1),

$$ \varepsilon = {\dot e}_\mathrm {ref\,} - {\dot e}_d = B_\mathrm {ref\,}{\tilde \theta } ^\mathrm {T}\omega = B_\mathrm {ref\,}\left ({\hat \theta }^\mathrm {T} - \theta ^\mathrm {T} \right )\omega = B_\mathrm {ref\,}\left ({\hat \theta }^\mathrm {T}\omega - y\right ), $$

(3.2)

where $y$ is the ideal value of the parametric disturbance in system (2.12).

Equation (3.2) implies that

$$ B_\mathrm {ref\,}^\dag \varepsilon = {\tilde \theta }^\mathrm {T}\omega = \left ({\hat \theta }^\mathrm {T} - \theta ^\mathrm {T}\right )\omega = {\hat \theta }^\mathrm {T}\omega - y. $$

(3.3)

At this stage, following the recursive least squares method, we introduce the measurements $y(\tau )$ and $\omega (\tau )$, $0\leqslant \tau <t$, to construct the identification loop $\hat \theta \left (t \right )$ for the ideal parameters $\theta$ at time $t$. Taking into account the new time, we write Eq. (3.3) as

$$ B_\mathrm {ref\,}^\dag \varepsilon = {\hat \theta ^\mathrm {T}}\left ( t \right )\omega \left ( \tau \right ) - y\left ( \tau \right ).$$

(3.4)

In this case, the target criterion for minimizing the expression (3.4) according to the recursive least squares method with exponential forgetting factor is written in the integral form

$$ Q\left ( {\hat \theta } \right ) = \dfrac {1}{2}\displaystyle \int \limits _0^{t} {{e^{ - \lambda \left ( {t - \tau } \right )}}{{\left ( {B_\mathrm {ref\,}^\dag \varepsilon } \right )}^\mathrm {T}}B_\mathrm {ref\,}^\dag \varepsilon } d\tau ,$$

(3.5)

where $\lambda$ is the exponential forgetting factor.

The condition for the minimum of the criterion (3.5) is that its gradient with respect to the adjusted parameters is zero,

$$ {\nabla _{{{\hat \theta }^\mathrm {T}}}}{Q^\mathrm {T}}\left ( {\hat \theta } \right ) = \displaystyle \int \limits _0^{t} {{e^{ - \lambda \left ( {t - \tau } \right )}}\omega \left ( \tau \right )\left [ {{\omega ^\mathrm {T}}\left ( \tau \right )\hat \theta \left ( t \right ) - {y^\mathrm {T}}\left ( \tau \right )} \right ]d} \tau = 0.$$

(3.6)

In the expression (3.6), we use the property of the sum of integrals, multiply out, and transpose the term containing the ideal value of the parametric disturbance to the right-hand side of the equation,

$$ \displaystyle \int \limits _0^{t} {{e^{ - \lambda \left ( {t - \tau } \right )}}\omega \left ( \tau \right ){\omega ^\mathrm {T}}\left ( \tau \right )\hat \theta \left ( t \right )d} \tau = \displaystyle \int \limits _0^{t} {{e^{ - \lambda \left ( {t - \tau } \right )}}\omega \left ( \tau \right ){y^\mathrm {T}}\left ( \tau \right )d} \tau .$$

(3.7)

From (3.7), using the least squares method, one can obtain an estimate $\hat { \theta }$ for the ideal parameters of the controller $\theta$,

$$ {\hat \theta }\left (t\right ) = \underbrace { \left [ \displaystyle \int \limits _0^t e^{-\lambda \left (t-\tau \right )} \omega \left (\tau \right )\omega ^\mathrm {T} \left (\tau \right )d\tau \right ]^{-1} }_{\Gamma \left (t\right )} \enspace \displaystyle \int \limits _0^t e^{-\lambda \left (t- \tau \right )} \omega \left (\tau \right )y^\mathrm {T}\left (\tau \right )\,d\tau .$$

(3.8)

Here $\Gamma (t)$ is the gain matrix of the parameter adjustment law for the approximating linear regression.

The time variation law of the matrix $\Gamma ^{-1} (t)$ can be found from the theorem on the derivative of an integral with respect to the upper limit,

$$ \dfrac {{d{\Gamma ^{ - 1}}}}{{dt}} = \omega ( t ){\omega ^\mathrm {T}} ( t ) - \lambda \displaystyle \int \limits _0^{t} {{e^{ - \lambda ( {t - \tau } )}}\omega ( \tau ){\omega ^\mathrm {T}} ( \tau )d} \tau = \omega ( t ){\omega ^\mathrm {T}} ( t ) - \lambda {\Gamma ^{ - 1}} ( t ). $$

(3.9)

At this stage, we introduce the auxiliary equation

$$ \dfrac {{dI}}{{dt}} = \dfrac {d}{{dt}}\left [ {\Gamma \left ( t \right ){\Gamma ^{ - 1}}\left ( t \right )} \right ] = \dfrac {{d\Gamma \left ( t \right )}}{{dt}}{\Gamma ^{ - 1}}\left ( t \right ) + \dfrac {{d{\Gamma ^{ - 1}}\left ( t \right )}}{{dt}}\Gamma \left ( t \right ) = 0. $$

(3.10)

Taking into account the expression (3.10) and the earlier-introduced definitions of the matrices $\Gamma (t)$ and $\Gamma ^{-1}(t)$, we obtain the time variation law of the matrix $\Gamma (t)$,

$$ \dfrac {{d\Gamma \left ( t \right )}}{{dt}} = - \Gamma \left ( t \right )\dfrac {{d{\Gamma ^{ - 1}}\left ( t \right )}}{{dt}}\Gamma \left ( t \right ) = \lambda \Gamma \left ( t \right ) - \Gamma \left ( t \right )\omega \left ( t \right ){\omega ^\mathrm {T}}\left ( t \right )\Gamma \left ( t \right ).$$

(3.11)

We find a formula for estimating the parameters of the ideal control law (2.7) with allowance for the expression (3.11) by differentiating the estimate (3.8) with respect to time,

$$ \begin {aligned} \dfrac {{d\hat \theta \left ( t \right )}}{{dt}} &= \dfrac {{d\Gamma \left ( t \right )}}{{dt}}\int \limits _0^{t} {{e^{ - \lambda \left ( {t - \tau } \right )}}\omega \left ( \tau \right ){y^\mathrm {T}}\left ( \tau \right )d} \tau + \Gamma \left ( t \right )\dfrac {d}{{dt}}\left [\, {\int \limits _0^{t} {{e^{ - \lambda \left ( {t - \tau } \right )}}\omega \left ( \tau \right ){y^\mathrm {T}}\left ( \tau \right )d} \tau } \right ] \\ &= \left ( {\lambda - \Gamma \left ( t \right )\omega \left ( t \right ){\omega ^\mathrm {T}}\left ( t \right )} \right )\hat \theta \left ( t \right ) - \lambda \hat \theta \left ( t \right ) + \Gamma \left ( t \right )\omega \left ( t \right ){y^\mathrm {T}}\left ( t \right ) \\ &= \Gamma \left ( t \right )\omega \left ( t \right )\left [ {{y^\mathrm {T}}\left ( t \right ) - {\omega ^\mathrm {T}}\left ( t \right )\hat \theta \left ( t \right )} \right ]. \end {aligned} $$

(3.12)

In view of (3.4), Eq. (3.12) can be reduced to the form

$$ \dfrac {{d\hat \theta \left ( t \right )}}{{dt}} = - \Gamma \left ( t \right )\omega \left ( t \right ){\left ( {B_\mathrm {ref\,}^\dag \varepsilon } \right )^\mathrm {T}}.$$

(3.13)

Thus, the identification loop for ideal parameters of the controller (2.7) is described by the evolution law (3.11) for the gain matrix and directly by the adaptation law (3.13),

$$ \begin {aligned} \dot {\hat \theta } &= - \Gamma \omega {\left ( {B_\mathrm {ref\,}^\dag \varepsilon } \right )^\mathrm {T}},\\ \dot \Gamma &= \lambda \Gamma - \Gamma \omega {\omega ^\mathrm {T}}\Gamma . \end {aligned}$$

(3.14)

Let us state the properties of the estimation loop (3.14) in the form of a theorem.

Theorem 1.

The estimation loop (3.14) for the error $\tilde \theta$ ensures the following properties:

• 1. The error $\tilde \theta$ is a bounded function, $\tilde \theta \in {L_2} \cap {L_\infty }$;

• 2. If the persistent excitation condition (2.13) holds and the first derivative of the regressor is bounded, $\dot \omega \in {L_\infty }$, then the error $\tilde \theta$ decays exponentially at a rate faster than $\kappa$ (its value is determined in the Appendix).

The proof of Theorem 1 is given in the Appendix.

4. SYNTHESIS OF ADAPTIVE CONTROL WITH A VARIABLE ADJUSTMENT-LOOP GAIN

Earlier in the present paper, we have proved the convergence of the parametric error $\tilde \theta$ to zero and hence the identification properties of the estimation loop (3.14) for the ideal controller parameters. However, the convergence of the entire vector $\xi$ to zero and hence the stability of the closed-loop control (2.12) when using the resulting estimates of the parameters have not been considered. Therefore, let us take formulas (3.14) as basic ones and modify them so as to ensure the convergence to zero not only of the parameter error $\tilde \theta$ but also of the tracking error $e_\mathrm {ref}$. We present the results of this modification as the following theorem.

Theorem 2.

Let the adaptation loop for the closed control loop (2.12) be described by the expressions

$$ \begin {aligned} \dot {\hat \theta } &= - \Gamma \omega {\left [ {B_\mathrm {ref\,}^\dag \varepsilon + B_\mathrm {ref\,}^\mathrm {T}P{e_\mathrm {ref\,}}} \right ]^\mathrm {T}},\\ \dot \Gamma &= \lambda \Gamma - 2\Gamma \omega {\omega ^\mathrm {T}}\Gamma , \end {aligned} $$

(4.1)

where $P$ is a matrix obtained by solving the Lyapunov equation

$$ A_\mathrm {ref\,}^{T}P + P{A_\mathrm {ref\,}} = - Q, $$

and $Q$ is a matrix to be chosen experimentally.

Then

• 1. The error $\xi$ is a bounded function, $\xi \in {L_2}\cap {L_\infty }$ .

• 2. Condition (2.13) ensures the exponential decay of the error $\xi$ at a rate faster than $\eta _{\min }$.

• 3. Under condition (2.13), the maximum convergence rate $\eta _{\max }$ of the error $\xi$ to zero can be made arbitrarily high by increasing the parameter $\lambda$.

The proof of Theorem 2, as well as the values of $\eta _{\min }$ and $\eta _{\max }$, is given in the Appendix.

5. EXAMPLE

The efficiency of our approach was demonstrated by mathematical modeling of the closed-loop system (2.12) when adapting the parameters of the control law (2.8) according to formulas (4.1). Modeling was performed in Matlab/Simulink based on numerical integration by the Euler method. In all the experiments, we used the constant discretization step $\tau _s = 10^{-6}$ s. The plant was described in the experiments by the equation

$$ \dot x = \left [ {\begin {array}{*{20}{c}} 0&1\\ 4&2 \end {array}} \right ]x + \left [ {\begin {array}{*{20}{c}} 0\\ 2 \end {array}} \right ]u.$$

Fig. 1.

Norm of the adaptation process gain matrix.

Fig. 2.

Transients of the norms of the parameter error $\tilde {\theta }$ and the error $\xi$.

The reference model for the plant was chosen according to the equation

$$ {\dot x_\mathrm {ref\,}} = \left [ {\begin {array}{*{20}{c}} 0&1\\ { - 8}&{ - 4} \end {array}} \right ]{x_\mathrm {ref\,}} + \left [ {\begin {array}{*{20}{c}} 0\\ 8 \end {array}} \right ]r.$$

According to the results presented, e.g., in [7], to ensure the persistent excitation condition for a second-order plant, one should use a harmonic signal with at least two frequencies for the input signal. Therefore, the persistent excitation condition (2.13) for the predictor $\omega$ was satisfied in the experiments by using the harmonic signal

$$ r = 125\sin \left ( t \right ) + 250\sin \left ( 125t \right ) + 500\sin \left ( 250t \right ).$$

All in all, we carried out two experiments. In the first experiment (see Figs. 1 and 2), the initial value of the matrix $\Gamma (0)$, the initial values of the parameters of the control law (2.8), and the value of the forgetting factor $\lambda$ were selected as follows:

$$ \Gamma \left ( 0 \right ) = 0{,}1I;\quad {\hat \theta ^\mathrm {T}}\left ( 0 \right ) = \left [ {\begin {array}{*{20}{c}} 0&0&1 \end {array}} \right ];\quad \lambda = 25. $$

It follows from the modeling results (Figs. 1 and 2) that the proposed adaptation loop (4.1) ensures the exponential decay of the parameter error $\tilde \theta$ and the error $\xi$, with a variable adaptation-loop gain used in the adaptation process.

In the second experiment, we used different values of the forgetting factor $\lambda$,

$$ \lambda _1 = 25;\quad {\lambda _2} = 100;\quad {\lambda _3} = 1000.$$

However, the initial value of the matrix $\Gamma (0)$ and the initial values of the coefficients of the control law (2.8) were the same as in the first experiment.

Fig. 3.

Transients of the norms of the parameter error $\tilde {\theta }$ and the error $\xi$ for various $\lambda$.

It follows from the modeling results (Fig. 3) that, when increasing the forgetting factor, the rate of convergence of the parameter error and the error $\xi$ increases as well. This confirms the results obtained in the proof of Theorem 2.

It can also be seen from Fig. 3 that significant oscillations arise as $\lambda \to \infty$; this also confirms the conclusions made in the Remark to Theorem 2. To eliminate this drawback, in further research we plan to modify the developed adaptation loop (4.1) by using methods of extension and filtering of the predictor [6] with the aim to minimize the value of $T$ (maximize the admissible value of $\lambda$).

6. CONCLUSIONS

In the present paper, we have proposed an adaptive control system that, under the persistent excitation condition, does not require experimental, manual selection of the adaptation process gain matrix and, at the same time, ensures the exponential decay of the tracking error and the parameter error with an adjustable upper bound for the convergence rate.

Unlike the classical gradient scheme, which has a limit convergence rate for the current regressor [6, 13, 14], in the developed scheme, according to the proof of Theorem 2, the analysis performed, and the results of experiments, the upper bound for the convergence rate can be made arbitrarily large by increasing the forgetting factor $\lambda$.

In further studies, we plan to modify the developed adaptation loop so as to relax the assumptions used (the persistent excitation condition and the availability of the first derivative of the state coordinate vector) and improve its properties (eliminate the oscillations at large $\lambda$ and ensure the monotone exponential convergence).

APPENDIX

Proof of Theorem 1. To prove the theorem, we substitute the expression (3.3) into Eq. (3.13). Then, under the condition $\theta = \mathrm{const}$, we have the equation

$$ \dot {\tilde \theta } = - \Gamma \omega {\omega ^\mathrm {T}}\tilde \theta .$$

(A.1)

We select a candidate for the Lyapunov function as the quadratic form

$$ \begin {gathered} V = {{\tilde \theta }^\mathrm {T}}{\Gamma ^{ - 1}}\tilde \theta ,\\ {\lambda _{\min }}\left ( {{\Gamma ^{ - 1}}} \right ){\left \| {\tilde \theta } \right \|^2} \leqslant V \leqslant {\lambda _{\max }}\left ( {{\Gamma ^{ - 1}}} \right ){\left \| {\tilde \theta } \right \|^2}, \end {gathered}$$

(A.2)

where $\lambda _{\min }(.)$ and $\lambda _{\max }(.)$ are the minimum and maximum eigenvalues of a matrix.

In view of Eqs. (3.9) and (3.13), the derivative of the quadratic form (A.2) along the trajectories of Eq. (A.1) is as follows:

$$ \begin {aligned} \dot V &= 2{{\tilde \theta }^{^\mathrm {T}}}{\Gamma ^{ - 1}}\dot {\tilde \theta } + {{\tilde \theta }^\mathrm {T}}{{\dot \Gamma }^{ - 1}}\tilde \theta = - 2{{\tilde \theta }^{^\mathrm {T}}}{\Gamma ^{ - 1}}\left [ {\Gamma \omega {\omega ^\mathrm {T}}\tilde \theta } \right ] + {{\tilde \theta }^\mathrm {T}}\left [ {\omega {\omega ^\mathrm {T}} - \lambda {\Gamma ^{ - 1}}} \right ]\tilde \theta \\ &= - {{\tilde \theta }^\mathrm {T}}\omega {\omega ^\mathrm {T}}\tilde \theta - \lambda {{\tilde \theta }^\mathrm {T}}{\Gamma ^{ - 1}}\tilde \theta = - \left ( {B_\mathrm {ref\,}^\dag \varepsilon } \right ){\left ( {B_\mathrm {ref\,}^\dag \varepsilon } \right )^\mathrm {T}} - \lambda {{\tilde \theta }^\mathrm {T}}{\Gamma ^{ - 1}}\tilde \theta \\ &\leqslant - {\left \| {B_\mathrm {ref\,}^\dag } \right \|^2}{\left \| \varepsilon \right \|^2} - \lambda {\lambda _{\min }}\left ( {{\Gamma ^{ - 1}}} \right ){\left \| {\tilde \theta } \right \|^2}. \end {aligned}$$

(A.3)

The derivative (A.3) of the positive definite quadratic form (A.2) is a negative semidefinite function, and therefore, the parameter error is $\tilde \theta \in {L_\infty }$, the generalized error is $\varepsilon \in {L_\infty }$, and Eq. (A.2) is a Lyapunov function for system (A.1). At the same time, the Lyapunov function (A.2) has a finite limit as $t\to \infty$,

$$ \begin {gathered} V\left ( {\tilde \theta \left ( {t \to \infty } \right )} \right ) = V\left ( {\tilde \theta \left ( {{t_0}} \right )} \right ) + \displaystyle \int \limits _{{t_0}}^\infty {\dot Vd} t = V\left ( {\tilde \theta \left ( {{t_0}} \right )} \right ) - \displaystyle \int \limits _{{t_0}}^\infty {\left [ {\left ( {B_\mathrm {ref\,}^\dag \varepsilon } \right ){{\left ( {B_\mathrm {ref\,}^\dag \varepsilon } \right )}^\mathrm {T}} + \lambda \left ( {{{\tilde \theta }^\mathrm {T}}{\Gamma ^{ - 1}}\tilde \theta } \right )} \right ]d} t\\ \Rightarrow \displaystyle \int \limits _{{t_0}}^\infty {\left [ {{{\left \| {B_\mathrm {ref\,}^\dag } \right \|}^2}{{\left \| \varepsilon \right \|}^2} + \lambda {\lambda _{\min }}\left ( {{\Gamma ^{ - 1}}} \right ){{\left \| {\tilde \theta } \right \|}^2}} \right ]d} t {}= V\left ( {\tilde \theta \left ( {{t_0}} \right )} \right ) - V\left ( {\tilde \theta \left ( {t \to \infty } \right )} \right ) < \infty , \end {gathered}$$

and then $\tilde \theta \in {L_2} \cap {L_\infty }$ and $\omega \in {L_\infty }$ (as a result of the fact that $\varepsilon \in {L_2} \cap {L_\infty }$).

We have thus proved the first part of Theorem 1. To prove the second part of Theorem 1, we find the second derivative of the Lyapunov function (A.2),

$$ \begin {aligned} \ddot V &= - 2\left ( {B_\mathrm {ref\,}^\dag \dot \varepsilon } \right ){\left ( {B_\mathrm {ref\,}^\dag \varepsilon } \right )^\mathrm {T}} - \lambda \left ( {2{{\tilde \theta }^\mathrm {T}}{\Gamma ^{ - 1}}\dot {\tilde \theta } + {{\tilde \theta }^\mathrm {T}}{{\dot \Gamma }^{ - 1}}\tilde \theta } \right ) \\ &= - 2\left ( {B_\mathrm {ref\,}^\dag \dot \varepsilon } \right ){\left ( {B_\mathrm {ref\,}^\dag \varepsilon } \right )^\mathrm {T}} - \lambda \left ( {2{{\tilde \theta }^\mathrm {T}}\left [ { - \omega {\omega ^\mathrm {T}}\tilde \theta } \right ] + {{\tilde \theta }^\mathrm {T}}\left [ {\omega {\omega ^\mathrm {T}} - \lambda {\Gamma ^{ - 1}}} \right ]\tilde \theta } \right ) \\ &= - 2\left ( {B_\mathrm {ref\,}^\dag \dot \varepsilon } \right ){\left ( {B_\mathrm {ref\,}^\dag \varepsilon } \right )^\mathrm {T}} + \lambda \left ( {2{{\tilde \theta }^\mathrm {T}}\omega {\omega ^\mathrm {T}}\tilde \theta - {{\tilde \theta }^\mathrm {T}}\left [ {\omega {\omega ^\mathrm {T}} - \lambda {\Gamma ^{ - 1}}} \right ]\tilde \theta } \right ). \end {aligned}$$

(A.4)

Based on the expression (A.4), it is difficult to draw a conclusion on the boundedness of the second derivative of the function (A.2); therefore, in view of the relation $\dot {\tilde \theta } = \dot {\hat \theta }$, we find the derivative of the generalized parameter error (3.2),

$$ \dot \varepsilon = B_\mathrm {ref\,}\left [ \dot {\tilde \theta }^\mathrm {T}\omega + {\tilde \theta }^\mathrm {T}\dot \omega \right ] = B_\mathrm {ref\,}\left [ - \Gamma \omega \omega ^\mathrm {T}\tilde \theta \omega + {\tilde \theta }^\mathrm {T}\dot \omega \right ].$$

(A.5)

Taking into account the expression (A.5), for calculation we rewrite Eq. (A.4) as

$$ \ddot V = - 2\left [ { - \Gamma \omega {\omega ^\mathrm {T}}\tilde \theta \omega + {{\tilde \theta }^\mathrm {T}}\dot \omega } \right ]{\left ( {B_\mathrm {ref\,}^\dag \varepsilon } \right )^\mathrm {T}} + \lambda \left ( {2{{\tilde \theta }^\mathrm {T}}\omega {\omega ^\mathrm {T}}\tilde \theta - {{\tilde \theta }^\mathrm {T}}\left [ {\omega {\omega ^\mathrm {T}} - \lambda {\Gamma ^{ - 1}}} \right ]\tilde \theta } \right ). $$

According to what has been proved, we have $\tilde \theta \in {L_2} \cap {L_\infty }$, $\varepsilon \in {L_2} \cap {L_\infty }$, and $\omega \in {L_\infty }$, and by the statement of Theorem 1, $\,\dot \omega {\,\in \,}{L_\infty }$. Then, to conclude that $\ddot V {\,\in \,}{L_\infty }$, it remains to prove the $L_\infty$-boundedness of the matrices $\Gamma$ and $\Gamma ^{-1}$. To this end, we obtain a solution of the differential equation (3.9),

$$ {\Gamma ^{ - 1}}\left ( t \right ) = {\Gamma ^{ - 1}}\left ( 0 \right ){e^{ - \lambda t}} + \displaystyle \int \limits _0^{t} {{e^{ - \lambda \left ( {t - \tau } \right )}}\omega \left ( \tau \right ){\omega ^\mathrm {T}}\left ( \tau \right )d} \tau . $$

Under the persistent excitation condition (2.13), it can readily be shown that for all $t \geqslant T$ the value of $\Gamma ^{-1}$ is bounded below by the expression

$$ \begin {aligned} {\Gamma ^{ - 1}}\left ( t \right ) &\geqslant \displaystyle \int \limits _0^{t} {{e^{ - \lambda \left ( {t - \tau } \right )}}\omega \left ( \tau \right ){\omega ^\mathrm {T}}\left ( \tau \right )d} \tau \\ &= \displaystyle \int \limits _{t - T}^{t} {{e^{ - \lambda \left ( {t - \tau } \right )}}\omega \left ( \tau \right ){\omega ^\mathrm {T}}\left ( \tau \right )d} \tau + \displaystyle \int \limits _0^{t - T} {{e^{ - \lambda \left ( {t - \tau } \right )}}\omega \left ( \tau \right ){\omega ^\mathrm {T}}\left ( \tau \right )d} \tau . \end {aligned}$$

(A.6)

Now we obtain upper bounds for each of the two integrals on the right-hand side in (A.6) by the mean value theorem. To this end, we rewrite the persistent excitation condition (2.13) in the equivalent form

$$ \displaystyle \int \limits _{t - T}^{t} {\omega \left ( \tau \right ){\omega ^\mathrm {T}}\left ( \tau \right )d} \tau \geqslant \alpha I. $$

(A.7)

Then, in view of the expression (A.7), the lower bound for the first integral has the form

$$ \displaystyle \int \limits _{t - T}^{t} {{e^{ - \lambda \left ( {t - \tau } \right )}}\omega \left ( \tau \right ){\omega ^\mathrm {T}}\left ( \tau \right )d} \tau \geqslant {e^{ - \lambda T}}\displaystyle \int \limits _{t - T}^{t} {\omega \left ( \tau \right ){\omega ^\mathrm {T}}\left ( \tau \right )d} \tau \geqslant {e^{ - \lambda T}}\alpha I. $$

(A.8)

In a similar manner, we produce a lower bound for the second integral,

$$ \displaystyle \int \limits _0^{t - T} {{e^{ - \lambda \left ( {t - \tau } \right )}}\omega \left ( \tau \right ){\omega ^\mathrm {T}}\left ( \tau \right )d} \tau \geqslant {e^{ - \lambda T}}\displaystyle \int \limits _0^{t - T} {\omega \left ( \tau \right ){\omega ^\mathrm {T}}\left ( \tau \right )d} \tau \geqslant 0.$$

(A.9)

Adding (A.8) and (A.9), we obtain a lower bound for the entire matrix $\Gamma ^{-1}$,

$$ {\Gamma ^{ - 1}}\left ( t \right ) \geqslant {e^{ - \lambda T}}\alpha I.$$

(A.10)

Now we obtain a lower bound for the matrix $\Gamma ^{-1}$ $\forall t\leqslant T$,

$$ {\Gamma ^{ - 1}}\left ( t \right ) \geqslant {\Gamma ^{ - 1}}\left ( 0 \right ){e^{ - \lambda T}} \geqslant {\lambda _{\min }}\left ( {{\Gamma ^{ - 1}}\left ( 0 \right )} \right ){e^{ - \lambda T}}I. $$

(A.11)

Then, in view of the estimates (A.10) and (A.11), the lower bound for the matrix $\Gamma ^{-1}$ for all $t \geqslant 0$ has the form

$$ {\Gamma ^{ - 1}}\left ( t \right ) \geqslant {\min }\left \{ {{\lambda _{\min }}\left ( {{\Gamma ^{ - 1}}\left ( 0 \right )} \right ),\alpha } \right \}{e^{ - \lambda T}}I.$$

(A.12)

Since $\omega \in {L_\infty }$ by what has been proved, it follows that the expression $\omega \omega ^\mathrm {T}$ satisfies the inequality

$$ {\lambda _{\min }}\left ( {\omega {\omega ^\mathrm {T}}} \right ) \leqslant \omega {\omega ^\mathrm {T}} \leqslant {\lambda _{\max }}\left ( {\omega {\omega ^\mathrm {T}}} \right ).$$

(A.13)

Taking into account inequality (A.13), we obtain an upper bound for the matrix $\Gamma ^{-1}$,

$$ \Gamma ^{-1} \left (t\right ) \leqslant \Gamma ^{-1} \left (0\right )+\lambda _{\max } \left (\omega \omega ^\mathrm {T}\right ) \displaystyle \int \limits _0^t e^{-\lambda \left (t-\tau \right )}\,d\tau I \leqslant \lambda _{\max }\left (\Gamma ^{-1}\left (0\right )\right )I + \dfrac {\lambda _{\max }\left (\omega \omega ^\mathrm {T}\right )}{\lambda } I. $$

(A.14)

By combining the expressions (A.12) and (A.14), we obtain inequalities for $\Gamma$ and $\Gamma ^{-1}$,

$$ \begin {aligned} {\min }\Big \{\lambda _{\min }\left (\Gamma ^{-1}\left (0\right )\right ),\alpha \Big \} e^{-\lambda T}I &\leqslant \Gamma ^{-1}\left ( t \right )\leqslant \lambda _{\max }\left (\Gamma ^{-1}\left (0\right )\right )I + \dfrac {\lambda _{\max }\left (\omega \omega ^\mathrm {T}\right )}{\lambda }I, \\[.3em] \left (\lambda _{\max }\left (\Gamma ^{-1}\left (0\right )\right ) + \dfrac {\lambda _{\max }\left (\omega \omega ^\mathrm {T}\right )}{\lambda }\right )^{-1}I &\leqslant \Gamma \left (t\right ) \leqslant \max \Big \{\lambda _{\min }^{-1}\left (\Gamma ^{-1}\left (0\right )\right ),\alpha ^{-1} \Big \}e^{\lambda T}I. \end {aligned} $$

(A.15)

It clearly follows from the expressions (A.15) that $\Gamma \in L_\infty$, $\Gamma ^{-1}\in L_\infty$, and hence $\ddot V \in {L_\infty }$. Then the derivative (A.3) of the Lyapunov function (A.2) is uniformly continuous, and $\dot V \to 0$ by Barbalat’s lemma. Accordingly, we achieve the convergence $\tilde \theta \to 0$ as $t \to \infty$.

To find an estimate for the convergence rate of the error $\tilde \theta$ to zero, we obtain an upper bound for the derivative (A.3) with allowance for inequality (A.13),

$$ \dot V = - {\tilde \theta ^\mathrm {T}}\omega {\omega ^\mathrm {T}}\tilde \theta - \lambda {\tilde \theta ^\mathrm {T}}{\Gamma ^{ - 1}}\tilde \theta \leqslant - {\lambda _{\min }}\left ( {\omega {\omega ^\mathrm {T}}} \right ){\left \| {\tilde \theta } \right \|^2} - \lambda {\lambda _{\min }}\left ( {{\Gamma ^{ - 1}}} \right ){\left \| {\tilde \theta } \right \|^2}. $$

(A.16)

Further, to determine the minimum convergence rate, we proceed from the lower and upper bounds (A.15) for the matrix $\Gamma ^{-1}$ to an expression for the lower and upper bounds for its norm,

$$ \begin {aligned} \left \| {{\Gamma ^{ - 1}}} \right \| &\geqslant \underbrace {\sqrt {n + 1} \left [ {{\min }\left \{ {{\lambda _{\min }}\left ( {{\Gamma ^{ - 1}}\left ( 0 \right )} \right ),\alpha } \right \}{e^{ - \lambda T}}} \right ]}_{{\lambda _{\min }}\left ( {{\Gamma ^{ - 1}}} \right )} ,\\ \left \| {{\Gamma ^{ - 1}}} \right \| &\leqslant \underbrace {\sqrt {n + 1} \left [ {{\lambda _{\max }}\left ( {{\Gamma ^{ - 1}}\left ( 0 \right )} \right ) + \dfrac {{{\lambda _{\max }}\left ( {\omega {\omega ^\mathrm {T}}} \right )}}{\lambda }} \right ]}_{{\lambda _{\max }}\left ( {{\Gamma ^{ - 1}}} \right )}. \end {aligned}$$

(A.17)

Taking into account the expression (A.17), we rewrite the upper bound (A.16) as

$$ \begin {aligned} \dot V &\leqslant - {\lambda _{\min }}\left ( {\omega {\omega ^\mathrm {T}}} \right ){\left \| {\tilde \theta } \right \|^2} - \lambda \sqrt {n + 1} \left [ {{\min }\left \{ {{\lambda _{\min }}\left ( {{\Gamma ^{ - 1}}\left ( 0 \right )} \right ),\alpha } \right \}{e^{ - \lambda T}}} \right ]{\left \| {\tilde \theta } \right \|^2} \\ &\leqslant - \left [ {\dfrac {{\lambda {\lambda _{\min }}\left ( {\omega {\omega ^\mathrm {T}}} \right ) + {\lambda ^2}\sqrt {n + 1} \left [ {{\min }\left \{ {{\lambda _{\min }}( {{\Gamma ^{ - 1}}( 0 )} ),\alpha } \right \}{e^{ - \lambda T}}} \right ]}}{{\sqrt {n + 1} \left [ {\lambda {\lambda _{\max }}\left ( {{\Gamma ^{ - 1}}\left ( 0 \right )} \right ) + {\lambda _{\max }}\left ( {\omega {\omega ^\mathrm {T}}} \right )} \right ]}}} \right ]{\lambda _{\max }}( {{\Gamma ^{ - 1}}} ) {\left \| {\tilde \theta } \right \|^2} \leqslant - \kappa V. \end {aligned} $$

Let us solve the resulting differential inequality substituting the lower bound

$$ \left \| {\tilde \theta } \right \| \leqslant \sqrt {\lambda _{\min }^{ - 1}\left ( {{\Gamma ^{ - 1}}} \right ){e^{ - \kappa \cdot t}}V\left ( 0 \right )}$$

(A.18)

for the Lyapunov function into the left-hand side of the solution.

It follows from the expression (A.18) that the error $\tilde \theta$ decays exponentially at a rate faster than $\kappa$, which is exactly what is claimed in the second part of Theorem 1. $\quad \blacksquare$

Proof of Theorem 2. A candidate for the Lyapunov function in the study of the stability of the closed-loop system (2.12) can be selected in the form of the sum of two quadratic forms,

$$ \begin {gathered} V = {\xi ^\mathrm {T}}H\xi = e_\mathrm {ref\,}^\mathrm {T}P{e_\mathrm {ref\,}} + {{\tilde \theta }^\mathrm {T}}{\Gamma ^{ - 1}}\tilde \theta ,\\[.03em] H = \mathrm {blockdiag} \left \{ {\begin {array}{*{20}{c}} P&{{\Gamma ^{ - 1}}} \end {array}} \right \},\\[.03em] {\lambda _{\min }}\left ( H \right ){\left \| \xi \right \|^2} \leqslant V \leqslant {\lambda _{\max }}\left ( H \right ){\left \| \xi \right \|^2}. \end {gathered} $$

(A.19)

In view of the relation $\dot {\tilde \theta } = \dot {\hat \theta }$ and Eq. (3.3), the derivative of the quadratic form (A.19) according to the deviation equation (2.12) and the adaptation loop equations (4.1) acquire the form

$$ \begin {aligned} \dot V &= \dot e_\mathrm {ref\,}^\mathrm {T}P{e_\mathrm {ref\,}} + e_\mathrm {ref\,}^\mathrm {T}P{{\dot e}_\mathrm {ref\,}} + 2{{\tilde \theta }^\mathrm {T}}{\Gamma ^{ - 1}}\dot {\tilde \theta } + {{\tilde \theta }^\mathrm {T}}{{\dot \Gamma }^{ - 1}}\tilde \theta \\ &= e_\mathrm {ref\,}^\mathrm {T}\left [ {A_\mathrm {ref\,}^\mathrm {T}P + P{A_\mathrm {ref\,}}} \right ]{e_\mathrm {ref\,}} + 2e_\mathrm {ref\,}^\mathrm {T}P{B_\mathrm {ref\,}}{{\tilde \theta }^\mathrm {T}}\omega - 2{{\tilde \theta }^\mathrm {T}}\omega {\left [ {B_\mathrm {ref\,}^\dag \varepsilon + B_\mathrm {ref\,}^\mathrm {T}P{e_\mathrm {ref\,}}} \right ]^\mathrm {T}} + {{\tilde \theta }^\mathrm {T}}{{\dot \Gamma }^{ - 1}}\tilde \theta \\ &= - e_\mathrm {ref\,}^\mathrm {T}Q{e_\mathrm {ref\,}} - 2{{\tilde \theta }^\mathrm {T}}\omega {\omega ^\mathrm {T}}\tilde \theta + {{\tilde \theta }^\mathrm {T}}\left [ {2\omega {\omega ^\mathrm {T}} - \lambda {\Gamma ^{ - 1}}} \right ]\tilde \theta \\ &= - e_\mathrm {ref\,}^\mathrm {T}Q{e_\mathrm {ref\,}} - \lambda {{\tilde \theta }^\mathrm {T}}{\Gamma ^{ - 1}}\tilde \theta \leqslant - {\lambda _{\min }}\left ( Q \right ){\left \| {{e_\mathrm {ref\,}}} \right \|^2} - \lambda {\lambda _{\min }}\left ( {{\Gamma ^{ - 1}}} \right ){\left \| {\tilde \theta } \right \|^2}. \end {aligned}$$

(A.20)

The derivative (A.20) of the positive definite quadratic form (A.19) is a negative semidefinite function; therefore, the error is $\xi {\, \in \,} {L_\infty }$, and Eq. (A.19) is a Lyapunov function for system (2.12). At the same time, the Lyapunov function (A.19) has a finite limit as $t \to \infty$,

$$ \begin {aligned} &V\left ( {\tilde \theta \left ( {t \to \infty } \right )} \right ) = V\left ( {\tilde \theta \left ( {{t_0}} \right )} \right ) + \displaystyle \int \limits _{{t_0}}^\infty {\dot Vd} t = V\left ( {\tilde \theta \left ( {{t_0}} \right )} \right ) - \displaystyle \int \limits _{{t_0}}^\infty {\left [ {e_\mathrm {ref\,}^\mathrm {T}Q{e_\mathrm {ref\,}} + \lambda \left ( {{{\tilde \theta }^\mathrm {T}}{\Gamma ^{ - 1}}\tilde \theta } \right )} \right ]d} t\\ &\qquad {}\Rightarrow \displaystyle \int \limits _{{t_0}}^\infty {\left [ {{\lambda _{\min }}\left ( Q \right ){{\left \| {{e_\mathrm {ref\,}}} \right \|}^2} + \lambda {\lambda _{\min }}\left ( {{\Gamma ^{ - 1}}} \right ){{\left \| {\tilde \theta } \right \|}^2}} \right ]d} t = V\left ( {\tilde \theta \left ( {{t_0}} \right )} \right ) - V\left ( {\tilde \theta \left ( {t \to \infty } \right )} \right ) < \infty , \end {aligned} $$

and then $\xi \in {L_2} \cap {L_\infty }$ and $\omega \in {L_\infty }$ (because ${e_\mathrm {ref\,}} \in {L_2} \cap {L_\infty }$).

We have thus proved the first part of Theorem 2. To prove the second part of Theorem 2, we find the second derivative of the Lyapunov function (A.19) taking into account Eq. (3.3),

$$ \begin {aligned} \ddot V &= - \dot e_\mathrm {ref\,}^\mathrm {T}Qe_\mathrm {ref\,} - e_\mathrm {ref\,}^\mathrm {T}Q{\dot e}_\mathrm {ref\,} - \lambda \left ( {\tilde \theta }^\mathrm {T}{\dot \Gamma }^{ - 1}\tilde \theta + 2{\tilde \theta }^\mathrm {T}\Gamma ^{ - 1}\dot {\tilde \theta } \right ) \\ &= - 2e_\mathrm {ref\,}^\mathrm {T}Q\left [ A_\mathrm {ref\,}e_\mathrm {ref\,} + B_\mathrm {ref\,}{\tilde \theta }^\mathrm {T}\omega \right ] + 2\lambda {\tilde \theta }^\mathrm {T}\omega \left [ B_\mathrm {ref\,}^\dag \varepsilon + B_\mathrm {ref\,}^\mathrm {T}Pe_\mathrm {ref\,} \right ]^\mathrm {T} \\ &\qquad {}- \lambda \left ( {\tilde \theta }^\mathrm {T}\left [ 2\omega \omega ^\mathrm {T} - \lambda \Gamma ^{ - 1} \right ]\tilde \theta \right ) = - 2e_\mathrm {ref\,}^\mathrm {T}Q\left [ A_\mathrm {ref\,}e_\mathrm {ref\,}+ B_\mathrm {ref\,}{\tilde \theta }^\mathrm {T}\omega \right ] \\ &\qquad {} + 2\lambda {\tilde \theta }^\mathrm {T}\omega e_\mathrm {ref\,}^\mathrm {T}PB_\mathrm {ref\,} + \lambda ^2\left ( {\tilde \theta }^\mathrm {T}\Gamma ^{ - 1}\tilde \theta \right ). \end {aligned}$$

Since it has been proved that $\tilde \theta \in {L_2} \cap {L_\infty }$, ${e_\mathrm {ref\,}} \in {L_2} \cap {L_\infty }$, and $\omega \in {L_\infty }$, it follows under the persistent excitation condition that $\Gamma \in L_{\infty }$ and $\Gamma ^{-1} \in L_{\infty }$ (the proof is similar to (A.6)–(A.15) in the proof of Theorem 1) and hence $\ddot V \in {L_\infty }$ as well. In this case, the derivative (A.20) of the Lyapunov function (A.19) is uniformly continuous, and $\dot V \to 0$ by Barbalat’s lemma; accordingly, the convergence $\xi \to 0$ as $t \to \infty$ is achieved.

To determine an estimate for the rate of convergence of the error $\xi$ to zero, we rewrite the upper bound for the derivative (A.20) as

$$ \dot V\leqslant - \dfrac {\lambda _{\min }\left ( Q \right )}{\lambda _{\max }\left ( P \right )}\lambda _{\max }\left ( P \right ) \left \|e_\mathrm {ref\,}\right \|^2- \dfrac {\lambda {}\lambda _{\min }\left (\Gamma ^{-1}\right )} {\lambda _{\max }\left (\Gamma ^{-1}\right )} \lambda _{\max }\left (\Gamma ^{-1}\right )\left \|\tilde \theta \right \|^2. $$

(A.21)

Further, to determine the minimum convergence rate using the results obtained when proving Theorem 1, we write the lower and upper bounds for the norm $\Gamma ^{-1}$ for the adjustment law $\Gamma$ in the adaptation loop (4.1),

$$ \begin {aligned} \left \| {{\Gamma ^{ - 1}}} \right \| &\geqslant \underbrace {\sqrt {n + 1} \Big [ {{\min }\left \{ {{\lambda _{\min }}\left ( {{\Gamma ^{ - 1}}\left ( 0 \right )} \right ),2\alpha } \right \}{e^{ - \lambda T}}} \Big ]}_{{\lambda _{\min }}\left ( {{\Gamma ^{ - 1}}} \right )} ,\\ \left \| {{\Gamma ^{ - 1}}} \right \| &\leqslant \underbrace {\sqrt {n + 1} \left [ {{\lambda _{\max }}\left ( {{\Gamma ^{ - 1}}\left ( 0 \right )} \right ) + \dfrac {{2{\lambda _{\max }}\left ( {\omega {\omega ^\mathrm {T}}} \right )}}{\lambda }} \right ]}_{{\lambda _{\max }}\left ( {{\Gamma ^{ - 1}}} \right )}. \end {aligned}$$

(A.22)

Taking into account (A.22), we rewrite the upper bound for the derivative (A.21) as

$$ \begin {aligned} \dot V &\leqslant -\frac {\lambda _{\min }(Q)}{\lambda _{\max }(P)} \lambda _{\max }(P)\left \|e_\mathrm {ref\,}\right \|^2 \\ &\qquad {}- \frac {\lambda ^2\min \left \{\lambda _{\min }\left (\Gamma ^{-1}(0)\right ),2\alpha \right \}e^{-\lambda T}} {\lambda {}\lambda _{\max }\left (\Gamma ^{-1}(0)\right )+2\lambda _{\max }\left (\omega {}\omega ^\mathrm {T} \right )} \lambda _{\max }\left (\Gamma ^{-1}\right )\left \|\tilde \theta \right \|^2 \leqslant -\eta _{\min }V, \\ {\eta _{\min }} &= {\min }\left \{ {\frac {{{\lambda _{\min }}\left ( Q \right )}}{{{\lambda _{\max }}\left ( P \right )}}{\rm {; }}\dfrac {{{\lambda ^2}{\min }\left \{ {{\lambda _{\min }}\left ( {{\Gamma ^{ - 1}}\left ( 0 \right )} \right ),2\alpha } \right \}{e^{ - \lambda T}}}}{{\lambda {}\lambda _{\max }\left ( {{\Gamma ^{ - 1}}\left ( 0 \right )} \right ) + 2{\lambda _{\max }}\left ( {\omega {\omega ^\mathrm {T}}} \right )}}} \right \}. \end {aligned}$$

(A.23)

Let us solve the resulting differential inequality while substituting the lower bound for the Lyapunov function into the left-hand side of the solution,

$$ \left \| \xi \right \| \leqslant \sqrt {\lambda _{\min }^{ - 1}\left ( H \right ){e^{ - {\eta _{\min }} \cdot t}}V\left ( 0 \right )}. $$

(A.24)

It follows from the majorant (A.24) that the error $\xi$ decays exponentially at a rate faster than $\eta _{\min }$; this is exactly what is claimed in the second part of Theorem 2.

To prove the third part of Theorem 2, we write a lower bound for the derivative (A.20),

$$ \begin {gathered} \dot V \geqslant - \dfrac {\lambda _{\max }\left ( Q \right )} {\lambda _{\max }\left (P\right )}{\lambda _{\max }\left (P\right )\left \| e_\mathrm {ref\,} \right \|^2} - \lambda {\lambda _{\max }}\left ( {{\Gamma ^{ - 1}}} \right ){\left \| {\tilde \theta } \right \|^2} \geqslant - {\eta _{\max }}V,\\ {\eta _{\max }} = {\max }\left \{\dfrac {\lambda _{\max }\left ( Q \right )}{\lambda _{\max }\left ( P \right )};\lambda \right \}. \end {gathered}$$

(A.25)

We solve the differential inequality (A.25) while substituting the upper bound for the Lyapunov function into the left-hand side of the solution,

$$ \left \| \xi \right \| \geqslant \sqrt {\lambda _{\max }^{ - 1}\left ( H \right ){e^{ - {\eta _{\max }} \cdot t}}V\left ( 0 \right )}. $$

(A.26)

It follows from the definition of $\eta _{\max }$ in (A.25) and the minorant (A.26) that by increasing the parameter $\lambda$, one can make the maximum rate of convergence of the error $\xi$ arbitrarily large; this is what is claimed in the third part of Theorem 2. $\quad \blacksquare$

Remark.

As $\lambda \to \infty$, the maximum convergence rate satisfies $\eta _{\max }\to \infty$, but the minimum convergence rate satisfies $\eta _{\min }\to 0$. Since $\lambda T\to \infty$ in (A.23), this leads to a considerable increase in the distance between the majorant (A.24) and the minorant (A.26); this, in turn, leads to oscillations with respect to $\xi$. Therefore, in practice, it makes little sense to use values of $\lambda$ exceeding $\lambda _{\max }=T^{-1}$.