Cutting Polygons Composed of Equal Rectangles into Similar Rectangles

Abstract

Assume that a polygon is composed of equal rectangles. We find all quadratic irrationalities $r$ for which the polygon under study can be cut into similar rectangles with aspect ratio $r$.

We consider the following problem: What polygons can be cut into rectangles similar to a given one?

The problem is very complicated and can hardly be solved in a reasonable sense in its general form. However, there are interesting particular cases. We will show how the fact that a polygon can be cut into equal rectangles allows one to determine whether the polygon can be cut into similar rectangles with a prescribed aspect ratio. By a polygon we mean a closed connected bounded part of the plane bounded by one or several nonintersecting and non-self-intersecting closed broken lines. In particular, the polygon need not be simply connected. We denote $\mathbb{Q}[\sqrt{p}\,]=\{a+b\sqrt{p} : a,b \in \mathbb{Q}\}$.

FormalPara Theorem.

Let $a,b,p \in \mathbb{Q}$ , $p>0$ , and $\sqrt{p} \notin \mathbb{Q}$ . Assume that a polygon all of whose sides belong to $\mathbb{Q}[\sqrt{p}\,]$ is cut into equal rectangles with aspect ratio $y \in \mathbb{R}$ . The polygon can be cut into similar rectangles with aspect ratio $a+b\sqrt{p}$ if and only if the rectangle with aspect ratio $y$ can be cut into similar rectangles with aspect ratio $a+b\sqrt{p}$ .

FormalPara Corollary 1.

Let the assumptions of the theorem be fulfilled. Then:

• (1) if $a-b\sqrt{p} > 0$ , then the polygon can be cut into rectangles with aspect ratio $a+b\sqrt{p}$ if and only if

  $$y \in \biggl\{e+f\sqrt{p} : e, f \in \mathbb{Q},\,e > 0,\,\frac{|f|}{e} \le \frac{|b|}{a}\biggr\};$$

• (2) if $a-b\sqrt{p} < 0$ , then the polygon can be cut into rectangles with aspect ratio $a+b\sqrt{p}$ if and only if

  $$y \in\biggl\{e+f\sqrt{p} : e,f \in \mathbb{Q},\,f > 0,\,\frac{|e|}{f} \le \frac{|a|}{b}\biggr\}.$$

As another consequence, we consider the case of cutting a “square with a hole” (Fig. 1).

Fig. 1.

FormalPara Corollary 2.

Let $a,b,p \in \mathbb{Q}$ , and let $\sqrt{p} \notin \mathbb{Q}$ . Consider a polygon between two homothetic concentric squares with sides $u > v$ . Then

• (1) if $a-b\sqrt{p} > 0$ , then this polygon can be cut into rectangles with aspect ratio $a+b\sqrt{p}$ if and only if

  $$\frac{u+v}{u-v} \in\biggl\{e+f \sqrt{p} : e,f \in \mathbb{Q},\,e > 0,\,\frac{|f|}{e} \le \frac{|b|}{a}\biggr\};$$

• (2) if $a-b\sqrt{p} < 0$ , then this polygon can be cut into rectangles with aspect ratio $a+b\sqrt{p}$ if and only if

  $$\frac{u+v}{u-v} \in\biggl\{ e+f \sqrt{p} : e, f \in \mathbb{Q},\,f > 0,\,\frac{|e|}{f} \le \frac{|a|}{b}\biggr\}.$$

We briefly consider the history of the problem of cutting rectangles into similar rectangles. For details, see, e.g., [1, “Survey of known results”]. One of the first nontrivial results was the fact proved by M. Dehn in 1903 that only the rectangles with rational aspect ratio can be tiled by squares [2]. In 2016, F. Sharov [1] generalized Dehn’s theorem determining all rectangles that can be cut into rectangles with a given aspect ratio from $\mathbb{Q}[\sqrt{p}\,]$. Using Sharov’s theorem, we will obtain the theorem and Corollaries 1 and 2. In [3], Freiling, Laczkovich and Rinne found an algebraic criterion for the possibility of cutting a rectangle into similar rectangles. However, this criterion does not provide an algorithm for verifying the possibility of a given cutting.

We fix a number $p \in \mathbb{Q}$ such that $p > 0$, $\sqrt{p} \notin \mathbb{Q}$. A polygon is said to be good if its sides have the form $\alpha+\beta\sqrt{p}$ for some $\alpha,\beta \in \mathbb{Q}$. Starting from that point, we assume that the sides of all polygons under study are parallel to the coordinate axes, i.e., they are vertical and horizontal.

We will use the following notions similar to those introduced in [4], cf. [3].

FormalPara Definition 1.

A basis is an ordered set of real numbers linearly independent over the field $\mathbb{Q}[\sqrt{p}\,]$. We will say that a number can be written in the basis ($e_1,e_2,\dots,e_k$) if it is equal to a linear combination of the numbers $e_1,e_2,\dots,e_k$ with coefficients from $\mathbb{Q}[\sqrt{p}\,]$.

FormalPara Definition 2.

Let $E=(e_1,e_2,\dots,e_k)$ be a basis, and let $z \in \mathbb{R}$. The $z$-area in the basis $E$ (or the Hamel area) of a rectangle

$$(a_1 e_1+a_2 e_2+\cdots+a_k e_k) \times (b_1 e_1+b_2 e_2+\cdots+b_k e_k),$$

is defined to be the number $(a_1+a_2 z)(b_1+b_2 z)$, where $a_1,a_2,\dots,a_k,b_1, b_2,\dots,b_k \in \mathbb{Q}[\sqrt{p}\,]$.

FormalPara Lemma 1.

If a rectangle is cut into rectangles whose sides can be written in a basis $E$ , then the $z$ -area in the basis $E$ of the considered rectangle is equal to the sum of $z$ -areas in the basis $E$ of the rectangles into which it was cut.

FormalPara Proof.

The proof of this property of $z$-areas almost word for word repeats the proof of Lemma 8 in [1].

FormalPara Lemma 2 (see Fig. 2).

For any good polygon $M$ whose angles are multiples of $90^\circ$ , there are good rectangles $R,R_1,\dots,R_n$ such that $R$ can be cut into $M, R_1,\dots,R_n$ .

Fig. 2.

FormalPara Proof.

The sought rectangle $R$ was obtained as the intersection of continuations of the highest and lowest horizontal sides of the polygon $M$ with its leftmost and rightmost vertical sides. To obtain the other sought rectangles $R_1,\dots,R_n$, we extend each side of the polygon up to its intersection with the boundary of the polygon $M$ or the rectangle $R$. Thus, we obtain a good rectangle $R$ together with the cutting into good rectangles $R_1,\dots,R_n$ and the original polygon $M$.

FormalPara Lemma 3.

If a good polygon is cut into equal rectangles, then these equal rectangles are good.

FormalPara Proof.

Assume that a good polygon is cut into $N$ equal rectangles $c \times d$. Assume the converse, namely, assume that one of the numbers $c$ or $d$ does not belong to $\mathbb{Q}[\sqrt{p}\,]$. The area of a good polygon is $Ncd \in \mathbb{Q}[\sqrt{p}\,]$; hence if $d \in \mathbb{Q}[\sqrt{p}\,]$, then also $c \in \mathbb{Q}[\sqrt{p}\,]$. This means that $c \notin \mathbb{Q}[\sqrt{p}\,]$ and $d \notin \mathbb{Q}[\sqrt{p}\,]$. Consider the basis

$$E=\begin{cases} (c,d,1)&\text{if the triple}\ (c,d,1)\ \text{is linearly independent over}\ \mathbb{Q}[\sqrt{p}\,]; \hspace{50pt} (1) \\ (1,c)&\text{if the triple}\ (c,d,1)\ \text{is linearly dependent over}\ \mathbb{Q}[\sqrt{p}\,]. (2) \end{cases}$$

In the case (2), let $d=a_1+a_2 c$ for some $a_1, a_2 \in \mathbb{Q}[\sqrt{p}\,]$. Then $a_2 \ne 0$, because otherwise, $d$ would belong to the set $\mathbb{Q}[\sqrt{p}\,]$.

By Lemma 2, we complement the polygon to the good rectangle $R$. We thus cut the good rectangle $R$ into good rectangles and the rectangles $c \times d$. Then the $z$-area in the basis $E$ of any good rectangle is independent of $z$. This means that the $z$-area of the rectangle $R$ is independent of $z$. The sum of the $z$-areas of the rectangles into which is was cut is equal to $N z$ in the case (1) and to $C+N a_1 z+N a_2 z^2$, where $C$ is a number independent of $z$, in the case (2). By Lemma 1, we obtain that the $z$-area of the rectangle $R$ depends on $z$, because $a_2 \ne 0$ and $N \ne 0$. This is a contradiction.

FormalPara Lemma 4.

If a good polygon is cut into rectangles whose aspect ratios belong to the set $\mathbb{Q}[\sqrt{p}\,]$ , then these rectangles are good.

FormalPara Proof.

Assume the converse; namely, assume that, in the cutting, there is a rectangle $c \times k c$, where $k \in \mathbb{Q}[\sqrt{p}\,]$, $k > 0$, $c \notin \mathbb{Q}[\sqrt{p}\,]$. We complement the set $(1,c)$ to a basis as follows. Let us consider the set of all sides of the rectangles in the cutting and, one by one, complement our set with the lengths of the sides that leave the set linearly independent over $\mathbb{Q}[\sqrt{p}\,]$. As a result, we obtain a basis $E=(1,c,e_3,\dots,e_n)$. Then the $z$-area of an arbitrary rectangle in the cutting

$$(a_1+a_2 c+a_3 e_3+\cdots+a_n e_n) \times b (a_1+a_2 c+a_3 e_3+\cdots+a_n e_n),$$

where $b \in \mathbb{Q}[\sqrt{p}\,]$, $b > 0$, is equal to $b a_1^2+2 b a_1 a_2 z+b a_2^2 z^2$ in the basis $E$. The coefficient of $z^2$ is nonnegative for any rectangle in the cutting and positive for the rectangle $c \times k c$. This means that the sum of the $z$-areas of all rectangles in the cutting nontrivially depends on $z$. By Lemma 2, we complement the polygon to a good rectangle. Then the $z$-area of the obtained rectangle, as well as of the added rectangles, is independent of $z$. Thus, by Lemma 1, we arrive at a contradiction.

We will need another notion introduced in [1].

FormalPara Definition 3 [1, Definition 5].

Let $A,B,C \in \mathbb{R}$, $\alpha$, $\beta$, $\gamma$, $\delta$, $p \in \mathbb{Q}$, and $\sqrt{p} \notin \mathbb{Q}$. Then the $ABC$-area of the rectangle $(\alpha+\beta\sqrt{p}\,) \times (\gamma+\delta\sqrt{p}\,)$ is the number $S:=\alpha\gamma A+\alpha\delta B+\beta\gamma B+\beta\delta C$.

FormalPara Example.

Let $p=2$, $A=-1$, $B=1$, and $C \in \mathbb{R}$. Then the $ABC$-area of the rectangle $(\sqrt{2}+1) \times 1$ is equal to 0, and the $ABC$-area of the similar rectangle $(\sqrt{2}-1)\times 1$ is equal to 2.

FormalPara Lemma 5 [1, Lemma 8].

If a rectangle is cut into good rectangles, then the $ABC$ -area of the cut rectangle is equal to the sum of the $ABC$ -areas of the obtained rectangles.

FormalPara Definition 4.

Assume that there is at least one cutting of a given good polygon into good rectangles. Then we let the $ABC$-area of the polygon be equal to the sum of the $ABC$-areas of all rectangles in any such a cutting.

Now we prove that the $ABC$-area of a polygon is well defined.

FormalPara Lemma 6.

If a polygon is cut into good rectangles in two ways, then the sum of the $ABC$ -areas of the rectangles is the same in both cases.

FormalPara Proof.

By Lemma 2, we complement the polygon to a good rectangle. By Lemma 5, for the obtained cutting of a good rectangle, the $ABC$-area is equal to the sum of the $ABC$-areas of the added good rectangles and the $ABC$-areas of the rectangles into which the polygon was cut. Thus, the sum of the $ABC$-areas of the rectangles in the cutting is equal to the difference between the $ABC$-areas of the rectangle and of the added good rectangles, and for them, the $ABC$-area is defined uniquely and is independent of the cutting. Thus, the $ABC$-area of the polygon is also independent of the cutting.

Now we formulate a lemma which we use to derive the theorem.

FormalPara Lemma 7.

Let $a,b,e,f,p \in \mathbb{Q}$ , $\sqrt{p} \notin \mathbb{Q}$ , $e+f\sqrt{p} > 0$ , and $a+b\sqrt{p} > 0$ . Assume that one of the following two conditions is satisfied:

• (a) $a-b\sqrt{p} > 0$ , $|f|/e > |b|/a$ ;

• (b) $a-b\sqrt{p} < 0$ , $|e|/f > |a|/b$ .

In the definition of $ABC$ -area, we put $A=f$ , $B=-e$ , and $C=(2fa^2/b^2)-pf$ . Then

• (1) the $ABC$ -area of the rectangle with sides $e+f\sqrt{p}$ and 1 is zero;

• (2) the $ABC$ -areas of all rectangles with aspect ratio $a+b\sqrt{p}$ and sides from $\mathbb{Q}[\sqrt{p}\,]$ are different from zero and have the same sign.

FormalPara Proof of the theorem (under the assumption that Lemma 7 is proved).

We will prove the “only if” part. We consider two cuttings of a polygon: the first, into equal rectangles, and the second, into similar good rectangles. Then by Lemmas 3 and 4, the sides of all these rectangles belong to the set $\mathbb{Q}[\sqrt{p}\,]$. Without loss of generality, we assume that the sides of equal rectangles in the first cutting are equal to $e+f\sqrt{p}$ and $1$ (this can be achieved with appropriate homothety). If the numbers $a$, $b$, $p$ are such that both conditions (a) and (b) of Lemma 7 are not satisfied, then, by the “if” part in Theorem 1 in [1], we obtain the required cutting of the rectangle with aspect ratio $y$ (for the direct construction of the cutting, see [5, Sec. 1]). Otherwise, by assertion (1) in Lemma 7, the $ABC$-area of the polygon is equal to zero (as the sum of the $ABC$-areas of equal rectangles). But by assertion (2) in Lemma 7, the sum of the $ABC$-areas of the rectangles with aspect ratios $a+b\sqrt{p}$ is always different from zero. Therefore, the $ABC$-area of the polygon is not equal to zero. This is a contradiction.

It remains to prove Lemma 7. In fact, it was proved in [1, pp. 209–211, see “Proof of the main theorem for $n=1$”], but it was not explicitly formulated there. We here present its proof, which is actually borrowed from [1].

FormalPara Proof of Lemma 7.

(1) The $ABC$-area of the rectangle $(e+f\sqrt{p}\,) \times 1$ is equal to

$$S=e \cdot 1 \cdot f+e \cdot 0 \cdot (-e)+ f \cdot 1 \cdot(-e)+f \cdot 0 \cdot \biggl(\frac{2fa^2}{b^2}-pf\biggr)=0.$$

(2) Let us consider the rectangle $(\alpha+\beta\sqrt{p}\,) \times (\gamma+\delta\sqrt{p}\,)$, where

$$\frac{\gamma+\delta\sqrt{p}}{\alpha+\beta\sqrt{p}}=a+b\sqrt{p}\,.$$

Then $\gamma+\delta\sqrt{p}=\alpha a+p\beta b+ \sqrt{p}\,(\beta a+\alpha b)$, and hence $\gamma=\alpha a+p\beta b$, $\delta=\beta a+\alpha b$. Therefore, the $ABC$-area of the rectangle can be written as

$$\begin{aligned} \, S&=\alpha \gamma f-\beta\gamma e-\alpha\delta e+ \beta \delta \biggl(\frac{2fa^2}{b^2}-p f\biggr) \\& =\alpha f(\alpha a+p\beta b)-\beta e(\alpha a+p \beta b)- \alpha e(\beta a+\alpha b)+\beta\biggl(\frac{2fa^2}{b^2}-pf\biggr) (\beta a+\alpha b) \\& ={\alpha}^2(fa-e b)+2\alpha\beta\biggl(\frac{fa^2}{b}- ea\biggr)+{\beta}^2\biggl(\frac{2fa^3}{b^2}- p f a-p e b\biggr). \end{aligned}$$

We note that if condition (a) is satisfied, then we have $a-b\sqrt{p} > 0$ and $a+b\sqrt{p} > 0$, and hence $a > 0$. Since $|f|/e > |b|/a$ in this case, it follows that $e > 0$. We have

$$\frac{|f|}{e} \ne \frac{|b|}{a} \quad\Longleftrightarrow\quad \biggl|\frac{f}{e}\biggr| \ne \biggl|\frac{b}{a}\biggr| \quad\Longleftrightarrow \quad|fa| \ne |be| \quad\Longrightarrow\quad fa \ne be.$$

If condition (b) is satisfied, we similarly obtain $f a-e b \ne 0$. Thus, $f a-e b \ne 0$ in both cases (a) and (b). Therefore, the expression $S/\beta ^2$ is a square trinomial in $\alpha / \beta$. We show that its discriminant $D$ is negative. Thus, we prove that, for fixed numbers $a$, $b$, $e$, $f$ the quantity $S$ is either always positive or always negative.

Indeed,

$$\begin{aligned} \, \frac{D}{4}&=\frac{f^2 a^4}{b^2}-\frac{2 f e a^3}{b}+e^2 a^2- \frac{2 f^2 a^4}{b^2}+p f^2 a^2+p f a e b+\frac{2 f e a^3}{b}- p f a e b-p e^2 b^2 \\& =\frac{-f^2 a^4}{b^2}+e^2 a^2+p f^2 a^2-p e^2 b^2= (a^2-p b^2)\biggl(e^2-\frac{f^2 a^2}{b^2}\biggr) < 0, \end{aligned}$$

because, under condition (a), it follows from the statement of the lemma that the first bracket is positive and the second bracket is negative, and conversely, under condition (b).

Thus, assertion (2) is proved, as well as the assertion of the theorem.

Now we prove the above-formulated corollaries.

FormalPara Proof of Corollary 1.

The proof immediately follows from the theorem and [1, Theorem 1].

FormalPara Proof of Corollary 2.

We cut the square with a hole into four equal rectangles $(u+v)/2 \times(u-v)/2$; see Fig. 3. We put $u=1$ without loss of generality.

Fig. 3.

If $(u+v)/(u-v) \in \mathbb{Q}[\sqrt{p}\,]$, then the square with a hole is a good polygon and, by Corollary 1, we obtain Corollary 2.

If $(u+v)/(u-v) \notin \mathbb{Q}[\sqrt{p}\,]$, then Corollary 1 cannot be applied, because the polygon is not good. We will prove that, in this case, the square with a hole cannot be cut into rectangles with aspect ratio $a+b\sqrt{p}$. Assume that there exists a cutting into rectangles with aspect ratio $a+b\sqrt{p}$. Adding the square $v \times v$ to the cutting, we obtain a cutting of the square $u \times u$. By Lemma 4, the sides of all rectangles in the cutting (including the square $v \times v$) lie in the set $\mathbb{Q}[\sqrt{p}\,]$. Then $v \in \mathbb{Q}[\sqrt{p}\,]$ and $(u+v)/(u-v) \in \mathbb{Q}[\sqrt{p}\,]$. This is a contradiction.

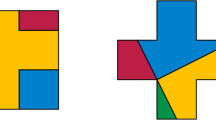
The theorem does not imply any universal method for solving the problem formulated at the beginning of the paper. For example, there is a good polygon which can be cut into similar good rectangles, but it cannot be cut into equal ones. Figure 4 shows such a polygon and its cutting into similar rectangles. The proof of the fact that it cannot be cut into equal rectangles is omitted.

In conclusion, we formulate several open questions related to the theorem in the form of problem.

Fig. 4.

FormalPara Problem.

Does the theorem remain true if “ $a+b\sqrt{p}$ ” is replaced in it by:

• (1) the set $a_1+b_1\sqrt{p},\dots,a_n+b_n\sqrt{p} \in \mathbb{Q}[\sqrt{p}\,]$ (to which the aspect ratios of the rectangles must belong);

• (2) the root $r$ of a polynomial of degree 3 with integer coefficients (and $\mathbb{Q}[\sqrt{p}\,]$ is replaced by $\mathbb{Q}[r]$ );

• (3) an arbitrary $r \in \mathbb{R}$ (and $\mathbb{Q}[\sqrt{p}\,]$ is replaced by $\mathbb{R}$ )?

Acknowledgments

The author wishes to express gratitude to M. B. Skopenkov for constant attention to this work.