Enhancing robustness to forecast errors in availability control for airline revenue management

Abstract

Traditional revenue management systems are built under the assumption of independent demand per fare. The fare adjustment theory is a methodology to adjust fares that allows for the continued use of optimization algorithms and seat inventory control methods, even with the shift toward dependent demand. Since accurate demand forecasts are a key input to this methodology, it is reasonable to assume that for a scenario with uncertainties it may deliver suboptimal performance. Particularly, during and after COVID-19, airlines faced striking challenges in demand forecasting. This study demonstrates, firstly, the theoretical dominance of the fare adjustment theory under perfect conditions. Secondly, it lacks robustness to forecast errors. A Monte Carlo simulation replicating a revenue management system under mild assumptions indicates that a forecast error of $\pm 20\%$ can potentially prompt a necessity to adjust the margin employed in the fare adjustment theory by $-10\%$. Moreover, a tree-based machine learning model highlights the forecast error as the predominant factor, with bias playing an even more pivotal role than variance. An out-of-sample study indicates that the predictive model steadily outperforms the fare adjustment theory.

Introduction and motivation

Formerly, most of the traditional airline revenue management (ARM) methods assumed independent demand for each fare class, meaning that passengers who acquire a specific fare class are presumed to be willing to purchase solely that particular fare class. This assumption was facilitated by the fare structures based on sets of restrictions, such as minimum stay prerequisites or cancelation charges.

However, the introduction of low-cost carriers led to the establishment of restriction-free fares, inducing prevalent demand dependencies across booking classes (Vinod 2021). Even though independent demand was never a solid assumption, it turned to be almost impracticable. Consequently, traditional models assuming only independent demand started to overestimate low-fare demand at the expense of high-fare demand. This incentivized the systems to account for an even greater extent of low-fare demand, inciting a higher number of high-fare customers to opt for lower priced options, known as spiral down effect (Cooper et al. 2006).

To tackle this issue, novel methodologies emerged to account for demand dependencies. In spite of the new forecasting methods, the remaining components of the ARM system still needed to be adjusted to account for demand dependencies. To solve it, Fiig et al. (2010) introduced the fare adjustment theory, which allows for the use of previously developed optimization methods. The fare adjustment theory is a theoretical dominant method under perfect conditions. However, in the presence of uncertainty, it might fail to be optimal, potentially leading to over-protection and, consequently, spoilage.

Due to many uncertainties, it remains challenging to achieve high levels of forecast accuracy. Within ARM, there is a lack or bad quality of historical booking data, which is most of the times adjusted by manual intervention, inaccurate demand models, when disregarding key customer decision drivers, and possibly inaccurate demand estimates. Beyond ARM, there is the inherent demand variability, or even changing customer behavior. On top of all these aspects, the recent global pandemic has brought up unprecedented challenges. According to Garrow and Lurkin (2021), the traditional demand forecasting approaches strongly struggled to adapt to the high schedule volatility and unstable travel restrictions. Thus, it is essential to analyze the performance of the fare adjustment theory across diverse scenarios characterized by escalating levels of uncertainty.

Forecasting dependent demand

To mitigate the prominent demand dependencies, one of the primary methods was Q-forecasting, which proposes to forecast demand for the lowest existing fare and scale it to higher fares using an exponential sell-up function, which is a willingness-to-pay (WTP) estimate (Belobaba 2011). Guo (2008) provides an overview of upsell estimation methods. Q-forecasting implies fully dependent demand, which is an accurate assumption if fare families are built in a way that fare products with similar restrictions are clustered into one family, following the work by Fiig et al. (2014).

A Poisson arrival process incorporates demand’s stochastic nature. For each fare family with booking classes $k=1,\ldots ,\ n$, sorted by fares in such a way that $r_1>r_2>\cdots >r_n$, a global homogeneous Poisson arrival process with expected value $\lambda$ can be considered for the minimum fare ($n$). The Poisson arrival process for the lowest available class $k$ is modeled, generally, as $\lambda {psup}^{n-k}$, where $psup$ represents the probability of a customer requesting a higher priced booking class if there is no availability for the demanded one.

The forecaster needs to derive the probabilities $P_k^t$ that a customer requests the lowest available fare product $k$ at each point in time $t$. Then, the booking horizon needs to be discretized in such an extent that, at maximum, one request arrives per time interval. For that, the booking period is first divided into data collection points (DCPs), each of which encompasses a set of requests following the above-mentioned Poisson arrival process. Current practices to define the DCP structure aim at including an approximately equal proportion of demand in each DCP, while assuring a constant arrival rate throughout a DCP interval.

Each DCP can then be divided into smaller time intervals of equal length, each of which follows a Poisson process with an expected number of bookings proportional to its length (Lee and Hersh 1993). Hence, the global Poisson process for a certain DCP is further subdivided into an amount of reduced time intervals such that

$$\begin{aligned} P(x>1)<\varepsilon , \end{aligned}$$

(1)

where $x$ is the random variable representing the number of requests that arrive during a time interval. $\varepsilon$ should be negligible. Figure 1 computes the impact of the number of time intervals on $P(x>1)$ for the expected demand values that are used as input for the simulations in next chapters. Note that even though the time intervals division occurs at each DCP, under the assumption that demand is equally divided per DCP, the plot would be identical.

Fig. 1

Impact of number of time intervals in $P(x>1)$

Bid price control

A bid price control is an origin–destination (OD) control for network optimization. A bid price is the shadow price for the capacity constraint, meaning the incremental network revenue that would be reached if the capacity constraint was increased by one unit, ceteris paribus. The idea behind the bid price is to establish a threshold to make decisions on whether to accept or reject a request: originally, a given booking class would only be available in a certain OD if the corresponding fare was greater than the sum of the bid prices of the comprised legs.

In a twofold work, Gallego and van Ryzin (1997) and Talluri and van Ryzin (2004) proposed a dynamic programming (DP) method for bid price determination, which considers the possibility of sell-up. Modeling the arrival of passengers through a Poisson process, which implies that past bookings only relate to future demand by absorbing a seat, allows to employ a DP formulation and, thus, the Bellman equation to calculate the expected revenue as value function:

$$\begin{aligned} V_t(x){} & {} = \underset{S\subseteq N}{\max }\ \left\{ \sum _{j\in S}\lambda {\ P}_j(S)(r_j+V_{t-1}(x-1))\right. \nonumber \\{} & {} \quad \left. +(\lambda {\ P}_0(S)+1-\lambda )V_{t-1}(x)\right\} , \end{aligned}$$

(2)

where $N=\left\{ 1,\ldots ,n\right\}$ is a set of fare products, $S\subseteq N$ a subset of fares, $r_j$ the revenues from each product $j\in N$ such that $r_1>r_2>\cdots >r_n$, $P_j(S)$ the probabilities of choosing product $j\in S$ when the fares $S$ are offered ($j=0$ denotes the no purchase decision), and $V_t(x)$ the value function (maximum expected revenue) from periods $t,\ t-1,\ldots ,\ 1$ for seat index $x$. Bid prices can be derived as follows:

$$\begin{aligned} \Delta V_t(x)=V_t(x)-V_t(x-1) . \end{aligned}$$

(3)

Yet, in practice, the network DP is impossible to solve for real airline networks due to the curse of dimensionality (Rauch et al. 2018). Instead, it is common to apply first a heuristic decomposition to reduce the state space, and just then apply DP to single legs to consider the stochasticity of the demand. This heuristic usually considers a deterministic linear program to calculate the displacement costs for each leg and decomposes the network, normally by prorating the OD fare to the enclosed legs.

Fare adjustment theory

Originally, literature stated that a certain fare should only be available if its value exceeded the bid price. However, Fiig et al. (2010) introduced the fare adjustment theory, which supports that the bid price, considered a marginal opportunity cost, should be compared to the marginal revenue instead. The main goal is to maximize revenue for a variety of fare structures, including the case of fully unrestricted ones, for which the marginal revenue is modeled with an upsell probability ${psup}_k$ for each fare $k=1,\ldots ,\ n$, with demand $D_k$ and revenues $r_1>r_2>\cdots >r_n$, as follows:

$$\begin{aligned} {r\prime }_k=\frac{r_k\ D_k-r_{k-1}\ D_{k-1}}{D_k-D_{k-1}}=\frac{r_k\ {psup}_k-r_{k-1}\ {psup}_{k-1}}{{psup}_k-{psup}_{k-1}} . \end{aligned}$$

(4)

Basically, the fare is being subtracted by a price elasticity cost, to take into consideration the possible risk of buy-down under dependent demand. This is why the marginal revenue is also designated as buy-down adjusted fare (BDAF). In this sense, as the customers’WTP rises, the price elasticity cost also rises and, thus, the BDAF decreases. Now, comparing this BDAF to a given bid price, it is more likely inferior, leading to a faster closing of lower fare classes.

Assuming an exponential sell-up, if the interval between fare levels is constant, the upsell probability is also constant, and the BDAF can be formulated, generally, as $r_k-margin$, where $margin$ is a constant.

Simulation framework

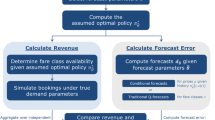
The fare adjustment theory is theoretically dominant under perfect conditions. However, there are many uncertainties in ARM, which might result in a suboptimal performance. It might cause over-protection for high-fare customers, ultimately leading to a lack of opportunities for low-fare customers and subsequent revenue loss. To investigate this, a Monte Carlo simulation aims to study the relevance of the $margin$ on the calculation of the BDAF, by computing different scenarios for both a psychic and distorted forecasts, where $margin$ is adjusted by a factor $\delta$:

$$\begin{aligned} {r\prime }_k=r_k-margin\times \left( 1+\delta \right) . \end{aligned}$$

(5)

The simulation starts by calculating the number of time steps given the expected demand. With that and the upsell probability, the forecaster derives the request probabilities for each booking class and time step. Then, considering this, the capacity and fare structure, the optimization step produces the bid price vectors. From there on, simulation runs are generated, by creating a set of requests and proceeding to the availability control with the comparison of bid prices and BDAFs. Resulting expected revenues are gathered until a certain confidence level is reached. In this case, the half-length of the $100 (1-\alpha )\%$ confidence interval (CI) needs to fall below a sufficiently small value $\gamma$:

$$\begin{aligned} z\left( \frac{\alpha }{2}\right) \times \frac{\sigma }{\sqrt{N}}<\gamma , \end{aligned}$$

(6)

where the sample mean of the random variable expected revenue is assumed to tend toward a normal distribution according to the Central Limit Theorem, since thousands of independent and identically distributed simulation runs are executed.

This simulation relies on a series of underlying assumptions. Similar hypothesis can be found, among others, in Bitran (2003), Rauch et al. (2018), Fiig et al. (2010), Fiig et al. (2012), and Lee and Hersh (1993), and is as follows:

• There are no explicit costs associated with the production of the final product.

• The seller is risk-neutral. The goal is to maximize revenue without considering the variance of the expected revenue.

• Each compartment is treated as a separate flight with fixed capacity.

• An exponential sell-up is considered: $D_k=\ D_n\ {psup}_k=D_n\ exp(-\beta (r_k-r_n))$, according to the notation in Equation (4). This means that for a set of fares arranged in equal increments, the margin in Equation (5) is the same for every fare product.

• Cancelations, no-shows, upgrades, multiple seat bookings, competition, and cross-price elasticity of demand are ignored for the sake of simplicity.

In order to test and evaluate the scenarios, it is essential to establish a set of parameters that govern the interactions within the simulated environment. Table 1 summarizes the base input values that are used in the simulation. It is noteworthy that, even though the upsell probability may vary along the booking horizon, it is treated as a constant here, since the goal is just to test different magnitudes. Regarding availability control alternatives, 100 equally spaced scenarios from $50\%$ up to $150\%$ of the original margin are compared. After analyzing Fig. 1, $\varepsilon =0.01$ was selected since it indicates a cutoff point where the additional returns in terms of $P(x>1)$ are not worth the additional computational cost. For $\gamma$, the reasoning was similar.

Table 1 Parametrization of the simulation

Psychic forecast

Since demand is modeled artificially in the simulation, a psychic forecast can be derived by encompassing known information regarding the Poisson arrival distribution, volume of demand, and upsell probability. Figure 2 displays the expected revenue for each margin correction. As anticipated, the fare adjustment theory retrieves optimal results. Negative margin corrections lead to under-protection, resulting in a high share of low-yield customers, and vice versa.

Fig. 2

Expected revenue by margin correction for psychic forecast

Assessing it from a different angle, Pang et al. (2015) demonstrate that, for optimal controls, bid prices do not exhibit a trend throughout the booking horizon. Figure 3 plots the average bid price across all simulation runs for each time step before departure, and shows that, from a bid price quality standpoint, the margin obtained from the fare adjustment theory appears to be the most suitable. It also supports the conclusions previously reached, since lower margins display an evident upward trend due to negligence of upsell potential, resulting in premature overselling, while higher margins exhibit a downward trend due to over-protecting.

Fig. 3

Bid price development according to margin correction

As input parameters are ad-hoc, there is a higher degree of uncertainty and, thus, it is of utmost importance to perform a sensitivity analysis on them. Figure 4 deep dives into the upsell probability parameter and shows that the fare adjustment theory is robust to different levels of upsell potential. Moreover, similar studies for both expected demand and capacity lead to identical conclusions.

Fig. 4

Sensitivity analysis on upsell probability for psychic forecast

Distorted forecast

Assuming the psychic forecast as given tends to artificially enhance forecast accuracy and diverge from reality (Frank et al. 2008). The main objective is, therefore, to analyze the performance of the fare adjustment theory under adverse conditions.

Hence, a simple forecasting process is considered since the main goal is to include the inherent variability of the demand (distorted forecast). For that, 1000 flights and the corresponding set of requests across the booking horizon are created from the same demand process. The same amount of random availabilities is generated, and from there a simple ratio of demand per availability counts is calculated for each booking class. This simply disregards the censored data, meaning the time steps where booking classes are not available, which is a Naïve technique.

Preserving the remaining parameters, Fig. 5 provides the results of the simulation and proves that the fare adjustment theory may lack robustness to forecast errors. Now, the optimal margin is the one with a $-13\%$ correction. Even though the delta to the new optimal margin is relatively low (approximately 8 units), for a network that operates thousands of flights a year, and for higher yield fares, it might have a significant impact. Besides that, poorer forecast accuracies might affect it even further.

Fig. 5

Expected revenue by margin correction for distorted forecast

For a concrete view of the impact of forecast error on the optimal margin correction, a sensitivity analysis must be performed. However, the introduction of forecast error with an average of previous flights makes it harder to quantify it. Hence, a new method to induct and quantify forecast error is employed: the request probabilities are adjusted by $\Delta$, which is composed by random values between a lower and upper bounds for the forecast error:

$$\begin{aligned} \lambda ^\prime =\lambda \times \Delta . \end{aligned}$$

(7)

Figure 6 plots the results for three levels of forecast error, and suggests that poorer forecast accuracies tend to lower optimal margins: forecast errors of $\pm 10\%$, $\pm 20\%$, and $\pm 30\%$ tend to, respectively, optimal margin corrections of $-4\%$, $-10\%$, and $-17\%$.

Fig. 6

Sensitivity analysis on forecast error for distorted forecast

Even though the variation of input parameters does not have an impact in a psychic forecast scenario, as previously concluded, it is important to test it under a distorted scenario. In fact, Fig. 7 indicates that varying ranges of upsell probability can influence the optimal margin correction. Similar studies for expected demand and capacity confirm that both variables can also influence the optimal margin. Yet, these relationships seem highly complex. Next section explores nonparametric models, which offer the flexibility required to uncover hidden patterns and nonlinear interactions that may exist among the variables.

Fig. 7

Sensitivity analysis on upsell probability for distorted forecast

Improving robustness to forecast errors

Leveraging the proposed Monte Carlo simulation, it is possible to generate a representative dataset of optimal margin corrections for the combination of parameters exhibited in Table 2. It is important to note that expected demand seeks higher values than the available capacities in order to analyze the problem with significant bid prices. Otherwise, the margin correction would not pose significant differences (only for cases where the BDAF gets negative) and, thus, it would not be relevant for this study.

Table 2 Range of parameters for data generation

An exhaustive combination of the parameters is done and, therefore, a synthetic set with 1440 data points is gathered. For each combination, the margin correction that maximizes revenue is collected. If two or more margin corrections result in the maximum expected revenue, the one with the narrower confidence interval is selected. With this dataset, the goal is to employ tree-based machine learning (ML) models to analyze the interaction between input variables and optimal margin corrections. These are effective in capturing complex relationships with remarkable performance.

First of all, it is necessary to define the features to use as input for the models. Expected demand, capacity, and upsell probability are equivalent to their parameter values. Regarding the fare structure, the minimum fare and step between fares are considered. Lastly, the forecast error is subdivided in a bias (middle point of the interval) and variance (amplitude of the interval) indicators.

To track the bias-variance trade-off, $80\%$ of the dataset is allocated for training, and $20\%$ for testing. The training data are then further divided into 4 subsets for k-fold cross-validation, in order to tune the hyperparameters. For tuning, a Tree-Structured Parzen Estimator with 100 iterations is applied. For model performance evaluation, two metrics are analyzed: mean absolute error (MAE) and root mean squared error (RMSE)—for hyperparameter tuning and model selection, RMSE carries more significance, since the curves of expected revenue are somewhat flat and, thus, it is worth to penalize more larger errors, since smaller errors might not imply a significant loss of revenue most of the times.

A random forest (RF) and gradient boosting machine (GBM) algorithms are employed. Table 3 indicates that whereas the GBM model shows a proper fitting with the default hyperparameter values, the RF model is suffering from overfitting. The optimization of the number of estimators, maximum depth, maximum number of features in each split (only for RF), and learning rate (only for GBM) mitigated the overfitting of the RF model and, consequently, enhanced the testing performance, while for the GBM the improvements were not significant.

Table 3 Models evaluation before and after hyperparameter tuning

Even though the models are very similar, moving forward only the RF model is considered, since it has a slightly better performance. Now, in order to understand the relevance of each input feature in predicting the optimal margin correction, it is possible to retrieve their importance scores. By inspecting the decrease in the sum of squared errors after the splits made using a specific feature, the RF model is able to depict the most important variables. Accordingly, Fig. 8 indicates that the forecast error variables are unequivocally the most significant ones, especially the bias indicator. These are followed by the upsell probability, expected demand, capacity, and fare structure related variables, in this order. However, their importance scores are substantially lower.

Fig. 8

Feature importance scores

After recognizing the forecast error variables as highly important, it is crucial to unravel their specific impact on the dependent variable. Partial dependence plots are universal methods to illustrate the marginal effect of a certain feature on the predicted outcome, after removing the influence of the other features. Figure 9 implements it for both the bias and the variance indicators. The findings are coherent: for the bias indicator, negative values mean that the forecasted values are lower than the real demand. Thus, the logical outcome is a trend to increase the margins, leading to lower BDAFs and, consequently, more strict availabilities. On the other hand, positive values imply over-forecasting, and the natural result is to decrease margins, causing more liberal availabilities. As for the variance indicator, as it increases, the margins need to be lower—the worse the forecast accuracy is, the less robust the fare adjustment theory is.

Fig. 9

Partial dependence plots for bias (left) and variance (right) indicators

Validation study

This section performs an out-of-sample validation with 100 generated flights to verify if the optimal margin correction being predicted really yields a superior performance when compared to the standard fare adjustment theory.

For the upsell probability, expected demand, capacity, and fare-related features, the ranges are simply the ones considered for the training data of the model. However, here, a random value between the lower and upper bounds is used for each feature. Regarding the forecast error variables, three distinct scenarios with increasing inaccuracy are evaluated. Scenario A accounts only for variance, with the forecast error ranging from $\pm 10$ to $\pm 20\%$. Scenario B is similar, but allows the forecast error to range from $\pm 10$ to $\pm 40\%$. Scenario C, besides this level of variance, also considers the possibility for bias in the forecast, ranging from $-10$ to $10\%$.

Table 4 proves that, in fact, a margin correction over the fare adjustment theory produces improved results, although with different magnitudes. As expected, the positive impact increases from scenario A to C, since the forecast accuracy is decreasing and, thus, it is more crucial to correct the margins in availability control. Focusing solely on the expected values, in scenario A, the margin correction strategy yields an expected revenue $0.0034\%$ higher than the one for no margin correction; in scenario B, the difference rises to $0.0093\%$; and in scenario C, to $0.0144\%$. Furthermore, when inspecting Table 5, it is also possible to assess that the margin correction strategy provides enhanced results regarding the number of passengers, which might represent a competitive edge for market share.

Table 4 Expected revenue for validation study

Table 5 Expected passengers for validation study

Conclusion and recommendations

This article studies the performance of the fare adjustment theory under distinct scenarios. Firstly, the Monte Carlo simulation validates that this methodology is a dominant methodology under a psychic forecast. Moreover, it is robust to variations in upsell probability, expected demand, and capacity.

Secondly, it proves that the fare adjustment theory lacks some robustness to forecast errors. Furthermore, it is clear that the greater the inaccuracy, the more the margin needs to be adjusted down. Additionally, for each level of forecast error, other variables might influence the optimal margin correction.

Thirdly, the variables that impact the most the optimal margin correction are, in this order, the bias indicator, variance indicator, upsell probability, expected demand, capacity, and fare-related variables. The forecast error variables are markedly the most essential ones, with importance scores of 0.47 for the bias indicator, and 0.23 for the variance indicator. When the bias indicator conveys positive values, the standard margins need to be reduced, leading to more permissive availabilities (and vice versa); for the variance indicator, the higher the forecast inaccuracy, the less robust the fare adjustment theory is.

For further validation, an out-of-sample study demonstrates that the strategy with the optimal margin correction from the predictive model steadily outperforms the fare adjustment theory in terms of expected revenue. Even though these are low differences, for an airline with thousands of flights a year it can have a significant impact.

As a final point, it is argued that, even though measuring forecast accuracy for dependent demand is far from trivial, there needs to be a standardized method to compute the forecast errors, as the one proposed by Fiig et al. (2014), to ensure the accurate functionality of the predictive model for optimal margin correction.