Introduction

Pricing decision is critical as it is responsible for a significant share (e.g. up to 90%) of the final product cost (Davenport and Kalagnanam 2001; Noori-daryan et al. 2018). Since pricing is directly related to sales, revenues, and profits, it is an effective tool to manipulate the demand in the short run (Bitran and Caldentey 2003; Lund et al. 2018). Hence, many companies (e.g. in airline and hospitality industries) apply dynamic pricing strategies to improve customer services and to attract strategic customers (Abrate et al. 2012; Bayoumi et al. 2013; Lehtimäki et al. 2018; Fiig et al. 2018; Bansal and Maglaras 2009). They fluctuate the price to adjust with the supply or to cope up with the competition in the market (Hönig et al. 2018) that improves social welfare and consumer’s surplus (Chen and Gallego 2018). Thus, it benefits both the seller and the buyer (Dugar et al. 2015). However, changing prices can be costly as well (Lanquepin-Chesnais 2014; Kareem Abdul 2018). Moreover, fluctuation of prices can lead to a market speculation and an increased uncertainty. It creates information distortions in order quantity and inventory (also known as the ‘bullwhip effect (BW)’) which adversely affects the supply chain in terms of excess inventories, backorders, inefficient use of resources etc. (Lee et al. 2004). Therefore, it is necessary to study the fluctuation of price in the supply chain.

Price variation may occur due to internal or external factors such as managerial decisions, cost changes, scarcity of resources, supplier quantity discounts, promotional sales, or future market speculations. In this study, we focus on the external cost changes and then analyze the impact of the cost change on the supply chain optimal pricing. Interestingly, the price variation does not remain constant always across the various stages of supply chain. It may propagate in an increased or decreased fashion towards the downstream (i.e. towards the customer side) supply chain depending on the demand function, supply chain structure, etc. We name the amplified or absorbed variability of prices as the ‘Bullwhip effect in Pricing (BP)’. If the variability of price is amplified towards the downstream supply chain, then researchers named it as ‘reverse bullwhip effect in pricing (RBP)’ (Özelkan and Çakanyıldırım 2009). On the other hand, if the variability of price is absorbed towards the downstream supply chain, we name it here as ‘Forward Bullwhip effect in Pricing (FBP)’. The ‘reverse’ and ‘forward’ directions refer to the direction of the classical bullwhip effect in the order quantity and the inventory decision. In classical bullwhip effect, the variability of the order information towards the upstream of a supply chain is higher. Hence, if the variability of price towards the downstream of a supply chain is higher, then the direction is referred as ‘reverse’; on the other hand, if the variability of price towards upstream is more (i.e. downstream is less), then the direction is referred as ‘forward’.

Figure 1 shows several empirical evidences of amplified and reduced variations in prices using real market data (from USDA and FRED). It shows an amplified variability in the case of the U.S. beef market (Fig. 1a), and the potato prices in Chicago, IL (Fig. 1b). These are two examples of RBP.

Fig. 1
figure 1

Empirical examples of RBP

Full size image

On the other hand, Borenstein and Cameron (1992) found a reduced variability in oil retail prices compared to the terminal prices and spot gasoline prices (e.g. standard deviations are 2.91, 4.12, 5.74 respectively). This is an example of the FBP phenomenon. Additional empirical examples of FBP are observed in U.S. and German coffee markets. Leibtag et al. (2007) show that a 10% increase in coffee cost results in a 3% increase in the retail price in US. Similarly, Bonnet et al. (2013) show that a reduced variability in coffee retail prices occurs in the German Market.

Existing research is centered on the occurrence of RBP, but not FBP (Özelkan and Çakanyıldırım 2009; Özelkan and Lim 2008; Özelkan et al. 2018). To figure out the required conditions for the occurrence of RBP, researchers considered a game theoretic model of a multi-stage linear supply chain, where a leader–follower type ‘Stackelberg’ game was considered in which a supplier or an upstream supply chain player act as the leader. However, previous research did not consider the flipped case of the game where powerful retailers (or downstream supply chain players) may act as leaders too. A simultaneous game structure was not considered either. Based on previous studies, research questions that we are trying to answer in this paper can be summarized as follows:

  1. (1)

    Can bullwhip effect in pricing propagate in the forward direction? Alternately, does FBP occur?

  2. (2)

    Does bullwhip effect in pricing exist if retailers or downstream supply chain players act as leaders in ‘Stackelberg’ game?

In the next section, we review the related literature in more detail. Then, we discuss the conditions for the occurrence of BP in “Conditions for the occurrence of BP”. In “BP in different game leadership structures”, we provide analytical results under different game leadership scenarios. In “Simulation results”, we present numerical simulation examples and relate the BP to price markups under different game leadership scenarios. Then finally, in “A discussion on price variations and markup profits”, we summarize and conclude the research outcomes, and suggest future research directions.

Literature review

In this section, we review several streams of literature related to the research presented here, such as the effect of price variation on bullwhip effect in order quantity (BW), bullwhip effect in pricing (BP), and “cost-pass-through”.

The term ‘Bullwhip effect’ was originally introduced by Lee et al. (1997). Lee et al. (2004) identified four sources of BW i.e. demand signal processing, rationing game, order batching, and price variations. Later, other researchers found several other sources of BW (Bhattacharya and Bandyopadhyay 2011). Among various causes, Paik and Bagchi (2007) emphasized price variations as one of three most significant causes of BW. Therefore, reducing or managing price variations may reduce BW.

In the analytical investigation of price-variation, the cost-pass-through coefficient is a useful economic tool (Weyl 2008; Fabinger and Weyl 2012). Cost-pass-through is defined as the marginal rate of price-changes in cost (e.g. \(\frac{{{\text{d}}p}}{{{\text{d}}c}},\frac{{{\text{d}}w}}{{{\text{d}}c}},\frac{{{\text{d}}p}}{{{\text{d}}w}}\) etc.).Footnote 1 The cost-pass-through reflects the retailer’s optimal pricing response to manufacturer’s price change. Tyagi (1999) shows the conditions on demand functions to conclude about the cost-pass-through. Based on the cost-pass-through, Weyl (2008) extracted conclusions about profits and markups in a simultaneous and a wholesale leading game in a simple supply chain with two stages. However, he did not consider the retail leading game. Some researchers related the cost-pass-through with profit margins in a double marginalization problem (see e.g. Bresnahan and Reiss 1985; Adachi and Ebina 2014). Empirical research of cost-pass-through includes Villas-Boas (2007); Nakamura and Zerom (2010); Nakamura et al. (2011); Bonnet et al. (2013) etc. To study empirical examples of price variation, publicFootnote 2 and subscription-basedFootnote 3 database can be accessed as well.

Özelkan and Çakanyıldırım (2009) identified the amplified fluctuation in prices towards downstream supply chain and referred it as ‘reverse bullwhip effect in pricing (RBP)’. They considered a wholesale-leading Stackelberg game (a.k.a. leader–follower game) framework in the supply chain and related the cost-pass-through coefficient to capture the ratio of price-variances. They derived the conditions on price-sensitive demand function for which price-variation may be amplified. Özelkan and Lim (2008) extended the previous analysis considering a stochastic demand function and added some stronger and weaker conditions on the demand function. Later, Özelkan et al. (2018) derived additional conditions considering joint replenishment and pricing decisions. They derived conditions for the occurrence of RBP under infinite horizon newsvendor model and continuous review inventory model.

In this research, we primarily follow Özelkan and Çakanyıldırım (2009)’s methodology of relating the cost-pass-through to conjecture the price-variation ratio. We extend the analysis by considering different types (retail leading and simultaneous) of supply chain pricing games. In order to consider simultaneous and retail leading games, we follow the markup pricing game model of Wang et al. (2013). For the cost-pass-through calculations, we are following the methodology of Tyagi (1999) and Weyl (2008). We extend their analysis in the case of a N-stage supply chain and relate that to BP.

Conditions for the occurrence of BP

In this section, we discuss the conditions for the occurrence of bullwhip effect in Pricing (BP) and relate it with the cost-pass-through and the concavity coefficient. After that, we discuss the occurrence of BP for some common demand functions.

Cost-pass-throughs and the occurrence of BP

In order to quantify BP, we first check the ratios of standard deviations of prices between two stages \(\left({\frac{{\sigma_{n}}}{{\sigma_{n + 1}}}} \right)\), referred as BP ratios. As shown in Özelkan and Çakanyıldırım (2009), the BP ratios are closely related with the cost-pass-through coefficients (i.e. rate of change of prices with respect to cost). The relation between the cost-pass-through and the BP ratio can be explained using a simple example case. Let assume, \(p = ac + b\) and \(w = Ac + B\), where p denotes the retail price, w is the wholesale price, c is the cost, and \(\left\{{a,b,A,B} \right\}\) are constants. Hence, \(\frac{{{\text{d}}p}}{{{\text{d}}c}} = a,\frac{{{\text{d}}w}}{{{\text{d}}c}} = A, \sigma_{\text{p}}^{2} = a^{2} \times \sigma_{\text{c}}^{2}, \sigma_{\text{w}}^{2} = A^{2} \times \sigma_{\text{c}}^{2}\). Therefore, \(\frac{{\sigma_{\text{p}}}}{{\sigma_{\text{c}}}} = a\) and \(\frac{{\sigma_{\text{w}}}}{{\sigma_{\text{c}}}} = A\). [Here, \(\sigma_{\text{p}}^{2}\) and \(\sigma_{\text{w}}^{2}\) are variances, and \(\sigma_{\text{p}}\) and \(\sigma_{\text{w}}\) are standard deviations of the random retail price and wholesale price respectively]. Then, algebraically, we can show, \(\frac{{\sigma_{\text{p}}}}{{\sigma_{\text{w}}}} = \frac{a}{A}\). Thus, we can conjecture the BP ratio from the cost-pass-through. (For a formal mathematical proof of the relationship, please check the proposition 8 of Özelkan and Çakanyıldırım (2009). In their analysis, they assumed p and w as random variables and related as \(p = g\left(w \right)\). They concluded, if \(\frac{{{\text{d}}g\left(w \right)}}{{{\text{d}}w}}\) is greater or equal to a constant (for all \(w > 0\)), then \(\frac{{\sigma_{\text{p}}}}{{\sigma_{\text{w}}}}\) is also greater or equal to that constant).

Accordingly, if the cost-pass-through is greater than one, then the BP ratio is also greater than one, hence ‘Reverse Bullwhip effect in Pricing’ (RBP) occurs (Özelkan and Çakanyıldırım 2009; Özelkan and Lim 2008). Similarly, if the cost-pass-through or BP ratio is less than one, then we will conclude that FBP occurs. If the BP ratio equals to one, we conclude that “no BP” occurs.

Concavity coefficients and the occurrence of BP

The occurrence of BP can also be identified through checking the value of the concavity coefficient of the demand functions. The concavity coefficient is defined as \(\Phi = \frac{{qq^{\prime\prime}}}{{\left({q^{\prime}} \right)^{2}}}\), where \(q^{\prime}\) is the first order derivative and \(q^{\prime\prime}\) is the second order derivative of the demand function, q with respect to the price, p (Tyagi 1999). It is also referred as the ‘relative curvature’ (Cowan 2004). The second order condition on the profit function (i.e. profit function to be concave in price) ensures that the concavity coefficient, \(\Phi\) is less than two.Footnote 4 However, based on the structure of the demand function, the concavity coefficient, \(\Phi\) can also be greater/less/equal to one. The cost-pass-through and the concavity coefficient are related such that \(\frac{{{\text{d}}p}}{{{\text{d}}w}} = \left({2 - \Phi} \right)^{- 1}\) (Tyagi 1999). Hence, if \(\Phi\) is between 1 and 2, \(\frac{{{\text{d}}p}}{{{\text{d}}w}}\) is greater than one, which results in RBP (Özelkan and Çakanyıldırım 2009). Here, in addition, we recognize that if \(\Phi\) is less than one, then, the cost-pass-through, \(\frac{{{\text{d}}p}}{{{\text{d}}w}}\) and the BP ratio, \(\frac{{\sigma_{\text{p}}}}{{\sigma_{\text{w}}}}\) are also less than one; thus, FBP occurs. Similarly, if \(\Phi = 1\), then, the cost-pass-through, \(\frac{{{\text{d}}p}}{{{\text{d}}w}}\) and the BP ratio, \(\frac{{\sigma_{\text{p}}}}{{\sigma_{\text{w}}}}\) are equals to one which results in the “no BP” scenario.

Proposition 1

For a linear supply chain with one retailer and one wholesaler in a wholesale leading game framework,

  • if \(\Phi = \frac{{qq^{\prime\prime}}}{{\left({q^{\prime}} \right)^{2}}} < 1\) , then, \(\frac{{{\text{d}}p}}{{{\text{d}}w}} < 1\) and \(\frac{{\sigma_{\text{p}}}}{{\sigma_{\text{w}}}} < 1\) ; thus, FBP occurs.

  • if \(\Phi = \frac{{qq^{\prime\prime}}}{{\left({q^{\prime}} \right)^{2}}} = 1\) , then, \(\frac{{{\text{d}}p}}{{{\text{d}}w}} = 1\) and \(\frac{{\sigma_{\text{p}}}}{{\sigma_{\text{w}}}} = 1\) ; thus, no BP occur.

Here, \(q^{\prime}\) is the first order derivative and \(q^{\prime\prime}\) is the second order derivative of the demand function, q with respect to the price, p.

Proof

The proof of Proposition 1 is omitted since the result directly follows from previous results cited above.

Occurrence of BP for some common demand functions

Concavity coefficients, cost-pass-throughs and occurrence of BP for some commonly used demand functions are shown in Table 1. It is to be mentioned, some of the results are adapted from Özelkan and Çakanyıldırım (2009) and Adachi and Ebina (2014).Footnote 5 Özelkan and Çakanyıldırım (2009) discussed that for isoelastic demand, RBP always occur; for logarithmic demand, RBP occurs if \(ue^{- b - 1} < p < ue^{- 1}\); for linear and logit demands, RBP do not occur. However, they didn’t focus on the occurrence of FBP or no BP cases, which are included in the Table 1 along with some additional demand functions.

Table 1 BP in some common demand functions
Full size table

Proposition 2

Occurrence of BP for some common demand functions are as follows

  • For a log-concave, linear, logit, and Type I extreme value distribution type demand functions, FBP occurs.

  • For an isoelastic demand function, RBP occurs

  • For a logarithmic demand function, RBP occurs if \(ue^{- b - 1} < p^{*} < ue^{- 1}\) ; FBP occurs if \(ue^{- 1} < p^{*}\) ; and no BP occurs if \(p^{*} = ue^{- 1}\)

  • For a negative exponential demand function, no BP occurs.

Proof

Based on the values of the concavity coefficients and cost-pass-throughs in Table 1, the conclusions in this proposition are obtained.

BP in different game leadership structures

In this section, we consider a simple linear supply chain with centralized demand. Note that a similar setting has been considered in previous studies as well (Chen et al. 2000). We consider a game theoretical model to identify the optimal markup pricing. If the associated manufacturing/procurement cost changes due to external reasons (e.g. tax increment, change of exchange rate, scarcity of resources etc.), then the optimal prices will also change accordingly. Thus, both the retail and wholesale prices will fluctuate because of the cost changes. We analyze the fluctuation of prices and conclude whether RBP or FBP occur in different game structures.

We are interested in a price-setting game, where supply chain firms (e.g. wholesaler, retailer etc.) decide on their prices to maximize their profit. In the next section, we discuss the game theoretic model.

Markup pricing game description

The wholesaler and the retailer decide on their per-unit markups \(u_{\text{w}}\) and \(u_{\text{r}}\), respectively. Both the retailer and wholesaler intend to maximize their own profit \(\Pi_{\text{W}}\) and \(\Pi_{\text{R}}\), respectively, by charging higher markups. On the other hand, higher markups result to higher prices that adversely affect the demand quantity and eventually affect the earned profit. Moreover, each of their decisions affect their profits. Therefore, both the wholesaler and the retailer need to consider the reaction functions of each other’s decision.

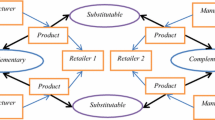
We consider three types of game scenarios, namely simultaneous, wholesale leading and retail leading games between the wholesaler and the retailer. In a simultaneous game, we solve for the Nash equilibrium where both wholesaler and retailer decide on their optimal markups considering another player’s markup as unknown. In a sequential game, we solve for the Stackelberg equilibrium, considering one player (i.e. either the wholesaler or the retailer) as the leader and the other as the follower in the decision-making. The leadership role (e.g. wholesale-leading, or retail-leading) is externally determined by the market type. In the case of a wholesale leading game, the wholesaler declares its markup first then the retailer decides on its markup. In the case of a retail leading game, the retailer announces its markup first, and then the wholesaler sets its markup. We assume the manufacturing cost, c to be a common knowledge.

The game is solved through backward induction. In the case of a wholesale leading game, the wholesaler anticipates the retailer’s best action assuming a given wholesale per-unit markup. Further considering this anticipated retailer’s action (i.e. retail per-unit markup), the wholesaler decides on its own profit maximization, and calculates the optimal wholesale markup. Finally, for the optimal wholesale markup, the retailer decides on the optimal retail markup that maximizes the retail profit. Thus, optimal actions are determined for the wholesale leading case. Similarly, the retail leading game is solved. For the simultaneous game, a response function need not be calculated. Rather, optimal actions are calculated by solving the system of equations where both the wholesaler and retailer have no knowledge of the other party’s actions. The games are illustrated in Fig. 2. The detailed formulation including objective functions, optimal actions, cost-pass-throughs etc. are summarized in Table 2.

Fig. 2
figure 2

Game description (2-stage supply chain with markup pricing)

Full size image
Table 2 Game description
Full size table

Analytical results of the cost-pass-throughs and BP ratios for 2-stage and N-stage supply chains are discussed in the following sections.

Two-stage supply chain

First, we will consider a two-stage supply chain (i.e. one retailer and one wholesaler) and solve the game theoretic model for specific demand functions (i.e. log-concave, isoelastic and negative exponential) considering three different game scenarios (i.e. simultaneous, wholesale leading and retail leading). Table 3 shows the resulting cost pass-throughs (i.e. \(\frac{{{\text{d}}w}}{{{\text{d}}c}}\) and \(\frac{{{\text{d}}p}}{{{\text{d}}c}}\)) and the BP ratios (i.e. \(\frac{{\sigma_{\text{p}}}}{{\sigma_{\text{w}}}}\)).

Table 3 Cost-pass-through and BP ratio (2-stage supply chain)
Full size table

As seen from Table 3, for a log-concave type demand functionFootnote 6 [i.e. \(q = \left({a - bp} \right)^{1/v}\)], the cost-pass-throughs are less than one, and their interrelation can be expressed as \(\frac{{{\text{d}}p}}{{{\text{d}}c}} < \frac{{{\text{d}}w}}{{{\text{d}}c}} < 1\). In the case of a wholesale-leading and a retail-leading games, the cost-pass-through of the retail price is 0.25 for a linear demand; for a convex demand, it is between 0.25 and 1, and for a concave demand, it is less than 0.25. That means, for $1 change in cost, the retail price will be changed by $0.25 for a linear demand (or less than $0.25 for a concave demand). In the case of a simultaneous game, the cost-pass-through of the retail price is 1/3 for a linear demand. Similarly, for a convex demand, it is between 1/3 and 1 and for concave demand, it is less than 1/3.

For an isoelastic demand function, the cost-pass-throughs are greater than one, and the interrelation can be expressed as \(1 < \frac{{{\text{d}}w}}{{{\text{d}}c}} < \frac{{{\text{d}}p}}{{{\text{d}}c}}\). In the case of wholesale leading and retail leading games, the cost-pass-through of the retail price is \(\left({\frac{l}{l - 1}} \right)^{2}\) for an isoelastic demand, which is greater than one, but the value varies based on the elasticity, l. That means, if l = 3, then for $1 change in cost, the retail price will be changed by \(\$ 2.25\). In the case of a simultaneous game, the cost-pass-through of the retail price is \(\frac{l}{l - 2}\). If \(l = 3\), then for $1 increase/decrease in cost, the retail price will be increased/decreased by $3.

For a negative exponential demand function (i.e. \(q = a\exp \left({- p/b} \right)\)), the cost-pass-throughs of the wholesale and the retail prices are equal to one in all game scenarios, which means for $1 change in cost, the wholesale and retail prices will be changed by $1. Note that, for a negative exponential demand, the concavity coefficient equals to one, which means the optimal markup for both parties (the wholesaler and retailer) is constant (i.e. \(\$ b\)) as well (Fabinger and Weyl 2012). Thus, for this demand function, optimal markup pricing is equivalent to the fixed dollar (\(\$ b\)) markup pricing. Hence, no RBP or FBP occur.

From the quantitative values of \(\frac{{{\text{d}}w}}{{{\text{d}}c}}\) and \(\frac{{{\text{d}}p}}{{{\text{d}}c}}\) in Table 3, we can conjecture the values of \(\frac{{\sigma_{\text{w}}}}{{\sigma_{\text{c}}}}\) and \(\frac{{\sigma_{\text{p}}}}{{\sigma_{\text{c}}}}\). Then, algebraically, we can calculate the value of \(\frac{{\sigma_{\text{p}}}}{{\sigma_{\text{w}}}}\) (see the bottom part of Table 3). The BP ratios are less, greater or equal to one for a linear, an isoelastic, or a negative exponential demand functions, respectively.

For a linear demand, the retail price fluctuates less than the wholesale price (Table 3). In the case of a simultaneous and a wholesale leading game, the BP ratio, \(\frac{{\sigma_{\text{p}}}}{{\sigma_{\text{w}}}}\) is \(\frac{1}{2}\). We interpret this result as the retail price fluctuates less (i.e. 50%) compared to the wholesale price. In the case of a retail leading game, the BP ratio is \(\frac{1}{3}\); that means, the retail price’s fluctuation is one-third of the fluctuation of the wholesale price.

For an isoelastic demand, the retail price fluctuates more than the wholesale price. In the case of a simultaneous and a wholesale leading game, the BP ratio, \(\frac{{\sigma_{\text{p}}}}{{\sigma_{\text{w}}}}\) is \(\frac{l}{l - 1}\), where l is the price-elasticity of the demand function. In the case of a retail leading game, the BP ratio is \(\frac{{l^{2}}}{{l^{2} - \left({l - 1} \right)}}\), which is also greater than one.

For a negative exponential demand, the retail price fluctuates at the same rate with respect to the wholesale price (i.e. \(\frac{{\sigma_{\text{p}}}}{{\sigma_{\text{w}}}} = 1\)).

N-stage supply chain

In this section, we extend the results for an N-stage supply chain (Table 4). N refers the total number of supply chain stages, and n refers to a specific stage in the supply chain. Here, we assume that under the wholesale-leading game of N-stages, the top most stage commits its action first; lower stages react accordingly one by one, and each stage considers it upper stage’s action as an input. On the other hand, under the retailer-leading game, the bottom most stage commits its action first and the upper stages react accordingly. In this latter case, each stage considers it lower stage’s action as an input. Under the simultaneous game, all stages take decision independently.

Table 4 Cost pass-through and BP ratio (N-stage supply chain; Total stage N, any stage n, top stage n = N, bottom stage n = 1)
Full size table

For a log-concave type demand function (or a linear demand as a special case), the cost pass-through at any stage, \(\frac{{{\text{d}}p_{n}}}{{{\text{d}}c}}\) is less than one and decreasing towards the downstream. In the case of a wholesale leading and a retail leading game, the cost-pass-through of the retail price, \(\frac{{{\text{d}}p_{1}}}{{{\text{d}}c}}\) is \(\frac{1}{{\left({v + 1} \right)^{N}}}\) (or, \(\frac{1}{{2^{N}}}\) for a linear demand). In the case of a simultaneous game, the cost-pass-through of the retail price, \(\frac{{{\text{d}}p_{1}}}{{{\text{d}}c}}\) is \(\frac{1}{1 + Nv}\) (or, \(\frac{1}{1 + N}\) for a linear demand).

For an isoelastic demand function, in the case of a wholesale-leading and a retail-leading game, the cost-pass-through at the retail price, \(\frac{{{\text{d}}p_{1}}}{{{\text{d}}c}}\) is \(\left({\frac{l}{l - 1}} \right)^{N}\). In the case of a simultaneous game, it is \(\frac{l}{l - N}\). As an example, if we assume an elasticity of \(l = 5\) and the total number of stages in the supply chain as \(N = 4\), then, \(\frac{{{\text{d}}p_{1}}}{{{\text{d}}c}}\) would be \(\left({\frac{5}{4}} \right)^{4} = 2.44\), in the case of wholesale-leading and retail-leading games. In the case of a simultaneous game, it would be \(\frac{5}{5 - 4} = 5\). That means, \(\$ 1\) increase in cost will result \(\$ 2.44\) increase in the retail price in the case of wholesale-leading and retail-leading games. But in the case of a simultaneous game, the retail price will be increased by \(\$ 5\) for \(\$ 1\) increase in cost.

Based on the value of the cost-pass-through, \(\frac{{{\text{d}}p_{n}}}{{{\text{d}}c}}\), the BP ratio between two consecutive stages, \(\frac{{\sigma_{n}}}{{\sigma_{n + 1}}}\) is also calculated in Table 4. As seen in this table, for a linear demand function, BP ratios are less than one; but for an isoelastic demand function, BP ratios are greater than one. In the case of a wholesale-leading game, BP ratios are constant. For the linear demand function, it is ½ and for the isoelastic demand function, it is \(\frac{l}{l - 1}\). In the case of a simultaneous and a retail leading game, the ratio is decreasing in n. In the case of a simultaneous game, the BP ratio does not depend on the number of total supply chain stages. That means, in the case of a simultaneous game, irrespective of the total number of stages, the BP ratio between the retail and the wholesale price (i.e. between the bottom two stages, \(\frac{{\sigma_{1}}}{{\sigma_{2}}}\) or \(\frac{{\sigma_{\text{p}}}}{{\sigma_{\text{w}}}}\)) will be the same. Figure 3 illustrates the BP ratios for a 4-stage supply chain, where \(\sigma_{1}, \ldots,\sigma_{4}\) are the standard deviation of prices at various stages [1 is the bottom stage; 4 is the top supplier stage], and \(\sigma_c\) is the standard deviation of the top supplier’s procurement cost.

Fig. 3
figure 3

BP ratios (4-stage) [1 is the bottom stage; 4 is the top supplier stage]

Full size image

Simulation results

In this section, we run simulations to illustrate the analytical results presented in “BP in different game leadership structures”. For illustration purposes, we will consider a two-stage supply chain (with a retailer and a wholesaler). For the simulations, we randomly fluctuate the cost, calculate the optimal wholesale and retail price for each random cost. The parameters (e.g. the distribution function, the demand function parameters, the upper or lower limit of costs, number of stages etc.) for the simulation are also chosen randomly (but within the limit of the constraints) for illustration purposes. Similar results can be obtained for other parameters as well.

In this simulation, the cost is uniformly distributed between $8 and $10. The demand functions are \(q = 20 - p\) (linear), \(q = ap^{- 2.5}\) (isoelastic), and \(q = a\exp \left({- p/8} \right)\) (negative exponential). We run the simulation for 300 times. Then, finally compare the standard deviation of the costs, the wholesale prices and the retail prices. Here, we consider nine scenarios (as a combination of three demand functions and three game structures). The results of this simulation are summarized in Table 5 and illustrated in Figs. 4 and 5.

Table 5 Results of simulation (markup pricing game)
Full size table
Fig. 4
figure 4

Price fluctuation under different games

Full size image
Fig. 5
figure 5

Constant price fluctuations under different games for a negative exponential demand

Full size image

For a linear demand, the standard deviation of the retail price is less than the standard deviation of the wholesale price and the cost. Hence, the price variation is absorbed. In the case of a simultaneous, a wholesale-leading, and a retail-leading game, the ratio of standard deviations of the retail price and the wholesale price are \(\frac{0.202}{0.403} = 0.501\), \(\frac{0.151}{0.302} = 0.5\), and \(\frac{0.151}{0.454} = 0.33\) respectively. These ratios match very closely with the BP ratio mentioned in Table 3 as expected.

For an isoelastic demand, the standard deviation of the retail price is greater than the standard deviation of the wholesale price and the cost. Hence, the price variation is amplified. In the case of a simultaneous, a wholesale-leading, and a retail-leading game, the ratios of standard deviation of the retail and wholesale price are \(\frac{3.024}{1.814} = 1.667\), \(\frac{1.68}{1.008} = 1.667\), and \(\frac{1.68}{1.277} = 1.316\) respectively. Analytical results of BP ratios from Table 3 are \(\frac{l}{l - 1} = \frac{2.5}{2.5 - 1} = 1.667\) and \(\frac{{l^{2}}}{{l^{2} - \left({l - 1} \right)}} = \frac{{\left({2.5} \right)^{2}}}{{\left({2.5} \right)^{2} - \left({2.5 - 1} \right)}} = 1.316\) and. Again, the results of Table 5 match the results of Table 3 as expected.

From Fig. 4, it is clearly visible that, for a linear (or an isoelastic) demand, the price variability is decreased (or amplified) towards the downstream supply chain. For a negative exponential demand, the variability of the cost, the wholesale price, and the retail price remain constant (Fig. 5).

We want to remark that this section is meant to be for illustration purposes only and not meant to present a comprehensive numerical experiment since the results are already analytically driven and proven in “BP in different game leadership structures”. More specifically, here we first calculate the cost-pass-throughs and decide on the occurrence of BP analytically (“BP in different game leadership structures”). Then through the simulation, we obtain standard deviations and variances, and illustrate the amplified or absorbed fluctuation of prices that conform the analytical results of the occurrence of BP. In the simulation, a uniform cost distribution is assumed. Hence, the cost pattern looks the same through all the runs. The simulation would be more comprehensive if other types of distributions are considered as well.

A discussion on price variations and markup profits

Comparing the price variations among various game structures (Fig. 4, and Table 5), it is seen that the retail price variability is same in the case of a wholesale-leading and a retail-leading game for both a linear and an isoelastic demand. But in the case of a simultaneous game, the retail price variability increases compared to other game scenarios. Because, for a linear demand, the more the markups the less the variability of prices. In other words, the closer the price to the cost, it captures more of the variability of the cost. For a linear demand, the far the price from the cost, the variability is absorbed more. On the other hand, for an isoelastic demand, the price variability is amplified for higher markups. In other words, the closer the price to the cost, the variability is less.

Regarding the comparative markups under different game leadership, it is known from the literature (Moorthy and Fader 1989) that the concept of strategic complementarity or substitutability plays an important role here. For a linear demand, the optimal retail price is less under a simultaneous game compared to leader–follower games. On the other hand, for an isoelastic demand, it is vice versa.

Hence, for a linear demand, the optimal price is closer to the cost (i.e. less markup) under a simultaneous game compared to the Stackelberg games; thus, it shows less absorption in variation of prices. For an isoelastic demand, the optimal retail price is far from the cost (i.e. greater markup) under a simultaneous game compared to the Stackelberg games; thus, it shows more amplification in variability of prices.

Conclusion and future directions

In this paper, after discussing the conditions for the occurrence of BP, we considered a markup-pricing model with three game rules (e.g. simultaneous, wholesale leading, and retail leading) and three types of demand functions (e.g. log-concave type (linear as a special case), isoelastic, and negative exponential). We showed that an isoelastic demand gives RBP, a log-concave (or linear as a special case) demand and a logit demand give FBP, a negative exponential demand gives no BP, a logarithmic demand gives RBP, FBP, or no BP based on the range of the optimal price. Moreover, for a linear demand, higher markups correspond to less price variability; on the other hand, for an isoelastic demand, higher markups correspond to higher price variability. The supply chain game comparison shows, that the demand function dictates the occurrence of BP but the cost-pass-throughs and BP ratios change under different game structures. We extended the cost-pass-through analysis for a N-stage supply chain and conjecture the BP ratios for a N-stage supply chain. The results show that a linear and isoelastic demand functions give constant cost-pass-throughs and BP ratios in the case of a wholesale leading game; but in the case of a simultaneous and a retail leading game, the cost-pass-through and BP ratio depend on the number of stages.

The results can aid managers in their pricing decisions. Since the occurrence of BP is affected by the demand function and market structure (e.g. game rule, number of stages etc.), managers can have an idea of the expected price fluctuations at the consumer level for a particular market. Moreover, the derived cost-pass-throughs also reflect on how retailers react to suppliers’ price-discounts or cost-increases.

Future research can include analysis of supply chain contracts (such as revenue-sharing, buyback contracts etc.), and consideration of competing retailers. The relationship between the occurrence of BP and the supply chain profits can also be investigated. Also, a more advanced perhaps integrated model may be developed to analyze the interaction between bullwhip effect in price (BP) and bullwhip effect in order quantity (BW).